1. Introduction
As oilfields progress into the mid-to-late stages of water injection development, the intense water flooding of the high-permeability layer at the bottom due to the longitudinal heterogeneity of the thick sand body in narrow channels results in ineffective circulation of injected water. Meanwhile, the low-permeability zone at the top of the sand body contains a significant amount of residual oil, which is distributed in small blocks or dispersed states within the pores at the microscopic scale and forms strip-like patterns in plan level, creating small-scale residual oil. Such residual oil cannot be effectively developed through vertical wells, as neither waterflooding nor chemical flooding can effectively mobilize the residual oil at the top of the thick sandstone layer [
1]. Consequently, a large number of low-producing wells, inefficient wells, and shut-in wells have formed, severely hindering the further improvement of recovery rates during the high water-cut stage of mature oilfields.
Traditional horizontal well technology, characterized by large curvature radii, long horizontal sections, high drilling costs, and significant risks [
2,
3,
4,
5,
6,
7,
8], is not applicable in 5.5-inch and 7-inch casings [
9], and is unsuitable for the exploitation of small-scale residual oil. Ultra-short-radius horizontal wells (USRHWs) are implemented through ultra-short-radius sidetracking from existing wells. They enable rapid and tortuous penetration into the target formation and the extension of a horizontal section of a certain length, to expand the contact area with remaining oil and improve the swept volume [
10,
11,
12,
13]. In contrast to traditional horizontal well drilling techniques, which require a travel distance of over 900 m to increase the wellbore angle from 0° to 90° and a horizontal distance of over 300 m to reach the target reservoir, this technology requires only 35 m and 22 m, respectively. This significantly reduces drilling costs and effectively addresses the key challenges of accessing residual oil-rich zones in near-wellbore areas—zones that traditional horizontal well technology cannot reach. Thus, USRHWs have emerged as a critical low-cost, high-efficiency method for the precise tapping of residual oil at the top of thick layers in mature oilfields during the high water-cut stage. They have achieved favorable practical application effects in blocks with small sand body development scales and poor vertical well development benefits, particularly suitable for reconstructing old wells such as casing-damaged wells, high-shut-in wells and low-efficiency wells [
14,
15].
USRHWs have the following technical advantages, by sidetracking horizontally 20–60 m from a vertical well opening, which achieve significant oil increase and water reduction effects while keeping the exploitation method unchanged. With a small curvature radius of only approximately 3 m, they can satisfy horizontal well drilling in small-scale sand bodies, effectively avoiding water layers without the need for cementing and water plugging, and achieving one-time completion of drilling and completion operations. They can implement multi-branch drilling with simple procedures and short operation cycles, generally requiring only 2–3 days and an additional drilling cost of CNY 500,000–1,200,000. USRHWs offer advantages such as low pollution, fast speed, short effect cycles and the ability to rapidly increase oil and gas production; compared to traditional methods, they feature lower development costs and superior economic benefits. Due to these unique advantages, they have been widely applied in both onshore and offshore oilfields in China and have been shown to increase the productivity of old wells by an average of 3–5 times [
16]. This performance establishes them as an important technological approach for enhancing productivity and economic efficiency in mature oilfields.
The horizontal section length is a crucial parameter for USRHWs. On the one hand, a longer horizontal section results in a larger drainage area and correspondingly boosts oil and gas production. On the other hand, increasing the horizontal section length leads to a substantial increase in drilling and completion costs, as well as increased friction in the horizontal section, reducing production. Therefore, determining the optimal length for the horizontal section is a key issue in the deployment and construction of USRHWs. The optimization of traditional horizontal well lengths generally falls into three categories: reservoir numerical simulation method [
17,
18,
19,
20], friction productivity formula method [
21,
22,
23], and economic benefit maximization method [
24,
25,
26]. However, these methods cannot be simply applied to USRHWs. Moreover, there is currently no literature reporting on the optimization of the horizontal section length for USRHWs.
This paper focuses on the optimization of the horizontal section length for USRHWs. The reservoir numerical simulation method was employed to determine the horizontal section length range under actual injection–production conditions. Then, considering the friction effect of the horizontal section, the productivity formula method was used to obtain the optimal horizontal section length with the optimization goal of achieving the best productivity. Finally, by considering the net income from drilling cost investment and oil and gas sales revenue as the optimization goal, the optimal horizontal section length was obtained via the economic benefit method. From multiple perspectives, including numerical simulation, technology, and economics, the optimal horizontal section length of USRHWs was precisely defined, thereby attaining maximum economic benefits.
2. Methods
2.1. Reservoir Numerical Simulation Method
Based on the theoretical foundation of oil–water two-phase fluid seepage and according to the actual formation system and the basic petrophysical characteristics of the reservoir, a numerical simulation model of the formation reservoir was established. Under the action of the pressure difference between the wellbore and the formation, the production process of the reservoir was simulated. The basic assumptions of reservoir numerical simulation are as follows:
The seepage in the reservoir is isothermal;
There are oil and water phases in the reservoir, and the seepage of each phase follows Darcy’s law;
Oil and water are immiscible;
The thickness of the oil layer is uniform;
Both the formation rock and the fluid are compressible;
The effects of gravity and capillary pressure are considered.
The seepage equations for the water phase and the oil phase are established as shown in Equations (1) and (2):
where
is the formation permeability,
;
and
are the relative permeabilities of the oil phase and the water phase, respectively;
and
are the densities of the oil phase and the water phase, respectively,
;
and
are the viscosities of the oil phase and the water phase, respectively,
;
and
are the pressures of the oil phase and the water phase, respectively,
;
and
are the flow rates of the oil phase and the water phase, respectively,
;
and
are the specific gravities of the oil phase and the water phase, respectively,
;
is the depth gradient,
;
is the time,
;
is the formation porosity, %;
and
are the oil saturation and the water saturation, respectively, %; and
.
The initialization of the oil–water two-phase model refers to the initial distribution of unknown quantities such as the pressure and saturation of the oil and water phases in the reservoir. The initial conditions of the model are as follows:
where
is the initial formation pressure,
;
is the initial formation water saturation, %;
is the radial radius of the formation,
;
is the wellbore radius,
.
The inner boundary with a constant pressure condition and the outer boundary with a sealed condition were adopted as the boundary conditions of the model, as shown below:
where
is the bottom-hole flowing pressure,
;
is the outer boundary of the formation,
.
To obtain the variations in formation pressure, saturation and mixed water salinity of different positions at different times, the partial differential equations need to be solved in combination with the boundary conditions and the initial conditions. Considering the applicable conditions and simulation conditions of the formation model, the finite difference method was used in this study to solve the seepage equations. The region to be solved was divided into a finite number of difference grids, which were used to replace the continuous solution domain. The flow variables to be solved were stored at each grid point, and the differential terms in the partial differential equations were replaced by the corresponding difference quotients. That is, the partial differential equations were transformed into difference equations in algebraic form, thus obtaining a system of difference equations with a finite number of unknown variables at discrete points. By solving the system of difference equations, the numerical solutions of the flow variables at the grid points can be obtained.
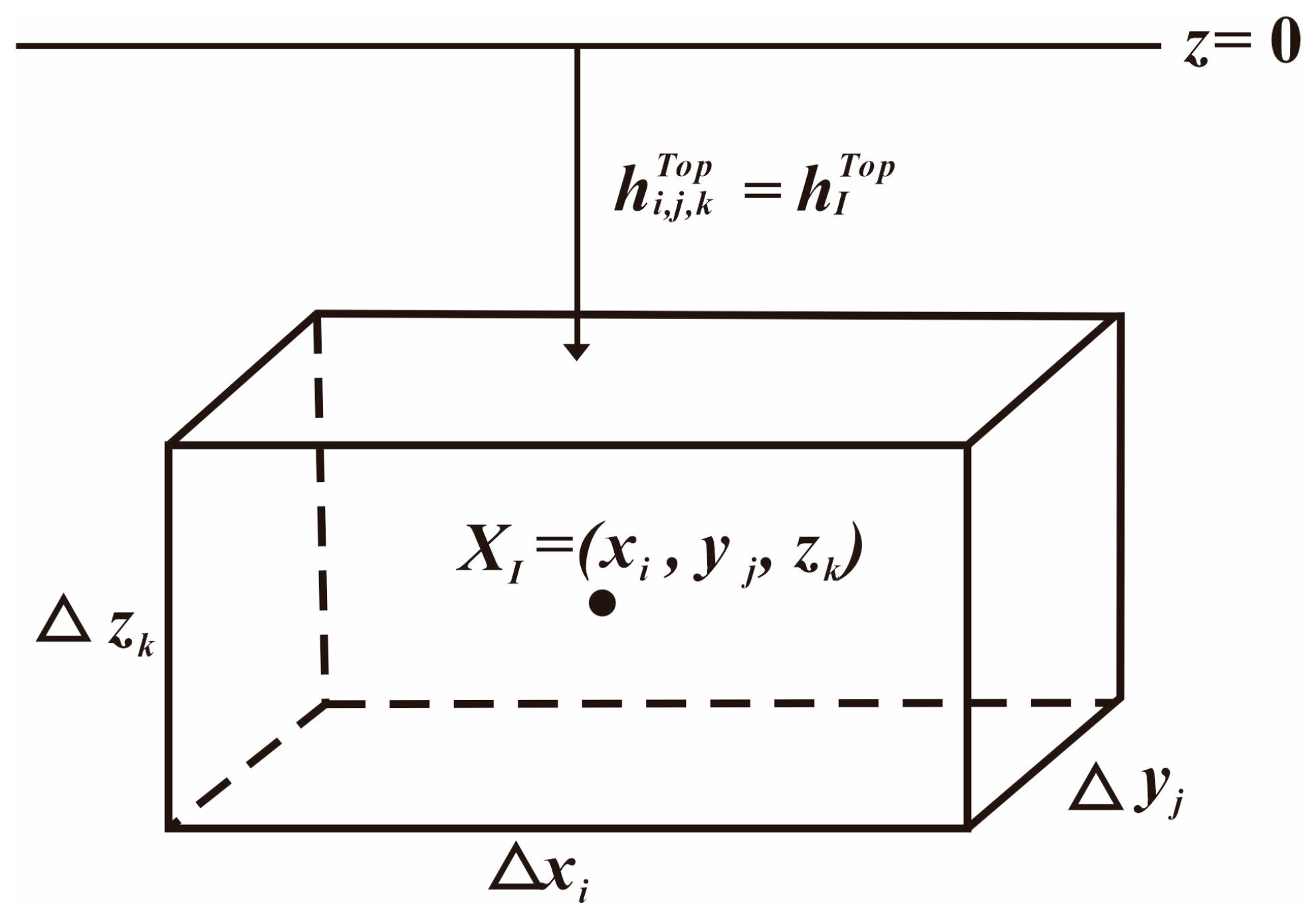
In this section, a three-dimensional block-centered grid with a Cartesian coordinate system was adopted. This coordinate system is a right-handed screw system with the
z-axis pointing vertically downward. The reservoir area was divided into cuboid grids. The number of grid blocks in the x-direction was 100, in the y-direction was 100, and in the z-direction was 10, as shown in
Figure 1 and
Figure 2.
2.2. Friction Productivity Formula Method
Traditional horizontal well productivity formulas, such as the Joshi formula, generally assume infinite wellbore conductivity, where productivity is considered to be approximately linearly correlated with well length. However, subsequent studies have indicated that the increase in horizontal well productivity is not linearly related to the length of the horizontal section. Instead, as the horizontal section extends, the frictional pressure drop generated by the fluid in the wellbore significantly reduces the contribution from the distal end of the well, leading to diminishing productivity gains. This implies the existence of an optimal well length that maximizes the productivity of the horizontal well [
27,
28,
29]. Based on this physical mechanism, a productivity calculation model is established through the coupling of reservoir seepage flow and wellbore flow by the friction productivity formula method, with the aim of identifying the optimal horizontal section length that maximizes productivity.
2.2.1. Flow in the Reservoir
Due to frictional losses in the horizontal well section, the pressure drop along the horizontal section is non-uniform, and the flow rate entering each part of the horizontal section is also non-uniform. Assuming that the horizontal section is parallel to the oil–water or oil–gas interface, the productivity index per unit length of the horizontal well (
) (where
denotes the productivity index and
represents the length of the horizontal section) can be approximately considered a constant. Setting the origin of the coordinate system at the initial position of the horizontal well and the
x-axis along the extension direction of the horizontal well, the equation for flow in the reservoir (ignoring the pressure gradient inside the horizontal wellbore) is
where
is the productivity index per unit length of the horizontal well,
;
is the flow rate of the reservoir flowing into the wellbore per unit length of the horizontal well,
;
is the pressure at the constant-pressure boundary,
;
is the flowing pressure at position x along the horizontal wellbore due to pressure loss caused by frictional resistance,
. The formula for calculating the productivity index per unit length of the horizontal well is
where
is the horizontal permeability,
μm
2;
is the vertical permeability,
μm
2;
is the oil viscosity,
;
is the horizontal well radius,
;
is the anisotropy ratio of the reservoir;
is the distance from the horizontal section to the bottom of the reservoir,
.
2.2.2. Flow in the Wellbore
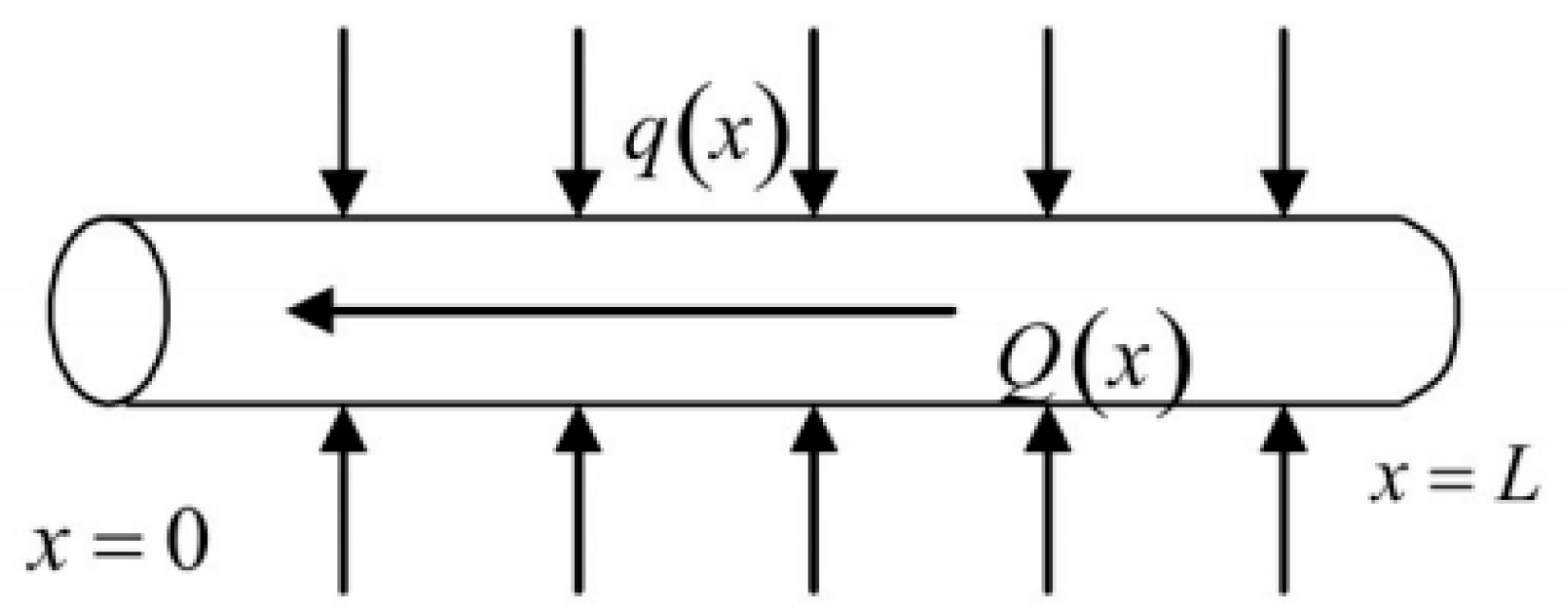
Assuming that the fluid in the horizontal wellbore is in single-phase turbulent flow and that the fluid flowing into the completion section is uniformly distributed, and considering the horizontal well section as open-hole completion, the physical model of coupled flow between the reservoir and the wellbore is shown in
Figure 3.
In the wellbore flow model, the entire horizontal section is assumed to be open for production (this assumption is applicable to open-hole completion, slotted liner completion, slotted screen completion, and perforated completion where the entire horizontal section is perforated). The pressure gradient equation in the horizontal section of the horizontal well caused by frictional resistance is
where
is the flow rate in the horizontal well,
; d is the inner diameter of the horizontal section (
), m;
is the underground oil density,
;
is the flow velocity at position
in the horizontal section, m/d; 4
is the friction factor, dimensionless. In the case of turbulent flow in a rough wellbore,
where
is the pipe wall roughness, m.
is the Reynolds number, dimensionless.
The volume balance equation was applied to connect the flow in the reservoir and the flow in the wellbore, and then the relationship between the local flow rate change in the horizontal section of the horizontal well and the reservoir flow rate towards the well was established:
where “—” indicates that the fluid flow direction is opposite to the
-direction.
Based on Equations (7), (9) and (11), the following equation can be obtained through theoretical derivation:
where
; for a specific slotted liner or screen in the fully turbulent flow region, the friction factor is a constant:
The corresponding boundary conditions for Equation (12) are
where
,
Pb is the pressure at the initial section of the horizontal well,
; the oil production rate at a position in the horizontal section is expressed as
In Equation (16), the productivity represented by
is the total productivity for
,
is a certain position in the horizontal section. For a horizontal section of length L, the productivity after accounting for frictional losses is
where
is the productivity considering wellbore frictional losses,
.
If the frictional losses in the wellbore are ignored, the pressure is uniformly distributed in the horizontal section, and the horizontal well productivity increases linearly with the length of the horizontal section. At this time, the horizontal well productivity is
where
is the productivity without considering wellbore frictional losses,
.
Dikken defined the optimal horizontal section length as the length at which frictional losses reduce the horizontal well productivity by 20%. Since the horizontal section length of USRHWs is relatively short and the frictional losses are small, the optimal length can instead be defined as the length at which frictional losses reduce productivity by 5%. That is, when the error in productivity calculation caused by ignoring the wellbore pressure drop is 5%, or when the horizontal well productivity considering frictional losses reaches 95% of the productivity without considering frictional losses, the optimal length of the horizontal section can be determined according to the following principle:
Thus, the following optimization equation is obtained:
The optimal horizontal section length can be obtained by iteratively solving Equation (20).
2.3. Economic Benefit Maximization Method
The Dikken criterion for calculating the optimal length of the horizontal section in a horizontal well only considers the proportional relationship of well production under two conditions: neglecting friction and considering friction. It does not take into account the impact of factors such as drilling and completion costs or oil prices on the design of the horizontal section length. As the length of the horizontal section increases, drilling and completion costs will rise significantly, leading to a substantial increase in actual expenses. Therefore, the calculation method for the optimal length of the horizontal section in a horizontal well was improved in this paper by incorporating relevant economic factors, thereby enhancing the practicality of the calculation method.
For horizontal wells in simpler scenarios, drilling and completion costs can be divided into fixed costs for vertical drilling, costs for drilling the horizontal well section, and operational expenses. The net profit of a horizontal well is the difference between its total revenue and total expenses, expressed as
where
is the net profit of the horizontal well, CNY;
is the production time instant,
;
is the production time period,
;
is the oil price at time
, CNY/d;
is the productivity of the horizontal well considering wellbore friction pressure differential at time
,
;
is the interest rate, %;
is the fixed cost for vertical drilling, CNY;
is the fixed cost for horizontal drilling, CNY/m;
is the operational expense, CNY/d.
For the convenience of theoretical research, it is assumed that the oil flow is steady, which means the oil production rate remains constant over time, and that the oil price remains unchanged within the considered time period. Under these assumptions, Equation (21) is transformed into
where
By substituting the steady-state productivity
Qfric of the horizontal well considering the wellbore friction pressure differential into Equation (22), the relationship between the net profit of the horizontal well and the length of the horizontal section can be derived. Consequently, a method for determining the optimal horizontal section length that considers economic benefits can be obtained.
The derivative of the net profit R with respect to L is obtained as follows:
By setting
, the formula for the optimal length of the horizontal well can be obtained:
Equation (26) represents the calculation formula for the optimal length of the horizontal section that considers economic benefits.
3. Results
3.1. Results Analysis of Numerical Simulation Method
Based on the theoretical foundation of two-phase fluid seepage, a numerical simulation model of the injection–production well formation was established using the reservoir numerical simulation method. Under the pressure differential between the formation pressure and the bottom-hole flowing pressure, the process of fluid seepage in the production well was simulated. Based on reservoir characteristics in the study area, core analysis data, oil testing geological data, etc., were referenced. In accordance with formation conditions, rock physical properties, and experimental data on high-temperature and high-pressure reservoir properties, considering isotropic permeability, a sensitivity analysis of factors affecting the productivity of sidetracked horizontal wells was conducted using the numerical simulation method. This provided a reliable basis for optimizing the parameters of sidetracked horizontal wells. The basic parameter settings for the numerical simulation model in this paper are shown in
Table 1.
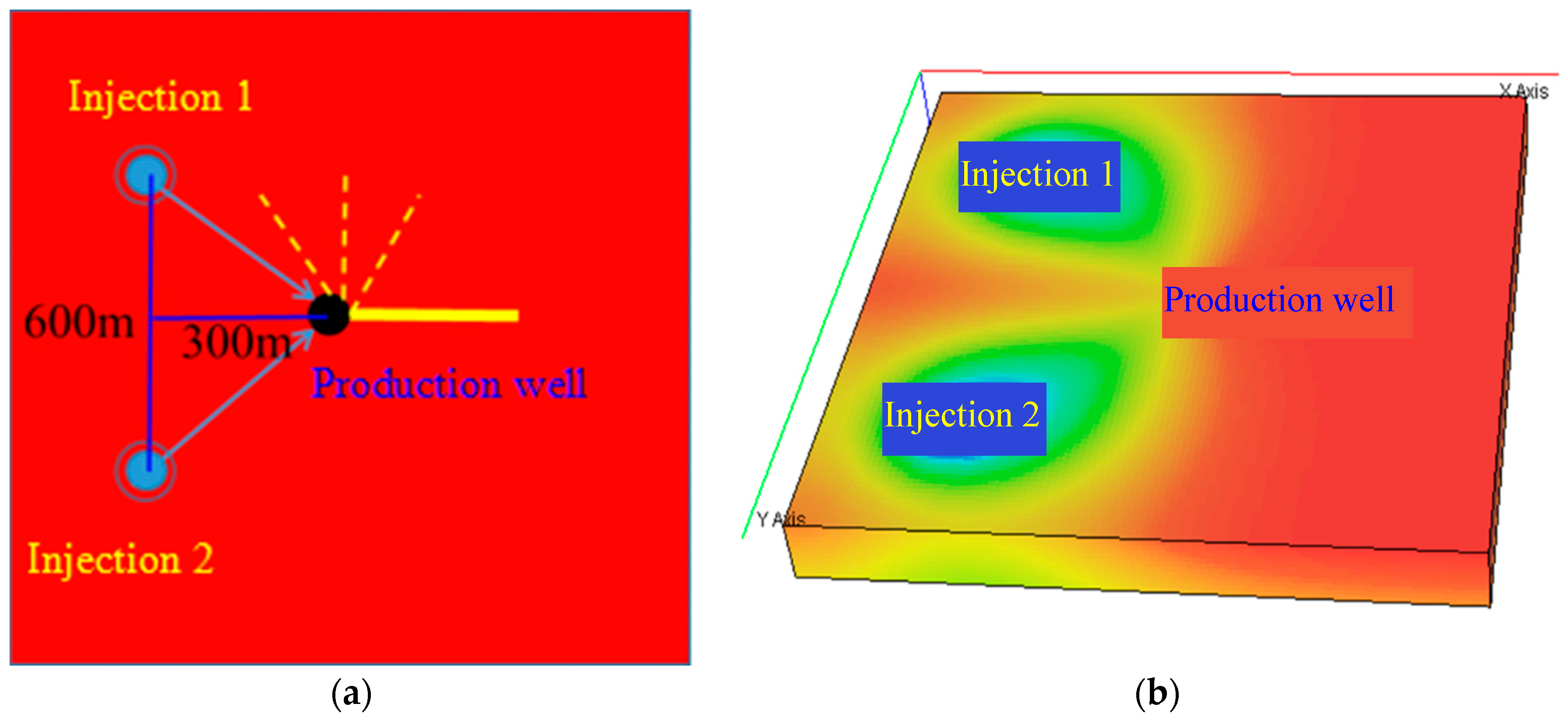
As the reservoir is an oilfield developed by water injection, the working system of constant liquid production was adopted during the history matching process to reduce the impact of history matching errors on pressure. Flowing pressure and static pressure data over the years were compiled as reference for matching the pressure and flowing pressure of the formation series. Through numerical simulation pre-processing, historical production data of oil and water wells in the area were directly invoked. A schematic diagram of the relative positions of injection and production wells and a schematic diagram of the initial fluid distribution in the horizontal well simulation are shown in
Figure 4.
To simulate the impact of horizontal well length on productivity, and to meet the needs of residual oil development at different scales, horizontal well lengths of 50 m, 80 m, 100 m, 150 m, 200 m, and 250 m were set, covering various well types such as ultra-short-radius, short-radius and medium-radius horizontal wells. The reservoir numerical simulation method was used to simulate changes in daily and cumulative production of production wells under different horizontal well lengths using the Eclipse (4.32) software. Other basic simulation conditions for the horizontal wells were entry depth of 50 m, angle between the horizontal well and the mainstream line of 135°, and being located in the middle of the oil reservoir.
Figure 5 shows the numerical simulation results of daily and cumulative production for different horizontal well lengths. From the simulation results, it can be observed that as the horizontal well length increases, daily and cumulative oil productions gradually increase for small-scale residual oil reservoirs (with horizontal section lengths generally less than 100 m). After the length of the horizontal well is extended to 80 m, any further increase in its length does not result in a notable rise in daily or cumulative oil production increment from small-scale residual oil. Therefore, 80 m is identified as the theoretical upper limit for the optimal horizontal section length in small-scale residual oil development.
3.2. Results Analysis of Technical and Economic Methods
Due to the small scale of residual oil accumulation zones, the sand bodies are small in size and have low or even no water flooding. The USRHWs are short in length, and the physical properties of the sand bodies do not change significantly across the horizontal section. Therefore, these zones can be regarded as homogeneous reservoirs with single-phase fluid flow, satisfying the basic assumptions of the friction production method. This method can be used to determine the optimal length of the horizontal section.
Using the same reservoir parameters as above, the vertical permeability of the reservoir was set at 50 × 10−3 μm2, and the relative roughness of the wellbore was set at 0.1. The friction productivity formula method was adopted. After solving through linear programming, the optimal length of USRHWs was obtained as 43.4 m, complementing for the accuracy error caused by the inability of reservoir numerical simulation methods to consider friction losses. For stable production of horizontal wells in bottom water drive reservoirs, the current stable production time was 29 days, the drilling cost per meter of the horizontal section was CNY 30,000, and other costs were negligible for USRHWs. According to the current market fixed price of oil at CNY 3525/ton and an interest rate of zero, based on the formula for calculating the optimal horizontal section length of USRHWs under turbulent flow (rough pipe wall) conditions, the optimal horizontal length was obtained as 23.1 m. After the well was put into production, it produced 86.8 cubic meters of fluid per day and 9.3 tons of oil per day; production increased by 7.8 times. The current economic benefit is CNY 258,000, and good application results have been achieved in terms of single-well production increase and economic benefits.
4. Discussion
The reservoir numerical simulation method, characterized by rigorous physical models, comprehensively accounts for actual injection–production well patterns, reservoir static conditions, and multiphase fluid seepage factors. It is the most widely applied technique for determining the optimal horizontal well length. However, this method is highly sensitive to the accuracy of reservoir parameters, with its simulation precision heavily relying on data quality. Since these parameters are indirectly derived from logging and well testing data, they inherently carry significant uncertainty. Additionally, actual formations exhibit substantial vertical and planar heterogeneity; an excessively long horizontal section may cause the horizontal well to traverse low-permeability zones and thin interlayers, thereby increasing the length of ineffective horizontal segments. As shown in the numerical simulation results in
Figure 5, even under unchanged reservoir conditions, there exist optimal lengths for different scales. For instance, at 80 m and 200 m, the daily oil production and cumulative oil production no longer increase significantly, indicating that the optimal length of 80 m is applicable to small-scale reservoirs, while 200 m is suitable for medium-scale marginal reservoirs. This is consistent with the research conclusions of Jiang (2025) [
30].
Another drawback of the reservoir numerical simulation method is that it simplifies the coupled flow physical processes between the wellbore and the formation and neglects frictional losses along the wellbore, which leads to an overestimation of the distal productivity and thus results in the obtained horizontal section length being a theoretical upper limit. In contrast, the friction-based productivity formula method, grounded in the coupled seepage theory of the reservoir and wellbore, fully considers frictional losses within the wellbore, serving as an effective analytical method for determining the optimal length of the horizontal section. Nevertheless, the 80% Dikken criterion is only applicable to medium-to-large-scale reservoirs. Based on this criterion, different authors have obtained optimal lengths for different reservoir scales: 188 m, 200 m, 350 m, 488 m, 509 m, and 1220 m [
31,
32]. For small-scale reservoirs, the horizontal section length should not be excessive, as wellbore friction losses are relatively minor in such cases. Therefore, applying a 95% optimization criterion is appropriate, which yields the horizontal section length as the technical optimal solution for small-scale reservoirs.
Both the friction-based productivity formula method and numerical simulation methods focus on productivity prediction, neglecting economic factors such as drilling costs and oil price fluctuations, which may result in a disconnect between the technically optimal and economically optimal horizontal section lengths. The economic methods proposed by Penmatcha (1999) [
33] and Cho (2001) [
34] consider economic factors, but they are primarily applicable to economic optimization of large-scale horizontal wells, requiring comprehensive consideration of drilling costs, operational costs, corporate management fees, project capital costs, and corresponding taxes and profits. USRHWs are sidetracked from existing vertical wells, involving only horizontal drilling costs. In contrast, traditional horizontal wells feature an extended stable production period, enabling substantial net revenue over the long term. USRHWs have a limited stable production period; thus, the factor of stable production duration must be carefully evaluated to avoid irrationality in this aspect, which could otherwise compromise the optimization effectiveness of economic benefit methods.
Statistics show that USRHWs have been widely applied in the exploitation of remaining oil in the high water-cut stage of Oilfield D, China. Over 100 such wells have been drilled, with an average horizontal section length of 20–30 m, an average daily oil increment of 3.2 t, and a 3–5-fold average increase in oil production compared to the pre-measurement stage. Additionally, the average water cut has decreased by 1–4 percentage points, with a cumulative oil increment of 39,000 t. These results fully validate the significant role of USRHWs in remaining oil development.
5. Conclusions
(1) This paper proposes a method for optimizing the horizontal section length of USRHWs suitable for small-scale residual oil development. The method first determines the maximum upper limit of the horizontal section length via reservoir numerical simulation, then uses the friction-based productivity formula method to obtain the technically optimal length, and finally employs the economic benefit maximization method to determine the final economically optimal solution. This integrated approach for determining the optimal horizontal section length of USRHWs offers distinct advantages, as the derived length can both meet production enhancement requirements and achieve maximum economic benefits.
(2) USRHWs serve as a technical tool for the precise tapping of small-scale residual oil at the top of narrow-channel sand bodies during the high water-cut stage of mature oilfields. Characterized by low drilling costs and favorable economic returns, they represent a critical stimulation measure for residual oil enriched in near-wellbore zones of old wells, including casing-damaged wells, high-shut-in wells, and low-efficiency wells. This technology significantly extends oilfield lifespan and effectively enhances development performance during the high water-cut stage of mature oilfields.
(3) Research demonstrates that traditional methods and criteria for optimizing horizontal well lengths are no longer applicable to USRHWs. In light of the actual characteristics of small-scale residual oil, this study proposes an integrated optimization approach for horizontal section length, combining numerical simulation, the friction-based productivity formula method, and economic benefit analysis, along with corresponding criteria. These three methods mutually reinforce and validate each other, yielding optimal horizontal section lengths with high reliability. The effectiveness of this methodology is verified by the processing results of actual reservoir parameters and post-drilling production performance.