A Novel Electric Load Prediction Method Based on Minimum-Variance Self-Tuning Approach
Abstract
1. Introduction
- Generalization problem: The LSTM method highly depends on the quality and quantity of historical data. In practical applications, an LSTM model that performs well on one dataset may exhibit poor performance on another [14].
- High computational resource consumption: Because of the generalization problem, when using it in time-series forecasting, rolling predictions are often needed. This means the model must be retrained repeatedly, using historical data combined with a small amount of new data for each cycle. This process requires significant computational resources and may take hours for each prediction, depending on the dataset size, model architecture, and available computational resources. Consequently, the slow prediction speed makes it challenging to apply these methods in real-time power system scheduling. In the era of artificial intelligence, where numerous applications require substantial computational resources, this challenge has become increasingly prominent [15,16,17,18].
- Lack of model interpretability: LSTM networks are considered “black-box” models because the predictions rely on a complex architecture with non-linear transformations and numerous parameters. The lack of transparency makes it difficult to understand how specific inputs influence the output, limiting interpretability and posing challenges for trust, debugging, and ethical considerations in critical applications [19].
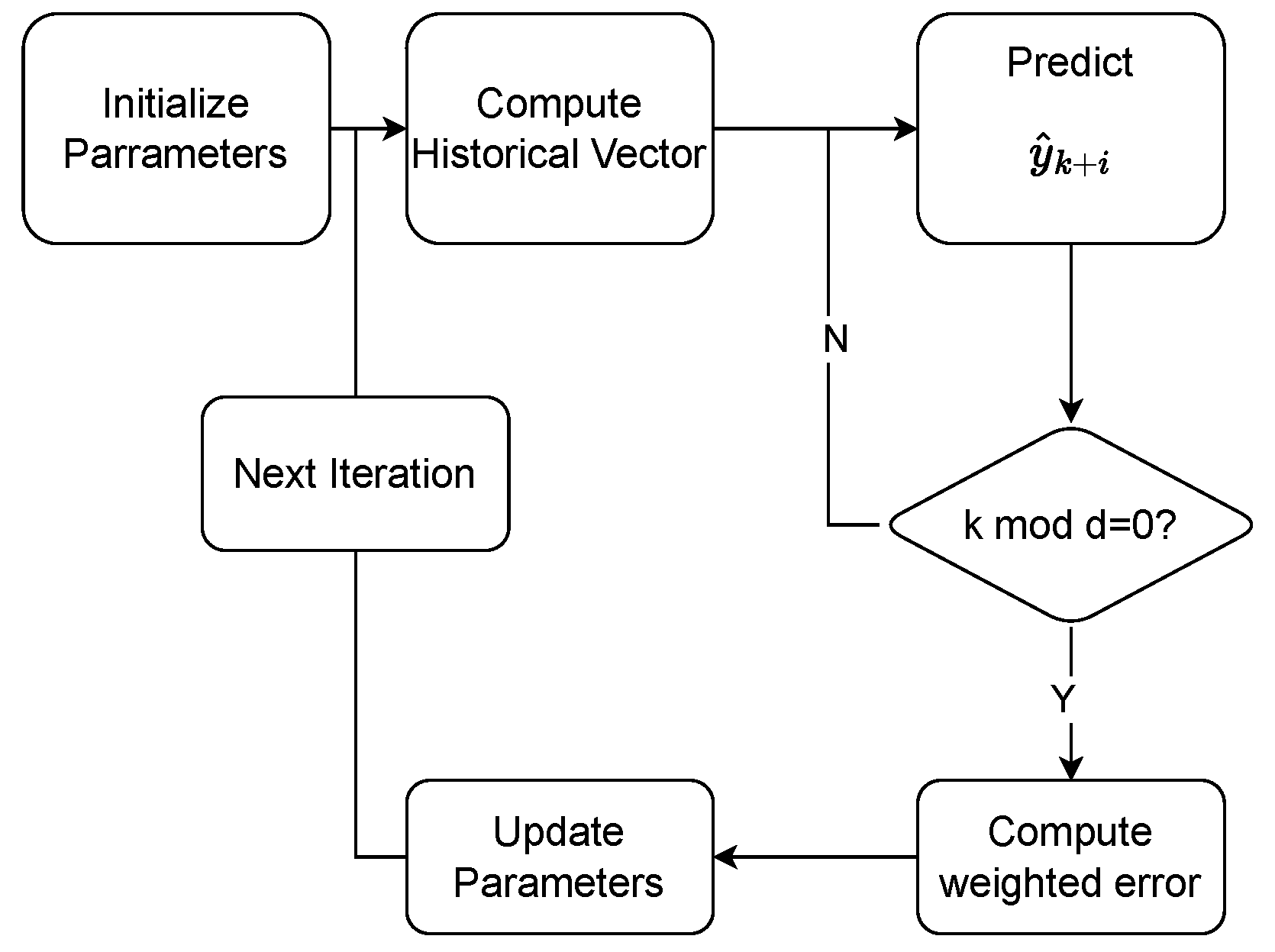
2. The MVST Prediction Algorithm
2.1. Deduction of the MVST Prediction Algorithm
| Algorithm 1 MVST Prediction Algorithm |
|
2.2. Analysis of MVST Prediction Algorithm
3. Numerical Experiments
3.1. Data Source
- Carbon emission prediction in the USA (small dataset): This case predicts emissions in the USA using annual emissions and electricity consumption data from 1971 to 2021, totaling 51 data pairs. Both datasets are publicly available from the International Energy Agency (IEA) [32] and the U.S. Energy Information Administration (EIA) [33], respectively.
- Transformer load prediction (medium dataset): This case predicts transformer load using data from a rural area in northern China, spanning 13–23 December 2023. The dataset includes load data at a 15 min resolution and hourly outdoor temperature data provided by the local electricity department and local government, respectively. The temperature data is processed with spline interpolation to match the 15 min resolution, yielding 1056 data pairs.
- Electricity consumption prediction of an office building (large dataset): This case predicts office building load consumption using hourly data from the Building Data Genome 2 (BDG2) dataset [34], spanning 1 January 2016–31 December 2017. The dataset, publicly available from BDG2, includes 731 days of electricity consumption and outdoor temperature data, totaling 17,544 samples, with a few missing temperature values that were filled with spline interpolation.
3.2. Test Environment
3.3. Validation Method
4. Results and Analysis
4.1. Significant Prediction Error Reduction with MVST
4.2. Substantial Computational Time Reduction with MVST
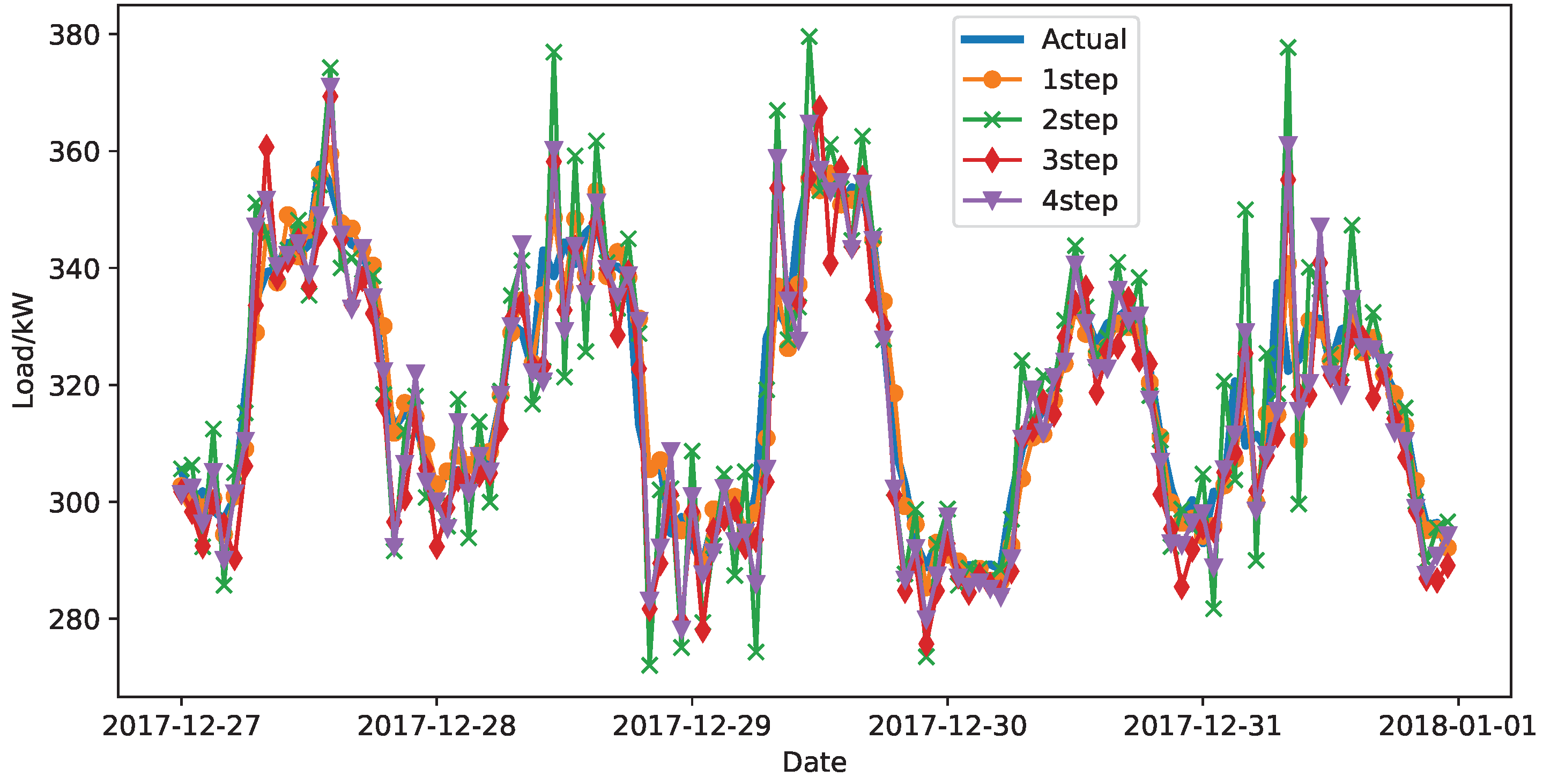
4.3. MVST Enables Multi-Step Prediction
4.4. Sensitivity of Error Weights
4.5. Limitations of the MVST Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, W.; Zhang, B.; Lu, R. A Novel Hybrid Deep Learning Model for Photovoltaic Power Forecasting Based on Feature Extraction and BiLSTM. IEEJ Trans. Electr. Electron. Eng. 2024, 19, 305–317. [Google Scholar] [CrossRef]
- L’Heureux, A.; Grolinger, K.; Capretz, M.A.M. Transformer-Based Model for Electrical Load Forecasting. Energies 2022, 15, 4993. [Google Scholar] [CrossRef]
- Sajjad, M.; Khan, Z.A.; Ullah, A.; Hussain, T.; Ullah, W.; Lee, M.Y.; Baik, S.W. A Novel CNN-GRU-Based Hybrid Approach for Short-Term Residential Load Forecasting. IEEE Access 2020, 8, 143759–143768. [Google Scholar] [CrossRef]
- Imani, M. Electrical load-temperature CNN for residential load forecasting. Energy 2021, 227, 120480. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chen, B.; Kawasaki, S. High Accuracy Short-term Wind Speed Prediction Methods based on LSTM. IEEJ Trans. Power Energy 2024, 144, 518–525. [Google Scholar] [CrossRef]
- Goh, H.H.; Ding, C.; Dai, W.; Xie, D.; Wen, F.; Li, K.; Xia, W. A Hybrid Short-Term Wind Power Forecasting Model Considering Significant Data Loss. IEEJ Trans. Electr. Electron. Eng. 2024, 19, 349–361. [Google Scholar] [CrossRef]
- Islam, B.u.; Ahmed, S.F. Short-Term Electrical Load Demand Forecasting Based on LSTM and RNN Deep Neural Networks. Math. Probl. Eng. 2022, 2022, 2316474. [Google Scholar] [CrossRef]
- Ullah, K.; Ahsan, M.; Hasanat, S.M.; Haris, M.; Yousaf, H.; Raza, S.F.; Tandon, R.; Abid, S.; Ullah, Z. Short-Term Load Forecasting: A Comprehensive Review and Simulation Study with CNN-LSTM Hybrids Approach. IEEE Access 2024, 12, 111858–111881. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, L.; Hu, F.; Zhu, Z.; Zhang, Q.; Kong, W.; Zhou, G.; Wu, C.; Cui, E. ISSA-LSTM: A new data-driven method of heat load forecasting for building air conditioning. Energy Build. 2024, 321, 114698. [Google Scholar] [CrossRef]
- Baba, A. Electricity-consuming forecasting by using a self-tuned ANN-based adaptable predictor. Electr. Power Syst. Res. 2022, 210, 108134. [Google Scholar] [CrossRef]
- Nabavi, S.A.; Mohammadi, S.; Motlagh, N.H.; Tarkoma, S.; Geyer, P. Deep learning modeling in electricity load forecasting: Improved accuracy by combining DWT and LSTM. Energy Rep. 2024, 12, 2873–2900. [Google Scholar] [CrossRef]
- Sato, R.; Fujimoto, Y. Rainfall Forecasting with LSTM by Combining Cloud Image Feature Extraction with CNN and Weather Information. IEEJ J. Ind. Appl. 2024, 13, 24–33. [Google Scholar] [CrossRef]
- Wazirali, R.; Yaghoubi, E.; Abujazar, M.S.S.; Ahmad, R.; Vakili, A.H. State-of-the-art review on energy and load forecasting in microgrids using artificial neural networks, machine learning, and deep learning techniques. Electr. Power Syst. Res. 2023, 225, 109792. [Google Scholar] [CrossRef]
- Neto, Á.C.L.; Coelho, R.A..; de Castro, C.L. An Incremental Learning Approach Using Long Short-Term Memory Neural Networks. J. Control Autom. Electr. Syst. 2022, 33, 1457–1467. [Google Scholar]
- Rokhsatyazdi, E.; Rahnamayan, S.; Amirinia, H.; Ahmed, S. Optimizing LSTM Based Network For Forecasting Stock Market. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Sagheer, A.; Kotb, M. Unsupervised Pre-training of a Deep LSTM-based Stacked Autoencoder for Multivariate Time Series Forecasting Problems. Sci. Rep. 2019, 9, 19038. [Google Scholar] [CrossRef]
- Yadav, H.; Thakkar, A. NOA-LSTM: An efficient LSTM cell architecture for time series forecasting. Expert Syst. Appl. 2024, 238, 122333. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning: A Guide For Making Black Box Models Explainable, 3rd ed.; Leanpub: Victoria, BC, Canada, 2020. [Google Scholar]
- Shin, Y.; Pesaran, M.H. An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis; Cambridge University Press: Cambridge, UK, 1999; pp. 371–413. [Google Scholar]
- Kondaiah, V.Y.; Saravanan, B.; Sanjeevikumar, P.; Khan, B. A review on short-term load forecasting models for micro-grid application. J. Eng. 2022, 2022, 665–689. [Google Scholar] [CrossRef]
- Negara, H.R.P.; Syaharuddin; Kusuma, J.W.; Saddam; Apriansyah, D.; Hamidah; Tamur, M. Computing the auto regressive distributed lag (ARDL) method in forecasting COVID-19 data: A case study of NTB Province until the end of 2020. J. Phys. Conf. Ser. 2021, 1882, 012037. [Google Scholar] [CrossRef]
- Madziwa, L.; Pillalamarry, M.; Chatterjee, S. Gold price forecasting using multivariate stochastic model. Resour. Policy 2022, 76, 102544. [Google Scholar] [CrossRef]
- Dai, Y.; Yang, X.; Leng, M. Forecasting power load: A hybrid forecasting method with intelligent data processing and optimized artificial intelligence. Technol. Forecast. Soc. Change 2022, 182, 121858. [Google Scholar] [CrossRef]
- Liu, S.; An, Q.; Zhao, B.; Hao, Y. A Novel Control Forecasting Method for Electricity-Carbon Dioxide Based on PID Tracking Control Theorem. In Proceedings of the 2024 4th Power System and Green Energy Conference (PSGEC), Shanghai, China, 22–24 August 2024; pp. 500–504. [Google Scholar]
- Álvarez, V.; Mazuelas, S.; Lozano, J.A. Probabilistic Load Forecasting Based on Adaptive Online Learning. IEEE Trans. Power Syst. 2021, 36, 3668–3680. [Google Scholar] [CrossRef]
- Åström, K.J.; Wittenmark, B. On self tuning regulators. Automatica 1973, 9, 185–199. [Google Scholar] [CrossRef]
- Achouri, F.; Mendil, B. Wind speed forecasting techniques for maximum power point tracking control in variable speed wind turbine generator. Int. J. Model. Simul. 2019, 39, 246–255. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.; Wang, H.; Wang, X.; Lu, R.; Man, Z. Tracking Control of a Linear Motor Positioner Based on Barrier Function Adaptive Sliding Mode. IEEE Trans. Ind. Inform. 2021, 17, 7479–7488. [Google Scholar] [CrossRef]
- Zhao, L.; Li, J.; Li, H.; Liu, B. Double-loop tracking control for a wheeled mobile robot with unmodeled dynamics along right angle roads. ISA Trans. 2023, 136, 525–534. [Google Scholar] [CrossRef]
- Woodbury, M.A. Inverting Modified Matrices; Department of Statistics, Princeton University: Elizabeth, NJ, USA, 1950. [Google Scholar]
- IEA. Greenhouse Gas Emissions from Energy Highlights—Data Product; Technical Report; IEA: Paris, France, 2024. [Google Scholar]
- EIA. Electricity Consumption in the United States Was About 4 Trillion Kilowatthours (kWh); Technical Report; EIA: Paris, France, 2022. [Google Scholar]
- Miller, C.; Kathirgamanathan, A.; Picchetti, B.; Arjunan, P.; Park, J.Y.; Nagy, Z.; Raftery, P.; Hobson, B.W.; Shi, Z.; Meggers, F. The Building Data Genome Project 2, energy meter data from the ASHRAE Great Energy Predictor III competition. Sci. Data 2020, 7, 368. [Google Scholar] [CrossRef]

| Method | MAE ( t) | RMSE ( t) | MAPE (%) | Time Usage (s) | p-Value (vs. MVST) |
|---|---|---|---|---|---|
| LSTM | 550.73 | 588.26 | 10.95 | 2.66 | 0.014 |
| ARDL | 152.99 | 191.90 | 3.08 | 0.209 | 0.235 |
| PID | 215.38 | 290.88 | 4.34 | 0.015 | 0.783 |
| XGBoost | 237.85 | 302.67 | 4.81 | 0.734 | 0.706 |
| Prophet | 173.97 | 194.24 | 3.35 | 0.44 | 0.723 |
| MVST | 218.33 | 280.02 | 4.39 | 0.208 | - |
| Method | MAE (kW) | RMSE (kW) | MAPE (%) | Time Usage (s) | p-Value (vs. MVST) |
|---|---|---|---|---|---|
| LSTM | 15.45 | 17.39 | 35.35 | 17.4 | <1 × 10−10 |
| ARDL | 28.66 | 29.96 | 70.39 | 0.5 | 9.22 × 10−6 |
| PID | 6.81 | 8.56 | 15.88 | 0.17 | 0.0133 |
| XGBoost | 14.90 | 17.27 | 35.02 | 1.09 | 5.82 × 10−8 |
| Prophet | 12.89 | 14.69 | 28.28 | 0.331 | <1 × 10−10 |
| MVST | 3.41 | 5.17 | 7.51 | 0.11 | - |
| Method | MAE (kW) | RMSE (kW) | MAPE (%) | Time Usage (s) | p-Value (vs. MVST) |
|---|---|---|---|---|---|
| LSTM | 60.53 | 69.28 | 15.62 | 185 | <1 × 10−10 |
| ARDL | 53.76 | 62.34 | 14.34 | 3.67 | <1 × 10−10 |
| PID | 9.89 | 11.98 | 3.11 | 1.54 | <1 × 10−10 |
| XGBoost | 72.19 | 75.70 | 23.05 | 1.47 | <1 × 10−10 |
| Prophet | 40.44 | 49.62 | 12.23 | 6.11 | <1 × 10−10 |
| MVST | 3.52 | 5.45 | 1.10 | 1.88 | - |
| Error Type | 1 Step | 2 Step | 3 Step | 4 Step | 5 Step | 6 Step |
|---|---|---|---|---|---|---|
| MAE (in kW) | 3.52 | 9.49 | 7.09 | 7.32 | 7.99 | 10.39 |
| RMSE (in kW) | 5.45 | 13.32 | 9.61 | 9.95 | 11.35 | 13.08 |
| MAPE (in percent) | 1.10 | 2.98 | 2.22 | 2.29 | 2.47 | 3.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yuan, Z.; An, Q.; Zhao, B. A Novel Electric Load Prediction Method Based on Minimum-Variance Self-Tuning Approach. Processes 2025, 13, 2599. https://doi.org/10.3390/pr13082599
Liu S, Yuan Z, An Q, Zhao B. A Novel Electric Load Prediction Method Based on Minimum-Variance Self-Tuning Approach. Processes. 2025; 13(8):2599. https://doi.org/10.3390/pr13082599
Chicago/Turabian StyleLiu, Sijia, Ziyi Yuan, Qi An, and Bo Zhao. 2025. "A Novel Electric Load Prediction Method Based on Minimum-Variance Self-Tuning Approach" Processes 13, no. 8: 2599. https://doi.org/10.3390/pr13082599
APA StyleLiu, S., Yuan, Z., An, Q., & Zhao, B. (2025). A Novel Electric Load Prediction Method Based on Minimum-Variance Self-Tuning Approach. Processes, 13(8), 2599. https://doi.org/10.3390/pr13082599







