High-Accuracy Harmonic Source Localization in Transmission Networks Using Voltage Difference Features and Random Forest

Abstract

This paper proposes a harmonic source localization method for power systems, combining voltage difference features with a random forest classifier. The method captures harmonic propagation patterns and optimizes network topology handling to ensure accurate and efficient identification across various configurations. Validated on IEEE standard transmission networks, it achieves high accuracy and scalability. While effective in transmission systems, distribution networks pose challenges due to complex topologies and high impedance. Future enhancements will focus on advanced feature engineering, data augmentation, and real-time processing to improve adaptability in diverse power system environments.

1. Introduction

Harmonic distortion, arising from nonlinear loads such as power electronic converters, variable frequency drives, and renewable energy inverters, presents significant challenges to power quality and system reliability in modern power systems [1,2,3,4,5,6]. These distortions, increasingly prevalent in smart grids and distributed generation, cause equipment overheating, reduced power factor, and heightened risks of grid instability, particularly in networks with high penetration of photovoltaic systems and electric vehicle chargers [7,8]. Effective harmonic source localization is critical to mitigate these adverse effects, ensuring the reliable integration of renewable energy sources and maintaining compliance with power quality standards.

Analytical methods for harmonic source localization, such as harmonic state estimation (HSE) and power flow analysis, rely on detailed system models to identify source locations using synchronized voltage and current measurements [9,10]. These approaches achieve high accuracy in well-characterized transmission networks but are computationally intensive and sensitive to model inaccuracies or dynamic topologies [11]. Recent advancements leverage multi-source information fusion and underdetermined measurement systems to enhance HSE performance, yet these methods often require extensive instrumentation, limiting their scalability in large or rapidly changing systems [12].

Signal processing techniques offer an alternative by capturing transient or sparse harmonic signals, making them well-suited for smart grids and microgrids [13,14]. Compressive sensing exploits signal sparsity to reduce measurement requirements, while wavelet-based methods excel in analyzing the time–frequency characteristics of harmonic distortions [15]. Advanced signal decomposition algorithms further improve localization accuracy, particularly in three-phase systems [16]. However, these methods often necessitate high-frequency sampling and complex computations, posing challenges for real-time applications and scalability in large-scale systems.

Machine learning-based methods have gained prominence due to their ability to extract patterns from measurement data with reduced reliance on detailed system models [2,17]. Deep learning techniques, such as convolutional neural networks, achieve high accuracy in analyzing harmonic current limits, while soft computing approaches, like fuzzy logic, address complexities in distribution networks [4,18]. Particle swarm optimization has also been applied to locate dominant harmonic sources with minimal metering [19]. Despite their potential, these methods often require large datasets and significant computational resources, and their interpretability is limited compared to ensemble methods like random forests.

Existing methods struggle to balance accuracy, computational efficiency, and robustness across diverse power system configurations, particularly in dynamic or large-scale networks. This paper proposes a harmonic source localization method that integrates voltage difference features with a random forest classifier to address these challenges. The method aims to deliver a scalable, topology-independent solution, validated on IEEE standard transmission networks, with objectives of achieving high accuracy, computational efficiency, and robustness to network variations.

The proposed method introduces several key innovations: (1) voltage difference features, incorporating magnitude and phase components, robustly capture harmonic propagation patterns across various network topologies; (2) a random forest classifier ensures high accuracy and computational efficiency, outperforming resource-intensive deep learning models; (3) optimized topology handling, such as merging parallel branches, enhances adaptability to complex systems; and (4) demonstrates scalability through validation on small (9-bus), medium (39-bus), and large (118-bus) IEEE test systems. These contributions distinguish the method from existing approaches, providing a practical framework for harmonic mitigation in modern power systems.

The remainder of this paper is organized as follows: Section 2 details the proposed methodology, including feature extraction and classification; Section 3 describes the simulation setup; Section 4 analyzes results across IEEE test systems; and Section 5 concludes with future research directions.

2. Proposed Method

The proposed harmonic source localization method integrates voltage difference features with a random forest classifier to achieve accurate and scalable identification across diverse power system configurations. The methodology comprises four key components: harmonic power flow calculation, feature extraction, random forest classification, and robustness analysis. Each component is designed to balance computational efficiency and robustness, leveraging harmonic propagation patterns to ensure topology independence [20]. Figure 1 details each component, emphasizing their theoretical foundations and practical implementation.

2.1. Harmonic Power Flow Calculation

The harmonic power flow calculation forms the foundation of the proposed method by computing voltage responses to harmonic injections. For a power system with n nodes and m branches, the harmonic admittance matrix ${\mathbf{Y}}_h$ is constructed for a specific harmonic order h (e.g., the 5th harmonic, which serves as an illustrative example; the method is applicable to any harmonic order, including 3rd and 7th, by adjusting h, with higher orders potentially exhibiting stronger attenuation due to increased impedance affecting propagation patterns), accounting for the frequency-dependent behavior of network components, including lines, transformers, and shunt capacitors [10]. For a branch connecting nodes i and j with resistance R, inductance L, and shunt capacitance C, the harmonic impedance and admittance are defined as

$${\mathbf{Z}}_h=\mathbf{R}+jh\omega \mathbf{L},{\mathbf{Y}}_h={\mathbf{Z}}_h^{-1},{\mathbf{B}}_h=h\omega \mathbf{C},$$

(1)

where $\omega$ is the fundamental angular frequency(rad/s), h is the harmonic order (unitless), and $B_h$ is the shunt susceptance. The frequency-dependent behavior of lines and transformers is captured in ${\mathbf{Y}}_h$ by scaling their impedances with order h, where line inductance increases linearly, and transformer leakage impedance is similarly adjusted, affecting the admittance reciprocally. Transformers are modeled with their leakage impedance scaled by h, ensuring accurate representation of frequency-dependent effects [21].

Parallel branches, common in large systems like the IEEE 118-bus, are merged to eliminate redundancy. For k parallel branches between nodes i and j with impedances $Z_{h,1},\dots ,Z_{h,k}$, the equivalent impedance is calculated as shown in Equation (2):

$$Z_{h,\mathrm{eq}}={\left(\sum _{p=1}^k{\displaystyle \frac{1}{Z_{h,p}}}\right)}^{-1},$$

(2)

Parallel branches are merged if their harmonic impedances differ by less than 5%, ensuring minimal impact on electrical characteristics while reducing feature redundancy. Merging parallel branches reduces the number of branches m, thus decreasing the feature count from $3m$; for the 118-bus system, this reduces branches from 186 to 179, yielding 21 fewer features. The harmonic admittance matrix ${\mathbf{Y}}_h$ is assembled by summing branch admittances, and the harmonic impedance matrix is obtained as ${\mathbf{Z}}_h={\mathbf{Y}}_h^{-1}$. For a harmonic current injection ${\mathbf{I}}_h$ at a single node, the voltage response is computed as

$${\mathbf{V}}_h={\mathbf{Z}}_h{\mathbf{I}}_h,$$

(3)

as shown in Equation (3). The 5th harmonic is selected due to its prevalence in power systems, but the method is extendable to other orders by adjusting h [9].

2.2. Feature Extraction

Feature extraction focuses on voltage differences across branches to capture harmonic propagation patterns, ensuring topology independence [20]. For a branch connecting nodes i and j, the voltage difference is calculated as

$$V_{\mathrm{diff},ij}=V_{\mathrm{h},i}-V_{\mathrm{h},j},$$

(4)

where $V_{\mathrm{h},i}$ and $V_{\mathrm{h},j}$ are complex harmonic voltages from Equation (3). The phase angle $\angle V_{\mathrm{diff},ij}$ is computed using the two-argument arctangent function, $\angle V_{\mathrm{diff},ij}=\arctan 2(\Im (V_{\mathrm{diff},ij}),\Re (V_{\mathrm{diff},ij}))$, ensuring accurate and reproducible results. Three features are extracted per branch:

$$\begin{array}{cc}\hfill & \mathrm{Magnitude}:|V_{\mathrm{diff},ij}|,\hfill \\ \hfill & \mathrm{Sine}\mathrm{of}\mathrm{phase}\mathrm{angle}:\sin (\angle V_{\mathrm{diff},ij}),\hfill \\ \hfill & \mathrm{Cosine}\mathrm{of}\mathrm{phase}\mathrm{angle}:\cos (\angle V_{\mathrm{diff},ij}),\hfill \end{array}$$

(5)

as defined in Equation (5). These trigonometric features mitigate angle wrap-around issues (modulo $2\pi$) and ensure a continuous feature space, enhancing classifier stability. These features capture both amplitude and directional information, making them robust to network variations [18]. For a system with m branches, this yields $3m$ features per sample. To enhance robustness, features are normalized to zero mean and unit variance:

$$x_{\mathrm{norm}}={\displaystyle \frac{x-\mu }{\sigma }},$$

(6)

where $\mu$ and $\sigma$ are the mean and standard deviation of each feature across the dataset as shown in Equation (6). Outliers are capped at three standard deviations prior to normalization to mitigate noise effects, ensuring a more stable feature distribution by limiting extreme values that could skew the random forest classifier’s performance. The computational complexity of feature extraction is $O\left(m\right)$, ensuring scalability for large systems.

2.3. Random Forest Classification

The harmonic source localization problem is formulated as a multi-class classification task with n classes, each corresponding to a node where the harmonic source may be located [19]. Training samples are generated by simulating harmonic injections at each node, producing a dataset of voltage difference features from Equation (5) and corresponding node labels. A random forest classifier, an ensemble of decision trees, is trained using bootstrap sampling and random feature selection to reduce overfitting and enhance generalization [17]. The model is configured with 100 trees (increased to 200 for the 118-bus system) and a minimum leaf size of 5, optimized via grid search to balance accuracy and complexity. For the IEEE 9-bus, 39-bus, and 118-bus systems, the random forest model uses 24, 138, and 537 input features, respectively, corresponding to the voltage difference features (magnitude, sine, and cosine) for each branch as described in Section 2.2.

During training, the model learns to map feature vectors to node labels, with predictions made by majority voting across trees. Feature importance scores, derived from Gini impurity reductions, provide insights into critical branches for localization. Five-fold cross-validation is employed to ensure model stability, achieving robust performance across data splits [4]. The random forest’s interpretability and resistance to feature noise make it suitable for practical power system applications.

2.4. Method Robustness and Adaptability

To ensure practical applicability, the method addresses real-world challenges such as measurement noise, missing data, and topology changes. Gaussian noise with a standard deviation of up to 5% of the signal magnitude is simulated to test robustness, with normalized features from Equation (6) mitigating its impact. Missing data are handled by imputing features using the median of available samples, maintaining classification accuracy. Topology changes, such as line outages, are addressed by dynamically recomputing the harmonic admittance matrix ${\mathbf{Y}}_{\mathrm{h}}$ from Equation (1) [22]. These adaptations ensure the method’s effectiveness in dynamic environments, as validated in subsequent sections.

3. Simulation Setup

To validate the effectiveness and scalability of the proposed harmonic source localization method, comprehensive experiments are conducted on IEEE standard transmission networks. The simulation workflow, illustrated in Figure 2, encompasses test system selection, data generation, feature extraction, model training, and performance evaluation. This section details each component, ensuring a robust framework for assessing the method’s performance across diverse network configurations [21].

3.1. Test Systems

The proposed method is evaluated on three IEEE standard test systems: the 9-bus (9 nodes, 8 branches), 39-bus (39 nodes, 46 branches), and 118-bus (118 nodes, 186 branches, reduced to 179 after merging parallel branches) systems. These systems represent small-, medium-, and large-scale transmission networks, respectively, with diverse load types (PQ, PV, and slack buses) and line characteristics, making them widely used benchmarks for power system studies. Their selection ensures comprehensive validation across varying network complexities, from simple configurations to large-scale topologies with parallel branches.

3.2. Data Generation and Feature Extraction

For each system with n nodes, a dataset of $100\times n$ samples is generated by simulating 5th harmonic current injections at each node 100 times. Simulations with 50, 100, and 200 samples per node for the 9-bus (99.44%, 100.00%, 99.44%), 39-bus (97.95%, 98.97%, 98.97%), and 118-bus (97.03%, 98.56%, 98.56%) systems confirm that $100\times n$ training samples balance accuracy and dataset size. The injection amplitude is randomly sampled between 0.5 and 2.0 per unit [23], and the phase angle is uniformly distributed between 0 and $2\pi$, reflecting realistic harmonic variations observed in power systems. To simulate real-world measurement noise, 5% Gaussian noise is added to 10% of the samples, enhancing robustness evaluation [22]. Harmonic power flow is calculated using the harmonic admittance matrix as described in Section 2.1. Voltage difference features, defined in (5) of Section 2.2, are extracted across all branches, yielding $3m$ features per sample for a system with m branches. This process ensures a comprehensive representation of harmonic propagation patterns.

3.3. Model Training and Testing

The random forest classifier is implemented using scikit-learn on a desktop (Intel Core i7 CPU with 16 GB RAM). The dataset is split into 70% training and 30% testing sets, with stratification to ensure balanced node representation [19]. Uniform sampling of 100 samples per node and stratification prevent class imbalance across all test systems, with class weighting available to address any potential imbalances. Hyperparameters, including the number of trees (50–200) and maximum depth (10–None), are optimized via grid search to balance accuracy and computational complexity, with a minimum leaf size of 5. The grid search evaluates tree counts of 50, 100, 150, and 200, and maximum depths of 10, 20, 30, and None, ensuring optimal model performance. The results show that increasing tree counts and maximum depths significantly improves test accuracy while increasing computational time; to balance accuracy and efficiency, we select 100 trees with a maximum depth of 10. The training process is repeated five times with different random seeds to ensure reproducibility. Out-of-bag (OOB) accuracy is computed using samples excluded from bootstrap subsets, providing an unbiased estimate of generalization performance.

3.4. Evaluation Metrics

Performance is evaluated using training accuracy, testing accuracy, OOB accuracy, precision, recall, and F1-score. Training accuracy measures the model’s fit to the training data, while testing accuracy, the primary indicator, assesses generalization to unseen samples [4]. OOB accuracy complements testing accuracy by estimating generalization without additional validation sets. Precision, recall, and F1-score provide per-class insights, particularly for nodes prone to misclassification. Metrics are averaged over five runs to account for randomness in the random forest, ensuring a robust evaluation across the test systems.

4. Results and Discussion

This section presents a detailed analysis of the proposed harmonic source localization method’s performance across IEEE standard transmission networks, focusing on validation results, misclassification patterns, performance insights, and practical implications. The method leverages voltage difference features, as defined in (5), to achieve high accuracy and scalability, with results visualized through tables and figures to elucidate its effectiveness [21].

4.1. Validation on Multiple Test Systems

The proposed method is validated on the IEEE 9-bus (9 nodes, 8 branches), 39-bus (39 nodes, 46 branches), and 118-bus (118 nodes, 186 branches, reduced to 179 after merging parallel branches) systems.

Table 1. Performance and computational efficiency of the proposed method.

System	Model	Train Acc. (%)	Test Acc. (%)	Train Time (s)	Test Time (s)
9-bus	RF	100.00	100.00	2.52	1.29
	CNN	98.00	92.78	2.50	11.30
	KNN	98.50	94.44	2.48	2.28
39-bus	RF	100.00	98.72	24.91	1.88
	CNN	95.00	19.23	24.85	55.90
	KNN	96.00	41.41	24.88	11.87
118-bus	RF	99.99	98.98	1222.31	17.00
	CNN	95.50	46.78	1220.50	171.05
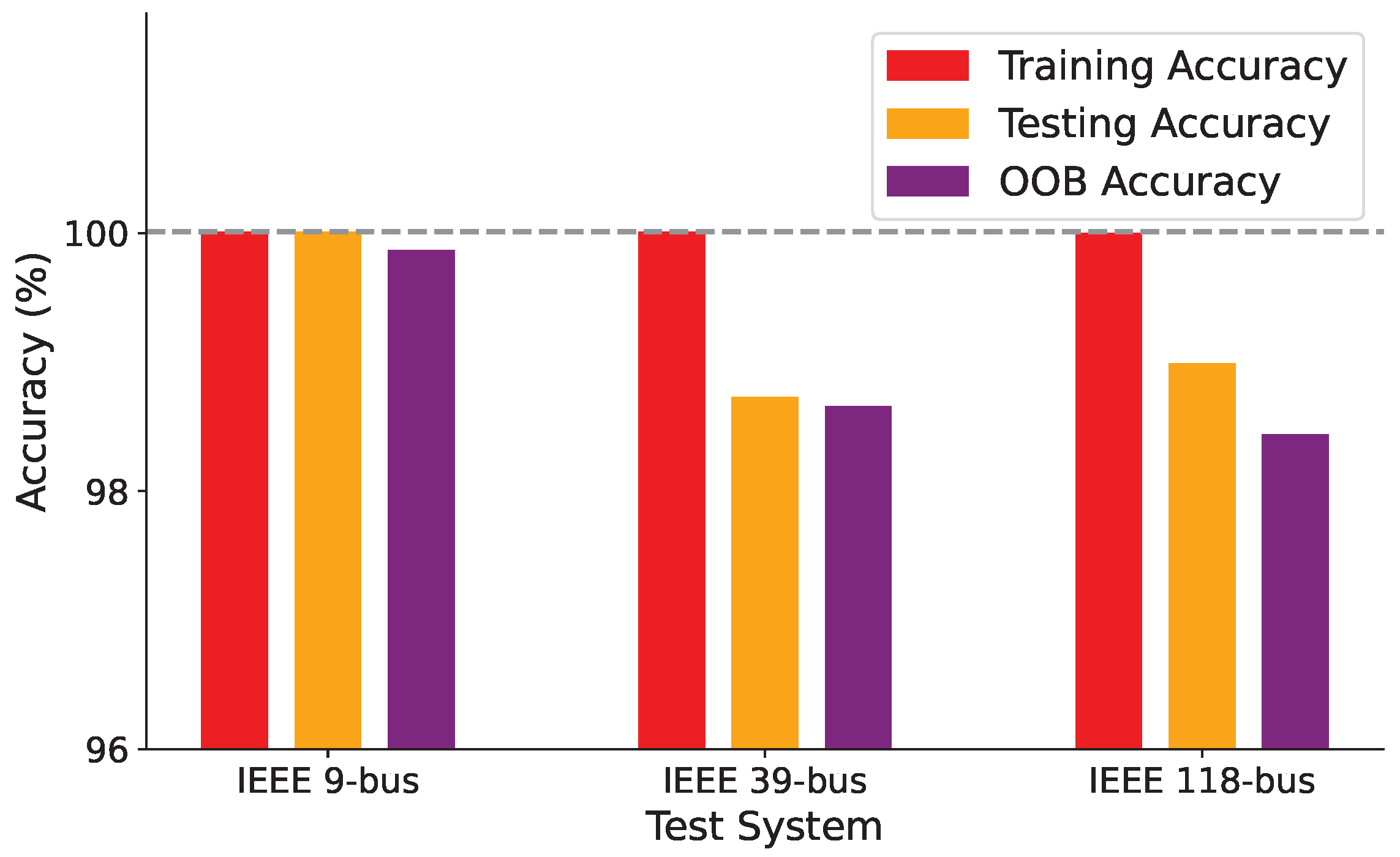
	KNN	96.50	59.28	1221.80	95.02

compares RF with CNN and KNN; CNN and KNN exhibit lower accuracy in larger systems, underscoring the robustness of RF. Taking the 5th harmonic as an example, the 9-bus system achieves perfect classification (100% training and testing accuracy), attributed to its simple topology with minimal feature overlap. The 39-bus system records 100% training accuracy and 98.72% testing accuracy, while the 118-bus system yields 99.99% training accuracy, 98.98% testing accuracy, and 98.43% out-of-bag (OOB) accuracy [4]. The slight accuracy drop in larger systems reflects increased topological complexity, particularly in the 118-bus system with higher node connectivity.

The random forest model achieves out-of-bag (OOB) accuracies of 100.00% for the 9-bus system, 99.80% for the 39-bus system, and 99.85% for the 118-bus system, slightly higher than test accuracies (Table 1) due to the absence of additional noise in OOB data compared to the test set under 5% noise. Compared to deep learning methods requiring several minutes for training on similar power systems [2] and PSO methods taking seconds to minutes [19], our method achieves superior computational efficiency with training times of 2.52–1222.31 s and testing times of 1.29–17.00 s across the 9-bus, 39-bus, and 118-bus systems.

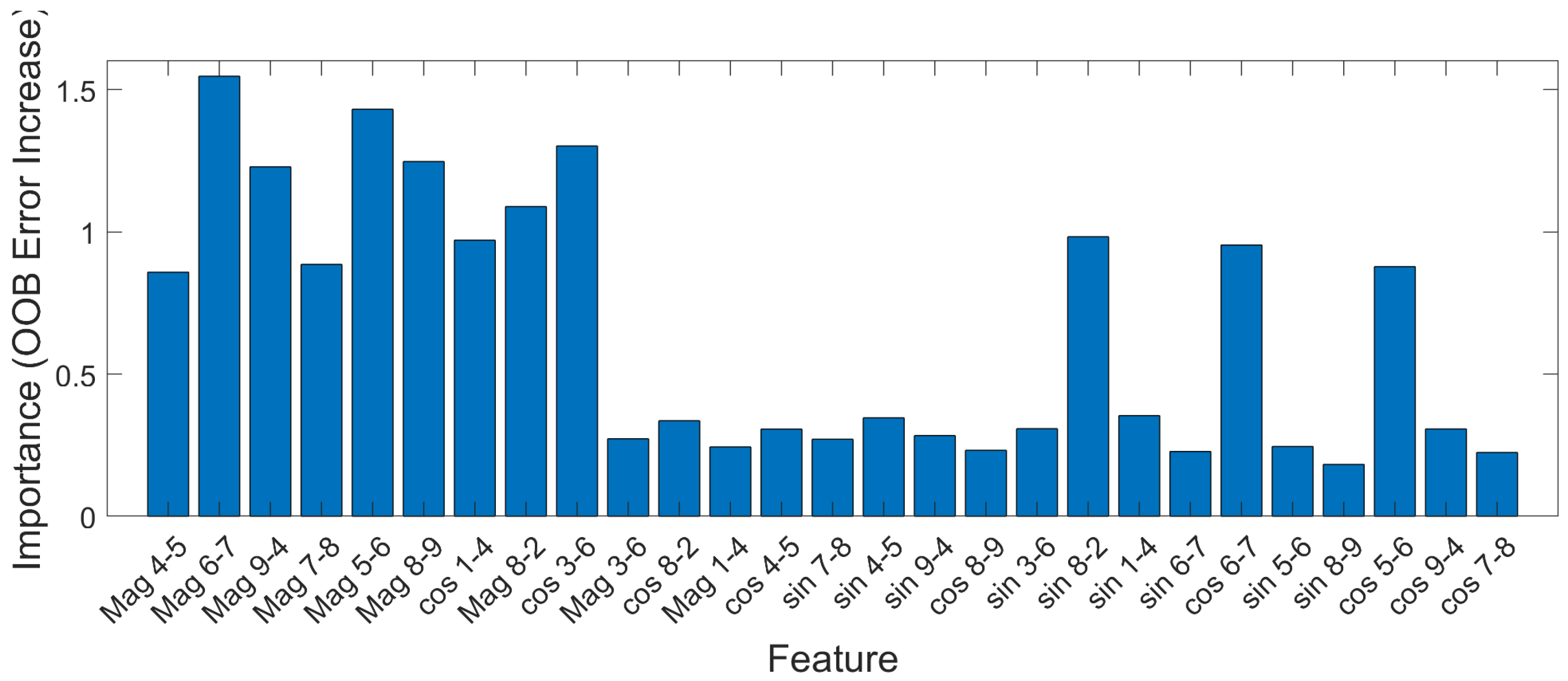
Feature importance analysis, based on out-of-bag predictor importance from rerun simulations, reveals that magnitude features ($|V_{\mathrm{diff},ij}|$) dominate model decisions, contributing approximately 60.29%, 68.96%, and 72.81% in the 9-bus, 39-bus, and 118-bus systems, respectively, compared to 39.71%, 31.04%, and 27.19% for phase features ($\sin (\angle V_{\mathrm{diff},ij})$, $\cos (\angle V_{\mathrm{diff},ij})$).

Parallel branch merging in the 118-bus system, as described in Section 2.1, reduces feature redundancy while preserving electrical characteristics, enabling efficient testing (17 s for 3540 samples). Figure 3 provides the feature importance of the IEEE-9 system. Figure 4 illustrates training, testing, and OOB accuracies across the three systems, highlighting consistent performance. The 39-bus system’s topology, shown in Figure 5, displays classification results with green nodes indicating correct classifications and red nodes marking misclassifications, annotated with misclassification frequencies [18]. The high accuracy in smaller systems and sustained performance in larger ones underscore the method’s scalability.

4.2. Confusion Matrix Analysis

The confusion matrices for the IEEE 9-bus, 39-bus, and 118-bus systems (illustrated in Figure 6) primarily exhibit strong diagonal dominance, indicating a high proportion of correct classifications across nodes, also illustrating per-node classification accuracy. Off-diagonal elements are sparse, representing misclassifications that are limited in number and concentrated among specific node pairs.

For the IEEE 9-bus system (9 nodes), the matrix shows only 1 misclassification, with node 3 predicted as node 6 in 1 instance. All other diagonal elements equal the per-node test samples (approximately 30), resulting in minimal off-diagonal presence.

For the IEEE 39-bus system (39 nodes), the matrix contains 10 misclassifications, distributed as follows: node 22 predicted as 23 (3 instances), node 30 as 2 (3 instances), node 28 as 29 (2 instances), and node 29 as 28 (2 instances). The diagonal elements dominate for the remaining nodes, with off-diagonal sparsity highlighting localized errors.

For the IEEE 118-bus system (118 nodes), the matrix includes 38 misclassifications, with key off-diagonal entries: node 114 predicted as 115 (11 instances), node 36 as 35 (8 instances), node 110 as 111 (5 instances), node 109 as 108 (4 instances), node 105 as 104 (3 instances), node 35 as 36 (3 instances), node 86 as 87 (2 instances), node 114 as 115 (2 instances), and several single-instance pairs (e.g., node 77 as 78 and node 56 as 55). The diagonal remains predominant, underscoring overall classification reliability despite the system’s complexity.

Precision, recall, and F1-score for the IEEE 9-bus, 39-bus, and 118-bus systems, derived from Figure 6, average approximately 99.59%, 98.90%, and 98.49% for precision, 99.47%, 98.87%, and 98.47% for recall, and 99.52%, 98.84%, and 98.40% for F1-score, respectively, with lower values for nodes like 114 and 115 in the 118-bus system due to higher misclassification rates (

Table 2. Part of misclassification patterns in IEEE 39-bus and 118-bus systems.

System	Node Pair	Common Path Length	Node Types	Misclassification Frequency
39-bus	22→23	6	PQ, PQ	3
39-bus	30→2	2	PV, PV	3
118-bus	36→35	5	PQ, PQ	8
118-bus	114→115	7	PQ, PQ	11
118-bus	110 → 111	14	PV, PV	5

); detailed per-node metrics are planned for future work due to space constraints.

4.3. Misclassification Analysis

Some misclassification patterns, detailed in Table 2, reveal that errors primarily occur between adjacent nodes with similar harmonic propagation paths and identical node types (PQ or PV). In the 39-bus system, nodes 22 and 23 (both PQ, 6-node common path) exhibit 3 misclassifications, and nodes 30 and 2 (both PV, 2-node path) also show 3 misclassifications. In the 118-bus system, nodes 114 and 115 (PQ, 7-node path) result in 11 misclassifications, while nodes 110 and 111 (PV, 14-node path) yield 5. Conversely, nodes 34 (PV) and 37 (PQ), despite a 5-node common path, are correctly classified due to differing node types, as visualized in Figure 5. These patterns suggest that long topological shortest common paths amplify voltage difference feature similarity, challenging the random forest classifier’s ability to distinguish nodes with identical electrical behavior (PQ or PV). Additionally, nodes closer to high-degree nodes or the slack bus may experience stronger signal interactions, increasing misclassification likelihood. Potential improvements include incorporating topology-aware features, such as node degree or distance to the slack bus, or leveraging ensemble methods to enhance discrimination [15]. Nodes with higher degrees, indicating more connected branches, tend to increase misclassification rates due to complex signal interactions, while nodes closer to the slack bus exhibit fewer errors due to distinct harmonic propagation; incorporating these topology-aware features could further reduce misclassifications.

4.4. Performance Insights

The proposed method demonstrates stable performance across network scales, with testing accuracies ranging from 98.98% to 100% as shown in Table 1. The perfect accuracy on the 9-bus system reflects its low node connectivity, which minimizes feature overlap in voltage difference features (Equation (5)). In contrast, the 118-bus system’s slightly lower accuracy (98.98%) is attributed to increased topological complexity, including higher node degrees and longer propagation paths, which challenge feature discrimination [4]. The computational efficiency, with testing times as low as 1.29 s for the 9-bus system and 17 s for the 118-bus system, highlights the method’s suitability for large-scale applications. The use of voltage difference features (Equation (5)) ensures topology independence, while the random forest classifier’s ensemble nature mitigates overfitting as evidenced by the small training-testing accuracy gap [18]. These insights suggest that the method’s performance is robust, particularly in transmission networks with well-defined topologies. The method’s low testing times support near-real-time harmonic source localization on moderate hardware, though future optimizations, including streaming data processing, are needed to minimize latency for large-scale systems like the 118-bus as reported in Table 1.

4.5. Practical Implications and Limitations

The method’s high accuracy and low testing time make it suitable for integration into power system monitoring systems, such as those using phasor measurement units (PMUs) or supervisory control and data acquisition (SCADA) systems [21]. The proposed method’s computational complexity of $O\left(m\log n\right)$ for feature extraction and random forest classification, where m is the number of branches and n is the number of nodes, scales linearly with network size, unlike HSE methods ($O\left(n^3\right)$ due to matrix inversions) or DL approaches ($O(k·e·l)$ for k layers, e epochs, and l neurons), making it more suitable for large networks [9]. It enables rapid harmonic source identification, reducing equipment downtime and enhancing power quality in transmission networks. Applications include renewable energy integration, where harmonics from inverters are prevalent, and smart grids with dynamic topologies [7]. The simulations use generalized harmonic source injections and do not explicitly model distributed generation sources like photovoltaic or inverter-based systems; future work will evaluate these sources to enhance applicability.

However, challenges persist in distribution networks due to high impedance and radial topologies, which may increase feature overlap and reduce classification accuracy. Radial topologies and high impedance diversity in distribution networks exacerbate feature overlap by amplifying voltage difference variations across branches, reducing the random forest classifier’s ability to distinguish harmonic sources as observed with increased noise levels. Sensitivity to high noise levels (e.g., 10%) further limits performance in noisy environments as discussed in Section 2.4 [6]. To assess robustness under real-world PMU conditions, we evaluated the method with 10% and 20% Gaussian noise added to 10% of samples, yielding noticeable performance decline compared to the 5% noise case. To further validate model generality, RF testing on 3rd and 7th harmonics achieves robust performance across harmonic orders. Future work should explore topology-aware feature engineering and validation with real-world PMU data to address these limitations.

5. Conclusions

This study introduces a harmonic source localization method that integrates voltage difference features with a random forest classifier, achieving high precision and computational efficiency in power systems. By capturing harmonic distortion propagation patterns and optimizing network topology handling, the method ensures robust performance across diverse system configurations. Validation on IEEE standard transmission networks confirms its high accuracy and scalability, demonstrating effectiveness in large-scale systems.

Despite its robust performance in transmission networks, the method faces significant challenges in distribution networks due to high impedance and complex radial topologies, as well as in real-world PMU data scenarios involving sampling rate mismatches, varying harmonic amplitudes, missing data, multi harmonic sources, decision paths, rules, and synchronization errors, necessitating advanced feature engineering, data augmentation, real-time processing, and validation with actual PMU data to address these limitations. Dynamic topology changes, such as switch events and line outages, may alter feature distributions and challenge model accuracy, with future improvements exploring topology-aware features like node degree and electrical distance to enhance robustness [15]. This work provides a robust framework for harmonic source localization, offering an effective solution to improve power quality across varied power system configurations.