Incentive-Compatible Mechanism Design for Medium- and Long-Term/Spot Market Coordination in High-Penetration Renewable Energy Systems
Abstract
1. Introduction
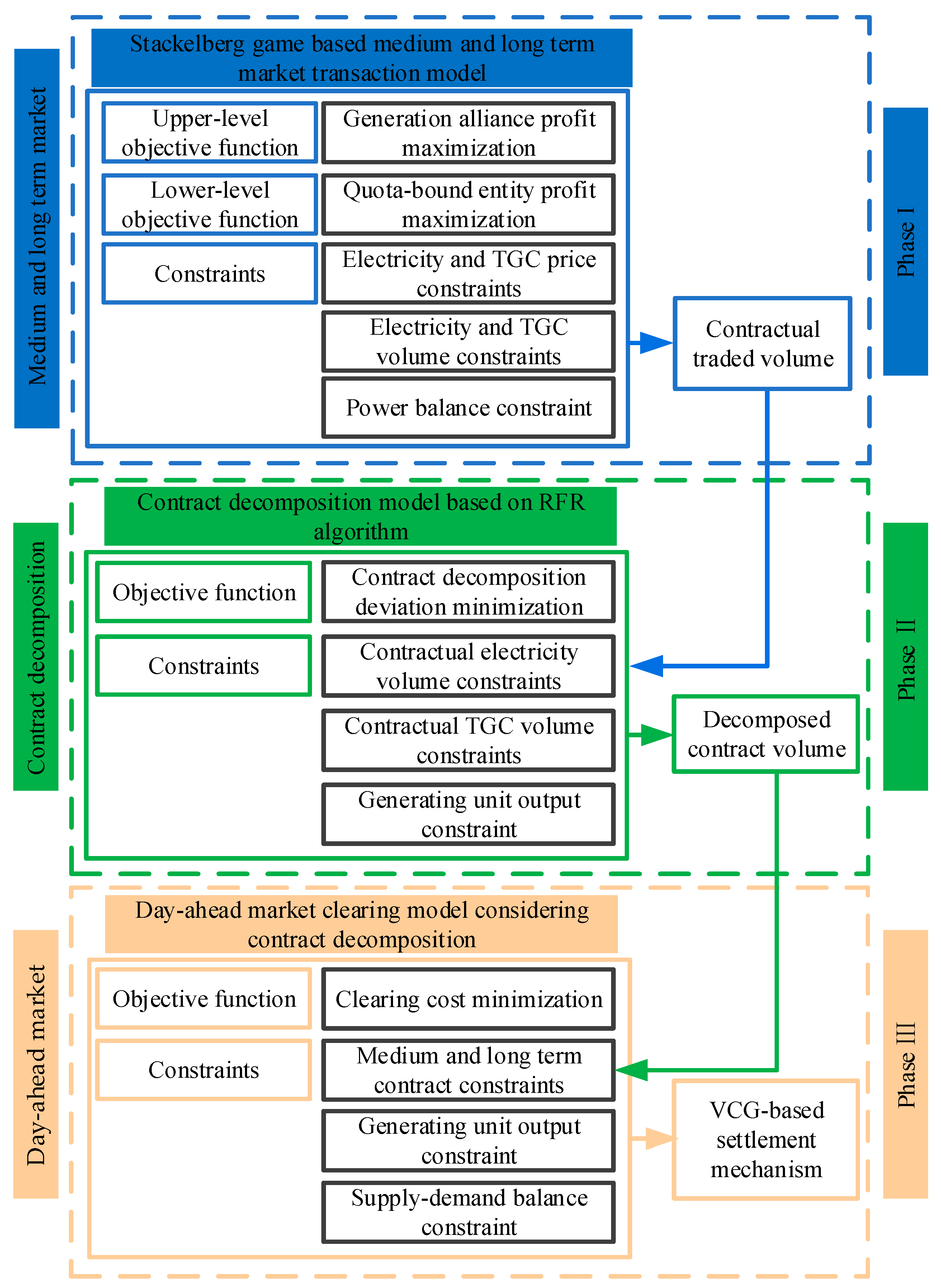
2. Three-Phase Integrated Framework for Coordinated Medium- and Long-Term/Spot Market Operations
- (1)
- Aggregating information on different types of generation units within the Alliance, the load of quota-bearing entities, and TGC demand;
- (2)
- Monitoring quota policy compliance and TGC settlement.
3. Three-Phase Coordinated Operational Decision-Making Model for Medium- and Long-Term/Spot Markets
3.1. Phase I: Stackelberg Game-Based Medium- and Long-Term Market Transaction Model
3.1.1. Generation Alliance Objective Function
3.1.2. Quota-Bound Entity Objective Function
3.1.3. Stackelberg Game Model Constraints
- (1)
- Operational constraints governing medium- and long-term transactions—
- (2)
- Medium- and long-term traded electricity/TGC volume constraints—
- (3)
- Thermal units’ output constraints—
- (4)
- TGC trading volume constraints for thermal units—
- (5)
- Renewable energy unit capacity constraints—
- (6)
- TGC trading volume constraints for renewable energy units—
- (7)
- Power balance constraints—
- (8)
- TGC volume balance constraints—
3.1.4. Proof of Stackelberg Game Equilibrium Existence
3.2. Phase II: Medium- and Long-Term Contract Volume Decomposition Mechanism Integrated with RFR
3.2.1. RFR-Based Predictive Model
3.2.2. Medium- and Long-Term Contract Decomposition Objective Function
3.2.3. Constraints for Contract Decomposition
- (1)
- Aggregate contractual balance constraints—
- (2)
- Generation unit output constraints—
3.3. Phase III: Provincial Day-Ahead Market Clearing Strategy Incorporating Contract Decomposition
3.3.1. Objective Function
3.3.2. Day-Ahead Market Clearing Constraints
- (1)
- Power balance constraints—
- (2)
- Renewable generation output constraints—
- (3)
- Thermal unit output constraints—
- (4)
- Thermal unit ramp rate constraints—
- (5)
- Thermal unit commitment constraints—
- (6)
- System standby constraints—
- (7)
- TGC trading constraints—
- (8)
- Medium- and long-term contractual constraints—
3.4. Trade Settlement Model Based on VCG Mechanism
3.4.1. Payment Rules
3.4.2. Validation of Model Properties
- (1)
- Incentive compatibility
- (2)
- Individual rationality
- (3)
- Maximizing social welfare
4. Model Solving
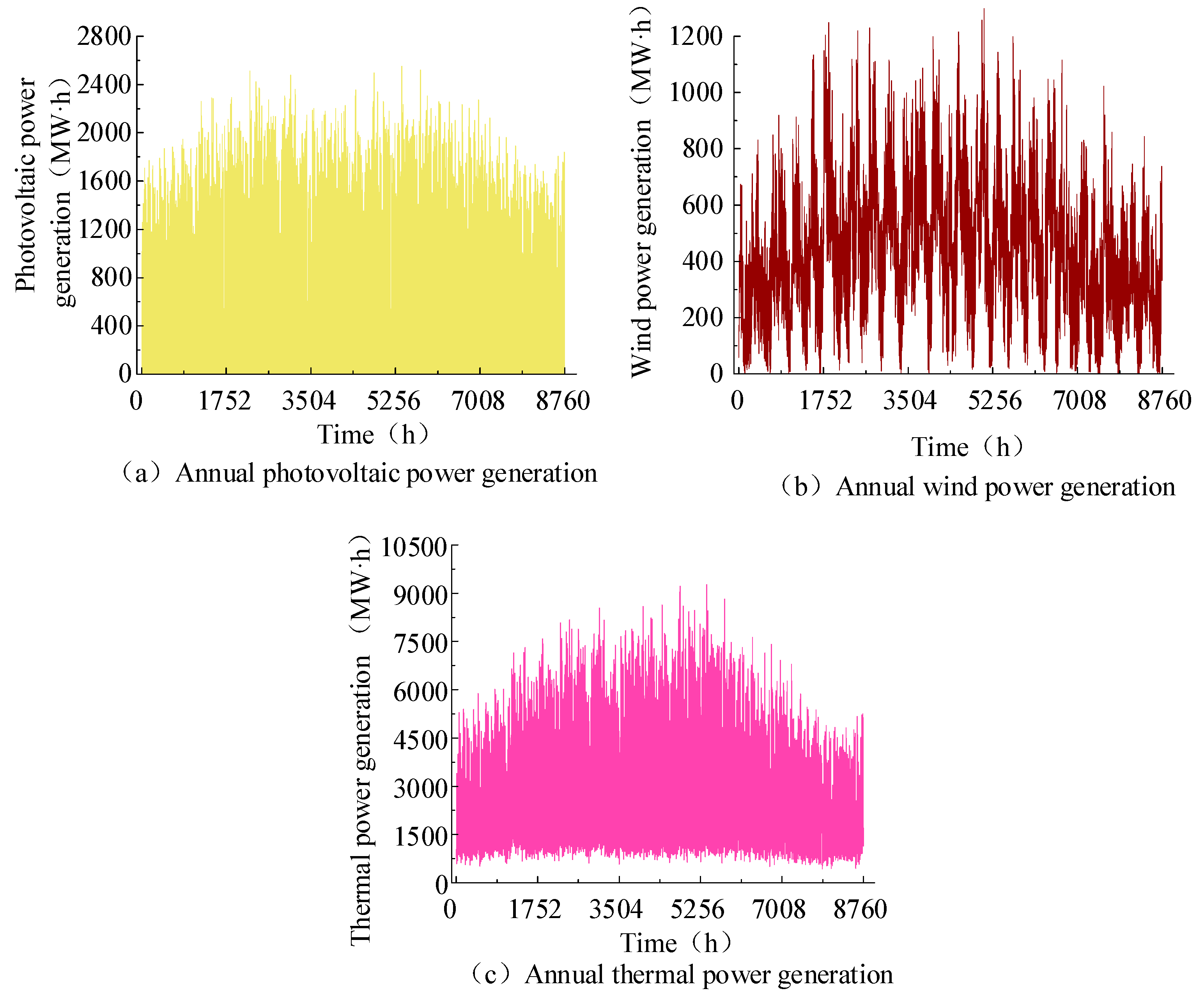
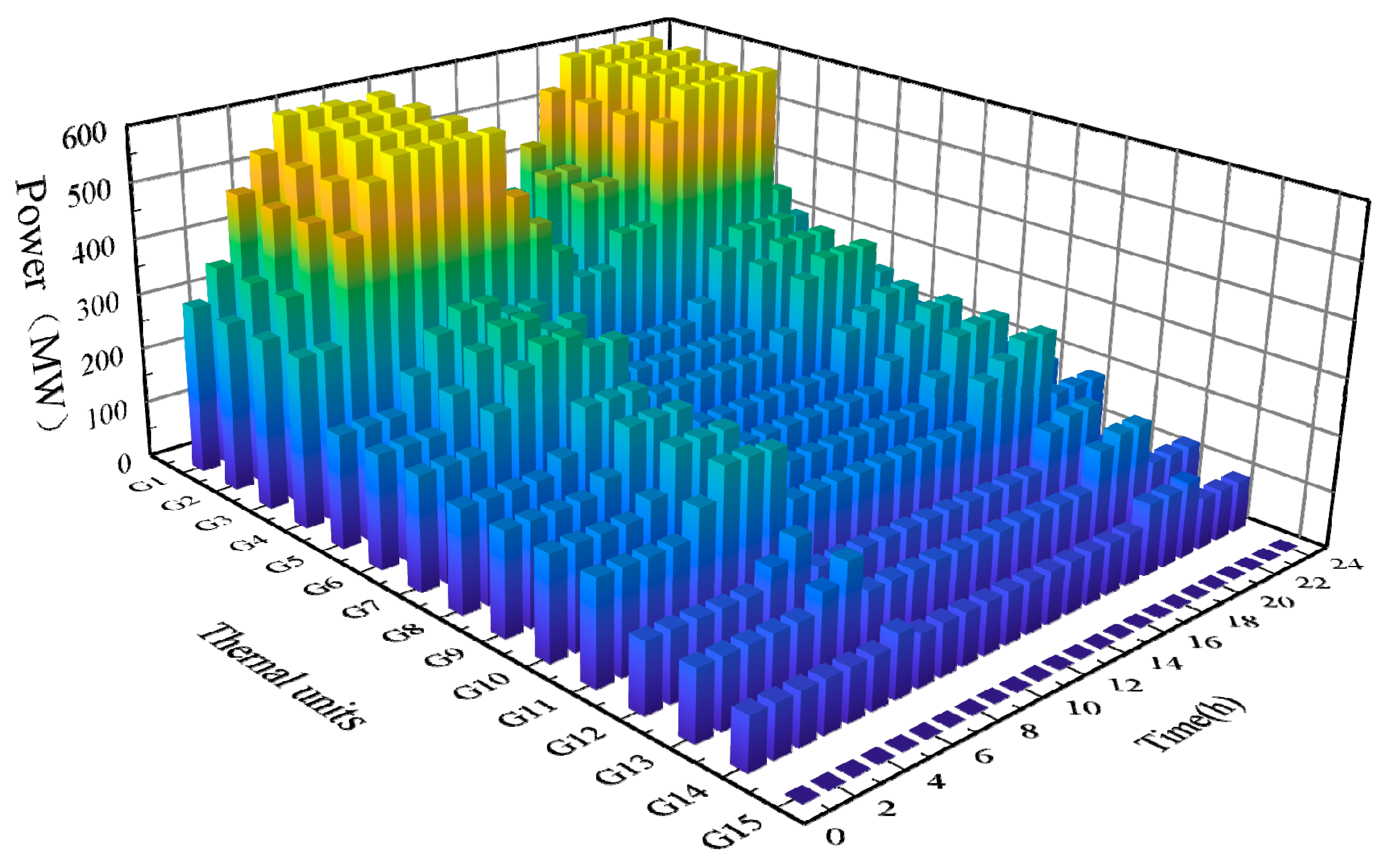
5. Example Analysis
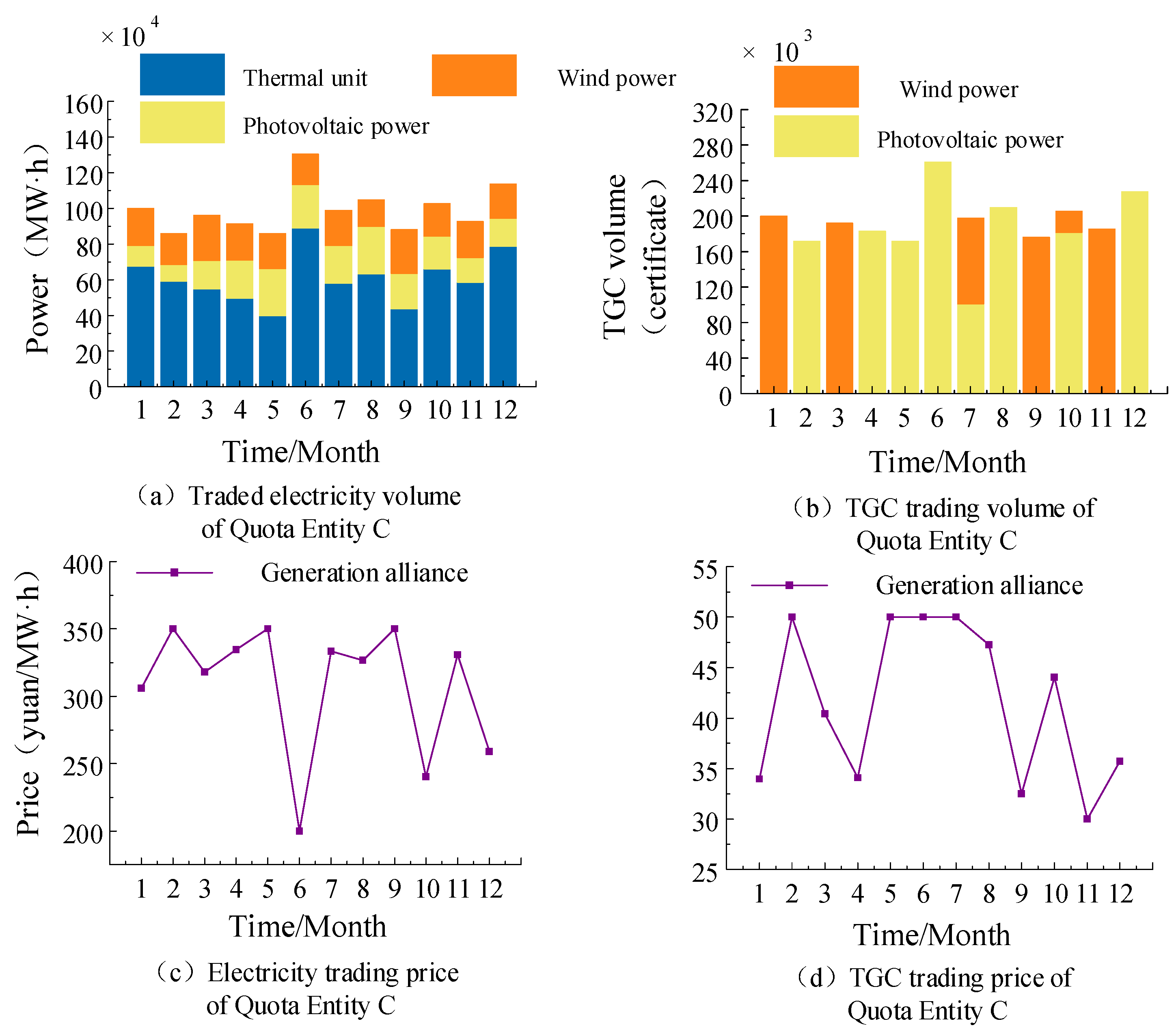
5.1. Analysis of Monthly Medium- and Long-Term Trading Results
- Quota-bound Entity A achieved a 6.23% annual increase in transacted energy;
- Quota-bound Entity B recorded a 3.44% increase;
- Quota-bound Entity C saw 1.03% growth.
- A 10.61% increase in renewable energy absorption capacity;
- A 13.47% improvement in TGC utilization efficiency.
5.2. Medium- and Long-Term Contract Decomposition Results
5.3. Analysis of the Convergence Between Day-Ahead Market Outcomes and Operational Linkages
5.4. Analysis of Results Based on the VCG Settlement Mechanism
6. Conclusions
- (1)
- A two-layer game-theoretic framework is established between provincial multi-type generation unit coalitions and quota-bound entities, achieving the joint optimization of electricity and TGC transactions. This mechanism ensures balanced revenue distribution among market participants, with thermal power units experiencing a 19.12% revenue increase. Also, wind and photovoltaic units achieve more substantial gains of 38.76% and 47.52%, while the generation alliance attains a 32.76% aggregate revenue increase. Simultaneously, the framework promotes rational resource allocation through systematic optimization, leading to a 10.61% increase in renewable energy accommodation capacity and a 13.47% improvement in TGC utilization efficiency. These results establish a novel paradigm for resource optimization in power systems with high renewable energy penetration;
- (2)
- A machine learning-optimization integrated methodology is developed for decomposing medium- and long-term contracts. Utilizing RFR for the multivariate correlation analysis of renewable energy output characteristics, this approach applies convex optimization techniques to achieve the cross-temporal smoothing of contractual energy volumes and TGC. The proposed method enhances contract executability amid renewable energy output volatility, providing technical support for physical delivery coordination between dual market tiers;
- (3)
- Finally, the VCG mechanism is indispensable in high-renewable-penetration electricity markets. Traditional marginal pricing fails to resolve incentive compatibility issues, enabling strategic bidding that manipulates dispatch sequences and prices, thereby causing market inefficiencies. In contrast, VCG enforces truthful cost reporting by quantifying units’ social welfare contributions, establishing honest bidding as the dominant strategy. Crucially, it internalizes environmental externalities—incorporating renewable energy’s carbon reduction benefits into settlements—to ensure equitable profit distribution between thermal and renewable generation, directly advancing China’s “Dual Carbon” goals. Building on this foundation, decomposed medium- and long-term contracts are integrated into a day-ahead market clearing model with environmentally weighted settlement. This mechanism balances energy value and ecological considerations, enhancing operational coherence between contracts and spot schedules while guaranteeing physical delivery. Dispatch prioritizes units based on economic–environmental attributes, and the VCG framework optimally allocates benefits among heterogeneous generators, effectively curbing strategic bidding across participants. Together, these innovations deliver a market-based paradigm for renewable-dominated power systems.
- Introduce behavioral game theory or evolutionary game approaches to characterize the bounded rational learning processes and adaptive behaviors of market participants;
- Model information asymmetry problems more deeply—for instance, considering private information related to renewable energy forecast errors or cost parameters—and investigate corresponding signaling mechanisms, mechanism design, or information incentive schemes to address them;
- Investigate how participants’ risk preferences influence their optimal strategies within multi-market coupled environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Value of the Parameter |
|---|---|
| /(CNY·MWh−1) | 200 |
| /(CNY·MWh−1) | 350 |
| /(CNY·MWh−1) | 30 |
| /(CNY·MWh−1) | 50 |
| /(CNY·MWh−1) | 220 |
| /(CNY·t−1)90 | 90 |
| /(t·MWh−1) | 0.79 |
| /(CNY/count) | 60 |
| /(CNY·MWh−1) | 900 |
| 0.2 | |
| 160/220 | |
| 570/523/618 | |
| /(10−4) | 1.76/1.90/1.60 |
| Thermal Units Number | Installed Capacity/ MW | Minimum Output/ MW | Ramp-Up Rate/(MW·h−1) | Start-Up and Shut-Down Cost/(CNY) | /(10−3yuan·MW−2) | /(yuan· MW−1) | /(CNY) | Carbon Emission Factor/(TCO2·MWh−1) |
|---|---|---|---|---|---|---|---|---|
| 1~4 | 600 | 300 | 300 | 256 | 14.1 | 187.60 | 25.6 | 0.8067 |
| 5~7 | 350 | 200 | 200 | 223 | 31.78 | 190.96 | 22.3 | 0.8385 |
| 8~11 | 300 | 180 | 180 | 162 | 23.59 | 197.26 | 16.2 | 0.8875 |
| 12~13 | 200 | 120 | 120 | 123 | 46.62 | 198.45 | 12.3 | 0.9363 |
| 14~15 | 135 | 90 | 90 | 46 | 65.17 | 201.81 | 4.6 | 0.9363 |
References
- Sun, X.; He, Y.; Ding, T.; Sun, J.; Yuan, B.; Huang, Y. An Elastic Mechanism and Its Practice for Inter-provincial Mid- and Long term Electricity Transactions in the Context of High Renewable Energy Integration. Proc. CSEE 2025, 45, 2472–2485. [Google Scholar] [CrossRef]
- Ma, L.; Fan, M.; Qu, H.; Li, J.; Zhao, Z.; Wu, Z.; Chen, K. The construction path of China’s electricity market and the key issues of market operation. Electr. Power 2020, 53, 1–9. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, T.; Li, Y.; Li, L.; Chi, F.; Wang, K.; Wang, X.; Wang, X. A review of low-carbon energy technologies in the context of carbon neutrality and its enlightenment for the development of new power systems. Proc. CSEE 2021, 41, 28–51. [Google Scholar] [CrossRef]
- Yan, S.; Wang, W.; Wang, H.; Wu, J.; Li, X.; Qi, Y. Research on the operation strategy of cross-regional system with uncertainty at both ends of source and load. Acta Solarica Sin. 2022, 43, 8–16. [Google Scholar] [CrossRef]
- Li, X.; Hu, J.; Zhang, Y.; Wang, Q.; Li, F. Multi-time scale market-oriented operation and scheduling strategy of wind-solar-water-storage consortium. Proc. CSEE 2025, 1–17. [Google Scholar]
- Zhang, X.; Liu, D.; Wang, X.; Xue, X.; Li, Z.; Han, J.; Liang, J. Research on intra-month integrated trading mode and unified price limit considering the connection between medium and long-term power and spot market. Power Syst. Technol. 2024, 48, 1418–1430. [Google Scholar] [CrossRef]
- Wu, G.; Xiang, Y.; Liu, J.; Zhang, X.; Tang, S. Chance-constrained optimal dispatch of integrated electricity and natural gas systems considering medium and long term electricity transactions. CSEE J. Power Energy Syst. 2019, 5, 315–323. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, B.; Ding, W.; Zhang, M.; Gong, S.; Zhang, W. Medium and long term electricity contract decomposition method considering cascade water matching constraints. Yunnan Electr. Power Technol. 2020, 48, 21–26. [Google Scholar]
- He, L.; Bao, T.; Liu, C.; Liu, L.; Lv, X. Optimization decomposition and rolling correction algorithm of annual contract electricity for renewable energy. J. Electr. Power Syst. Autom. 2021, 33, 56–65. [Google Scholar] [CrossRef]
- Miao, S.; Luo, B.; Shen, J.; Cheng, C.; Li, G.; Sun, Y. Short-term multi-objective power generation dispatch of hydrothermal power considering market transition and medium and long term contract power splitting. Power Syst. Technol. 2018, 42, 2221–2231. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, Y.; Li, P.; Geng, T.; Li, F. Medium and long term trading power decomposition method of renewable energy considering priority and power balance. Autom. Electr. Power Syst. 2021, 45, 117–125. [Google Scholar] [CrossRef]
- Zhao, S.; Hu, L.; Tian, J.; Xu, Z.Y. Contract power decomposition model of multi-energy power system based on medium and long term wind power photovoltaic prediction. Electr. Power Autom. Equip. 2019, 39, 13–19. [Google Scholar] [CrossRef]
- Fan, W.; Huang, L.L.; Cong, B.; Tan, Z.; Xing, T. Research on an optimization model for wind power and thermal power participating in two-level power market transactions. Int. J. Electr. Power Energy Syst. 2022, 134, 107423. [Google Scholar] [CrossRef]
- Xu, Y. Spot market in consideration of medium and long term trading restrictions of electricity sales company decision. Energy Policy 2021, 54, 79–85. [Google Scholar]
- Do Prado, J.C.; Qiao, W. A stochastic bilevel model for an electricity retailer in a liberalized distributed renewable energy market. IEEE Trans. Sustain. Energy 2020, 11, 2803–2812. [Google Scholar] [CrossRef]
- Lu, X.; Qiu, J.; Zhang, C.; Lei, G.; Zhu, J. Seizing unconventional arbitrage opportunities in virtual power plants: A profitable and flexible recruitment approach. Appl. Energy 2024, 358, 122628. [Google Scholar] [CrossRef]
- Mondal, S.; Ruffini, M. Fairness Guaranteed and Auction-Based x-Haul and Cloud Resource Allocation in Multi-Tenant O-RANs. IEEE Trans. Commun. 2023, 71, 3452–3468. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yang, L.; Su, Z.; Hou, C.; Bai, Y.; Wang, T.; Kong, J. Soil Moisture Content Retrieval in Arid Area Based on Random Forest Using Polarimetric SAR Data. J. Jilin Univ. (Earth Sci. Ed.) 2022, 52, 1255–1264. [Google Scholar] [CrossRef]
- Wei, M.; Yu, X.; Yang, X.; Xiao, X. Accuracy analysis of regional ZTD modeling based on random forest and back propagation neural network machine learning method. J. Geod. Geodyn. 2023, 43, 755–760. [Google Scholar] [CrossRef]
- You, J.S.; Juarez, R. Incentive-compatible simple mechanisms. Econ. Theory 2021, 71, 1569–1589. [Google Scholar] [CrossRef]
- An, Q.; Wang, J.; Wu, Z.; Zhong, H.; Li, G. Benefit Allocation Mechanism Design of Electricity Markets with Penetration ofHigh Proportion of Renewable Energy. Autom. Electr. Power Syst. 2022, 46, 13–22. [Google Scholar] [CrossRef]
- Wang, R.; Cheng, S.; Wang, Y.; Dai, J.; Zuo, X. Low-carbon economic optimal scheduling of regional integrated energy system based on multi-agent master-slave game. Power Syst. Prot. Control 2022, 50, 12–21. [Google Scholar] [CrossRef]
- Pan, B.; Fang, S.; Li, G.; Lu, X.; Zhou, Z.; Wang, P. Robust optimization economic dispatch method for grid-connected virtual power plant with distributed generation. Renew. Energy Resour. 2022, 50, 12–21. [Google Scholar] [CrossRef]
- Li, X. Research on Robust Trading and Operation Strategy Considering Uncertainty Under Dual-Track System. Ph.D. Thesis, Xinjiang University, Ürümqi, China, 2021. [Google Scholar] [CrossRef]
- Zhang, Y. Research on Bilateral Transaction Mode and Trading Strategies of Tradable Green Certificates. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2021. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, X.; Yu, X.; Zhang, Y. Cost-benefit evolution for concentrated solar power in China. J. Clean. Prod. 2018, 190, 471–482. [Google Scholar] [CrossRef]
- Wang, G.; You, D.; Lou, S.; Zhang, Z.; Dai, L. Economic valuation of low-load operation with auxiliary firing of coal-fired units. Energies 2017, 10, 1317. [Google Scholar] [CrossRef]
- Schiro, D.A.; Zheng, T.; Zhao, F.; Litvinov, E. Convex hull pricing in electricity markets: Formulation, analysis, and implementation challenges. IEEE Trans. Power Syst. 2015, 31, 4068–4075. [Google Scholar] [CrossRef]













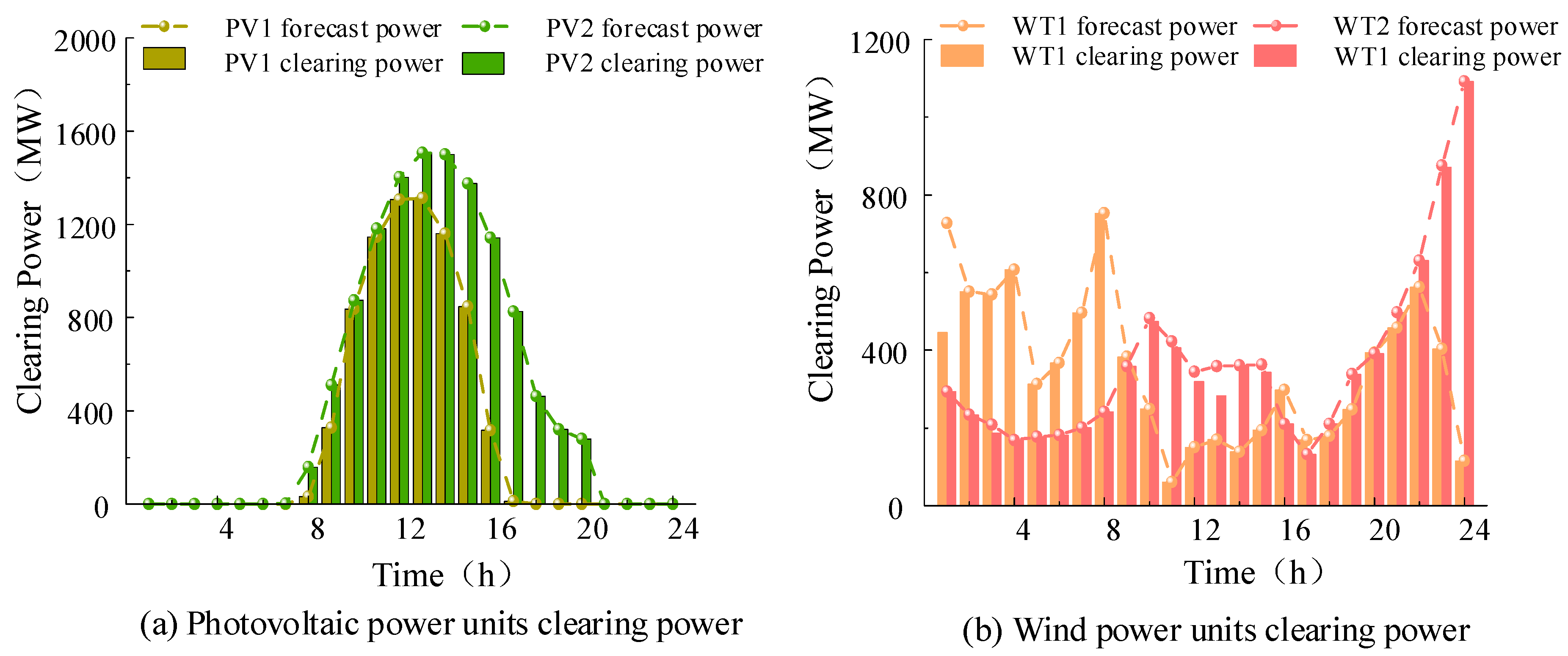

| Profits/(×108 yuan) | Scenario 1 | Scenario 2 |
|---|---|---|
| Thermal unit profits | 7.46 | 8.88 |
| Wind power profits | 6.21 | 8.61 |
| Photovoltaic power profits | 4.35 | 6.41 |
| Generation alliance profits | 18.01 | 23.91 |
| Quota entity A profits | 12.96 | 15.35 |
| Quota entity B profits | 10.15 | 9.77 |
| Quota entity C profits | 20.58 | 20.08 |
| Quota entities profits | 43.68 | 45.21 |
| Cleared Energy/(×103 MW) | Decomposed Energy from Medium- and Long-Term Contracts | Day-Ahead Cleared Energy |
|---|---|---|
| Thermal unit | 44.09 | 94.08 |
| Wind power | 16.89 | 17.03 |
| Photovoltaic power | 17.76 | 18.84 |
| Unit Number | Revenue/(×CNY 104) | Cost/(×CNY 104) | Profit/(×CNY 104) |
|---|---|---|---|
| G1 | 376.58 | 268.48 | 108.10 |
| G2 | 374.60 | 266.50 | 108.10 |
| G3 | 372.07 | 263.98 | 108.10 |
| G4 | 369.11 | 261.01 | 108.10 |
| G5 | 185.86 | 148.10 | 37.75 |
| G6 | 185.33 | 147.57 | 37.75 |
| G7 | 185.86 | 148.10 | 37.75 |
| G8 | 147.77 | 125.82 | 21.95 |
| G9 | 147.73 | 125.78 | 21.95 |
| G10 | 147.22 | 125.27 | 21.95 |
| G11 | 146.78 | 124.83 | 21.95 |
| G12 | 88.59 | 83.47 | 5.12 |
| G13 | 88.62 | 83.50 | 5.12 |
| G14 | 61.02 | 61.02 | 0.00 |
| G15 | 0.00 | 0.00 | 0.00 |
| PV1 | 223.78 | 160.59 | 63.19 |
| PV2 | 273.19 | 192.96 | 80.22 |
| WT1 | 280.93 | 209.55 | 71.38 |
| WT2 | 247.51 | 172.65 | 74.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, W.; Yan, S.; Li, Q. Incentive-Compatible Mechanism Design for Medium- and Long-Term/Spot Market Coordination in High-Penetration Renewable Energy Systems. Processes 2025, 13, 2478. https://doi.org/10.3390/pr13082478
Wang S, Wang W, Yan S, Li Q. Incentive-Compatible Mechanism Design for Medium- and Long-Term/Spot Market Coordination in High-Penetration Renewable Energy Systems. Processes. 2025; 13(8):2478. https://doi.org/10.3390/pr13082478
Chicago/Turabian StyleWang, Sicong, Weiqing Wang, Sizhe Yan, and Qiuying Li. 2025. "Incentive-Compatible Mechanism Design for Medium- and Long-Term/Spot Market Coordination in High-Penetration Renewable Energy Systems" Processes 13, no. 8: 2478. https://doi.org/10.3390/pr13082478
APA StyleWang, S., Wang, W., Yan, S., & Li, Q. (2025). Incentive-Compatible Mechanism Design for Medium- and Long-Term/Spot Market Coordination in High-Penetration Renewable Energy Systems. Processes, 13(8), 2478. https://doi.org/10.3390/pr13082478






