A Stackelberg Game-Based Joint Clearing Model for Pumped Storage Participation in Multi-Tier Electricity Markets
Abstract
1. Introduction
2. Strategy Modeling Framework for Cross-Market Bidding of PSPSs
3. Modeling of Coordinated Multi-Market Trading Mechanism for PSPSs
3.1. Bidding Strategy Model of PSPSs
3.1.1. Objective Function
3.1.2. Constraints
- Output constraints of pumped storage:
- Bidding constraints for pumped storage:
3.2. Coordinated Market Clearing Model
3.2.1. Objective Function
3.2.2. Constraints
- Bidding award constraints:
- Regulation demand constraints:
- Generation capacity limits:
- Node power balance constraint:
- Line transmission limits:
4. Model Reformulation and Solution Approach
- 1.
- Initialize the iteration counter , and formulate the PSPS’s initial bidding strategy aimed at maximizing its profit;
- 2.
- Input initial market-clearing prices and bidding information of other market participants;
- 3.
- Conduct a multi-agent bidding game under the joint clearing framework of the energy and ancillary service markets;
- 4.
- Perform joint market clearing to determine clearing prices and awarded quantities;
- 5.
- Calculate the revenue of the PSPS unit based on the clearing results;
- 6.
- Compare the current revenue with the previous value ; if , update the bidding strategy, and continue to the next iteration; otherwise, terminate the process;
- 7.
- Output the optimal bidding strategy and corresponding expected revenue.
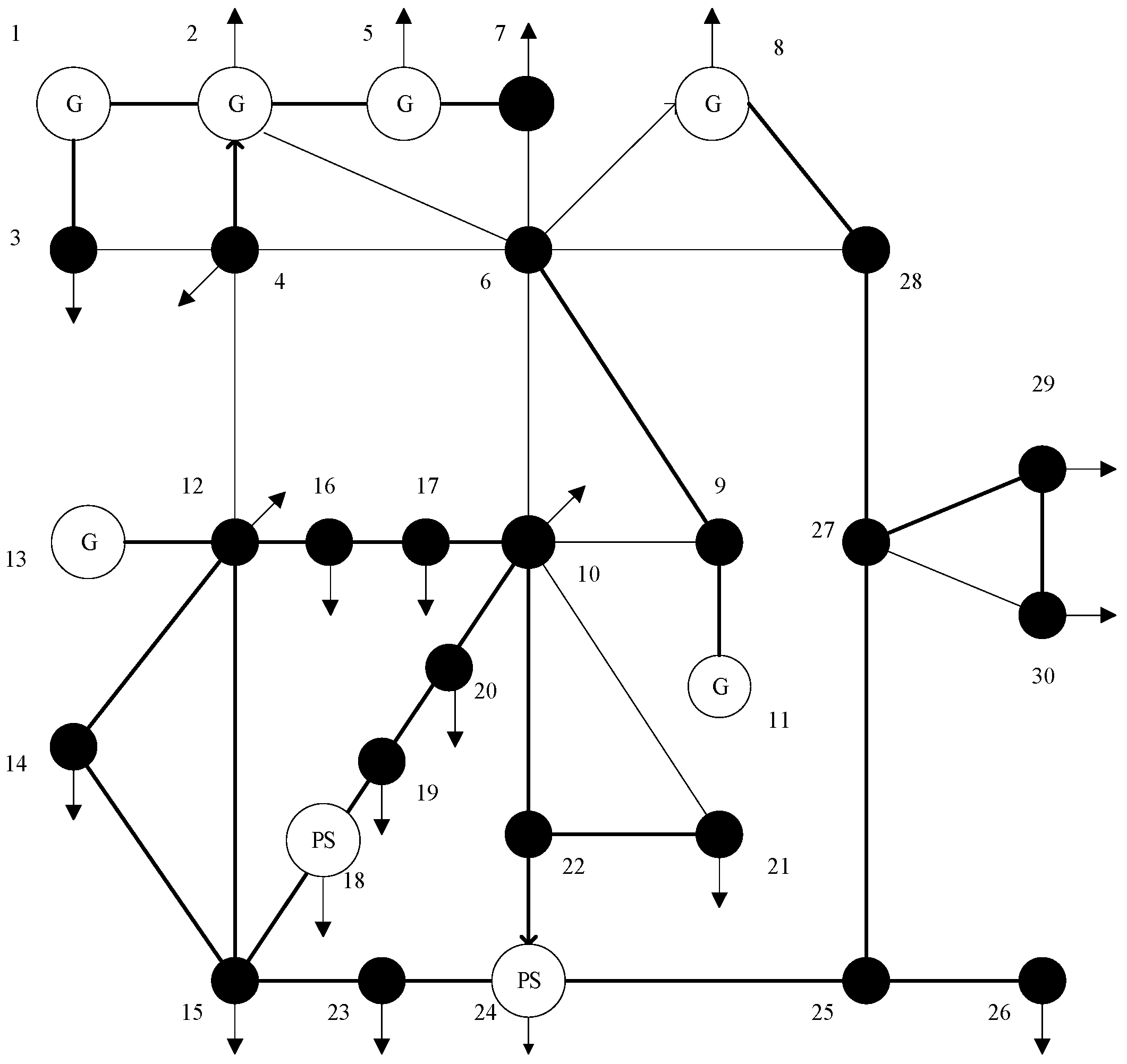
5. Case Study and Analysis
5.1. Basic Data and Parameters
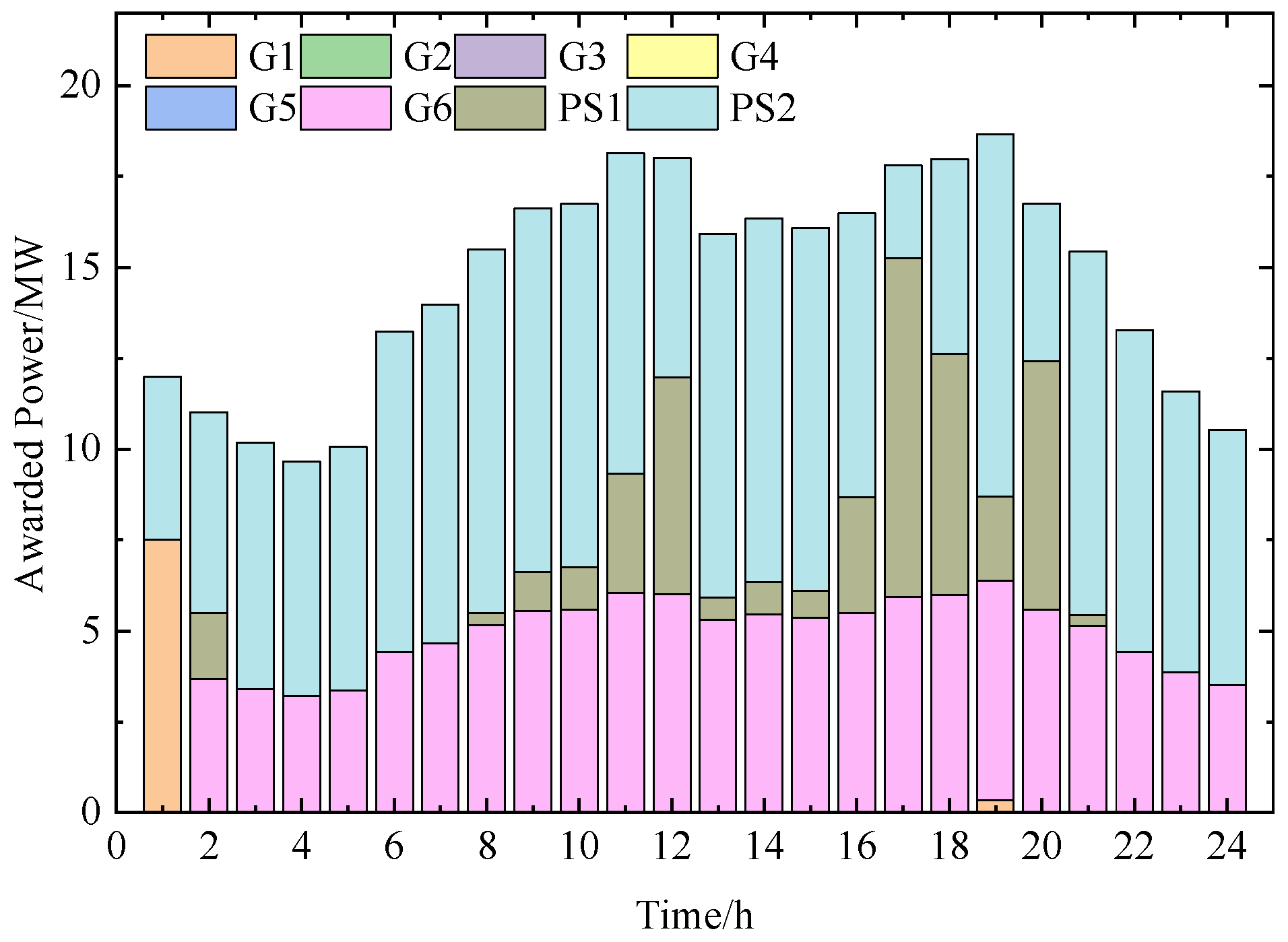
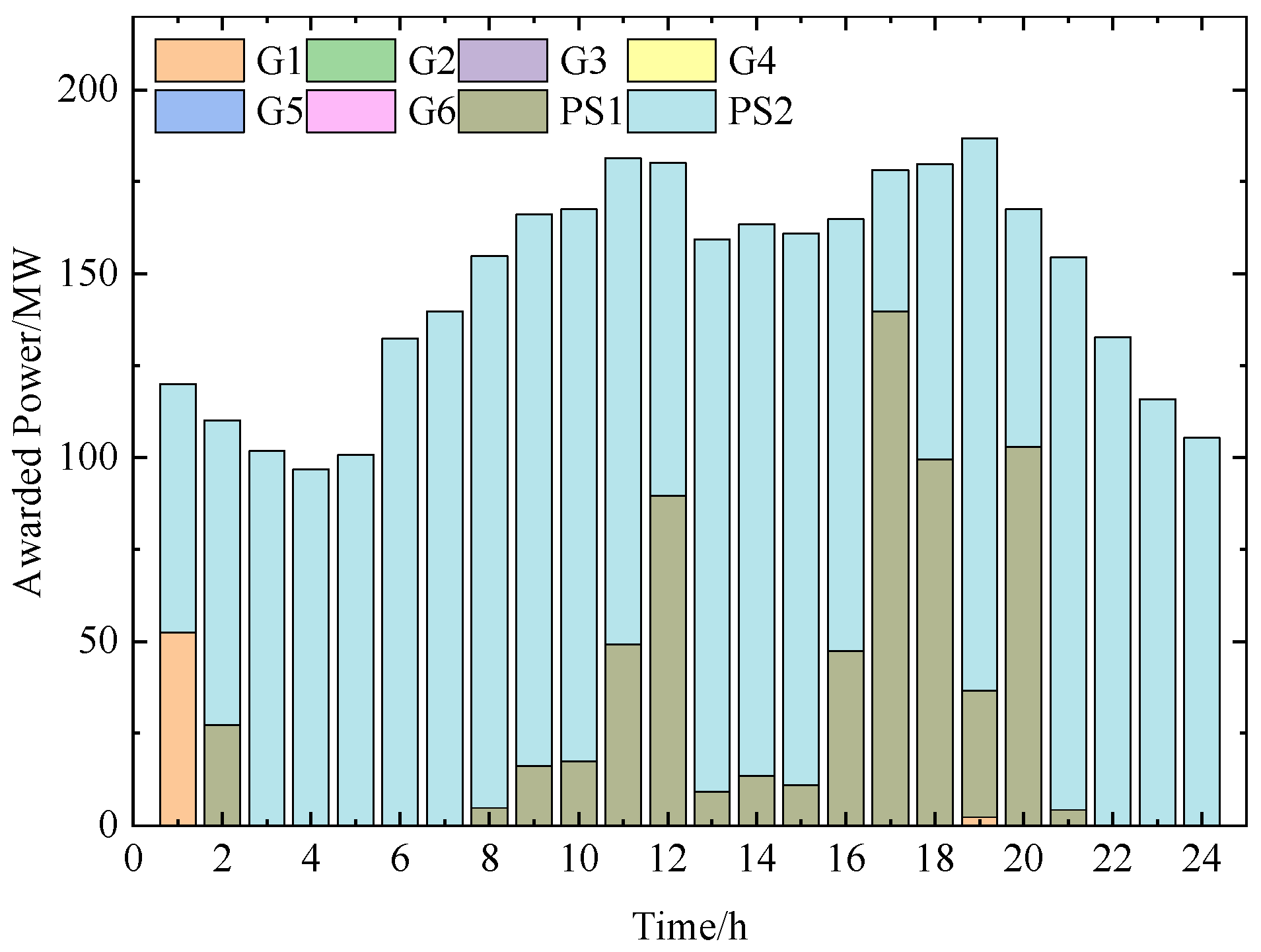
5.2. Clearing Results of the Energy Market
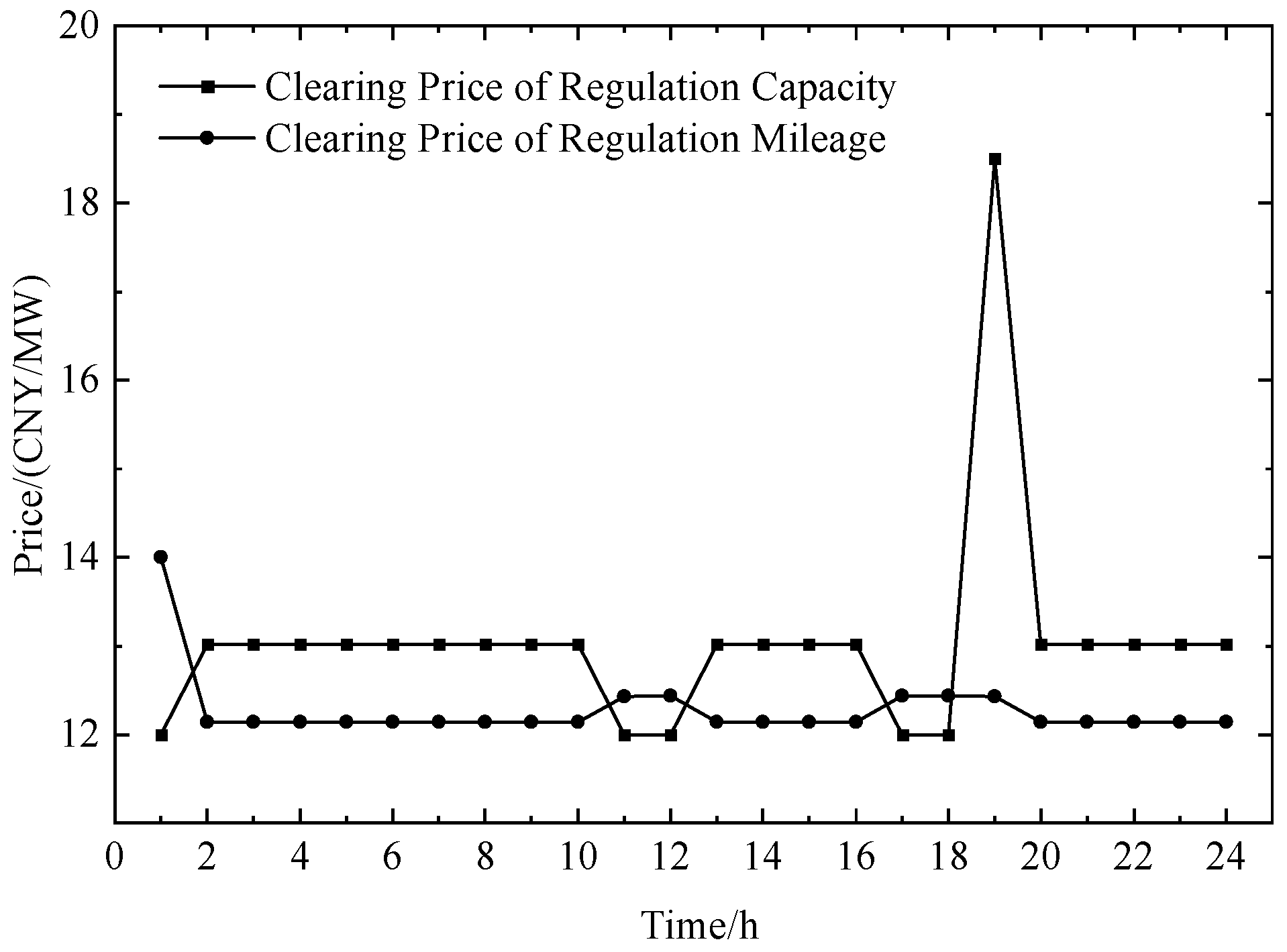
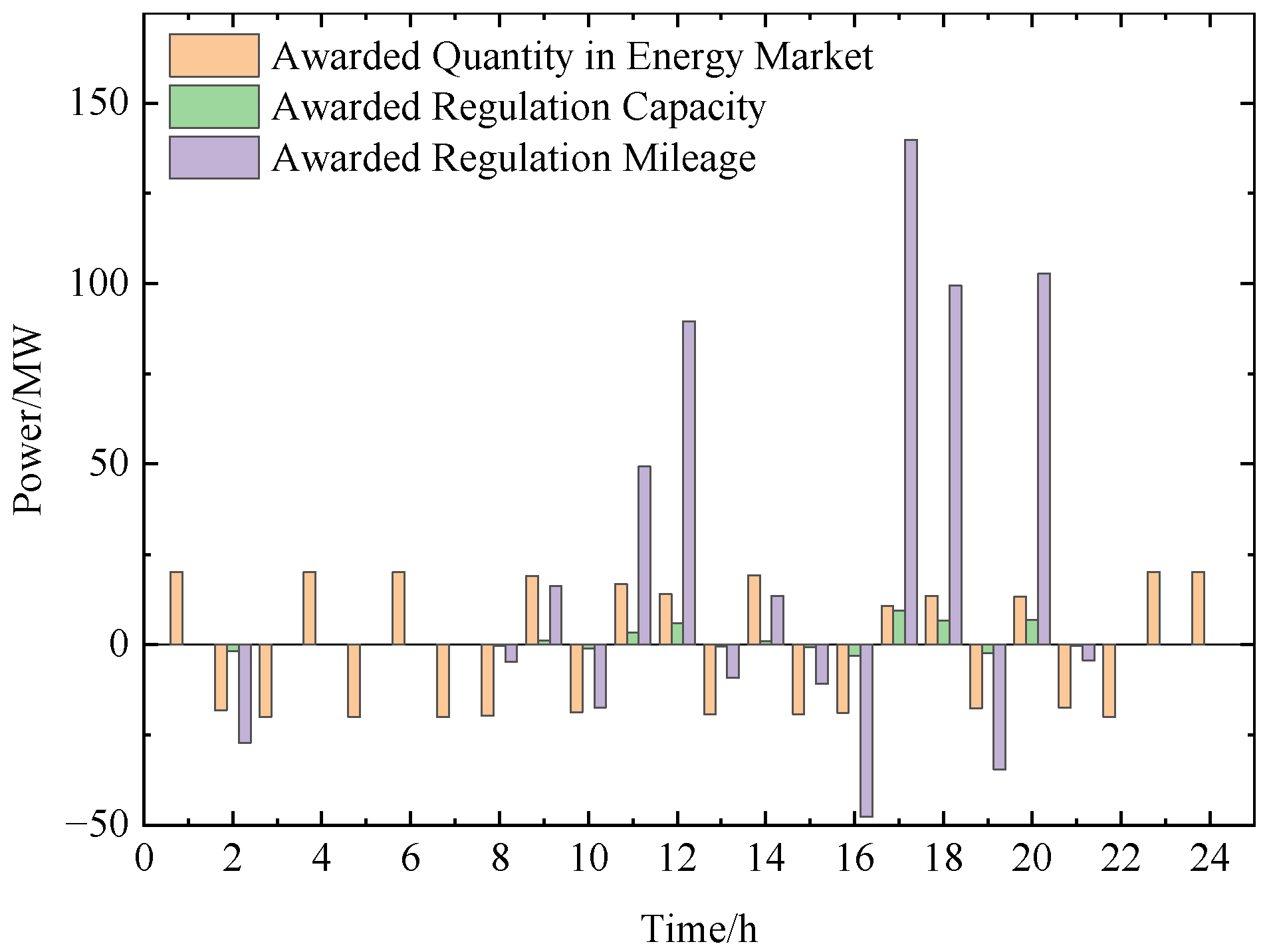
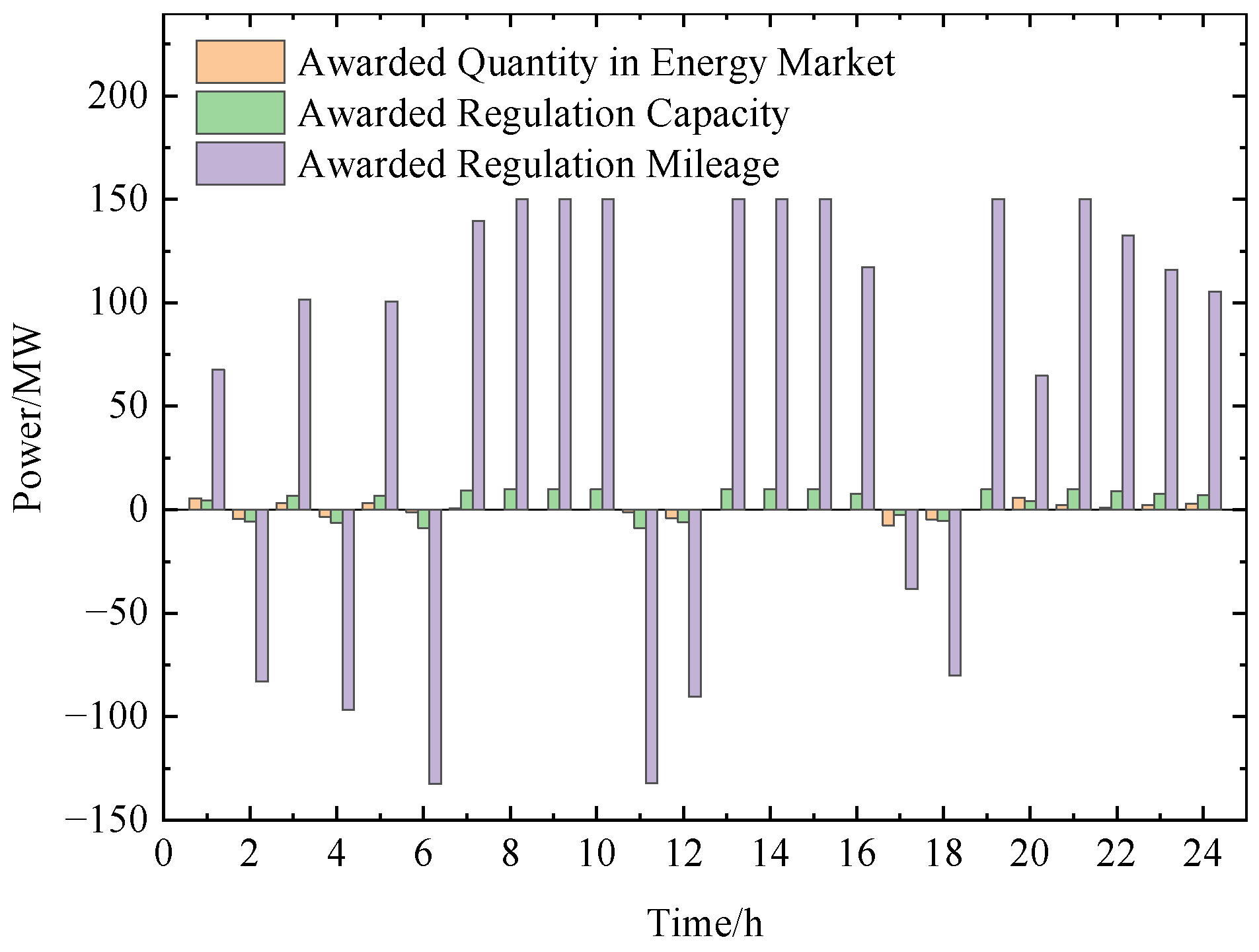
5.3. Clearing Results of the Frequency Regulation Market
5.4. Pumped Storage Operational Strategy
5.5. Profit Analysis of Market Participants
5.6. Economic Benefit Analysis of Pumped Storage
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| PSPS | Pumped storage power station |
| LMP | Locational marginal price |
| MILP | Mixed-integer linear programming |
| KKT | Karush–Kuhn–Tucker |
| The clearing price in the energy market at time t, CNY/MWh | |
| The clearing price in the regulation capacity market at time t, CNY/MW | |
| The clearing price in the regulation mileage market at time t, CNY/MW | |
| The objective function of the upper level | |
| The objective function of the lower level | |
| The total energy procurement cost from thermal generators | |
| The total cost of frequency regulation services | |
| The declared generation power of PSPS unit n at time t, MW | |
| The declared pumping power of PSPS unit n at time t, MW | |
| The declared regulation capacity of PSPS unit n at time t, MW | |
| The declared regulation mileage of PSPS unit n at time t, MW | |
| The declared energy bid of thermal unit m at time t, MW | |
| The declared regulation capacity bid of unit m at time t, MW | |
| The declared regulation mileage bid of unit m at time t, MW | |
| The awarded generation power of PSPS unit n at time t, MW | |
| The awarded pumping power of PSPS unit n at time t, MW | |
| The awarded regulation capacity of PSPS unit n at time t, MW | |
| The awarded regulation mileage of PSPS unit n at time t, MW | |
| The awarded generation power of thermal unit m at time t, MW | |
| The awarded regulation capacity of unit m at time t, MW | |
| The awarded regulation mileage of unit m at time t, MW | |
| The generation bid price of PSPS unit n at time t, CNY/MWh | |
| The pumping bid price of PSPS unit n at time t, CNY/MWh | |
| The regulation capacity bid price of PSPS unit n at time t, CNY/MW | |
| The regulation mileage bid price of PSPS unit n at time t, CNY/MW | |
| The generation bid price of thermal unit m at time t, CNY/MWh | |
| The regulation capacity bid price of unit m at time t, CNY/MW | |
| The regulation mileage bid price of unit m at time t, CNY/MW | |
| The state of charge of PSPS unit n at time t, MWh | |
| The maximum energy storage of unit n, MWh | |
| The minimum energy storage of unit n, MWh | |
| The efficiency coefficient for generation of unit n | |
| The efficiency coefficient for pumping of unit n | |
| The binary variable indicating generation status, | |
| The binary variable indicating pumping status, | |
| The total regulation capacity demand at time t, MW | |
| The total regulation mileage demand at time t, MW | |
| The mileage-to-capacity ratio of PSPS unit n | |
| The mileage-to-capacity ratio of thermal unit m | |
| The voltage angle at node i and time t | |
| The line susceptance between nodes i and k | |
| The transmission limit of line l, MW |
References
- National Energy Administration. Blue Book on Development Planning of National Unified Electricity Market; National Energy Administration: Beijing, China, 2024. [Google Scholar]
- National Development and Reform Commission; National Energy Administration. Notice on Establishing and Improving the Price Mechanism for Power Auxiliary Services. 2024. Available online: https://www.gov.cn/zhengce/zhengceku/202402/content_6931026.htm (accessed on 25 June 2025).
- Papalexopoulos, A.D.; Andrianesis, P.E. Performance-Based Pricing of Frequency Regulation in Electricity Markets. IEEE Trans. Power Syst. 2014, 29, 441–449. [Google Scholar] [CrossRef]
- MISO. Business Practices Manual: Energy and Operating Reserve Markets. Available online: https://www.misoenergy.org/legal/business-practice-manuals/ (accessed on 25 June 2025).
- PJM. PJM Manual 11: Energy and Ancillary Services Market Operations. Available online: https://www.pjm.com/~/media/documents/manuals/m11.ashx (accessed on 25 June 2025).
- ISO-NE. Market Rule 1: Standard Market Design. Available online: https://iso-ne.com/staticassets/documents/2014/12/mr1_sec_1_12.pdf (accessed on 25 June 2025).
- ERCOT. Market Rule 1: Standard Market Design. Available online: http://www.ercot.com/content/wcm/libraries/151823/April_11__2018_Nodal_Protocols.pdf (accessed on 25 June 2025).
- NYISO. Market Administration and Control Area Services Tariff. Available online: https://www.nyiso.com/public/markets_operations/documents/tariffs/index.jsp (accessed on 25 June 2025).
- Liu, X.; Zhao, S.; Bo, L.; Jin, Z.; Liang, H. Comparative Study on Sequential Clearing and Joint Clearing of Joint Markets under Different Load Conditions. J. N. China Electr. Power Univ. 2025, 52, 107–125. [Google Scholar] [CrossRef]
- Nazari, M.E.; Ardehali, M.M. Optimal Bidding Strategy for a GENCO in Day-Ahead Energy and Spinning Reserve Markets with Considerations for Coordinated Wind-Pumped Storage-Thermal System and CO2 Emission. Energy Strategy Rev. 2019, 26, 100405. [Google Scholar] [CrossRef]
- Igder, M.A.; Niknam, T.; Khooban, M.H. Bidding Strategies of the Joint Wind, Hydro, and Pumped-Storage in Generation Company Using Novel Improved Clonal Selection Optimisation Algorithm. IET Sci. Meas. Technol. 2017, 11, 991–1001. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, N.; Chen, B.; Li, Y.; Zhao, M. Optimal Operation Strategy for Pumped Storage Participating in Energy Market under Electricity Market Environment. Electr. Power Constr. 2020, 41, 45–52. [Google Scholar]
- Liang, N.; Li, P.; Liu, Z.; Song, Q.; Luo, L. Optimal Scheduling of Island Microgrid with Seawater-Pumped Storage Station and Renewable Energy. Processes 2020, 8, 737. [Google Scholar] [CrossRef]
- Chen, X.; Wu, P.; He, H.; Song, B.; Qin, K.; Teng, X.; Yang, F.; Li, D. Optimal Flexibility Dispatching of Multi-Pumped Hydro Storage Stations Considering the Uncertainty of Renewable Energy. Symmetry 2024, 16, 1404. [Google Scholar] [CrossRef]
- Fan, H.; Wu, H.; Li, S.; Han, S.; Ren, J.; Huang, S.; Zou, H. Optimal Scheduling Method of Combined Wind–Photovoltaic–Pumped Storage System Based on Improved Bat Algorithm. Processes 2025, 13, 101. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; Bie, Z.; Liu, H.; Zhang, X. Research on Electricity Price Mechanism and Market Bidding Mode for Pumped Storage Power Stations. Smart Power 2019, 47, 47–55. [Google Scholar]
- Qiao, H.; Zhang, Y.; Gao, M.; Song, X.; Wei, J. Thoughts on Electricity Price Mechanism of Pumped Storage in New Power Systems. Hydropower Pumped Storage 2021, 7, 24–27. [Google Scholar] [CrossRef]
- Feng, C.; Guo, Q.; Liu, Q.; Jian, F. An Optimized Dynamic Benefit Evaluation Method for Pumped Storage Projects in the Context of the “Dual Carbon” Goal. Energies 2025, 18, 2815. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, M.; Zhang, M.; Li, R.; Jin, P. Operation Strategy and Benefit Analysis of Pumped Storage Power Stations in Electricity Market. J. N. China Electr. Power Univ. 2021, 48, 71–80. [Google Scholar] [CrossRef]
- Li, Y.; Fan, Y.; Ke, X.; Huo, C.; Zhou, M.; Yang, Y.; Wang, J.; Xin, Y. Cost Recovery for Variable-Speed Pumped Storage Power Plants in the Market Environment. Energies 2025, 18, 153. [Google Scholar] [CrossRef]
- Ma, L.; Zhai, H.; Yang, W.; Chen, C.; Hu, Y. Analysis of Electricity Revenue and Comprehensive Benefits of Pumped Storage Power Stations in Spot Market. Water Resour. Hydropower Eng. 2023, 54 (Suppl. S1), 283–289. [Google Scholar] [CrossRef]
- Liu, F.; Che, Y.; Tian, X.; He, J.; Wu, D. Cost Transmission Mechanism of Pumped Storage Power Stations in New Power Systems: A Review and Prospects. J. Shanghai Jiao Tong Univ. 2023, 57, 757–768. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, L.; Zhang, X.; Sun, W.; Luo, J. Coordinated Clearing Mechanism for Spot Energy and Frequency Regulation Ancillary Service Markets Incorporating Independent Energy Storage. Proc. CSEE 2020, 40 (Suppl. S1), 167–180. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Cong, Y.; Chen, H.; Zhang, F. Designing a Clearing Model for the Regional Electricity Spot Market Based on the Construction of the Provincial Electricity Market: A Case Study of the Yangtze River Delta Regional Electricity Market in China. Processes 2025, 13, 492. [Google Scholar] [CrossRef]
- Lu, Q.; Chen, L.; Mei, S. Typical Applications of Game Theory in Power Systems and Some Prospects. Proc. CSEE 2014, 34, 5009–5017. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; Cheng, H.; Li, K.; Wang, L. Application Research Review of Stackelberg Game in Electricity Markets. Trans. China Electrotech. Soc. 2022, 37, 3250–3262. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Y.; Yi, Z.; Tu, Z.; Rong, S.; Zhao, G. Coordinated Operation Strategy of Energy Storages with Reactive Power Compensators in Joint Active and Reactive Power Market Environment. Processes 2025, 13, 16. [Google Scholar] [CrossRef]




| Unit | Rated Power (MW) | Energy Bid (CNY/MW) | Regulation Capacity Bid (CNY/MW) | Regulation Mileage Bid (CNY/MW) | Mileage-to-Capacity Ratio |
|---|---|---|---|---|---|
| G1 | 150 | 191 | 14 | 12 | 7 |
| G2 | 110 | 183 | 12 | 15 | 12 |
| G3 | 60 | 201 | 16 | 15 | 7 |
| G4 | 80 | 190 | 14 | 18 | 9 |
| G5 | 40 | 230 | 15 | 14 | 8 |
| G6 | 40 | 192 | 12 | 16 | 12 |
| Market Participant | Energy Market Revenue (CNY) | Regulation Capacity Revenue (CNY) | Regulation Mileage Revenue (CNY) |
|---|---|---|---|
| Thermal Units G1–G6 | 1,302,629.62 | 1578.02 | 763.88 |
| Pumped Storage PS1 | −4589.00 | 565.35 | 8211.70 |
| Pumped Storage PS2 | 72.43 | 2456.14 | 34,247.64 |
| Market Participation | Revenue/Cost (CNY) | Two-Part Tariff Scheme | Revenue/Cost (CNY) |
|---|---|---|---|
| Daily Energy Market Revenue | 44,535.50 | Energy Charge | 24,657.53 |
| Daily Regulation Capacity Revenue | 3021.49 | Capacity Charge | 12,328.76 |
| Daily Regulation Mileage Revenue | 42,459.34 | - | - |
| Daily Power Purchase Cost | –49,052.07 | - | - |
| Daily Net Profit | 40,964.26 | Daily Net Profit | 36,986.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Huang, M.; Xu, H.; Chen, Z.; Li, W.; Zhang, J.; Ran, S.; Chen, X. A Stackelberg Game-Based Joint Clearing Model for Pumped Storage Participation in Multi-Tier Electricity Markets. Processes 2025, 13, 2472. https://doi.org/10.3390/pr13082472
Zeng L, Huang M, Xu H, Chen Z, Li W, Zhang J, Ran S, Chen X. A Stackelberg Game-Based Joint Clearing Model for Pumped Storage Participation in Multi-Tier Electricity Markets. Processes. 2025; 13(8):2472. https://doi.org/10.3390/pr13082472
Chicago/Turabian StyleZeng, Lingkang, Mutao Huang, Hao Xu, Zhongzhong Chen, Wanjing Li, Jingshu Zhang, Senlin Ran, and Xingbang Chen. 2025. "A Stackelberg Game-Based Joint Clearing Model for Pumped Storage Participation in Multi-Tier Electricity Markets" Processes 13, no. 8: 2472. https://doi.org/10.3390/pr13082472
APA StyleZeng, L., Huang, M., Xu, H., Chen, Z., Li, W., Zhang, J., Ran, S., & Chen, X. (2025). A Stackelberg Game-Based Joint Clearing Model for Pumped Storage Participation in Multi-Tier Electricity Markets. Processes, 13(8), 2472. https://doi.org/10.3390/pr13082472





