Optimizing Multi-Cluster Fracture Propagation and Mitigating Interference Through Advanced Non-Uniform Perforation Design in Shale Gas Horizontal Wells

Abstract

The persistent challenge of fracture-driven interference (FDI) during large-scale hydraulic fracturing in the southern Sichuan Basin has severely compromised shale gas productivity, while the existing research has inadequately addressed both FDI risk reductions and the optimization of reservoir stimulation. To bridge this gap, this study developed a mechanistic model of the competitive multi-cluster fracture propagation under non-uniform perforation conditions and established a perforation-based design methodology for the mitigation of horizontal well interference. The results demonstrate that spindle-shaped perforations enhance the uniformity of fracture propagation by 20.3% and 35.1% compared to that under uniform and trapezoidal perforations, respectively, with the perforation quantity (48) and diameter (10 mm) identified as the dominant control parameters for balancing multi-cluster growth. Through a systematic evaluation of the fracture communication mechanisms, three distinct inter-well types of FDI were identified: Type I (natural fracture–stress anisotropy synergy), Type II (natural-fracture-dominated), and Type III (stress-anisotropy-dominated). To mitigate these, customized perforation schemes coupled with geometry-optimized fracture layouts were developed. The surveillance data for the offset well show that the pressure interference decreased from 14.95 MPa and 6.23 MPa before its application to 0.7 MPa and 0 MPa, achieving an approximately 95.3% reduction in the pressure interference in the application wells. The expansion morphology of the inter-well fractures confirmed effective fluid redistribution across clusters and containment of the overextension of planar fractures, demonstrating this methodology’s dual capability to enhance the effectiveness of stimulation while resolving FDI challenges in deep shale reservoirs, thereby advancing both productivity and operational sustainability in complex fracturing operations.

1. Introduction

Deep shale gas has emerged as a strategic frontier for China’s natural gas exploration and development, with horizontal well drilling and multi-stage fracturing technologies serving as pivotal enablers for efficient exploitation [1,2,3]. Advances in staged volume fracturing techniques have driven rapid growth in the production in the deep shale gas reservoirs of the Sichuan Basin. However, as the cluster spacing continues to shrink and fracturing operations intensify, the hydraulic fractures generated during multi-stage fracturing in horizontal wells increasingly interconnect with NF networks in adjacent layers [4,5]. This leads to high-pressure fluid channeling between wells (termed “fracture-driven interference”), resulting in the invasion of proppant into neighboring wells, causing deformation or damage and significant production disruptions [6,7,8]. By the end of 2020, 80 instances of fracture-driven interference (FDI) were documented in the Changning region, cumulatively reducing the gas production by 136.386 × 10⁸ m³ between 2015 and 2024, severely undermining the productivity of the shale gas field [9].

The escalation of volume fracturing operations, characterized by larger fluid injection volumes, generates longer hydraulic fractures that intersect with natural fractures (NFs), forming complex inter-well fracture networks [10,11,12]. These NF networks play a critical role in FDI. Research results indicate that when large-scale NFs span multiple wells, they can easily connect with the fracture networks formed by these wells, leading to widespread inter-well interference [13]. Research underscores that the stress field distribution is a dominant factor controlling fracture propagation. Hydraulic fracturing inherently alters the pore pressure, inducing rock deformation and stress redistribution. This creates non-uniform stress fields, reducing the pore pressure in adjacent regions while elevating matrix and closure stresses, thereby driving fractures to preferentially propagate toward low-stress zones [14,15,16]. Additionally, during multi-cluster fracturing in horizontal wells, stress interference among simultaneously propagating fractures exacerbates asymmetric growth [17,18].

Therefore, during the process of multi-cluster fracturing in horizontal well stages, FDI is influenced by multiple factors, such as the development of NFs, the heterogeneity of reservoir stresses, and interference between fractures [19,20,21]. Competition in fluid allocation results in dominant fractures capturing the majority of the injected fluid while the other clusters fail to develop effective fractures, compromising the stimulation efficiency [22]. Moreover, an excessive influx of fluid into the dominant fractures also risks uncontrolled planar extension, invading neighboring wells and causing interference [3,23,24]. Consequently, achieving a balanced fluid distribution among clusters and suppressing dominant fracture growth are critical to promoting uniform fracture propagation and mitigating FDI [25].

Key to mitigating these issues is achieving a balanced fluid distribution among clusters and suppressing dominant fracture growth [26,27]. Field practices demonstrate that non-uniform perforation strategies (varying the perforation density and diameter) can effectively regulate the allocation of fluid across clusters in both homogeneous and heterogeneous reservoirs [28,29,30]. Previous studies, such as Settgast et al.’s [31] finite element models analyzing perforation patterns and friction effects; Guo et al.’s [32] 3D multi-fracture propagation models highlighting the impacts of spacing; and Lu et al.’s [33] mathematical models incorporating stress shadowing and fluid loss, have established foundational insights. These works emphasize that a closer cluster spacing intensifies the stress interference, while a higher fluid viscosity can counteract such effects by modifying the fracture width [34,35,36,37,38]. However, systematic studies on non-uniform perforation-based anti-interference mechanisms tailored to diverse FDI scenarios remain scarce.

This study bridges this gap by establishing a theoretical model for competitive multi-cluster fracture propagation under non-uniform perforation conditions. Leveraging enhanced coupled fluid flow–stress–fracture simulations, a 3D finite element model for elucidating the fluid allocation dynamics and fracture competition mechanisms in deep shale gas reservoirs was developed. Building on this, a non-uniform perforation-based design methodology for mitigating FDI was proposed and applied. These findings aim to optimize reservoir stimulation while minimizing FDI, enhancing the efficiency and sustainability of deep shale gas development.

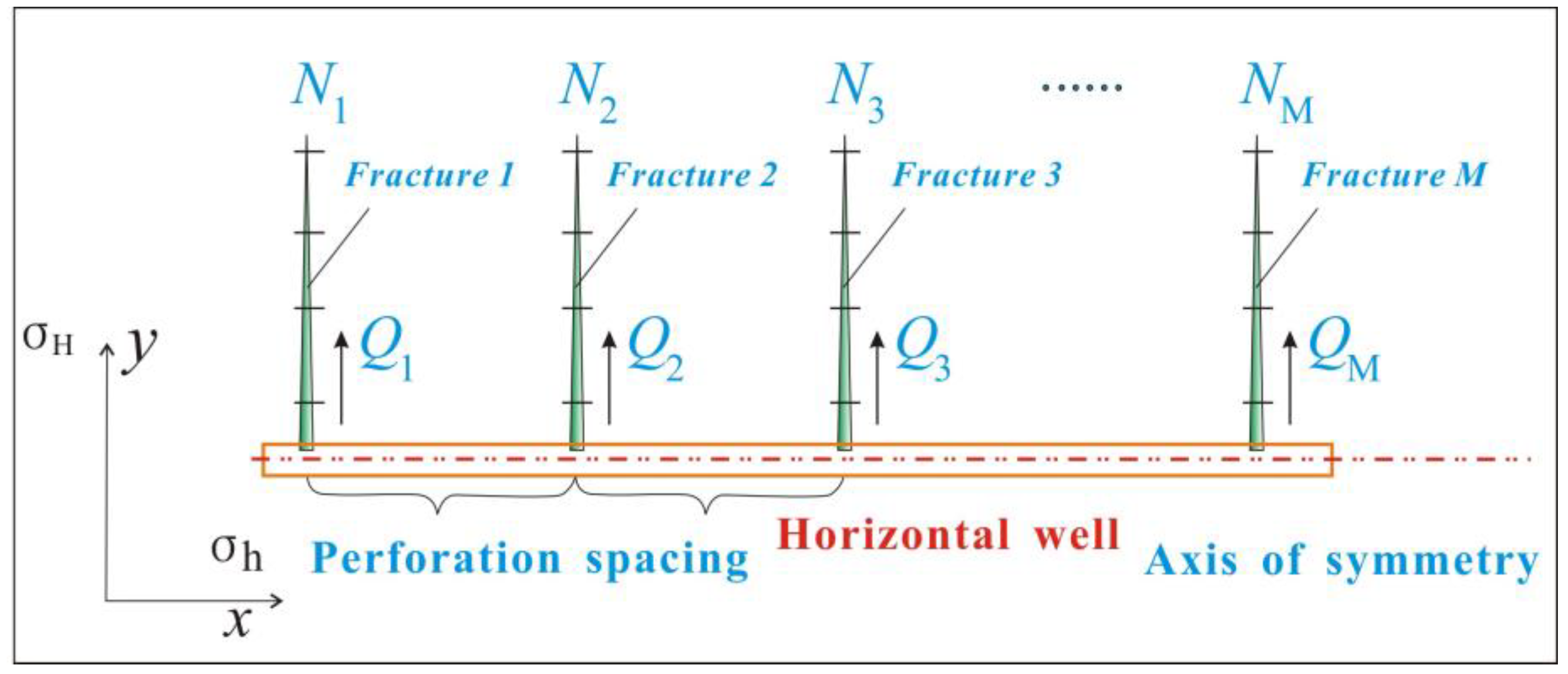
2. The Model for the Simultaneous Propagation of Multiple Fractures

2.1. The Model of the Fracturing Fluid Flow

The controlling equations for fracture expansion include rock deformation, the fluid flow in the seam, and the flow distribution in the wellbore. The model assumes that the fluid inside the fracture in the direction of the fracture length and height flows according to a two-dimensional plane and the horizontal cross-section of the hydraulic fracture satisfies the plane strain condition of elasticity.

The fluid flow inside the fracture is characterized by the Navier–Stokes equation of fluid mechanics. Assuming that the two surfaces of the fracture are parallel and smooth and the pressure gradient is uniform, the Navier–Stokes equation can be simplified as follows [39]:

$${\displaystyle \frac{\partial p}{\partial l}}=C_f{H}^{-n’}{w}^{-(2n’+1)}{q}^{n’}$$

(1)

in which

$$C_f=2^{n’+1}k’{\left({\displaystyle \frac{1+2n’}{n’}}\right)}^{n’}$$

(2)

where: p is the fluid pressure inside the crack, MPa; q is the flow rate inside the crack, m³/min; h is the height of the crack, m; w is the width of the crack, m; l is the distance along the crack, m; n’ is the fluidity index of the fluid, dimensionless; and k’ is the power law coefficient of the fluid, Pa·s.

Considering the leakoff of the fracturing fluid along the hydraulic fracture surface, the material balance equation is satisfied:

$${\displaystyle \frac{\partial q\left(l,t\right)}{\partial l}}+{\displaystyle \frac{2H{C}_L}{\sqrt{t-t_0(l)}}}+{\displaystyle \frac{\partial A(l,t)}{\partial t}}=0$$

(3)

The leakoff of the fracturing fluid is calculated using the Carter leakoff model [40]:

$$q_l(s,t)={\displaystyle \frac{2H{C}_L}{\sqrt{t-\tau (l)}}}$$

(4)

where q(l,t) is the flow rate through the crack section, m³/min; A(l,t) is the cross-sectional area of the fracture, m²; q_l(s,t) is the leakoff rate of the fracturing fluid per unit length of the fracture, m²/min; C_L is the filtration coefficient of the fracturing fluid, m·min^−1/2; and τ(l) is the time at which the crack reaches position l, min.

Basically, the HF’s width equals zero before fracture initiation. If the injection rate at the wellbore remains constant and no flow exists at the fracture tip, the boundary conditions and the initial conditions are

$$q(0,t) = Q_c, q(L_f,t) = 0, w(s,0) = 0$$

(5)

where Q_c is 1/2 (m³/s) of the displacement of the fracturing pump; L_f is the half-length of the crack (m).

Under the interference of stress, the uneven distribution of fluid can lead to the differential initiation and propagation of cracks. When multiple cracks (N) expand synchronously in the increased area, the distribution of fracturing fluid in each crack satisfies (Figure 1)

$$Q(x,t)={\displaystyle \sum _{i=1}^N{Q}_i(l,t)}$$

(6)

Assume that the crack is divided into M boundary cells, with each cell approximated by a straight-line segment, where Q_i is the fluid displacement into the i-th crack; k is the k-th cell of the i-th crack. In this case, the cumulative flow rate injected into each crack can be obtained from the sum of the total volume and the leakoff of each crack:

$$\begin{array}{c}{\displaystyle {\int }_0^t{Q}_i}(x,t)dt={\displaystyle {\int }_0^{L_i(k)}{H}_i}{w}_{i}dl+{\displaystyle {\int }_0^{L_i(k)}{\displaystyle {\int }_0^{L_i(k)}{q}_i(l,t)}}dtdl\\ (i=1,2,\dots ,N;k=1,2,\dots ,M)\end{array}$$

(7)

where q_i is the flow rate along the crack’s cross-section in crack i (m³/s); L_i(k) is the length of crack i (m); H_i is the height of crack i (m); w_i is the width of crack i (m); and l is the length of the k-th tiny cell of crack i (m).

At this point, the fluctuating flow of the unsteady fluid in crack i can be described as

$$u_i(x,t)={\displaystyle \frac{Q_i(x,t)}{H_i{w}_i}}$$

(8)

By coupling Equations (1)–(8) using Newton’s iterative method, the pressure distribution and the flow distribution of multiple hydraulic fractures can be solved.

2.2. The Stress Model of the Hydraulic Fracture

We assume that there is a stress concentration area composed of N fracturing perforation clusters on the wall of a horizontal wellbore. Assuming that the initiation pressures of these fracturing perforation clusters are P_f1, P_f2 …… P_fn, the force acting on each fracturing perforation cluster is

$$P_{fnp}(l,t)=P_{fc}(l,t)-P_{fn}$$

(9)

where P_fnp(l,t) is the net pressure at any point within the crack, MPa; P_fc(l,t) is the pressure at any point within the crack, MPa; and P_fn is the critical initiation pressure for the cracks, MPa.

$$P_{f\min }=\min \left\{\left.P_{f1},P_{f2}, ..., P_{fn}\right\}\right.$$

(10)

According to the average circumferential stress criterion, the clusters with the minimum breakdown pressure are usually located within the maximum principal stress orientation. During the hydraulic fracturing process, a crack initiates when the hydraulic fracturing reaches the minimum crack breakdown pressure P_fmin.

2.3. The Model of Fracture Initiation Propagation

Under the action of injection, the continuous change in the fracture net pressure P_fc(x,t) will inevitably induce significant changes in the stress at the crack tip, which will affect the initiation and propagation of the fracture. According to the theory of fracture mechanics, the stress strength factor of the fracture tip under high pressure can be expressed according to the equivalent strength of the stress [41]:

$$K_{eq}={\displaystyle \frac{1}{2}}\cos ({\displaystyle \frac{\phi }{2}})\left[K_{{\rm I}}(1+\cos \phi )-3K_{\Pi }\sin \phi \right]$$

(11)

where $\phi$ is the angle measured from the fracture tip in the counterclockwise direction, and K_I and K_II are the stress strength factors at the fracture tips of I and II, respectively:

$$K_{{\rm I}}=-{\displaystyle \frac{E}{8(1-v^2)}}\sqrt{{\displaystyle \frac{2\pi }{l}}}\left[{\sigma }_n-p_{fc}(x,t)\right].$$

(12)

$$K_{\Pi }=-{\displaystyle \frac{E}{8(1-v^2)}}\sqrt{{\displaystyle \frac{2\pi }{l}}}\left\{\left.\tau -c-\left[({\sigma }_n-p_{fc}(x,t))\tan \varphi \right]\right\}\right..$$

(13)

Once the equivalent stress strength factor, K_eq, reaches the toughness of a Type I fracture, K_IC, a hydraulic fracture begins to propagate, and the angle of propagation is determined by the equation [42]

$$\phi =2\arctan \left[{\displaystyle \frac{1}{4}}({\displaystyle \frac{K_{{\rm I}}}{K_{\Pi }}}-\mathrm{sgn}(K_{\Pi })\sqrt{8+{({\displaystyle \frac{K_{{\rm I}}}{K_{\Pi }}})}^2})\right].$$

(14)

To determine the hydraulic fracture length l_eq, considering the effect of osmotic pressure on hydraulic fractures, the fracture model established by Horri and Nemat-Nasser is modified as follows:

$$K_{eq}={\displaystyle \frac{2a{\tau }_e\sin \phi }{\sqrt{\pi (l_{eq}+0.27l_{eq})}}}-\left[{\sigma }_n-p_{fc}(x,t)\right]\sqrt{\pi l_{eq}}$$

(15)

By combining (12), (13), and (15) with Equation (11), the response relationship between fluid injection, pressure migration, and fracture initiation and propagation can be obtained.

2.4. Constitutive Model Calculation

TOUGH2-Biot adopts a modular design idea, in which the fracture damage module can use the stress state and fluid pressure for each unit to calculate the additional strain and damage variables [43]. The coupled simulation program (TOUGH-EPFD3D) is reconstructed based on the theory of competitive fracture initiation and propagation among multiple clusters. The structure of the designed and improved program and the calculation flow are shown in Figure 2.

TOUGH-EPFD3D is divided into three functional modules according to different physical processes: a hydrothermal transport module, an elastic–plastic mechanics module, and a fracture damage module. Since the time change in the solution of the coupled multi-physics process is only in the hydrothermal transport module, the overall simulation control part is also controlled by the hydrothermal transport part.

The mechanics module is for calculating the stress and displacement at each point in the model using the nonlinear finite element method based on the incoming temperature, the stress boundary conditions, and the physical parameters. The fracture damage module explicitly calculates the current fracture damage state and the additional deformation resulting from the fracture damage based on the stress conditions and the fluid pressure obtained from the mechanics module and the hydrothermal transport module (Figure 3).

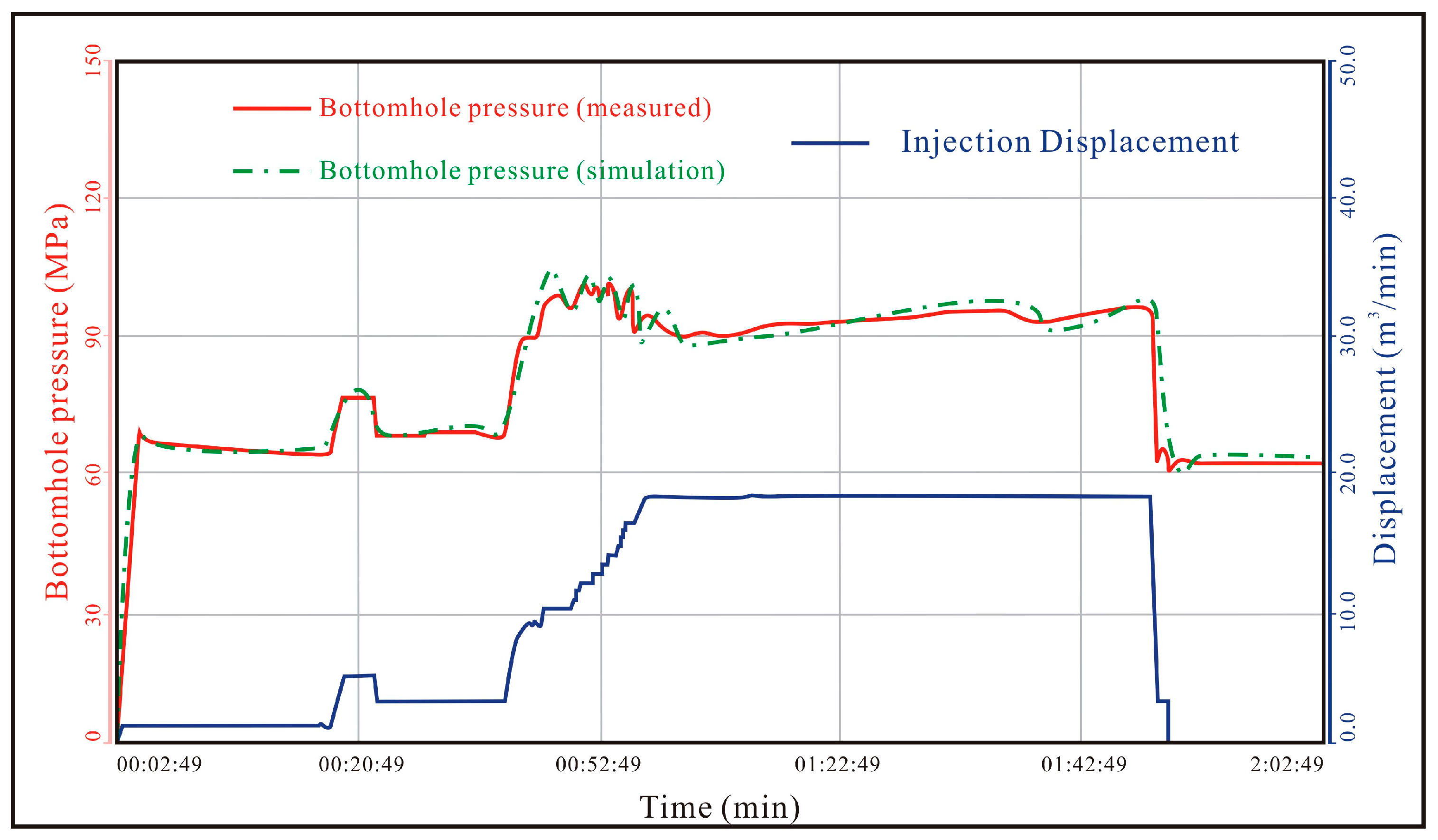
2.5. Model Verification

The KGD fracturing model is a mathematical model that can accurately describe and analyze the fracture propagation and fluid flow in rock media. This model also assumes that the horizontal plane satisfies the plane strain condition. Therefore, the model with the analytical solution of the KGD model was calibrated using the fracturing parameters of the horizontal wells in the Shunan gas field (

Table 1. The simulation parameters of horizontal well fracturing in Shunan gas field.

Parameter	Value	Parameter	Value
σH	95 MPa	H	80 m
σh	85 MPa	μ	3 mPa·s
E	51 GPa	n	1
V	0.25	Q	18 m3/min
T	10 MPa	CL	0.03 cm/min0.5

).

Where the geological conditions and engineering measures of the comparison model are consistent (Table 1), the comparison results indicate that the fracture lengths and widths obtained by the model are in good agreement with the results of the KGD model under the conditions of using the given parameters. Leakoff of the fracturing fluid into the formation during hydraulic fracturing results in a lower fracture propagation rate and a narrower fracture width. Since the KGD model does not consider the leakoff from the hydraulic fracture’s surface, the fracture length and width obtained from the model calculations are slightly lower than those from the KGD model (Figure 4).

The model is designed to simulate the competitive expansion of multiple fractures, and using only the KGD model to verify a single crack is insufficient. Therefore, the model was validated further based on data on the bottomhole pressure from the shale gas horizontal well fracturing site. The calibration results show that the numerical simulation also compares well with the actual data for the site. The newly developed numerical procedure can accurately simulate the simultaneous propagation of multiple fractures in horizontal wells (Figure 5).

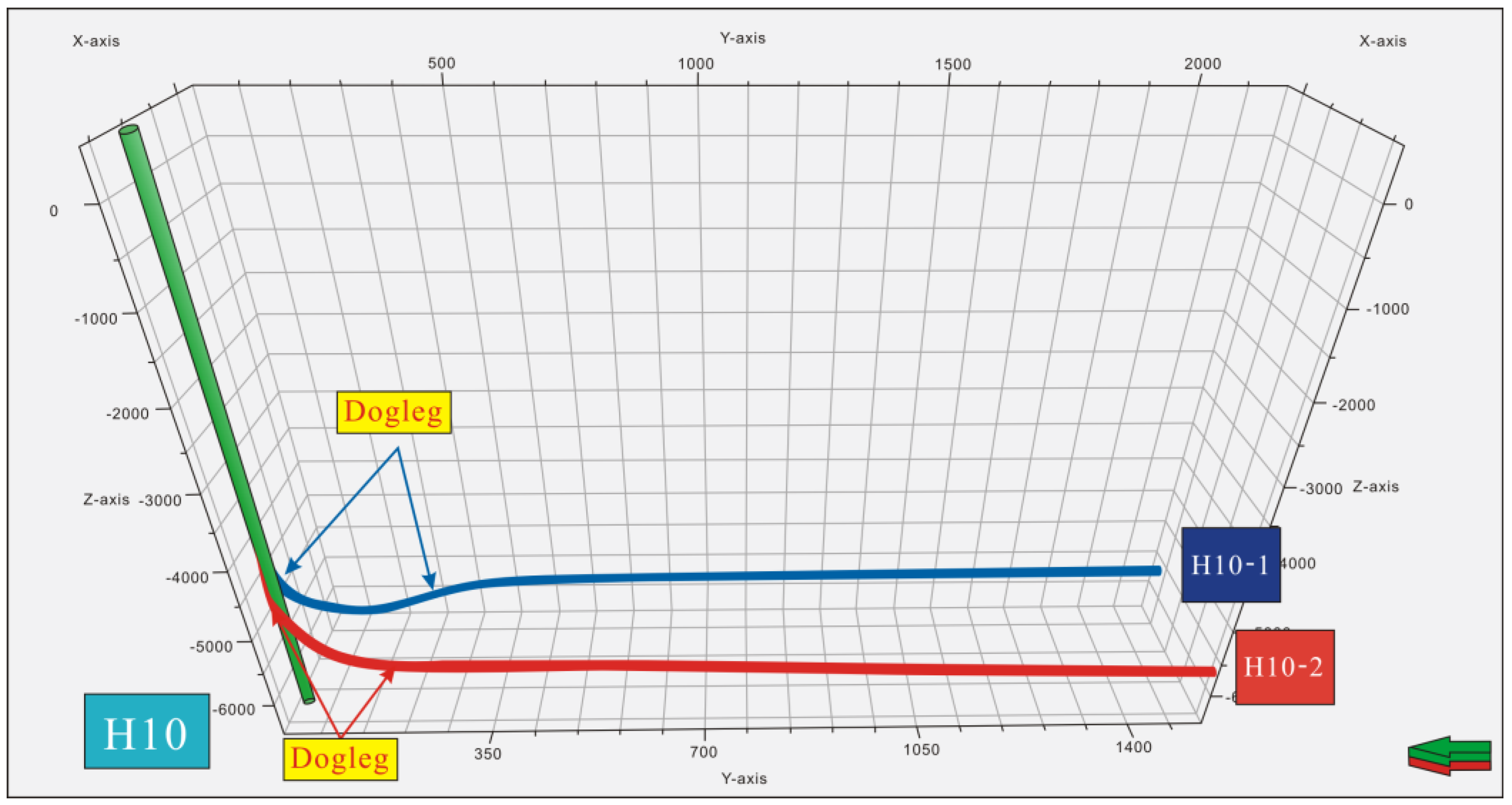
3. Reservoir Simulations

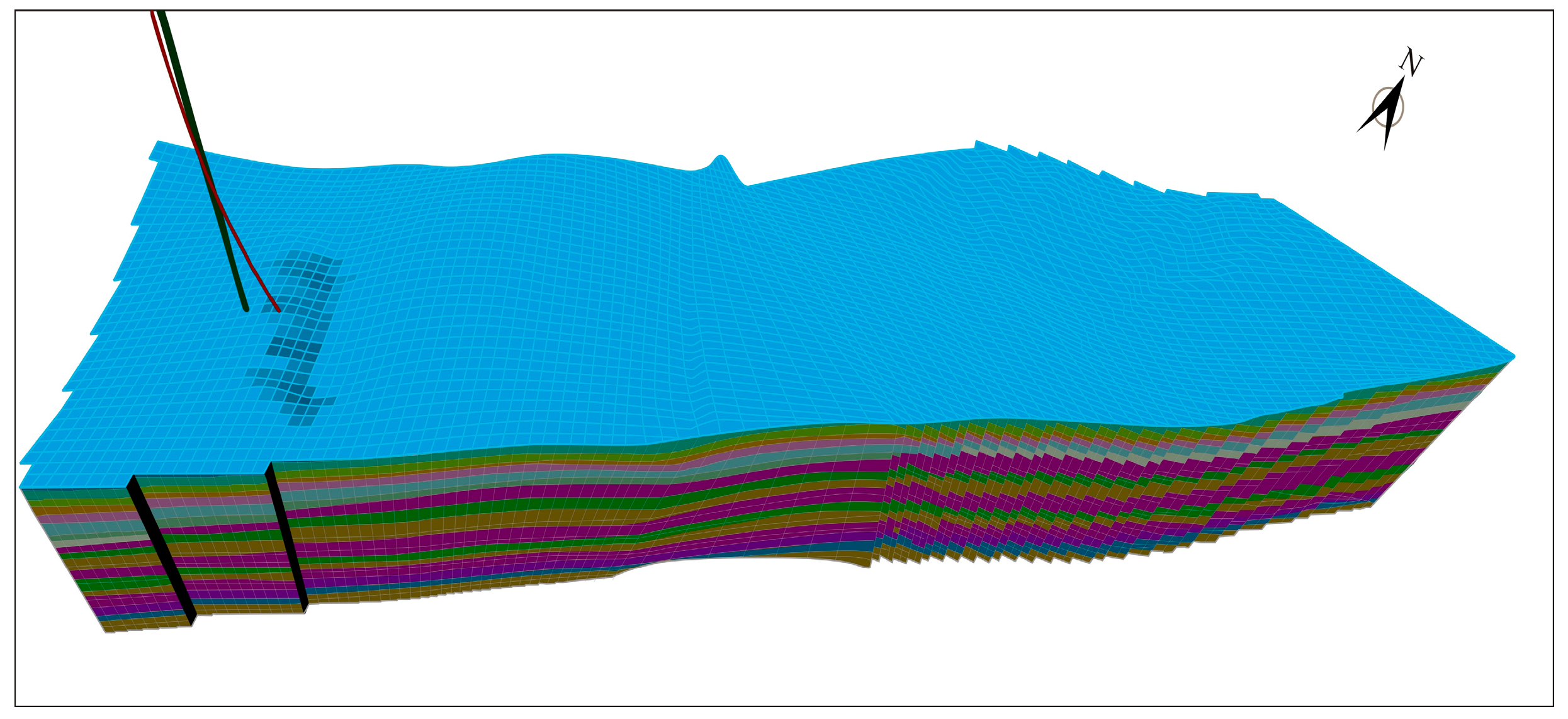
3.1. DFN Construction

The interaction between hydraulic fractures and natural fractures in our model was simulated using discrete fracture network (DFN) coupling criteria, which were grounded in prior validated methodologies [44]. NFs with different occurrences are randomly distributed in the formation, and the volumetric fracture network has the structural characteristics of the main fractures and branch fractures being intertwined with each other. These features are the causes of inter-well fracture communication and fracturing interference. Therefore, it is necessary to describe the distribution characteristics of the NFs through uncertainty fracture modeling.

Considering the spatial distribution and the application of ant-body characterization, the discrete fracture network (DFN) model was adopted to effectively inscribe the reservoir fracture system. In the data sorting, the seepage path for each fracture from the injection point was analyzed, and fractures >600 m from the injection point were deleted. Second, considering that the model cannot handle the expansion behavior of multi-scale natural cracks, natural cracks with a length less than 100 m are not included in the model. Finally, repeated fractures with intersection angles of less than 5° and distances of less than 10 m were integrated. After simplification, there are approximately 2100 fractures in the DFN model. Through analysis using the ant body from the M507H10 platform, the discrete fracture constructed using the model matches well with the ant body method’s portrayal (Figure 6).

3.2. The Reservoir Model

Based on the geological stratification data for the study area, the geological model was divided into three-layer segments vertically, representing the upper, lower, and destination layers. The 3D dimensions of the model are 1500 m × 1500 m × 32 m (Figure 7). The dogleg of the heel of the M1 horizontal well is located at 4175.00 m. The fracturing section of this well is 1400 m, with an average section length of 77.7 m. Each section is designed with 6 clusters of fractures, with an average spacing of 12.9 m between clusters.

The dogleg at the heel of M2 is located at 4315.00 m. The fracturing section of this well is 1420 m, with an average section length of 74.7 m. There are 19 designed fracturing sections with an average cluster spacing of 12.5 m. Fracturing well M1 and the adjacent well M2 are located on both sides of the model, with 350 m between these two horizontal wells (Figure 8).

3.3. Boundary Conditions and Parameters

Based on field measurements, the initial temperature of the model was set to 112 °C. Due to the limited thickness of the reservoir and the relatively high thermal conductivity of the shale formation, the temperature within the model was assumed to be uniform. Additionally, using field-measured data, the initial pore pressure of the model was defined as 72.5 MPa. The rock’s mechanical properties were determined through core experiments and geophysical logging data. The vertical principal stress at the top of the model is 90 MPa, calculated based on a gradient of 22.54 kPa/m. The maximum principal stress in the reservoir is 95 MPa, and the minimum horizontal principal stress is 85 MPa. The range of directions of the maximum horizontal principal stress in the reservoir is 100° to 105° N–E. In the model, the direction is set to 102° N–E. The reservoir properties and geomechanical parameters are shown in

Table 2. The rock properties, reservoir parameters, and in situ stress used in the model.

Category	Parameter	Value	Unit
Mechanical parameters	Density, D	2500	kg/m3
	Tensile strength, TO	6.0	MPa
	Cohesion, c	12	MPa
	Friction angle, φ	35	°
	Young’s modulus, E	45.6	GPa
	Poisson’s ratio	0.24
	Friction coefficient, μ	0.21
Reservoir parameters	Reservoir temperature	112	°C
	Pore pressure	72.5	MPa
	Porosity	4.6	%
In-situ stress	Maximum horizontal principal, SH	95	MPa
	Minimum horizontal principal, Sh	85	MPa
	Vertical principal, Sv	90	MPa

.

For the boundary conditions, the outer boundaries were assigned zero-flux (free) thermal and pressure boundaries, as their extended spatial range ensured negligible external influences during the simulation period. Additionally, the symmetric boundaries (the x = 0 and y = 0 coordinate planes) were also set to free thermal/pressure boundaries following symmetry principles to maintain the geometric and physical consistency of the system. The fluid flow’s boundary was assumed to be a closed boundary.

4. Results and Analyses

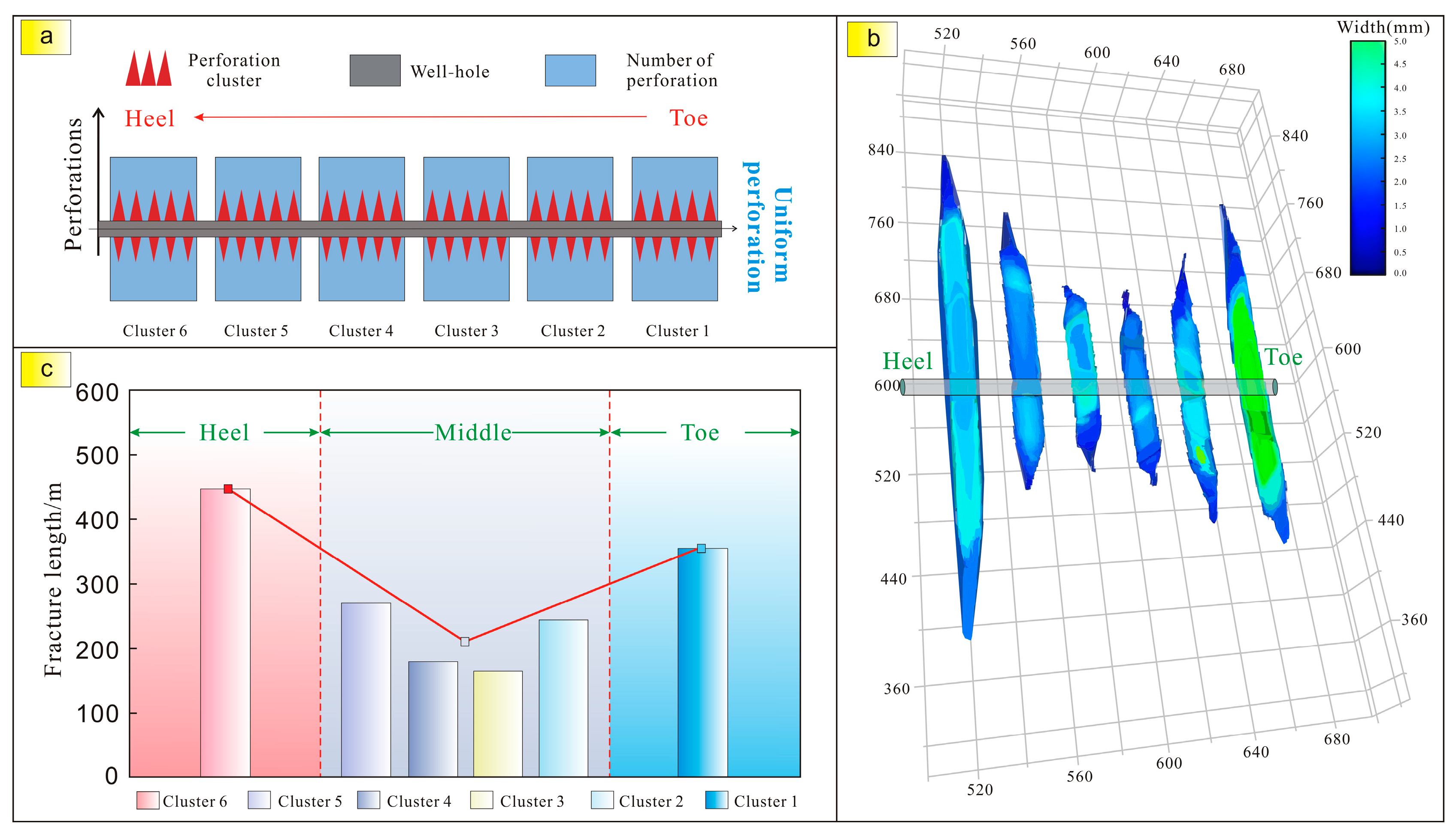
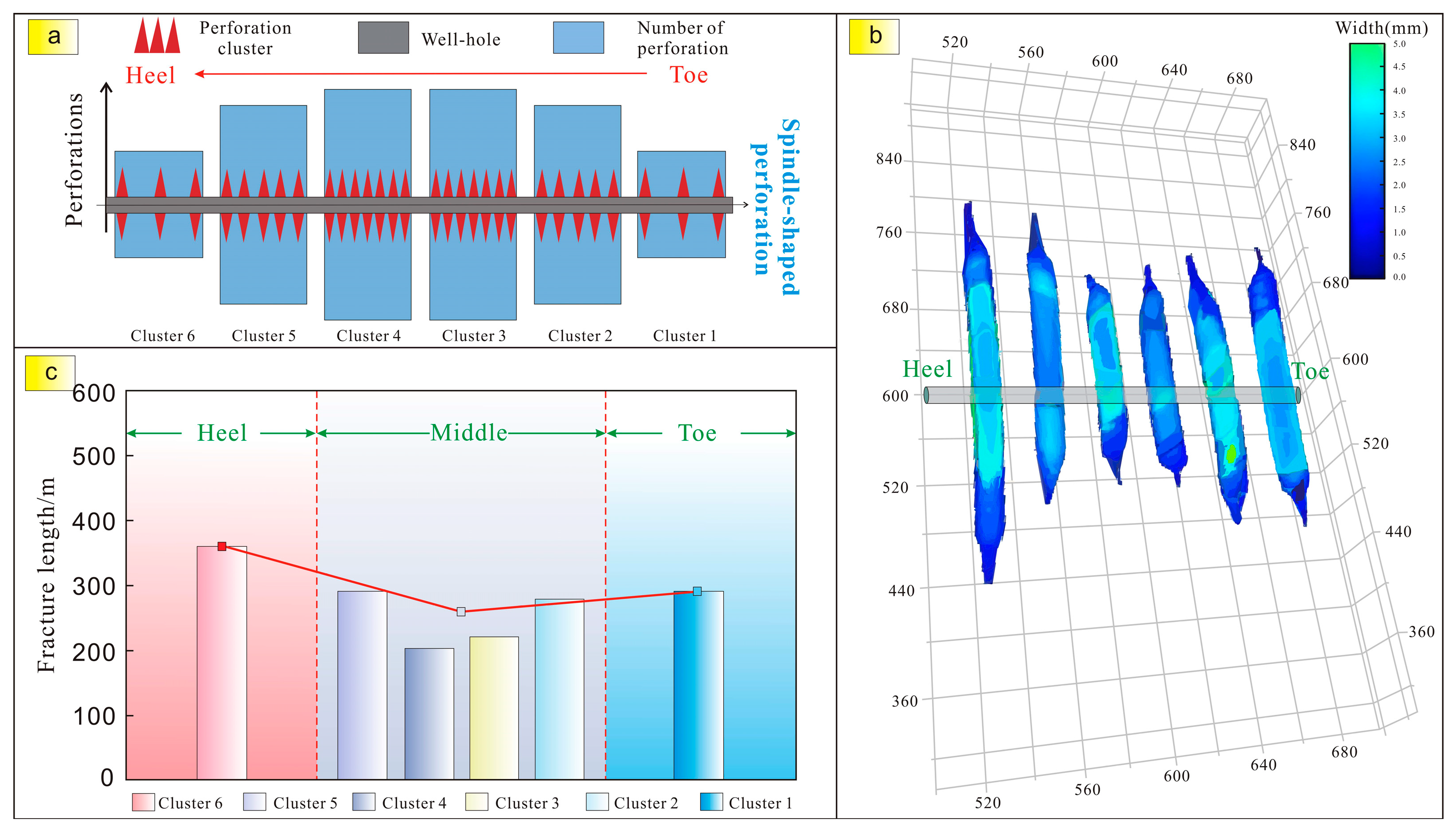
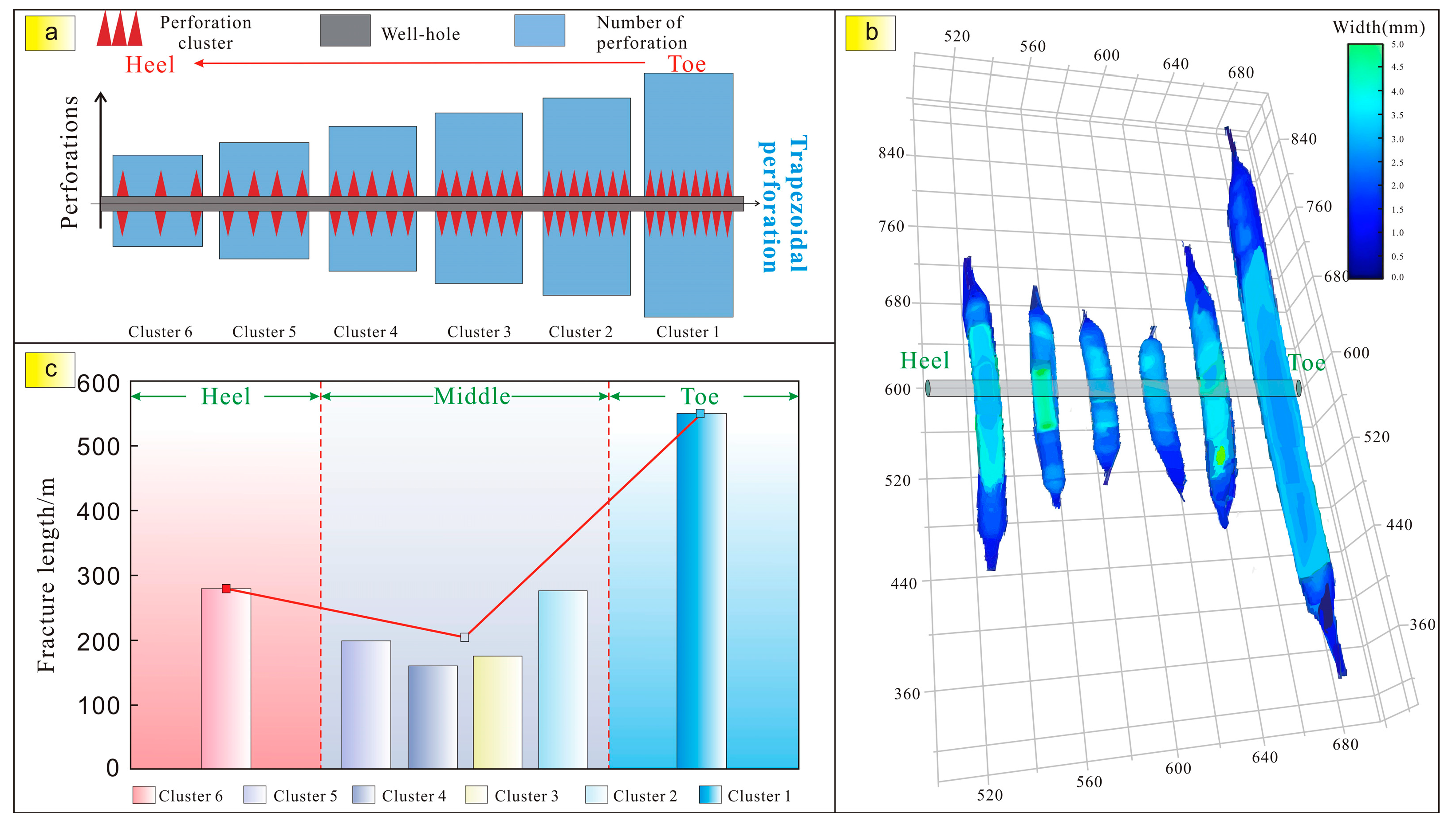
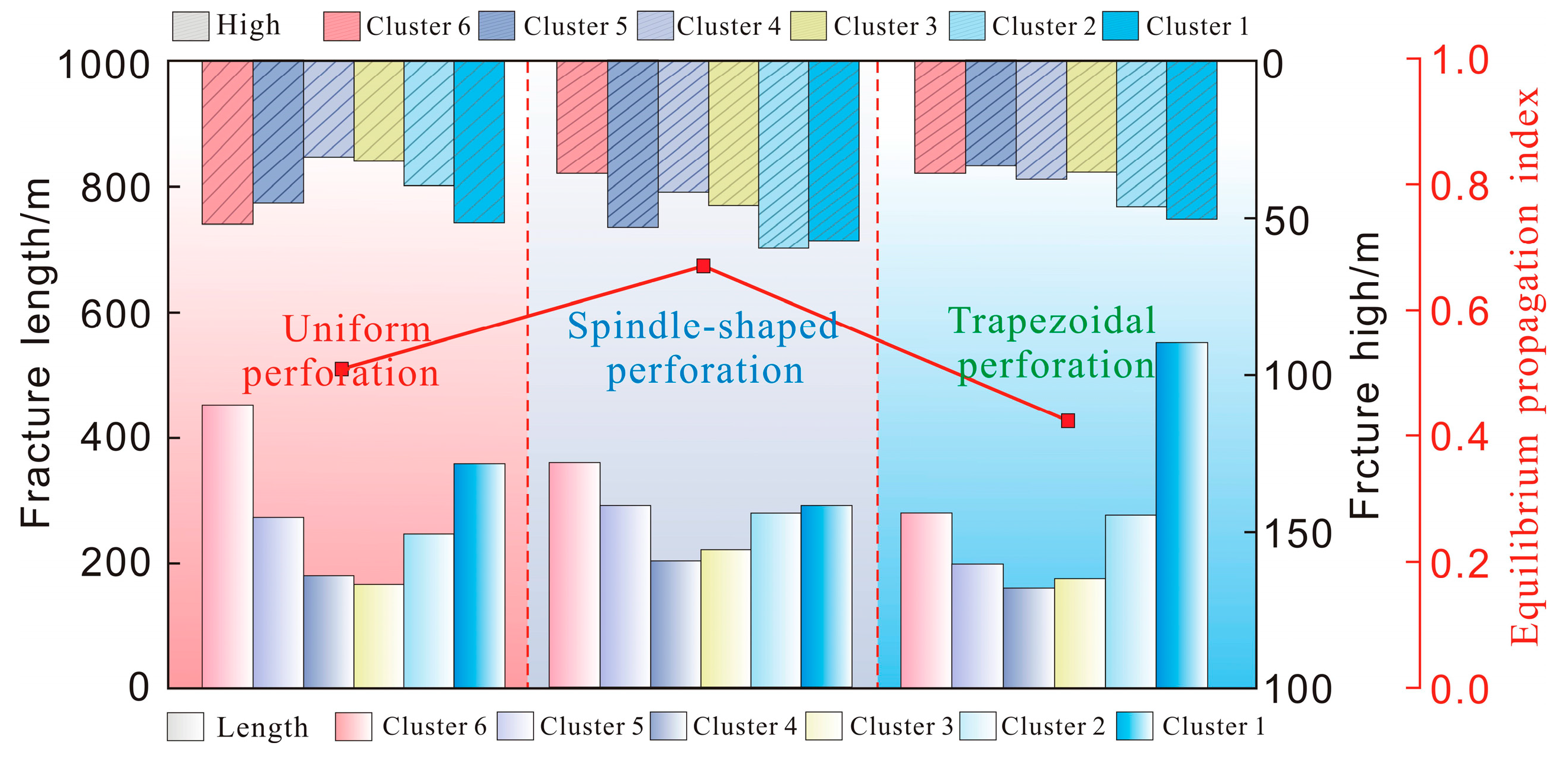
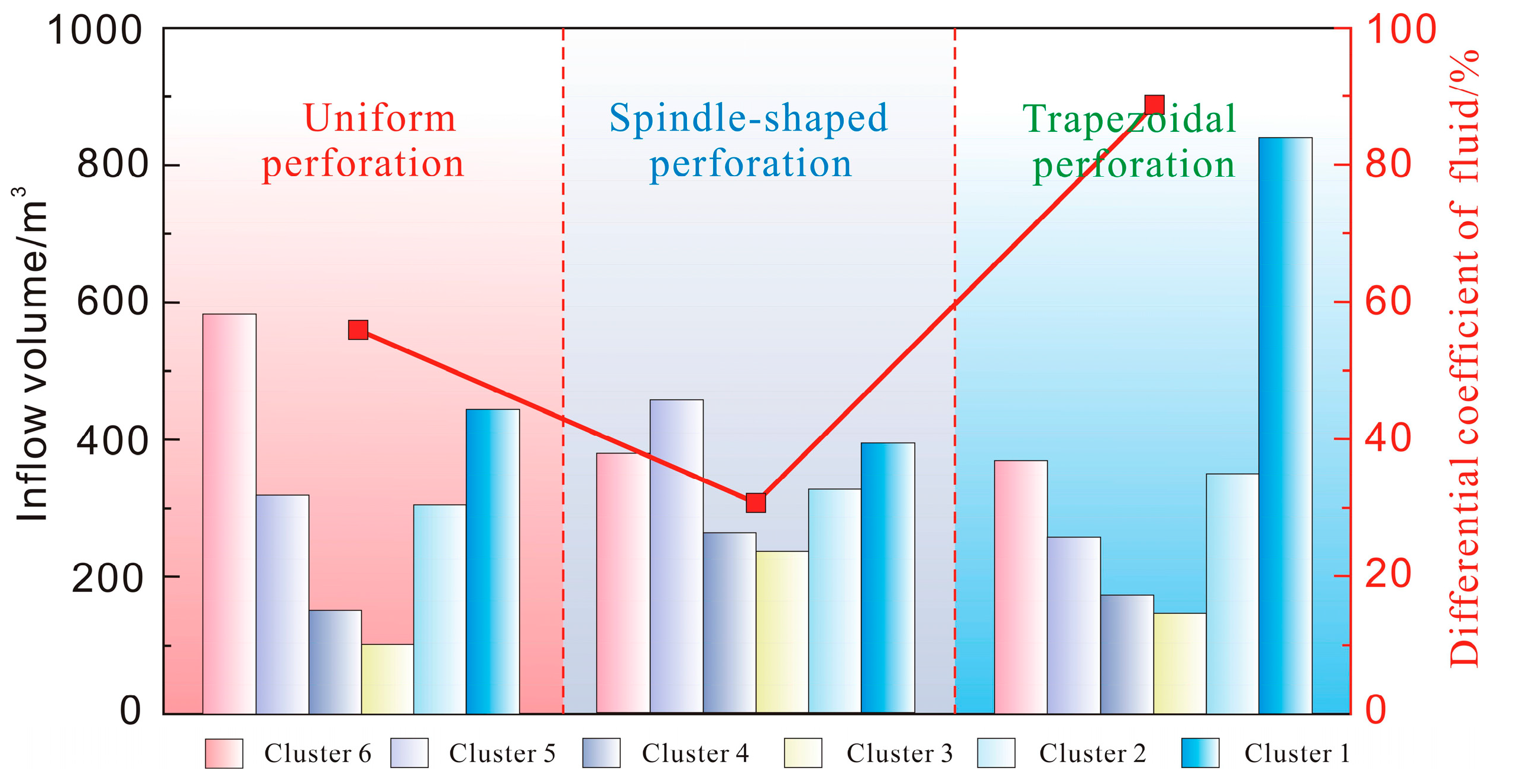
4.1. The Competitive Propagation of Multi-Clusters Under Non-Uniform Perforations

4.1.1. The Influence Mechanism of Perforation Methods on Balanced Fracture Propagation

This study comparatively analyzes the fracture propagation mechanisms among three perforation configurations—uniform (Figure 9a), spindle-shaped (Figure 10a), and trapezoidal patterns (Figure 11a)—focusing on their ability to achieve a uniform fluid distribution and balanced cluster fracture development. Utilizing a controlled experimental framework, all configurations were evaluated under consistent geological conditions (including the wellbore depth, in situ stress field, and rock mechanics properties) and identical operational parameters (i.e., fluid injection rates), thereby eliminating interference from external variables. This methodological rigor enabled a direct comparison of the intrinsic performance characteristics between the three designs. The detailed fracturing simulation parameters are systematically outlined in

Table 3. No-uniform perforation methods in horizontal sections.

Scheme Number	Simulation Scheme		Number of Perforations	Diameter/m	Number of Perforations from Toe to Heel
1	Perforation method	Uniform perforations	48	0.01	8-8-8-8-8-8
2		Spindle-shaped perforations	48	0.01	5-8-11-11-8-5
3		Trapezoidal perforations	48	0.01	13-11-9-7-5-3

.

For the uniform perforations, the hydraulic fractures in the horizontal section exhibited dominant propagation at the heel and toe clusters due to the interference of stress, while the middle clusters were restricted, forming a “concave” fracture geometry with significant non-uniformity (Figure 9).

Under trapezoidal perforations, the reduced perforation density at the ends shortened the end-cluster fractures but caused excessive toe-cluster propagation, increasing the risks of inter-well communication. The middle clusters remained restricted, retaining a “concave” geometry (Figure 10). In contrast, spindle-shaped perforations (fewer perforations at the ends/toes and more in the middle) significantly reduced the interference of stress in the middle clusters. This allowed for the full propagation of the middle clusters, achieving the optimal fracture balance and lowering the FDI risks (Figure 11).

The hydraulic fractures in the horizontal wells exhibited preferential propagation at the terminal clusters (the first and sixth clusters) while showing restricted expansion in the middle clusters (the third/fourth clusters). An analysis of the fluid intake revealed that uniform perforations allocated 55% of the fluid to the heel/toe clusters (clusters 1 and 6), while the middle clusters (clusters 3/4) received only 13%, limiting their propagation (Figure 12).

For trapezoidal perforations, the HFs demonstrate extreme propagation at the toes and limited expansion in the middle. The analysis reveals a 41% contribution to the fluid intake from a single toe cluster, while the middle clusters remain constrained (15%). Spindle-shaped perforations effectively reduce the dominance of terminal fractures while enabling full propagation of the middle clusters. Terminal clusters (first/sixth) exhibit reduced fluid intake (38%), whereas middle clusters demonstrate significantly enhanced allocation (24%), achieving a balanced fracture propagation (Figure 13).

A comparative analysis of the fracture morphology and fluid distribution across clusters across the perforation layouts reveals the mechanisms governing balanced fracture propagation. Uniform designs exhibit the progressive intensification of stress at the central clusters, diminishing the fluid intake and creating concave geometries dominated by heel/toe clusters. The trapezoidal configuration allocates 38% of the perforation density to toe clusters, achieving 41% fluid dominance through amplified suppression of stress in the central clusters, while elevated allocation of fluid to the heel-ends enables competitive propagation. The spindle-shaped perforations demonstrate dual functionality: the elevated perforation density in the middle clusters reduces the stress interference induced while restricting the fluid intake of the edge clusters. These perforations enhance the propagation uniformity by 20.3% and 35.1% compared to that under uniform and trapezoidal perforations, respectively, demonstrating superior coordination of the stress interactions and fluid allocation across clusters.

Additionally, the preliminary analysis indicates that spindle-shaped perforations reduce the stress concentration compared to that under trapezoidal and uniform layouts, suggesting potential benefits in terms of seismic risk mitigation. However, field microseismic monitoring data collected during hydraulic fracturing operations revealed no statistically significant correlation between the perforation geometry and frequency (M < 1.5) or magnitude of seismic events. This discrepancy may arise from scale-dependent stress redistribution mechanisms or subsurface heterogeneities that were not fully captured in the current simulations. Future studies will integrate real-time distributed acoustic sensing (DAS) and advanced geomechanical modeling to systematically track the stress–seismicity couplings across varying completion designs.

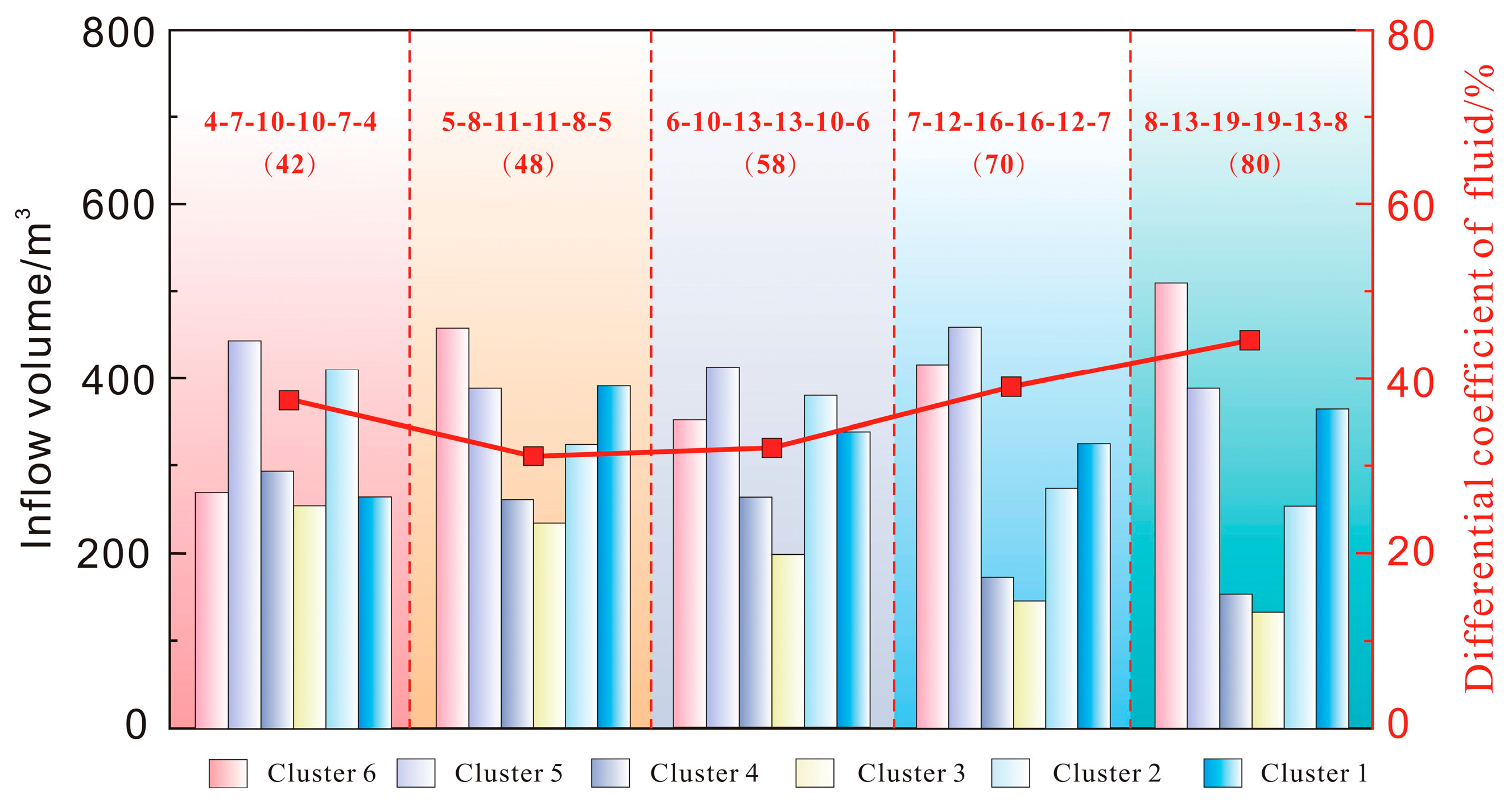
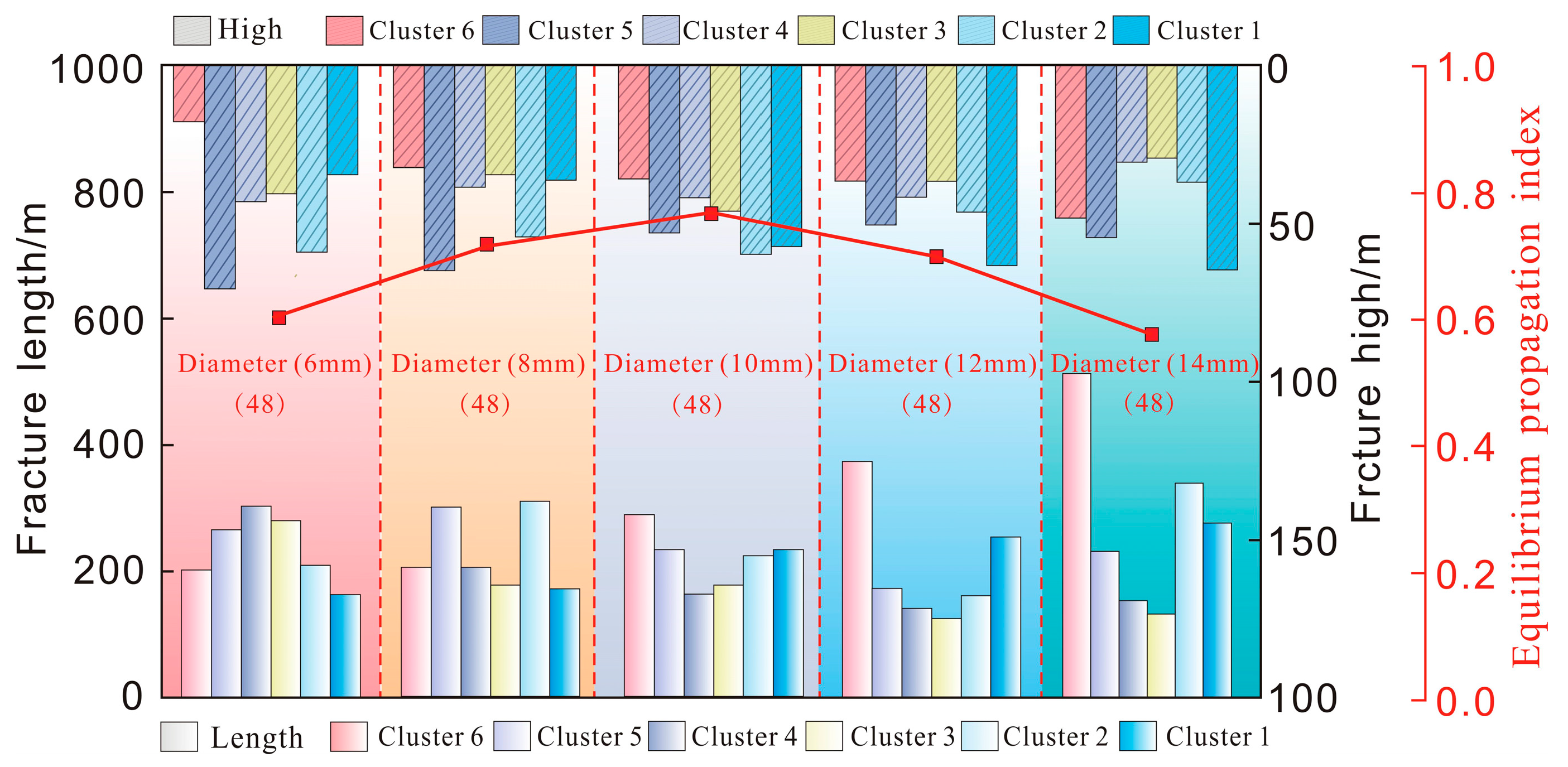
4.1.2. The Influence of the Perforation Parameters on Balanced Fracture Propagation

(1)

The Perforation Quantity

For the spindle-shaped perforations, variations in the perforation quantity significantly affect the fracture length/height development, inter-cluster fluid allocation, and propagation patterns (Figure 14). As the perforation quantity decreases, the middle cluster fractures exhibit gradual increases in their lengths and heights, while heel/toe clusters progressively decrease. The uniformity of fracture propagation initially improves but declines afterward. At perforation quantities of 42 and 80, the fracture propagation uniformity index drops to 0.63 and 0.61, respectively. Under the optimal conditions (48 perforations), the uniformity index peaks at 0.72, achieving the most balanced inter-cluster propagation (Figure 14).

Figure 14 demonstrates that as the number of perforations decreases from 80 to 42, the coefficient for the difference in the inter-cluster fluid allocation initially decreases and then increases, reaching minimal variation (26.3%) at 48 perforations (Figure 15). This contrasts sharply with the patterns for uniform (57.1%) and trapezoidal (83.8%) perforations, confirming the spindle-shaped design’s superiority in terms of the uniformity of the fluid distribution.

(2)

The Perforation Diameter

Reducing the perforation diameter from 14 mm to 6 mm enhances the fracture lengths/heights in the middle clusters while suppressing terminal cluster propagation (Figure 16). At 6 mm, middle clusters dominate, whereas 14 mm favors terminal clusters, yielding poor uniformity indices of 0.61 and 0.57, respectively. The optimal balance occurs at 10 mm, where the uniformity index peaks at 0.77. Similarly, the coefficient for the difference in the inter-cluster fluid allocation is lowest at 24.8% for 10 mm perforations (Figure 17), demonstrating a “first decrease, then increase” trend with a reduction in the diameter.

The perforation quantity and diameter are pivotal for balanced multi-cluster propagation. Adjusting these parameters optimizes the inter-cluster fluid distribution and mitigates the interference if stress. A spindle-shaped perforation design with 48 total perforations with 10 mm diameters achieves the peak uniformity.

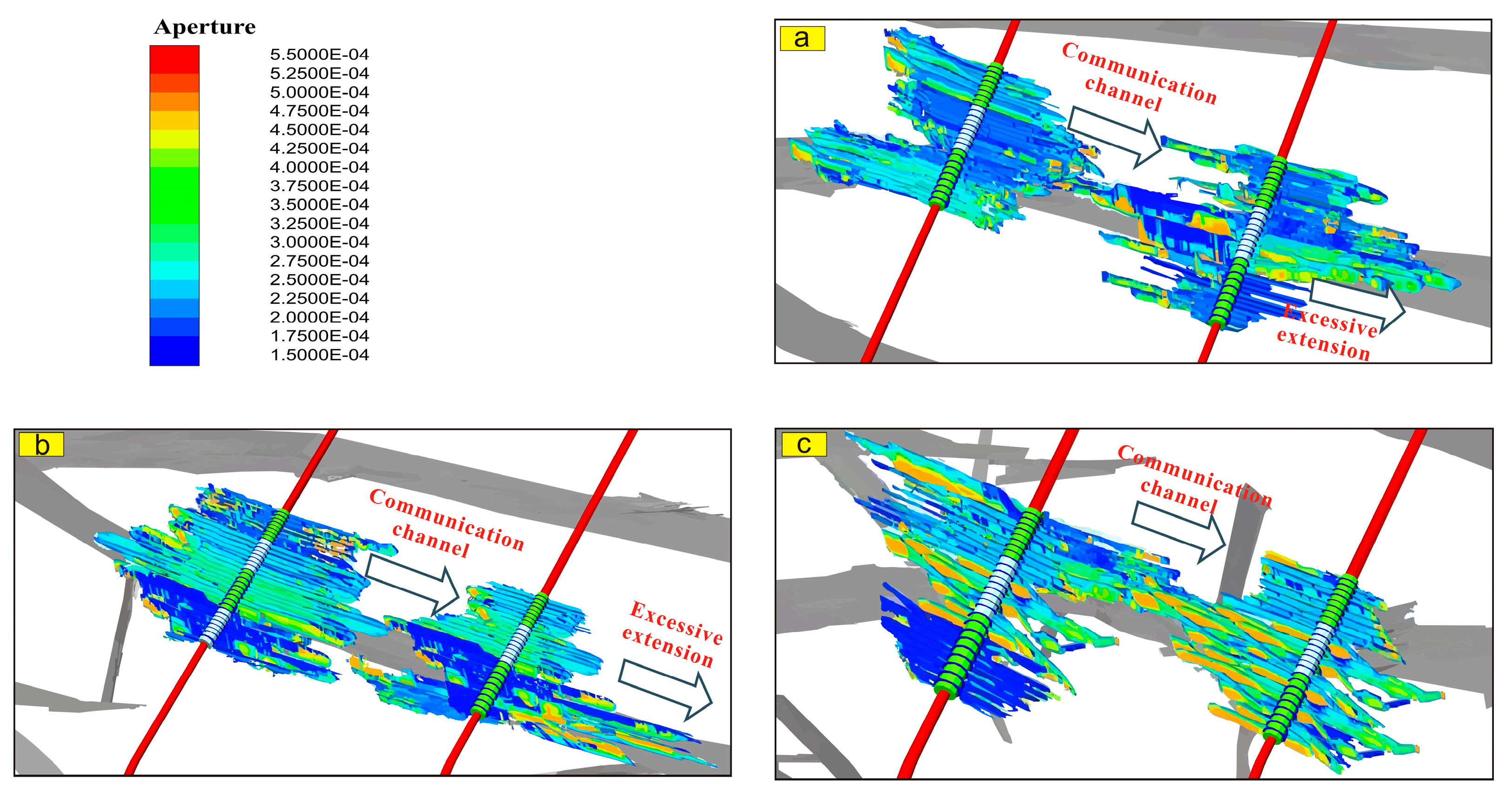
4.2. The Fracturing Interference Under Multi-Cluster Competitive Propagation

During hydraulic fracturing operations on the M507H10 platform, adjacent well monitoring revealed the significant interference of pressure (frac hits) between the H10-M1 and M2 wells, indicating strong inter-well connectivity. Taking wells M507H10-1 and M507H10-2 as examples, the FDI mechanisms were analyzed (Figure 18).

Four major FDI events (pressure surges > 5 MPa) occurred during fracturing of M507H10-1 and M507H10-2, primarily associated with large-scale NF zones. Notably, Stage 3 for M2 exhibited the most severe interference, with a pressure surge in neighboring wells of 14.95 MPa (

Table 4. FDI events and pressure rises between M1 and M2 wells.

Well Number	Fracturing Stage	Pressure Increase/MPa	FDI Types
M507H10-2	1	2.71	Stress-Dominated
	3	14.95	NF–Stress Synergy
	7	6.8	NF-Dominated
	12	6.23	NF-Dominated
	16	5.6	NF-Dominated
	17	2.8	Stress-Dominated

). Surprisingly, significant inter-well connectivity was also observed in fracturing stages where NFs did not develop.

(1)

Natural Fractures

Severe FDI events correlate strongly with large-scale intersecting NF zones. An analysis of the overlay between interference-prone stages and the NF distribution revealed multiple cross-well NF systems bridging M1 and M2. These fractures act as preferential pathways, enabling hydraulic fractures to overextend along natural networks, forming “bridges” for pressure communication (Figure 19).

(2)

The Horizontal Stress Difference

Hydraulic fractures preferentially propagate along low-stress orientations. In zones with NFs, the stress contrast amplifies the risks of FDI by synergistically guiding fractures toward adjacent wells. Notably, in some stages, the fractures overcame stress barriers and extended against stress gradients (low to high stress) via the NFs, forming interference dominated by NFs (Figure 20).

The simulation results also show that even in non-fractured intervals, stress alone drove the growth of asymmetric fractures in low-stress directions, inducing stress-dominated interference (Figure 20).

(3)

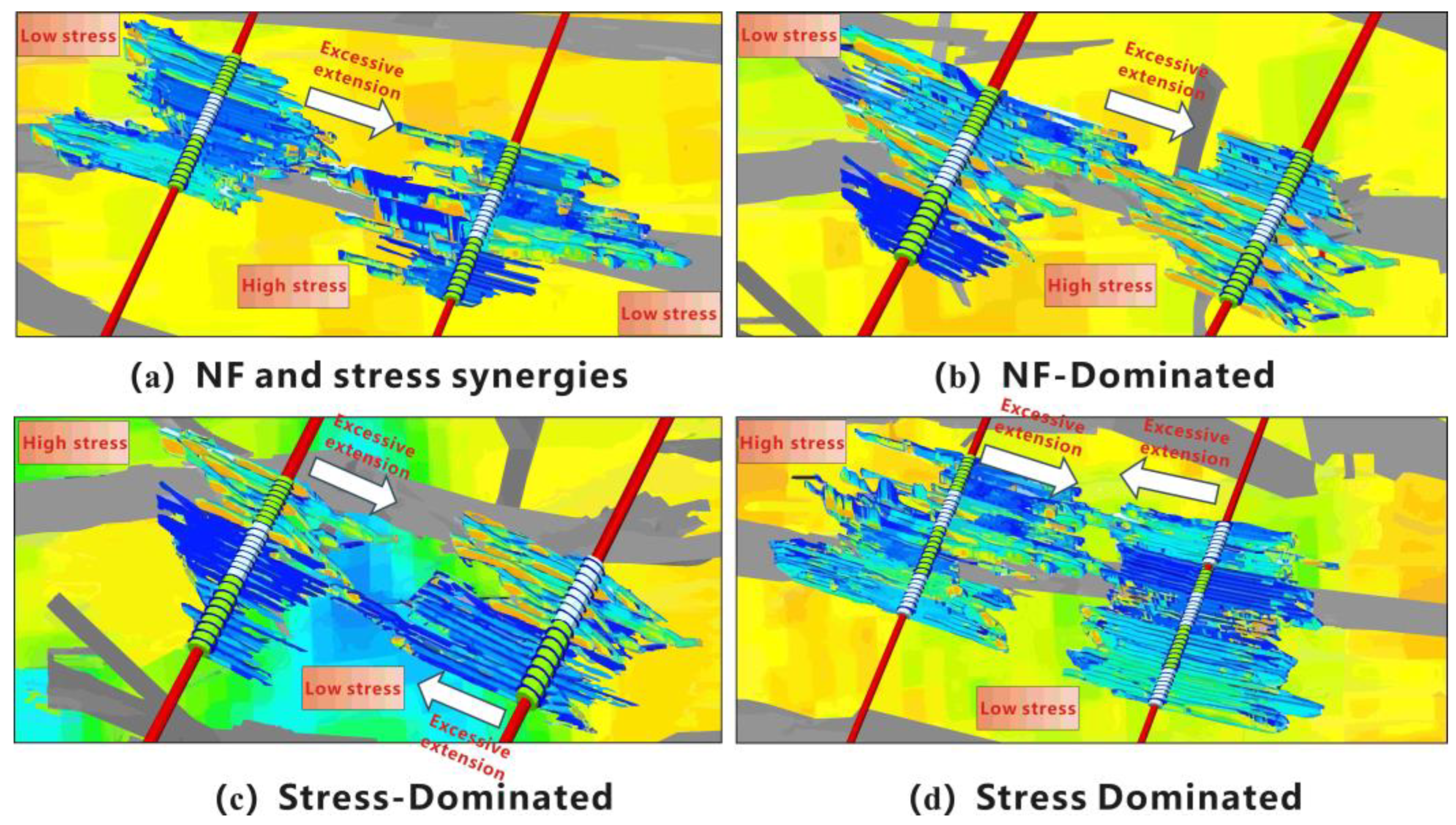
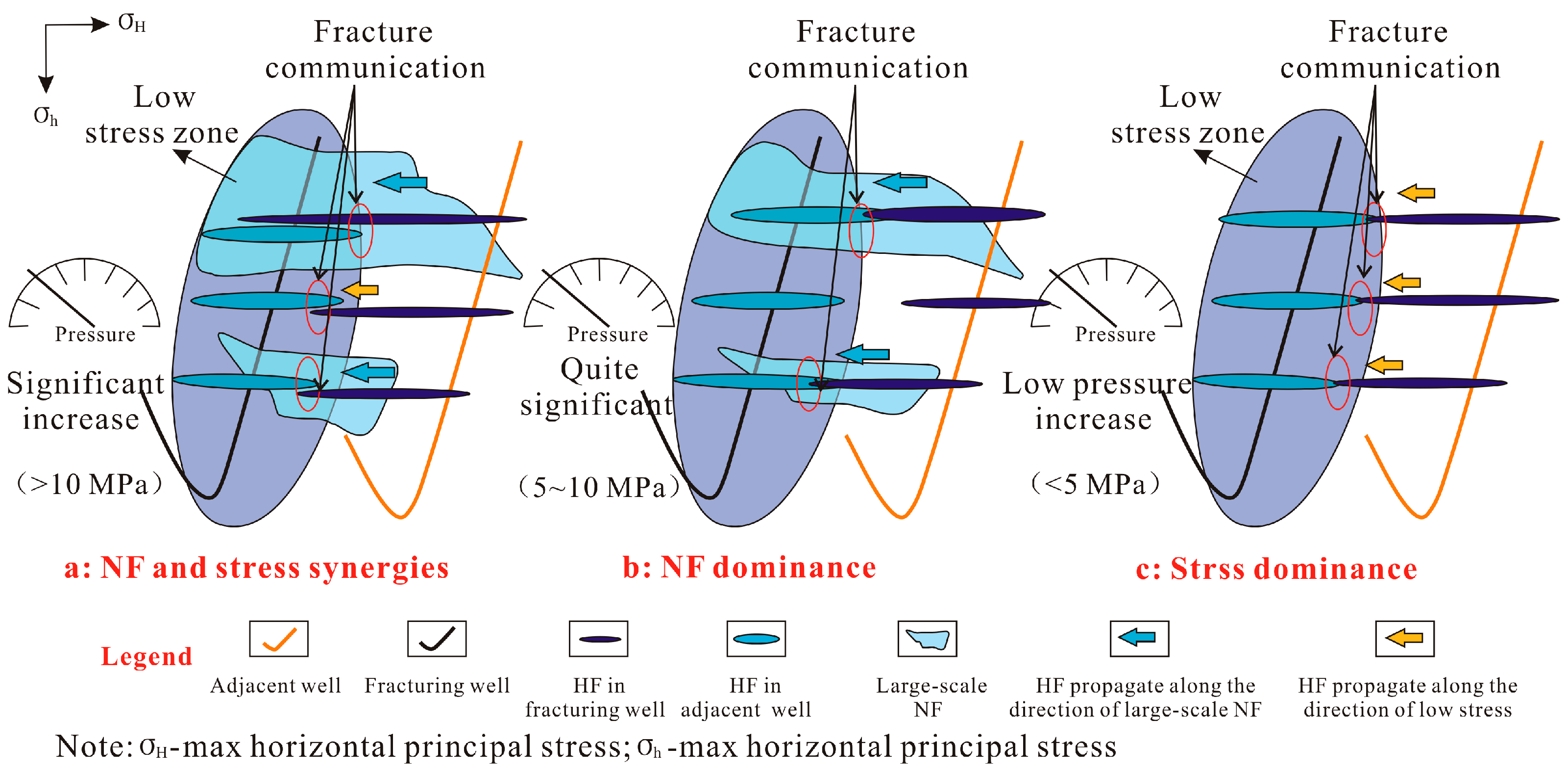
FDI Classification

Through a systematic evaluation of the fracture communication mechanisms, three types of FDI were identified:

Type I: NF–stress synergy. This is prevalent in low-stress regions intersecting with large, unidirectional NFs. Hydraulic fractures extend preferentially along these paths, forming ultra-long fractures that severely impact neighboring wells (Figure 21). According to the statistical results of adjacent well pressure monitoring, the pressure surges typically exceed 10 MPa (Table 4).

Type II: NF-dominated. This occurs where large, unidirectional NFs traverse multiple horizontal wellbores. Fractures follow these natural pathways, causing pressure surges in adjacent wells (Figure 21). According to the statistical results of adjacent well pressure monitoring, these pressure surges are typically 5~10 MPa (Table 4).

Type III: Stress-dominated. This constitutes the matrix-mediated interference driven by the stress differentials. FDI results from the transmission of stress through the matrix (Figure 21). According to the statistical results of adjacent well pressure monitoring, these pressure surges are typically less than 5 MPa (Table 4).

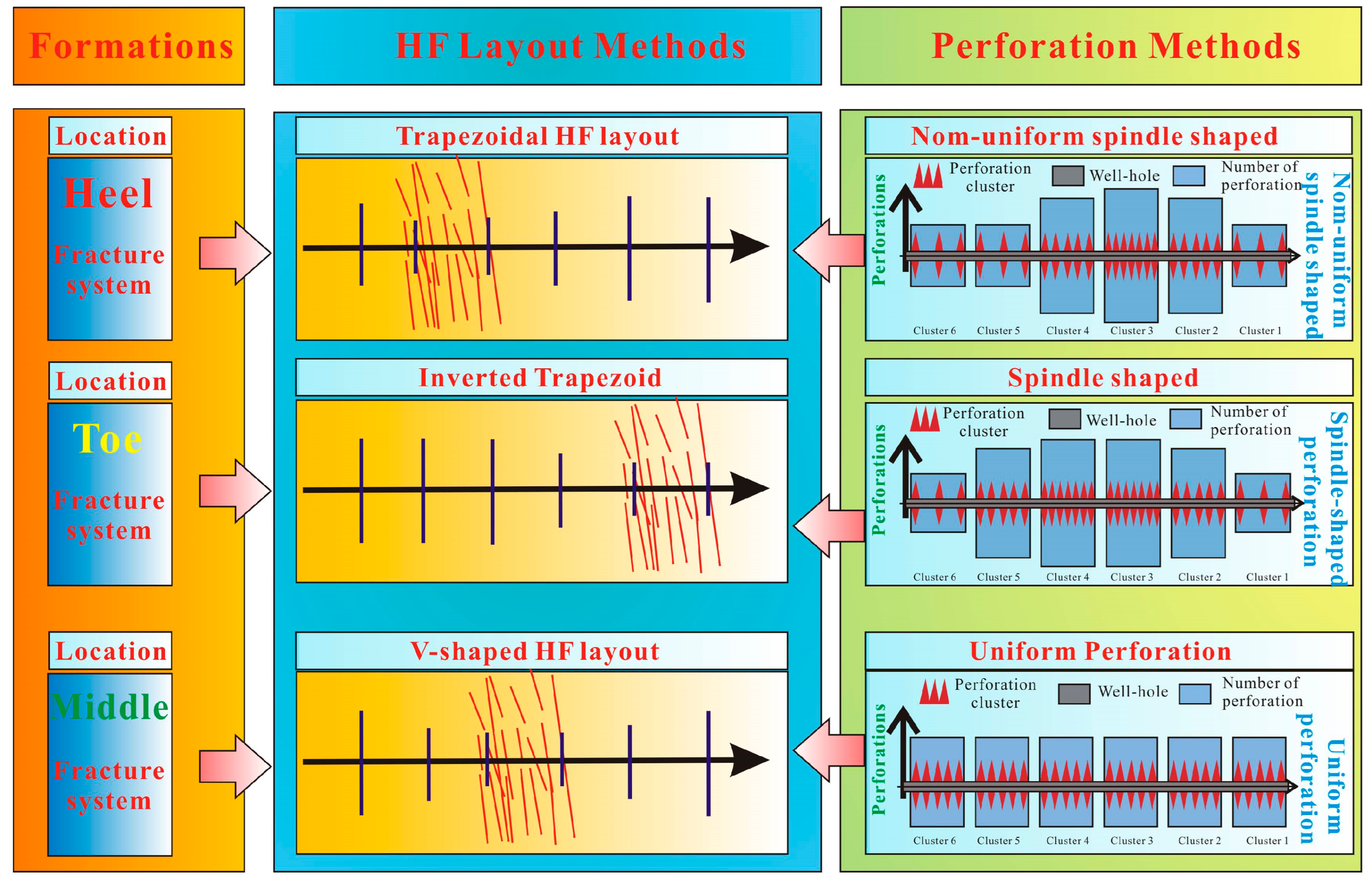
4.3. Mitigationof FDI Based on Multi-Fracture Diversion Regulation

The simulation results indicate that adjusting the perforation configurations and key parameters in horizontal wellbores during hydraulic fracturing can regulate the inflow of fluid into individual fracture clusters, promoting balanced propagation. Accordingly, a FDI mitigation strategy was proposed based on the competitive propagation mechanisms of multi-cluster fractures under a system of non-uniform perforations.

When developed fracture systems exist near the heel, a trapezoidal fracture layout is adopted to prevent the excessive intake of fluid through these systems. This approach implements non-uniform spindle-shaped perforations to restrict the fluid intake near root zones and fracture systems while maintaining an adequate fluid inflow in the middle and the toe (Figure 22).

For fracture systems developed near the toe of the horizontal fracturing stages, an inverted trapezoidal fracture layout was proposed. To achieve this, uniform spindle-shaped perforations were applied to reduce the fluid intake in both the heel and toe fracture systems while ensuring an adequate inflow in the middle (Figure 22). For central fracture system development, a V-shaped fracture layout was introduced. This employed uniform perforations to maintain the fluid intake in the heel and toe systems while preventing excessive inflow in the middle (Figure 22).

The FDI within primary treatment zones (lacking large-scale NFs) predominantly originates from significant stress differentials. To mitigate localized fluid over-inflow and the associated connectivity risks, the fracture network geometry and perforation strategies should align with the protocols established for fracture-developed segments (Figure 22). Notably, spindle-shaped perforations were implemented in homogeneous stress environments to optimize the uniformity of the fracture distribution and enhance the stimulation effectiveness in the primary zones (Figure 23).

Through a systematic analysis of the characteristics of the fracture system in high-risk intervals, three specialized fracture architectures were formulated: trapezoidal, inverted trapezoidal, and V-shaped fracture layouts. Each geometric pattern was synergistically paired with customized perforation designs, thereby establishing a comprehensive optimization framework for the prevention of FDI through multi-cluster fracture competition and fluid diversion control.

4.4. The Prevention of Fracturing Interference Through Diversion Regulation

The surveillance of microseismic events and pressure during Stage 3 and Stage 12 fracturing of well M507H10-2 identified NF10 and NF12 activation, respectively, inducing critical inter-well communication (M1 and M2). Numerical simulations further confirmed the hydraulic connectivity between (1) M2-Stage 3 and M1-Stage 5 via the NF10 system and (2) M2-Stage 12 and M1-Stage 13 via the NF12 system.

Example 1: M1 well Stage 5 and M2 well Stage 3 (NF10)

NF10 predominantly intersects with the toe–mid section (M1 well Stage 5), exhibiting excessive mid-zone propagation. The implementation of uniform perforations effectively restricted the flow to the central fracture clusters. Post-optimization pressure data confirmed controlled fracture growth in the mid–toe region under flow-diversion-controlled fracturing (Figure 24). The NF10 concentration near the heel region drove root-zone (M2 well Stage 3) overextension. A spindle-shaped perforation design optimized the cluster flow distribution, achieving a 68% reduction in heel-dominated fracture growth while maintaining effective mid-zone propagation (Figure 24).

The simulation results demonstrated that the optimized flow diversion technology effectively regulated the allocation of fluid among fracture clusters, preventing the excessive invasion of fluid into NFs in high-risk zones while suppressing their activation and over-propagation (Figure 24). Comparative pressure monitoring showed a reduction in the surge in inter-well pressure from 14.95 MPa to 0.7 MPa, conclusively mitigating the NF10-mediated connectivity between the M1 and M2 wells (Figure 24).

Example 2: M1 well Stage 13 and M2 well Stage 12 (NF12)

The natural fracture NF12, predominantly located in the toe section of well M1 Stage 13, exhibited excessive toe-zone propagation. A non-uniform spindle-shaped perforation design was implemented to restrict the fluid inflow into the toe clusters. Post-optimization diagnostics confirmed effective control of the toe-dominated fracture growth under the flow-diversion protocols (Figure 25). In well M2 Stage 12, NF12 concentrated near the heel region drove root-zone overextension. A spindle-shaped perforation reduced the fluid intake by the heel cluster, with the post-treatment results demonstrating stabilized fracture propagation in the heel section (Figure 25).

Tailored perforation strategies, designed based on the spatial characteristics of the fracture system, enabled precise control over the fluid distribution across clusters. The optimized flow diversion process effectively regulated the inter-cluster fluid allocation, preventing the excessive invasion of fluid into NFs in high-risk zones while suppressing NF12’s reactivation and over-propagation (Figure 25). Furthermore, offset well pressure monitoring recorded complete elimination of the pressure transmission (reduced from 6.23 MPa to 0 MPa), successfully mitigating the NF12-mediated inter-well FDI between wells M1 and M2.

5. Conclusions

To address the FDI caused by an imbalanced multi-cluster fracture propagation in horizontal wells, a theoretical model for the competitive multi-cluster fracture propagation under non-uniform perforation conditions was established. Leveraging enhanced coupled fluid flow–stress–fracture simulations, a 3D finite element model was developed, and a non-uniform perforation-based design methodology for mitigating FDI was proposed.

(1)

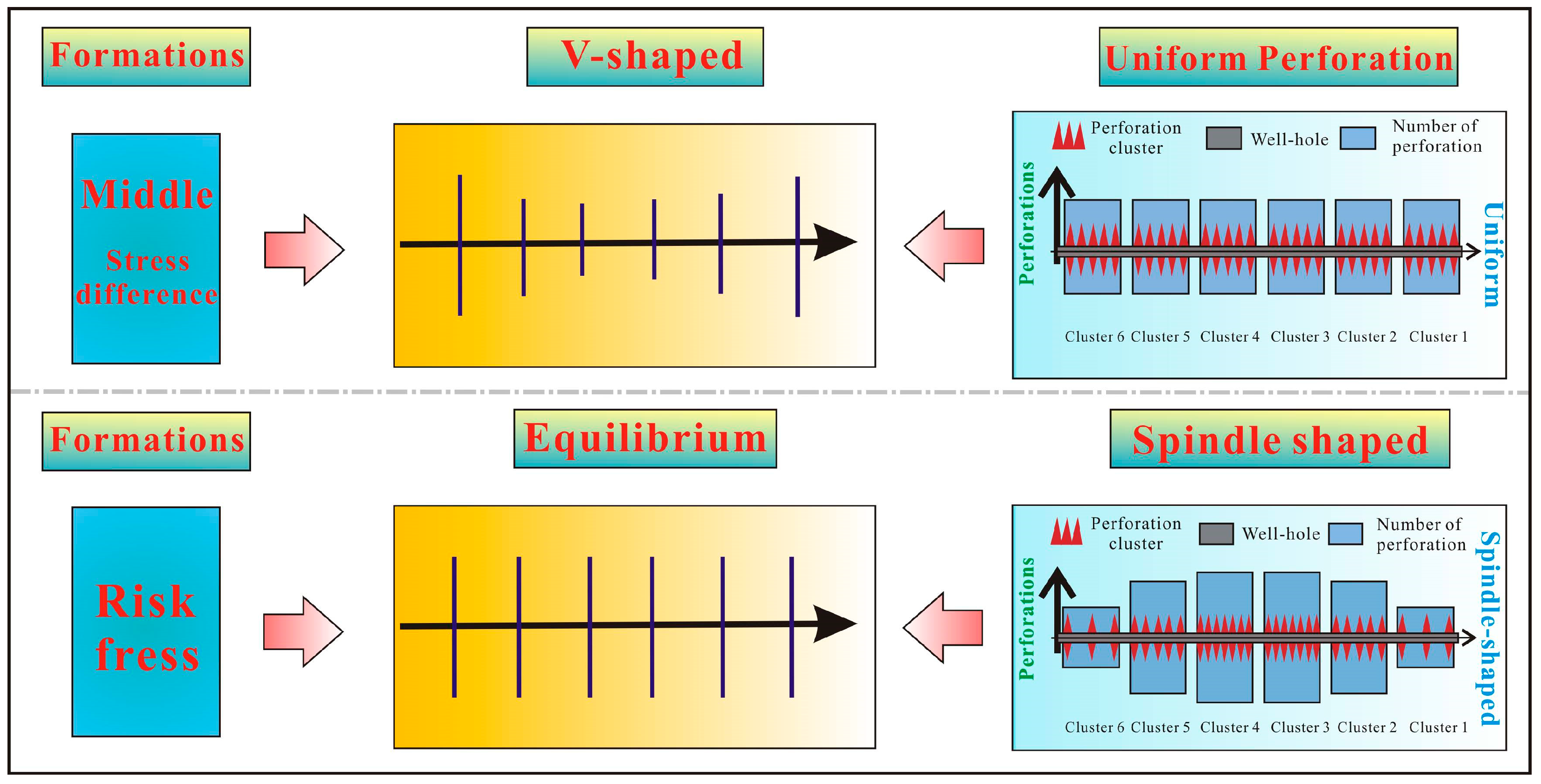
Spindle-shaped perforations, characterized by a higher density in the middle clusters and a lower density at the terminals, reduce the stress induced in the mid-clusters compared to that under uniform/stepped patterns. This design improves the allocation of fluid to the mid-cluster, enhancing the uniformity of fracture propagation by 20.3% and 35.1% versus that under uniform and trapezoidal perforations, respectively.

(2)

A novel numerical simulation framework was established based on the fracture damage mechanics to model simultaneous multi-cluster propagation in horizontal well fracturing of shale gas. The advanced model precisely captured the dynamic coupling between the fluid injection, three-dimensional stress evolution, and fracture network development, while providing a quantitative analysis of complex fracture propagation patterns under various interference scenarios. Through a systematic evaluation of the fracture communication mechanisms and intensity of interference, three distinct inter-well types of FDI were identified: Type I: natural fracture–stress anisotropy synergy; Type II: natural-fracture-dominated; and Type III: stress-anisotropy-dominated.

(3)

Based on the mechanisms of fracturing interference in the study area, three fracture placement patterns were developed: trapezoidal, inverted trapezoidal, and V-shaped layouts. Corresponding perforation schemes were designed for each pattern, establishing an integrated optimization methodology for control over inter-well interference through multi-cluster competition and flow diversion regulation. The optimized flow diversion technique effectively balanced the fluid distribution among the clusters, suppressing preferential fracture growth. Field monitoring demonstrated s significant reduction in the interference of pressure from 14.95/6.23 MPa to 0.7/0 MPa in the offset wells, successfully preventing the dominant fracture pathways and inter-well communication.