Economic Dispatch Strategy for Power Grids Considering Waste Heat Utilization in High-Energy-Consuming Enterprises

Abstract

Under the construction background of carbon peak and carbon neutrality, high-energy-consuming enterprises, represented by the electrolytic aluminum industry, have become important carriers for energy conservation and emission reduction. These enterprises are characterized by significant energy consumption and high carbon emissions, greatly impacting the economic and environmental benefits of regional power grids. Existing research often focuses on grid revenue, leaving high-energy-consuming enterprises in a passive regulatory position. To address this, this paper constructs an economic dispatch strategy for power grids that considers waste heat utilization in high-energy-consuming enterprises. A typical representative, electrolytic aluminum load and its waste heat utilization model, for the entire production process of high-energy-consuming loads, is established. Using a tiered carbon trading calculation formula, a low-carbon production scheme for high-energy-consuming enterprises is developed. On the grid side, considering local load levels, the uncertainty of wind power output, and the energy demands of aluminum production, a robust day-ahead economic dispatch model is established. Case analysis based on the modified IEEE-30 node system demonstrates that the proposed method balances economic efficiency and low-carbon performance while reducing the conservatism of traditional optimization approaches.

1. Introduction

Climate change is a global challenge facing humanity. With the development of industrialization, greenhouse gas emissions have surged, posing a threat to ecosystems. Moreover, as a major manufacturing country, China’s industrial production capacity continues to grow, yet its oil and gas resources are relatively scarce. Advocating for low-carbon production and developing a low-carbon economy holds significant security implications for achieving the dual-carbon goals [1]. The high-energy-consuming industry is a key sector for carbon neutrality in industrial production [2]. According to relevant statistics, taking the electrolytic aluminum industry as an example, China’s aluminum output in 2020 was 37.124 million tons, with a total electricity consumption of approximately 501.174 billion kWh, accounting for about 6.67% of the nation’s total electricity consumption. Meanwhile, the total CO₂ emissions reached about 426 million tons, representing roughly 5% of the country’s net CO₂ emissions. Formulating a low-carbon production plan suitable for aluminum enterprises is of great significance for enhancing their core competitiveness and sustainable development.

High-energy-consuming enterprises are characterized by their sensitivity to electricity prices and high production flexibility, creating conditions for coordinated dispatch between the source and load sides. Runze Chen and Hongyang Jin et al. conducted a detailed analysis of the operational and power consumption characteristics of high-energy-consuming loads in [3,4], establishing refined mathematical models for smelting and electrolytic loads, and thoroughly discussing various collaboration methods for their participation in economic dispatch. A robust unit commitment algorithm is proposed in [5], considering the dual uncertainties of high-energy-consuming load power and renewable energy output, analyzing the impact of load power fluctuations on system revenue. To enhance the system’s ability to absorb renewable energy, such as hydropower and photovoltaics, Yu Qian et al. [6] designed a collaborative framework where high-energy-consuming loads work with cascaded hydropower to mitigate fluctuations in wind and solar power output, significantly increasing the renewable integration capacity. Pi Xia and Zhao Yuyang et al. [7] considered the impact of wind power forecasting errors on the revenue of high-energy-consuming enterprises and proposed a predictive revenue model based on predictive control theory. These studies primarily focus on grid-enterprise collaborative dispatch and uncertainty modeling of renewable energy but overlook the carbon emission constraints of high-energy-consuming enterprises, prioritizing economic benefits at the expense of environmental considerations.

Some experts and scholars have also conducted research on low-carbon production and dispatch in power systems. Tian Biyuan and Chang Xiqiang et al. [8] achieved low-carbon economic dispatch in distribution networks through demand response and shared energy storage usage rights. Cui Yang and Deng Guibo et al. [9] designed a low-carbon economic dispatch strategy for a concentrated solar power-wind hybrid system, considering carbon trading mechanisms and analyzing technical and policy aspects to reduce overall operational costs. Chen Jinpeng and Kang Lihong et al. [10,11] accounted for the actual carbon emissions of loads, refined carbon emission models, and introduced carbon trading mechanisms to further constrain emissions in integrated energy systems, balancing economic and low-carbon objectives through flexible scheduling of heating and cooling loads. However, these low-carbon dispatch studies primarily target renewable energy and integrated energy systems, excluding high-energy-consuming enterprises. In fact, as early as 2019, the China Nonferrous Metals Industry Association issued the “Technical Guidelines for Carbon Emission Trading in Electrolytic Aluminum Enterprises” [12], detailing the carbon trading management system and technical specifications for such enterprises, with pilot programs implemented in multiple provinces. Some AI technologies have also been introduced into the field of power system scheduling to enhance decision-making efficiency and accuracy. Fan Shixiong et al. [13] proposed a framework and key technologies for a human–machine hybrid augmented intelligence system for large-scale power grid dispatching and control. This study offers new ideas and methods for the dispatching and control of large-scale power grids. Z. Liu et al. [14] presented a brain-inspired collaborative power dynamic dispatch method for digital twin smart generation systems. By drawing on the brain’s collaborative mechanisms, this method provides an innovative solution for power dynamic dispatch in digital twin environments. J. Chen et al. [15] achieved stochastic dynamic power dispatch with human knowledge transfer using inverse reinforcement learning assisted by Graph-GAN. M. Li and J. Mohammadi [16] conducted research on optimization learning for joint chance-constrained power dispatch problems, offering an effective approach to handling uncertainty factors in power dispatching. D. Ma et al. [17] proposed an implicit dual gradient tracking algorithm under a randomly triggered transmission protocol for distributed economic dispatch with dynamic power demands. Y. Zhang et al. [18] introduced a PI + R control scheme based on a multi-agent system for economic dispatch in isolated battery energy storage systems. This scheme leverages the advantages of multi-agent systems and combines them with the PI + R control strategy to achieve effective economic dispatch in isolated battery energy storage systems. Additionally, the abundant waste heat resources in electrolytic aluminum enterprises have rarely been addressed in previous dispatch and production studies. The aluminum production process involves stages such as petroleum coke calcination and anode baking, generating large amounts of high-temperature flue gas. Preliminary estimates suggest that adopting waste heat recovery technology can reduce energy consumption by 200–300 kWh per ton of aluminum, equivalent to saving 1.5–2 million tons of standard coal [19]. Today, Organic Rankine Cycle (ORC) technology, based on different working fluids, has advanced significantly, enabling the recovery of low-grade waste heat from electrolytic cells [20,21]. Many domestic aluminum enterprises have already implemented waste heat recovery systems. For instance, since its launch in 2019, Yunnan Aluminum’s flue gas waste heat utilization system has cumulatively reduced greenhouse gas emissions by 7566 tons and achieved energy-saving benefits worth 6.9137 million yuan. This demonstrates that integrating aluminum production waste heat into power system dispatch and internal production processes, while consolidating waste heat resources of varying grades, can significantly improve resource utilization efficiency and enhance both economic and environmental benefits.

To address the aforementioned issues and gaps in existing research, this paper designs a collaborative day-ahead low-carbon economic dispatch strategy for electrolytic aluminum enterprises and power grids. The scheduling method proposed in this paper differs significantly from traditional power grid scheduling strategies, primarily in the following aspects: Firstly, traditional scheduling methods typically make decisions with the power grid as the main entity, treating high-energy-consuming enterprises as passive recipients of scheduling. They overlook the substantial waste heat resources generated by these enterprises during production, resulting in energy waste and low resource utilization efficiency. Secondly, traditional methods solely pursue economic benefits on the grid side and fail to fully consider the carbon emission issues of high-energy-consuming industries, leading to poor environmental performance of the overall system. Thirdly, traditional optimization methods often adopt relatively conservative scheduling strategies, which are difficult to adapt to the uncertainty of renewable energy output, such as wind power, and fail to effectively coordinate the relationship between industrial production and clean energy consumption. The organizational framework of this paper is as follows: First, Section 2 conducts an analysis of waste heat sources, pointing out the sources of waste heat in the three stages of petroleum coke calcination, green anode baking, and electrolytic aluminum production during the electrolytic aluminum manufacturing process, and establishes corresponding mathematical models. In Section 3.1, an optimal production model for the electrolytic aluminum enterprise side is established, taking into account electrolyzer production constraints, captive power plant unit constraints, and a carbon emissions model. Finally, in Section 3.2, a robust economic dispatch model for the power grid is presented, and its effectiveness and feasibility are verified through a case study in Section 4. Lastly, Section 5 summarizes the entire paper.

The main innovative points of this paper are summarized as follows:

(1) This paper constructs a model that considers waste heat utilization in high-energy-consuming enterprises, represented by the electrolytic aluminum industry, and formulates a low-carbon production scheme using a tiered carbon trading calculation formula, thereby changing the passive regulatory status of high-energy-consuming enterprises in research.

(2) By comprehensively considering factors such as local load levels, uncertainty in wind power output, and energy demands for aluminum production, this paper establishes a robust day-ahead economic dispatch model for the power grid side, balancing economic efficiency and low-carbon performance while reducing the conservatism of traditional optimization methods.

2. Modeling and Utilization Methods of Waste Heat in High Energy-Consuming Loads

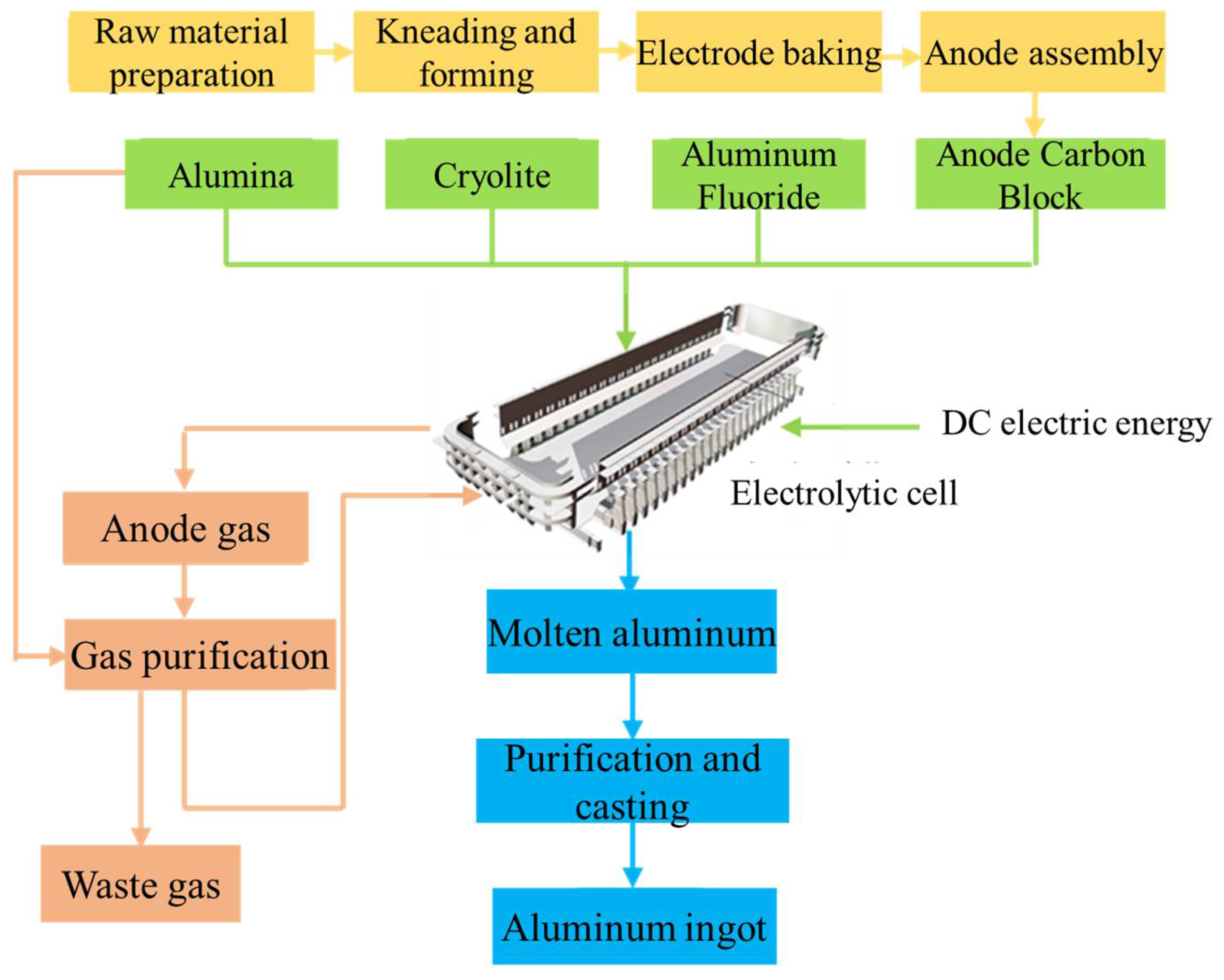
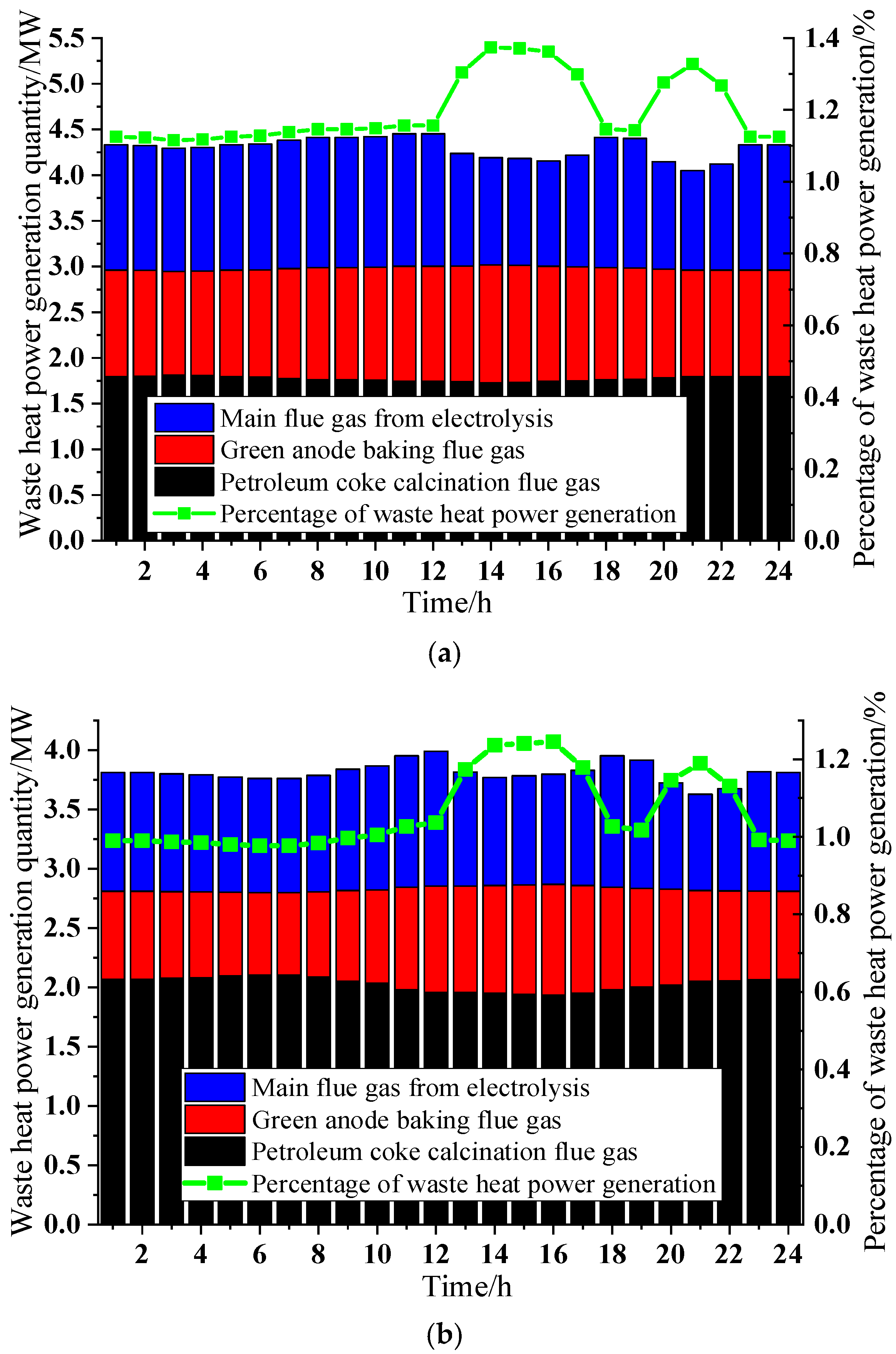
Due to technological advancements in recent years, aluminum production enterprises primarily use prebaked anode cells for electrolytic aluminum production. Figure 1 illustrates the electrolytic aluminum production process, showing that prebaked anode electrolytic aluminum production requires significant amounts of prebaked anodes. Therefore, electrolytic aluminum plants typically perform processes such as calcination, baking, and assembly to produce sufficient prebaked anodes. Since some production stages generate waste heat with low calorific value, making it unsuitable for utilization, this paper focuses on analyzing, modeling, and utilizing the waste heat generated during the calcination of petroleum coke, green anode baking, and the electrolytic aluminum production process.

Equation (1) presents the calculation formula for the utilizable energy of flue gas waste heat. Here, P_t represents the utilizable energy of flue gas waste heat, c_p denotes the average specific heat capacity of the flue gas, m is the flue gas flow rate, T₀ and T represent the thermodynamic temperatures of the flue gas and the environment, respectively, and η_t signifies the efficiency during flue gas collection and transmission.

$$P_t=c_{p}m(T-T_0)\left[1-{\displaystyle \frac{T_0}{T-T_0}}\ln {\displaystyle \frac{T}{T_0}}\right]{\eta }_t$$

(1)

Petroleum coke calcination is the first step in producing anode carbon. During calcination, the generated flue gas has a high temperature, typically above 900 °C, making it a high-quality heat source with significant thermal value. In addition to power generation, this flue gas is often used to meet the plant’s thermal energy demands. Equations (2)–(8) describe the mathematical model for waste heat utilization in petroleum coke calcination. Here, P_y1,t represents the utilizable energy from high-temperature flue gas generated during calcination at time t, the specific value of which can be calculated using Equation (1). P_e1,t and P_h1,t represent the electrical and thermal energy produced from flue gas utilization at time t, respectively, while η_e1 and η_h1 represent the power generation efficiency and heat production efficiency, respectively. η_loss represents the energy loss efficiency, and P_hL,t represents the thermal load power at time t. C_s,min and C_s,max represent the lower and upper limits of the thermal storage capacity, respectively. In Equation (8), P_c,max and P_f,max represent the maximum charging and discharging power of the thermal storage system, respectively. $C_{s,t}$ and $C_{s,t-1}$ represents the thermal storage capacity at time t and t − 1, respectively. $C_{s,t0}$ represents the initial thermal storage capacity before production begins.

$$P_{e1,t}=P_{y1,t}{\eta }_{e1}$$

(2)

$$P_{h1,t}=P_{y1,t}{\eta }_{h1}$$

(3)

$${\eta }_{h1}=1-{\eta }_{e1}-{\eta }_{loss}$$

(4)

$$P_{h1,t}\ge P_{hL,t}$$

(5)

$$C_{s,\min }\le C_{s,t}\le C_{s,\max }$$

(6)

$$C_{s,t}=C_{s,t0}+{\displaystyle \sum _{i=1}^t(P_{c,t}-P_{f,t})}$$

(7)

$$-P_{f,\max }\le C_{s,t}-C_{s,t-1}\le P_{c,\max }$$

(8)

The final stage in anode production is the baking of green anodes. When air flows into the packing material layer with sufficient oxygen content, the baking furnace achieves complete combustion, generating flue gas typically at temperatures between 150 and 250 °C. Although this temperature is significantly lower than that of the calcination process, the large flue gas flow rate—often exceeding 100,000 Nm³/h—still presents substantial potential for energy recovery. Due to the relatively low flue gas temperature, Organic Rankine Cycle (ORC) technology is widely adopted for waste heat power generation both domestically and internationally. For simplicity in calculations, the cooling water flow rate, heat exchange area, and working fluid efficiency of the ORC system are collectively converted into a single ORC power generation efficiency value, η_ORC. The waste heat utilization model for green anode baking can thus be expressed by Equations (9)–(11). Here, P_e2,t and P_e2,t−1 represent the electricity generated from the baking flue gas via ORC technology at time t and t − 1, while P_y2,t denotes the recovered energy from the flue gas, which can be calculated using Equation (1). $P_{ORC,\max }$ and $P_{ORC,\min }$ represent the upper and lower limits of the electricity generated from ORC technology. $\mathrm{\Delta }{P}_{ORC,\max }$ and $\mathrm{\Delta }{P}_{ORC,\min }$ represent the upper and lower limits of adjustment inertia given by ORC technology. Equations (10) and (11) define the upper and lower limits for power generation capacity and the ramp rate constraints, respectively.

$$P_{e2,t}={\eta }_{orc}{P}_{y2,t}$$

(9)

$$P_{ORC,\min }\le P_{e2,t}\le P_{ORC,\max }$$

(10)

$$\mathrm{\Delta }{P}_{ORC,\min }\le P_{e2,t}-P_{e2,t-1}\le \mathrm{\Delta }{P}_{ORC,\max }$$

(11)

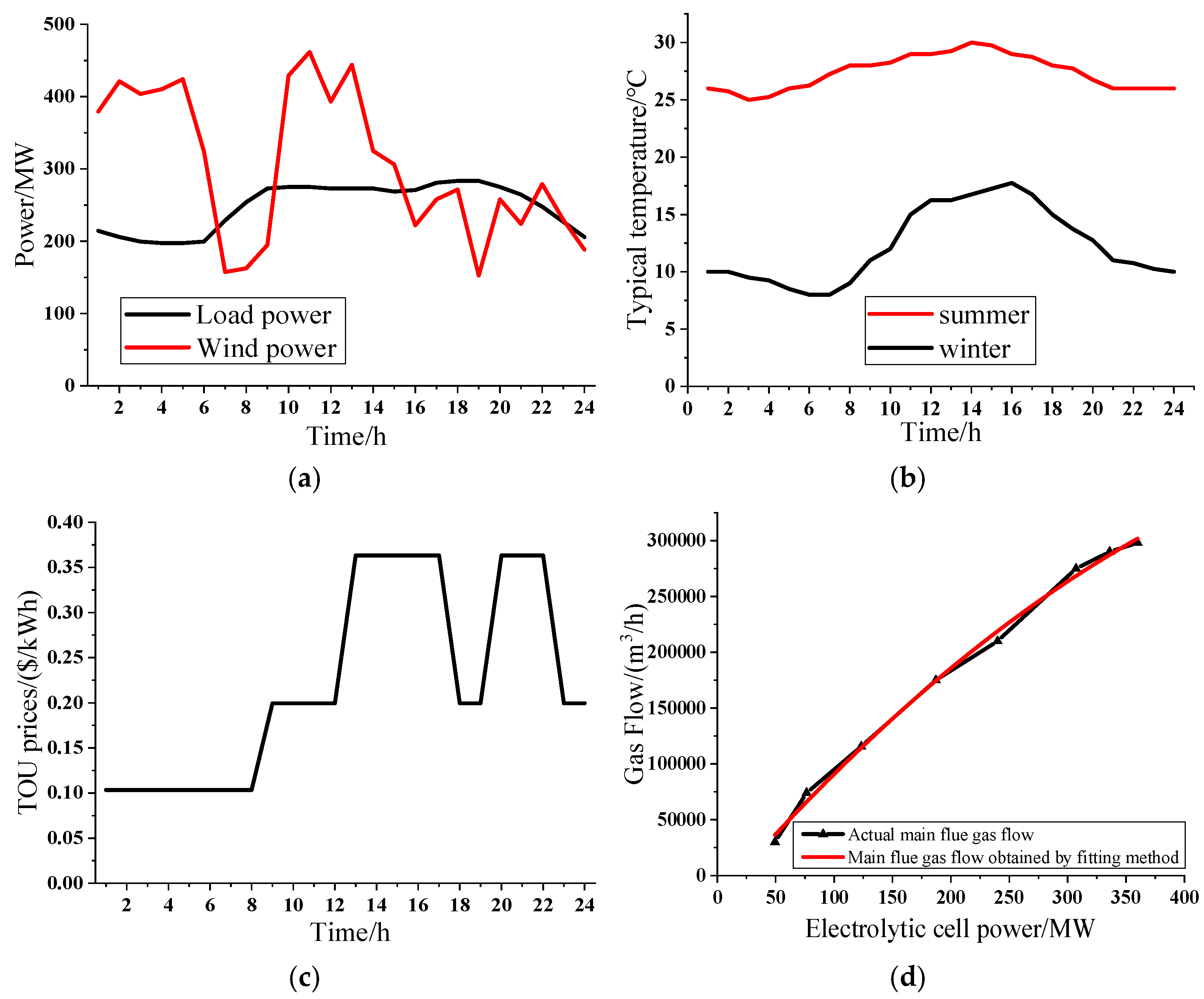
Finally, the aluminum electrolysis process also generates a significant amount of low-temperature flue gas, which is discharged through the main flue. The temperature of this flue gas typically ranges between 100 and 200 °C, making ORC technology suitable for its recovery. However, unlike the relatively stable flue gas flow rates in the lime coke calcination and green anode baking processes, the main flue gas flow fluctuates depending on the operating conditions of the electrolytic cells. In this study, the relationship between the main flue gas flow rate and the electrolytic cell power is derived using the least squares fitting method, with the detailed calculation formula provided in Equation (12). Here, m_al represents the main flue gas flow rate of the electrolytic cells, P_al,t represents the electrolytic cell power, and a, b, and c are the least squares fitting coefficients. The waste heat power generation P_e3,t from this source can be calculated using Equation (1) in conjunction with Equations (9)–(11).

$$m_{al}=a{(P_{al,t})}^2+b{P}_{al,t}+c$$

(12)

3. An Economic Dispatch Model for Power Grids Considering Waste Heat Utilization in Energy-Intensive Enterprises

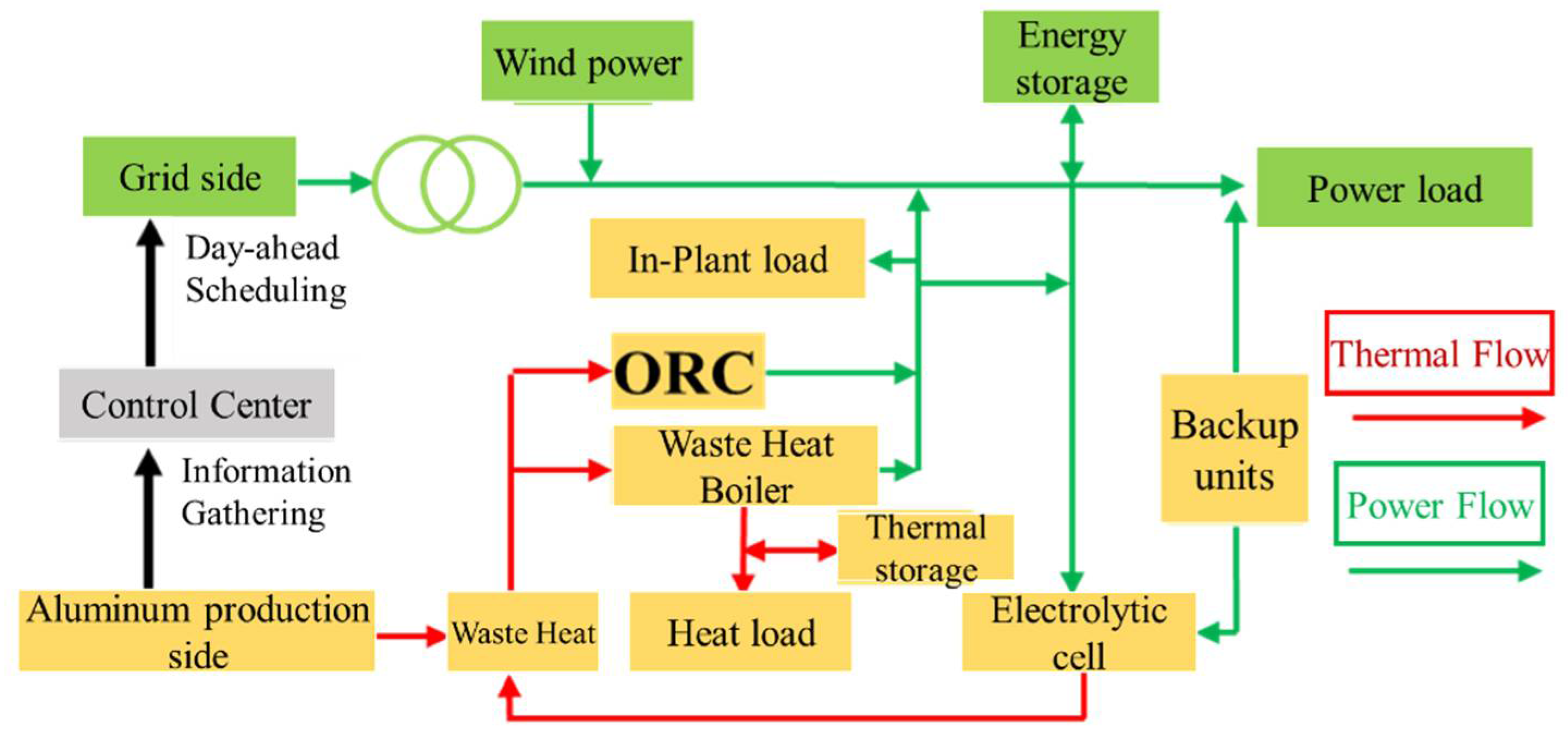
Figure 2 illustrates the schematic diagram of power grid economic dispatch considering waste heat utilization in energy-intensive enterprises. The aluminum production enterprise formulates its optimal production plan by comprehensively considering electrolytic cell energy consumption, standby unit output, and waste heat utilization, while simultaneously feeding back the required electricity purchase quantity to the control center. The control center then develops a robust day-ahead dispatch strategy by accounting for the aluminum enterprise’s power demand, renewable energy output, and load uncertainties. In terms of model characteristics, the aluminum electrolysis-grid-coordinated dispatch constitutes a two-stage optimization problem. The first-stage model, targeting the aluminum production enterprise, presents a mixed-integer nonlinear programming problem; the second-stage model, designed for the power grid, represents a robust mixed-integer linear programming problem considering uncertainties. The transmission variable between these two stages is precisely the electricity purchase quantity from the aluminum enterprise to the power grid.

3.1. Mathematical Model for Production on the Energy-Intensive Enterprise Side

The electrolytic cells accomplish production tasks through direct current. In actual production, these cells are formed by connecting multiple small-capacity electrolytic cells in series. Due to the highly time-consuming assembly process, power control of the electrolytic cells is typically achieved by adjusting the voltage across the terminals. The mathematical model for aluminum production via electrolysis can be expressed as follows:

(1) Electrolytic cell production constraints…

$$P_{al,\min }\le P_{al,t}\le P_{al,\max }$$

(13)

$$\mathrm{\Delta }{P}_{al,\min }\le P_{al,t}-P_{al,t-1}\le \mathrm{\Delta }{P}_{al,\max }$$

(14)

$$P_{al,t}-P_{al,t+x}=0,x\in \left[t,t+\mathrm{\Delta }t\right]$$

(15)

$${\displaystyle \sum _{t=1}^T(a_{al}{P}_{al,\min }+a_{al-ext}(P_{al,t}-P_{al,\min }))}\ge Y^{order}$$

(16)

Equations (13) and (14) represent the upper and lower power limits and ramp rate constraints of the electrolytic cells respectively; considering that frequent power adjustments may affect the electrolysis state of raw materials and the quality of the final product, Equation (15) is used to limit the power adjustment frequency of the electrolytic cells, with the adjustment time interval Δt set to 1 h in this study; the primary objectives of the aluminum electrolysis enterprise are to complete production tasks and achieve profitability, where Equation (16) represents the production output constraint, with a_al denoting the unit electricity production coefficient when the electrolytic cell operates at the minimum active power P_al,min, a_al-ext representing the corresponding unit electricity production coefficient when the active power ranges between P_al,min and P_al,max, and Y^order indicating the daily production requirement of the aluminum manufacturing enterprise. $\mathrm{\Delta }{P}_{al,\max }$ and $\mathrm{\Delta }{P}_{al,\min }$ represent the upper and lower regulation inertia limit of the electrolytic cells.

(2) Constraints related to self-generation power plant units

$$P_{ru,\min }{x}_t^G+r_t^{G,d}\le P_{ru,t}\le P_{ru,\max }{x}_t^G-r_t^{G,u}$$

(17)

$$\mathrm{\Delta }{P}_{ru,\min }{x}_t^G\le P_{ru,t}-P_{ru,t-1}\le \mathrm{\Delta }{P}_{ru,\max }{x}_t^G$$

(18)

$$-v_t^G\le x_t^G-x_{t-1}^G\le u_t^G$$

(19)

$$x_t^G-x_{t-1}^G⩽x_{\tau }^{\mathrm{G}}, \forall \tau \in \left[t+1,\min \left\{t+T^{G,on}-1,T\right\}\right]$$

(20)

$$x_{t-1}^G-x_t^G⩽1-x_{\tau }^G,\forall \tau \in \left[t+1,\min \left\{t+T^{G,off}-1,T\right\}\right]$$

(21)

Equation (17) represent the output constraints of self-generation power plant units considering reserve capacity; Equation (18) specify the ramp rate constraints of the units; Equation (19) define the value constraints for the operational status and start-up/shut-down states of self-generation power plant units; Equations (20) and (21) impose the minimum operating time and shut-down time constraints for the units, where P_ru,t denotes the output of self-generation units at time t, x_t^G represents the unit status variable at time t, and u_t^G and v_t^G indicate the unit start-up and shut-down variables at time t, respectively.

(3) Other constraints

$${\displaystyle \sum _{i=1}^3{P}_{ei,t}}+P_{buy,t}+P_{ru,t}=P_{al,t}+P_{in-L,t}$$

(22)

Equation (22) represents the power balance constraint within the aluminum electrolysis enterprise, where the left side of the equation consists of the total waste heat power generation, electricity purchased from the grid $P_{buy,t}$, and self-generated power output $P_{ru,t}$ at time t, while the right side represents the power consumption of the electrolytic cells $P_{al,t}$ and other internal loads within the enterprise $P_{in-L,t}$.

(4) Carbon emission modeling

The aluminum electrolysis industry is a key sector for carbon emissions. Calculating CO₂ emissions during aluminum production primarily depends on two factors: emissions converted from electricity consumption and emissions generated during raw material processing and product formation. The detailed calculation method is shown in Equation (23), where T_emi represents the total CO₂ emissions in aluminum production, Ψ denotes the electricity emission factor, Y_t represents production output at time t, and γ represents the CO₂ emission coefficient for raw material processing and product formation. According to the “Technical Guidelines for Carbon Emission Trading in Aluminum Electrolysis Enterprises”, the values used in this study are Ψ = 0.6858 tCO₂/MWh and γ = 2.5 tCO₂/tAl.

$$T_{emi}={\displaystyle \sum _{t=1}^T{P}_{al,t}}\psi +{\displaystyle \sum _{t=1}^T{Y}_t}\gamma$$

(23)

The current determination of free carbon emission allowances for aluminum electrolysis primarily adopts the baseline method, which calculates based on historical production and benchmark values as shown in Equation (24), where T_all represents the allocated free carbon emission allowance, S represents the emission benchmark value (taken as 9.1132 tCO₂/tAl in this study), and Y^order represents the daily production target (260 t in this case).

$$T_{all}=Y^{order}S$$

(24)

$$F_{C{O}_2}=\left\{\begin{array}{cc}\lambda k& k\le d\\ 1.25\lambda k-0.25\lambda k& d<k\le 2d\\ 1.5\lambda k-0.75\lambda k& 2d<k\le 3d\\ 1.75\lambda k-1.5\lambda k& 3d<k\le 4d\\ 2\lambda k-2.5\lambda k& 4d<k\end{array}\right.$$

(25)

$$k=T_{emi}-T_{all}$$

(26)

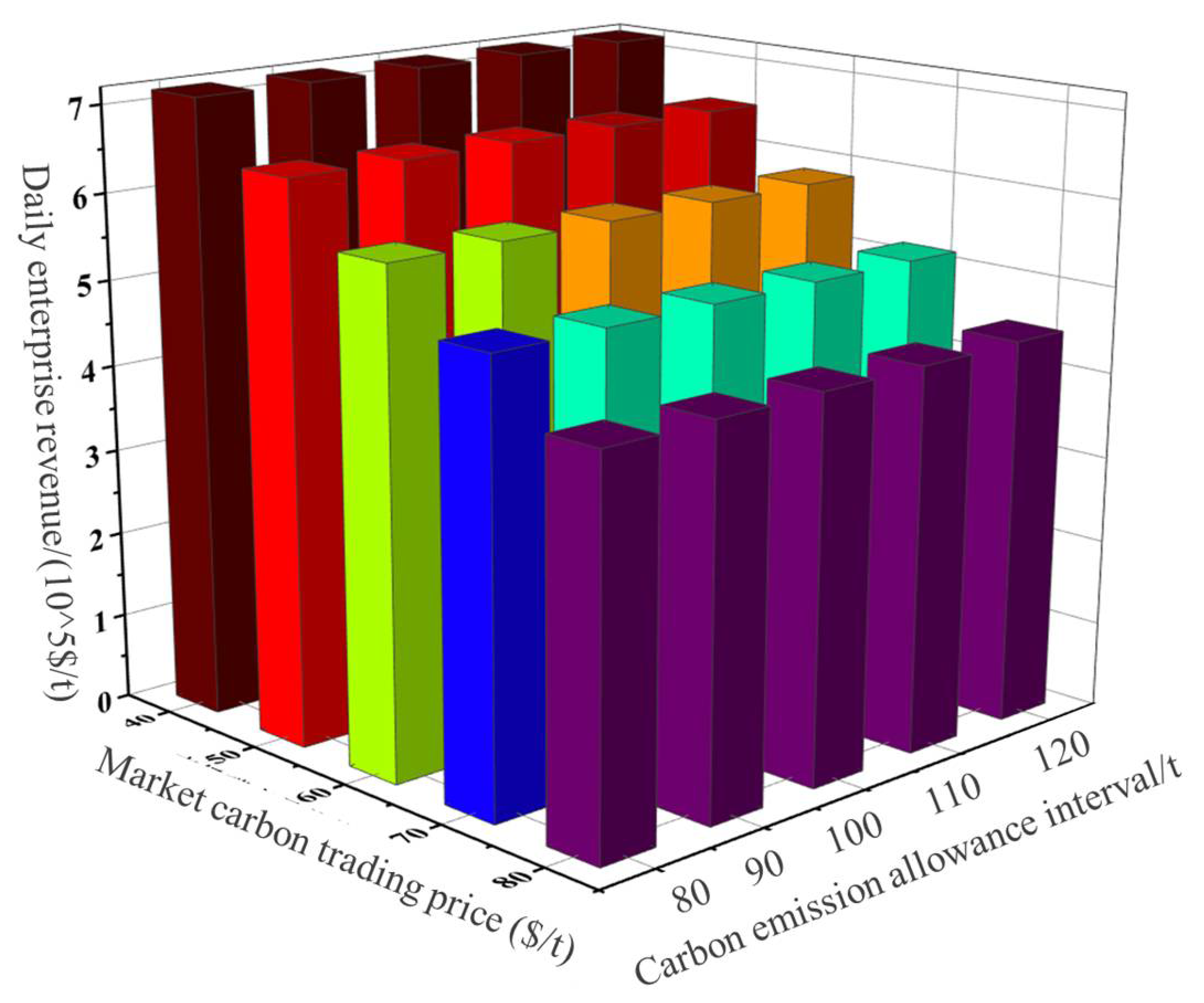
This paper adopts a tiered carbon trading cost calculation model that uses the allocated free carbon emission allowance as a baseline, dividing it into several intervals where higher emission ranges correspond to higher carbon trading prices. Equations (24) and (25) present the detailed calculation model, where λ represents the market unit carbon trading price and d represents the length of the carbon emission interval. When k is positive, it represents that the actual carbon emissions exceed the allocated free allowance, requiring the purchase of additional carbon credits from other producers; conversely, when k is negative, the actual emissions are below the allocated allowance, allowing the sale of surplus credits for profit.

In summary, the optimal production model for the aluminum electrolysis enterprise can be formulated as Equations (27) and (28), with the objective function minimizing the difference between the sum of electricity purchase costs, self-generation power plant costs, and carbon trading costs, and the revenue from aluminum sales.

$$Obj:\min (F_{buy}+F_{ru}+F_{CO2}-S_{al})$$

(27)

$$\begin{array}{c}s.t.(2)-(22)\end{array}$$

(28)

It can be observed that this optimization model contains integer variables such as unit status variables, along with a nonlinear constraint (12), making direct solution challenging. To simplify the computation, constraint (12) is piecewise linearized here, transforming the mixed-integer nonlinear programming problem into a mixed-integer linear programming problem, which can then be solved using established commercial solvers like CPLEX or Gurobi.

3.2. Mathematical Model for Power Grid Day-Ahead Dispatch

By solving Equations (27) and (28), the power grid dispatch control center obtains the aluminum electrolysis enterprise’s day-ahead electricity purchase demand, based on which it formulates the day-ahead dispatch plan. The detailed mathematical model is as follows:

(1) Constraints related to grid-connected generation units

The constraints for units within the power grid mainly include output limits, ramp rate constraints, unit status constraints, and minimum uptime/downtime constraints. The specific expressions are similar to Equations (17)–(21). To avoid repetitive descriptions and confusion, they are represented here in the general form shown in Equation (29).

$$\begin{array}{l}{P}_{i,t}^G\in {\mathrm{\Phi }}_i^G\\ {\mathrm{\Phi }}_i^G=\left\{\left.P_{i,t}^G,t\in [1,T]\right|\mathit{A}{P}_{i,t}^G+\mathit{F}{x}_i^G\ge \mathit{h}\right\}\end{array}$$

(29)

(2) Power flow constraints

$$L_{l,t}^{\min }\le L_{l,t}\le L_{l,t}^{\max }$$

(30)

Equation (30) represents the transmission line power flow constraint. Since this study focuses on day-ahead scheduling without considering voltage and reactive power issues, this constraint is implemented by solving the DC power flow to ensure secure power flow operation.

(3) Power balance constraint

$$z{P}_{buy,t}+P_{L,t}^{fore}+{\epsilon }_{L,t}^{fore}-(P_{w,t}^{fore}+{\epsilon }_{w,t}^{fore}-\mathrm{\Delta }{P}_{w,t}^{cur})-{\displaystyle \sum _{i=1}^N{P}_{i,t}^G}=0$$

(31)

When considering the uncertainty of wind power forecast output and load in the system, the strict power balance constraint can be described by Equation (31). Here, z represents the electricity purchase fluctuation coefficient. Since the waste heat recovery efficiency of aluminum electrolysis enterprises is affected by temperature, z is introduced to ensure that the power system maintains a sufficient electricity supply for aluminum production even when fluctuations occur in the thermoelectric conversion power on the enterprise side. P_L,t^fore and P_w,t^fore represent the forecasted load and wind power at time t, respectively; ε_L,t^fore and ε_W,t^fore represent the forecast errors for load and wind power, respectively; △P_w,t^fore represents the curtailed wind power. P_i,t^G represents the output of the i-th unit at time t. To facilitate subsequent solution, wind power fuzzy coefficient µ_w and load fuzzy coefficient µ_L are introduced, allowing Equation (31) to be relaxed into the chance-constrained form shown in Equation (32).

$$\begin{array}{c}\min credit\left\{{\mu }_w-{\mu }_L-z{P}_{buy,t}+{\displaystyle \sum _{i=1}^N{P}_{i,t}^G}\right\}\end{array}\ge r$$

(32)

Here, the credibility function represents the measure of event reliability, with r denoting the predetermined confidence level (set at 0.95 in this study). Compared to deterministic programming, Equation (32) employs credibility-based chance constraints to handle uncertainty factors, ensuring that the constraint satisfaction probability meets power grid dispatchers’ operational requirements. Following the equivalent transformation conditions and methods for fuzzy chance-constrained programming proposed in references [22,23], we convert this into the deterministic equivalent form of power balance constraints as shown in Equation (33), where P_w1,t, P_w2,t, P_L3,t, and P_L4,t represent the membership function parameters for wind power and load. Detailed derivation steps and parameter specifications can be found in reference [17], which are omitted here due to space limitations.

$$0.1(P_{L3,t}-P_{W2,t})+0.9(P_{L4,t}-P_{W1,t})-{\displaystyle \sum _{i=1}^N{P}_{i,t}^G}+z{P}_{buy,t}=0$$

(33)

(4) Wind farm power constraints

$$0\le P_{w,t}\le P_{w,t}^{fore}$$

(34)

In summary, the lower-level optimization model for the power grid can be formulated as shown in Equations (35)–(38).

$$Obj:\min (F_{Gu}+F_{pen}+F_{man})$$

(35)

$$F_{pen}=\xi {\displaystyle \sum _{t=1}^T(P_{w,t}^{fore}-P_{w,t})}$$

(36)

$$F_{man}=\omega {\displaystyle \sum _{t=1}^T{P}_{w,t}}$$

(37)

$$\begin{array}{c}s.t.(28)-(29)\end{array},(32)-(33)$$

(38)

In the objective function, F_Gu, F_pen, and F_man represent the generation cost of units, the penalty cost for wind curtailment, and the operation and maintenance (O&M) cost of wind power, respectively. Here, ξ represents the wind curtailment penalty coefficient, and w represents the O&M cost coefficient of wind power. At this point, the model becomes a mixed-integer linear programming (MILP) problem, which can be solved directly to obtain the day-ahead dispatch scheme for the grid side, under the uncertainties of wind power and load demand.

4. Case Study

This paper employs the IEEE-30 bus system for case validation, with a wind farm connected at bus 13 and an energy-intensive enterprise connected at bus 4, where the market carbon trading price λ is USD 40/t and the interval length d is 80 t. To better analyze the waste heat recovery efficiency in aluminum production, two scenarios are established: typical summer conditions and typical winter conditions. Detailed load curves, wind power output curves, temperature profiles, and time-of-use electricity prices are shown in Figure 3a–c, while Figure 3d displays the fitted relationship curve between the electrolyzer power and main flue gas flow rate according to the form specified in Equation (12). To meet the need of electrolytic aluminum plants for accurate recording and data retention of production waste heat, an integrated and traceable waste heat management solution can be constructed by combining industrial Internet of Things, intelligent monitoring, and energy management systems, so as to further advance industrial applications. High-precision temperature and pressure sensors should be installed at key nodes of waste heat sources, including electrolytic cells, flues, cooling systems, and conveying pipelines, to collect temperature and pressure data in real time, with the accuracy meeting industrial-grade standards. Electromagnetic flowmeters or ultrasonic flowmeters can be employed to measure the flow rate of the thermal medium, and the thermal power can be calculated in combination with temperature data. Infrared thermal imagers can conduct non-contact scanning of equipment surface temperatures to identify local heat loss points and assist in optimizing waste heat recovery paths. Edge computing gateways can be deployed on-site to perform real-time cleaning, calibration, and preliminary calculations of sensor data, reducing invalid data transmission and enhancing system response speed. Data can be labeled with timestamps, device IDs, and other tags to ensure data traceability.

The detailed parameters of the three types of flue gas are shown in

Table 1. Detailed parameters of flue gas in aluminum production.

Flue Gas Parameters	Main Flue Gas from Electrolytic Cells	Petroleum Coke Calcination Flue Gas	Green Anode Baking Flue Gas
Temperature/°C	100	1000	200
Specific Heat Capacity/(KJ/kg*K)	1.01	1.44	1.45
Flow rate/(m3/h)	Determined by Equation (12)	27,500	125,000

.

4.1. Analysis of Electrolyzer Operating Conditions

Under typical summer daily temperatures, the electrolyzer power and the aluminum production enterprise’s power purchase from the grid are shown in Figure 4.

Figure 4 reveals a clear complementary relationship between the aluminum electrolysis power curve and the time-of-use electricity price curve. During the low-price period from 0:00 to 8:00, the electrolyzers maintain high-power operation, while power consumption drops significantly during peak-price hours (12:00–16:00 and 20:00–22:00). This pattern occurs because aluminum electrolysis, as a typical energy-intensive industry with power consumption typically reaching several hundred megawatts, is highly sensitive to electricity prices as the primary factor affecting profitability. These findings demonstrate that grid operators can effectively adjust production schedules and enhance operational flexibility for energy-intensive enterprises like aluminum producers through well-designed time-of-use pricing strategies, thereby improving renewable energy integration and reducing grid stress during peak load periods.

4.2. Efficiency Analysis of Waste Heat Utilization

As indicated by Equation (1), ambient temperature significantly impacts flue gas waste heat recovery efficiency. This study analyzes both typical summer and winter conditions, with calculation results presented in Figure 5.

The calculation results in Figure 5a,b show that under typical summer day conditions, the waste heat utilization power generation mostly ranges between 4 and 4.4 MW, accounting for approximately 1.1–1.4% of the aluminum electrolysis enterprise’s total power consumption, with the enterprise’s total revenue reaching USD 71,701 in this scenario. Additionally, during peak electricity price periods such as 12:00–16:00, the enterprise reduces power consumption to save production costs, resulting in two peaks where waste heat generation accounts for the highest proportion of total power usage. Under typical winter day conditions, waste heat power generation mostly ranges between 3.6 and 4.0 MW, constituting about 0.9–1.1% of the enterprise’s total power consumption, with a total revenue of USD 71,190 in this scenario. It is evident that the winter scenario generally shows slightly lower values than the summer scenario in terms of waste heat recovery power, its proportion to total power consumption, and enterprise revenue, primarily due to lower winter temperatures reducing waste heat recovery efficiency and consequently affecting both final waste heat generation and enterprise profits.

4.3. The Impact of Carbon Trading Costs and Intervals on Aluminum Production Enterprise Revenue

Figure 6 demonstrates the impact of different market carbon trading prices (λ) and carbon emission interval lengths (d) on the daily revenue of aluminum production enterprises. The case results show that when the market carbon trading price λ is USD 40/t with an interval length d of 80 t, the enterprise’s revenue reaches USD 71,701. When λ remains at USD 40/t but d increases to 120 t, the revenue becomes USD 71,941; when λ rises to USD 80/t with d at 80 t, the revenue drops significantly to USD 44,415. Clearly, as the market carbon trading price increases, the enterprise’s carbon trading costs gradually rise, leading to a substantial reduction in profits. On the other hand, when the carbon trading price remains relatively stable, a larger allocated emission interval length results in higher enterprise revenue. However, due to the significant carbon emissions per ton of aluminum produced, the market carbon trading price has a more pronounced impact on the enterprise’s profitability compared to the emission interval length.

Table 2. Calculation results of day-ahead dispatch of power grid.

Dispatch Scheme	Wind Curtailment Percentage	Total Cost/USD
The proposed Day-Ahead Dispatch Scheme	7%	115,261
Day-Ahead Dispatch Scheme Without Considering Source-Load Uncertainty	16%	109,245

presents the effectiveness of the robust day-ahead dispatch scheme on the grid side, demonstrating that the proposed method sacrifices some economic efficiency to ensure system security under source-load uncertainty, while addressing potential renewable energy and load power fluctuations.

5. Conclusions

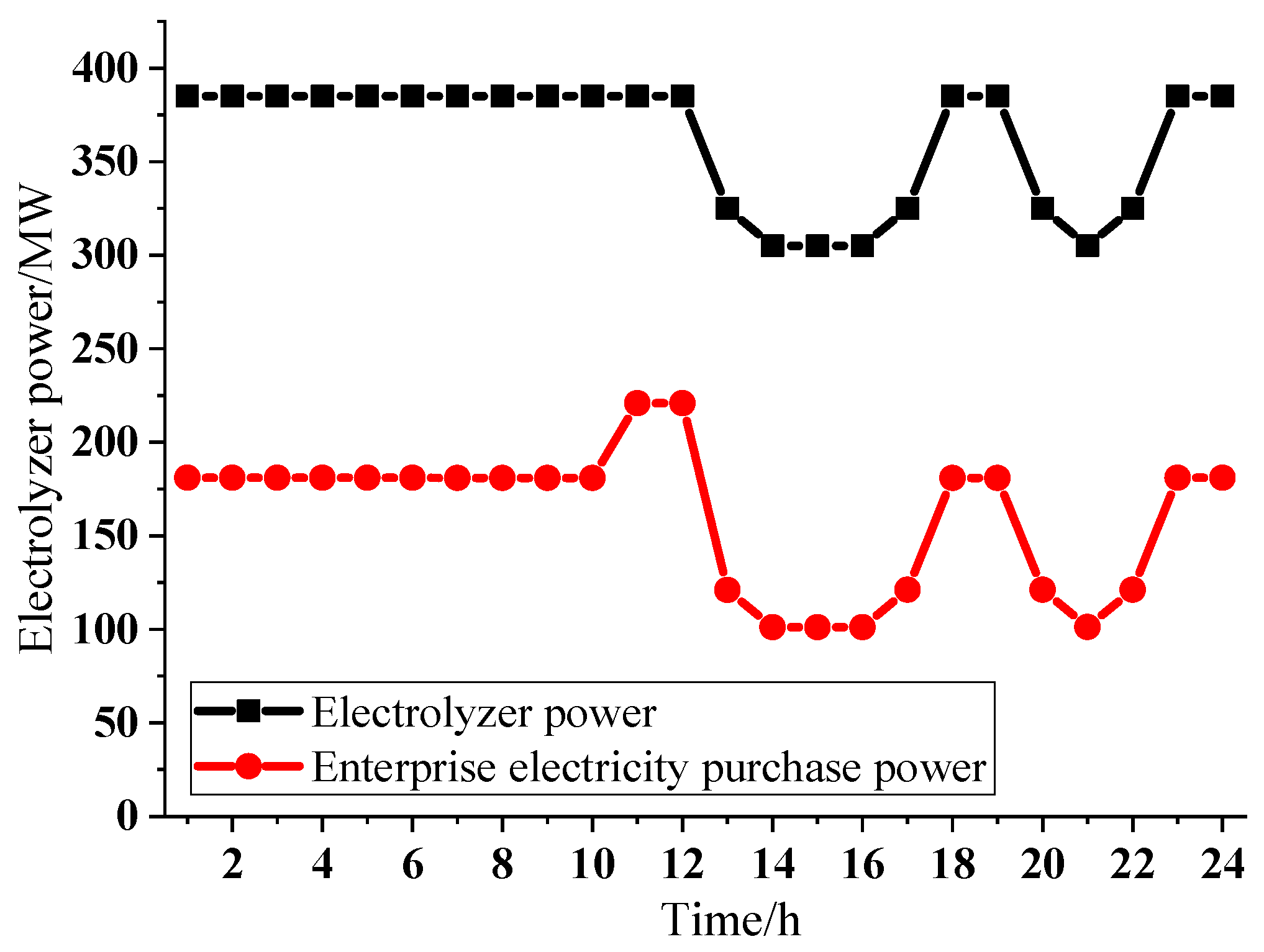
To evaluate both the economic and environmental benefits of internal production processes in aluminum manufacturing enterprises while simultaneously considering the economic interests of both aluminum producers and the power grid, this study designs a coordinated low-carbon economic dispatch strategy for aluminum electrolysis and the power grid that incorporates waste heat utilization. On the aluminum production side, the optimal production plan is formulated by accounting for flue gas waste heat and carbon emission models. On the power grid side, a robust day-ahead economic dispatch strategy is developed, fully considering the uncertainties in electricity demand from aluminum producers, renewable energy generation, and load fluctuations. The case study results lead to the following conclusions: (1) For aluminum producers, electricity prices are the primary factor influencing production output. Aluminum electrolysis enterprises typically reduce production during peak electricity price periods and increase output during low-price periods to meet minimum production constraints. When the power grid requires a response, the production power of electrolytic aluminum enterprises can be reduced by up to 45% or increased by up to 61%. (2) The substantial flue gas generated during petroleum coke calcination, green anode baking, and electrolysis in aluminum production holds significant utilization value. Case analysis shows that, in addition to meeting on-site thermal load demands, waste heat power generation from these three processes can account for up to 1.4% of the total energy consumption in aluminum production. Although this proportion appears modest, considering that aluminum electrolysis consumes hundreds of megawatts per hour, the resulting economic and environmental benefits remain substantial. Through waste heat utilization, enterprises can reduce carbon emissions by 11.4% and increase economic returns by 6.8%. (3) When carbon emission constraints are considered in aluminum production, both carbon market trading prices and carbon emission allowance ranges affect final profits. Carbon trading prices have a greater impact—higher prices lead to lower enterprise profits, while wider emission allowance ranges positively influence profits, albeit to a lesser degree. When the carbon trading price increases by 10%, the enterprise’s profit decreases by approximately 5.4%. (4) The power grid’s robust day-ahead dispatch strategy ensures stable and secure system operation amid renewable energy and load power fluctuations by increasing economic investment in reserve capacity. Through coordinated scheduling, the average renewable energy consumption rate has increased by 7.5%, while the system operating costs have decreased by 9.4%, achieving a win-win outcome.

Potential future research directions include the following: (1) Exploring the application of reinforcement learning in power grid economic dispatching. This involves constructing intelligent agents to interact with the power grid environment, optimizing dispatching decisions through continuous trial-and-error and learning to cope with the complex and ever-changing operational conditions of the power grid, as well as production variations in high-energy-consuming enterprises. (2) Taking data privacy protection into account. By employing techniques such as differential privacy and federated learning, the privacy information of enterprises and users can be safeguarded while ensuring data availability, thereby facilitating data sharing and collaboration.