Abstract
Flexible energy sources such as electric vehicles and the battery energy storage systems of intelligent distribution systems can provide system-wide auxiliary services such as frequency regulation for power systems. This paper proposes an optimal method for operating the local energy community that is based on two-stage scheduling. Firstly, the basic concepts of the local energy community and flexible service are introduced in detail. Taking LEC as the reserve unit of artificial frequency recovery, an energy information interaction model among LEC, balance service providers, and the power grid is established. Then, a two-stage scheduling framework is proposed to ensure the rationality and economy of community energy scheduling. In the first stage, day-ahead scheduling uses the energy community management center to predict the up/down flexibility capacity that LEC can provide by adjusting the BESS control parameters. In the second stage, real-time scheduling aims at maximizing community profits and scheduling LEC based on the allocation and activation of standby flexibility determined in real time. Finally, the correctness of the two-stage scheduling framework is verified through a case study. The results show that the control parameters used in the day-ahead stage can significantly affect the real-time profitability of LEC, and that LEC benefits more in the case of low BESS utilization than in the case of high BESS utilization and non-participation in frequency recovery reserve.
1. Introduction
With the popularization of renewable distributed energy, the flexibility of the power system will be greatly reduced [1,2]. The flexibility of electrical systems can be defined as the continuous adjustability of network operating points to adapt to changes in predicted/unpredictable demand/power generation fluctuations [3,4,5]. Flexible services can be provided by different flexible energy sources located in the transmission or distribution network, where generators are the only source of electrical energy used to meet system level flexibility requirements [6]. To meet the flexibility requirements of the power system, it is urgent to incorporate flexible energy sources such as electric vehicles, different types of energy storage devices, and controllable household appliances into the flexibility regulation of the power system.
The flexibility services used by power operators are mainly aimed at maintaining system frequency within a predefined range. Frequency reserve services can be divided into frequency containment reserve, automatic frequency recovery reserve, and manual frequency recovery reserve [7,8]. The manual frequency recovery reserve service is divided into an upward flexibility service and a downward flexibility service. Currently, relevant research has analyzed the economics and feasibility of different types of energy reserves participating in reserve market flexibility regulation. Based on the concept of multi-timescale flexibility in the context of high-proportion cogeneration, a coordinated optimization scheduling framework for the electric heating system is established, with the allowable heat output range of cogeneration units and the operating boundary of the electric heating system as constraints. The proposed optimization scheduling framework is analyzed using examples of cogeneration units to prove that it can effectively reduce abandoned air volume, increase system backup capacity, and reduce operating costs. It could help guide the study of flexibility of cogeneration units in centralized heating systems and wind power integration [9]. A source load storage coordinated rolling scheduling model considering wind power was established, constrained by the output characteristics and the supply capacity of flexible resources. The output status of various flexible resources was adjusted in a rolling manner, and the effectiveness and feasibility of the method were verified through numerical examples [10]. The use of a comprehensive energy system with multi-timescale optimization scheduling solves the uncertainty of new energy and load demand, coordinates equipment processing in the day-ahead stage to enhance flexibility, and smooths power fluctuations in the day-ahead stage. But none of them involve other flexible energy dispatches within the distribution network [11,12,13]. Firstly, an analysis was conducted of the flexibility requirements of high-penetration distributed power distribution networks. Based on the flexibility and adequacy of distribution network capacity and the adaptability of power supply acceptance, a multi-objective optimization scheduling model for improving distribution network flexibility was established [14]. A dual-layer optimization scheduling model considering photovoltaic flexibility was proposed, and intuitive fuzzy programming was adopted to meet the huge economic cost caused by flexibility requirements in extreme scenarios, in order to obtain a comprehensive optimal scheduling scheme [15]. A flexibility evaluation method for distribution networks considering the integration of electric vehicles was established based on multiple scenarios and timescales [16]. A load storage scheduling model for electric vehicle clusters was established using the Monte Carlo sampling method. Combining the interests of system operators and electric vehicles (EV) aggregators, as well as EV flexibility, a two-stage scheduling optimization operation strategy was proposed with the goal of maximizing the interests of both parties. By improving the IEEE 33 node system, it was proven that this method can effectively improve scheduling flexibility [17]. Based on the flexibility index of the distribution network, an optimization scheduling model considering EV charging, energy storage, and interruptible load scheduling was established. The effectiveness of the proposed flexibility index and ordered EV charging model was verified using an IEEE 33 node system [18]. However, the above literature did not address the interaction between EV charging and battery energy storage systems and the power grid.
In summary, this article proposes a method for optimizing the operation of local energy communities based on two-stage scheduling. A detailed introduction was given to the basic concepts of local energy communities and flexible services. The local energy community (LEC) was used as a reserve unit for artificial frequency recovery, and an energy information exchange model was established among the LEC, the balancing service provider (BSP), and the power grid. A two-stage scheduling framework is proposed to ensure the rationality and economy of community energy dispatching. In the first stage, day-ahead scheduling uses the energy community management center to predict the flexibility capacity that LEC can provide by deploying battery energy storage system (BESS) control parameters. In the second stage, real-time scheduling aims to maximize community profits and dispatches the LEC based on the real-time determined allocation and activation reserve flexibility. The correctness of the two-stage scheduling framework is verified through case studies.
2. LEC Model
2.1. Energy Community Flexibility Services
The energy community is composed of participants with different roles, including energy producers and consumers. These communities are usually equipped with various shared facilities, such as photovoltaic devices, wind power generation equipment, and battery energy storage systems. The core purpose of an LEC is to minimize operating costs and maximize collective benefits by participating in electricity market transactions and providing grid regulation services [19,20,21]. Based on member attributes (such as residents, businesses, agricultural users, etc.) or geographical distribution characteristics, energy communities can be divided into two models: regional communities and distributed communities. The former emphasizes geographical proximity between members and energy facilities, requiring the production of energy to be prioritized for local consumption, ensuring that both supply and demand sides are within the same regional scope. All local users can join the community and participate in internal energy trading, with related benefits and expenses shared by all members.
This study takes household users as the basic unit of residential energy communities, which are equipped with renewable facilities such as shared batteries, electric vehicles, and photovoltaic power generation systems to enhance the operational flexibility of the community. Community operation is managed by the Energy Community Management Center (ECMC), which coordinates and schedules various resources, increases revenue by providing flexible services to transmission grid operators (TSOs), and optimizes the collaborative management of electric vehicles and energy storage systems.
Manual frequency regulation services can be divided into two categories: upstream and downstream. When the power grid needs to increase power supply, the TSO purchases electricity from the BSP; when the power supply needs to be reduced, the TSO sells electricity to the BSP. The specific type of service depends on the dynamic needs of the TSO. This type of transaction is completed through the Balanced Capacity Market (BCM) and Balanced Energy Market (BEM): the BCM requires participants to submit capacity quotes at 11:00 am before the service day, and the TSO deploys resources and pays fees accordingly; the BEM allows participants to adjust their energy quotes 45 min before the service. The BSP needs to submit a quotation plan to the BEM that includes price, adjustment direction, and unit parameters. The TSO will then integrate these data to determine the optimal allocation plan for each time period. It should be noted that there is a fundamental difference between allocation flexibility and actual call flexibility: the former is determined by the TSO through BEM transactions, while the latter is dynamically adjusted based on real-time grid demand. Specifically, the TSO first plans flexible resources through market mechanisms and then determines the actual adjustment amount based on instantaneous equilibrium demand.
2.2. Model Building
The LEC can be used as a backup regulatory resource due to its ability to participate in manual frequency recovery reserve services. To support access by small-scale LECs, their flexible quotations need to be submitted to the BSP, integrated with quotations from other regulatory resources, and uniformly submitted to the balanced market. The LEC provides flexible services to TSOs through the BSP, while conducting energy trading with the higher-level grid to ensure its own supply–demand balance.
The two-stage scheduling framework of the LEC and its interaction with upstream institutions are shown in Figure 1. The main interaction object of the LEC is the BSP, which covers two timescales: day-ahead scheduling and real-time scheduling. The responsibilities of the BSP include formulating bidding strategies, acting as an agent to regulate resource participation in the BCM and the BEM, and decomposing the regulation tasks assigned by the TSO to various resources. The core functions of the TSO include balancing market clearing, allocating flexible capacity on demand, and actually calling for backup energy when the system needs it. The day-ahead dispatching is carried out by the Energy Community Management Center (ECMC) 24 h before the service day to predict the adjustable capacity of the LEC. This result needs to be submitted to the BSP before 11:00 am on the day before the service day so that the BSP can participate in the Balanced Capacity Market (BCM) and Balanced Energy Market (BEM) based on complete information. Real-time scheduling is executed within 1 h before the service period. The BSP represents its participation in market bidding to regulate resources, the TSO allocates flexibility tasks based on system requirements, and the BSP decomposes them into various resources. During this process, the ECMC optimizes the sharing of flexible resources such as energy storage and photovoltaics within the community to complete assigned tasks and maximize real-time revenue. This paper focuses on optimizing the operation and scheduling of the LEC, in which the availability of electric vehicles is obtained through daily LEC statistics, and the demand for electricity load and photovoltaic forecasting are obtained through the use of Gaussian mixture models and approximate linear programming methods. A related function model is established with the goal of maximizing the real-time profit of the LEC to complete FER scheduling and optimal trading. However, research has not been conducted on electricity market bidding, BSP reserve allocation and aggregation methods, reserve market clearing, etc., shown in the gray boxes in Figure 1.
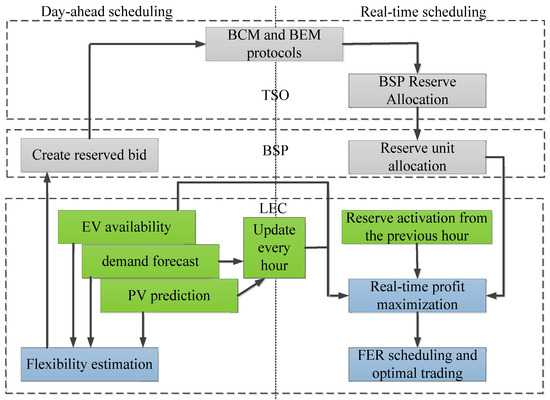
Figure 1.
Two-stage scheduling framework of LECs.
3. Two-Stage Scheduling
3.1. Day-Ahead Dispatching Stage
In the day-ahead scheduling phase, the ECMC executes the scheduling procedure to measure the maximum flexible supply capacity of the LEC in the next 24 h [22,23]. At this stage, it is assumed that the ECMC has obtained accurate capacity data for the electric vehicle’s next-day charging plan and the BESS, while predicting the net load of community members on an hourly basis (defined as the difference between aggregated electricity consumption and photovoltaic power generation). To address the uncertainty of net load fluctuations caused by random user behavior, a 24 h flexibility capacity assessment will be conducted at 1 h intervals. Within any 1 h, the community provides up/down flexibility based on its ability to regulate energy surplus and flexible resources (BESS and EV). During periods of energy surplus, all surplus will be declared as an increase in flexibility capacity, while during periods of energy shortage, the maximum consumption increment will be considered as a decrease in flexibility capacity. It should be emphasized that, if the LEC has both energy surplus and flexible resource adjustment space during a certain period, it can declare bidirectional flexibility [24,25].
The objective function of the ECMC aims to optimize the maximum bidirectional flexibility capacity that can be provided to the BSP in all scenarios within the next 24 h. The objective function of ECMC operation is shown in Formula (1):
where s represents the scenario; t represents the time period; πt,s represents the probability of scenario s at the t-th hour; Ft,s-up represents the upward flexibility for scenario s in the t-th hour; and Ft,s-down represents the downward flexibility for scenario s in the t-th hour.
The quotation for the BEM’s upward adjustment flexibility is usually higher than the price of selling electricity to the upstream power grid or energy market. On the contrary, the cost of purchasing reduced flexibility is generally lower than the cost of purchasing electricity from upstream sources. This price difference pattern makes it advantageous for LECs to participate in balancing the market overall. Therefore, the purpose of the LEC in the day-ahead scheduling phase is to determine the maximum flexible capacity Capt,s-up that can be provided to the balanced market. The calculation formula is shown in Formula (2):
where Pt,s-BESS,did,est represents the predicted value of BESS discharge power; Nt-EV,est represents the predicted number of charged electric vehicles for the t-th hour; PEV represents the charging power for electric vehicles; Lt-net,for represents the predicted net load for the t-th hour of LEC; and ∆εt,s represents the error related to the predicted net load for the t-th hour.
The upward adjustment capability of the LEC mainly comes from its production surplus, which is the difference between BESS discharge power and the sum of community net load plus EV charging power. The net load of the LEC in the t-th hour is shown in Formula (3):
where Pt-L,for represents the predicted load for the t-th hour and Pt-PV,for represents the predicted power generation of solar energy in the t-th hour.
Therefore, the maximum downward flexibility capacity that can be used to provide manual frequency recovery reserve is shown in Formula (4).
where Pt,s-BESS,ch,est represents the predicted value of BESS charging power.
The downward flexibility capacity represents the potential for the LEC to flexibly increase electricity consumption. This study considers the charging behavior of EV and BESS resources, forming the flexible consumption of the LEC. Therefore, during the time period t of scenario s, the total charging power of EVs and the BESS can be considered as the downward flexibility available to the LEC. The charging and discharging rates of the BESS are limited by its maximum power, as constrained by Formula (5):
where ut,s-BESS,est represents a binary variable that prevents the BESS from charging and discharging simultaneously. When the BESS is in a charging state, the variable is considered to be 1; otherwise it is 0.
Using a Gaussian mixture model to describe the joint probability distribution characteristics of photovoltaic and load power prediction errors can better consider their correlation and irregularity of probability distribution. GMMs approximate any joint probability density function with a linear weighted combination of multiple normal distribution functions, which can describe the joint probability distribution of any dependent, non-normally distributed random variable. The calculation formula for the random vector x is shown in Formula (6) below [26,27,28]:
where M represents the number of Gaussian sub terms; Nm represents the m-th Gaussian sub term; ωm represents the weight of the m-th Gaussian sub term; μm represents the expected value matrix; ∑m represents the covariance matrix; N represents the number of samples; and Det (·) represents finding the trace of the matrix (·). By adjusting the values of parameters θ = {ωm, μm, ∑m}, fGMM(x) can fit any probability density function.
When the upward flexibility capacity of the LEC is positive, this indicates its potential to provide upward adjustment services. Similarly, when the downward flexibility capacity is positive, this means that downward adjustment services can be provided, and the judgment criteria are shown in Formula (7).
Due to the need to submit charging time points and charging hours in advance for electric vehicles, the number of electric vehicles Nt,EV charged within the t-th hour is shown in Formula (8):
where Nt-plug and Nt-unplug represent the number of electric vehicles plugged in and unplugged at the t-th hour, respectively.
In day-ahead dispatching, the ECMC is faced with the uncertainty of balance service activation status, regulation direction (up/down), and photovoltaic forecast output and load demand. In order to avoid the risk of fines due to the inability to fulfill flexibility commitments in real time, the ECMC may choose to limit the utilization of the BESS in the current market for providing TSO-level flexibility services and reserve some capacity for real-time scheduling. To this end, the control parameters SOCt-min and SOCt-max are introduced for restriction. The constraint equations for BESS operation are shown in Formulas (9) and (10).
where SOCt,s-BESS,est represents the estimated SOC of the BESS within the t-th hour of scenario s; CapBESS represents the capacity of the BESS; and ηBESS,ch and ηBESS,dis represent the charging and discharging efficiencies, respectively.
Considering these constraints, if the gap between the adopted SOCt-min and SOCt-max is reduced, this means that ECMC is more inclined to provide less BESS flexible capacity for backup services and reserve some flexibility for real-time scheduling.
The expected amount of upward flexibility Qt-up and downward flexibility Qt-down provided to the BSP within the t-th hour are shown in Equation (11):
After ECMC provides downward/upward flexibility in total capacity, BSP will participate in balancing the market by consolidating the flexibility capacity of its reserve units.
3.2. Real-Time Scheduling Stage
BSP determines the total amount of flexibility that the LEC should provide based on the recent quotation. Community administrators need to arrange flexible energy resources to meet the specified power requirements of mFRR and maximize the real-time revenue of the LEC. Based on this flexible allocation value, the ECMC will complete the community flexible energy dispatch task for the next hour (covering four 15 min time periods) [29]. Therefore, the time window for this scheduling process is set to 1 h, with a time step of 15 min. At this stage, it is assumed that electric vehicle owners strictly adhere to their charging plan submitted the previous day, plug and unplug the electric vehicle within the specified time, and arrange their energy use based on the minimum charging time submitted by the owner; the ECMC updates SOC information about the BESS and electric vehicles based on the activated reserve capacity at the end of each hour; photovoltaic power generation and demand forecasting are updated every hour with very short intervals, and their forecast results are more accurate than daily forecasts. The results of PV/demand forecasting are considered deterministic and are not affected by any uncertainty. After fulfilling its flexibility service obligations to the TSO, the ECMC will trade surplus electricity with upstream power grids through distribution network operators or retailers.
The ECMC runs an optimization problem with the goal of maximizing real-time community profit Yt,m-RT, and the total profit calculation is shown in Formula (12):
where ICt,m-flex represents the revenue or cost generated by providing capacity and energy related to manual frequency recovery reserve services; It-Cap represents the profit obtained by LEC from providing reserve capacity in the t-th hour; It-en,up represents the profit obtained by LEC from providing upward reserve energy in the t-th hour; It-en,down represents the cost of purchasing downward reserve energy for LEC in the t-th hour; Pt,m-out and Pt,m-in are the output and input electrical energy of LEC, respectively; and λt-sell and λt-buy are the retail prices for selling and purchasing electricity to the grid in the t-th hour, respectively.
Under the determined conditions of BESS material and usage environment, the cyclic aging of the BESS is influenced by the depth of cycling and the number of cycles. The cost function ζBESS of the BESS for one discharge aging is shown in Formula (13) [30,31]:
where RCBESS represents the replacement cost of the BESS; ηdis represents the discharge efficiency of the battery; Erate represents the rated capacity of the battery pack; A represents the Arrhenius constant; Ea represents the activation energy; R represents the molar gas constant; T represents absolute temperature; ht represents the cycle depth of the battery pack at time t; and z represents the reaction rate constant.
The primary task of LEC real-time scheduling is to provide allocated flexible services (a and a). However, the ECMC must exchange power with the upstream power grid to meet the power balance constraints within the LEC. The power balance relationship of the LEC in providing upward and downward flexibility services is shown in Formula (14):
The binary parameters ut,m-up and ut,m-down are determined by the BSP based on the settlement results of the Balanced Energy Market (BEM). When providing downward flexibility services (ut,m-up = 0), the power required for net load, BESS charging, and EV charging is jointly supplied by electricity from the upstream grid and downward flexibility electricity purchased from BEM. Similarly, when providing upward flexibility services (ut,m-down = 0), the positive power surplus generated by the LEC will be sold back to the upstream grid after meeting the specified requirements for upward flexibility services.
In real-time scheduling, the charging arrangement of each EV is optimized with the goal of maximizing the overall community revenue. All EVs must maintain a constant charging power PEV, and the constraints on EV charging behavior are shown in Formulas (15)–(17):
where ui,t,m-EV is a binary decision variable, representing the charging status of electric vehicle i at the m-th hour and t-th time, with charging being 1, otherwise it is 0; Ψi-req is the minimum number of hours that electric vehicle i needs to be charged; and ∆ti-plug is the continuous charging time of electric vehicle i.
The SOC value of the EV at the beginning of the first time period in the t-th hour must be determined based on the actual SOC value at the end of the fourth time period in the (t−1)-th hour. This is because the actual activation value of the backup power may deviate from the planned allocation value, resulting in a difference between the actual SOC of the EV and the planned value at the end of the previous hour. Therefore, the actual SOC value needs to be used instead of the planned value for initialization. During the second to fourth time periods of the t-th hour, the SOC of the EV can be calculated based on the planned value at the end of the previous time period. The constraints related to the BESS are shown in Formulas (18)–(20) [32]:
The ECMC executes optimization solutions based on Equations (12)–(19) every hour to schedule its flexible energy sources such as the BESS and EVs, as well as trading power with upstream power grids, in order to maximize real-time community benefits. Before starting the next hour’s scheduling, the system will update the actual SOC values SOCi,(t−1),4-BESS,act and SOCi,(t-1),4-EV,act of the BESS and EVs at the end of the previous hour based on the operational data generated by the activated mFRR. Subsequently, the real-time scheduling program will perform calculations for the next hour’s four time periods based on this.
4. Numerical Study
4.1. Case Study
Take an LEC with 50 families in Kunming, Yunnan as an example, assuming each household has three people and an average of 21% electric vehicles per person. After calculation, there are about 10 electric vehicles in the community [33,34], with a dispatch cycle of 24 h and a time interval of 1 h. The community has a 100 kW photovoltaic system and flexible energy, including a 200 kWh BESS, with a maximum charge and discharge power of 50 kW, a maximum charge/discharge rate of 50 kW, a charge/discharge efficiency of 0.8, a discharge depth of 60%, and a service life of 12,000 charges. The plug-in/unplugged state and battery capacity information of the EV are shown in Table 1 [35].

Table 1.
Information about EVs owned by community members.
The temperature variation in the studied area is relatively small throughout the year, so the influence of climate was not taken into account. The predicted and actual values of load demand and solar power generation the next day are shown in Figure 2. GMMs are used in day-ahead dispatching to describe the joint probability distribution characteristics of PV power generation and load power prediction errors, taking into account their correlation and the irregularity of probability distribution.
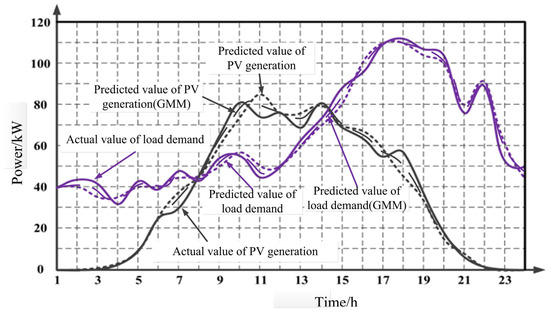
Figure 2.
Actual and forecasted values of demand and PV generation.
4.2. Day-Ahead Scheduling Analysis
This study uses Monte Carlo simulation technology to generate 1000 scenarios of photovoltaic output and hourly load demand to support stochastic optimization analysis, as shown in Figure 3. Based on these scenarios, solve the optimization problem defined by Formulas (1)–(11) and handle constraints Formulas (6) and (7) through linearization techniques. The total upward and downward flexibility that the BSP can provide daily was calculated for different values of state control parameters (kept constant within 24 h). The results are shown in Table 2. Compared with the extended Kalman particle filter control scheme used in reference [36], in terms of accurately tracking the SOC information of the BESS, the fixed control parameters have local deviations from the true state of SOC, but their prediction error can be controlled within 1%. The calculation results are shown in Figure 4. The yellow scenario in Table 2 is S1, the green scenario is S2, and the white scenario is S3. The data in Table 2 indicates that increasing the SOCt-min parameter usually leads to a decrease in the upward and downward flexibility provided by the BSP. However, when the parameter values of SOCt-max are low, this effect is not significant. Specifically, under the condition of 0.8, higher values do correspond to lower flexibility supply; however, at other values, the impact of increasing the value on flexibility changes is relatively weak, as the upward flexibility of 84.2 kW and the downward flexibility of 79.8 kW mainly come from other sources such as LECs and surplus photovoltaics from EVs.
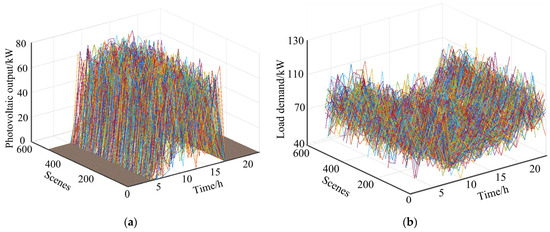
Figure 3.
Photovoltaic output and load demand scenarios: (a) photovoltaic output; (b) load demand.

Table 2.
Flexibility calculation results with different control parameters.
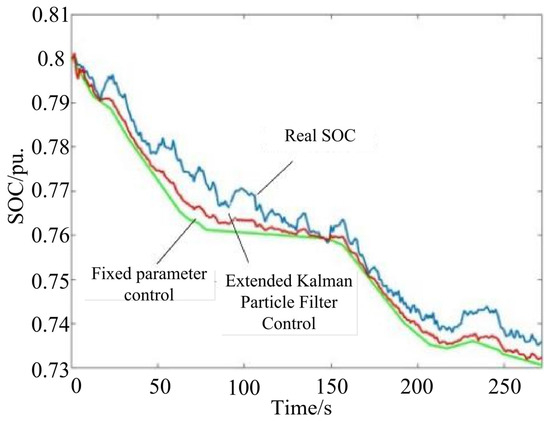
Figure 4.
Comparison of SOC calculation methods.
Overall, reducing parameters tends to decrease the predicted supply of upward/downward flexibility. From Table 2, it can be seen that scenario S1 provides the highest flexibility and utilization when the parameter combinations are (0.2, 0.8), (0.3, 0.8), and (0.2, 0.7). Following closely behind is scenario S2, whose parameter combinations with suboptimal flexibility are (0.4, 0.8), (0.2, 0.6), and (0.2, 0.5). In contrast, scenario S3 provides the least flexibility. From this, it can be seen that smaller values usually correspond to higher levels of flexibility, such as a combination of 0.2 occupying the top two positions in the flexibility supply ranking. The reason is that the community production surplus was negative in the early morning of the next day, and releasing the battery energy storage system (BESS) at this time can provide upward flexibility, while a smaller value allows the LEC to contribute more upward flexibility through BESS discharge.
Even under low utilization conditions, the LEC can still provide upward flexibility during the 09:00 to 14:00 period, as shown in Figure 5. During this period, the production surplus allows the LEC to provide upward flexibility without the assistance of the BESS. For scenario S1, LEC can provide upward flexibility in the vast majority of time periods. In addition, the only difference between scenario S2 and S3 is that S2 can utilize the BESS to provide additional flexibility supply at 05:00.
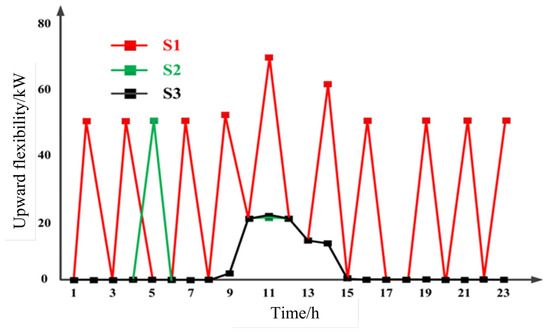
Figure 5.
Upward flexibility offer by the LEC considering different cases.
In all examined scenarios, the LECs of scenarios S1, S2, and S3 can provide downward flexibility during the charging period of electric vehicles, as shown in Figure 6. EVs and the BESS are the only two sources that provide flexibility in this direction. In scenario S3, due to the LEC using less than 50% of BESS capacity, its downward flexibility is mainly provided by EV charging. However, scenario S1 deployed a larger BESS capacity, allowing it to provide downward flexibility during most of the time. The downward flexibility provided by scenario S2 is similar to the total amount of scenario S3, but scenario S2 utilizes its BESS to obtain more supply at 07:00.
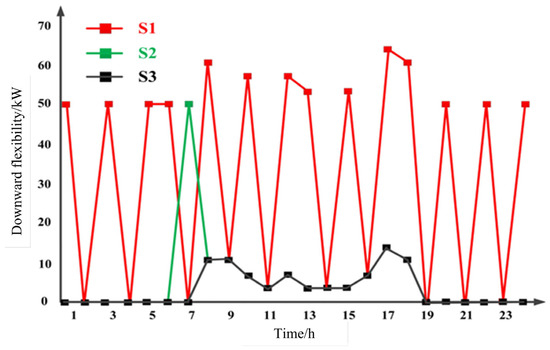
Figure 6.
Downward flexibility offer by the LEC considering different cases.
The 24 h charging and discharging schedule of the BESS in different scenarios is shown in Figure 7. The number “1” in the figure indicates that the BESS is in the charging state, “−1” indicates that the BESS is in the discharging state, and “0” indicates that the BESS is in the hot standby state. It can be seen that the charging and discharging states of the BESS in scenarios S1–S4 are roughly the same from 12:00 to 24:00, and charging and discharging of the BESS in scenario S1 are the most frequent, which corresponds to the up/down flexibility provided by the LEC in the day-ahead scheduling link.
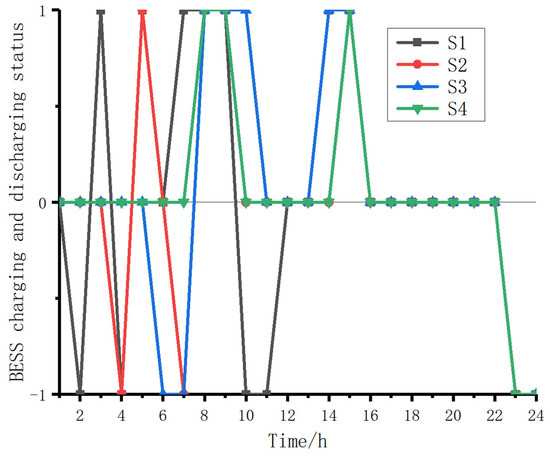
Figure 7.
The day-ahead charging and discharging schedules of the BESS in different scenarios.
4.3. Real-Time Scheduling Analysis
The BSP sets the flexibility scale that LECs should provide in real time. During a specific period of time, there is no need to accept any flexible resources, as there is no need to deploy manual frequency recovery backup. Assuming that the BSP fully accepts and allocates the capacity provided by the LEC to meet flexibility requirements, the allocation and actual call volume of upward and downward flexibility required by the LEC are shown in Figure 8 and Figure 9. These values were calculated in real-time by the BSP for the three scenarios (S1–S3) mentioned earlier.
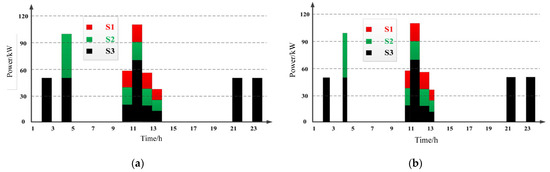
Figure 8.
The upward flexibility provided by the LEC in different scenarios: (a) allocated values; (b) activation values.
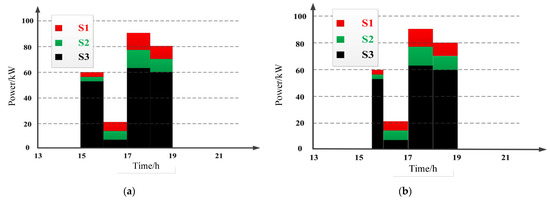
Figure 9.
The downward flexibility provided by the LEC in different scenarios: (a) allocated values; (b) activation values.
When the LEC generates surplus power, its profit during the period is positive. However, during most of the remaining time periods, profits are mostly negative, indicating that the community needs to purchase electricity from the upstream power grid or meet demand by providing downward flexibility services. The optimization results from different scenarios show that the LEC cannot provide its allocated backup energy during some time periods in scenarios S1 and S2. To achieve flexibility of commitment, the LEC needs to purchase the required electricity from the upstream power grid through DSO or retailers, which leads to a significant decrease in profits for scenarios S1 and S2 during certain periods of the day, and the profit fluctuation of scenario S1 is greater than that of scenario S3. Although scenario S1 obtains higher profits during a very small number of periods (such as 02:45, 11:15–11:45), it generates higher costs in the early morning hours (such as 02:02–02:15, 03:15, 05:15, and 15:00–15:45).
If the scenario without reserve participation is set as S4, the total net costs of the S1, S2, S3, and S4 scenarios are 24.7 k¥, 20.7 k¥, 19.6 k, and 20 k¥, respectively, as shown in Table 3. It can be seen that there is a correlation between the selection of control parameters and the real-time net cost of the LEC. The total net cost of S1 is higher than the other three scenarios; S2 also has a similar trend, but to a lower degree than S1, with a higher total net cost than S3. Compared with the other three scenarios, the total cost of the LEC not participating in the reserve supply scenario S4 ranks third, which means that the total net cost of the LEC not participating in the reserve supply is higher than that of S3, but lower than that of S1 and S2. By comparing situations with different control parameters, the LEC has higher profits when it provides smaller BESS capacity in its day-ahead flexibility plan. In other words, when choosing higher and lower values, the LEC’s profit is higher.

Table 3.
Total net cost in different scenarios.
The trough price during 00:00–08:00 is 0.3 yuan/kWh, the normal price during 08:00–18:00 is 0.6 yuan/kWh, and the peak price during 18:00–24:00 is 1 yuan/kWh. The time-of-use price is used to trade with the upstream grid, providing upward and downward balance flexibility. The price of selling flexibility up is always equal to or greater than the price of selling power to the grid, and the price of purchasing flexibility down is always equal to or lower than the price of purchasing power from the grid. The SOC input data of EVs and the BESS are updated based on the actual activation reserve to obtain 24 h capacity. The real-time profits of the community under the four scenarios are shown in Figure 10.
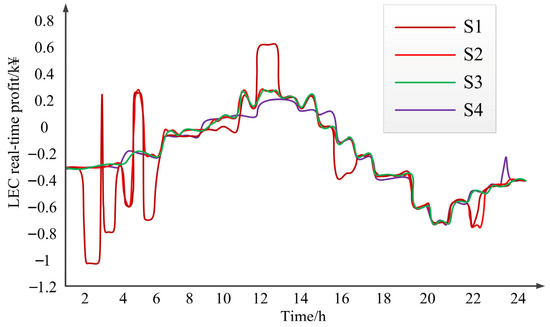
Figure 10.
LEC real-time profit under different scenarios.
The LEC costs and revenue sources under different circumstances are shown in Figure 11. According to the community’s recent plan, in terms of obtaining backup-related income, S1 benefits the most from participating in TSO-level flexibility trading, followed by S2 and S3. If the LEC does not declare its flexibility capability in advance, it will not be able to benefit from such services. But the real-time energy trading costs of S1 and S2 have increased, as they need to compensate during periods when flexibility commitments cannot be fulfilled. In these cases, the LEC has recently planned to sell a large amount of production capacity to provide TSO-level flexibility, resulting in the community being unable to sell this portion of capacity to upstream networks, thereby reducing energy trading revenue. The higher the participation of the LEC in the backup supply, the higher the real-time utilization of the BESS, but the flexibility capacity provided is more dynamic, and the operating cost of the BESS will also increase.
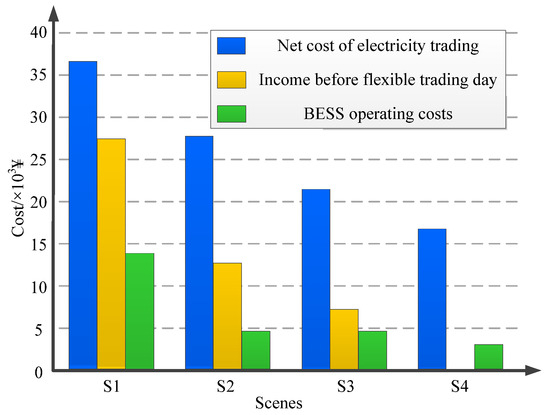
Figure 11.
The LEC’s monetary turnover in a single day, considering different cases.
In S1, S2, and S3, the capacity sold by the LEC to upstream networks is negligible; when there is no backup supply (S4), the community can sell all of the surplus electricity that it generated to the upstream power grid. This is because, in the S1–S3 scenarios, the LEC uses most of its production capacity to provide backup. In terms of energy input to the community, S1′s LEC shows short-term fluctuations, mainly due to the need for upward flexibility in its allocation, which is concentrated in the early morning and 21:00 to 23:00 periods. Similar fluctuations were also observed in some areas of S2′s LEC around 22:00. The SOC changes of the BESS under different conditions are shown in Figure 12, indicating that participating in the backup supply can improve the utilization rate of the BESS. The initial SOC value and minimum allowable value of the BESS are set to 0.2 and 0.5, respectively. Comparing the BESS capacity utilization of S1, S2, and S3, it can be seen that higher participation in the backup supply leads to increased SOC fluctuations, resulting in a more diverse distribution of capacity. The LEC of S1 utilizes higher BESS capacity, resulting in more significant capacity fluctuations. In contrast, the LEC fluctuations of S2 and S3 are reduced. In the S4 scenario without backup participation, BESS capacity utilization only occurs between 22:00 and 24:00, and its charging capacity is not utilized at all.
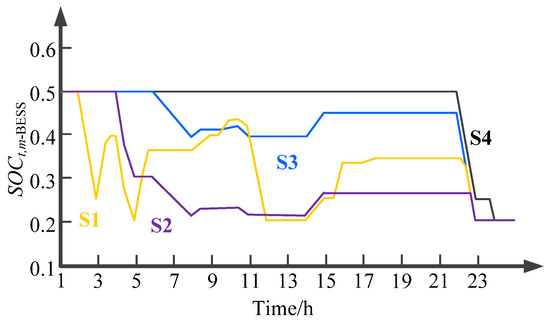
Figure 12.
SOC variation of the BESS considering different cases.
5. Conclusions
This paper proposes an optimal method of operating local energy communities based on two-stage scheduling. The basic concepts of local energy community and flexible service are described in detail, and an energy information interaction model among the local energy community, the BSP, and the power grid is established. The proposed two-stage scheduling framework is used to optimize the energy scheduling of the LEC, and the correctness of the proposed method is verified by a case study. The following conclusions are obtained:
- (1)
- A two-stage scheduling framework is proposed. In the day-ahead scheduling phase, the ECMC manages BESS utilization by changing the SOC control parameters and then determines the flexibility capacity that the LEC can provide, to submit to the BSP in the day-ahead phase. In the real-time scheduling phase, based on the distribution flexibility that the LEC should provide within 15 min of a quarter hour and the flexibility of activation in the first hour, the real-time profit of LEC is maximized under the control of the ECMC.
- (2)
- A simulation analysis of community cases including the LEC, the photovoltaic system, and the BESS is carried out. The day-ahead scheduling link calculates the up/down flexibility capacity that the LEC can provide and the charging and discharging schedule of the BESS. The real-time scheduling link calculates the allocation value and activation value of the up/down flexibility that the LEC needs to provide and then calculates the real-time profit of the LEC. The results show that the BESS control parameters used in day-ahead scheduling have a great impact on the real-time profitability of the LEC. The BESS with low utilization has more profits than the BESS with high utilization that does not participate in the frequency recovery reserve.
- (3)
- In the future, different types of flexible energy such as random behavior of electric vehicle charging and discharging modes, climate factors, thermostatically controllable loads, thermal storage, and wind power in the energy community can be taken into account. The model will also be extended to more complex environments or more large-scale and structured energy communities to further improve the flexibility of LECs.
Author Contributions
Conceptualization, P.H., L.Z., J.W., Z.Y., G.L., C.C., and H.Z.; methodology, P.H., L.Z., J.W., Z.Y., G.L., C.C., and H.Z.; software, P.H., L.Z., J.W., Z.Y., G.L., C.C., and H.Z.; investigation, P.H., L.Z., J.W., Z.Y., G.L., C.C., and H.Z.; writing—original draft preparation, P.H., L.Z., J.W., Z.Y., G.L., C.C., and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by State Grid Hubei Electric Power Co., Ltd. Project: 2024 User Side Load Resource Management Capability Deepening and Improvement Project—Economic Development Zone (Hannan District) Contract No.: SGHBWHJHKFJS2400248.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Ping He, Lei Zhou, Jingwen Wang, Zhuo Yang, Guozhao Lv were employed by State Grid Hubei Electric Power Co., Ltd. Wuhan Economic and Technological Development Zone (Hannan District) Power Supply Company. Author Can Cai was employed by Hunan Zhuoqun Electric Power Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The State Grid Hubei Electric Power Co., Ltd. Wuhan Economic and Technological Development Zone (Hannan District) Power Supply Company and Hunan Zhuoqun Electric Power Technology Co., Ltd. had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Xia, Y.; Li, Z.; Xi, Y.; Wu, G.; Peng, W.; Mu, L. Accurate Fault Location Method for Multiple Faults in Transmission Networks Using Travelling Waves. IEEE Trans. Ind. Inform. 2024, 20, 8717–8728. [Google Scholar] [CrossRef]
- Fan, W.; Li, X.; Wang, Y.; Li, X.; Wang, Y.; Tan, Z.; Ju, L. Two-stage Scheduling Optimization Model of Flexible Resource Aggregation in New Power System. Electr. Power Constr. 2023, 44, 25–37. [Google Scholar]
- Tong, H.; Zeng, X.; Yu, K.; Zhou, Z. A Fault Identification Method for Animal Electric Shocks Considering Unstable Contact Situations in Low-Voltage Distribution Grids. IEEE Trans. Ind. Inform. 2025, 21, 4039–4050. [Google Scholar] [CrossRef]
- Bian, X.; Yang, S.; Huang, L.; Zhao, J.; Li, L. Research on Power System Scheduling Flexibility of Virtual Power Plant Accessing to Distribution Network. Electr. Meas. Instrum. 2020, 57, 66–71. [Google Scholar] [CrossRef]
- Pan, C.; Wang, J.; Bao, Y.; Fan, G.; Meng, T. Interactive Control of Wind and Photovoltaic Power Consumption Considering Source-load Side Flexible Resources. Smart Power 2023, 51, 1–8. [Google Scholar]
- Yang, L.; Cao, X.; Zhou, Y.; Lin, Z.; Zou, J.; Guan, X.; Wu, Q. Frequency-Constrained Coordinated Scheduling for Asynchronous AC Systems Under Uncertainty via Distributional Robustness. IEEE Trans Netw. Sci. Eng. 2025, 1–18. [Google Scholar] [CrossRef]
- Khajeh, H.; Laaksonen, H.; Gazafroudi, A.S.; Shafie-Khah, M. Towards flexibility trading at TSO-DSO-customer levels: A review. Energies 2019, 13, 165. [Google Scholar] [CrossRef]
- Zhao, Y.; Xie, K.; Shao, C.; Lin, C.; Shahidehpour, M.; Tai, H.M.; Hu, B.; Du, X. Integrated Assessment of the Reliability and Frequency Deviation Risks in Power Systems Considering the Frequency Regulation of DFIG-based Wind Turbines. IEEE Trans Sustain. Energy 2023, 14, 2308–2326. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, Y.; Luo, H.; Miao, S.; Ye, J.; Zhou, G.; Sun, L. Scheduling of Integrated Heat and Power System Considering Multiple Time-scale Flexibility of CHP Unit Based on Heat Characteristic of DHS. Proc. CSEE 2018, 38, 985–998. [Google Scholar] [CrossRef]
- Huang, P.; Zhou, Y.; Xu, F.; Cui, D.; Ge, W.; Chen, X.; Li, T.; Jiang, F. Source-load-storage Coordinated Rolling Dispatch for Wind Power Integrated Power System Based on Flexibility Margin. Electr. Power 2020, 53, 78–88. [Google Scholar]
- Tang, X.; Hu, Y.; Geng, Q.; Xu, X. Multi-time-scale Optimal Scheduling of Integrated Energy System Considering Multi-energy Flexibility. Autom. Electr. Power Syst. 2021, 45, 81–90. [Google Scholar]
- Wu, Z.; Ai, X.; Hu, J. Reserve Optimization and Real-time Scheduling of Frequency Regulation Ancillary Service with Participation of Flexible Resource on Demand Side. Autom. Electr. Power Syst. 2021, 45, 148–157. [Google Scholar]
- Li, Y. Research on Power System Flexibility Dispatch and Its Assessment with Large Scale Renewable Energy Sources. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2020. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Pan, Z.; Wang, J. Optimized Dispatching Method for Flexibility Improvement of Distribution Network with High-penetration Distributed Generation. Autom. Electr. Power Syst. 2018, 42, 86–93. [Google Scholar]
- Zhang, X.; Guo, M.; Lin, Y.; Liang, C.; Li, Y.; Yang, Y.; Lin, S. A Bilayer Optimal Dispatch Approach for Distribution Networks with Distributed Photovoltaic Considering the Flexibility. J. Electr. Power Sci. Technol. 2021, 36, 56–66. [Google Scholar] [CrossRef]
- Sun, L.; Yu, T. Optimal Collaborative Scheduling Strategy of Mobile Energy Storage System and Electric Vehicles Considering Spatio Temporal Characteristics. Processes 2025, 13, 2242. [Google Scholar] [CrossRef]
- Zhang, P.; Xie, L.; Ma, R.; Lu, M.; Song, X.; Yang, J.; Bian, Y. Multi-player Two-stage Low Carbon Optimal Operation Strategy Considering Electric Vehicle Cluster Schedulability. Power Syst. Technol. 2022, 46, 4809–4825. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; Wang, H.; Wu, Z. Two-stage Flexibility Improvement Optimization Method of Distribution Network Considering EV Charging and Scheduling of Energy Storage and Interruptible loads. Electr. Power Autom. Equip. 2020, 40, 1–10. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, W.; Li, Y.; Zhang, Z. Constructing Low Carbon Energy Community Group Based on Multi-energy Net-work System. Comput. Simulator 2022, 39, 108–115. [Google Scholar]
- Lilla, S.; Orozco, C.; Borghetti, A.; Napolitano, F.; Tossani, F. Day Ahead Scheduling of a Local Energy Community: An Alternating Direction Method of Multipliers Approach. IEEE Trans. Power Syst. 2020, 35, 1132–1142. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, H.; Shen, X.; Ge, D.; Fu, L. Distributed Optimal Scheduling for Prosumer in Distribution Network for Energy Community Energy Management. Proc. CSEE 2022, 42, 4449–4459. [Google Scholar] [CrossRef]
- Zhang, G.; Li, F. Day-ahead Optimal Scheduling of Power System Considering Comprehensive Flexibility of Source-load-storage. Electr. Power Autom. Equip. 2020, 40, 159–167. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, R.; Li, F. A Novel Peer-to-Peer Local Electricity Market for Joint Trading of Energy and Uncertainty. IEEE Trans. Smart Grid 2020, 11, 1205–1215. [Google Scholar] [CrossRef]
- Kampouris, Y.; Mandoulidis, P.; Prionistis, G. Adaptive Day-ahead and Intra-day Frequency Restoration Reserves Calculation Methodology for Electricity Balancing Markets. In Proceedings of the 2023 IEEE Belgrade Power Tech, Belgrade, Serbia, 25–29 June 2023. [Google Scholar] [CrossRef]
- Pavić, I.; Pandžić, H.; Capuder, T. Day-ahead Energy and Balancing Capacity Bidding Considering Balancing Energy Market Uncertainty. In Proceedings of the 2022 International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, The Netherlands, 5–7 September 2022. [Google Scholar] [CrossRef]
- Hemmati, M.; Mohammadi-Ivatloo, B.; Abapour, M.; Anvari-Moghaddam, A. Optimal Chance-Constrained Scheduling of Reconfigurable Microgrids Considering Islanding Operation Constraints. IEEE Syst. J. 2020, 14, 5340–5349. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, C.; Gu, T.; Xue, F.; Gao, C.; Song, X. Corrective Control Method of Wind Power System Based on Gaussian Mixture Model and Approximate Linear Programming. Electr. Power Autom. Equip. 2022, 42, 35–42. [Google Scholar] [CrossRef]
- Li, J.; Jia, L.; Peng, D.; Hou, R. Auxiliary Modelling Error and Probability Density Function Based Neuro-fuzzy Short-term Wind Power Prediction. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023. [Google Scholar] [CrossRef]
- Wang, T.; Hu, L.; Liu, Z.; Zhu, H.; Li, F.; Xue, Y.; Liu, C. Distributionally Robust Real-time Dispatch Model Considering Flexibility Requirement and Correlations of Wind Powers. J. Glob. Energy Inter-Connect. 2021, 4, 585–594. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, M.; Lu, W. Control Method for Battery Energy Storage Participating in Frequency Regulation Market Considering Degradation Cost. Power Syst. Technol. 2021, 45, 3043–3051. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, Y.; Li, B.; Qian, X.; Zhang, S.; Wang, X.; Zhang, X.; Chen, M. Improved Cycle Aging Cost Model for Battery Energy Storage Systems Considering More Accurate Battery Life Degradation. IEEE Access 2022, 10, 297–307. [Google Scholar] [CrossRef]
- Chakkalakkal, S.; Sagar, S.M.V.; Mirfakhrai, T.; Liu, W.; Bhavaraju, V. Comparative Study of Battery Management Algorithms on Customer Return and Battery Life in Building Energy Storage Applications. In Proceedings of the IECON 2024-50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024. [Google Scholar] [CrossRef]
- Lu, Y. Research on Energy Storage Allocation and Energy Management Strategy of Community Microgrid Including Electric Vehicles. Master’s Thesis, Jiangnan University, Wuxi, China, 2021. [Google Scholar] [CrossRef]
- Gupta, A.; Suhag, S. Charging Station Control Strategy Considering Dynamic Behaviour of Electric Vehicles with Variable State of Charge Regulation for Energy Management of Autonomous Micro-grid. J. Energy Storage 2023, 59, 106460. [Google Scholar] [CrossRef]
- Kumar, R.R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in Batteries, Battery Modeling, Battery Management System, Battery Thermal Management, SOC, SOH, and Charge/Discharge Characteristics in EV Applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, R.; Qin, Y.; Sun, H. Energy Management of Battery Energy Storage System Based on Adaptive Inversion Sliding Mode. Electr. Meas. Instrum. 2022, 59, 67–74. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).