Hazelnut Kernel Percentage Calculation System with DCIoU and Neighborhood Relationship Algorithm
Abstract
1. Introduction
- X-ray hazelnut image dataset has been created.
- All hazelnut defects have been detected in hazelnut kernel percentage calculation.
- A new bounding box regression method DCIoU has been developed for anchor based deep learning methods.
- A Neighborhood Relationship Algorithm that can make a more appropriate bounding box selection for bounding box-based deep learning methods has been developed.
- A system model that minimizes errors that may occur while determining hazelnut kernel percentage has been proposed by performing the above-mentioned operations.
2. Materials and Methods
2.1. Hazelnut Quality Assessment System
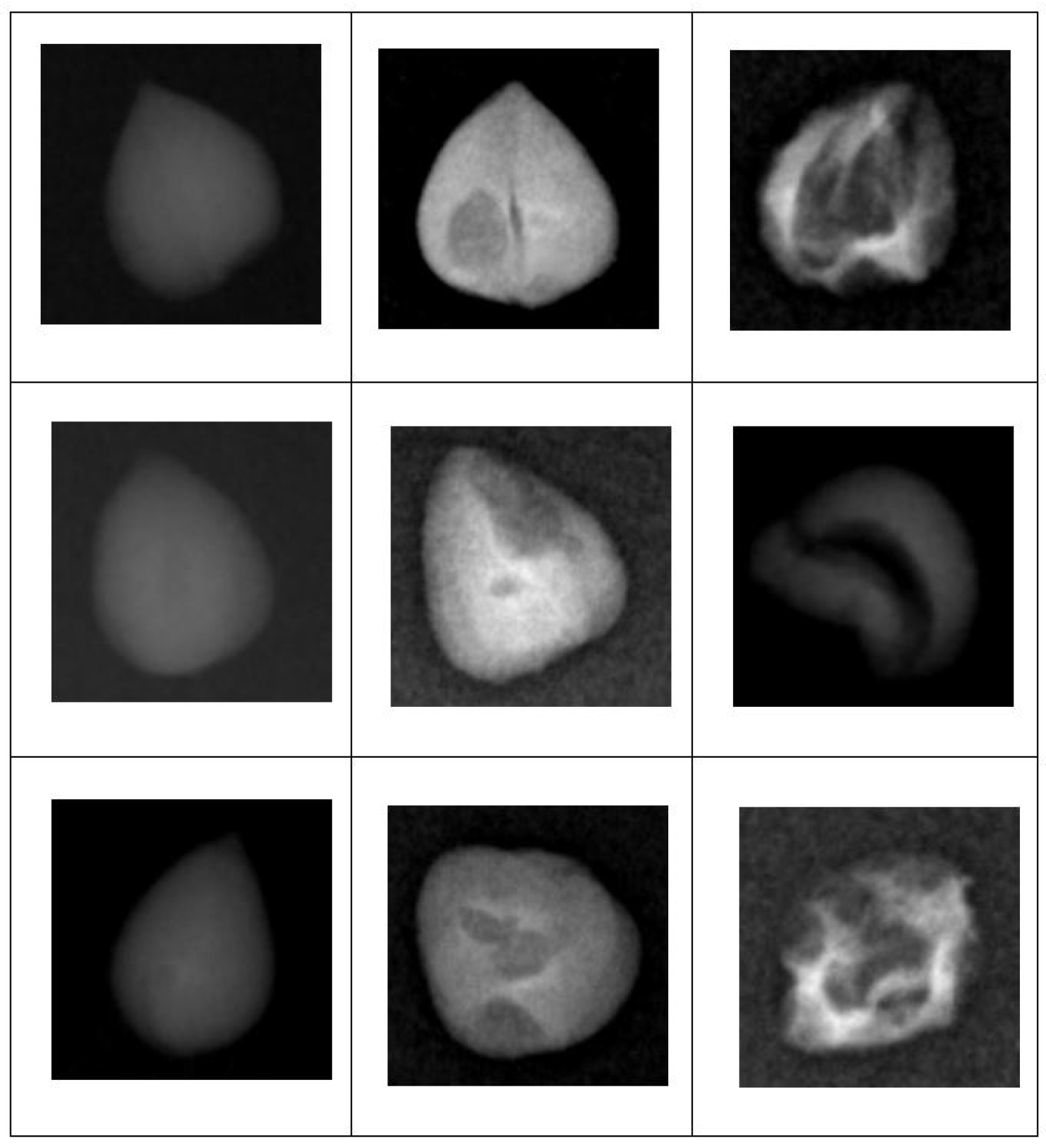
2.2. Dataset Creation
2.3. Preprocessing Stage
2.4. Deep Learning Method
2.5. Bounding Box Regression
2.5.1. Intersection over Union (IoU)
2.5.2. Generalized Intersection over Union (GIoU)
2.5.3. Distance Intersection over Union (DIoU) and Complete Intersection over Union (CIoU)
2.6. The Proposed Methods
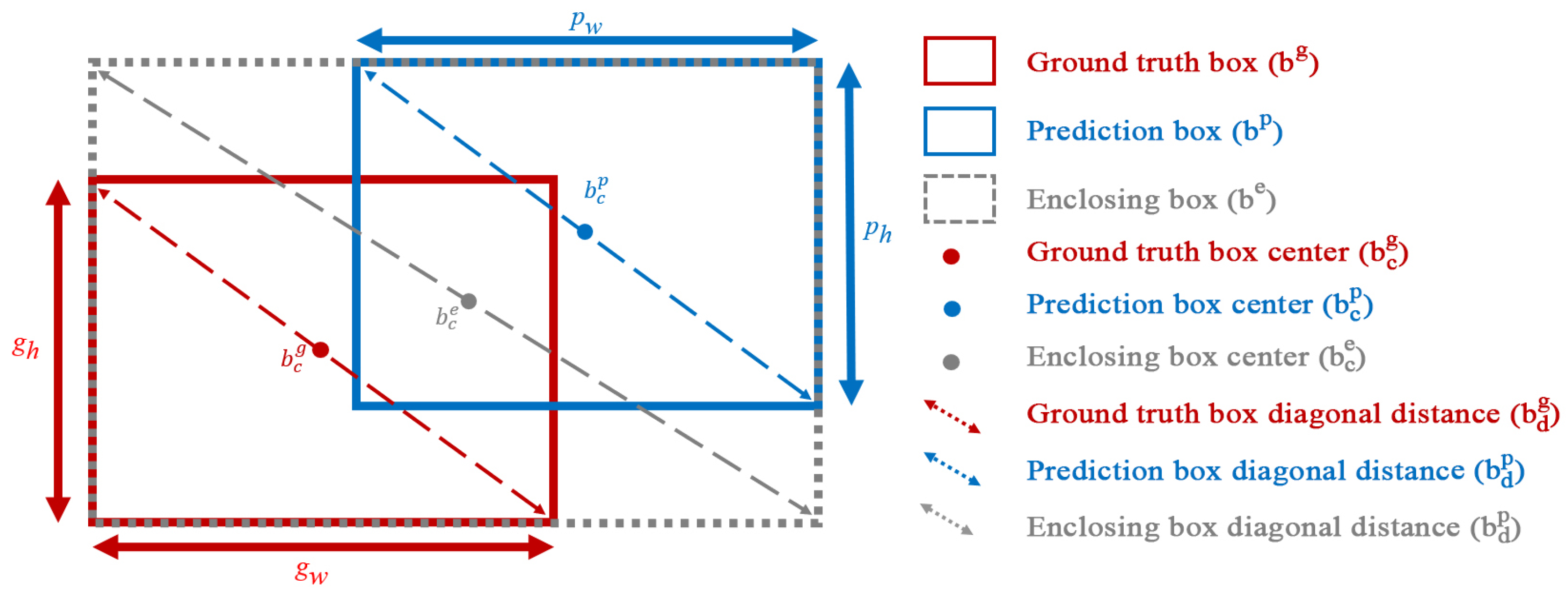
2.6.1. Distance Center Intersection over Union (DCIoU)
| Algorithm 1 DCIoU Algorithm |
| Input: Prediction box and ground-truth box coordinates: , Output: DCIoU
|
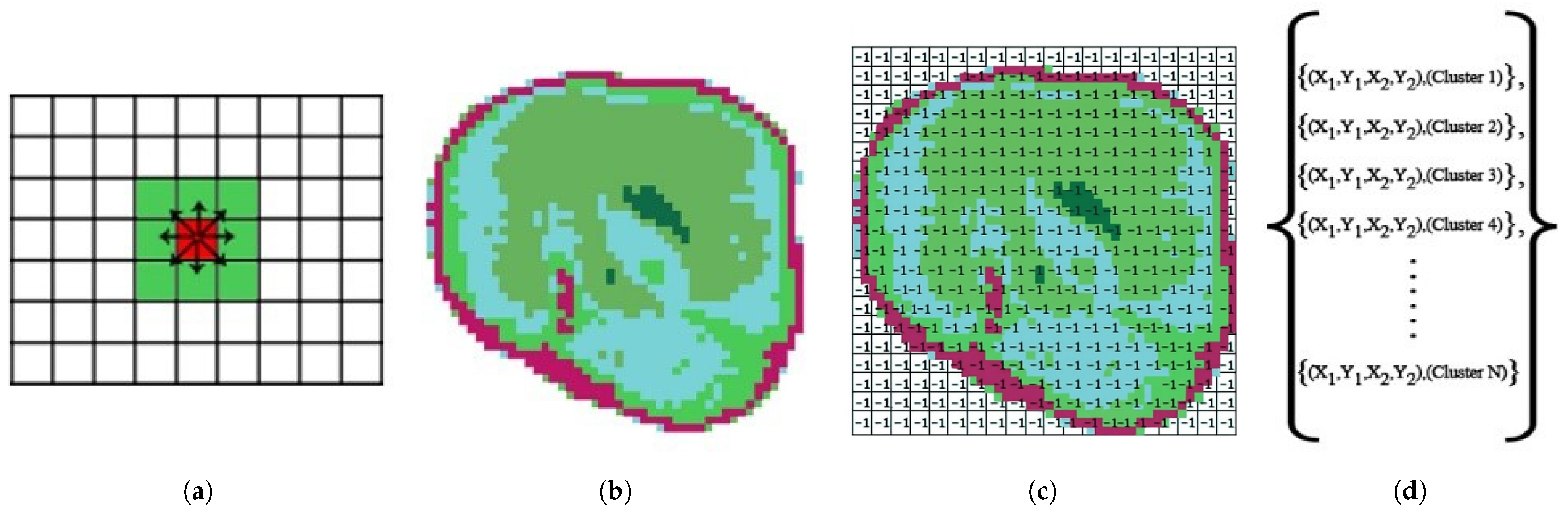
2.6.2. Neighborhood Relationship Algorithm
| Algorithm 2 Neighborhood Relationship Algorithm |
| Input: The image obtained during the preprocessing stage Output: Tensor
|
3. Results and Discussion
3.1. Tests for the DCIoU Method
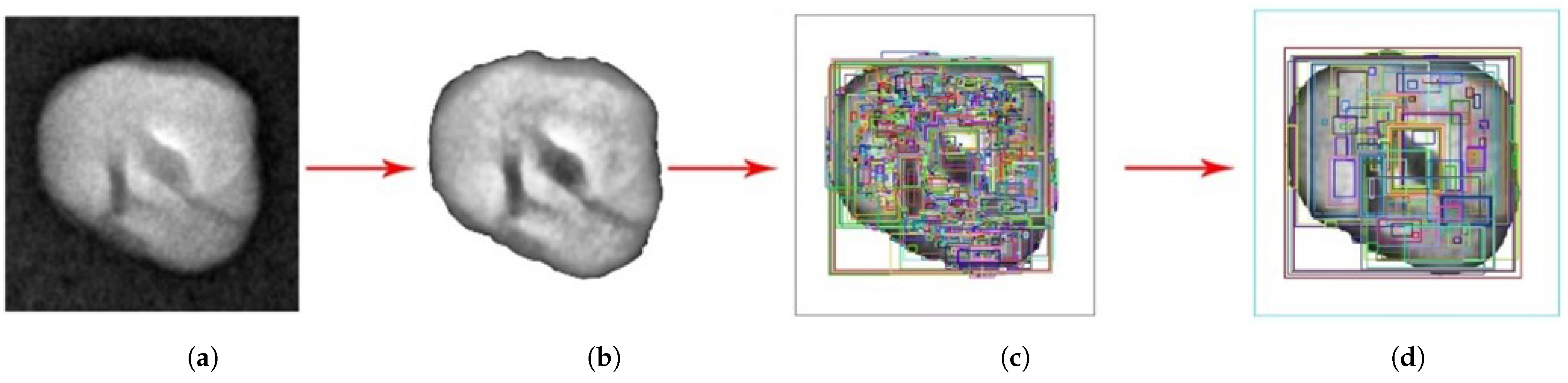
3.2. Neighborhood Relationship Algorithm Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| OECD | Organization for Economic Co-operation and Development |
| UNECE | United Nations Economic Commission for Europe |
| BiT | BigTransfer |
| OA-MIL | Object-Aware Multiple Instance Learning |
| AR | Alpha-Refine |
| IoU | Intersection over Union |
| GIoU | Generalized Intersection over Union |
| DIoU | Distance Intersection over Union |
| CIoU | Complete Intersection over Union |
| DCIoU | Distance Center Intersection over Union |
| CLAHE | Contrast Limited Adaptive Histogram Equalization |
| NMS | Non-Maximum Suppression |
References
- Król, K.; Gantner, M. Morphological Traits and Chemical Composition of Hazelnut from Different Geographical Origins: A Review. Agriculture 2020, 10, 375. [Google Scholar] [CrossRef]
- Romero-Aroca, A.; Rovira, M.; Cristofori, V.; Silvestri, C. Hazelnut Kernel Size and Industrial Aptitude. Agriculture 2021, 11, 1115. [Google Scholar] [CrossRef]
- Cabo, S.; Aires, A.; Carvalho, R.; Vilela, A.; Pascual-Seva, N.; Silva, A.P.; Gonçalves, B. Kaolin, Ascophyllum nodosum and salicylic acid mitigate effects of summer stress improving hazelnut quality. J. Sci. Food Agric. 2021, 101, 459–475. [Google Scholar] [CrossRef] [PubMed]
- Poșta, D.S.; Radulov, I.; Cocan, I.; Berbecea, A.A.; Alexa, E.; Hotea, I.; Iordănescu, O.A.; Băla, M.; Cântar, I.C.; Rózsa, S.; et al. Hazelnuts (Corylus avellana L.) Spontaneous Flora West Part Romania: A Source of Nutrients for Locals. Agronomy 2022, 12, 214. [Google Scholar] [CrossRef]
- FAOSTAT. Food and Agricultural Organization of the United Nations. 2023. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 10 April 2024).
- Pacchiarelli, A.; Silvestri, C.; Muganu, M.; Cristofori, V. Influence of the Plant Training System on Yield and Nut Traits of European Hazelnut (Corylus avellana L.) Cultiv. Nocchione. Agronomy 2025, 15, 345. [Google Scholar] [CrossRef]
- Ayyildiz, E.; Yildiz, A.; Taşkın, A.; Ozkan, C. An interval valued Pythagorean fuzzy AHP integrated quality function deployment methodology for hazelnut production in Turkey. Expert Syst. Appl. 2023, 231, 120708. [Google Scholar] [CrossRef]
- Günay, H.F.; Uyğun, U.; Yardımcıoğlu, F. Evaluation of Fiscal Support on Hazelnut Production in Point of Efficiency and Farmer Content. Sak. Univ. J. Econ. 2020, 9, 299–332. [Google Scholar]
- Valeriano, T.; Fischer, K.; Ginaldi, F.; Giustarini, L.; Castello, G.; Bregaglio, S. Rotten Hazelnuts Prediction via Simulation Modeling—A Case Study on the Turkish Hazelnut Sector. Front. Plant Sci. 2022, 13, 766493. [Google Scholar] [CrossRef] [PubMed]
- Bak, T.; Karadeniz, T. Effects of Branch Number on Quality Traits and Yield Properties of European Hazelnut (Corylus avellana L.). Agric. 2021, 11, 437. [Google Scholar] [CrossRef]
- Karakaya, O.; Yaman, M.; Balta, F.; Yilmaz, M.; Balta, M.F. Assessment of genetic diversity revealed by morphological traits and ISSR markers in hazelnut germplasm (Corylus avellana L.) East. Black Sea Reg. Turkey. Genet. Resour. Crop Evol. 2023, 70, 525–537. [Google Scholar] [CrossRef]
- Spataro, F.; Rosso, F.; Genova, G.; Caligiani, A. Untargeted UHPLC-HRMS as a new tool for the detection of rotten defect markers in hazelnuts of different origins. Microchem. J. 2024, 197, 109743. [Google Scholar] [CrossRef]
- Turan, A. Determination of Some Traits on Arrival of Hazelnut at Purchasing Points: The Case of Giresun. Akad. Ziraat Derg. 2023, 12, 99–108. [Google Scholar] [CrossRef]
- Ferrão, A.C.; Guiné, R.P.F.; Ramalhosa, E.; Lopes, A.; Rodrigues, C.; Martins, H.; Gonçalves, R.; Correia, P.M.R. Chemical and Physical Properties of Some Hazelnut Varieties Grown in Portugal. Agronomy 2021, 11, 1476. [Google Scholar] [CrossRef]
- Bostan, S.Z.; Karakaya, O. Morphological, chemical, and molecular characterization of a new late-leafing and high fruit quality hazelnut (Corylus avellana L.) Genotype. Genet. Resour. Crop Evol. 2024, 71, 5113–5126. [Google Scholar] [CrossRef]
- İşbakan, H.; Bostan, S.Z. Relationships between plant morphological traits, nut yield and quality traits in hazelnut. Ordu Univ. J. Sci. Technol. 2020, 10, 32–45. [Google Scholar]
- OECD. Organisation for Economic Co-Operation and Development. 2011. Available online: https://www.oecd.org/en/publications/inshell-hazelnuts-and-hazelnut-kernels_9789264166721-en-fr.html (accessed on 10 April 2024).
- UNECE. United Nations Economic Commission for Europe. 2010. Available online: https://unece.org/fileadmin/DAM/trade/agr/standard/dry/dry_e/04HazelnutKernels_e.pdf (accessed on 10 April 2024).
- Bostan, S.Z. Nut and kernel defects in hazelnut. Akad. Ziraat Derg. 2019, 8, 157–166. [Google Scholar] [CrossRef]
- Gavilán-CuiCui, G.; Padilla-Contreras, D.; Manterola-Barroso, C.; Morina, F.; Meriño-Gergichevich, C. Antioxidant Performance in Hazelnut (Corylus avellana L.) Cultiv. Shell Is Subst. Influ. Seas. Locality. Agronomy 2024, 14, 1412. [Google Scholar] [CrossRef]
- Kan, E.; Akgün, M.; Turan, A. Effect of Brown Marmorated Stink Bug [Halyomorpha halys Stal (Hemiptera: Pentatomidae)] on Physical Traits of Hazelnuts. Black Sea J. Sci. 2024, 14, 1654–1664. [Google Scholar] [CrossRef]
- Silvestri, C.; Bacchetta, L.; Bellincontro, A.; Cristofori, V. Advances in cultivar choice, hazelnut orchard management, and nut storage to enhance product quality and safety: An overview. J. Sci. Food Agric. 2020, 101, 27–43. [Google Scholar] [CrossRef] [PubMed]
- Pannico, A.; Schouten, R.E.; Basile, B.; Romano, R.; Woltering, E.J.; Cirillo, C. Non-destructive detection of flawed hazelnut kernels and lipid oxidation assessment using NIR spectroscopy. J. Food Eng. 2015, 160, 42–48. [Google Scholar] [CrossRef]
- Mahanti, N.K.; Pandiselvam, R.; Kothakota, A.; Ishwarya, S.P.; Chakraborty, S.K.; Kumar, M.; Cozzolino, D. Emerging non-destructive imaging techniques for fruit damage detection: Image processing and analysis. Trends Food Sci. Technol. 2022, 120, 418–438. [Google Scholar] [CrossRef]
- Abasi, S.; Minaei, S.; Jamshidi, B.; Fathi, D. Dedicated non-destructive devices for food quality measurement: A review. Trends Food Sci. Technol. 2018, 78, 197–205. [Google Scholar] [CrossRef]
- He, Y.; Xiao, Q.; Bai, X.; Zhou, L.; Liu, F.; Zhang, C. A Recent progress of nondestructive techniques for fruits damage inspection: A review. Crit. Rev. Food Sci. Nutr. 2021, 62, 5476–5494. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Khan, M.A.; Butola, R.; Singari, R.M. Advances in applications of Non-Destructive Testing (NDT): A review. Adv. Mater. Process. Technol. 2021, 8, 2286–2307. [Google Scholar] [CrossRef]
- Li, L.; Jia, X.; Fan, K. Recent advance in nondestructive imaging technology for detecting quality of fruits and vegetables: A review. Crit. Rev. Food Sci. Nutr. 2024, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Ropodi, A.I.; Panagou, E.Z.; Nychas, G.-J.E. Data mining derived from food analyses using non-invasive/non-destructive analytical techniques; determination of food authenticity, quality & safety in tandem with computer science disciplines. Trends Food Sci. Technol. 2016, 50, 11–25. [Google Scholar] [CrossRef]
- Torres-Cobos, B.; Tres, A.; Vichi, S.; Guardiola, F.; Rovira, M.; Romero, A.; Baeten, V.; Fernández-Pierna, J.A. Comparative analysis of spectroscopic methods for rapid authentication of hazelnut cultivar and origin. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 326, 125367. [Google Scholar] [CrossRef] [PubMed]
- Shakiba, N.; Gerdes, A.; Holz, N.; Wenck, S.; Bachmann, R.; Schneider, T.; Seifert, S.; Fischer, M.; Hackl, T. Determination of the geographical origin of hazelnuts (Corylus avellana L.) Near-Infrared Spectrosc. (NIR) A Low-Level Fusion Nucl. Magn. Reson. (NMR). Microchem. J. 2022, 174, 107066. [Google Scholar] [CrossRef]
- Xue, Q.; Miao, P.; Miao, K.; Yu, Y.; Li, Z. X-ray-based machine vision technique for detection of internal defects of sterculia seeds. J. Food Sci. 2022, 87, 3386–3395. [Google Scholar] [CrossRef] [PubMed]
- Zehi, Z.B.; Afshari, A.; Noori, S.M.A.; Jannat, B.; Hashemi, M. The Effects of X-Ray Irradiation on Safety and Nutritional Value of Food: A Systematic Review Article. Curr. Pharm. Biotechnol. 2020, 21, 919–926. [Google Scholar] [CrossRef] [PubMed]
- Kayakuş, M.; Kabas, Ö.; Ünal, İ.; Paçacı, S.; Dinca, M.N. Non-destructive prediction of hazelnut and hazelnut kernel deformation energy using machine learning techniques. Int. J. Food Prop. 2024, 27, 326–340. [Google Scholar] [CrossRef]
- El-Mesery, H.S.; Mao, H.; Abomohra, A.E.-F. Applications of Non-destructive Technologies for Agricultural and Food Products Quality Inspection. Sensors 2019, 19, 846. [Google Scholar] [CrossRef] [PubMed]
- Adak, M.F. Identification of Plant Species by Deep Learning and Providing as A Mobile Application. Sak. Univ. J. Comput. Inf. Sci. 2020, 3, 231–238. [Google Scholar] [CrossRef]
- Zhu, L.; Spachos, P.; Pensini, E.; Plataniotis, K.N. Deep learning and machine vision for food processing: A survey. Curr. Res. Food Sci. 2021, 4, 233–249. [Google Scholar] [CrossRef] [PubMed]
- Güney, E.; Bayılmış, C.; Çakar, S.; Erol, E.; Atmaca, Ö. Autonomous control of shore robotic charging systems based on computer vision. Expert Syst. Appl. 2024, 238, 122116. [Google Scholar] [CrossRef]
- Selamet, F.; Cakar, S.; Kotan, M. Automatic Detection and Classification of Defective Areas on Metal Parts by Using Adaptive Fusion of Faster R-CNN and Shape From Shading. IEEE Access 2022, 10, 126030–126038. [Google Scholar] [CrossRef]
- Cerezci, F.; Çakar, S.; Oz, M.A.; Oz, C.; Tasci, T.; Hizal, S.; Altay, C. Online metallic surface defect detection using deep learning. Emerg. Mater. Res. 2020, 4, 1266–1273. [Google Scholar] [CrossRef]
- Oztel, I.; Yolcu Oztel, G.; Sahin, V.H. Deep Learning-Based Skin Diseases Classification using Smartphones. Adv. Intell. Syst. 2023, 5, 2300211. [Google Scholar] [CrossRef]
- Taner, A.; Öztekin, Y.B.; Duran, H. Performance Analysis of Deep Learning CNN Models for Variety Classification in Hazelnut. Sustainability 2021, 13, 6527. [Google Scholar] [CrossRef]
- Gencturk, B.; Arsoy, S.; Taspinar, Y.S.; Cinar, İ.; Kursun, R.; Yasin, E.Y.; Koklu, M. Detection of hazelnut varieties and development of mobile application with CNN data fusion feature reduction-based models. Eur. Food Res. Technol. 2024, 250, 97–110. [Google Scholar] [CrossRef]
- Ünal, Z.; Aktaş, H. Classification of hazelnut kernels with deep learning. Postharvest Biol. Technol. 2023, 197, 112225. [Google Scholar] [CrossRef]
- Dönmez, E.; Kılıçarslan, S.; Diker, A. Classification of hazelnut varieties based on bigtransfer deep learning model. Eur. Food Res. Technol. 2024, 250, 1433–1442. [Google Scholar] [CrossRef]
- Keles, O.; Taner, A. Classification of hazelnut varieties by using artificial neural network and discriminant analysis. Span. J. Agric. Res. 2021, 19, e0211. [Google Scholar] [CrossRef]
- Aydin, S.; Aldara, D. Microservices-based databank for Turkish hazelnut cultivars using IoT and semantic web Technologies. Concurr. Comput. Pract. Exp. 2024, 36, e8062. [Google Scholar] [CrossRef]
- Shojaeian, A.; Bagherpour, H.; Bagherpour, R.; Parian, J.A.; Fatehi, F.; Taghinezhad, E. The Potential Application of Innovative Methods in Neural Networks for Surface Crack Recognition of Unshelled Hazelnut. J. Food Process. Preserv. 2023, 2023, 2177724. [Google Scholar] [CrossRef]
- Dönmez, E.; Ünal, Y.; Kayhan, H. Bacterial Disease Detection of Cherry Plant Using Deep Features. Sak. Univ. J. Comput. Inf. Sci. 2024, 7, 1–10. [Google Scholar] [CrossRef]
- Kayaalp, K.; Metlek, S. Classification of Robust and Rotten Apples by Deep Learning Algorithm. Sak. Univ. J. Comput. Inf. Sci. 2020, 3, 112–120. [Google Scholar] [CrossRef]
- Sasso, D.; Lodato, F.; Sabatini, A.; Pennazza, G.; Vollero, L.; Santonico, M.; Merone, M. Hazelnut mapping detection system using optical and radar remote sensing: Benchmarking machine learning algorithms. Artif. Intell. Agric. 2024, 12, 97–108. [Google Scholar] [CrossRef]
- Maier, G.; Shevchyk, A.; Flitter, M.; Gruna, R.; Längle, T.; Hanebeck, U.D.; Beyerer, J. Motion-based visual inspection of optically indiscernible defects on the example of hazelnuts. Comput. Electron. Agric. 2021, 185, 106147. [Google Scholar] [CrossRef]
- Khosa, I.; Pasero, E. Feature extraction in X-ray images for hazelnuts classification. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 4 September 2014. [Google Scholar] [CrossRef]
- Solak, S.; Altınışık, U. Detection and classification of hazelnut fruit by using image processing techniques and clustering methods. Sak. Univ. J. Sci. 2018, 22, 56–65. [Google Scholar] [CrossRef][Green Version]
- Kaur, R.; Singh, S. A comprehensive review of object detection with deep learning. Digit. Signal Process. 2023, 132, 103812. [Google Scholar] [CrossRef]
- Kaur, J.; Singh, W. Tools, techniques, datasets and application areas for object detection in an image: A review. Multimed. Tools Appl. 2022, 81, 38297–38351. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Lin, S.; Cheng, G.; Yao, X.; Ren, H.; Wang, W. Object Detection in Remote Sensing Images Based on Improved Bounding Box Regression and Multi-Level Features Fusion. Remote Sens. 2020, 12, 143. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Meng, F.; Song, Z.; Xu, L. Segmenting Beyond the Bounding Box for Instance Segmentation. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 704–714. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, F.; Liu, D.; Pu, W.; Zhang, Q. Manhattan-distance IOU loss for fast and accurate bounding box regression and object detection. Neurocomputing 2022, 500, 99–114. [Google Scholar] [CrossRef]
- Ravi, N.; Naqvi, S.; El-Sharkawy, M. BIoU: An Improved Bounding Box Regression for Object Detection. J. Low Power Electron. Appl. 2022, 12, 51. [Google Scholar] [CrossRef]
- Yuan, D.; Shu, X.; Fan, N.; Chang, X.; Liu, Q.; He, Z. Accurate bounding-box regression with distance-IoU loss for visual tracking. J. Vis. Commun. Image Represent. 2022, 83, 103428. [Google Scholar] [CrossRef]
- Liu, C.; Wang, K.; Lu, H.; Cao, Z.; Zhang, Z. Robust Object Detection with Inaccurate Bounding Boxes. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; ECCV Lecture Notes in Computer Science 2022. Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Vo, X.-T.; Jo, K.-H. Accurate Bounding Box Prediction for Single-Shot Object Detection. IEEE Trans. Ind. Inform. 2022, 8, 5961–5971. [Google Scholar] [CrossRef]
- Zhang, R.; Di, Y.; Lou, Z.; Manhardt, F.; Tombari, F.; Ji, X. RBP-Pose: Residual Bounding Box Projection for Category-Level Pose Estimation. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; ECCV Lecture Notes in Computer Science 2022. Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Yan, B.; Zhang, X.; Wang, D.; Lu, H.; Yang, X. Alpha-Refine: Boosting Tracking Performance by Precise Bounding Box Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Yu, J.; Jiang, Y.; Wang, Z.; Cao, Z.; Huang, T. UnitBox: An Advanced Object Detection Network. In Proceedings of the MM ’16: ACM Multimedia Conference, Amsterdam, The Netherlands, 15–19 October 2016. [Google Scholar]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 658–666. [Google Scholar]
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU loss: Faster and better learning for bounding box regression. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–8 February 2020; Volume 34, pp. 12993–13000. [Google Scholar]
- Ultralytics. COCO-128 Data Set. Available online: https://docs.ultralytics.com/tr/datasets/detect/coco128/ (accessed on 22 July 2025).
- Wong, K.Y. Official YOLOv7. 2023. Available online: https://github.com/WongKinYiu/yolov7 (accessed on 22 July 2025).
- Oztel, I.; Yolcu Oztel, G.; Akgun, D.A. hybrid LBP-DCNN based feature extraction method in YOLO: An application for masked face and social distance detection. Multimed. Tools Appl. 2023, 82, 1565–1583. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Yang, Y.; Li, M.; Yang, J.; Meng, B.; Bai, R. A Scale Balanced Loss for Bounding Box Regression. IEEE Access 2020, 8, 108438–108448. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Wang, H.; Zhang, S.; You, Y.; Yu, Z. Fused-IoU Loss: Efficient Learning for Accurate Bounding Box Regression. IEEE Access 2024, 12, 37363–37377. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Ren, W.; Zhang, Z.; Jia, Z.; Wang, L.; Tan, T. Focal and efficient IOU loss for accurate bounding box regression. Neurocomputing 2022, 506, 146–157. [Google Scholar] [CrossRef]
- Du, S.; Zhang, B.; Zhang, P. Scale-Sensitive IOU Loss: An Improved Regression Loss Function in Remote Sensing Object Detection. IEEE Access 2021, 9, 141258–141272. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, J. LCornerIoU: An Improved IoU-based Loss Function for Accurate Bounding Box Regression. In Proceedings of the 2021 International Conference on Intelligent Computing, Automation and Systems (ICICAS), Chongqing, China, 29–31 December 2021. [Google Scholar]
- Su, K.; Cao, L.; Zhao, B.; Li, N.; Wu, D.; Han, X. N-IoU: Better IoU-based bounding box regression loss for object detection. Neural Comput. Appl. 2024, 36, 3049–3063. [Google Scholar] [CrossRef]









| X-Ray Hazelnut | Precision | Recall | mAP@50 | mAP@50-95 | COCO-128 | Precision | Recall | mAP@50 | mAP@50-95 |
|---|---|---|---|---|---|---|---|---|---|
| IoU | 0.8872 | 0.8746 | 0.9175 | 0.7815 | IoU | 0.8924 | 0.8694 | 0.9428 | 0.7551 |
| GIoU | 0.9135 | 0.8665 | 0.9213 | 0.7886 | GIoU | 0.8988 | 0.8714 | 0.9475 | 0.7576 |
| DIoU | 0.9248 | 0.8765 | 0.9253 | 0.7893 | DIoU | 0.9213 | 0.8725 | 0.9512 | 0.7610 |
| CIoU | 0.9316 | 0.8790 | 0.9268 | 0.7904 | CIoU | 0.9240 | 0.8780 | 0.9573 | 0.7742 |
| DCIoU | 0.9448 | 0.8860 | 0.9373 | 0.7901 | DCIoU | 0.9348 | 0.8816 | 0.9632 | 0.7860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yılmaz, S.M.; Kaman, S.Ç.; Güler, E. Hazelnut Kernel Percentage Calculation System with DCIoU and Neighborhood Relationship Algorithm. Processes 2025, 13, 2414. https://doi.org/10.3390/pr13082414
Yılmaz SM, Kaman SÇ, Güler E. Hazelnut Kernel Percentage Calculation System with DCIoU and Neighborhood Relationship Algorithm. Processes. 2025; 13(8):2414. https://doi.org/10.3390/pr13082414
Chicago/Turabian StyleYılmaz, Sultan Murat, Serap Çakar Kaman, and Erkan Güler. 2025. "Hazelnut Kernel Percentage Calculation System with DCIoU and Neighborhood Relationship Algorithm" Processes 13, no. 8: 2414. https://doi.org/10.3390/pr13082414
APA StyleYılmaz, S. M., Kaman, S. Ç., & Güler, E. (2025). Hazelnut Kernel Percentage Calculation System with DCIoU and Neighborhood Relationship Algorithm. Processes, 13(8), 2414. https://doi.org/10.3390/pr13082414





