Life Cycle Cost Modeling and Multi-Dimensional Decision-Making of Multi-Energy Storage System in Different Source-Grid-Load Scenarios
Abstract
1. Introduction
- (1)
- A life-cycle cost (LCC)-based evaluation framework is established to quantify the economic performance of four representative energy storage technologies. This model comprehensively incorporates factors such as annual cycle frequency, operational efficiency, replacement costs, and discount rates, providing a more accurate and dynamic reflection of storage economics over the system’s operational lifespan.
- (2)
- A multi-attribute decision-making system is constructed that integrates economic indicators derived from LCC analysis with technical and environmental performance metrics. An improved G1-EWM method combined with a fuzzy comprehensive evaluation (FCE) model is employed to ensure balanced consideration of multi-dimensional performance attributes.
- (3)
- A scenario-based comparative analysis is conducted to evaluate the suitability of different energy storage technologies across the source, grid, and load sides in various application contexts. This enables targeted recommendations for energy storage deployment based on system needs and contextual constraints.
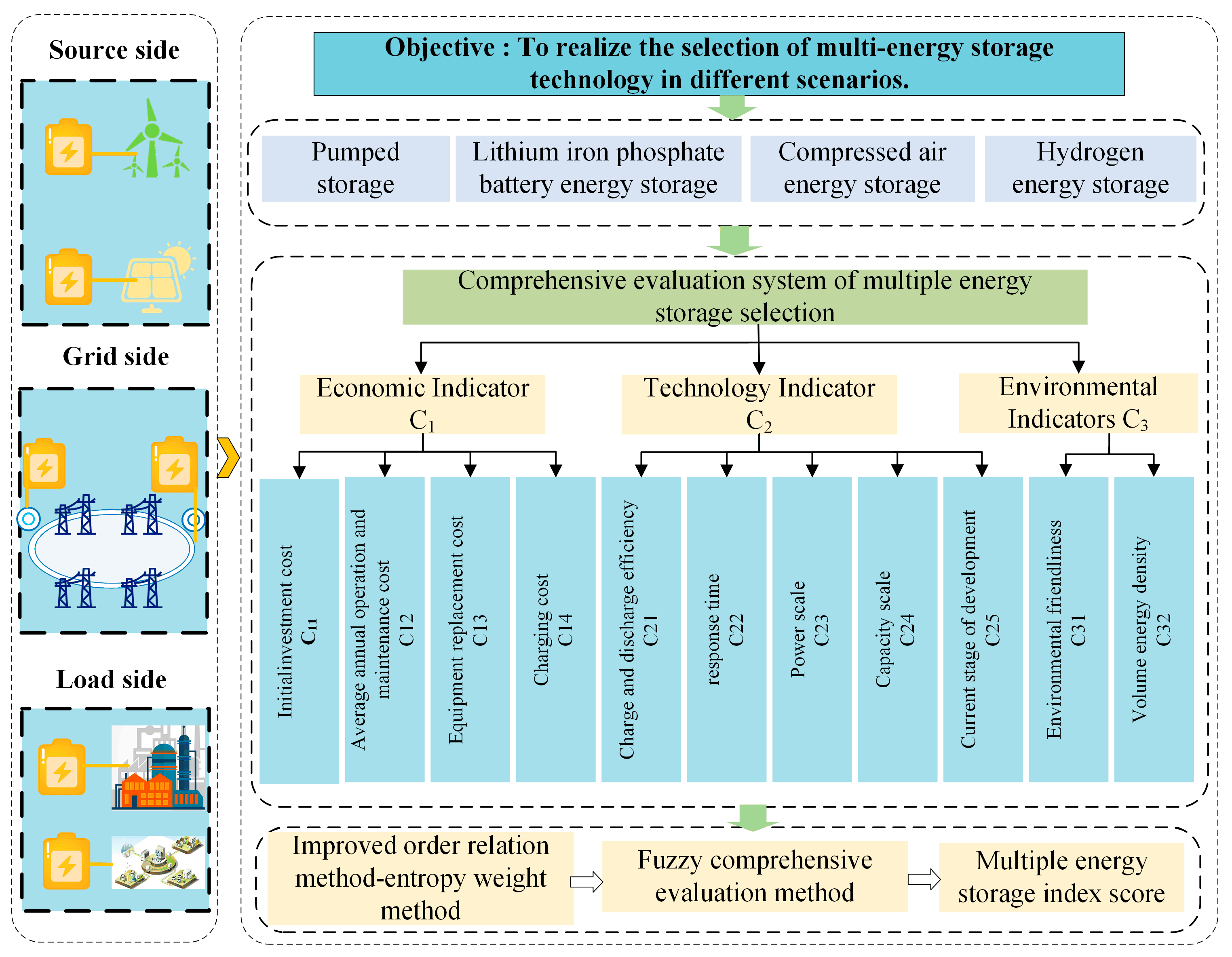
2. Characteristic Parameters of Energy Storage Technology in Power Systems
- (1)
- Economy (C1): This includes initial investment, operation and maintenance cost, equipment replacement cost, and charging cost, reflecting the capital investment and economic burden of the energy storage system in the whole life cycle.
- (2)
- Technical performance (C2): Covering charge and discharge efficiency, response time, and power and capacity scale, reflecting system operation efficiency, adjustment ability, and scale adaptability.
- (3)
- Environmental impact (C3): Including environmental friendliness and volumetric energy density, reflecting ecological impact and spatial utilization efficiency, respectively, this is an important basis for measuring green and low-carbon attributes. Environmental friendliness is included as a subjective indicator because different types of energy storage technologies have diverse environmental impacts across multiple dimensions, including resource extraction, manufacturing processes, operational emissions, and end-of-life disposal. A subjective indicator that comprehensively reflects environmental impact allows for a more holistic consideration of these factors. In contrast, relying on a single quantifiable metric—such as CO2 emissions per unit of energy or water consumption—may introduce bias due to incomplete data or limited representativeness. This could lead to evaluation bias against certain technologies and compromise the objectivity and fairness of the overall assessment results.
3. Life Cycle Cost Modeling
3.1. Life Cycle Cost Model of Energy Storage System
3.2. LCC Analysis of Energy Storage System
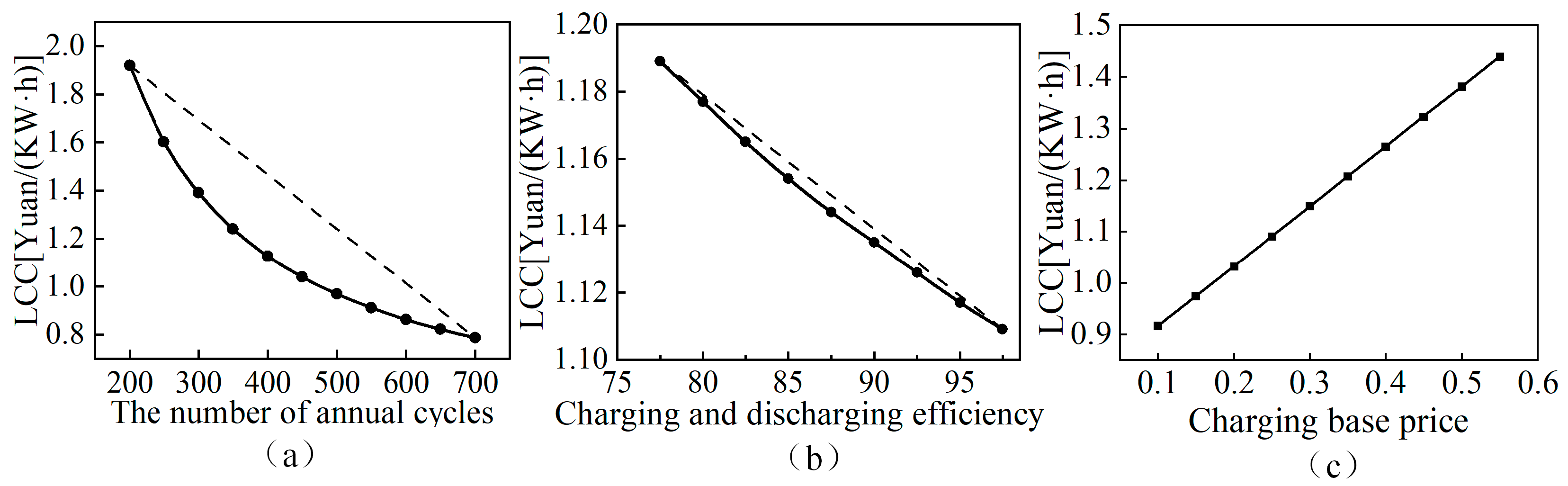
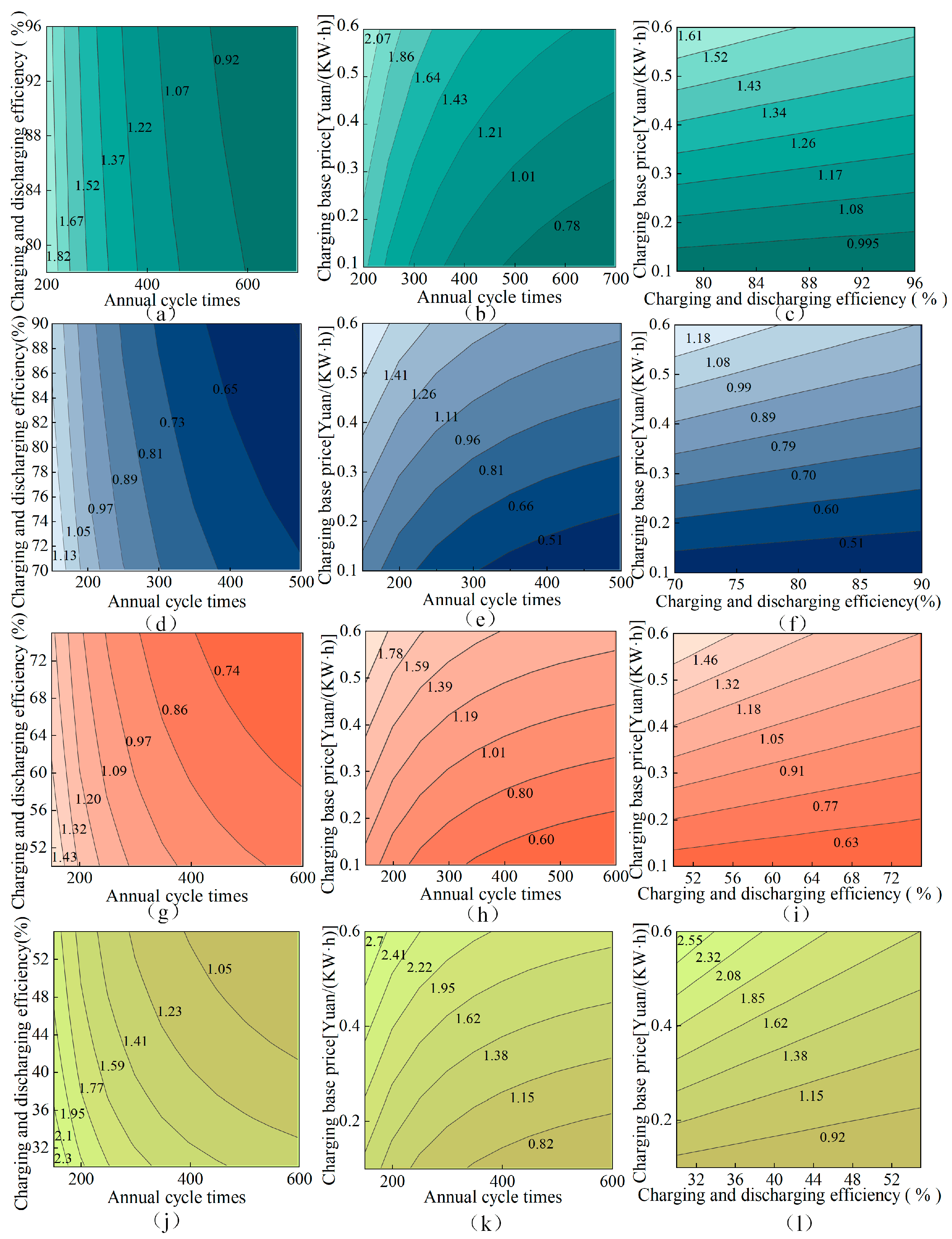
3.3. Analysis of the Influence of the LCC Parameters of the Energy Storage System
3.4. Comprehensive Comparison and Analysis
4. Multi-Energy Storage Technology Selection
4.1. Improved G1–EWM Comprehensive Weighting Method
4.1.1. Improved G1 Method
- (1)
- Determine the ranking of the indicators.
- (2)
- Constructing triangular fuzzy numbers.
- (3)
- Fuzzy judgment of the weight ratio of adjacent indicators.
- (4)
- Calculating Indicator Weight :
4.1.2. Comprehensive Empowerment Method
4.2. Fuzzy Comprehensive Evaluation Method
5. Typical Application Scenario Analysis
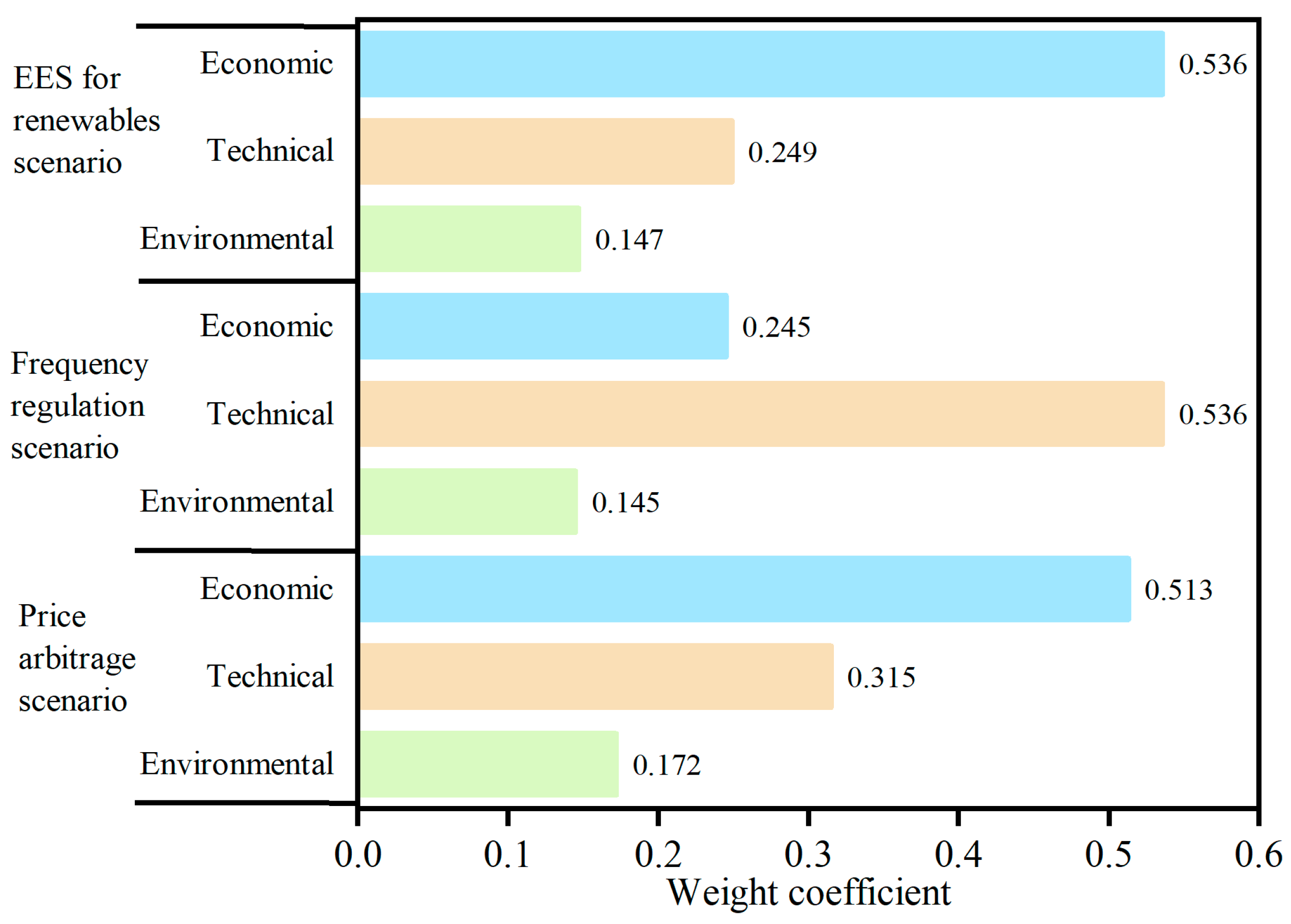
5.1. Indicator Weight of Different Application Scenarios
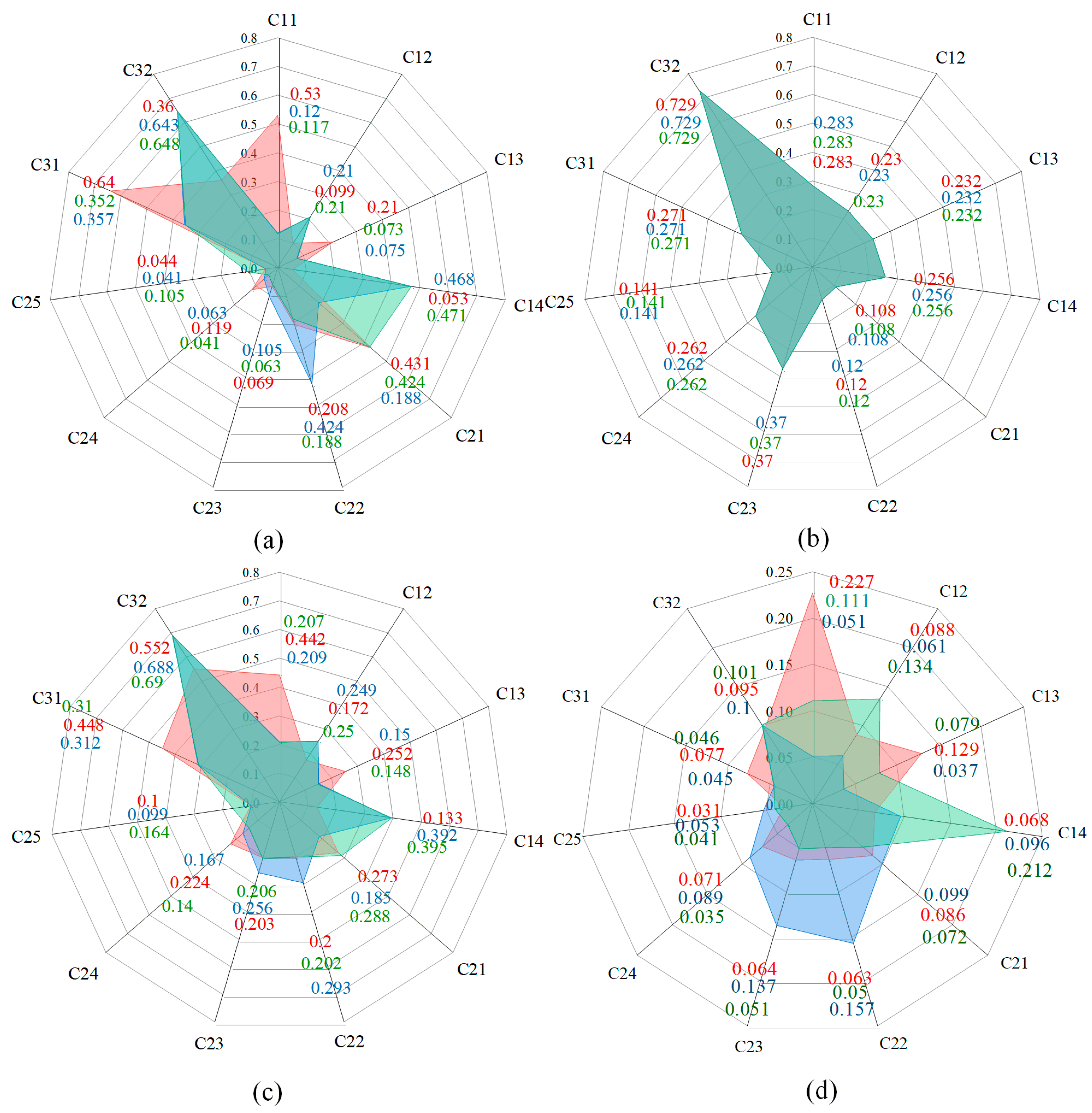
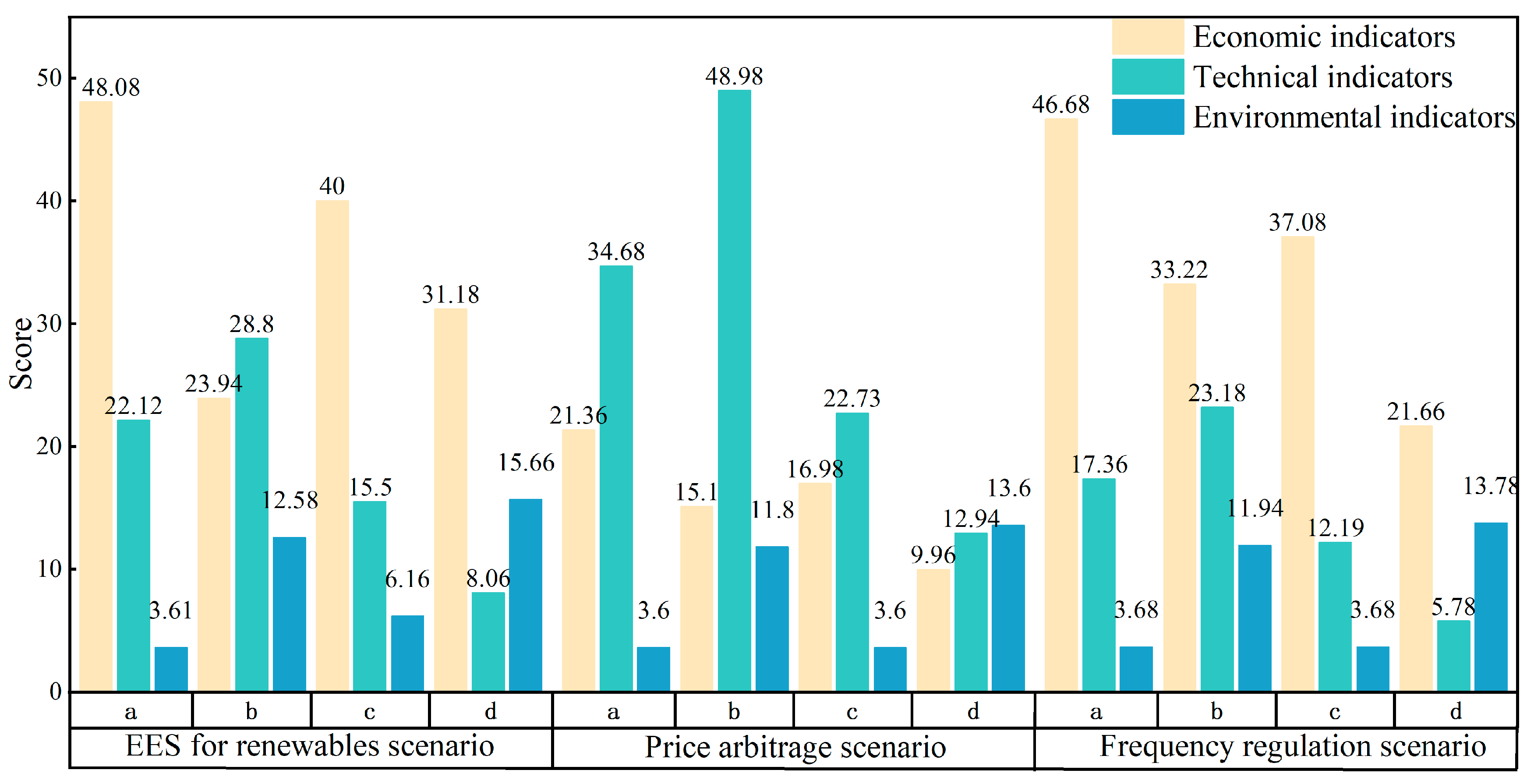
5.2. Comprehensive Evaluation of Multi-Energy Storage in Different Application Scenarios
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |||
| C | Cost | E | Scrapping cost rate |
| F | On-grid electricity | G | Gray range value |
| k | The number of experts participating in the evaluation | L | Conservative estimates of the ratio |
| M | Intermediate range value | N | Operation cycle |
| Q | Energy storage capacity | U | Factor set |
| V | Judgment set | W | Installed capacity |
| r | Discount rate | Weight | |
| Energy storage equipment parameters | Charge and discharge efficiency | ||
| Composition operator | |||
| Subscripts and superscripts | |||
| o | Objective weighting method | s | subjective weighting method |
| DOD | Charge and discharge depth | Deg | Annual cycle decay rate |
| E | Unit capacity | el | Electric charging price |
| ge | Geometric mean | Inv | Initial investment |
| j | Comprehensive weighting method | O&M | Operation and maintenance |
| P | Unit power | P-r | Unit power replacement |
| Pay | Annual cycle times | Repl | Replacement |
| pel | Charging | Eol | Recovery |
| Abbreviations | |||
| FCE | Fuzzy comprehensive evaluation | LCC | Life cycle cost |
| MADM | Multi-attribute decision-making | O&M | Operation and maintenance |
| G1-EWM | Ordinal relation-entropy weight method | G1 | Grade one |
| EWM | Entropy weight method | ||
Appendix A
| Membership Score | Very Good (100) | Better (80) | General (60) | Poor (40) | Very Poor (0) | |
| Indicators | ||||||
| Economic indicators | Initial investment cost | ≤0.3 | 0.3–0.45 | 0.45–0.55 | 0.55–0.65 | ≥0.65 |
| Average annual operation and maintenance cost | ≤0.02 | 0.02–0.05 | 0.05–0.12 | 0.12–0.18 | ≥0.2 | |
| Equipment replacement cost | ≤0.01 | 0.01–0.02 | 0.02–0.05 | 0.05–0.1 | ≥0.1 | |
| Charging cost | ≤0.35 | 0.35–0.45 | 0.45–0.55 | 0.55–0.65 | ≥0.65 | |
| Technical indicators | Charge and discharge efficiency | ≥90% | 80–90% | 60–80% | 40–60% | ≤ 40% |
| Charge and discharge response time | ms | 1 s | 5 s | 60 s | ≥60 s | |
| Power scale/MW | >100 | 50–100 | 10–50 | 1–10 | <1 | |
| Capacity scale/MWh | >500 | 100–500 | 10–100 | 1–10 | <1 | |
| Current stage of development | Large-scale development | Early commercialization | Demonstration application | technology research and development | Early stage of technology R & D | |
| Environmental indicators | Environmental friendliness | Excellent | Good | Medium | difference | Very poor |
| Volume energy density | ≥500 Wh/L | 350 Wh/L | 200 Wh/L | 50 Wh/L | ≦10 Wh/L |
Appendix B
| Scenarios | (Optimistic Value, Conservative Value) | |
| Frequency regulation scenario | Expert evaluation | |
| Deepseek evaluation | ||
| Price arbitrage scenario | Expert evaluation | |
| Deepseek evaluation | ||
| EES for renewables scenario | Expert evaluation | |
| Deepseek evaluation | ||
References
- Mentens, L.; Peremans, H.; Springael, J.; Nimmegeers, P. Flexibility in short-term electricity markets for renewable integration and uncertainty mitigation: A comprehensive review. Smart Energy 2025, 18, 100183. [Google Scholar] [CrossRef]
- Rahman, T.; Lipu, M.H.; Shovon, M.M.A.; Alsaduni, I.; Karim, T.F.; Ansari, S. Unveiling the impacts of climate change on the resilience of renewable energy and power systems: Factors, technological advancements, policies, challenges, and solutions. J. Clean. Prod. 2025, 493, 144933. [Google Scholar] [CrossRef]
- Suraparaju, S.K.; Samykano, M.; Vennapusa, J.R.; Rajamony, R.K.; Balasubramanian, D.; Said, Z.; Pandey, A.K. Challenges and prospectives of energy storage integration in renewable energy systems for net zero transition. J. Energy Storage 2025, 125, 116923. [Google Scholar] [CrossRef]
- Vilaplana, J.A.L.; Yang, G.; Ackom, E. From investment to net benefits: A review of guidelines and methodologies for cost–benefit analysis in the electricity sector. Energy Res. Soc. Sci. 2025, 124, 104052. [Google Scholar] [CrossRef]
- Weldu, Y.W.; Assefa, G. The search for most cost-effective way of achieving environmental sustainability status in electricity generation: Environmental life cycle cost analysis of energy scenarios. J. Clean. Prod. 2017, 142, 2296–2304. [Google Scholar] [CrossRef]
- Sadiq, M.; Mayyas, A.; Wei, M. A standardized parametric framework for techno-economic analysis of renewable and clean energy systems. Renew. Energy 2025, 243, 122493. [Google Scholar] [CrossRef]
- Yang, K.; Zou, R.; Zhang, W.; Zeng, X.; Li, Z.; Guo, J. Comprehensive review of Positive Energy Districts: Multidimensional analysis of energy, economic, social, and environmental aspects. Renew. Sustain. Energy Rev. 2025, 217, 115740. [Google Scholar] [CrossRef]
- Hottenroth, H.; Sutardhio, C.; Weidlich, A.; Tietze, I.; Simon, S.; Hauser, W.; Naegler, T.; Becker, L.; Buchgeister, J.; Junne, T.; et al. Beyond climate change. Multi-attribute decision making for a sustainability assessment of energy system transformation pathways. Renew. Sustain. Energy Rev. 2022, 156, 111996. [Google Scholar] [CrossRef]
- Chen, N.; Han, X.; Nie, L.; Li, Y.; Huang, X.; Yan, J. Assessment of energy storage technologies on life cycle sustainability for peak shaving scenario. Sol. Energy Mater. Sol. Cells 2025, 286, 113576. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Schmidt, O.; Melchior, S.; Hawkes, A.; Staffell, I. Projecting the Future Levelized Cost of Electricity Storage Technologies. Joule 2019, 3, 81–100. [Google Scholar] [CrossRef]
- Hamed, H.; AlEssa, A.; AlKhorafi, M.; AlDakheel, A.; AlDei, S.; Aleisa, E. Integrating renewable energy in Sabah Al-Ahmad City: A techno-economic and environmental analysis. J. Eng. Res. 2025, in press. [Google Scholar] [CrossRef]
- Mu, T.; Wang, Z.; Yao, N.; Zhang, M.; Bai, M.; Wang, Z.; Wang, X.; Cai, X.; Ma, Y. Technological penetration and carbon-neutral evaluation of rechargeable battery systems for large-scale energy storage. J. Energy Storage 2023, 69, 107917. [Google Scholar] [CrossRef]
- Zhou, Q.; He, Q.; Lu, C.; Du, D. Techno-economic analysis of advanced adiabatic compressed air energy storage system based on life cycle cost. J. Clean. Prod. 2020, 265, 121768. [Google Scholar] [CrossRef]
- Yao, X.; Ge, S.; Guo, Z.; Li, J.; Han, Y.; Liu, X.; Ahmed, D.; Tachega, M.A. Life cycle cost study of abandoned coal mine shaft-based pumped storage. China Min. Mag. 2020, 29, 50–56+65. [Google Scholar]
- Fu, X.; Li, F.; Yang, X.; Yang, P. Energy storage cost analysis based on life cycle cost. Distrib. Energy 2020, 5, 34–38. [Google Scholar]
- He, Y.; Chen, Y.; Liu, Y.; Liu, H.; Liu, D.; Sun, C. Analysis of levelized cost of electricity and mileage cost of energy storage. Adv. Technol. Electr. Eng. Energy 2019, 38, 1–10. [Google Scholar]
- Yang, H.; Zhou, M.; Zhang, M.; Wu, Z.; Du, J. Operation strategy and benefit analysis of pumped-storage power stations under electricity market environment. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2021, 48, 71–80. [Google Scholar]
- Meng, X.; Pang, X.; Chong, F.; Hou, S.; Qi, B. Application analysis and prospect of electrochemical energy storage in power grid. Energy Storage Sci. Technol. 2019, 8, 38–42. [Google Scholar]
- Zhang, W.; Qiu, M.; Lai, X. Application of energy storage technology in power system. Power Syst. Technol. 2008, 7, 1–9. [Google Scholar]
- Feng, J.; Zeng, P.; Li, Y.; Dai, Q.; Zhu, L. Optimal configuration of novel distributed energy storage considering impact of charge/discharge strategies on lifespan. Electr. Meas. Instrum. 2024, 61, 26–32. [Google Scholar]
- Bai, X. Application of lithium iron phosphate battery energy storage systems. Hi-Tech Ind. 2016, 4, 71–73. [Google Scholar]
- Cao, F.; Jin, Y.; Xu, D.; Li, B.; Liu, Q. Brief analysis of the impact of alternative and energy storage technologies on the development of pumped storage. China Foreign Energy 2021, 26, 89–95. [Google Scholar]
- Chai, M.; Gao, C.; Chen, T.; Hu, N.; Guan, Y. Economic analysis of energy storage configuration for industrial users in Jiangsu Province. Demand Side Manag. Electr. Power 2021, 23, 47–51. [Google Scholar]
- Paul, D.; Pechancová, V.; Saha, N.; Pavelková, D.; Saha, N.; Motiei, M.; Jamatia, T.; Chaudhuri, M.; Ivanichenko, A.; Venher, M.; et al. Life cycle assessment of lithium-based batteries: Review of sustainability dimensions. Renew. Sustain. Energy Rev. 2024, 206, 114860. [Google Scholar] [CrossRef]
- Tang, F.; Qin, Y.; Guo, M.; Wang, P.; Zhang, F.; Hou, H. Thermal risk assessment in the mine of TOPSIS based on game theory subjective and objective comprehensive weighting. Therm. Sci. Eng. Prog. 2025, 59, 103367. [Google Scholar] [CrossRef]
- Qian, Y.; Xu, Z.; Qin, Y.; Gou, X. A critical review on the multidimensional complexity of sustainable energy development. Appl. Energy 2025, 394, 126194. [Google Scholar] [CrossRef]
- Lei, S.; Ma, X.; Qin, H.; Ren, D.; Niu, X. A new three-way multi-attribute decision-making with objective risk avoidance coefficients based on q-rung orthopair fuzzy pre-order relations. Expert Syst. Appl. 2025, 268, 126252. [Google Scholar] [CrossRef]
- Si, T.; Wang, C.; Liu, R.; Guo, Y.; Yue, S.; Ren, Y. Multi-criteria comprehensive energy efficiency assessment based on fuzzy-AHP method: A case study of post-treatment technologies for coal-fired units. Energy 2020, 200, 117533. [Google Scholar] [CrossRef]
- Xu, C.; Xu, C.; Zhan, L.; Li, G. Establishment and validation of a novel composite index for energy efficiency evaluation of data center chilled water systems based on AHP and Entropy Weight Method. Energy Build. 2025, 337, 115677. [Google Scholar] [CrossRef]
- Wu, Y.; Jia, W.; Li, L.; Song, Z.; Xu, C.; Liu, F. Risk assessment of electric vehicle supply chain based on fuzzy synthetic evaluation. Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Zhang, T.; Ma, Y.; Wu, Y.; Yi, L. Optimization configuration and application value assessment modeling of hybrid energy storage in the new power system with multi-flexible resources coupling. J. Energy Storage 2023, 62, 106876. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Yan, Z.; Cao, H.; Shi, H.; Jia, Y. Optimization of energy output in multimodal and multi-load CCHP systems with integrated electric energy storage. Energy Rep. 2025, 13, 4734–4748. [Google Scholar] [CrossRef]

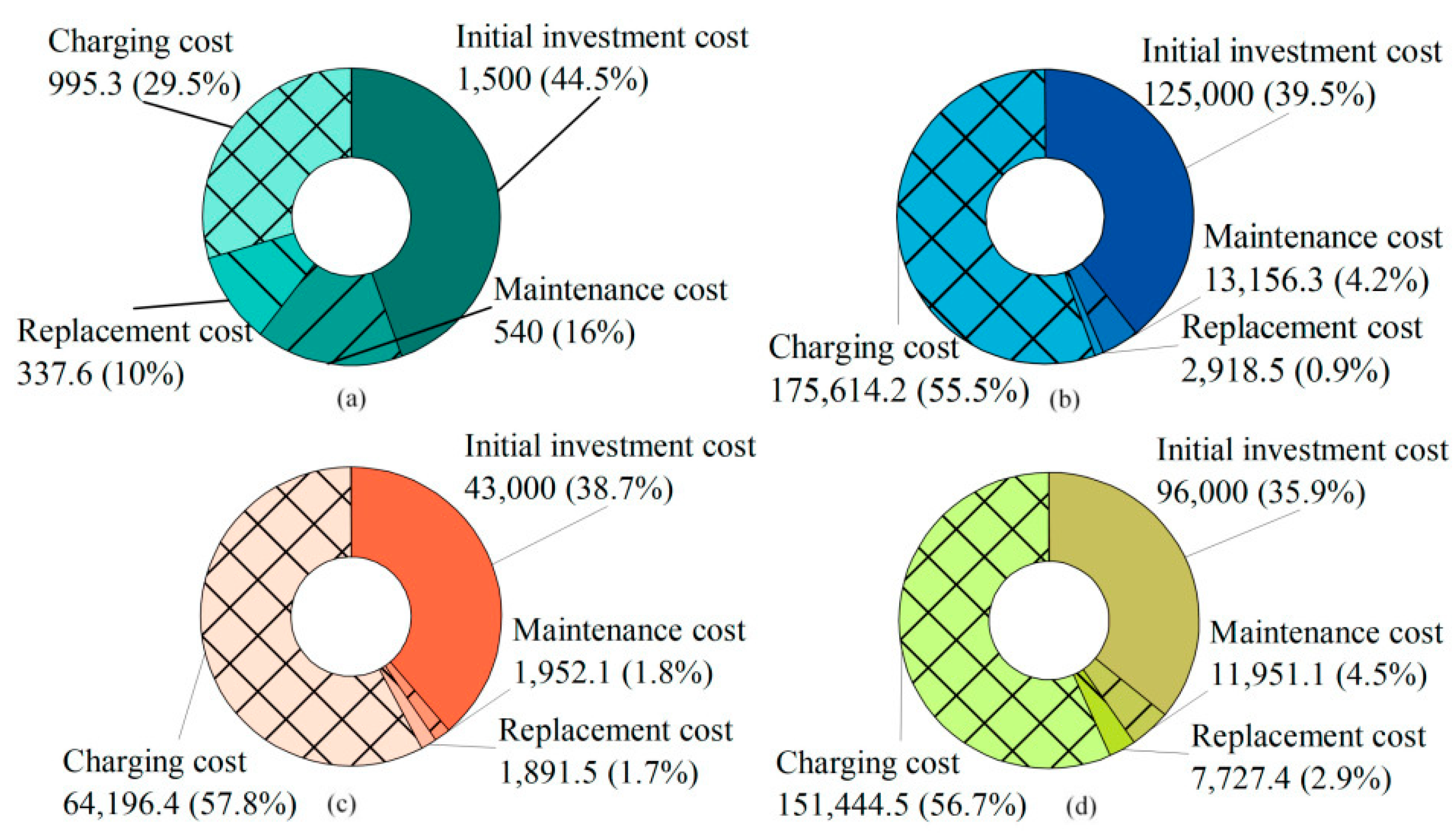
| Parameter | Lithium Iron Phosphate Battery | Pumped Storage | Compressed Air Energy Storage | Hydrogen Energy Storage | Data Source |
|---|---|---|---|---|---|
| /MW·h | 10 | 1000 | 300 | 800 | Setting value |
| /MW | 10 | 200 | 60 | 200 | Setting value |
| /ten thousand CNY | 1500 | 125,000 | 43,000 | 96,000 | Ref. [15] |
| /[CNY/(kW·year)] | 55 | 39 | 14.5 | 60 | Ref. [16] |
| /[CNY/(kW·year)] | 0 | 14.4 | 14.4 | 20 | Ref. [16] |
| /(CNY/kW) | 850 | 560 | 1000 | 1200 | Ref. [17] |
| /% | 0.08 | 0.08 | 0.08 | 0.08 | Ref. [18] |
| /% | 0.9 | 0.8 | 0.6 | 0.45 | Refs. [19,20] |
| /% | 0.8 | 1.0 | 1.0 | 1.0 | Ref. [21] |
| /(%/year) | 0.011 | 0.004 | 0.005 | 0.007 | Ref. [22] |
| /year | 20 | 55 | 30 | 20 | Ref. [23] |
| /times | 396 | 396 | 396 | 396 | Setting value |
| [CNY/(kW·h)] | 0.288 | 0.288 | 0.288 | 0.288 | Ref. [24] |
| LCC Under Different Scenarios [CNY/(KW·h)] | Lithium Iron Phosphate Battery | Pumped Storage | Compressed Air Energy Storage | Hydrogen Energy Storage |
|---|---|---|---|---|
| Consider the charging price | 1.135 | 0.667 | 0.853 | 1.157 |
| Do not consider the charging price a | 0.80 | 0.297 | 0.360 | 0.501 |
| Considering the charging price, do not consider the discount rate | 0.910 | 0.471 | 0.655 | 0.909 |
| The charging price is not considered and the discount rate is 0 | 0.573 | 0.098 | 0.158 | 0.248 |
| Selection Indicator | Pumped Storage | Lithium Iron Phosphate Battery | Compressed Air Energy Storage | Hydrogen Energy Storage |
|---|---|---|---|---|
| Initial investment cost/(CNY/kWh) | 0.2633 | 0.5047 | 0.3305 | 0.4157 |
| Average annual operation and maintenance cost/(CNY/kWh) | 0.0277 | 0.1817 | 0.0150 | 0.0518 |
| Equipment replacement cost/(CNY/kWh) | 0.0061 | 0.1136 | 0.0145 | 0.0335 |
| Charging cost/(CNY/kWh) | 0.3700 | 0.3349 | 0.4934 | 0.6558 |
| Efficiency/% | 90 | 80 | 60 | 45 |
| Response time | 5 min | 10 ms | 5 min | 10 min |
| Power scale/MW | 100–5000 | 100 | 5–300 | 10 |
| Capacity scale/(MWh) | 500–8000 | 200 | 600–3000 | 50 |
| Volume energy density/(Wh/L) | 2 | 500 | 6 | 3000 |
| Selection Indicator | Pumped Storage | Lithium Iron Phosphate Battery | Compressed Air Energy Storage | Hydrogen Energy Storage |
|---|---|---|---|---|
| Current stage of development | 4 | 3.3 | 3.2 | 2.8 |
| Environmental friendliness | 3.8 | 3.0 | 3.6 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, H.; Li, P.; Xin, C.; Wang, Y.; Zhou, Y.; Li, W.; Lu, Y.; Chen, T.; Wang, J. Life Cycle Cost Modeling and Multi-Dimensional Decision-Making of Multi-Energy Storage System in Different Source-Grid-Load Scenarios. Processes 2025, 13, 2400. https://doi.org/10.3390/pr13082400
Huo H, Li P, Xin C, Wang Y, Zhou Y, Li W, Lu Y, Chen T, Wang J. Life Cycle Cost Modeling and Multi-Dimensional Decision-Making of Multi-Energy Storage System in Different Source-Grid-Load Scenarios. Processes. 2025; 13(8):2400. https://doi.org/10.3390/pr13082400
Chicago/Turabian StyleHuo, Huijuan, Peidong Li, Cheng Xin, Yudong Wang, Yuan Zhou, Weiwei Li, Yanchao Lu, Tianqiong Chen, and Jiangjiang Wang. 2025. "Life Cycle Cost Modeling and Multi-Dimensional Decision-Making of Multi-Energy Storage System in Different Source-Grid-Load Scenarios" Processes 13, no. 8: 2400. https://doi.org/10.3390/pr13082400
APA StyleHuo, H., Li, P., Xin, C., Wang, Y., Zhou, Y., Li, W., Lu, Y., Chen, T., & Wang, J. (2025). Life Cycle Cost Modeling and Multi-Dimensional Decision-Making of Multi-Energy Storage System in Different Source-Grid-Load Scenarios. Processes, 13(8), 2400. https://doi.org/10.3390/pr13082400







