Short-Circuit Current Calculation of Single-Phase to Ground Fault in Petal-Shaped Distribution Network
Abstract
1. Introduction
- (1)
- A DG grid-connected mathematical model covering positive and negative dual sequence control was constructed through the grid-connected structure of DGs in a petal-shaped distribution network. A composite sequence network model considering the DG negative sequence current output was established based on the symmetrical component method.
- (2)
- An analytical short-circuit current calculation method based on nodal–voltage relationships, adaptable to multiple control goals (e.g., constant active power, constant reactive power, and symmetrical current output) was proposed, with demonstrated computational efficiency.
- (3)
- The effectiveness of the proposed method was verified in the two petal-shaped distribution network simulation models constructed, and the different performances of DGs’ output current under different voltage sag scenarios were also analyzed.
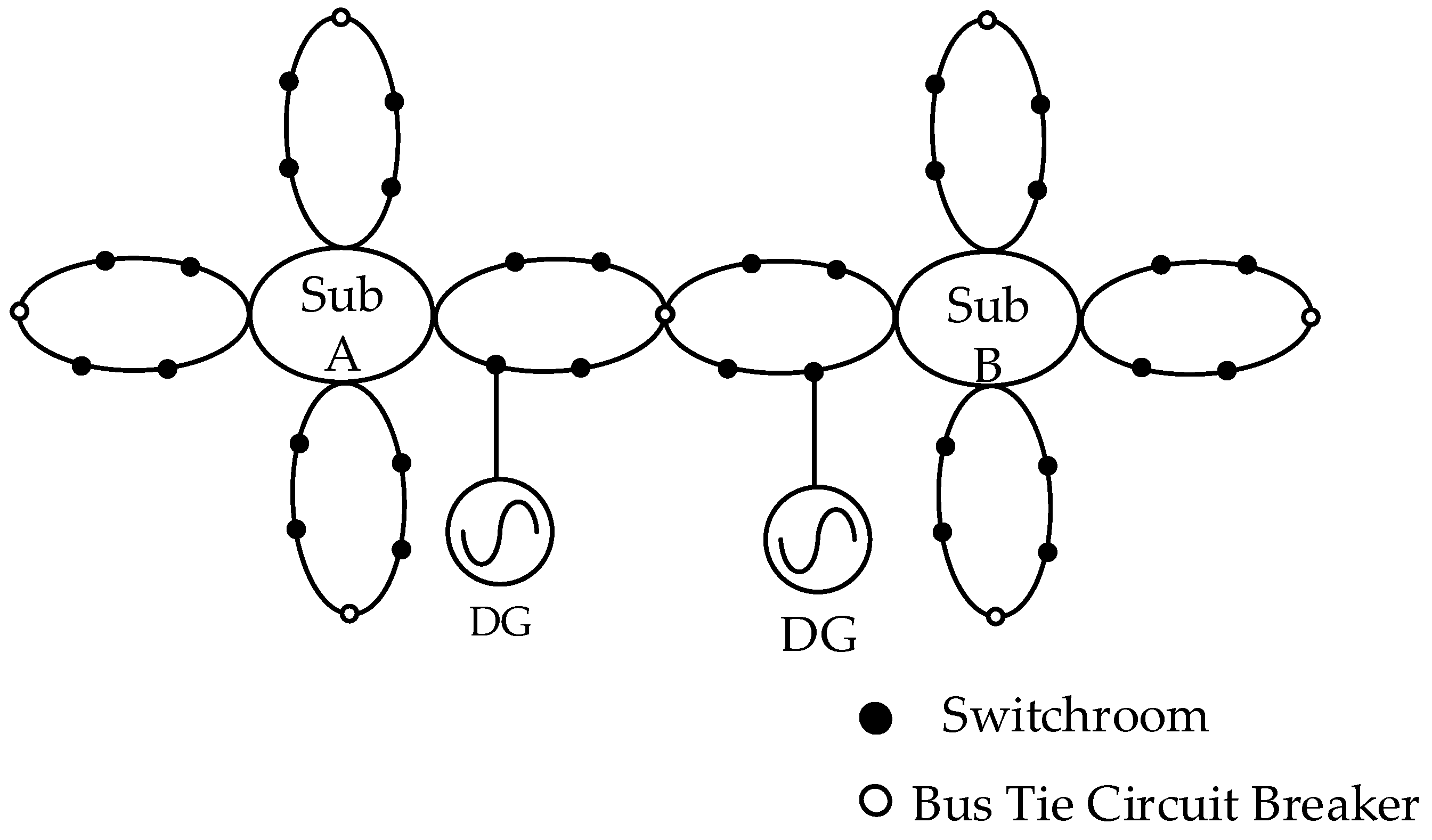
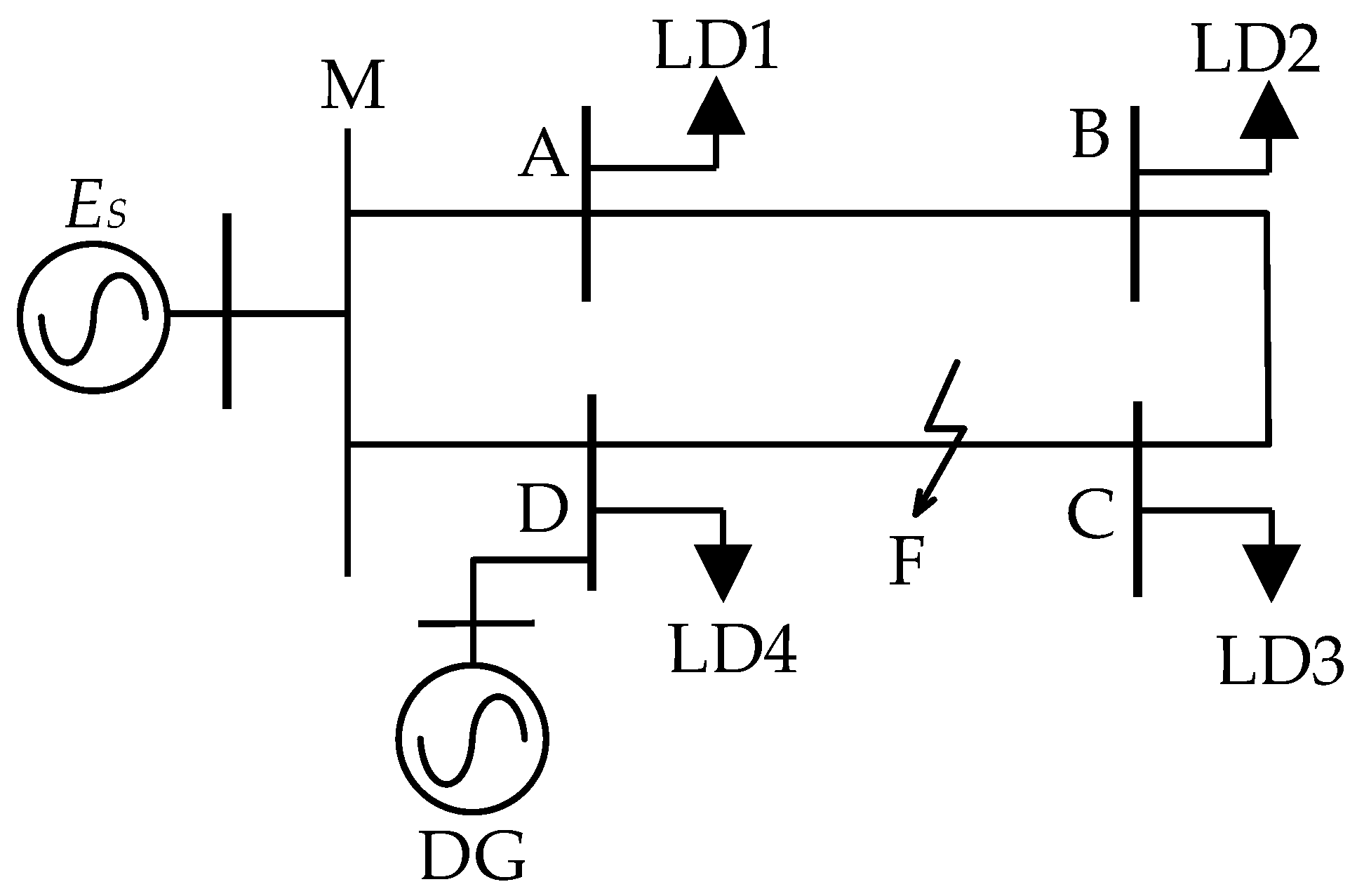
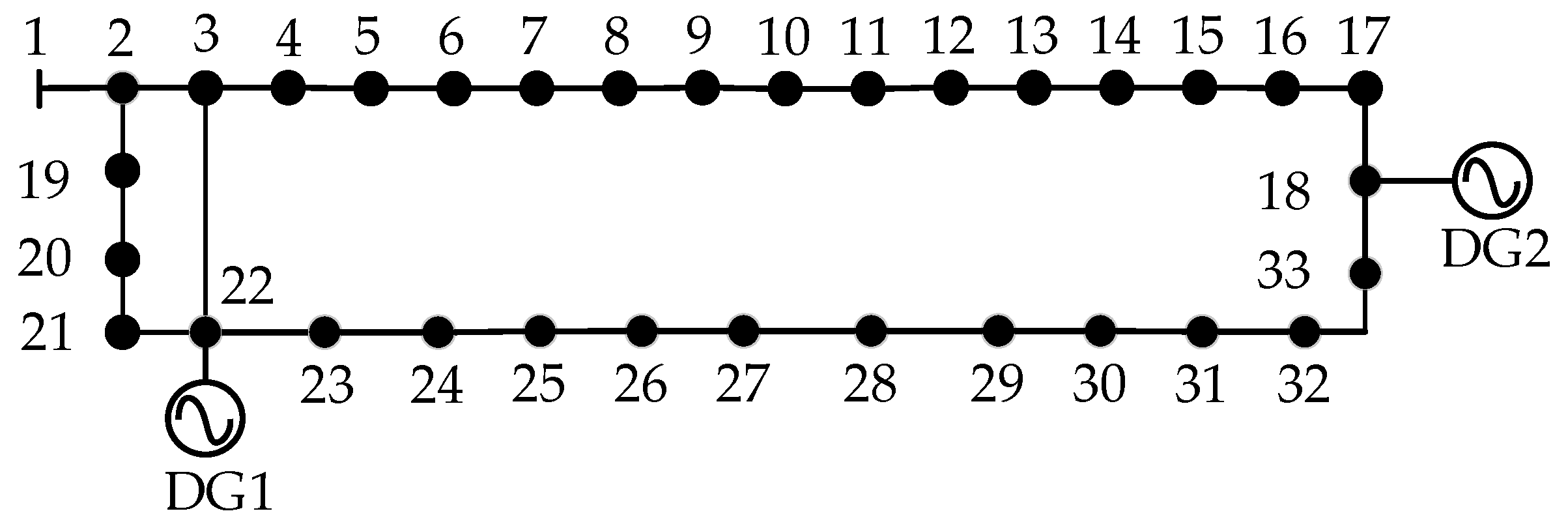
2. Topology of Petal-Shaped Distribution Network with DG Integration and Asymmetric Fault Control of DG
2.1. Topology of Petal-Shaped Distribution Network with DG Integration
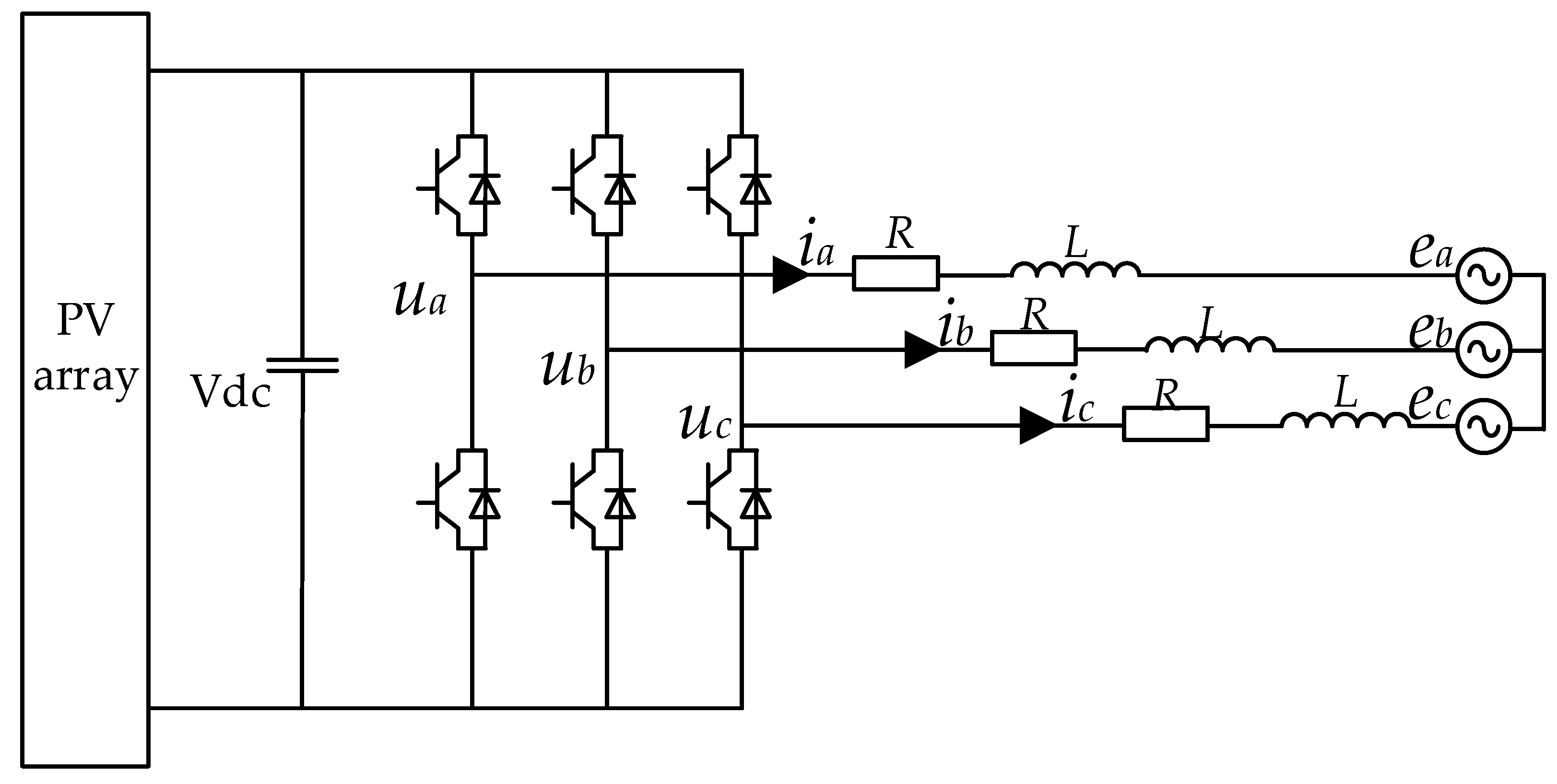
2.2. DG Control Principles Under Asymmetric Faults
2.3. DG Output Characteristics Under Asymmetric Faults
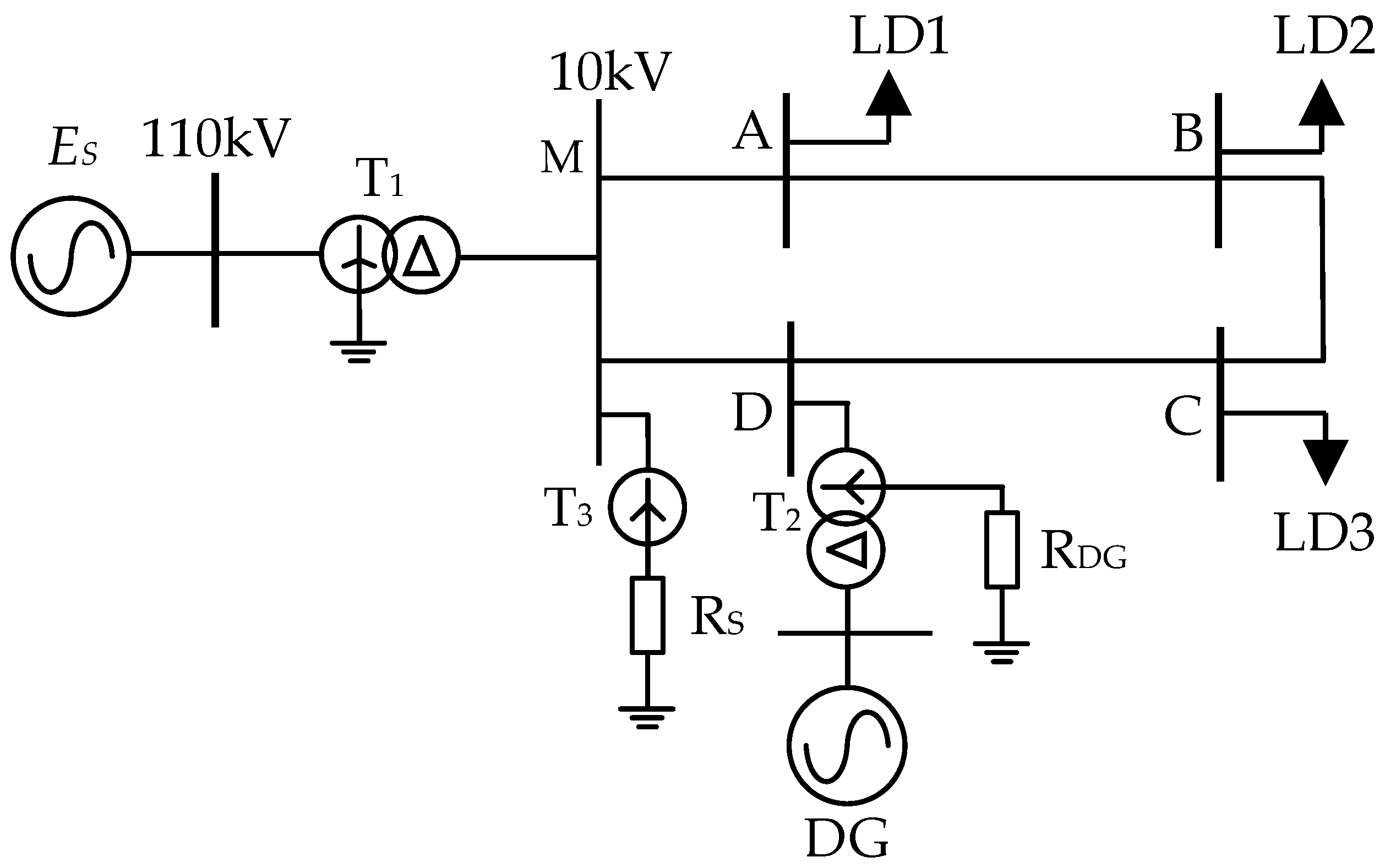
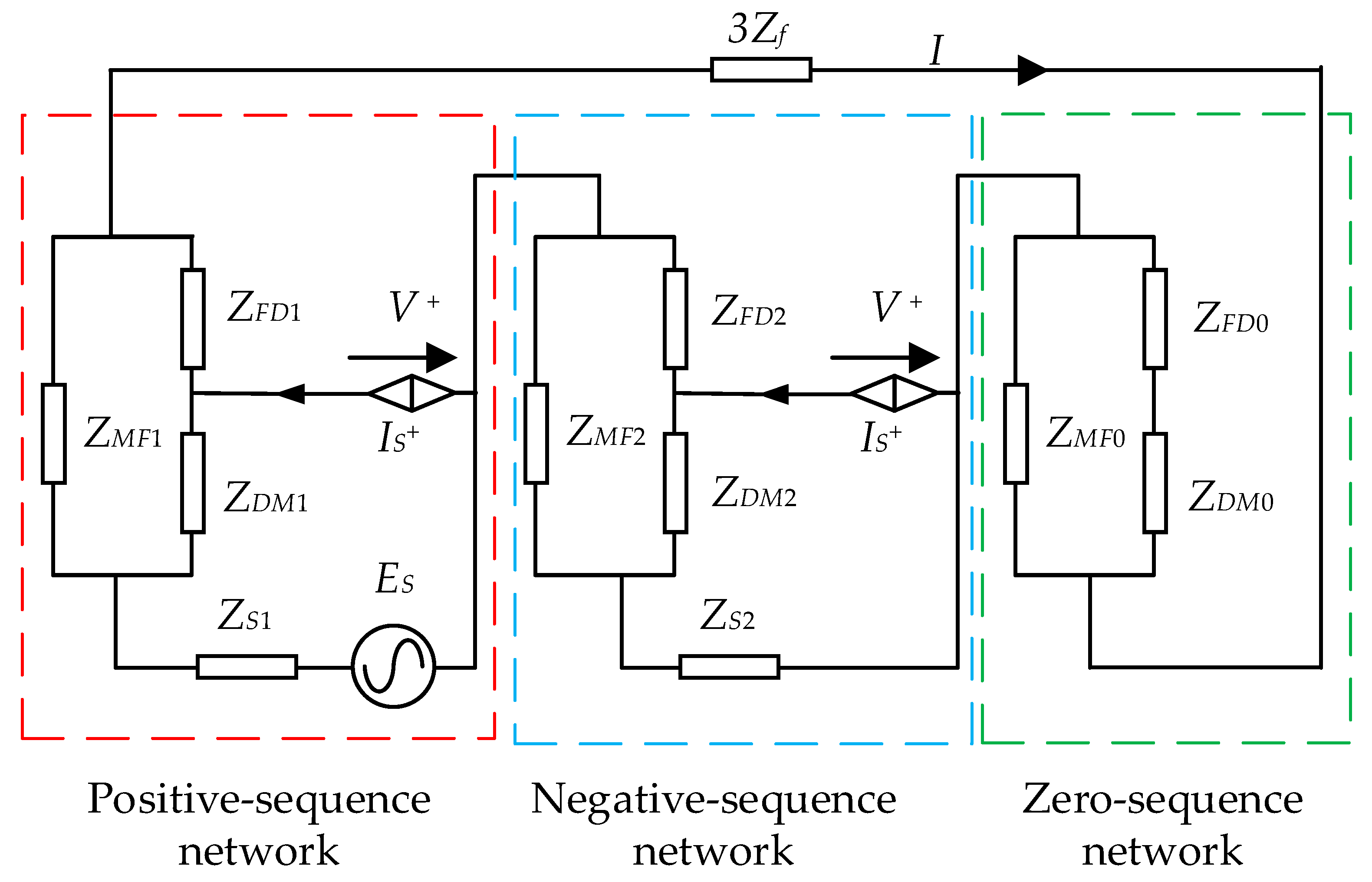
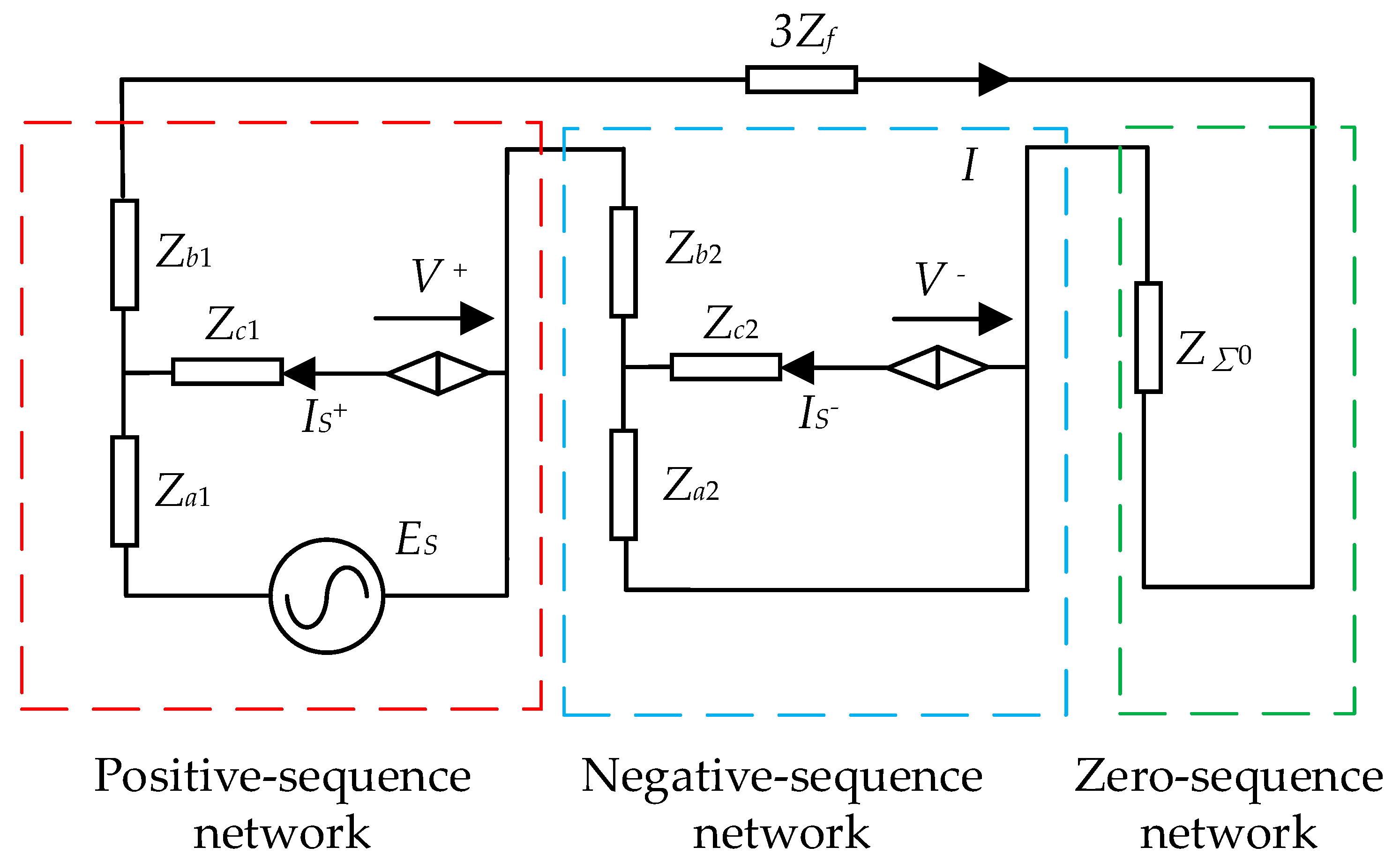
3. Single-Phase to Ground Fault Current Calculation in Petal Networks with DGs
3.1. Network Analysis for Single-Phase to Ground Fault
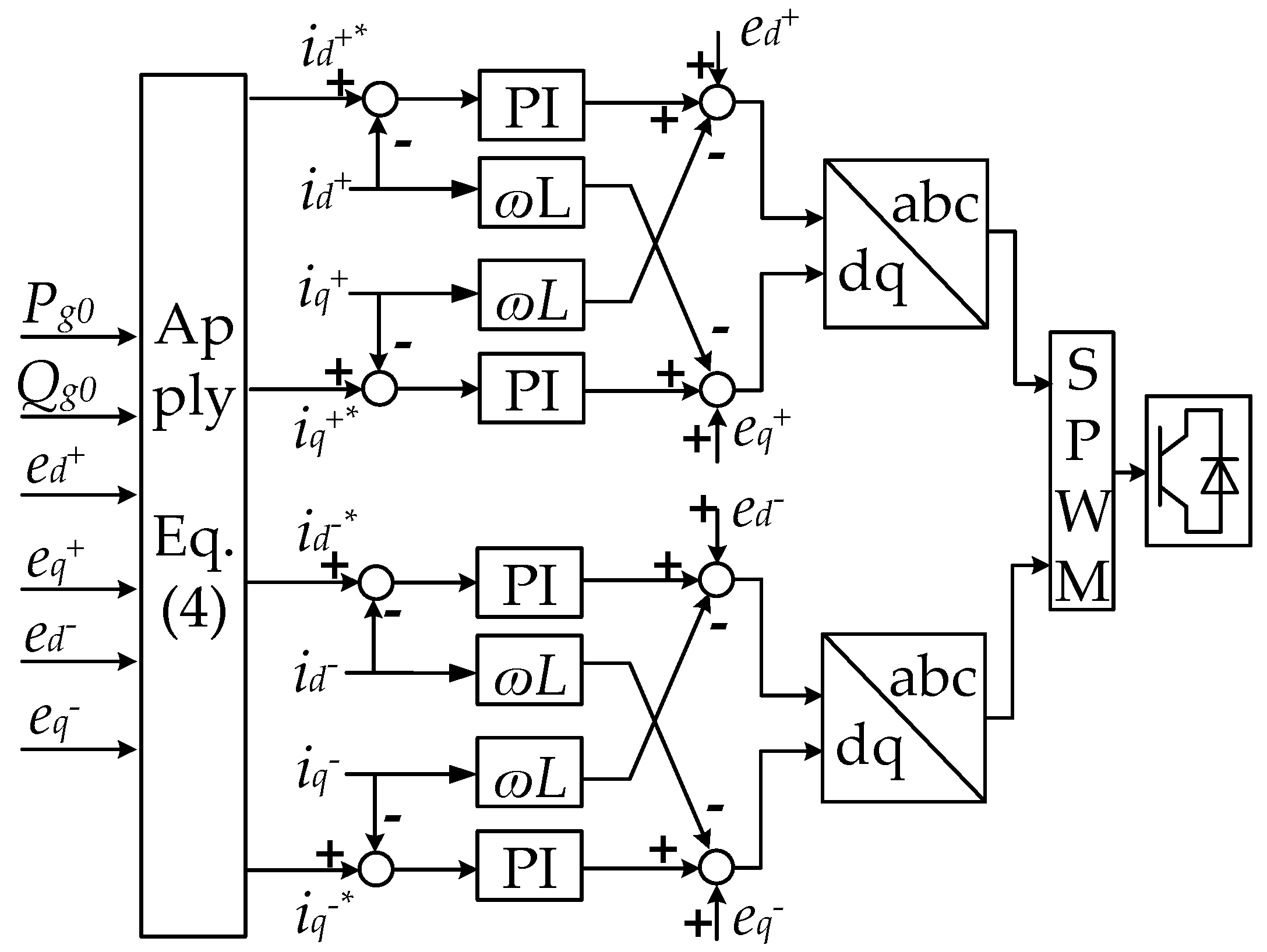
3.2. DG Output Current Calculation Under Asymmetric Faults
3.2.1. Calculation of DG Output Positive Sequence Current
3.2.2. Calculation of DG Output Negative Sequence Current
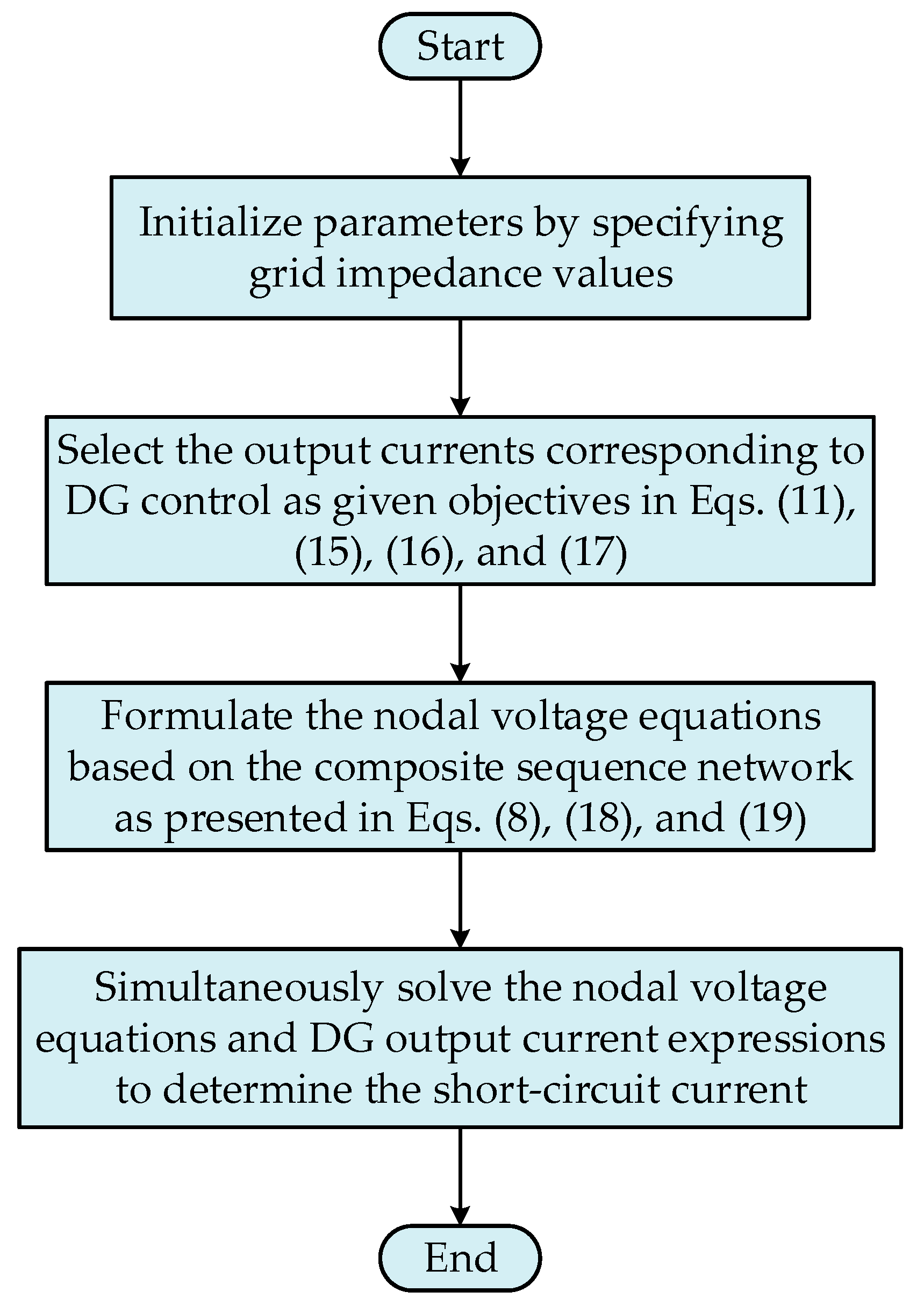
3.2.3. Short-Circuit Current Calculation Method and Flowchart
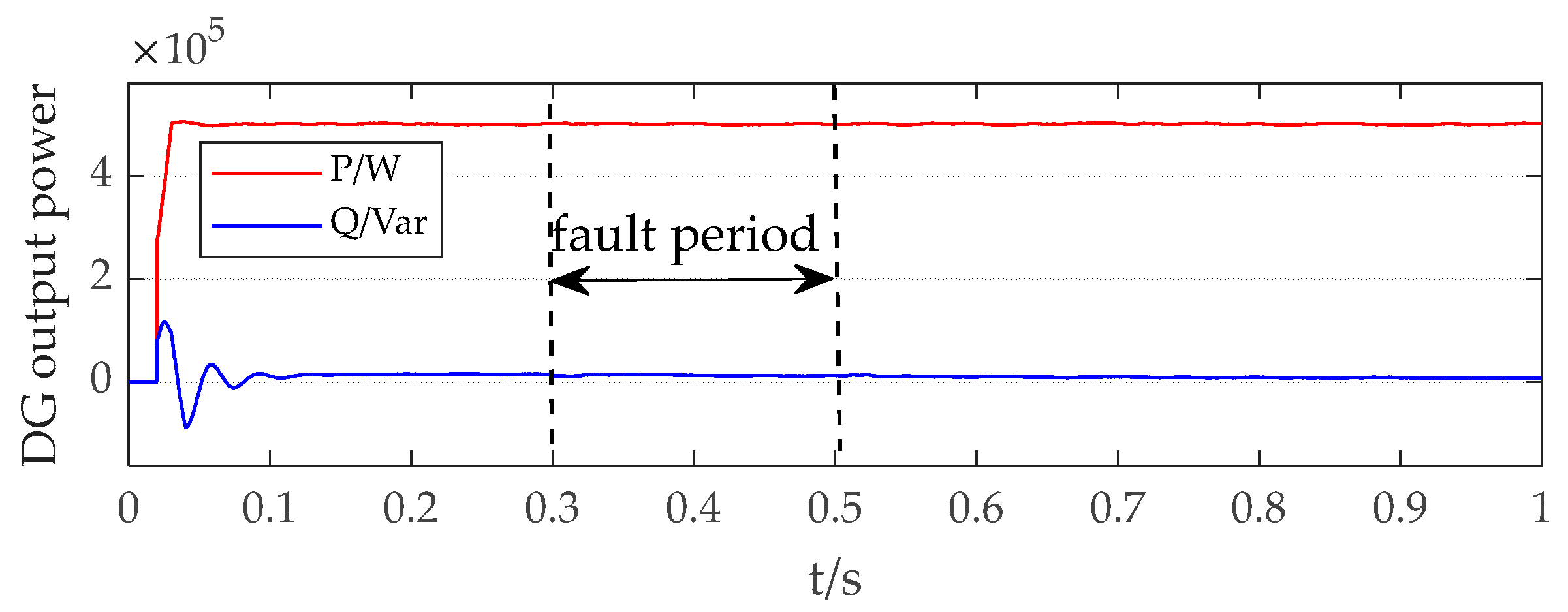
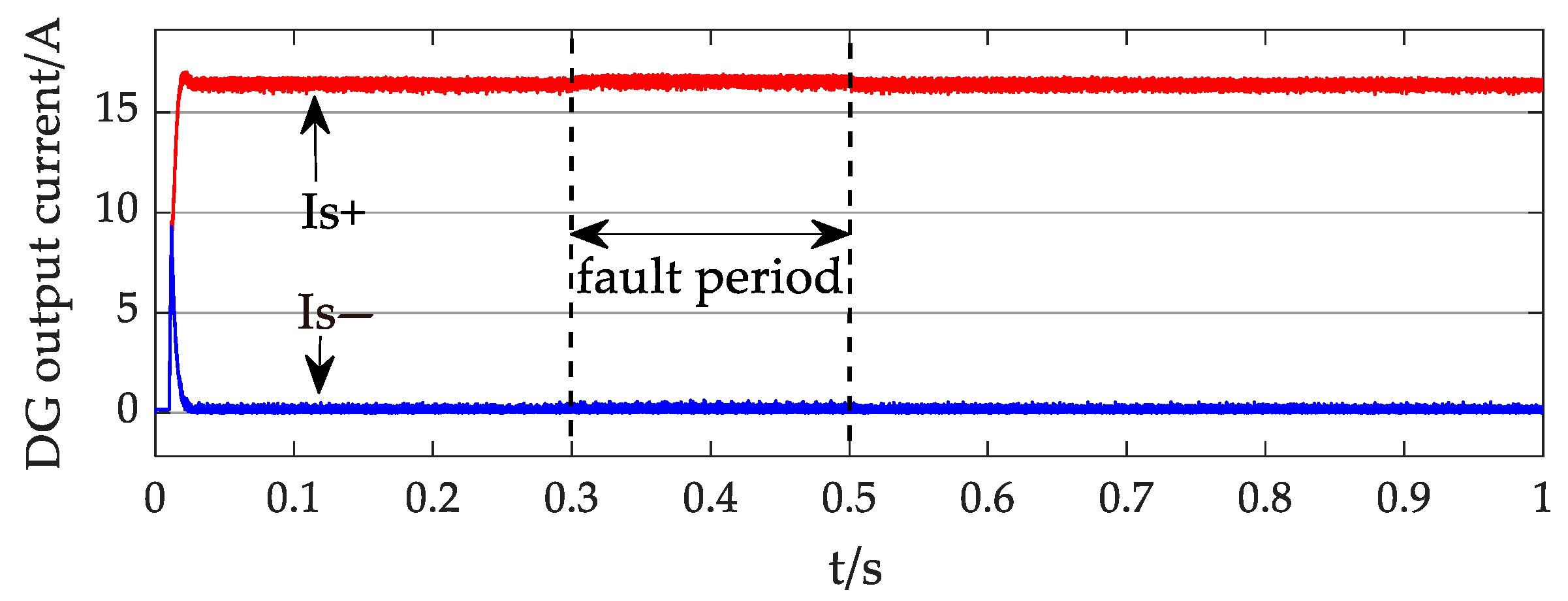
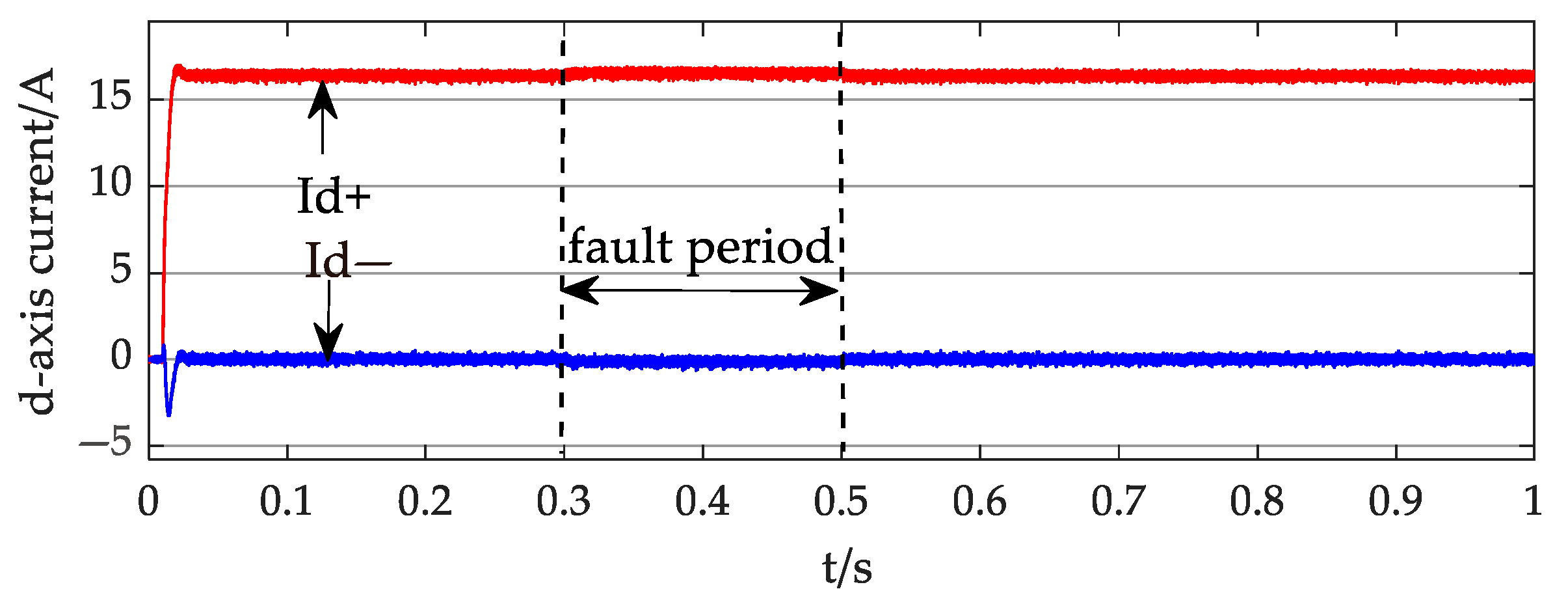
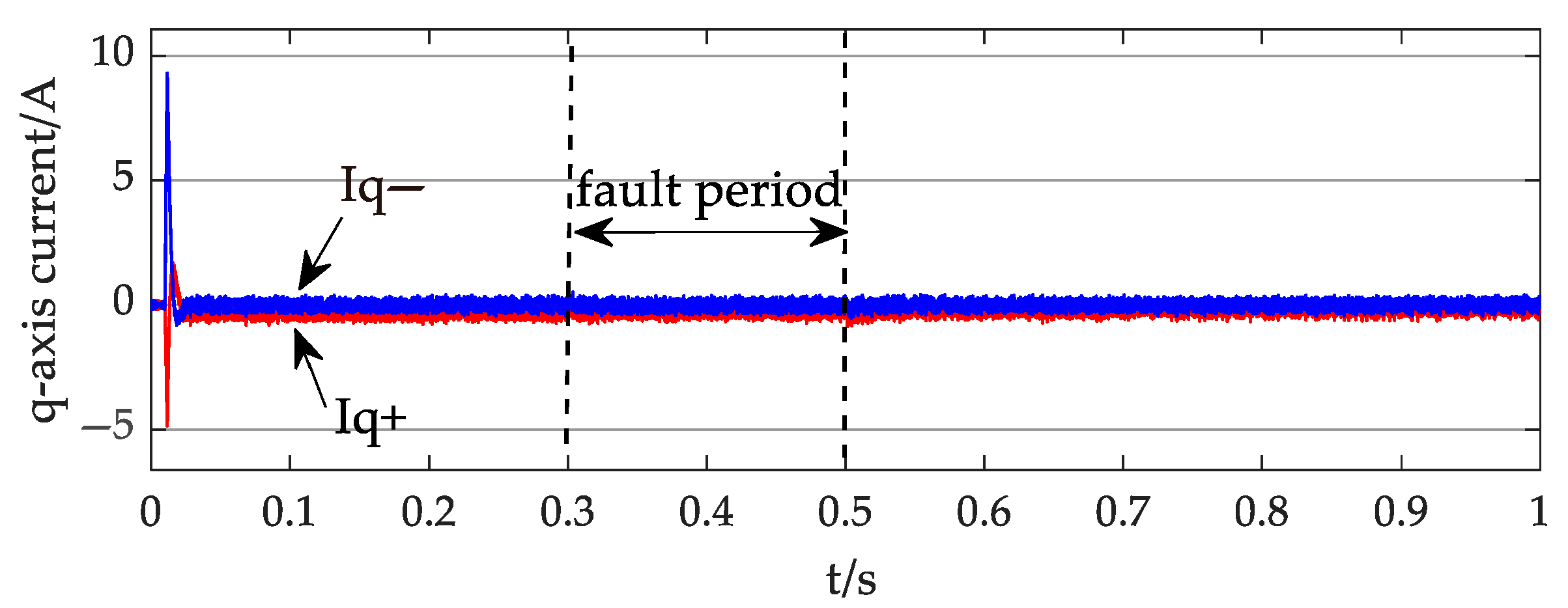
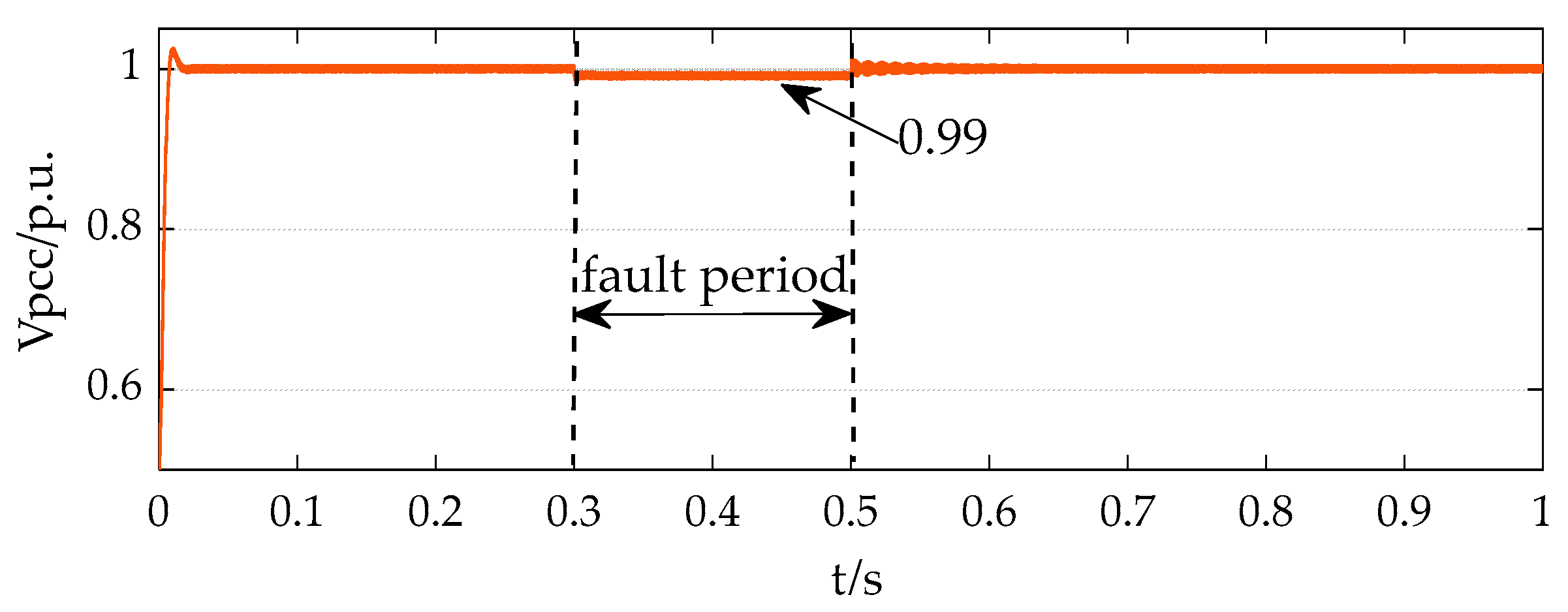
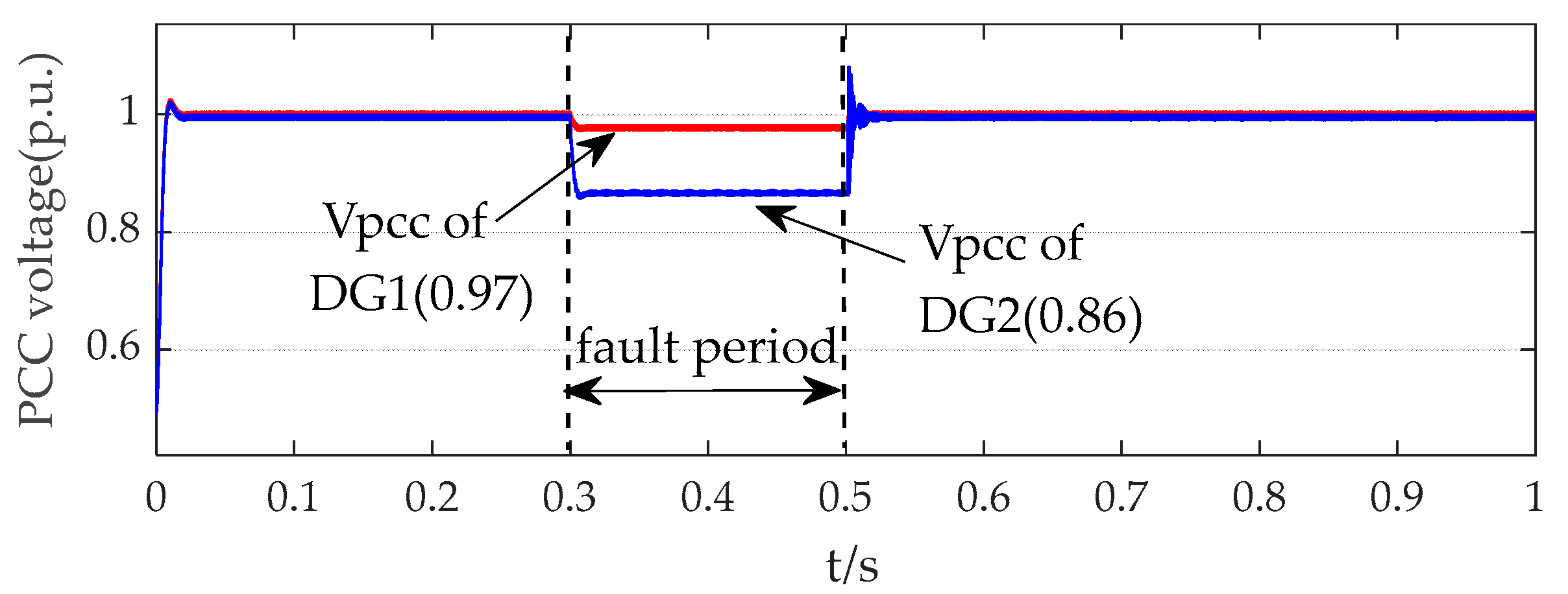
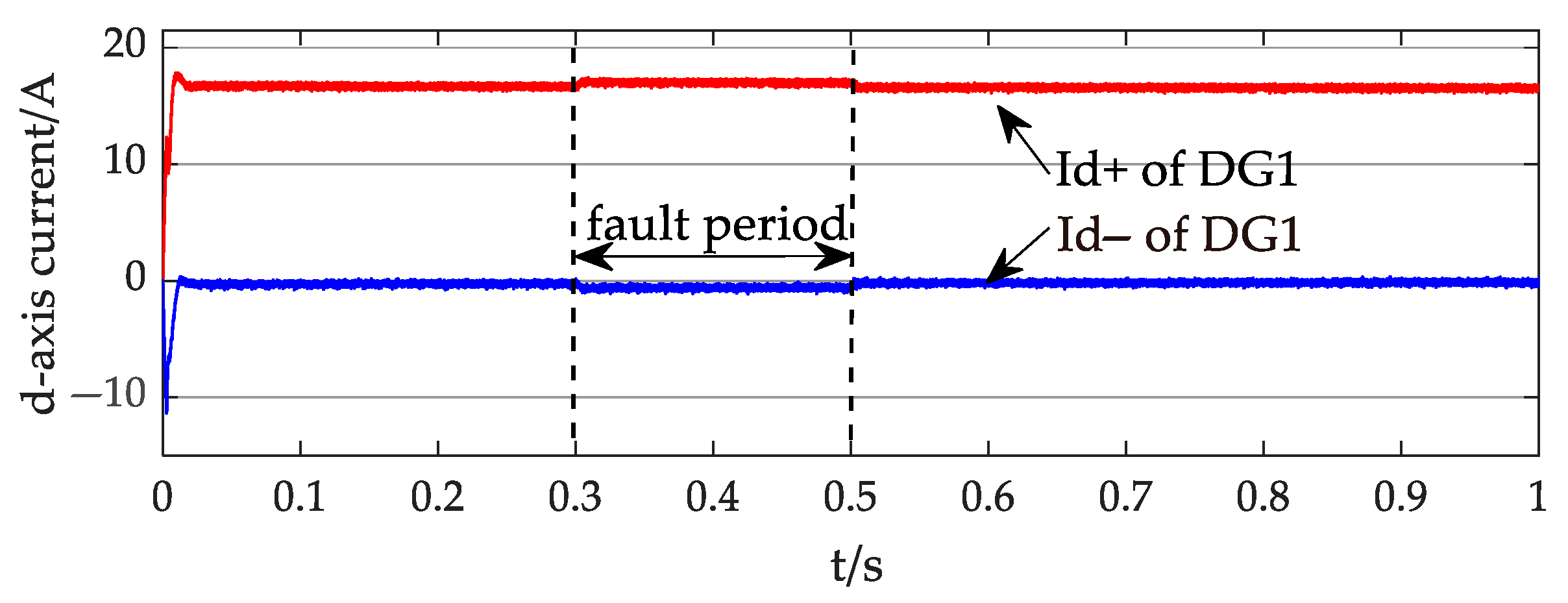
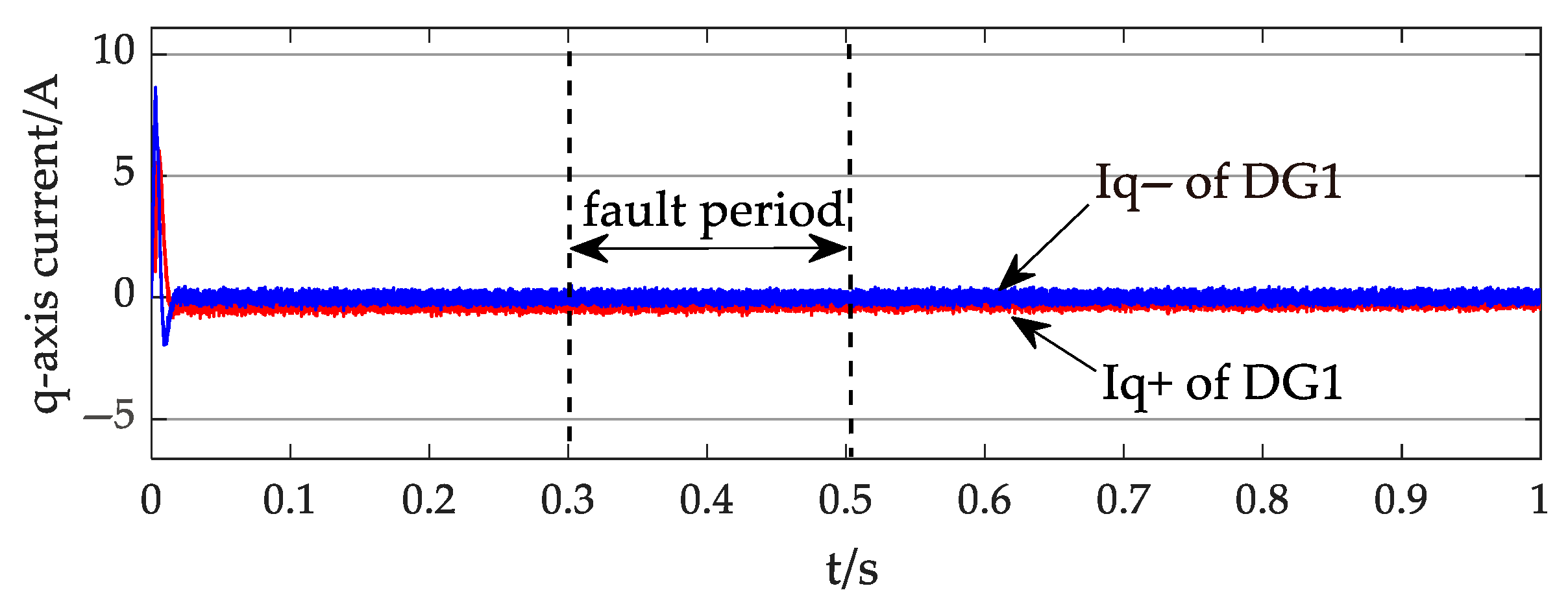
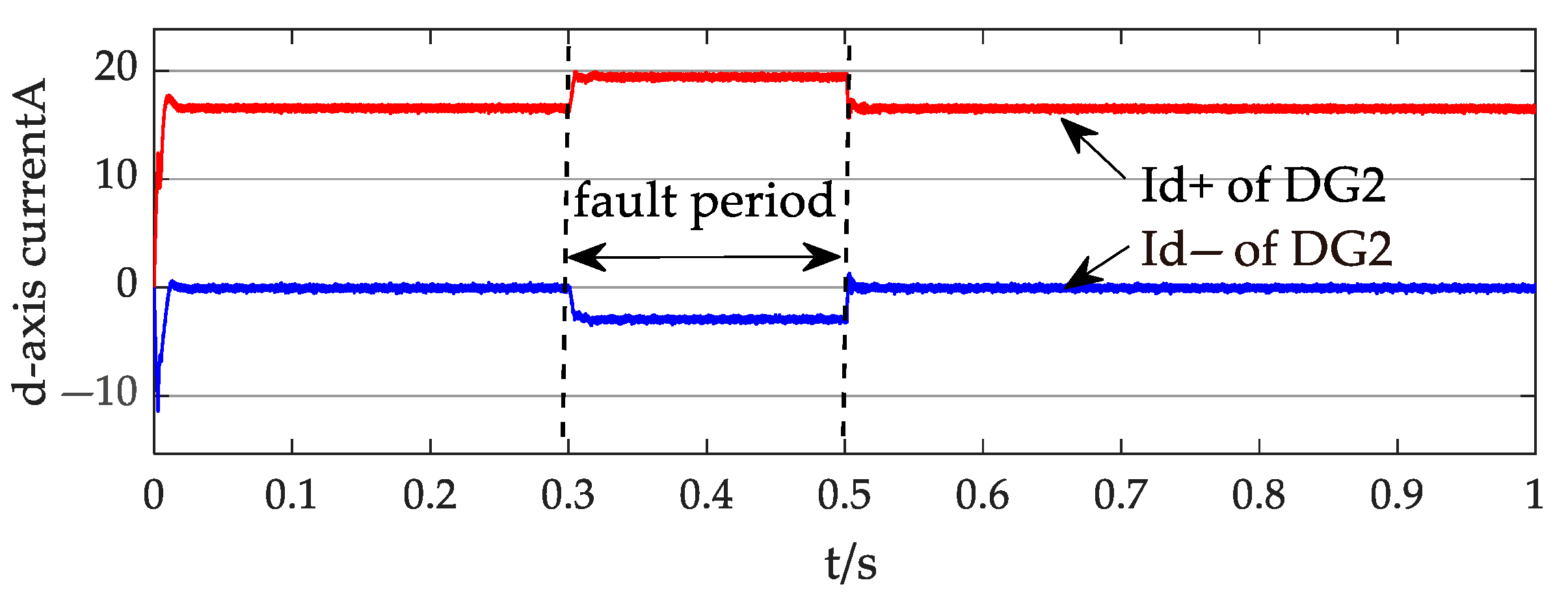
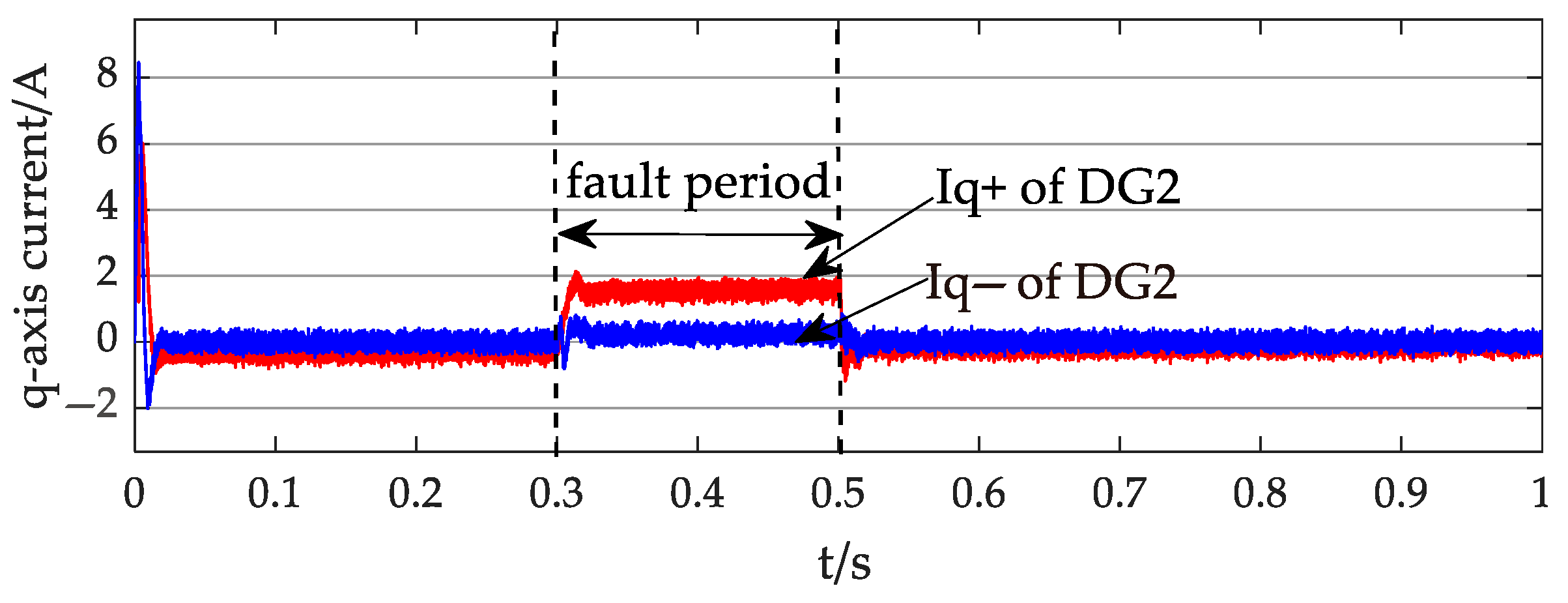
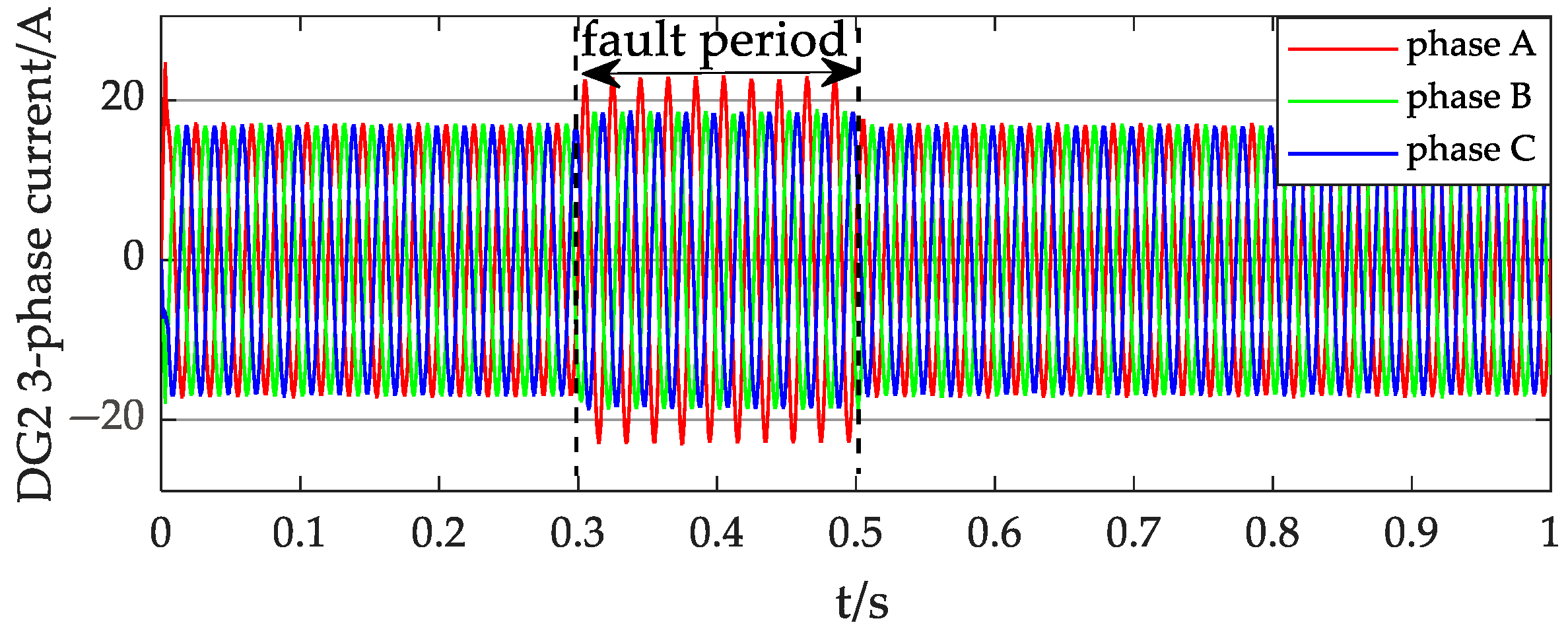
4. Simulation Results and Discussion
4.1. Case 1
4.2. Case 2
5. Conclusions
- (1)
- A comprehensive mathematical model for DG grid interconnection was established, incorporating both positive and negative sequence control strategies to accurately capture the inverter output characteristics during single-phase to ground faults, and the detailed mathematical formulations under various control goals were presented.
- (2)
- A composite sequence network model that integrates the negative sequence current output from DGs was developed, leveraging the symmetrical component method to enable precise analysis of fault currents in a petal-shaped distribution network, making up for the shortcomings of traditional methods that do not consider negative sequence control in a petal-shaped network.
- (3)
- An analytical short-circuit current calculation method based on the nodal–voltage relationships was proposed, adaptable to multiple control goals. The proposed method accurately calculates the short-circuit currents at fault locations, with maximum relative errors of only 0.31% in Case 1 and 2.04% in the modified IEEE 33-bus, demonstrating high computational precision that provides reliable theoretical support for fault analysis and protection design in petal networks. When the per-unit voltage at the DG’s PCC remains above 0.9, the negative sequence current minimally influences the distribution network’s short-circuit current, where the primary contributions originate from the DG’s positive sequence current. However, when the voltages drop below 0.9 per unit, negative sequence currents constitute 14.78% of the DG output current, making their impact non-negligible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shao, C.; Yan, X.W.; Jia, J.X.; Wu, W.L. Two-Stage Speed-Power Control Strategy for Rotating Power Flow Controller in “Petal-Shaped” Distribution Networks. Trans. China Electrotech. Soc. 2025, 1, 25–63. [Google Scholar] [CrossRef]
- Chen, J.F.; Ren, H.T. Failure Study of DC Distribution System with all Converters Resistance-Grounded. In Proceedings of the 2024 6th Asia Energy and Electrical Engineering Symposium, Chengdu, China, 28–31 March 2024. [Google Scholar] [CrossRef]
- Kamberi, K.; Shaliu, D.; Çelo, M.; Bualoti, R. Hosting capacity calculation of photovoltaic penetration in a closed-loop distribution network: A case study. IET Conf. Proc. 2025, 29, 113–118. [Google Scholar] [CrossRef]
- Zhao, S.J.; Yang, P.; Hao, P.F. Load Partition and Planning Research of Distribution Networks. Electr. Power Syst. Clean Energy 2016, 8, 79–85. [Google Scholar]
- Villa-Ávila, E.; Ochoa-Correa, D.; Arévalo, P. Advancements in Power Converter Technologies for Integrated Energy Storage Systems: Optimizing Renewable Energy Storage and Grid Integration. Processes 2025, 6, 1819. [Google Scholar] [CrossRef]
- Alanazi, M. Optimal Integration of Distributed Generators and Soft Open Points in Radial Distribution Networks: A Hybrid WCA-PSO Approach. Processes 2025, 6, 1775. [Google Scholar] [CrossRef]
- Parsadust, H.; Lotfi, H.; Hajiabadi, M.E. A Dual-Objective Approach to Load Management: Telecommunication Switch Optimization with Distributed Generation Integration. Processes 2025, 3, 716. [Google Scholar] [CrossRef]
- Das, S.S.; Kumar, J.; Dawn, S.; Salata, F. Existing Stature and Possible Outlook of Renewable Power in Comprehensive Electricity Market. Processes 2023, 6, 1849. [Google Scholar] [CrossRef]
- Yang, J.Z.; Fu, B.B.; Peng, J.Q.; Wang, G.B.; Yao, H. Integration of a salt cavern for large-scale hydrogen storage into a solar-wind-storage power system: Technical and economic advantages. Appl. Energy 2025, 9, 126073. [Google Scholar] [CrossRef]
- Ahang, M.; Granado, P.C.; Tomasgard, A. Investments in green hydrogen as a flexibility source for the European power system by 2050: Does it pay off? Appl. Energy 2025, 1, 124656. [Google Scholar] [CrossRef]
- Peng, X.; Jiang, F.; Tu, C.M.; Guo, Q. Optimal Voltage Support Strategy for Photovoltaic Inverters Under Asymmetric Faults. Power Syst. Technol. 2021, 11, 4259–4268. [Google Scholar]
- Pompodakis, E.E.; Katsigiannis, Y.; Karapidakis, E.S. Incorporating Modern Fault Ride-Through Standards into the Short-Circuit Calculation of Distribution Networks. Sensors 2023, 21, 8868. [Google Scholar] [CrossRef] [PubMed]
- Evangelos, E.P.; Strezoski, L.; Simic, N. Short-Circuit Calculation of Droop-Controlled Islanded AC Microgrids With Virtual Impedance Current Limiters. Electr. Power Syst. Res. 2023, 218, 109184. [Google Scholar]
- Ye, R.K.; Wang, H.F.; Zhang, S. Data-Driven Multi-Output Model for Short Circuit Current Calculation in Distribution Network with IIDGs. Electr. Power Autom. Equip. 2022, 9, 119–125+132. [Google Scholar]
- Strezoski, L.V.; Simic, N.G.; Loparo, K.A. A Robust Short-circuit Calculation Method for Islanded, Grid-connected, and Utility Microgrids. J. Mod. Power Syst. Clean Energy 2025, 1, 325–337. [Google Scholar] [CrossRef]
- Kim, I. A Calculation Method for the Short-Circuit Current Contribution of Current-Control Inverter-Based Distributed Generation Sources at Balanced Conditions. Electr. Power Syst. Res. 2021, 190, 106839. [Google Scholar] [CrossRef]
- Liu, M.X.; Shan, R.R.; Feng, S.Y. A Feeder Automation Solution for Petal-Shaped Distribution Networks. Autom. Instrum. 2015, 11, 68–69. [Google Scholar]
- Li, T.C.; Guo, S.F.; Wang, X.Z. Principle of Relay Protection for Petal-shape Distribution Network Based on Voltage Prediction Error. Proc. CSU-EPSA 2022, 6, 79–88. [Google Scholar]
- Gu, D.D.; Xiao, J.; Wei, M.L. Research on Fault Location Strategy for Petal-Shaped Distribution Network with Inverter-Interfaced Distributed Generation. Electr. Meas. Instrum. 2023, 11, 53–57. [Google Scholar]
- Guo, S.F.; Li, T.C.; Duan, J. Backup Protection for Tie Lines in a Petal Distribution Network. Power Syst. Clean Energy. 2022, 4, 10–18. [Google Scholar]
- Chen, X.L.; Yuan, S.; Li, Y.L. Analysis of Single-Phase Grounding Fault Characteristics in Petal-Shaped Distribution Network with Inverter-Interfaced Distributed Generator. Electr. Power Autom. Equip. 2022, 4, 129–137. [Google Scholar]
- Bakkar, M.; Bogarra, S.; Córcoles, F. Three-Level Secure Smart Protection for Ring Grid-Connected Distributed Generation. Energies 2024, 17, 3188. [Google Scholar] [CrossRef]
- Gómez-Luna, E.; De La Cruz, J.; Vasquez, J.C. New Approach for Validation of a Directional Overcurrent Protection Scheme in a Ring Distribution Network with Integration of Distributed Energy Resources Using Digital Twins. Energies 2024, 17, 1677. [Google Scholar] [CrossRef]
- Alamshah, A.; Ramli, S.P.; Mansor, N.N. Recent Developments of Directional Overcurrent Relay Coordination in Ring Distribution Network Based on Hybrid Optimization Techniques. IEEE Access 2025, 13, 14961–14982. [Google Scholar] [CrossRef]
- Cano, A.; Arévalo, P.; Benavides, D. Integrating discrete wavelet transform with neural networks and machine learning for fault detection in microgrids. Int. J. Electr. Power Energy Syst. 2024, 155, 109616. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, F.; Liu, Y. The Intelligent Sizing Method for Renewable Energy Integrated Distribution Networks. Energies 2024, 17, 5763. [Google Scholar] [CrossRef]
- Silveira, R.D.; Silva, S.A.O.; Sampaio, L.P. Full-order models and dynamic assessment of droop-controlled grid-connected and off-grid DC microgrids. Sustain. Energy Technol. Assess. 2024, 64, 103685. [Google Scholar] [CrossRef]
- Tan, Q.; Xu, Y.H.; Huang, H. A Control Strategy for Peak Output Current ff PV Inverter Under Unbalanced Voltage Sags. Power Syst. Technol. 2015, 3, 601–608. [Google Scholar]
- Pawar, V.S.; Gaidhane, P. A resilient approach for optimizing power quality in grid integrated solar photovoltaic with asymmetric 15-level inverter. Comput. Electr. Eng. 2024, 116, 109211. [Google Scholar] [CrossRef]
- Zhou, N.C.; Ye, L.; Wang, Q.G. Asymmetric Short-Circuit Current Calculation for Inverter Interfaced Distributed Generators with Negative Sequence Current Injection Integrated in Power Systems. Proc. CSEE 2013, 36, 41–49. [Google Scholar]
- Tan, H.Z.; Li, Y.L.; Chen, X.L. Influence of Inverter-Interfaced Distributed Generator with Low-Voltage Ride Through Capability on Short Circuit Current of Distribution Network. Electr. Power Autom. Equip. 2015, 8, 31–37. [Google Scholar] [CrossRef]

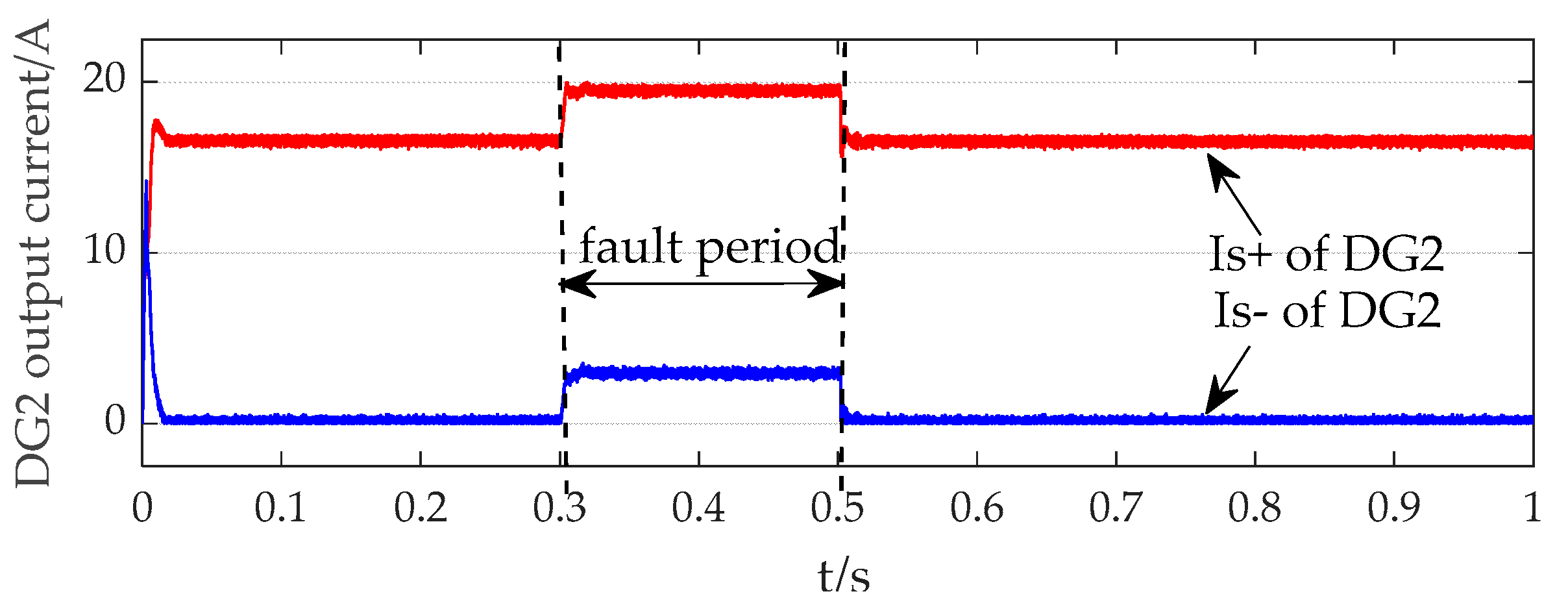
| Parameters | Value |
|---|---|
| DG capacity | 0.5 MW |
| positive sequence impedance | 0.047 + j0.062 Ω |
| negative sequence impedance | 0.047 + j0.062 Ω |
| zero-sequence impedance | 0.141 + j0.186 Ω |
| fault period | 0.3–0.5s |
| control goal | constant active power |
| Fault Position | Simulation Value/kA | Theoretical Value/kA | Relative Error | |
|---|---|---|---|---|
| Goal 1 | Bus A | 2.594 | 2.596 | 0.077% |
| Bus B | 2.566 | 2.568 | 0.078% | |
| Bus C | 2.566 | 2.567 | 0.039% | |
| Goal 2 | Bus A | 2.594 | 2.595 | 0.038 |
| Bus B | 2.566 | 2.566 | 0% | |
| Bus C | 2.566 | 2.567 | 0.039% | |
| Goal 3 | Bus A | 2.594 | 2.588 | 0.23% |
| Bus B | 2.566 | 2.559 | 0.27% | |
| Bus C | 2.566 | 2.558 | 0.31% |
| Voltage amplitude/kV | Bus A | Bus B | Bus C | Bus D | |
| Phase A | 7.865 | 7.783 | 7.701 | 7.823 | |
| Phase B | 8.347 | 8.399 | 8.451 | 8.372 | |
| Phase C | 8.106 | 8.09 | 8.075 | 8.097 |
| Fault Bus Node | Simulation Value/A | Theoretical Value/A | Relative Error |
|---|---|---|---|
| 28 | 912.9 | 921.8 | 0.98% |
| 9 | 951.1 | 955.5 | 0.47% |
| 24 | 1525.3 | 1531 | 0.38% |
| 5 | 1940.1 | 1944 | 0.2% |
| 32 | 720.7 | 735.4 | 2.04% |
| 14 | 701 | 708.5 | 1.01% |
| 17 | 690 | 703.5 | 1.95% |
| 30 | 792.86 | 804.1 | 1.42% |
| Assumptions | Control Strategy | Absolute Error | Voltage Level | |
|---|---|---|---|---|
| Reference [21] | Ignore negative sequence current | PQ control | Max absolute error 7A | Voltage > 0.9 p.u. |
| This study | Consider the impact of negative sequence current | Three control goals | Max absolute error 8A | Voltage < 0.9 p.u. (case 2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Qi, H.; Liu, R.; Yan, X.; Chen, C.; Guo, F.; Guo, F.; Dong, X. Short-Circuit Current Calculation of Single-Phase to Ground Fault in Petal-Shaped Distribution Network. Processes 2025, 13, 2393. https://doi.org/10.3390/pr13082393
Kang Y, Qi H, Liu R, Yan X, Chen C, Guo F, Guo F, Dong X. Short-Circuit Current Calculation of Single-Phase to Ground Fault in Petal-Shaped Distribution Network. Processes. 2025; 13(8):2393. https://doi.org/10.3390/pr13082393
Chicago/Turabian StyleKang, Yilong, Huanruo Qi, Rui Liu, Xiangyang Yan, Chen Chen, Fei Guo, Fang Guo, and Xiaoxiao Dong. 2025. "Short-Circuit Current Calculation of Single-Phase to Ground Fault in Petal-Shaped Distribution Network" Processes 13, no. 8: 2393. https://doi.org/10.3390/pr13082393
APA StyleKang, Y., Qi, H., Liu, R., Yan, X., Chen, C., Guo, F., Guo, F., & Dong, X. (2025). Short-Circuit Current Calculation of Single-Phase to Ground Fault in Petal-Shaped Distribution Network. Processes, 13(8), 2393. https://doi.org/10.3390/pr13082393






