Optimum Equipment Allocation Under Discrete Event Simulation for an Efficient Quarry Mining Process
Abstract
1. Introduction
2. Materials and Methods
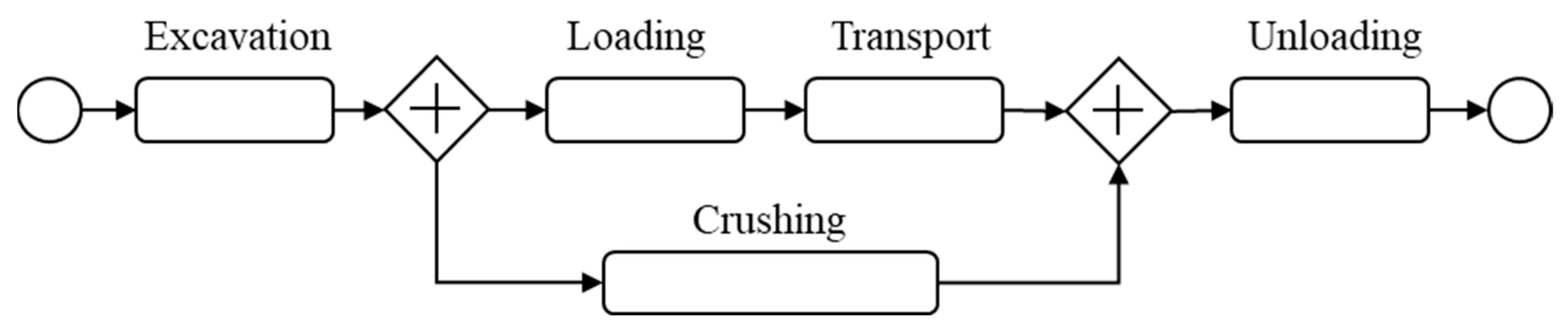
2.1. Quarry Mining Process
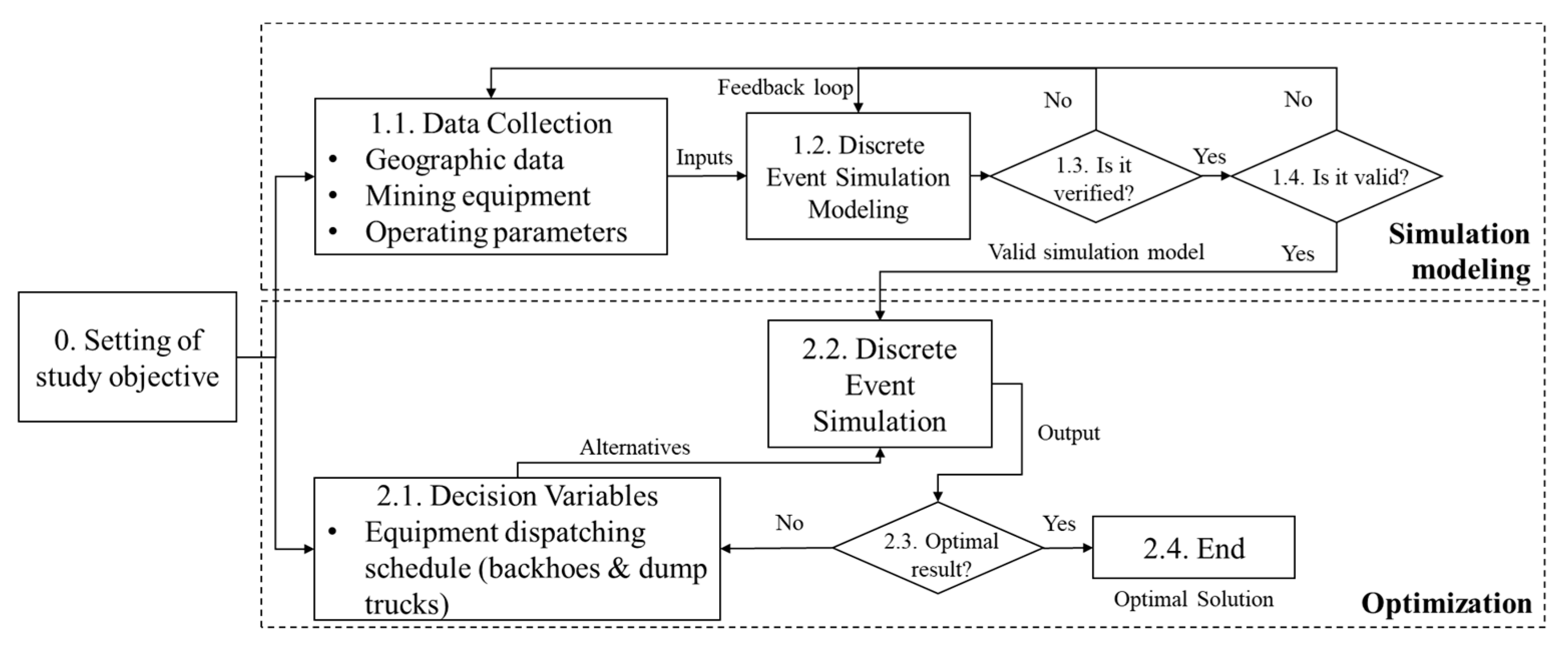
2.2. Simulation Modeling and Optimization in Quarry Mining
2.3. Simulation-Based Equipment Allocation in Quarry Mining
2.3.1. Optimization Model
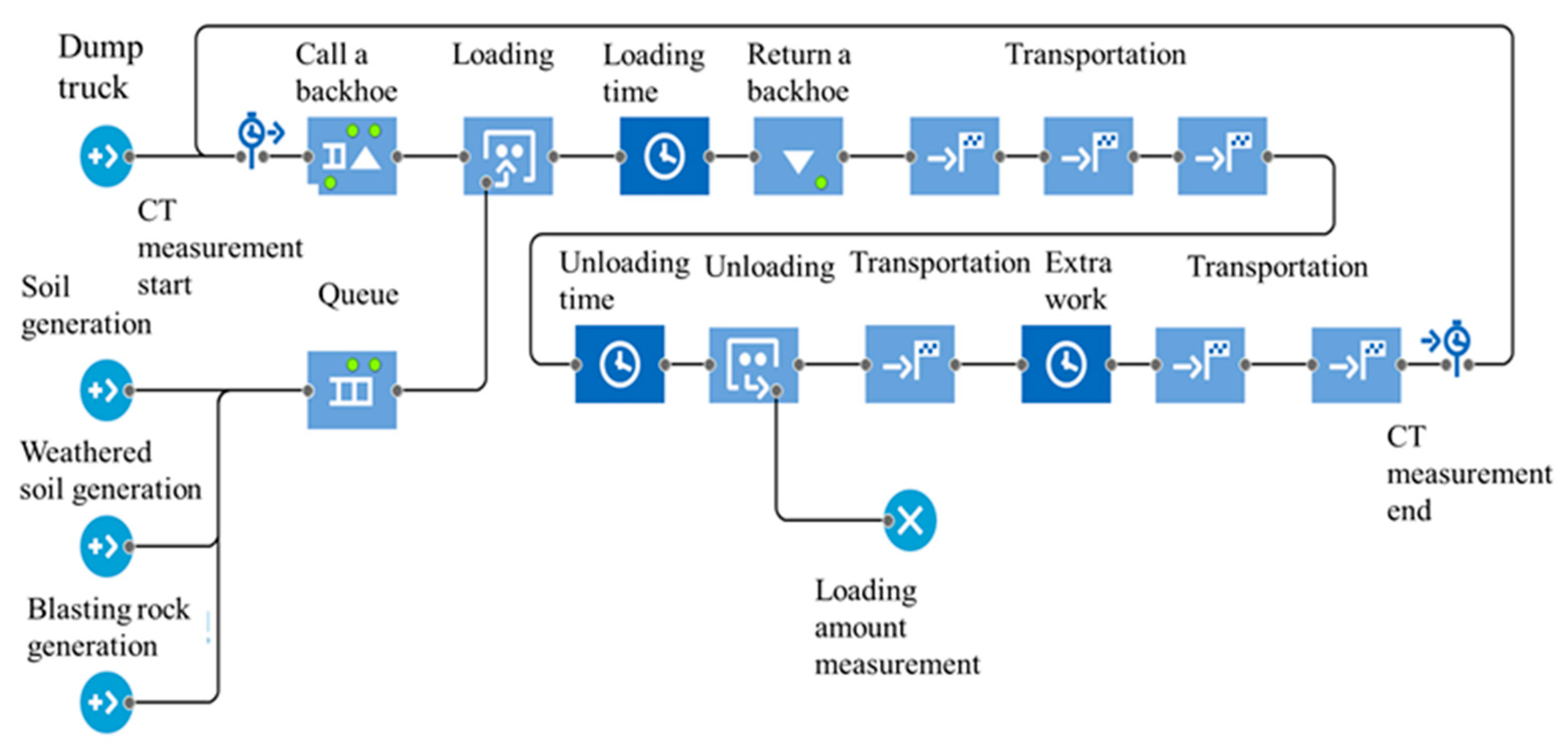
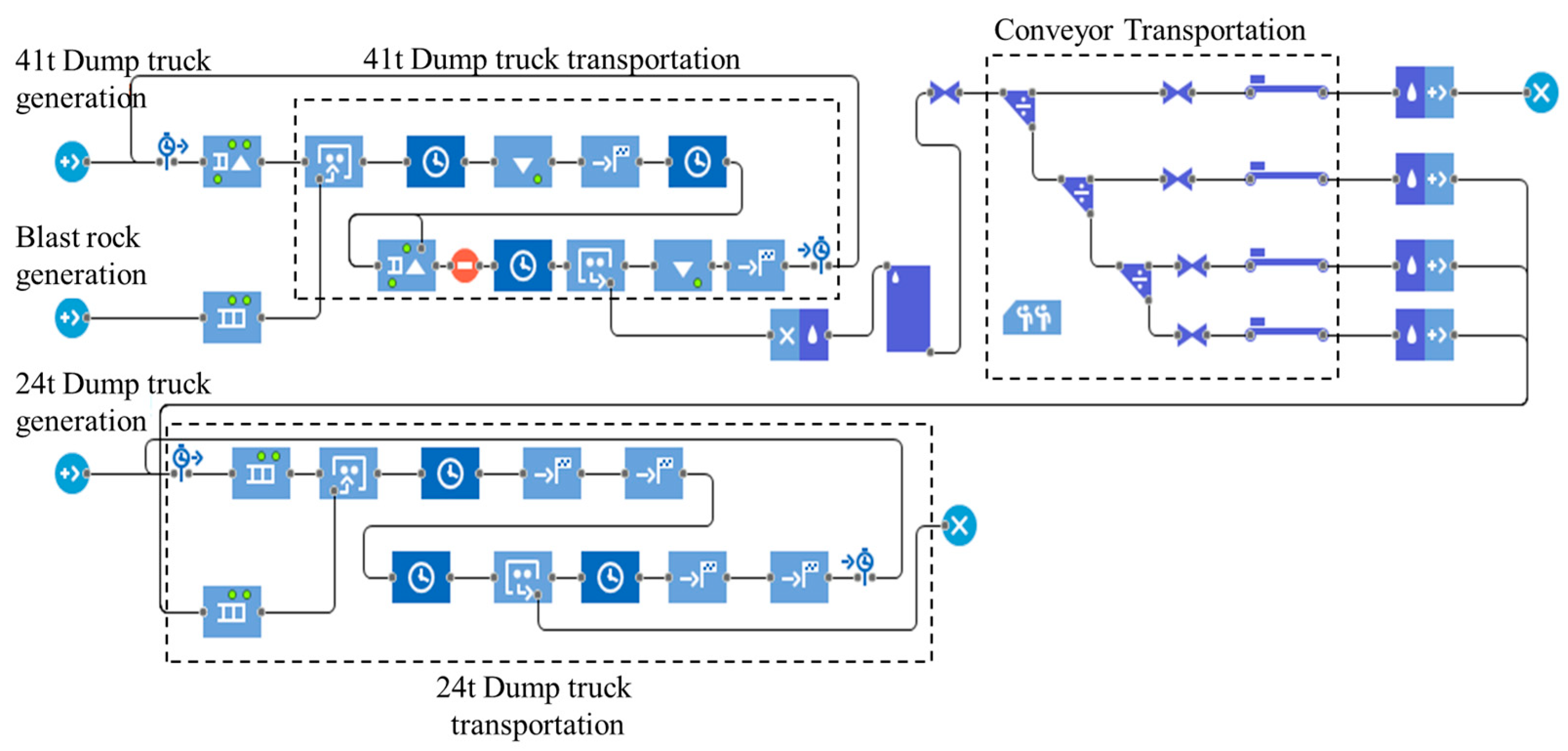
2.3.2. Simulation Model
3. Results
3.1. Scenario
3.2. Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Přikryl, R. Geomaterials as construction aggregates: A state-of-the-art. Bull. Eng. Geol. Environ. 2021, 80, 8831–8845. [Google Scholar] [CrossRef]
- Langer, W.H. An overview of aggregate resources in the United States. In Industrial Minerals and Extractive Industry Geology; Geological Survey of London: London, UK, 2002; pp. 9–16. [Google Scholar]
- Woodford, G. U.S. Aggregates Production Up 5% in 2021. Aggregates Business. Available online: https://www.aggbusiness.com/us-aggregates-production-5-2021 (accessed on 3 April 2025).
- Gran View Research. Aggregates Market Size, Share & Trends Analysis Report by Type (Gravel, Crushed Stone, Sand), by Application (Concrete, Road Base & Coverings), by Region (APAC, MEA), and Segment Forecasts, 2020–2027. Available online: https://www.grandviewresearch.com/industry-analysis/aggregates-market (accessed on 3 April 2025).
- Molit Statistics System. Construction Materials Status-Annual Aggregate Extraction Status. Available online: https://stat.molit.go.kr/portal/cate/statView.do?hRsId=344&hFormId=5393&hDivEng=&month_yn= (accessed on 3 April 2025).
- Rock Products. Aggregates Production. Available online: https://rockproducts.com/2020/07/06/aggregates-production-4/#:~:text=The%20U.S.%20Geological%20Survey%20Reports,the%20same%20period%20of%202019 (accessed on 3 April 2025).
- Oh, J.H. The Current Status of Aggregate Industry in Korea. Resour. Recycl. 2016, 25, 80–86. [Google Scholar]
- Deressa, G.W.; Choudhary, B.S. Evaluating Productivity in Opencast Mines: A Machine Learning Analysis of Drill-Blast and Surface Miner Operations. Nat. Resour. Res. 2025, 34, 215–251. [Google Scholar] [CrossRef]
- Sobko, B.; Lozhnikov, O.; Levytskyi, V.; Skyba, G. Conceptual development of the transition from drill and blast excavation to non-blasting methods for the preparation of mined rock in surface mining. Min.-Geol.-Pet. Bull. 2019, 34, 21–28. [Google Scholar] [CrossRef]
- Paricheh, M.; Osanloo, M.; Rahmanpour, M. A heuristic approach for in-pit crusher and conveyor system’s time and location problem in large open-pit mining. Int. J. Min. Reclam. Environ. 2018, 32, 35–55. [Google Scholar] [CrossRef]
- Sundar, D.K.; Acharya, D. Blast schedule planning and shiftwise production scheduling of an opencast iron ore mine. Comput. Ind. Eng. 1995, 28, 927–935. [Google Scholar] [CrossRef]
- Choudhary, R.P. Optimization of Load-Haul-Dump Mining System by OEE and Match Factor for Surface Mining. Int. J. Appl. Eng. Technol. 2015, 5, 96–102. [Google Scholar]
- Choi, Y.S.; Sun, W.C.; Park, H.D. Analysis of Optimal Haulage Routes for Dump Trucks in Large Open Pit Mines. J. Korean Soc. Geosystem Eng. 2007, 44, 447–491. [Google Scholar]
- Dabbagh, A.; Bagherpour, R. Investigating the Applicability of Imperialist Competitive Algorithm in the Problem of Allocating Truck to the Open Pit Mine. Min.-Geol.-Pet. Bull. 2019, 34, 35–42. [Google Scholar] [CrossRef]
- Pavloudakis, F.; Roumpos, C.; Spanidis, P.M. Planning the closure of surface coal mines based on circular economy principles. Circ. Econ. Sustain. 2024, 4, 75–96. [Google Scholar] [CrossRef]
- Mirzehi, M.; Afrapoli, A.M. Sustainable long-term production planning of open pit mines: An integrated framework for concurrent economical and environmental optimization. Resour. Policy 2024, 94, 105131. [Google Scholar] [CrossRef]
- Mirzaei-Nasirabad, H.; Mohtasham, M.; Askari-Nasab, H.; Alizadeh, B. An optimization model for the real-time truck dispatching problem in open-pit mining operations. Optim. Eng. 2023, 24, 2449–2473. [Google Scholar] [CrossRef]
- Peña-Graf, F.; Órdenes, J.; Wilson, R.; Navarra, A. Discrete event simulation for machine-learning enabled mine production control with application to gold processing. Metals 2022, 12, 225. [Google Scholar] [CrossRef]
- Whittle, D.; Brazil, M.; Grossman, P.A.; Rubinstein, J.H.; Thomas, D.A. Combined optimisation of an open-pit mine outline and the transition depth to underground mining. Eur. J. Oper. Res. 2018, 268, 624–634. [Google Scholar] [CrossRef]
- Ramani, R.V. Surface mining technology: Progress and prospects. Procedia Eng. 2012, 46, 9–21. [Google Scholar] [CrossRef]
- Omnia Machinery, What Is Underground Mining? Available online: https://www.omniamachinery.com/2021/05/what-is-underground-mining/ (accessed on 4 April 2025).
- Greberg, J.; Salama, A.; Gustafson, A.; Skawina, B. Alternative process flow for underground mining operations: Analysis of conceptual transport methods using discrete event simulation. Minerals 2016, 6, 65. [Google Scholar] [CrossRef]
- Dendle, N.; Isokangas, E.; Corry, P. Efficient simulation for an open-pit mine. Simul. Model. Pract. Theory 2022, 117, 102473. [Google Scholar] [CrossRef]
- Liu, S.Q.; Kozan, E. New graph-based algorithms to efficiently solve large scale open pit mining optimisation problems. Expert. Syst. Appl. 2016, 43, 59–65. [Google Scholar] [CrossRef]
- Drew, L.J.; Langer, W.H.; Sachs, J.S. Environmentalism and natural aggregate mining. Nat. Resour. Res. 2002, 11, 19–28. [Google Scholar] [CrossRef]
- Ercelebi, S.G.; Bascetin, A. Optimization of shovel-truck system for surface mining. J. South. Afr. Inst. Min. Metall. 2009, 109, 433–439. [Google Scholar]
- Ozdemir, B.; Kumral, M. A system-wide approach to minimize the operational cost of bench production in open-cast mining operations. Int. J. Coal Sci. Technol. 2019, 6, 84–94. [Google Scholar] [CrossRef]
- Campeau, L.P.; Gamache, M. Short-term planning optimization model for underground mines. Comput. Oper. Res. 2020, 115, 104642. [Google Scholar] [CrossRef]
- Ben-Awuah, E.; Richter, O.; Elkington, T.; Pourrahimian, Y. Strategic mining options optimization: Open pit mining, underground mining or both. Int. J. Min. Sci. Technol. 2016, 26, 1065–1071. [Google Scholar] [CrossRef]
- L’Heureux, G.; Gamache, M.; Soumis, F.J.M.T. Mixed integer programming model for short term planning in open-pit mines. Min. Technol. 2013, 122, 101–109. [Google Scholar] [CrossRef]
- Upadhyay, S.P.; Askari-Nasab, H. Simulation and optimization approach for uncertainty-based short-term planning in open pit mines. Int. J. Min. Sci. Technol. 2018, 28, 153–166. [Google Scholar] [CrossRef]
- Afrapoli, A.M.; Tabesh, M.; Askari-Nasab, H. A multiple objective transportation problem approach to dynamic truck dispatching in surface mines. Eur. J. Oper. Res. 2019, 276, 331–342. [Google Scholar] [CrossRef]
- Abolghasemian, M.; Ghane Kanafi, A.; Daneshmandmehr, M. A two-phase simulation-based optimization of hauling system in open-pit mine. Interdiscip. J. Manag. Stud. 2020, 13, 705–732. [Google Scholar]
- Runciman, N.; Vagenas, N.; Baiden, G. Evaluation of underground development mining systems using discrete-event simulation. Simulation 1999, 72, 4–11. [Google Scholar] [CrossRef]
- Banks, J. Handbook of Simulation: Principles, Methodology, Advances, Applications, and Practice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998; pp. 55–396. [Google Scholar]
- Hussain, Z.; Haider, H.U.D.; Li, J.; Yu, Z.; Fu, J.; Zhang, S.; Zhu, S.; Ni, W.; Hitch, M. Mapping, Modeling and Designing a Marble Quarry Using Integrated Electric Resistivity Tomography and Unmanned Aerial Vehicles: A Study of Adaptive Decision-Making. Drones 2025, 9, 266. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.; Kim, S. Simulation modeling in supply chain management research of ethanol: A review. Energies 2023, 16, 7429. [Google Scholar] [CrossRef]

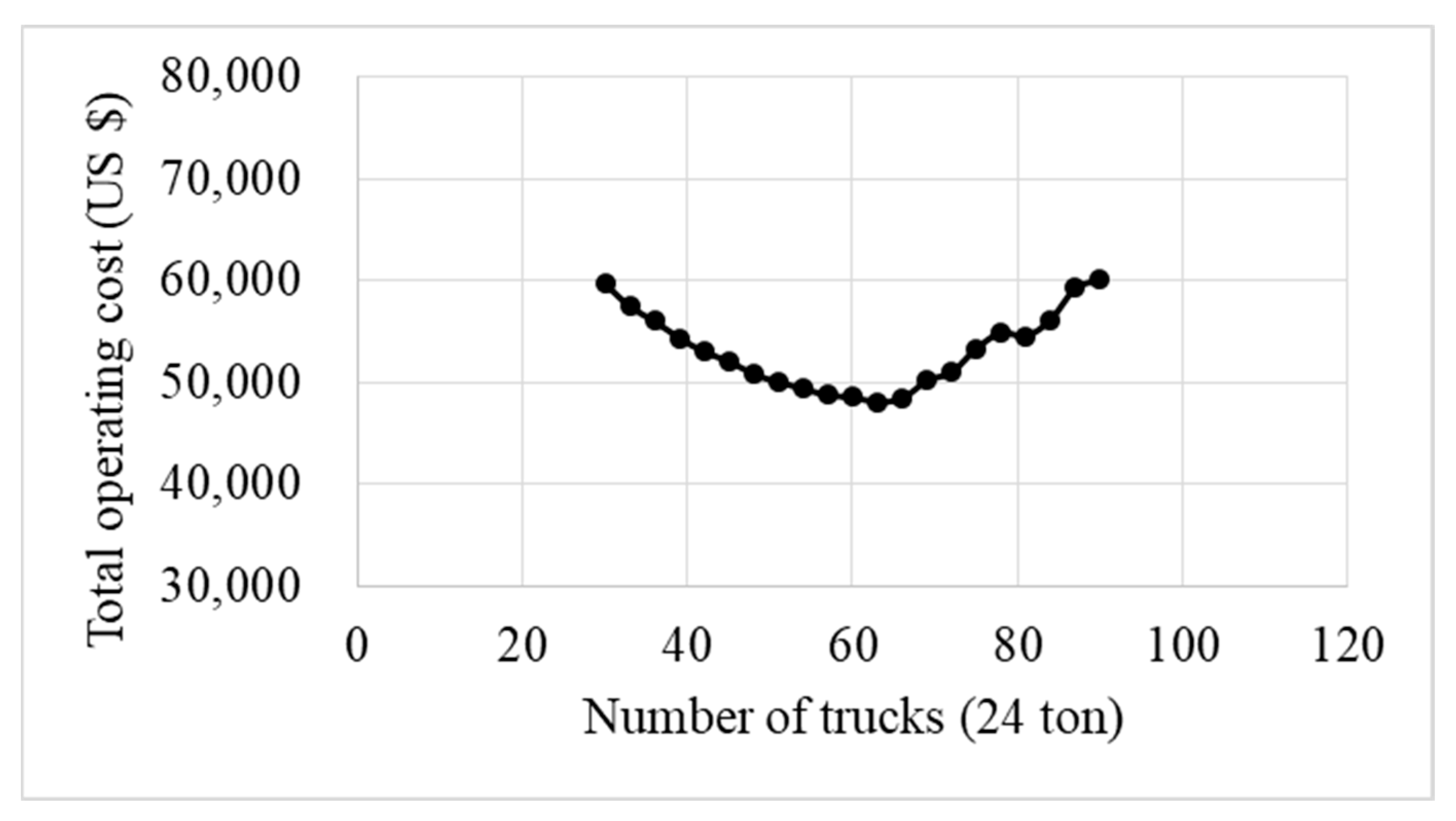
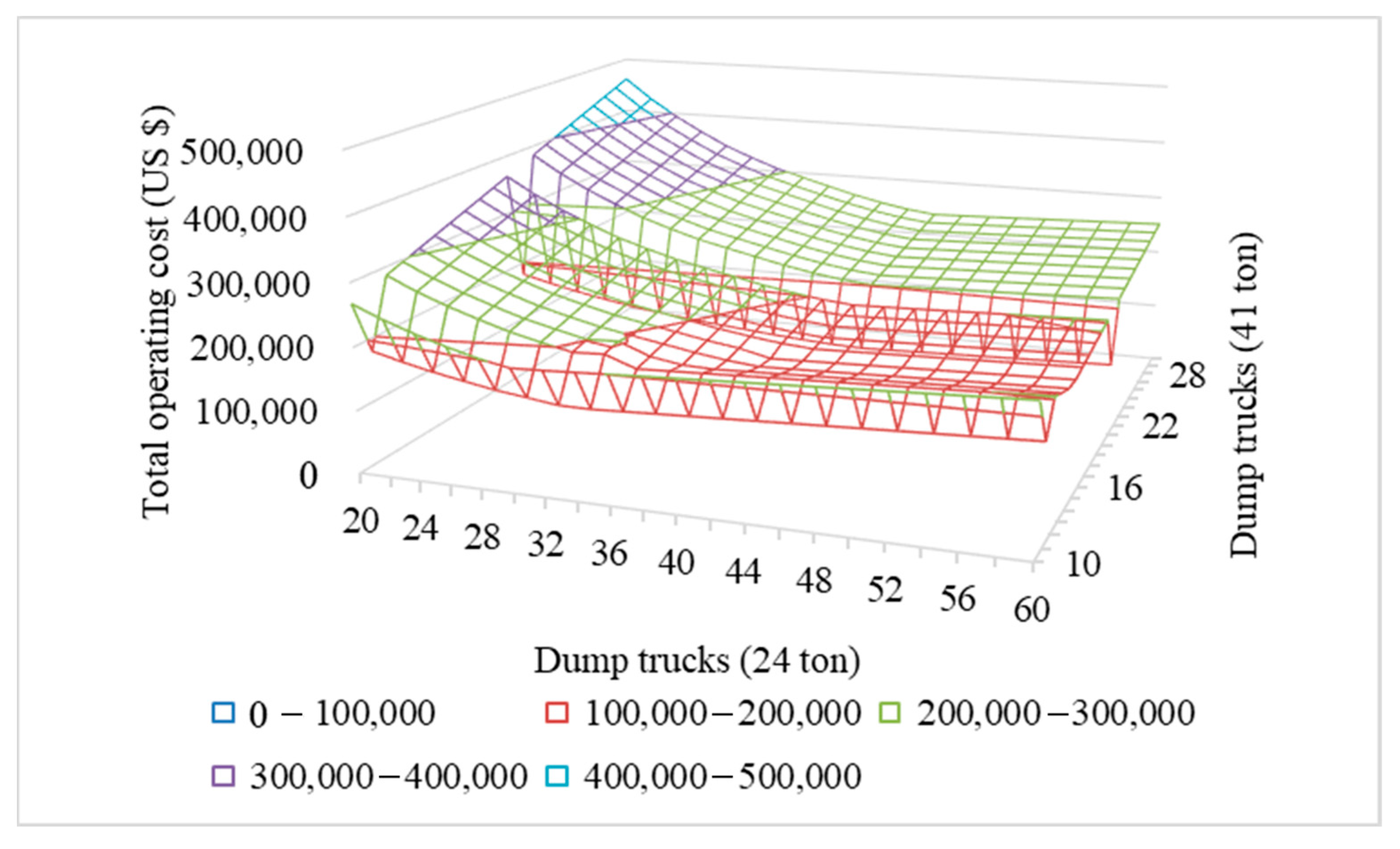
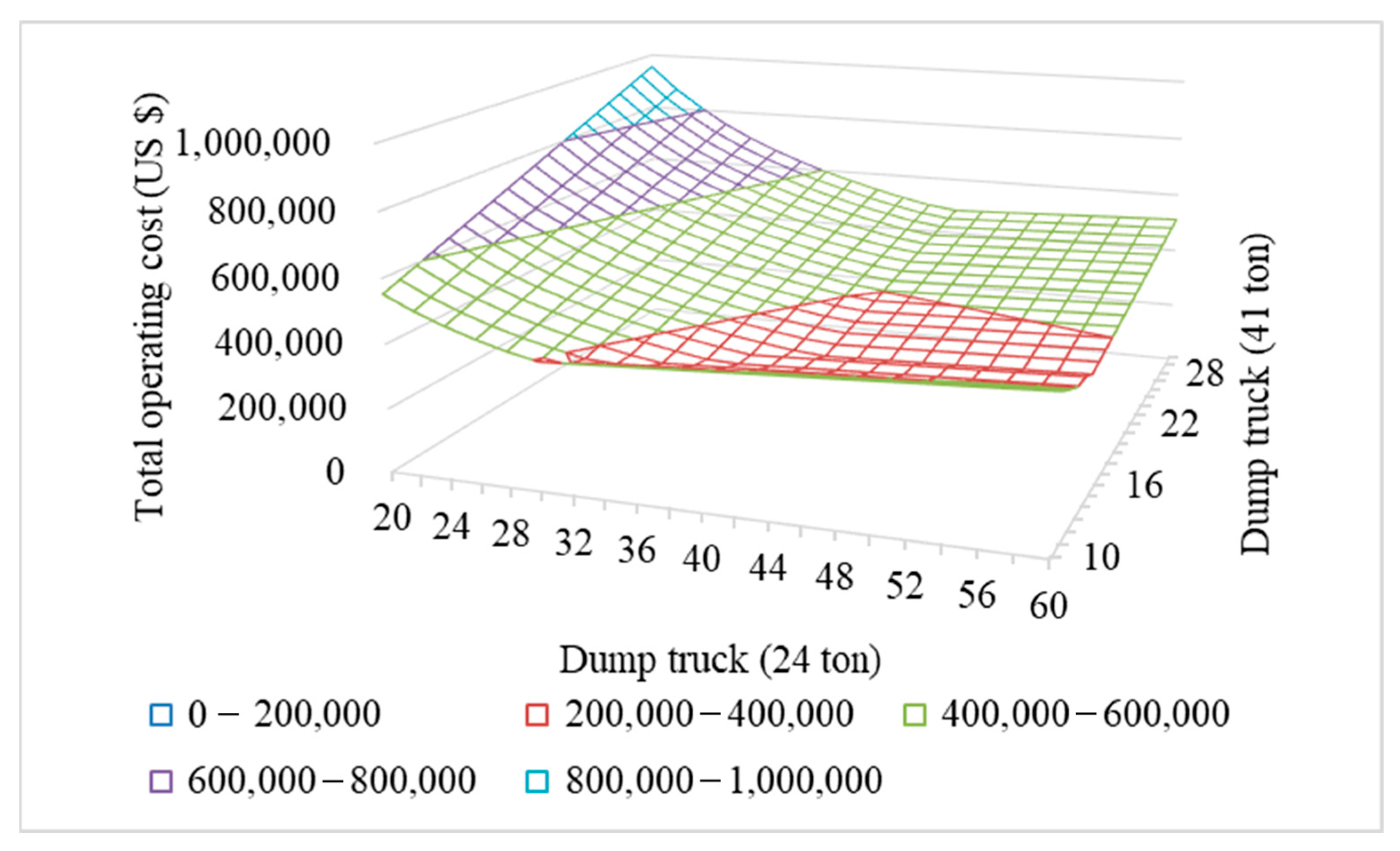
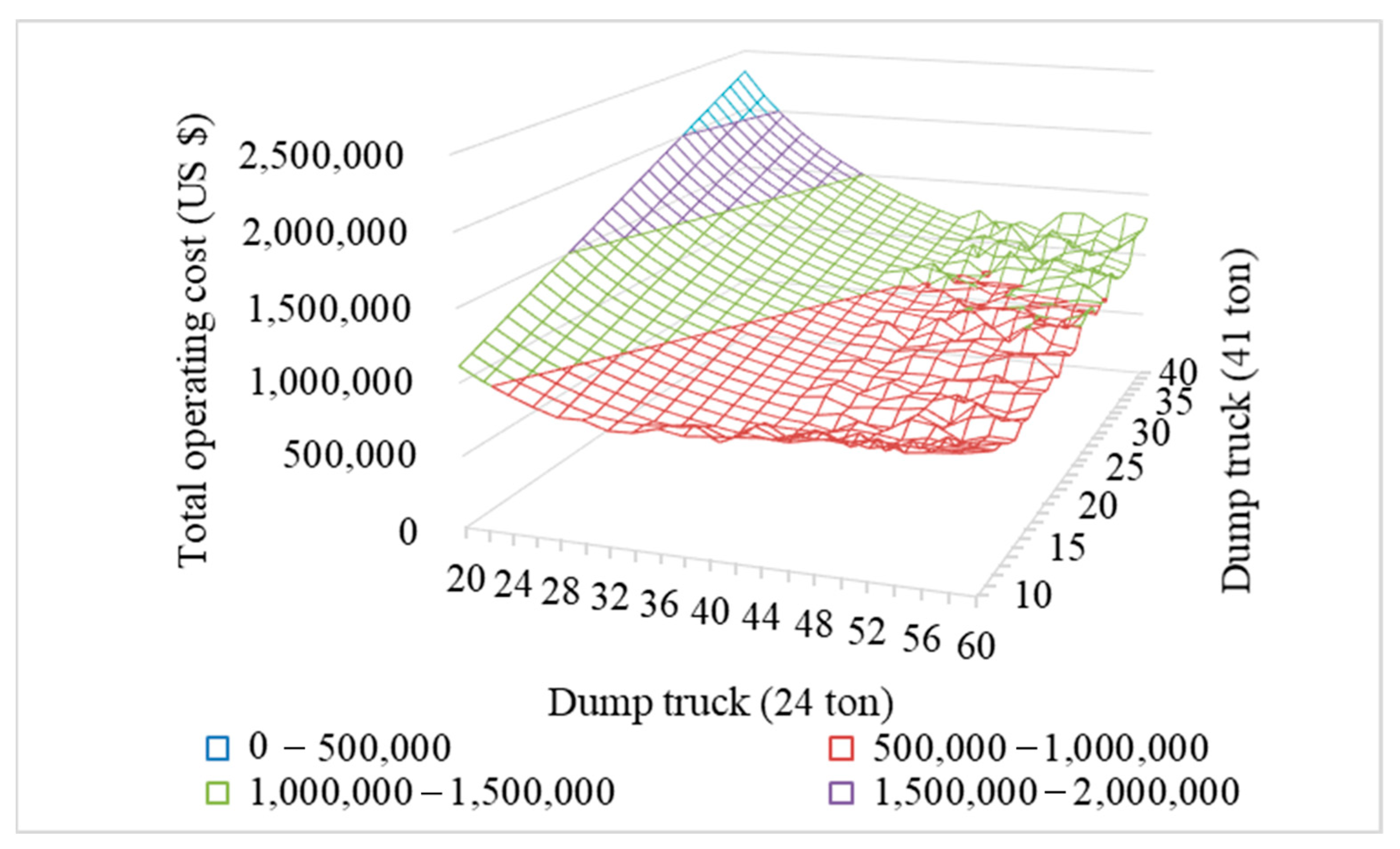
| Category | Stage | Depth (m) | Equipment |
|---|---|---|---|
| 1 | 1~3 (Open-pit mining) | 0~30 | Dump truck 24 t and backhoe 2.0 m3 |
| 2 | 4~6 (Open-pit and tunnel mining) | 30~60 | Dump truck 24 t, dump truck 41 t, backhoe 2.0 m3, and backhoe 4.64 m3 |
| 3 | 7~9 (Open-pit and tunnel mining) | 60~90 | Dump truck 24 t, dump truck 41 t, backhoe 2.0 m3, and backhoe 4.64 m3 |
| 4 | 10~13 (Open-pit and tunnel mining) | 90~130 | Dump truck 24 t, dump truck 41 t, backhoe 2.0 m3, and backhoe 4.64 m3 |
| Parameters | Value | Description |
|---|---|---|
| Triangular (2.87, 3.53, 5.03) min | Time required for loading soil into a dump truck (24 t) across all categories | |
| Triangular (4.7, 6.0, 8.52) min | Time required for loading ripped rock into a dump truck (24 t) across all categories | |
| Triangular (10.10, 12.06, 13.24) min | Loading time for blasting rock using a 24 t dump truck across all categories | |
| Triangular (9.5, 10.84, 12.24) min | Loading time for blasting rock using a 41 t dump truck across all categories | |
| 15.67 m3 | Soil loading capacity of a 24 t dump truck across all categories | |
| 15.16 m3 | Ripping rock loading capacity of a 24 t dump truck across all categories | |
| 15.16 m3 | Blasting rock loading capacity of a 24 t dump truck across all categories | |
| 24.47 m3 | Blasting rock loading capacity of a 41 t dump truck across all categories | |
| Uniform (11.7, 13.5) min | Transport time for a 24 t dump truck on route A across all categories | |
| Uniform (5.3, 7.5) min | Transport time for a 24 t dump truck on route B across all categories | |
| Uniform (3, 5.05) min | Travel time for a dump truck (24 t) on route C across all categories | |
| Uniform (3.88, 4.33) min | Vertical shaft travel time for a dump truck (41 t) across all categories | |
| Triangular (3.9, 4.1, 4.3) min | Unload duration for a dump truck (24 t, 41 t) across all categories | |
| USD 48.88/h | Operational cost of a dump truck (24 t) across all categories | |
| USD 266.80/h | Operational cost of backhoes (2.0 m3) across all categories | |
| USD 111.19/h | Operational cost of a dump truck (41 t) across all categories | |
| USD 255.74/h | Operational cost of backhoes (4.64 m3) across all categories | |
| - | Queue time for a dump truck (24 t, 41 t) across all categories |
| Category | Equipment | |||
|---|---|---|---|---|
| 1 (1~3 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 30~90 units |
| 2 (4~6 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 20~60 units |
| Backhoes (4.64 m3) | 10 units | Dump trucks (41 t) | 10~30 units | |
| 3 (7~9 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 20~60 units |
| Backhoes (4.64 m3) | 10 units | Dump trucks (41 t) | 10~30 units | |
| 4 (10~13 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 20~60 units |
| Backhoes (4.64 m3) | 10 units | Dump trucks (41 t) | 10~30 units | |
| Variables | Default Value | Description |
|---|---|---|
| 10 | Number of backhoes (2.0 m3) across all categories | |
| 10 | Number of backhoes (4.64 m3) assigned to category 2 | |
| 10 | Number of backhoes (4.64 m3) assigned to category 3 | |
| 10 | Number of backhoes (4.64 m3) assigned to category 4 | |
| 10 | Number of dump trucks (24 t) across all categories | |
| 10 | Number of dump trucks (41 t) assigned to category 2 | |
| 10 | Number of dump trucks (41 t) assigned to category 3 | |
| 10 | Number of dump trucks (41 t) assigned to category 4 |
| Category | Equipment | |||
|---|---|---|---|---|
| 1 (1~3 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 63 units |
| 2 (4~6 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 44 units |
| Backhoes (4.64 m3) | 10 units | Dump trucks (41 t) | 21 units | |
| 3 (7~9 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 46 units |
| Backhoes (4.64 m3) | 10 units | Dump trucks (41 t) | 15 units | |
| 4 (10~13 stages) | Backhoes (2.0 m3) | 10 units | Dump trucks (24 t) | 46 units |
| Backhoes (4.64 m3) | 10 units | Dump trucks (41 t) | 15 units | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Kim, S. Optimum Equipment Allocation Under Discrete Event Simulation for an Efficient Quarry Mining Process. Processes 2025, 13, 2215. https://doi.org/10.3390/pr13072215
Lee H, Kim S. Optimum Equipment Allocation Under Discrete Event Simulation for an Efficient Quarry Mining Process. Processes. 2025; 13(7):2215. https://doi.org/10.3390/pr13072215
Chicago/Turabian StyleLee, Hyunho, and Sojung Kim. 2025. "Optimum Equipment Allocation Under Discrete Event Simulation for an Efficient Quarry Mining Process" Processes 13, no. 7: 2215. https://doi.org/10.3390/pr13072215
APA StyleLee, H., & Kim, S. (2025). Optimum Equipment Allocation Under Discrete Event Simulation for an Efficient Quarry Mining Process. Processes, 13(7), 2215. https://doi.org/10.3390/pr13072215







