Research on the Damage Evolution Law of Branch Wellbore Based on Damage Mechanics
Abstract
1. Introduction
2. Multiphysics Coupling Mathematical Model for Wellbore Stability
2.1. Effective Stress Principle
2.2. Stress Equilibrium Equation
2.3. Seepage Continuity Equation
2.4. Elastoplastic Damage Theory
2.5. Damage Evolution Equation
2.6. Permeability Evolution Equation
2.7. Model Validation
3. Instability Mechanism of Wellbore Under Multiphysics Coupling Conditions
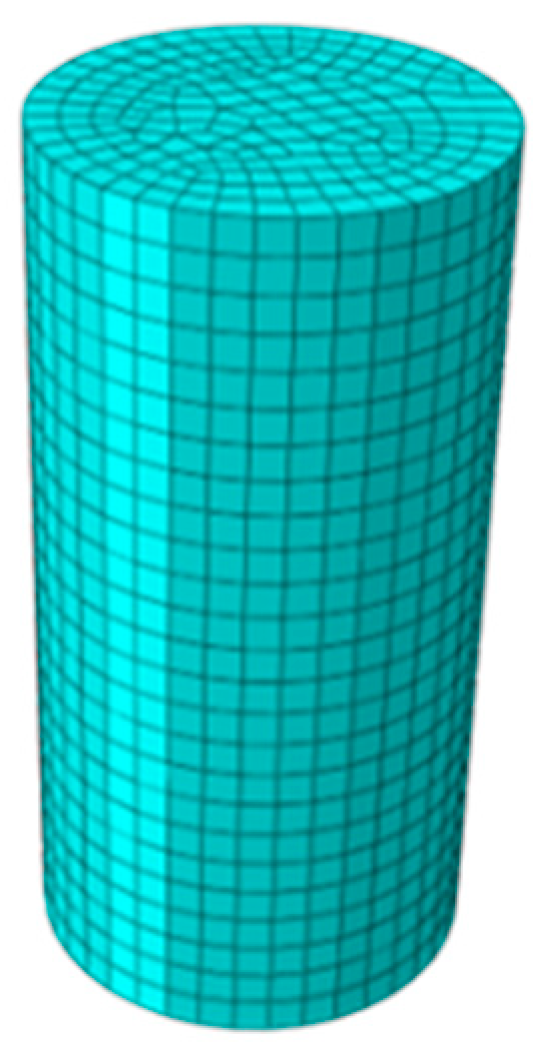
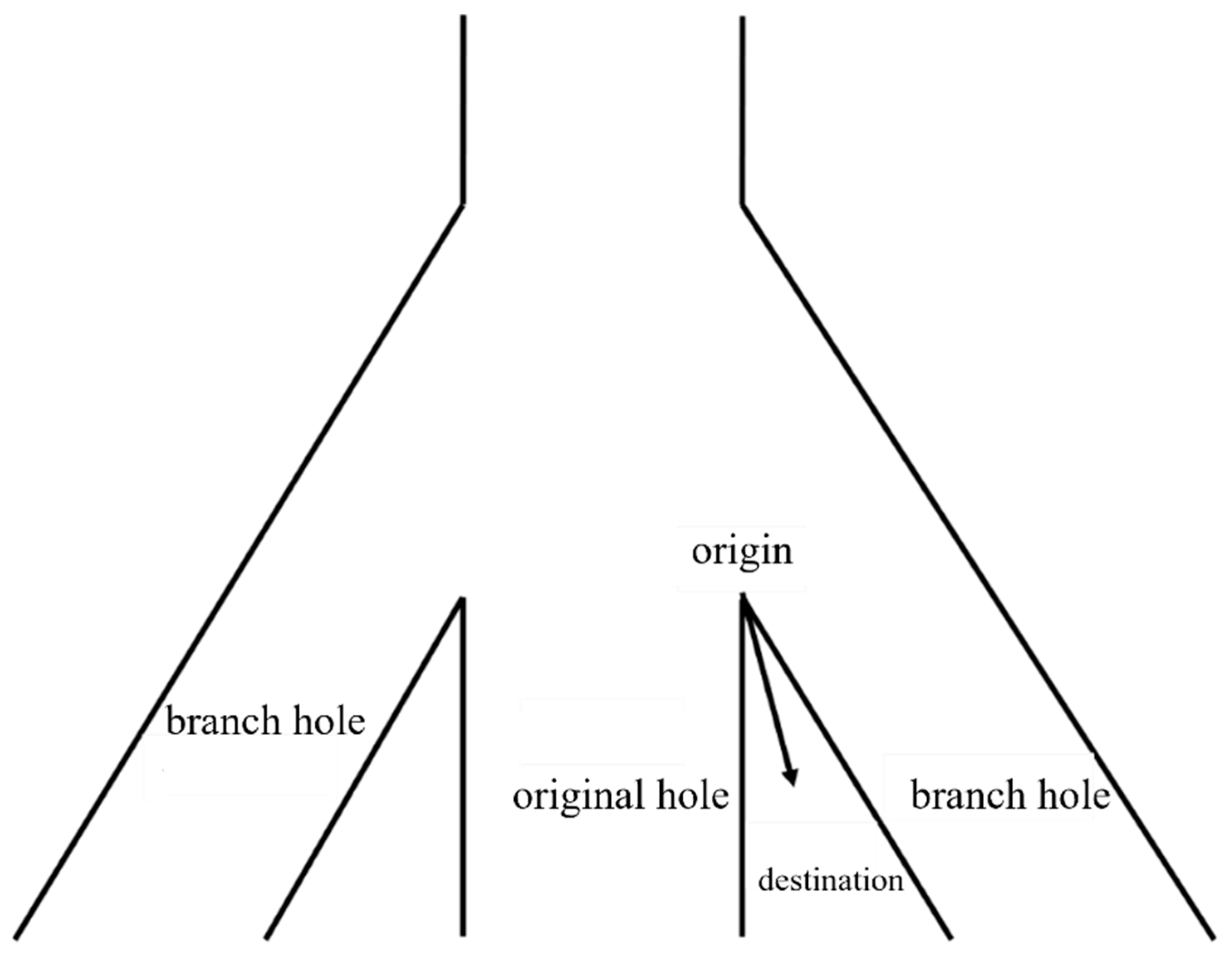
3.1. Geometric Model
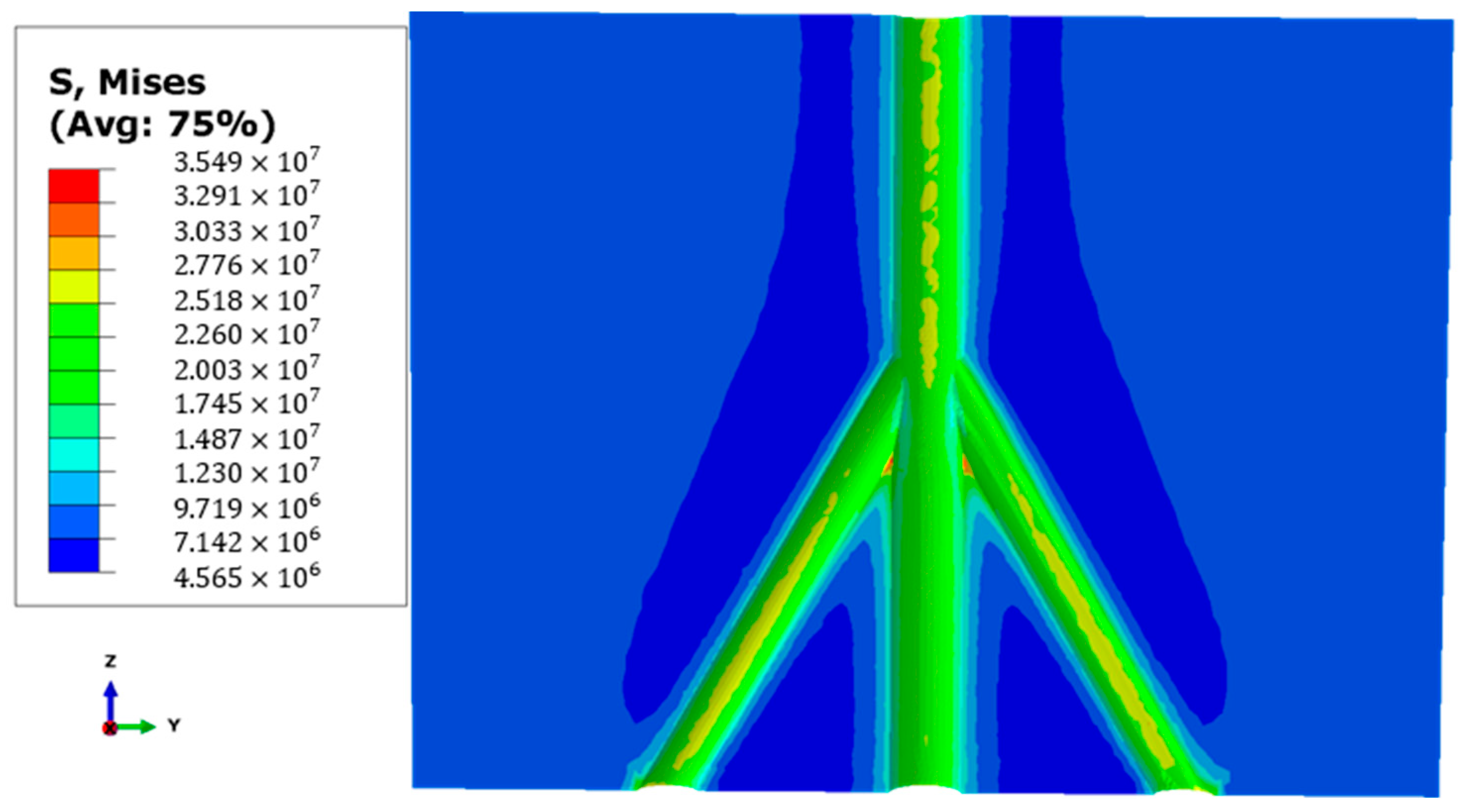
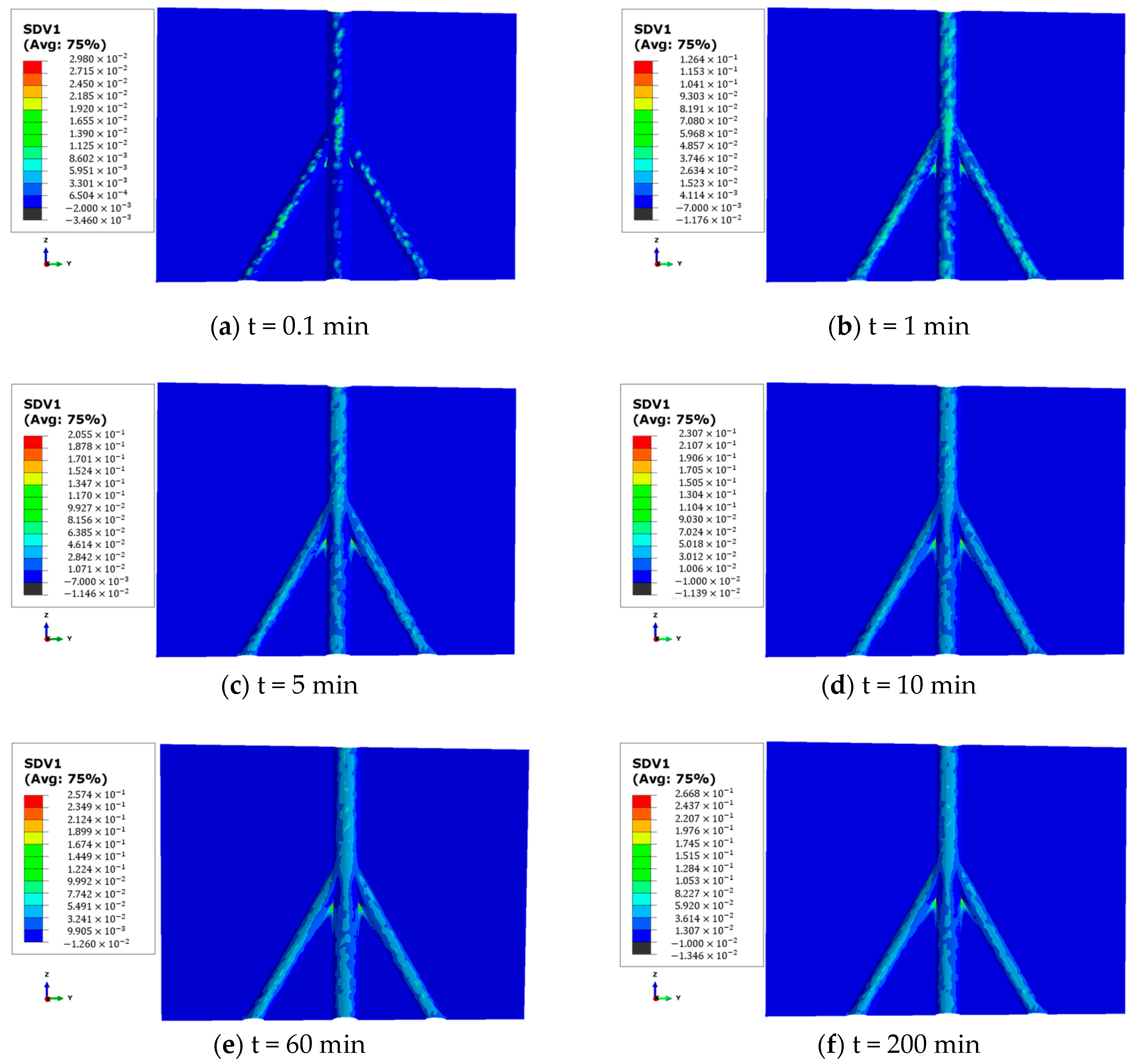
3.2. Evolution of Formation Damage Around Branch Wellbores
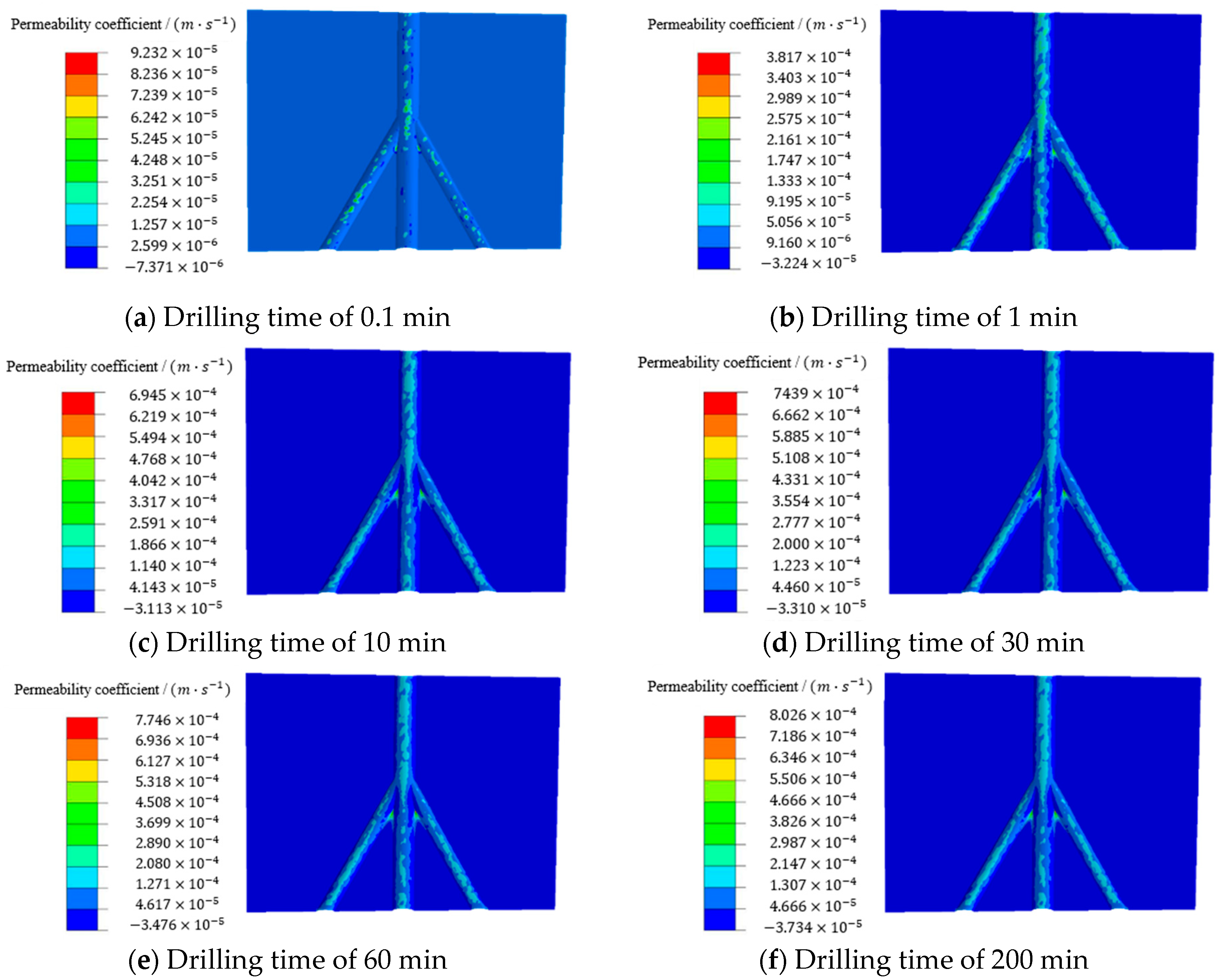
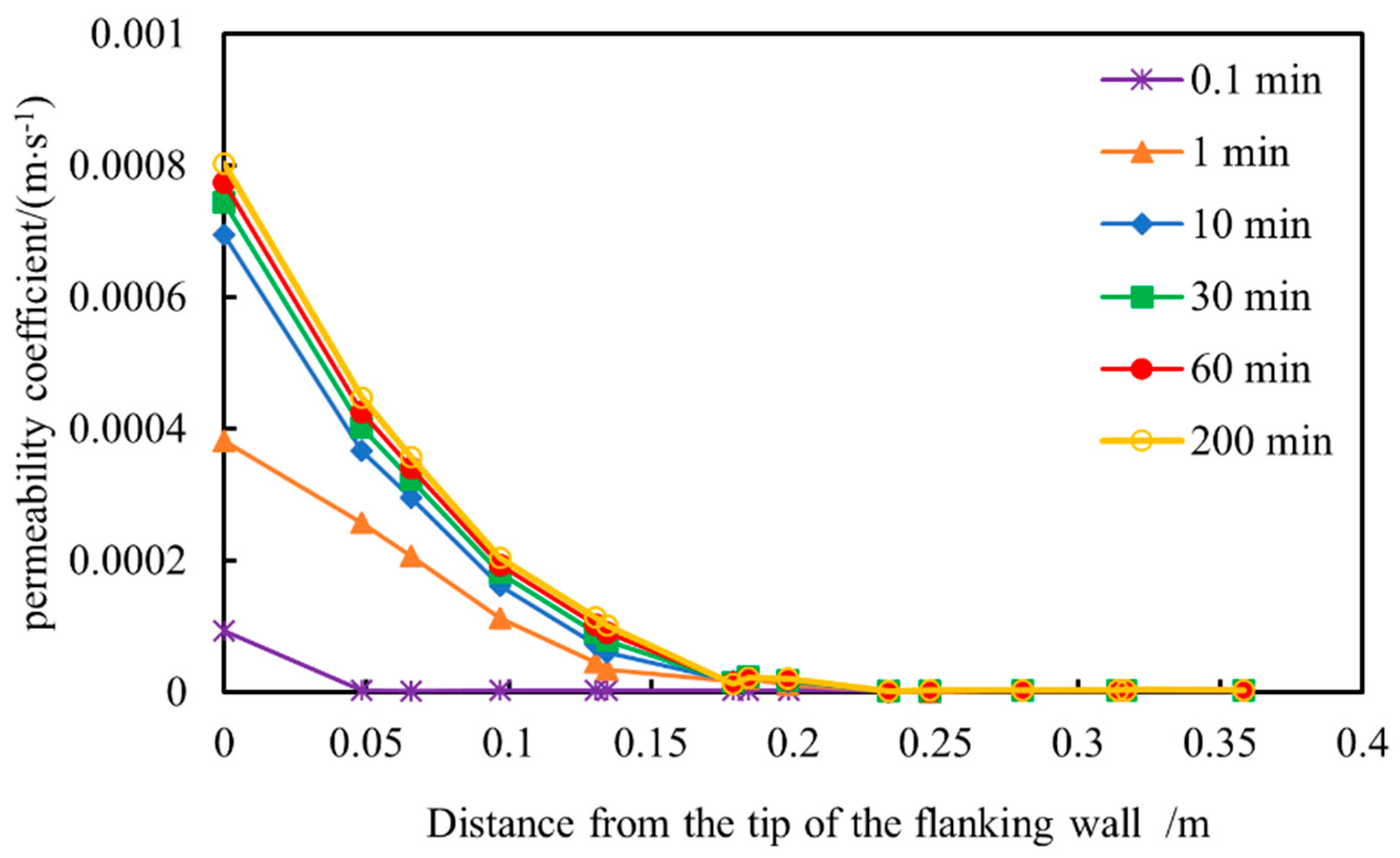
3.3. Evolution of Formation Permeability Around Branch Wellbores
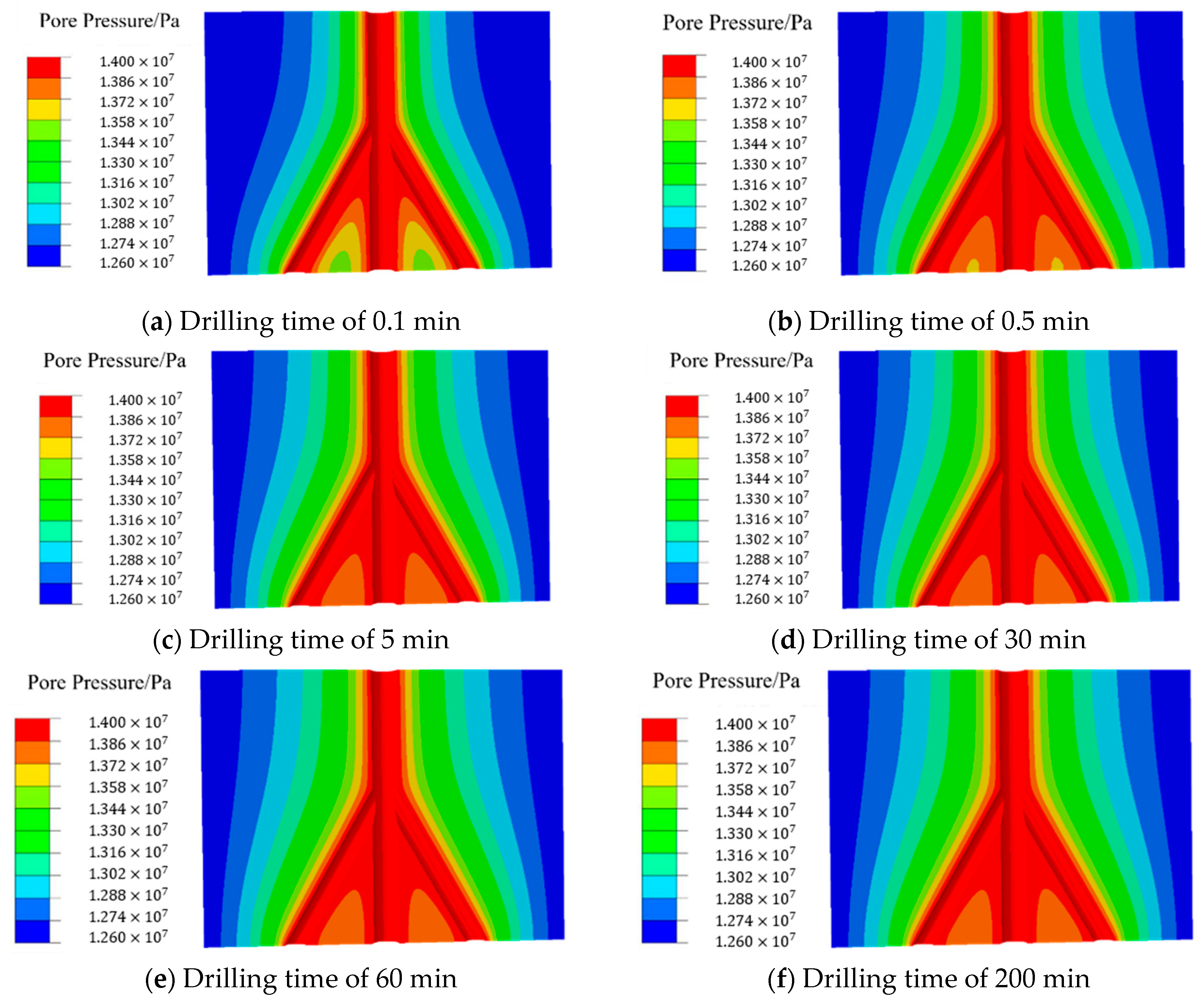
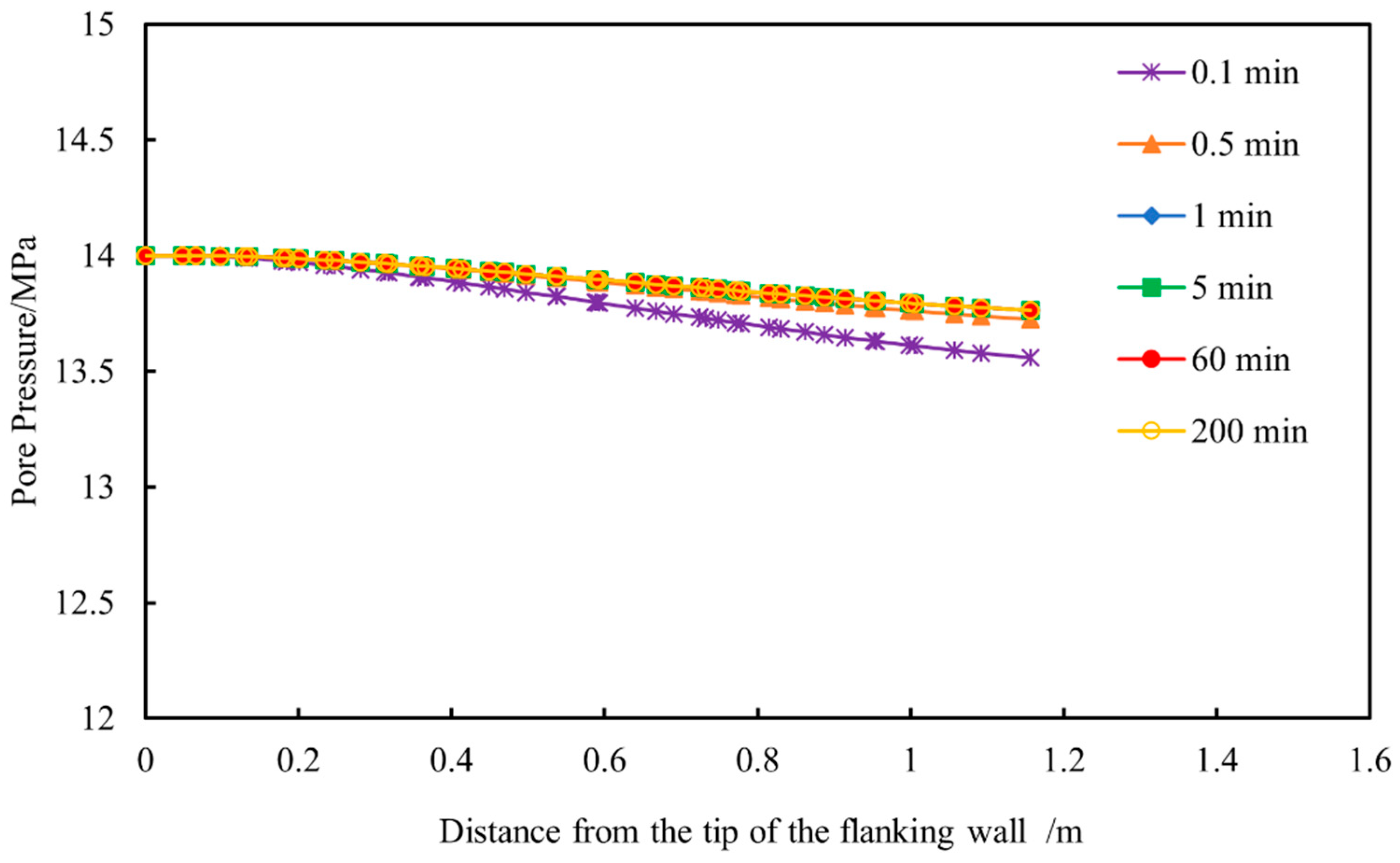
3.4. Distribution of Pore Pressure Around Branch Wellbores
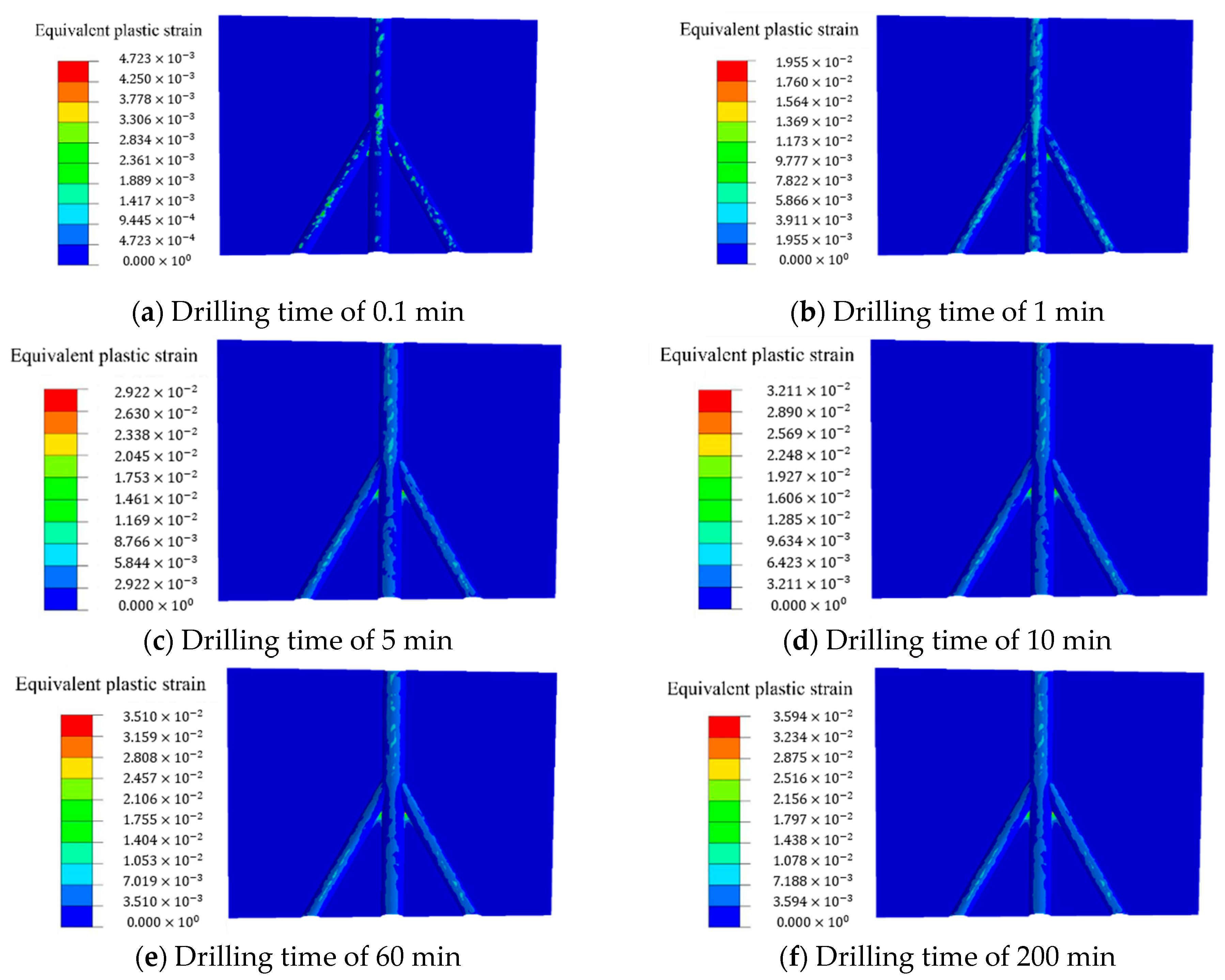
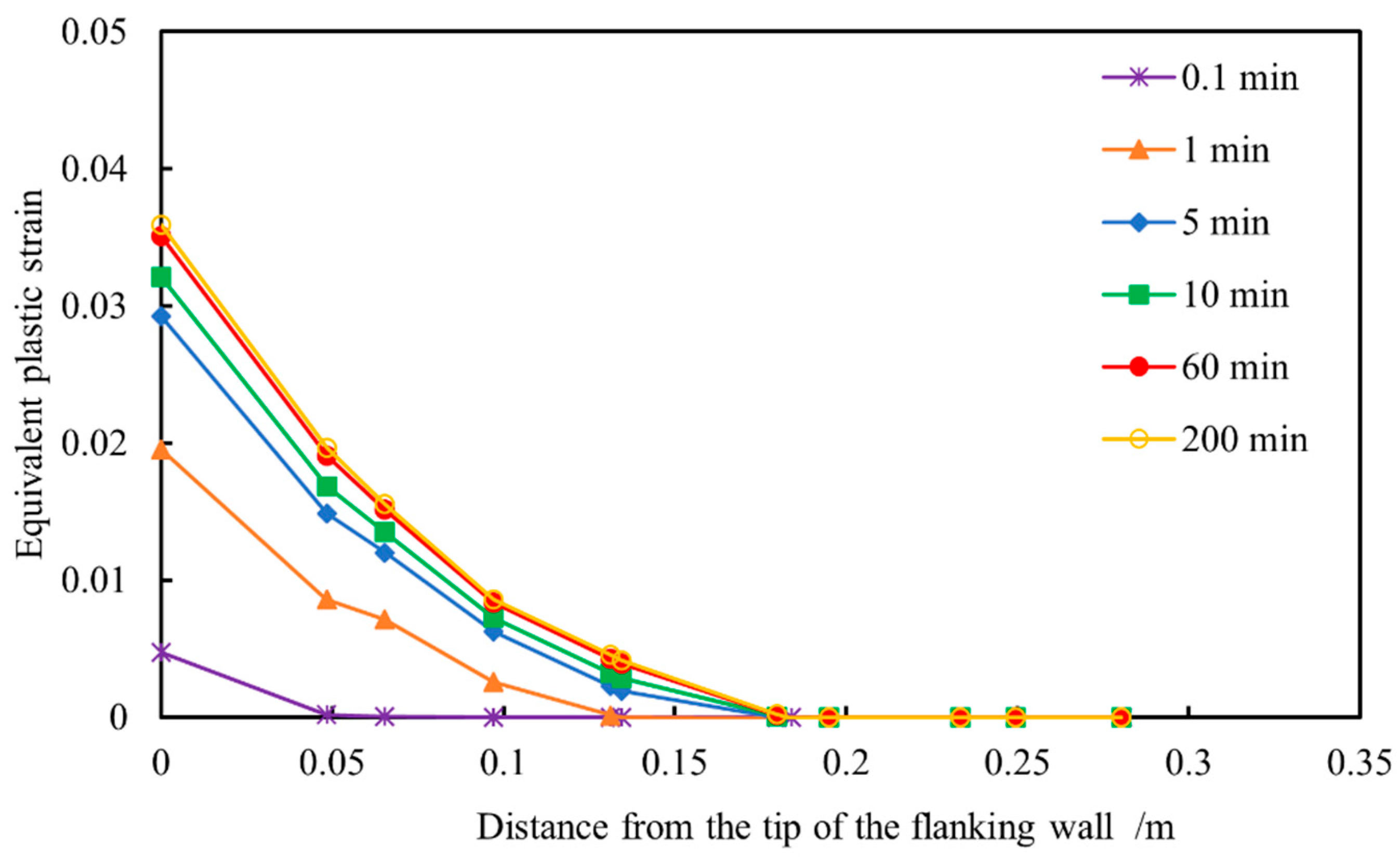
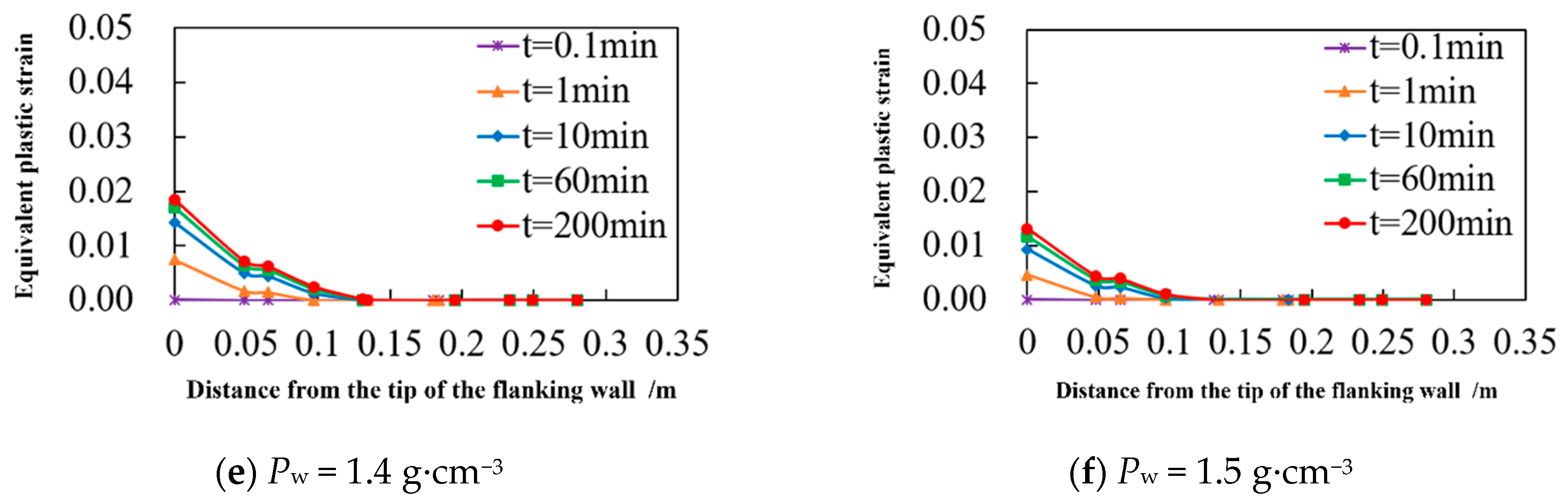
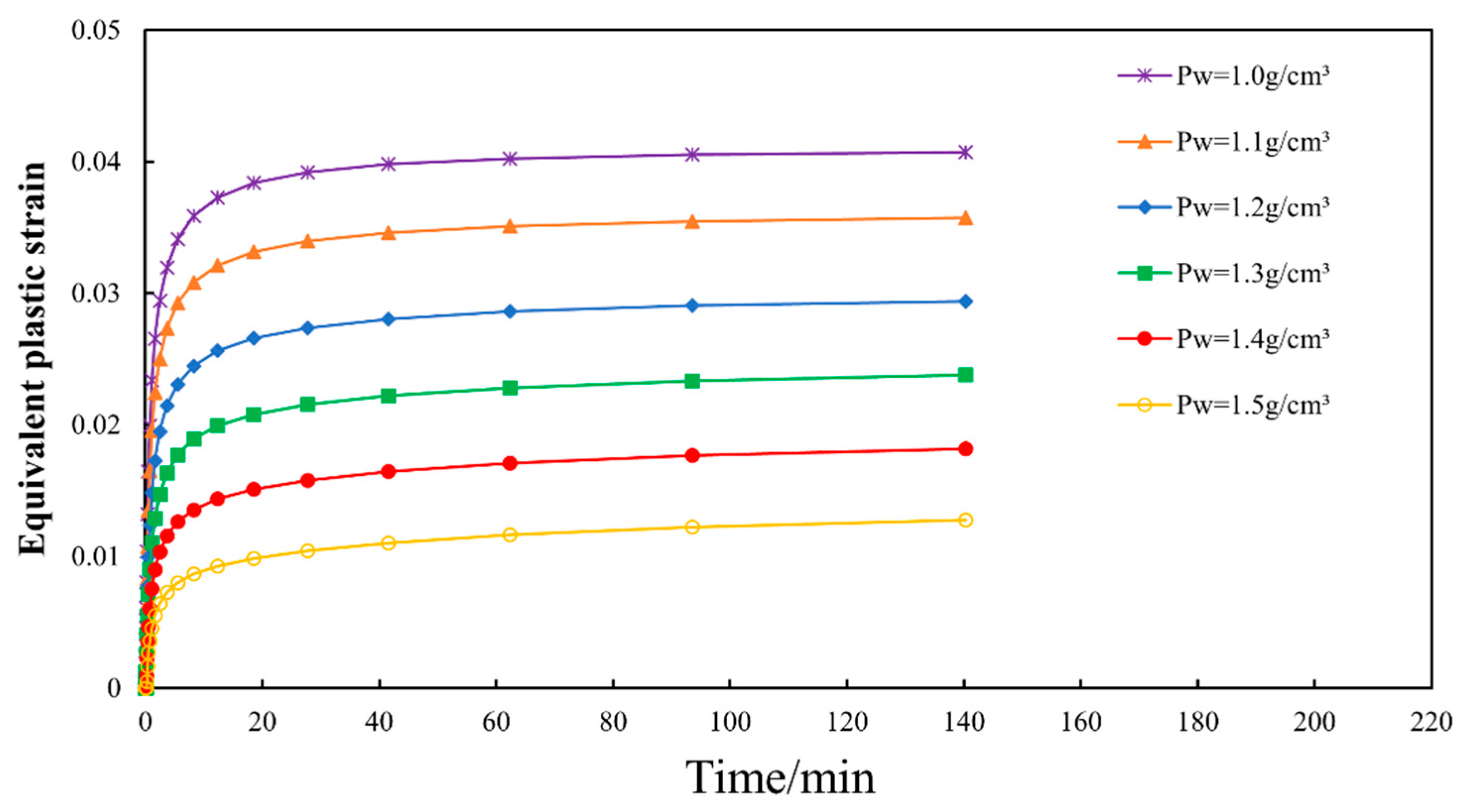
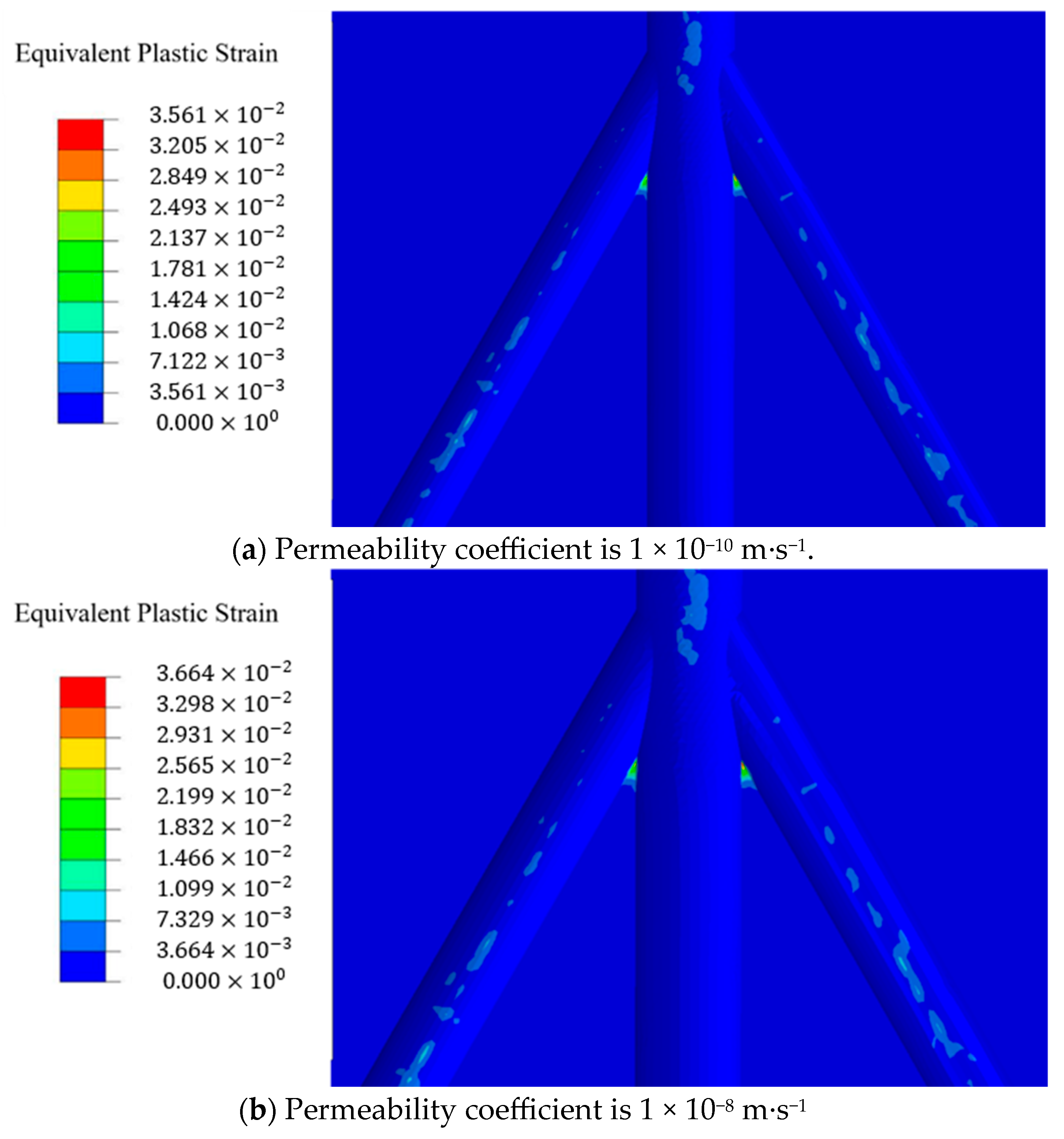
3.5. Evolution of Plastic Strain Around Branch Wellbores
4. Analysis of Sensitive Factors for Borehole Stability in Multilateral Wells
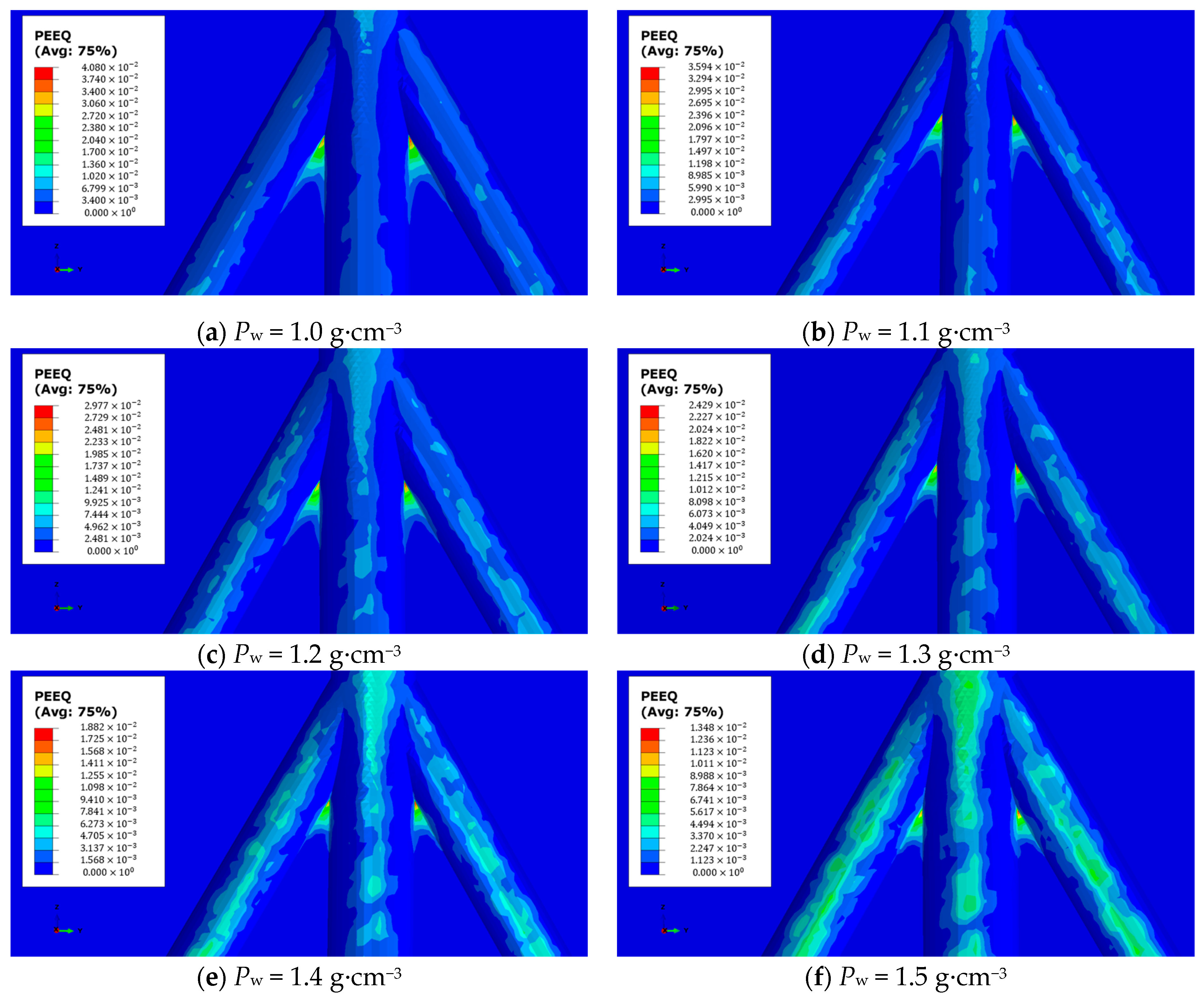
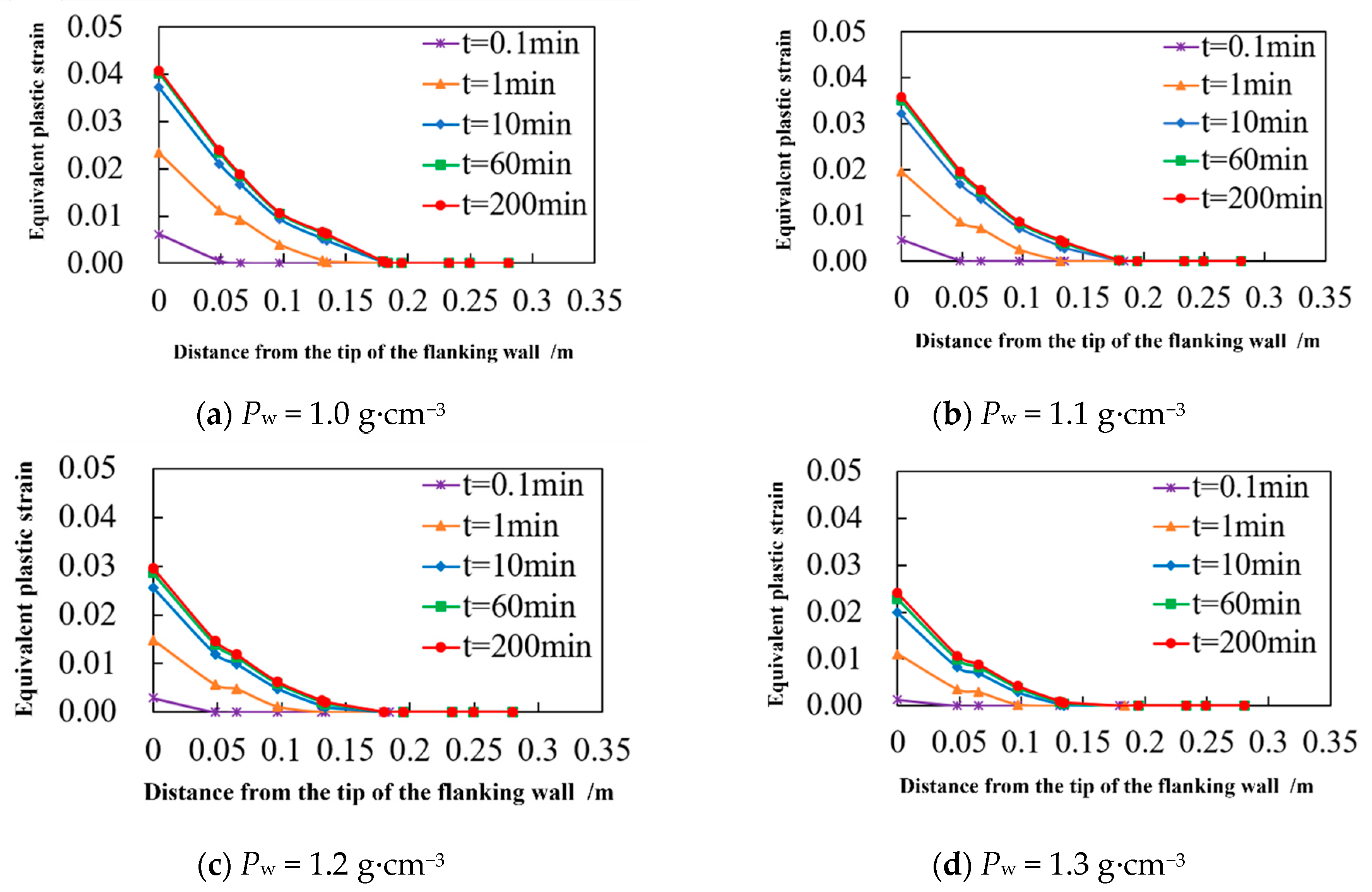
4.1. The Influence of Drilling Fluid Density
4.2. Influence of Permeability Coefficient
4.3. Influence of Cohesion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.H. New development on multi-lateral drilling and completion technologies. Oil Drill. Prod. Technol. 1900, 23, 1–3. [Google Scholar]
- Song, X.Z.; Zhang, C.K.; Shi, Y.; Li, G. Production performance of oil shale in-situ conversion with multilateral wells. Energy 2019, 189, 116145. [Google Scholar] [CrossRef]
- Almedallah, M.; Altaheini, S.K.; Clark, S.; Walsh, S. Combined stochastic and discrete simulation to optimise the economics of mixed single-horizontal and multilateral well offshore oil developments. Pet. Explor. Dev. 2021, 48, 1183–1197. [Google Scholar] [CrossRef]
- Wang, G.Y. The Multi-branch Well Drilling Technical Overview and the Latest Progress. Offshore Oil 2006, 26, 100–104. [Google Scholar]
- Chen, J.; Wu, G.; Zuo, K. The technology development of level 5 multilateral well. Oil Field Equip. 2019, 48, 80–84. [Google Scholar]
- Diggins, E. Classification provides framework for ranking multilateral complexity and well type. Oil Gas J. 1997, 95, 97. [Google Scholar]
- JPT Staff. Multilateral TAML levels reviewed, slightly modified. J. Pet. Technol. 2002, 54, 24–28. [Google Scholar] [CrossRef]
- Yin, H.; Huang, J.Z.; Liu, H. Wellbore stability of juncture of multilateral drilling well. Sci. Technol. Eng. 2012, 12, 4616–4619. [Google Scholar]
- Li, W.F. Analysis of stability of wellface of fish-bone multiple lateral horizontal wells. China Coalbed Methane 2012, 9, 17–20. [Google Scholar]
- Goshtasbi, K.; Elyasi, A.; Naeimipour, A. 3D numerical stability analysis of multi-lateral well junctions. Arab. J. Geosci. 2013, 6, 2981–2989. [Google Scholar] [CrossRef]
- Goshtasbi, K.; Elyasi, A.; Naeimipour, A. Stability assessment of a dual-opposing well junction. Pet. Sci. Technol. 2014, 32, 790–796. [Google Scholar] [CrossRef]
- Mohamad-Hussein, A.; Heiland, J. 3D finite element modelling of multilateral junction wellbore stability. Pet. Sci. 2018, 15, 801–814. [Google Scholar] [CrossRef]
- Wu, X.Y.; Lian, Z.H.; Jiang, W.; Ren, R.K. The fluid-solid coupling modelling and analysis of the connecting section in multilateral wells. China Pet. Mach. 2011, 39, 28–31. [Google Scholar]
- Wei, C.X.; Lian, Z.H.; Lin, T.J.; Wang, Y.M.; Guo, Y.R. Analysis of fluid-solid coupling seepage field for branch wells. Spec. Oil Gas Reserv. 2012, 19, 100–102+156. [Google Scholar]
- Xu, K.; Xiong, J.; Xu, H.; Lue, F.; Liu, H. Borehole stability research of plane dual-opposing laterals junction. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2012, 34, 132–138. [Google Scholar]
- Hoang, S.K.; Abousleiman, Y.N.; Ashraf, A.T. Multilaterals Drilling and Sustainable Openhole Production from Theory to Field-Case Studies. SPE J. 2010, 15, 878–892. [Google Scholar] [CrossRef]
- Zhang, G.Q. Plastic mechanics model for wellbore stability analysis of branched wells. J. China Univ. Pet. (Ed. Nat. Sci.) 2013, 37, 81–87. [Google Scholar]
- Oyedokun, O. Coupling a Void Growth Model with an Elastoplastic Material Model for a Simultaneous Prediction of the Borehole Plastic Zone and Critical Collapse Pressure. Geoenergy Sci. Eng. 2024, 233, 212448. [Google Scholar] [CrossRef]
- Haghgouei, H.; Lavrov, A.; Nermoen, A. Effect of Drill String Lateral Vibrations on Wellbore Stability and Optimal Mud Pressure Determination. Geoenergy Sci. Eng. 2025, 247, 213691. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, Y.; Gao, K.; Tian, B.; He, H.; Wang, J.; Qin, J.; Yin, Q. Experimental and Numerical Analyses of Rock Damage Behavior and Fragmentation Mechanism Under Enlarged Hole Impact Conditions. Geoenergy Sci. Eng. 2025, 249, 213778. [Google Scholar] [CrossRef]
- Han, L. Study on Stability of Shale Well Walls Based on Fluid-Structure Interaction Theory. Master’s Thesis, China University of Petroleum, Dongying, China, 2021. [Google Scholar]
- Ma, C. Wellbore Stability of Fragmented Coal Evaluation Under the Couple Effect of Seepage And Stress. Master’s Thesis, China University of Petroleum, Beijing, China, 2016. [Google Scholar]
- Ghassemi, A.; Zhang, Q. A Transient Fictitious Stress Boundary Element Method for Porothermoelastic Media. Eng. Anal. Bound. Elem. 2004, 28, 1363–1373. [Google Scholar] [CrossRef]
- Zhou, X.; Ghassemi, A. Finite Element Analysis of Coupled Chemo-Poro-Thermo-Mechanical Effects around a Wellbore in Swelling Shale. Int. J. Rock Mech. Min. Sci. 2009, 46, 769–778. [Google Scholar] [CrossRef]
- Zeng, Y.; Cai, M.; Zhong, L. A Coupled Method Combining Crouzeix-Raviart Nonconforming and Node Conforming Finite Element Spaces for Biot Consolidation Model. J. Comput. Math. 2024, 42, 911–931. [Google Scholar] [CrossRef]
- Jia, S.P. Hydro-mechanical coupled creep damage constitutive model of Boom clay, back analysis of model parameters and its engineering application. Chin. J. Rock Mech. Eng. 2009, 28, 2594. [Google Scholar]
- Souley, M.; Homand, F.; Pepa, S.; Hoxha, D. Damage-induced permeability changes in granite: A case example at the URL in Canada. Int. J. Rock Mech. Min. Sci. 2001, 38, 297–310. [Google Scholar] [CrossRef]
- Oda, M.; Takemura, T.; Aoki, T. Damage growth and permeability change in triaxial compression tests of Inada granite. Mech. Mater. 2002, 34, 313–331. [Google Scholar] [CrossRef]
- Sun, Q.; Jiang, Z.Q.; Zhu, S.Y. Experimental study on permeability of soft rock of Beizao Coal Mine. Chin. J. Geotech. Eng. 2012, 34, 540–545. [Google Scholar]
- Zhao, Z.Y.; Yan, C.L.; Xue, M.Y.; Sun, B.; Cheng, Y.; Han, Z.; Yang, J.; Chen, Y.; Zhang, Q. Geological Carbon Sequestration: Experimental Study of the Mechanical Response and Microscopic Mechanism of Shales Subjected to Gaseous CO2 and ScCO2. Energy Fuels 2025, 39, 6388–6399. [Google Scholar] [CrossRef]
- Jia, S.P.; Chen, W.Z.; Yu, H.D.; Li, X.L. Research on seepage-stress coupling damage model of Boom clay during tunneling. Rock Soil Mech. 2009, 30, 19–26. [Google Scholar]
- Liu, S.G.; Peng, Z.G.; Li, Z.G.; Chen, H. Numerical analysis of coalbed methane horizontal branch well stability. J. Liaoning Tech. Univ. Nat. Sci. 2015, 34, 769–773. [Google Scholar]
- Jing, L. A Review of Techniques, Advances and Outstanding Issues in Numerical Modelling for Rock Mechanics and Rock Engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Huang, S.H. The Analysis of Mechanical Parameters in Unconsolidated Sandstone. Master’s Thesis, China University of Petroleum, Beijing, China, 2016. [Google Scholar]









| Model Parameter | Value |
|---|---|
| Density/(kg·m−3) | 2300 |
| Elastic Modulus/MPa | 6000 |
| Poisson’s Ratio | 0.25 |
| Permeability/(m·s−1) | 1 × 10−6 |
| Porosity | 0.5 |
| Internal Friction Angle/° | 35 |
| Effective Stress Coefficient | 0.8 |
| Cohesion/MPa | 5.5 |
| Formation Pressure/MPa | 12.6 |
| Overburden Pressure MPa | 29 |
| Maximum Horizontal Principal Stress/MPa | 26 |
| Minimum Horizontal Principal Stress/MPa | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Han, C.; Meng, Y.; Dai, R.; Huang, H.; Chen, J.; Yan, C. Research on the Damage Evolution Law of Branch Wellbore Based on Damage Mechanics. Processes 2025, 13, 2172. https://doi.org/10.3390/pr13072172
Tian Q, Han C, Meng Y, Dai R, Huang H, Chen J, Yan C. Research on the Damage Evolution Law of Branch Wellbore Based on Damage Mechanics. Processes. 2025; 13(7):2172. https://doi.org/10.3390/pr13072172
Chicago/Turabian StyleTian, Qizhong, Chao Han, Yang Meng, Rongdong Dai, Haocai Huang, Jiaao Chen, and Chuanliang Yan. 2025. "Research on the Damage Evolution Law of Branch Wellbore Based on Damage Mechanics" Processes 13, no. 7: 2172. https://doi.org/10.3390/pr13072172
APA StyleTian, Q., Han, C., Meng, Y., Dai, R., Huang, H., Chen, J., & Yan, C. (2025). Research on the Damage Evolution Law of Branch Wellbore Based on Damage Mechanics. Processes, 13(7), 2172. https://doi.org/10.3390/pr13072172







