Gas Prediction in Tight Sandstone Reservoirs Based on a Seismic Dispersion Attribute Derived from Frequency-Dependent AVO Inversion
Abstract
1. Introduction
2. Methods
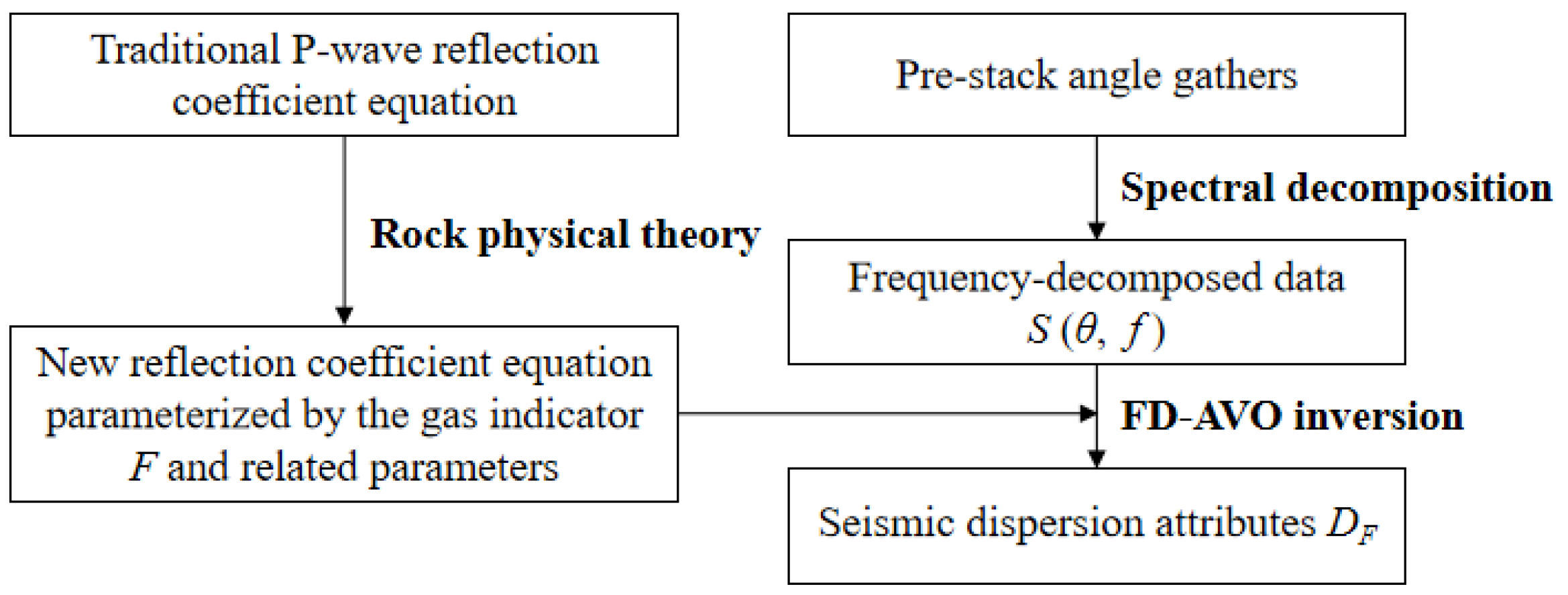
2.1. FD-AVO Inversion of Dispersion Attribute DF for Gas Prediction
2.2. Multi-Scale Fracture Theory
3. Results
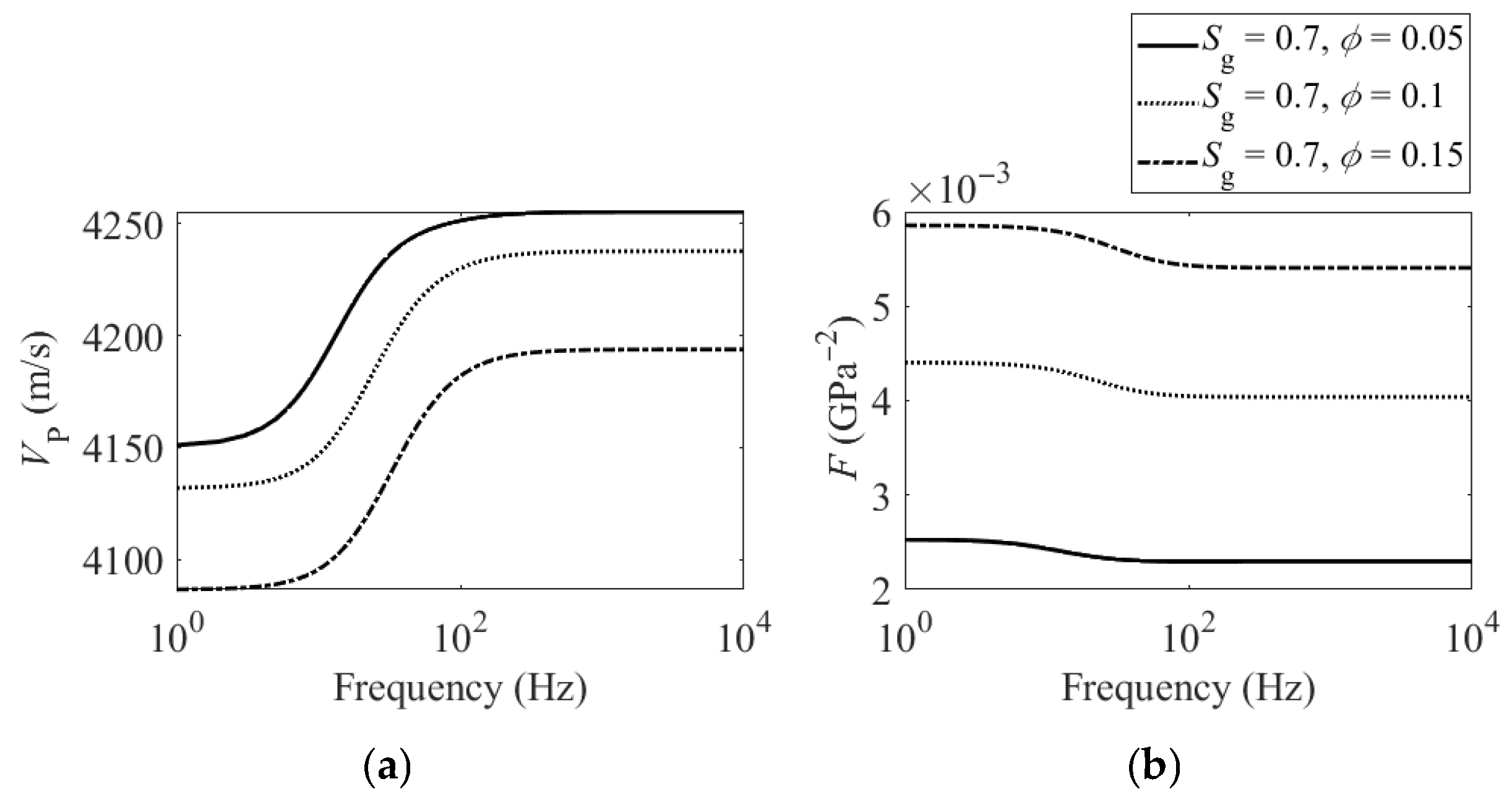
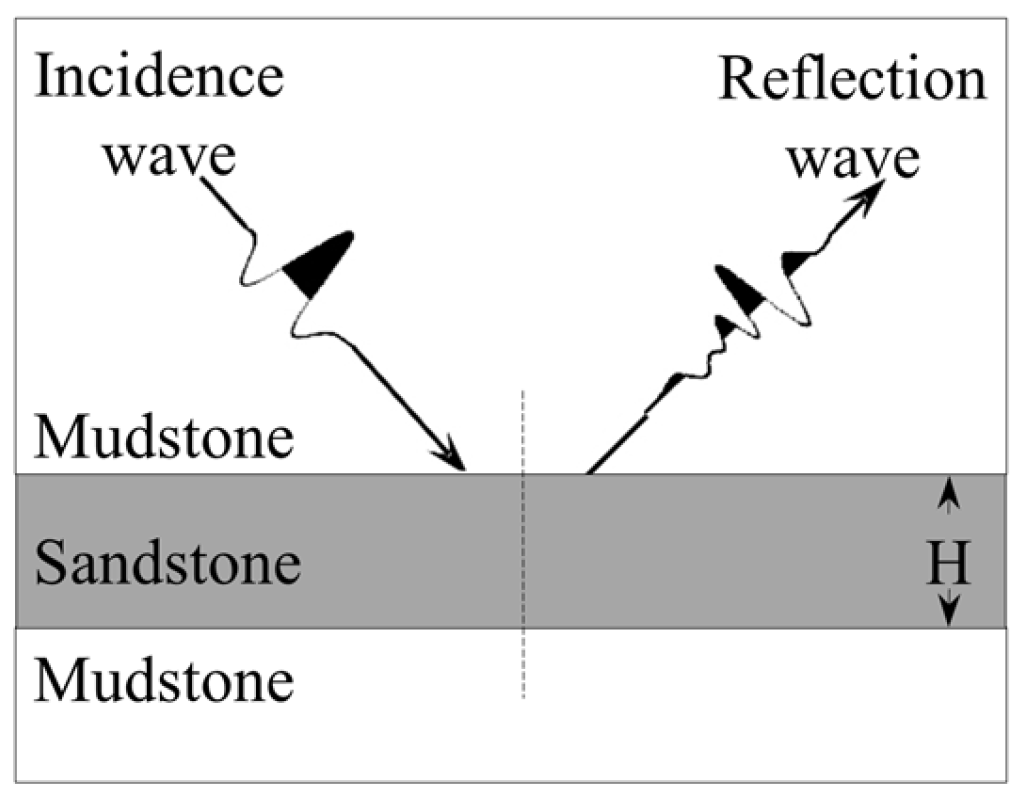
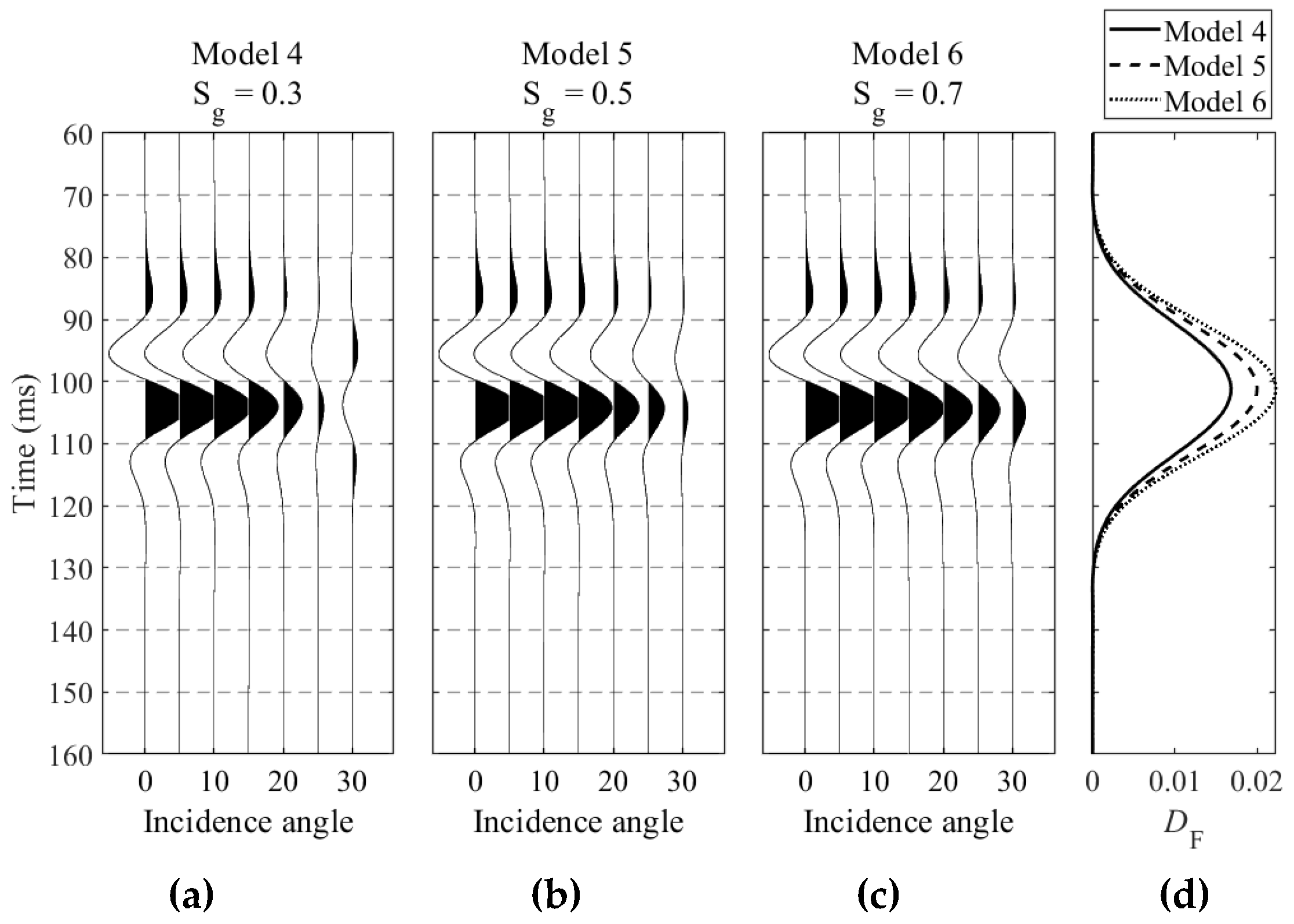
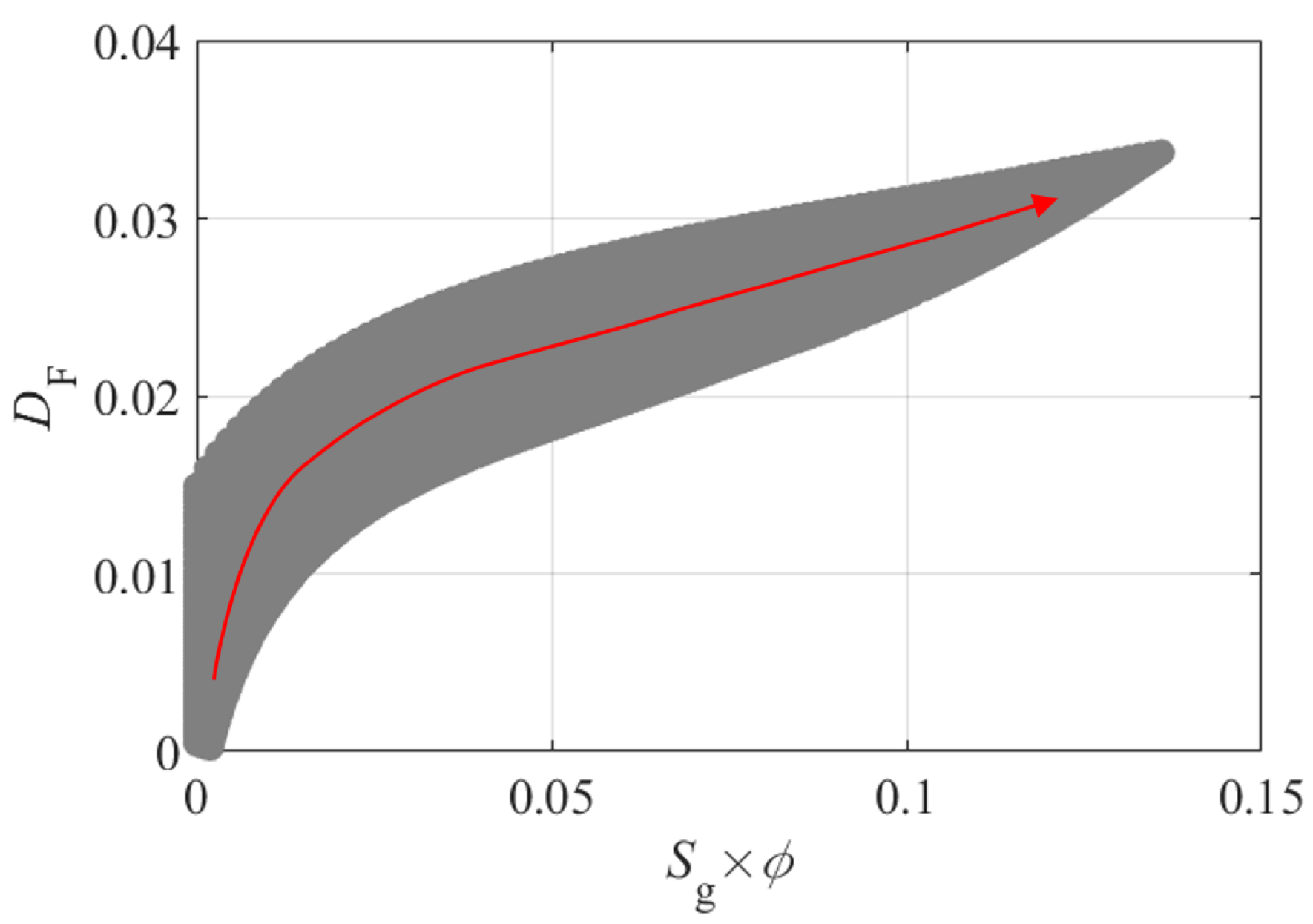
3.1. Synthetic Data Tests
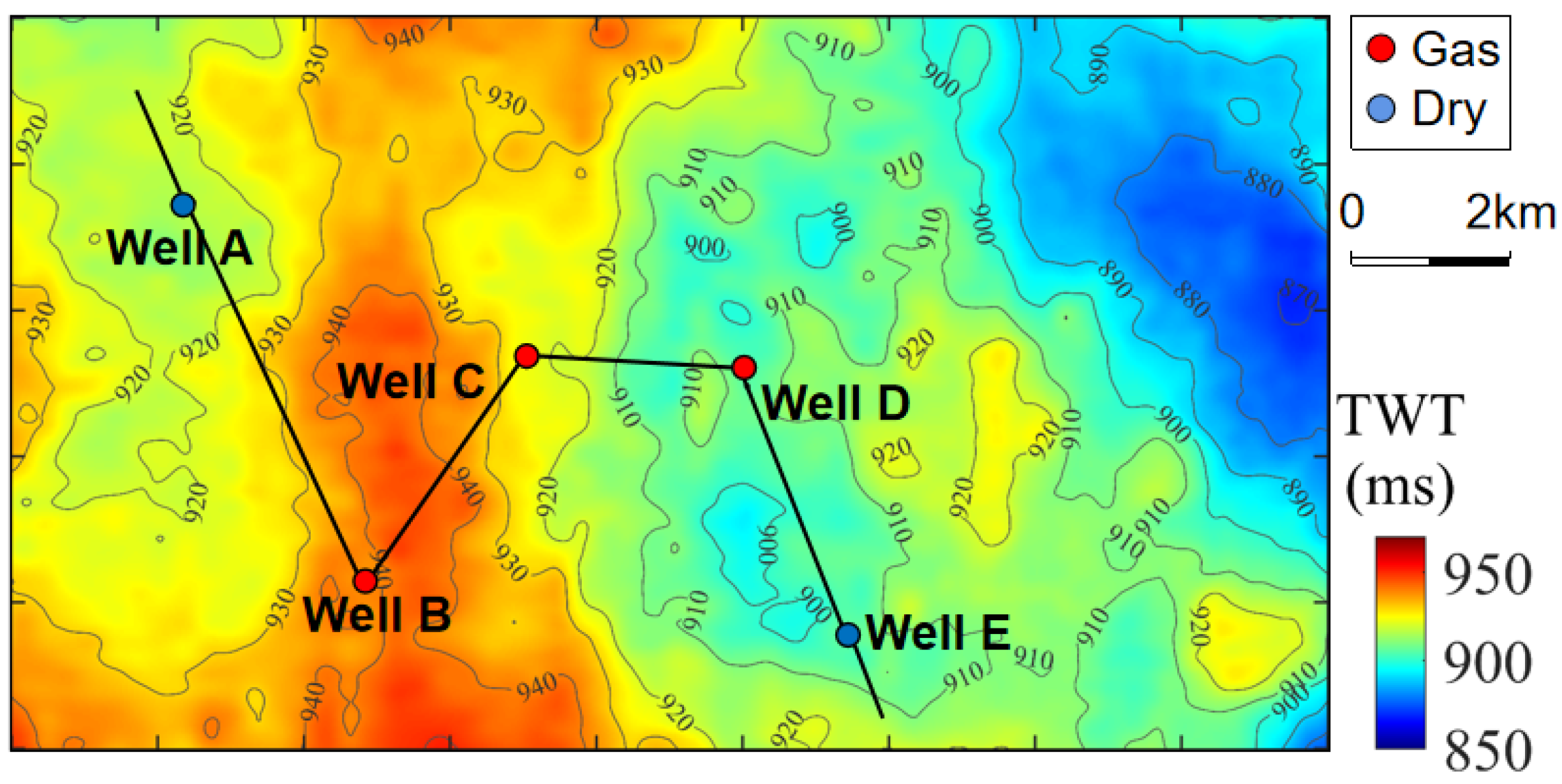
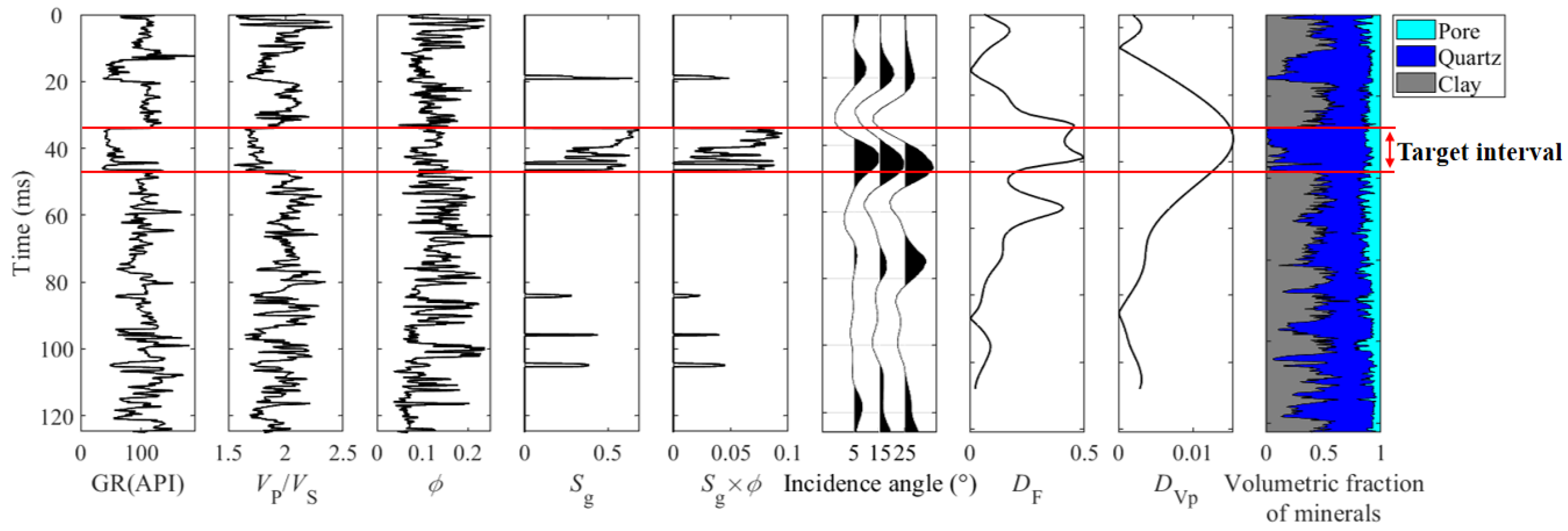
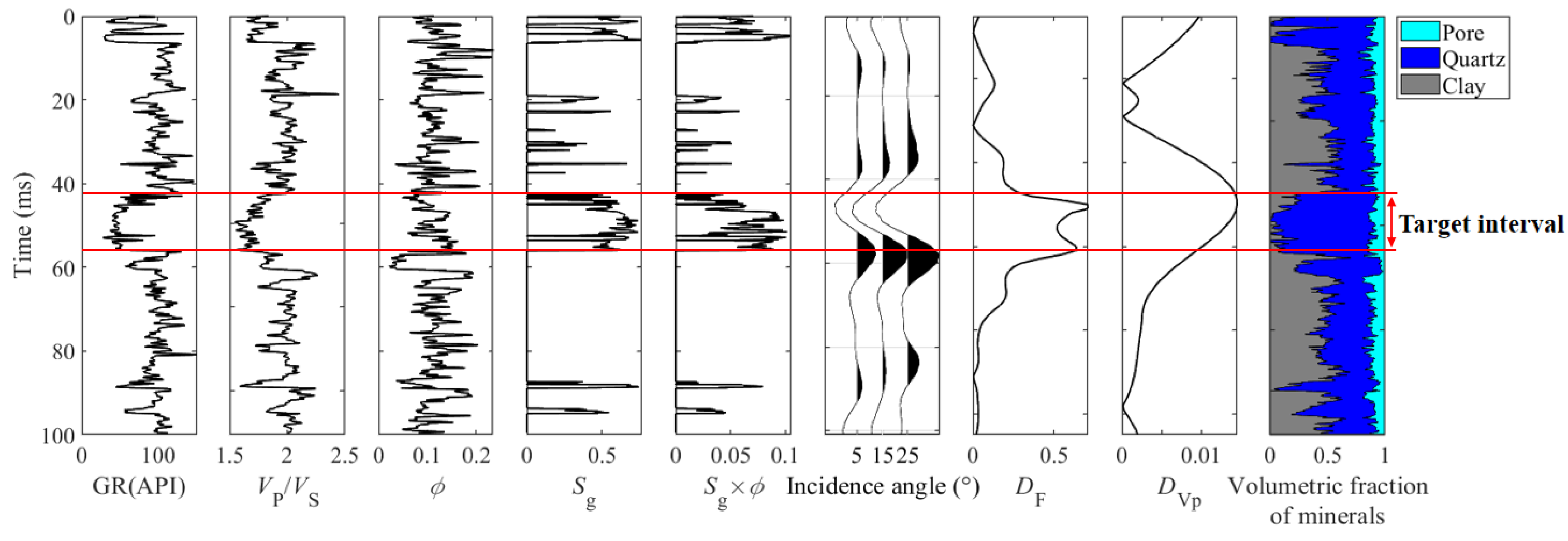
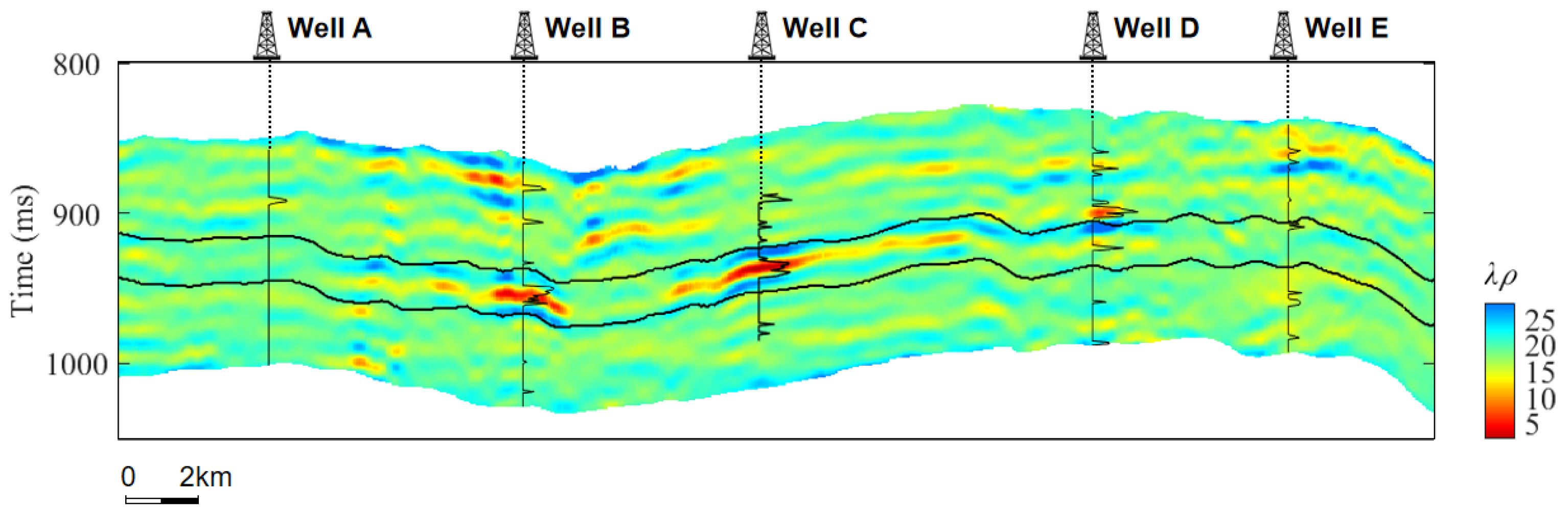
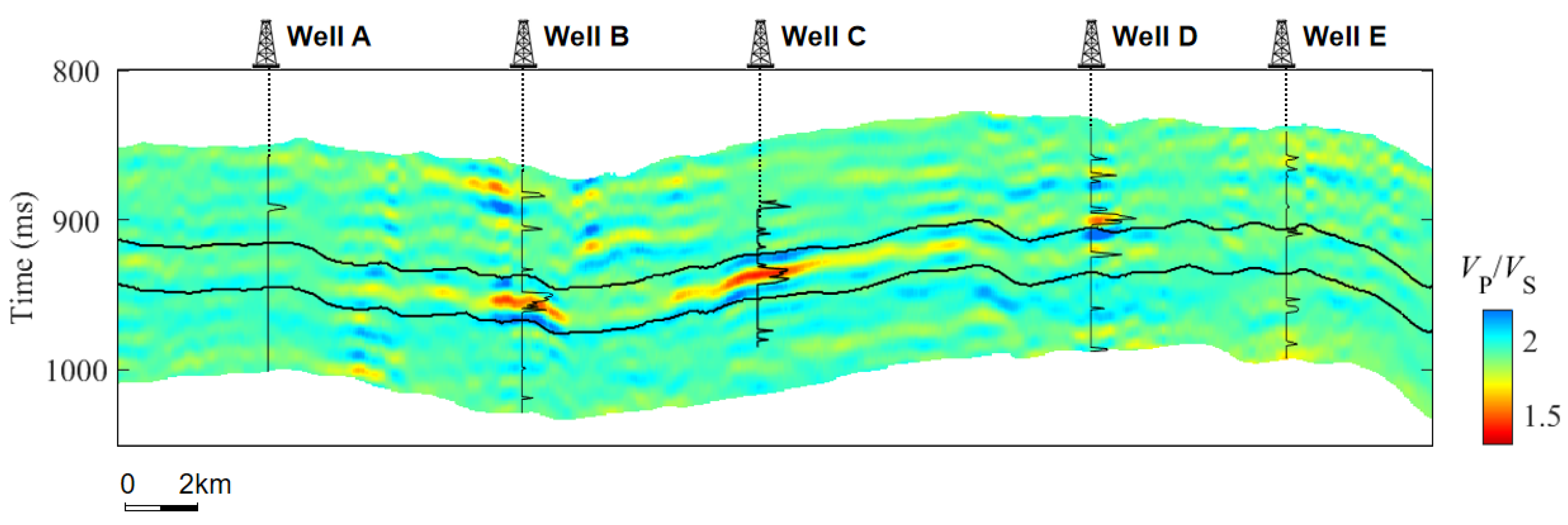
3.2. Real Data Applications
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AVO | Amplitude variation with offset |
| FD-AVO | Frequency-dependent amplitude variation with offset |
| Kf | Fluid bulk modulus |
| μ | Shear modulus of rock skeleton |
| F | Gas indicator |
| IS | S-wave impedance |
| ρ | Density |
| ϕ | Porosity |
| θ | Incidence angle |
| γsat | P- and S-wave velocity ratio of saturated rock |
| γdry | P- and S-wave velocity ratio of dry frame |
| ω0 | Reference frequency |
| DF | Dispersion attribute related to gas content |
| DϕIS | Dispersion attribute related to porosity and S-wave impedance |
| ΔS | Decomposed spectral components |
| ΔR | Reflection coefficient difference term |
| W | Wavelet spectrum |
| C0ijkl | Isotropic background stiffness coefficients |
| C1ijkl | The contributions of pore to stiffness coefficients |
| C2ijkl | The contributions of microcrack to stiffness coefficients |
| C3ijkl | The contributions of fracture to stiffness coefficients |
| ϕp | Porosity |
| εc | Microcrack density |
| εf | Fracture density |
| VP(ω) | Frequency-dependent P-wave velocity |
| VS(ω) | Frequency-dependent S-wave velocity |
| ρs | Density of the fluid-saturated tight sandstone |
Appendix A
References
- Liu, L.; Tang, D.Z.; Wo, Y.J.; Liu, L.H.; Sun, W.; Lu, H.M.; Yekikang, M.Q. Favorable area prediction of tight sandstone: A case study of the He8 formation in the Kangning area, Eastern Ordos Basin, China. J. Pet. Sci. Eng. 2019, 175, 430–443. [Google Scholar]
- Shu, Y.; Sang, S.X.; Lin, Y.X.; Zhou, X.Z.; Wang, H.; Wang, Z.L. The influence of magmatic-hydrothermal activities on porosity and permeability of sandstone reservoirs in the Linxing area, Ordos Basin, Northern China. J. Asian Earth Sci. 2021, 213, 104741. [Google Scholar] [CrossRef]
- Ba, J.; Cao, H.; Carcione, J.M.; Tang, G.; Yan, X.F.; Sun, W.T.; Nie, J.X. Multiscale rock-physics templates for gas detection in carbonate reservoirs. J. Appl. Geophys. 2013, 93, 77–82. [Google Scholar] [CrossRef]
- Pang, M.Q.; Ba, J.; Carcione, J.M.; Picotti, S.; Zhou, J.; Jiang, R. Estimation of porosity and fluid saturation in carbonates from rock-physics templates based on seismic Q. Geophysics 2019, 84, M25–M36. [Google Scholar] [CrossRef]
- Pang, M.Q.; Ba, J.; Fu, L.Y.; Carcione, J.M.; Markus, U.I.; Zhang, L. Estimation of microfracture porosity in deep carbonate reservoirs based on 3D rock-physics templates. Int. J. Subsurf. Charact. 2021, 8, SP43–SP52. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Qin, X.Y.; Liu, C. Quantitative characterization of tight gas sandstone reservoirs using seismic data via an integrated rock-physics-based framework. Pet. Sci. 2023, 20, 3428–3440. [Google Scholar] [CrossRef]
- Goodway, W.N.; Chen, T.; Downton, J. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters; “λρ”, μρ, λ/μ Fluid Stack,” from P and S inversions. In Proceedings of the 67th SEG Annual Meeting, Dallas, TX, USA, 2–7 November 1997; pp. 183–186. [Google Scholar]
- Quakenbush, M.; Shang, B.; Tuttle, C. Poisson impedance. Lead. Edge 2006, 25, 128–138. [Google Scholar] [CrossRef]
- Xu, C.X.; Ma, P.S.; Lai, L.B.; Sun, Y.H.; Li, Z.C. Sensitivity parameters of tight sand gas: A case study of Lower Cretaceous Yingcheng Formation of Yingtai gas field in Songliao Basin, NE China. Pet. Explor. Dev. 2014, 41, 712–716. [Google Scholar] [CrossRef]
- Huang, X.R.; Huang, J.P.; Li, Z.C. High-Sensitivity Fluid Identification Factor in Anisotropic Tight-Oil Sandstone Reservoirs. In SEG Annual Meeting; SEG: Houston, TX, USA, 2015; pp. 2688–2692. [Google Scholar]
- Wang, P.; Chen, X.H.; Li, X.Y.; Cui, Y.A.; Li, J.Y.; Wang, B.F. Analysis and Estimation of an Inclusion-Based Effective Fluid Modulus for Tight Gas-Bearing Sandstone Reservoirs. IEEE. Trans. Geosci. Remote Sens. 2022, 60, 4502710. [Google Scholar] [CrossRef]
- Yin, X.Y.; Zhang, S.X.; Zhang, F. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification. Chin. J. Geophys. 2013, 7, 2378–2390. [Google Scholar]
- Zong, Z.Y.; Yin, X.Y. Direct inversion of Young’s and Poisson impedances for fluid discrimination. Geofluids 2017, 16, 1006–1016. [Google Scholar] [CrossRef]
- Jia, L.Y.; Li, L.; Wang, Q.Y.; Ma, J.F.; Wang, H.F.; Wang, D.X. Fluid identification factor inversion based on generalized elastic impedance. Geophys. Prospect. Pet. 2018, 57, 302–311. [Google Scholar]
- Gao, G.; Yang, Y.H.; Zhao, B.; Duan, H.L.; Wang, X.Y.; Wei, Y.Z. A method for establishing and directly extracting sensitive identification factors of unconsolidated sandstones. Oil Geophys. Prospect. 2019, 54, 1329–1338. [Google Scholar]
- Ma, Z.Q.; Yin, X.Y.; Zong, Z.Y.; Tan, Y.Y.; Ji, L.X.; Yang, Z.F.; Yan, X.F. Sequential Bayesian seismic inversion for fracture parameters and fluid indicator in tilted transversely isotropic media. Geophysics 2023, 88, R355–R371. [Google Scholar] [CrossRef]
- Jin, H.; Liu, C.; Guo, Z.Q. Gas prediction in tight sandstones based on the rock-physics-derived seismic amplitude variation versus offset method. Pet. Sci. 2024, 21, 3951–3964. [Google Scholar] [CrossRef]
- Yin, H.j.; Zhao, J.G.; Tang, G.Y.; Zhao, L.M.; Ma, X.Y.; Wang, S.X. Pressure and fluid effect on frequency-dependent elastic moduli in fully saturated tight sandstone. J. Geophys. Res. Solid Earth 2017, 122, 8925–8942. [Google Scholar] [CrossRef]
- Chapman, M.; Liu, E.; Li, X. The influence of fluid-sensitive dispersion and attenuation on AVO analysis. Geophys. J. Int. 2006, 167, 89–105. [Google Scholar] [CrossRef]
- Chapman, M. Modeling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy. Geophysics 2009, 74, D97–D103. [Google Scholar] [CrossRef]
- Ba, J.; Carcione, J.M.; Cao, H.; Du, Q.Z.; Yuan, Z.Y.; Lu, M.H. Velocity dispersion and attenuation of P waves in partially-saturated rocks: Wave propagation equations in double-porosity medium. Chin. J. Geophys. 2012, 55, 219–231. [Google Scholar]
- Ba, J.; Xu, W.H.; Fu, L.Y.; Carcione, J.M.; Zhang, L. Rock anelasticity due to patchy saturation and fabric heterogeneity: A double double-porosity model of wave propagation. J. Geophys. Res. Solid Earth 2017, 122, 1949–1976. [Google Scholar] [CrossRef]
- Sun, W.T.; Ba, J.; Carcione, J.M. Theory of wave propagation in partially saturated double-porosity rocks: A triple-layer patchy model. Geophys. J. Int. 2016, 205, 22–37. [Google Scholar] [CrossRef]
- He, Y.X.; Wu, X.Y.; Fu, K.; Zhou, D.; Wang, S.X. Modeling the Effect of Microscopic and Mesoscopic Heterogeneities on Frequency-Dependent Attenuation and Seismic Signatures. IEEE. Trans. Geosci. Remote Sens. Lett. 2018, 15, 1174–1178. [Google Scholar] [CrossRef]
- He, Y.X.; Li, X.L.; Tang, G.Y.; Dong, C.H.; Chen, M.; Wang, S.X. Modeling the effects of fracture infill on frequency-dependent anisotropy and AVO response of a fractured porous layer. Pet. Sci. 2021, 18, 758–772. [Google Scholar] [CrossRef]
- Wilson, A.; Chapman, M.; Li, X.Y. Frequency-dependent AVO inversion. In Proceedings of the 79th Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 25–30 October 2009; pp. 341–345. [Google Scholar]
- Pang, S.; Liu, C.; Guo, Z.Q.; Liu, X.W.; Liu, Y.W. Gas identification of shale reservoirs based on frequency-dependent AVO inversion of seismic data. Chin. J. Geophys. 2018, 61, 4613–4624. [Google Scholar]
- Liu, W.; Cao, S.Y.; Jin, Z.Y.; Wang, Z.M.; Chen, Y.K. A novel hydrocarbon detection approach via high-resolution frequency-dependent AVO inversion based on variational mode decomposition. IEEE. Trans. Geosci. Remote Sens. 2018, 56, 2007–2024. [Google Scholar] [CrossRef]
- Luo, C.; Li, X.Y.; Huang, G.T. Hydrocarbon identification by application of improved sparse constrained inverse spectral decomposition to frequency-dependent AVO inversion. J. Geophys. Eng. 2018, 15, 1446–1459. [Google Scholar] [CrossRef]
- Huang, G.T.; Chen, X.H.; Luo, C.; Chen, Y.K. Mesoscopic Wave-Induced Fluid Flow Effect Extraction by Using Frequency-Dependent Prestack Waveform Inversion. IEEE. Trans. Geosci. Remote Sens. 2021, 59, 6510–6524. [Google Scholar] [CrossRef]
- Jin, H.; Liu, C.; Guo, Z.Q.; Zhang, Y.M.; Niu, C.; Wang, D.; Ling, Y. Rock physical modeling and seismic dispersion attribute inversion for the characterization of a tight gas sandstone reservoir. Front. Earth Sci. 2021, 9, 641651. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Li, Y.D.; Liu, C.; Zhang, D.; Li, A.B. Characterization of a Volcanic Gas Reservoir Using Seismic Dispersion and Fluid Mobility Attributes. Lithosphere 2021, 3, 9520064. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Zhao, D.Y.; Liu, C. Gas prediction using an improved seismic dispersion attribute inversion for tight sandstone gas reservoirs in the Ordos Basin, China. J. Nat. Gas. Sci. Eng. 2022, 101, 104499. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Zhang, X.D.; Liu, C.; Liu, X.W.; Liu, Y.W. Hydrocarbon Identification and Bedding Fracture Detection in Shale Gas Reservoirs Based on a Novel Seismic Dispersion Attribute Inversion Method. Surv. Geophys. 2022, 43, 1793–1816. [Google Scholar] [CrossRef]
- Luo, X.; Chen, X.H.; Lv, B.N.; Liu, J.J.; Wu, H.J.; Wang, P. Frequency-Dependent AVO Inversion Using a Modified Window-Parameter-Optimized S-Transform for High Gas-Saturation Reservoir Delineation. IEEE. Trans. Geosci. Remote Sens. Lett. 2023, 20, 3000805. [Google Scholar] [CrossRef]
- Li, Y.D.; Guo, Z.Q.; Liu, C. Characterization of Fluid-Saturated Fractures Based on Seismic Azimuthal Anisotropy Dispersion Inversion Method. IEEE. Trans. Geosci. Remote Sens. 2024, 62, 1–17. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.; Chen, X.H.; Wang, K.D.; Wang, B.F. Fluid Discrimination Based on Frequency-Dependent AVO Inversion with the Elastic Parameter Sensitivity Analysis. Feofluis 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Zhao, D.Y.; Liu, C. A New Seismic Inversion Scheme Using Fluid Dispersion Attribute for Direct Gas Identification in Tight Sandstone Reservoirs. Remote Sens. 2022, 14, 5326. [Google Scholar] [CrossRef]
- Tian, Y.; Gao, J.; Stovas, A.; Meng, C. Frequency-dependent AVO inversion via deep neural network and application on tight reservoir parameters prediction. In Proceedings of the 84th EAGE Annual Conference and Exhibition, Vienna, AT, USA, 5–8 June 2023. [Google Scholar]
- Tian, Y.J.; Stovas, A.; Gao, J.H.; Meng, C.J.; Yang, C. Frequency-Dependent AVO Inversion and Application on Tight Sandstone Gas Reservoir Prediction Using Deep Neural Network. IEEE. Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Fawad, M.; Hansen, J.A.; Mondol, N.H. Seismic-fluid detection-a review. Earth Sci. Rev. 2020, 210, 103347. [Google Scholar] [CrossRef]
- Chapman, M.; Zatsepin, S.v.; Crampin, S. Derivation of a microstructural poroelastic model. Geophys. J. Int. 2002, 151, 427–451. [Google Scholar] [CrossRef]
- Chapman, M. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity. Geophys. Prospect. 2003, 51, 369–379. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Liu, C.; Li, X.Y.; Lan, H.T. An Improved Method for the Modeling of Frequency-Dependent Amplitude-Versus-Offset Variations. IEEE. Geosci. Remote Sens. Lett. 2015, 12, 63–67. [Google Scholar]
- Guo, Z.Q.; Liu, X.W. Seismic rock physics characterization of anisotropic shale-a Longmaxi Shale case study. J. Geophys. Eng. 2018, 15, 512–526. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]




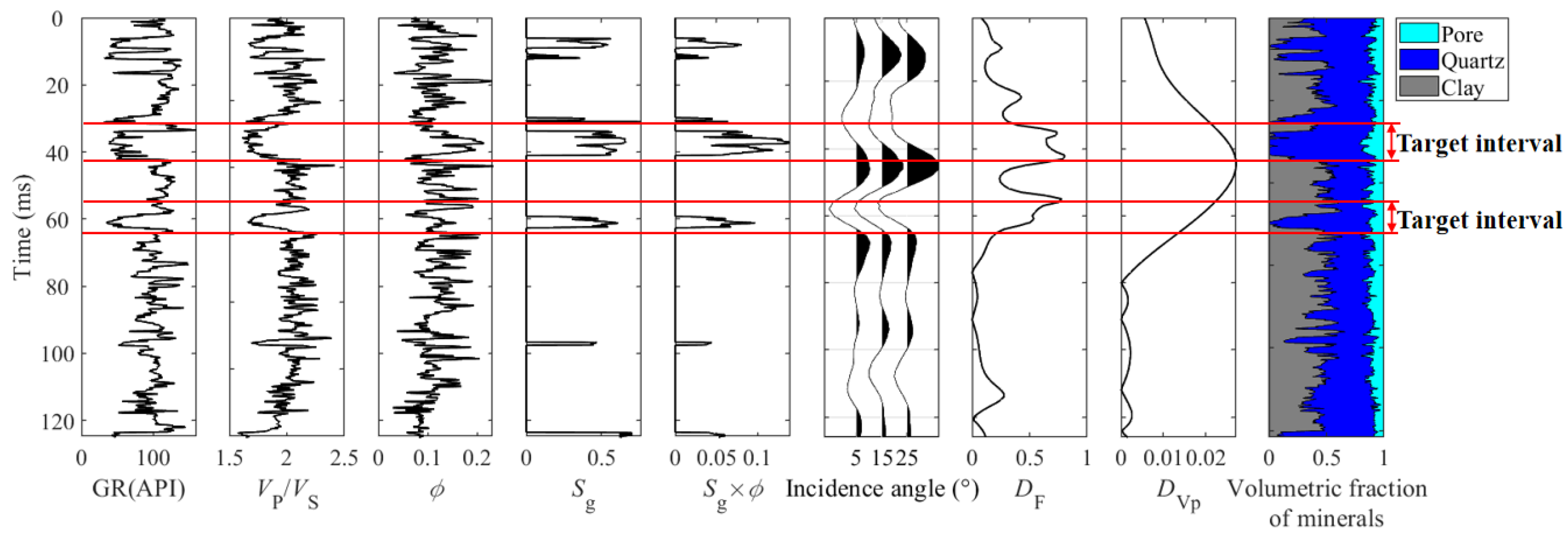

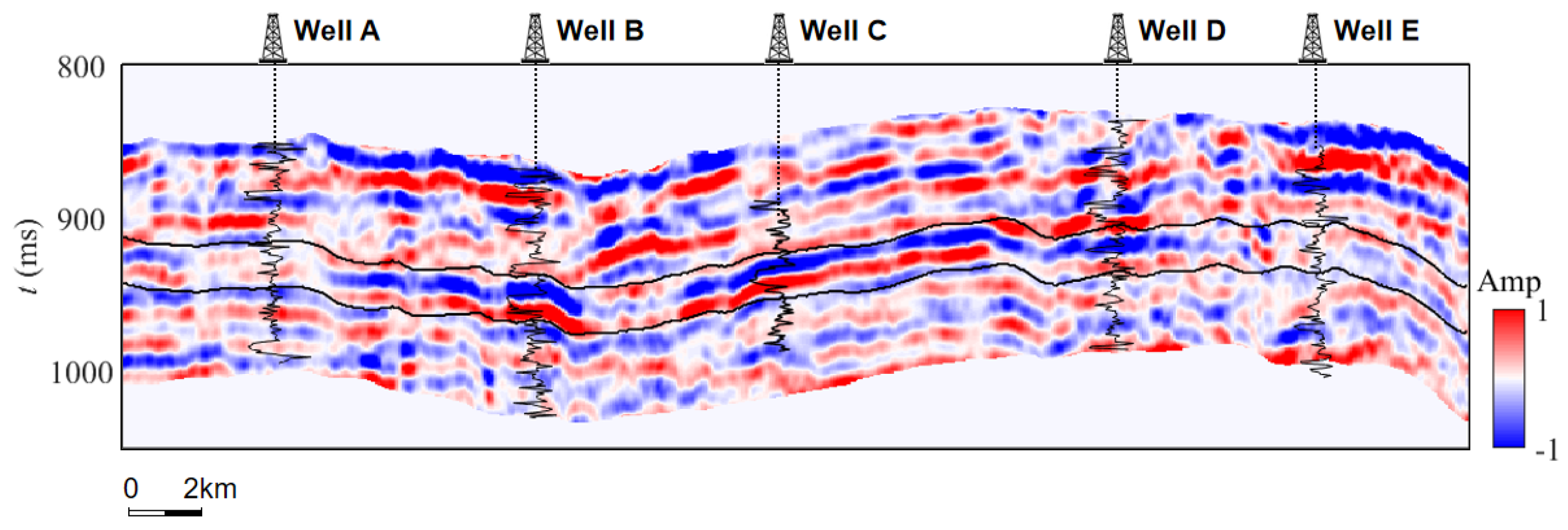


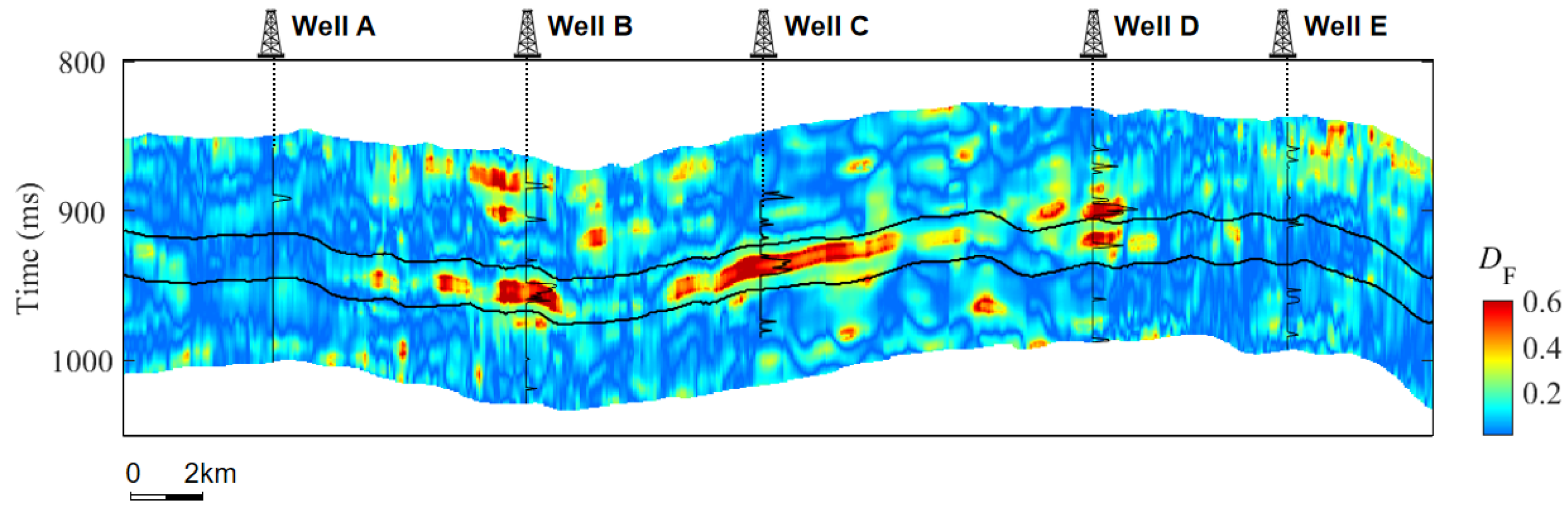
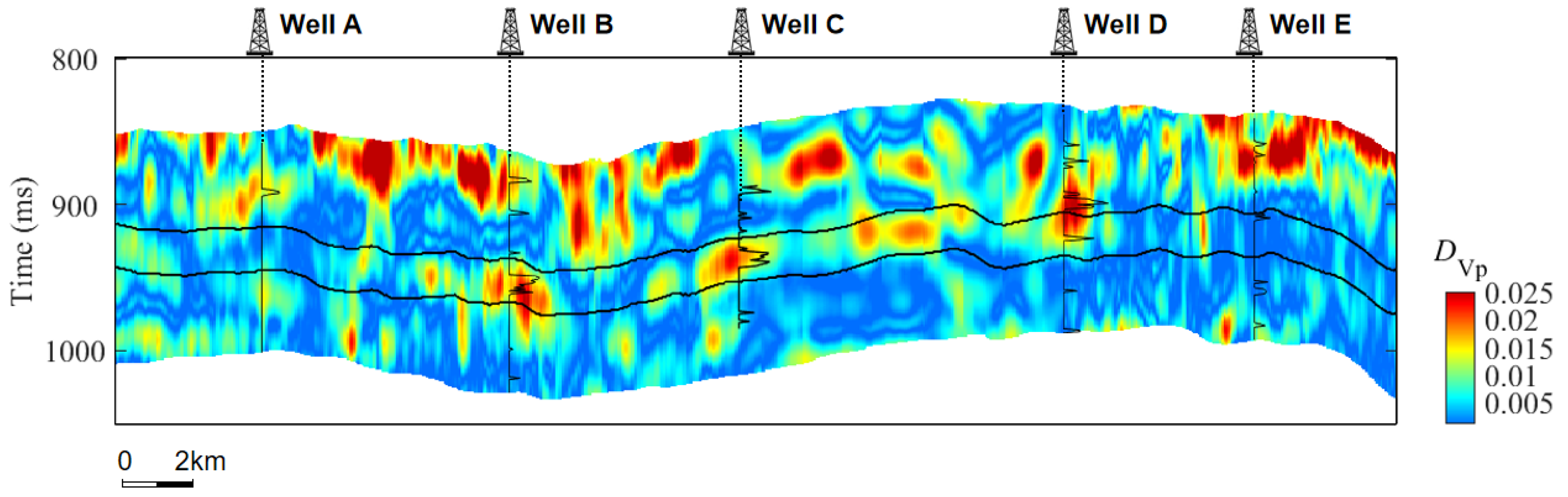
| Clay | Quartz | |
|---|---|---|
| VP (km/s) | 3.90 | 6.05 |
| VS (km/s) | 1.50 | 3.90 |
| ρ (g/cm3) | 2.58 | 2.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Chen, M.; Jin, H. Gas Prediction in Tight Sandstone Reservoirs Based on a Seismic Dispersion Attribute Derived from Frequency-Dependent AVO Inversion. Processes 2025, 13, 2210. https://doi.org/10.3390/pr13072210
Hu L, Chen M, Jin H. Gas Prediction in Tight Sandstone Reservoirs Based on a Seismic Dispersion Attribute Derived from Frequency-Dependent AVO Inversion. Processes. 2025; 13(7):2210. https://doi.org/10.3390/pr13072210
Chicago/Turabian StyleHu, Laidong, Mingchun Chen, and Han Jin. 2025. "Gas Prediction in Tight Sandstone Reservoirs Based on a Seismic Dispersion Attribute Derived from Frequency-Dependent AVO Inversion" Processes 13, no. 7: 2210. https://doi.org/10.3390/pr13072210
APA StyleHu, L., Chen, M., & Jin, H. (2025). Gas Prediction in Tight Sandstone Reservoirs Based on a Seismic Dispersion Attribute Derived from Frequency-Dependent AVO Inversion. Processes, 13(7), 2210. https://doi.org/10.3390/pr13072210





