Optimization of Process Parameters for WEDM Processing SiCp/Al Based on Graphene Working Fluid

Abstract

In the process of machining an aluminum matrix silicon carbide (SiCp/Al) composite material using wire electric discharge machining (WEDM), the thermal conductivity and dielectric properties of working fluid, such as discharge medium and cool carrier, directly determine the material removal rate (MRR) and surface roughness (R_a). In this paper, graphene-working fluid is innovatively used as working medium to optimize the discharge process due to its high thermal conductivity and field emission characteristics. The single-factor experiments show that graphene can increase the MRR by 11.16% and decrease the R_a by 29.96% compared with traditional working fluids. In order to analyze the multi-parameter coupling effect, an L16 (4⁴) orthogonal test is further designed, and the effects of the pulse width (T_on), duty cycle (DC), power tube number (PT), and wire speed (WS) on the MRR and R_a are determined using a signal-to-noise analysis. Based on a gray relational grade analysis, a multi-objective optimization model was established, and the priority of the MRR and R_a was determined using an AHP, and finally the optimal parameter combination (T_on = 22 μs, DC = 1:4, PT = 3, WS = 2) was obtained.

1. Introduction

Aluminum-based silicon carbide (SiC/Al) is a lightweight and high-strength particulate-reinforced composite material. SiC particles enhance hardness, wear resistance, and thermal resistance, while the aluminum matrix provides excellent thermal conductivity and workability, making it an ideal material for aerospace and electronic packaging [1]. Wire Electrical Discharge Machining (WEDM) technology is a key tool for machining difficult-to-machine materials like SiC/Al. Its performance is significantly affected by the dielectric properties and heat transfer ability of working fluids. Traditional working fluids often lead to low machining efficiency and surface quality degradation due to low heat conduction efficiency and uneven discharge. The research of nano-enhanced working fluids provides a new direction for breaking through this bottleneck [2]. Graphene shows remarkable advantages due to its unique structure and excellent physical properties. The ultra-high thermal conductivity of graphene can significantly improve the cooling efficiency of the working fluid. The conductive network composed of sp²-hybridized carbon atoms contributes to the uniform distribution of discharge channels. In addition, the field emission effect of graphene nanosheets during discharge can effectively reduce the breakdown voltage, so that the single-pulse energy utilization can be increased by more than 30% [3]. These characteristics not only restrain the thermal stress mismatch between SiC particles and aluminum matrix but also reduce the recasting defects of molten metal, which provides a physical basis for efficient precision machining.

Sivaprakasam et al. [4] performed micro-wire cutting on an Inconel alloy by adding graphite nano-powder to the dielectric. The results show that adding nano-graphite powder to the dielectric can significantly improve the surface morphology and roughness of the machined surface, and the material removal rate is higher. Paswan et al. [5] studied the machining possibility of graphene nanosheets as dielectric in an Inconel718 alloy during EDM and found that mixed-powder EDM was more stable than traditional EDM. Sivaprakasam et al. [6] verified that graphene nanosheets could improve the MRR (maximum +22.4%) and reduce R_a (−34.7%), which was demonstrated by EDS to reduce surface microcracks and recast the layer thickness. Singh et al. [7] demonstrated that the addition of graphene nanoparticles to an aqueous fluid can improve the conductivity and heat transfer of the fluid, resulting in improved material removal rates. Jain et al. [8] also found that graphene nanoparticles can significantly reduce the electrode wear, which is critical for the long-term process stability. Kuma’s [9] study highlights the enhanced dielectric properties of graphene aqueous solutions, enabling more stable spark discharge, reduced surface roughness, and minimized recast layers.

In the optimization of process parameters for the EDM of SiCp/Al composites, Rao et al. [10] optimized the process parameters of 5–15 vol.%SiCp/Al composites after WEDM using a response surface method and obtained the optimal processing parameters of material removal rate (MRR), surface roughness (Ra), and wire wear rate (WWR). Satishkumar et al. [11] proposed that the higher the SiCp/Al volume fraction, the slower the processing speed, and the worse the surface quality after machining; Chen et al. [12] adopted a back-propagation neural network (BPNN) to improve the overall efficiency of wire cutting, and a Taguchi L18 orthogonal array was used for experimental planning. Based on artificial neural network technology, the surface roughness was related to the relevant processing parameters. The experimental results show that pulse conduction time and input current play a leading role in response. Yusoff et al. [13] used an artificial neural network (ANN) to model the EDM performance. An orthogonal array was used to reduce the randomness of the ANN algorithm. By selecting the optimal dataset, the calculation and experiment time of the ANN were reduced.

In summary, many scholars have made important contributions in the field of mixed-powder WEDM processing of SiCp/Al composites, but there have been few studies on utilizing graphene nanoparticles as a working-fluid medium for the WEDM of materials. Based on this, this study relies on the research and development platform of the Jiangsu Key Laboratory of Advanced Materials Structural Component Design and Composite Manufacturing to propose a processing method based on the graphene working fluid for WEDM. This laboratory has profound research accumulation in the field of special processing of difficult-to-machine materials, which provides advanced experimental equipment and theoretical support for this study. The aim of this paper is to systematically study the process characteristics of SiCp/Al after processing under different working fluids and focus on the optimization of processing parameters to obtain the optimal combination of process parameters to improve the MRR and R_a of SiCp/Al after processing.

2. Experiment and Design

2.1. Mixed-Powder WEDM Principles and Devices

Mixed-powder WEDM is a special processing method based on traditional WEDM cutting by adding a conductive or semi-conductive micro-nano-powder (e.g., graphene, silicon carbide, aluminum, etc.) to the working fluid to enhance the processing performance [14]. The processing principle is: that under the action of a pulsed-power supply, a high-frequency discharge channel is formed between the electrode wire and the workpiece, and the mixed-powder particles in the working fluid are vaporized and ionized under the high temperature of the discharge to form a plasma, which increases the discharge gap and expands the discharge channel to improve the energy distribution [15]. Graphene nanoparticles can reduce the breakdown voltage and stabilize the discharge plasma due to their ultra-high specific surface area and excellent electron mobility, significantly improving the discharge efficiency. Mixed-powder particles accelerate the discharge of etching products by enhancing the thermal conductivity of the working fluid while dispersing the discharge points to make the energy distribution uniform and reduce the surface microcracks. Experiments used Hangzhou Huafang CNC machine tool Co., Ltd.’s (Hangzhou, China) HF320MZQ-G20 type in the wire WEDM cutting machine. The processing taper range is ±6°, with an octagonal cutting precision of ≤0.005 mm. The surface roughness, after multiple cuts, can reach R_a ≤ 1.0 μm. In terms of performance, the maximum cutting efficiency of this machine tool is ≥180 mm²/min, maintaining continuous processing of 400,000 mm² at a cutting speed of 110 mm²/min. Its principle of operation and processing site are shown in Figure 1a–c for the discharge channel micrograph.

2.2. Experimental Material

Aluminum-based silicon carbide (SiCp/Al) composites have become a key material in aerospace, automobile manufacturing, and other high-end equipment fields due to their excellent mechanical properties (high hardness, high wear resistance) and unique thermophysical properties (low coefficient of thermal expansion) [16]. In this paper, aluminum matrix composites reinforced with low-volume-fraction silicon carbide particles (SiCp/Al) were used as experimental materials, where the volume fractions of the SiC particles and Al matrix were 20% and 80%, respectively. The geometry of the specimens used for the experiments was 160 mm × 130 mm × 10 mm, and the size of the cut specimens was 10 mm × 10 mm × 3 mm, as shown in Figure 2. The main physical property parameters of SiCp/Al composites are listed in

Table 1. Parameters of physical properties of SiCp/Al.

Attribute	Values
Densities (g/cm3)	2.7–2.8
Thermal conductivity (W/m·K)	160
Coefficient of thermal expansion (10−6/K)	23
Modulus of elasticity (GPa)	100
Ultimate tensile strength (MPa)	300
Durometer (VHN)	90
Fracture toughness (MPa·m1/2)	25

. In addition, a Dick’s-brand-water-based working fluid was selected as the conventional working fluid, and graphene nanopowder was selected as the dielectric additive.

2.3. Experimental Design

In this study, the material removal rate (MRR) and surface roughness (R_a) are taken as the key evaluation indexes, focusing on the effects of four key process parameters, namely, pulse width (T_on), duty cycle (DC), number of power tubes (PT), and wire travel speed (WS), on the performance of SiCp/Al EDM wire cutting. Based on the benchmark process parameters (T_on = 22 μs, DC = 1:4, PT = 3, WS = 2 speeds), graphene working fluid concentration gradient experiments (0.1–0.4 wt%) were firstly carried out, and the optimal concentration was determined by comparing and analyzing the trends in the MRR and R_a. On this basis, comparison experiments with the conventional working fluid were carried out to preliminarily clarify the efficiency enhancement mechanism of the graphene working fluid. In order to further reveal the influence mechanism of the process parameters, a single-factor comparison experiment was designed to investigate the influence law of each parameter on the processing performance under the conditions of the two working fluids, respectively. The experiments were designed using the one-factor level design shown in

Table 2. Table of experimental parameters.

Experimental Parameters	Numerical Value
Materials	20 vol.%SiCp/Al
Electrode wire diameter/material	Φ0.18 mm/Mo
Working fluid	Dietrich-water-based working fluid/graphene mixing powder working fluid
Ton/μs	18, 22, 26, 30
DC/ratio	1:4, 1:5, 1:6, 1:7
PT	1, 2, 3, 4
WS/Gear	0, 1, 2, 3
Graphene working fluid’s concentration/wt%	0.1, 0.2, 0.3, 0.4

, in which the variation ranges of the key parameters were determined based on preliminary pre-tests, and all experimental groups kept the other parameters constant to ensure the reliability of the data.

After the single-factor experiment revealed the improvement effect of the graphene working fluid on the processing performance, in order to deeply analyze the multi-parameter coupling action mechanism [13], the L16 (4⁴) orthogonal experimental design (based on the graphene working fluid) was used to further analyze the degree of influence of each processing parameter on the process indexes. Each set of experimental data was measured four times repeatedly, and the average value was taken as the final result to ensure the reliability of the experimental data, and the orthogonal test factor levels are shown in

Table 3. Orthogonal test factor levels.

Level	Ton	DC	PT	WS
1	18	1:4	1	0
2	22	1:5	2	1
3	26	1:6	3	2
4	30	1:7	4	3

.

The machining effect is characterized by the material removal rate and surface roughness at the end of the experiment. Among them, the material removal rate is an important index to measure the efficiency of EDM wire cutting machining, and in this paper, Equation (1) is used to calculate the MRR of SiCp/Al composites after machining [17]:

$$\mathrm{MRR}={\displaystyle \frac{\mathrm{LH}}{\mathrm{t}}}$$

(1)

Equation (1): CE expression, where L is the length of the cut workpiece for one week (unit: mm), H is the thickness of the workpiece (unit: mm), and t is the time required to cut the workpiece within one week (unit: min).

The surface roughness R_a of the machined SiCp/Al composites was measured with a TR200 surface-roughness-measuring instrument. Each group of workpieces was measured four times and averaged, as represented by Equation (2) [18]:

$$\mathrm{Ra}={\displaystyle \frac{{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{R}}_{\mathrm{ai}}}}{\mathrm{n}}}$$

(2)

Equation (2): R_a expression, where R_ai is the R_a of the ith measurement (unit).

3. Results and Discussion

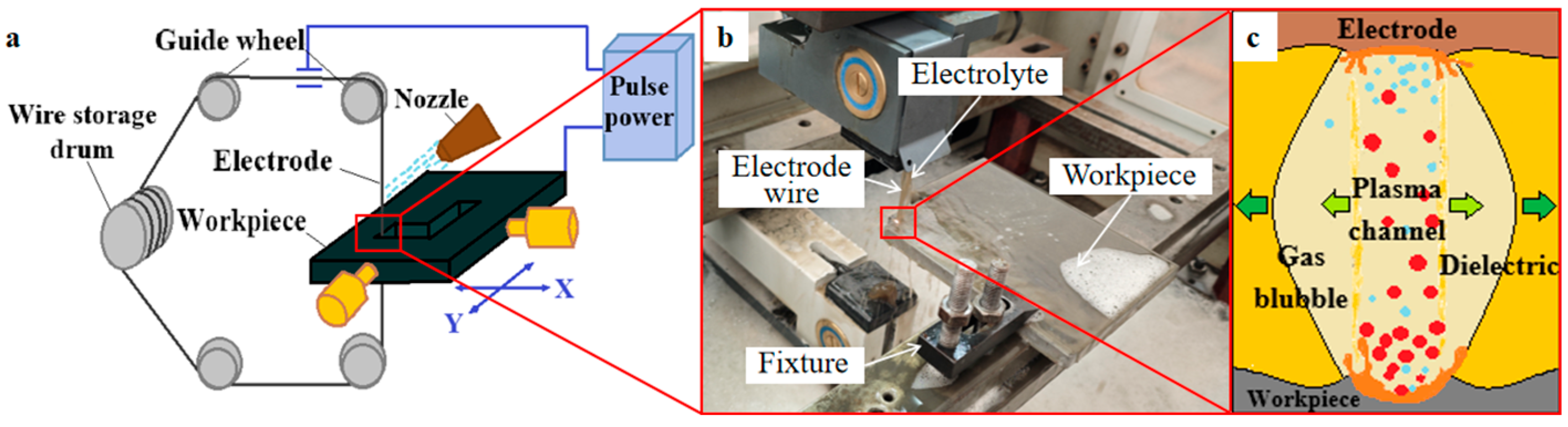
3.1. Experimental Analysis of Working-Fluid Performance

In order to clarify the influence mechanism of the graphene working solution concentration, the baseline process parameters (T_on = 22 μs, DC = 1:4, PT = 3, WS = 2 steps) were selected for the control experiment. The experimental results are shown in Figure 3, where it can be observed that the effects of different concentrations of the aqueous graphene working fluid on R_a and MRR show a tendency of first increasing and then decreasing. Specifically, when the graphene concentration increases from 0.1% to 0.2%, the R_a value decreases and the MRR value increases, while when the concentration exceeds 0.2%, the R_a value starts to increase, and the MRR value decreases. For MRR, the reason for the appearance of this trend is that, the increase in the graphene concentration is accompanied by a change in the viscosity of the working fluid, and the desirable viscosity can improve the cooling and chip removal ability of the machining fluid, which can improve the MRR [19]. However, a too-high viscosity may hinder the flow of the machining fluid, affecting the cooling and chip removal effects and leading to a decrease in the MRR. For the R_a, graphene acts as a lubricant during the machining process and optimizes the discharge channel, thus reducing the R_a [20]. However, when the concentration is too high, graphene flakes may produce aggregation, leading to an increase in the R_a.

The combination of experimental results and theoretical analysis revealed that graphene may provide the best electrical conductivity at a concentration of 0.2 wt%, so in the subsequent one-factor experiments, a graphene working fluid concentration of 0.2 wt% will be used for the experiments.

Then, a set of experiments comparing the ordinary working fluid with the graphene working fluid under fixed parameters (Ton = 22 μs, DC = 1:4, PT = 3, WS = 2 steps) were carried out after determining the graphene concentration, and the results of the experiments are as follows (

Table 4. Comparison of experimental results.

Working Fluid Type	Ra μm	MRR mm2/min
Conventional working fluid	4.527	55.87
Graphene working fluid	3.247	63.22

):

This improvement is mainly due to the triple mechanism of graphene [21]: (1) the “micro-explosion effect of nanoparticles in the discharge gap promotes the expansion of the discharge channel”, resulting in a more uniform distribution of energy; (2) the high thermal conductivity of graphene accelerates the discharging of etching products, and the SEM shows that the microcracks and exfoliation grooves on the surface of the processed surface are reduced (Figure 4); (3) the dispersion of discharge energy reduces local overheating, resulting in the selective etching of the Al substrate, which inhibits the over-oxidation of the Al substrate; (4) dispersing the discharge energy, reducing the selective etching of Al substrate caused by local overheating, and suppressing the excessive oxidation of Al substrate.

3.2. Results and Analysis of One-Way Comparison Experiments

According to the experimental design, one-factor comparative experiments were carried out using the ordinary working fluid and the graphene mixed-powder working fluid (wt%), respectively, to investigate the effects of the process parameters, such as pulse width (Ton), duty cycle (DC), number of power tubes (PT), and wire-walking speed (WS), on the MRR and Ra. The effects of different working fluids on the MRR and R_a after processing are shown in Figure 5 and Figure 6, respectively.

Figure 5 demonstrates the influence pattern of each process parameter on the MRR under different working fluids. The results show that the MRR increases with the increase in Ton, PT, and WS and decreases with the increase in DC. Among them, the most significant effect of the Ton on the MRR is due to the fact that the increase in the Ton directly increases the single-pulse discharge energy, leading to more SiCp/Al melting or vaporization. In addition, the MRR curve of the graphene working fluid is always located above the curve of the conventional working fluid, and its maximum MRR is calculated to be 11.16% higher than that of the conventional working fluid, and this enhancement is mainly attributed to the high electrical conductivity and the field emission effect of graphene, which promotes a uniform distribution of the discharge channels and reduces the local energy concentration, so that the etch rate of the SiC particles and the Al substrate tends to be synchronized. Thus, the MRR was effectively improved.

Figure 6 demonstrates the influence pattern of each process parameter on the R_a under different working fluids. The results show that the R_a increases with the increase in the Ton, PT, and WS and decreases with the increase in DC. Similarly, the R_a is still affected by the pulse energy: when the DC increases, the pulse energy decreases subsequently, which in turn reduces the discharge crater pulse depth and surface thermal damage, and the surface roughness decreases as a result. In addition, the MRR curve of the graphene working fluid is always located below the curve of the conventional working fluid, and its minimum R_a is calculated to be 29.96% less than that of the conventional working fluid. This optimization is mainly due to the high thermal conductivity of graphene nanoparticles, which significantly improves the heat dissipation efficiency of the working fluid and accelerates the solidification process of the molten material. This effectively inhibits the microcrack extension caused by rapid cooling and also reduces the thermal stress mismatch between the SiC particles and the Al matrix, decreasing the probability of particle shedding, thus effectively reducing the R_a.

3.3. Signal-to-Noise Ratio Analysis

In order to reduce the interference of random factors in repeated trials and accurately extract effective information, a signal-to-noise ratio analysis (SNR) was introduced [22]. Minitab 2023 software was used for the signal-to-noise ratio analysis and image processing. The signal-to-noise ratio value of each group of test results is used as the basis for data processing, which weakens the random interference when analyzing the controllable factors and improves the accuracy of calculation and analysis. The signal-to-noise ratio method divides the system response into the desired characteristics: the large desired characteristics and the small desired characteristics. For the MRR, the larger the value, the better; the MRR belongs to the large desired characteristics and is calculated according to the Formula (3) of the signal-to-noise ratio calculation for the large desired characteristics. Meanwhile, for the R_a, the smaller the value, the better; the R_a has the small desired characteristics and is calculated according to the Formula (4) of the signal-to-noise ratio calculation for the small desired characteristics [23]. The larger the value of the signal-to-noise ratio, the better the test results.

$$\mathrm{S}/\mathrm{N}=-10\ast \lg ({\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}\frac{1}{{\mathrm{y}}_{\mathrm{i}}^2}})$$

(3)

$$\mathrm{S}/\mathrm{N}=-10\ast \lg ({\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{y}}_{\mathrm{i}}^2})$$

(4)

where S/N is the signal-to-noise ratio value of the process target, n is the overall number of test samples, and n = 16 in this study. y_i is the ith group of level factor sample data. In the Taguchi analysis response table, the difference between the maximum average response value of the factor minus the minimum average response value is Delta, and the larger the value is, the greater the impact of the factor on the judging index, and the higher the factor ranks [24].

The results of the MRR and R_a were substituted into the calculation to obtain their respective signal-to-noise ratios, and the results are shown in

Table 5. Optimization metrics signal-to-noise ratio values.

No.	Signal-to-Noise Ratio Values
	MRR	Ra
1	28.35	−2.049
2	33.78	−2.997
3	35.60	−6.6
4	35.33	−4.464
5	36.02	−6.596
6	27.99	−6.307
7	36.83	−7.024
8	34.70	−0.906
9	36.23	−4.915
10	37.10	−8.379
11	27.00	−4.286
12	32.43	−5.235
13	37.82	−12.089
14	36.23	−4.297
15	31.97	−8.711
16	27.60	−5.818

. There are four levels for each factor, and a total of 16 groups of tests, so each level corresponds to four groups of experimental signal-to-noise ratio values.

The mean values of the MRR signal-to-noise ratios of the four groups of tests corresponding to each level of each factor were calculated and plotted in Figure 7 of the mean values of the MRR signal-to-noise ratios. Figure 7 shows that the S/N fluctuates with the increase in the Ton; the MRR tends to decrease with the increase in DC; the MRR increases and then tends to be stable with the increase in PT; and the MRR decreases, then increases, and then decreases when the increase in WS is observed. The range of changes in the mean values of the signal-to-noise ratios of the PT was the largest, which shows that the PT have the greatest influence. It is analyzed that the PT determines the energy intensity of a single pulse, and a higher PT means more energy release, which can melt the material faster and thus increase the MRR. Based on the levels corresponding to the maximum of the mean values of the signal-to-noise ratios of the factors, the combination of the processing parameters at the time of the maximum of the MRR is determined as follows: Ton = 22 μs, DC = 1:4, PT = 4 s, and WS = 2.

The mean values of the R_a signal-to-noise ratios of the four groups of tests corresponding to each level of each factor were calculated separately, and the mean values of the R_a signal-to-noise ratios were plotted in Figure 8. From Figure 8, it can be seen that the S/N showed a decreasing trend with the growth in the Ton; with the increase in DC, the S/N first decreased, then increased, and then decreased; with the growth in the PT, the S/N increased and then decreased; and with the increase in WS, the S/N increased first and then decreased. And from the figure, it can be seen that the range of variation in the mean value of the Ton signal-to-noise ratio is the largest, indicating that the Ton has the greatest influence on R_a. It is analyzed that a higher Ton produces a larger discharge pit, leading to an increase in R_a. Therefore, the higher the Ton, the more pronounced the R_a. The level corresponding to the maximum value of the mean value of the signal-to-noise ratio of each factor material was selected to form the processing parameter combination at the time of the maximum R_a. The processing parameter combinations were as follows: T_on = 22 μs, DC = 1:4, PT = 3, and WS = 2.

3.4. Multi-Objective Optimization Analysis by Gray Correlation Method

For different judging dimensions, the factors produce different effects; i.e., the combination of factors that is more optimal for the surface roughness is not necessarily optimal for the cutting speed [25]. In the actual EDM wire-cutting SiCp/Al processing, the MRR and R_a need to be considered comprehensively, so it is necessary to carry out a multi-objective optimization analysis, this study uses a gray correlation analysis, which is a multi-factor statistical analysis method that is based on the sample data of each factor, and the gray correlation is used to describe the strength, magnitude, and order of the relationship between the factors [26]. The process of calculating the gray correlation value is as follows [27,28]:

1.

Determine the number series to be compared

The compared columns are a set of data under two optimization metrics in Table 4, i.e., xe (k) represents the signal-to-noise ratio values for MRR and R_a, respectively, where e = 1,2. xe (k) is the MRR optimization metric for e = 1, xe (k) is the R_a optimization metric for e = 2, and k is the number of trials serial number.

2.

Determination of the reference sequence

The reference sequence ${\mathrm{y}}_{\mathrm{e}}^0\left(\mathrm{e}\right)$ is the ideal value under the eth optimization metric, and the largest signal-to-noise ratio value among the two optimization metrics is set as the reference sequence, i.e., ${\mathrm{y}}_{\mathrm{e}}^0\left(\mathrm{e}\right)$ = (35.485 − 0.906).

3.

Dimensionless data processing

Since the data of each factor may have different magnitudes and orders of magnitude, the data need to be normalized without dimension. The equation for normalizing the magnitude of the compared series is as follows:

$${\mathrm{y}}_{\mathrm{e}}\left(\mathrm{k}\right)={\displaystyle \frac{{\mathrm{x}}_{\mathrm{e}}\left(\mathrm{k}\right)-min{\mathrm{x}}_{\mathrm{e}}\left(\mathrm{k}\right)}{max{\mathrm{x}}_{\mathrm{e}}\left(\mathrm{k}\right)-min{\mathrm{x}}_{\mathrm{e}}\left(\mathrm{k}\right)}}$$

(5)

Equation (5): Normalized formula, where y_e (k) is the value under the eth indicator and after normalization of the kth test scale, k = 1,2,3,…,16.

4.

Calculating the gray correlation coefficient

The gray correlation coefficient ξ_e (k) is calculated as follows:

$${\xi }_{\mathrm{e}}\left(\mathrm{k}\right)={\displaystyle \frac{\mathrm{m}+\rho \mathrm{M}}{{\mathsf{\Delta }}_{\mathrm{e}}\left(\mathrm{k}\right)+\rho \mathrm{M}}}$$

(6)

Equation (6): Gray correlation coefficient.

${\mathsf{\Delta }}_{\mathrm{e}}\left(\mathrm{k}\right)={|\mathrm{y}}_{\mathrm{e}}^0\left(\mathrm{k}\right)-{\mathrm{y}}_{\mathrm{e}}\left(\mathrm{k}\right)|$: M is the maximum difference between the two levels, m is the minimum difference between the two levels, and ρ is the resolution factor. The value of ρ is calculated according to Equation (7):

$$\mathsf{\rho }={\displaystyle \frac{\sqrt{{\displaystyle \sum {\mathsf{\Delta }}_1\left(\mathrm{k}\right)\cdot {\displaystyle \sum {\mathsf{\Delta }}_2\left(\mathrm{k}\right)}}}}{2\mathrm{kM}}}$$

(7)

Equation (7): Distinguishing coefficient.

Since there were two optimization metrics in this experiment, one resolution factor was calculated for a set of two metrics, resulting in a final resolution factor ρ = 0.178 used in this study.

5.

Determine gray correlation coefficient weights

The gray correlation coefficient weights are determined using a hierarchical analysis method (AHP). After an expert analysis, the importance degree of the MRR for the R_a is selected as 3; then, the importance degree of the R_a for the MRR is 1/3, and then the evaluation matrix Q is established, and the response weight matrix β is obtained after normalization by finding the maximum eigenvalue λmax and the corresponding eigenvector x of matrix Q. The evaluation matrix Q is shown in Equation (8), with the maximum eigenvalue λmax = 2, and the eigenvector x as Equation (9) is shown in Equation (10), and the response weight matrix β is shown in Equation (10).

$$\mathrm{Q}=\left[\left.\begin{array}{cc}1& 3\\ {\displaystyle \frac{1}{3}}& 1\end{array}\right]\right.$$

(8)

Equation (8): Evaluation matrix.

$$\mathrm{x}=\left[\left.\begin{array}{cc}1.5& 0.5\end{array}\right]\right.$$

(9)

Equation (9): Eigenvector x.

$$\mathsf{\beta }=\left[\left.\begin{array}{cc}0.75& 0.25\end{array}\right]\right.$$

(10)

Equation (10): Weight matrix.

Therefore, the MRR weight β₁ = 0.75, and the R_a weight β₂ = 0.25, indicating that the most important optimization metric in this case is the MRR.

6.

Calculating Gray Correlation

The higher the correlation, the higher the degree of correlation between the comparison series and the reference series. The gray correlation value is calculated using the formula:

$${\mathrm{r}}_{\mathrm{k}}={\displaystyle {\sum }_{\mathrm{e}=1}^{\mathrm{n}}{\beta }_{\mathrm{e}}}{\xi }_{\mathrm{e}}\left(\mathrm{k}\right)$$

(11)

Equation (11): Gray relational grade.

β_e is the weight value of the eth optimization index; r_k is the gray correlation value.

The analysis results are shown in

Table 6. Grey relational analysis results.

No.	Normalize		Gray Correlation Coefficient		Gray Correlation Value
	MRR	Ra	MRR	Ra
1	0.125	0.145	0.205	0.172	0.1918
2	0.627	0.256	0.365	0.193	0.2962
3	0.796	1	0.536	1	0.7216
4	0.770	0.773	0.492	0.44	0.4712
5	0.833	0.98	0.518	0.9	0.6708
6	0.092	0.415	0.195	0.233	0.2102
7	0.909	0.686	0.667	0.362	0.545
8	0.713	0.39	0.423	0.226	0.3442
9	0.854	0.715	0.554	0.384	0.486
10	0.931	0.03	0.725	0.155	0.497
11	0	0.447	0.178	0.243	0.204
12	0.501	0.306	0.284	0.204	0.252
13	1	0.456	1	0.246	0.6984
14	0.854	0.35	0.554	0.215	0.4184
15	0.459	0	0.267	0.151	0.2206
16	0.558	0.211	0.187	0.184	0.1858

. Based on the gray correlation value in Table 6, the average gray correlation value under each level of the four process parameters is calculated, and at the same time, the extreme difference analysis is carried out, and the calculation results are shown in

Table 7. Average value of gray correlation degree of different technological parameters.

Level	Ton	DC	PT	WS
1	0.4202	0.51175	0.3261	0.3518
2	0.44255	0.35545	0.3599	0.3857
3	0.35975	0.4228	0.49255	0.5188
4	0.3808	0.3133	0.5529	0.347
Range	0.0828	0.19845	0.2268	0.1718
Sort	4	2	1	3

; then, the primary and secondary relationships of the influence of each machining process parameter on the evaluation indexes of the MRR and R_a are in the following order: DC, WS, PT, and Ton.

According to the gray correlation analysis method, the larger the mean value of the gray correlation degree, the better the target response corresponding to this level of this factor; then, this level is the optimal level of this factor. From the above table, it can be seen that the optimal process parameter combination of the multi-objective optimization is as follows: pulse width: 22 μs, duty ratio: 1:4, number of power tubes: 3, and wire speed: 2, and the comprehensive gray correlation value of the MRR and R_a reaches the maximum value of 0.756 under this processing condition, which proves the feasibility of the multi-objective optimization model of the gray correlation analysis method.

3.5. Confirmatory Experiment

Based on the optimized parameter combinations, the multi-objective optimal parameter combination G_max, the maximum MRR parameter combination MRR_max, and the minimum R_a parameter combination R_amin are determined. The test results of response to the optimal process parameter combination are shown in

Table 8. Validation experiment results.

Parameter Combination	Ra/μm	MRR (mm2/min)
MRRmax	5.68	73.65
Ramin	2.97	45.64
Gmax	3.21	68.28

. Compared with the MRR_max processing-parameter test, the R_a is reduced by 48.17%; compared with the R_amin processing-parameter test, the MRR is increased by 35.43%. Figure 9 shows the surface morphology after the G_max combination processing.

4. Conclusions

In this study, the optimization effect of the graphene-enhanced working fluid on the wire EDM of SiCp/Al composites was systematically explored. The key mechanism of the graphene-enhanced working fluid in improving the machining performance was revealed through experimental verification and theoretical analysis. The following conclusions were obtained:

1.

The results show that the addition of graphene nano-powder to traditional working fluid can significantly improve the machining performance of SiCp/Al composites. Through the single-factor experiment analysis, the MRR of the graphene working fluid can be increased by 11.16%, and R_a can be decreased by 29.96%. The optimization mechanism is mainly attributed to the high thermal conductivity and field emission effect of graphene, which can effectively improve the discharge uniformity, accelerate the discharge of etching products, and reduce the surface defects caused by thermal stress.

2.

Based on the gray correlation analysis and analytic hierarchy process (AHP), the optimal combination of process parameters considering MRR and R_a is determined: pulse width: 22 μs, duty ratio: 1:4, number of power tubes: 3, and wire speed: 2. Verification experiments show that the combination achieves the best balance between the MRR and R_a: the R_a is reduced by 48.17% compared with the combination of the maximum MRR, and the MRR is increased by 35.43% compared with the combination of the minimum R_a. The parameter sensitivity analysis showed that duty cycle had the most significant effect on the comprehensive index (range 0.198), followed by the WS and PT.