Abstract
To address the challenge of multimodal anomaly data governance in ship maintenance-cost prediction, this study proposes a three-stage hybrid data-cleansing framework integrating physical constraints and intelligent optimization. First, we construct a multi-dimensional engineering physical constraints rule base to identify contradiction-type anomalies through ship hydrodynamics validation and business logic verification. Second, we develop a Feature-Weighted Isolation Forest Algorithm (W-iForest) algorithm that dynamically optimizes feature selection strategies by incorporating rule triggering frequency and expert knowledge, thereby enhancing detection efficiency for discrete-type anomalies. Finally, we create a Genetic Algorithm-Ant Colony Optimization Collaborative Random Forest (GA-ACO-RF) to resolve local optima issues in high-dimensional missing data imputation. Experimental results demonstrate that the proposed method achieves a physical compliance rate of 88.2% on ship-maintenance datasets, with a 25% reduction in RMSE compared to conventional prediction methods, validating its superior data governance capability and prediction accuracy under complex operating conditions. This research establishes a reliable data preprocessing paradigm for maritime operational assurance, exhibiting substantial engineering applicability in real-world maintenance scenarios.
1. Introduction
1.1. Research Background
With the rapid development of global maritime industries, modern vessels increasingly operate under demanding schedules and extreme environmental conditions, including prolonged exposure to salt spray corrosion, mechanical vibration, and electromagnetic interference. Industry statistics reveal that maintenance costs now constitute 30–50% of total lifecycle expenditures for commercial fleets [1,2]. This cost escalation is further intensified by surging maintenance requirements driven by accelerated adoption of intelligent ship systems and frequent operational mode transitions in complex marine environments. In this context, building a highly accurate maintenance-cost prediction model is critical for optimizing ship lifecycle management, scientifically formulating maintenance budgets, precisely allocating spare parts resources, and ensuring operational readiness. It represents the key to reducing high operational costs. However, the engineering implementation of current predictive models faces multifaceted constraints stemming from foundational data-quality issues. Ship equipment typically has long service cycles and requires frequent maintenance, generating substantial data on equipment status, maintenance procedures, and operating conditions. However, inadequate development of data-management platforms across maintenance facilities has resulted in these valuable maintenance records being scattered across disparate business systems, hindering integration and utilization. Furthermore, the diversity of data sources and inconsistent formats compromise data reliability. This manifests in issues such as human input errors, inconsistent unit systems, and sensor failures or missing data. If these “dirty data” are not effectively cleansed, they will severely distort the output of predictive models. This distortion risks budget overruns, resource misallocation, and potentially delays to critical operations due to the failure to accurately anticipate high-cost maintenance events. Data-cleansing techniques, as critical preprocessing solutions to address these challenges, have established mature implementation frameworks in domains such as power equipment fault prediction [3] and wind turbine health management [4]. Wang et al. achieved enhanced electrical load forecasting performance by applying K-means and DBSCAN clustering algorithms for power load data sanitization, attaining a Relative Percentage Difference (RPD) of 3.053 and reducing MAPE to 4.332% [5]. In parallel, Shen developed a hybrid cleansing methodology integrating change-point grouping with quartile-based anomaly detection, effectively identifying aberrant power data in wind turbines with an approximately 20% data exclusion rate [6]. These cross-domain practices offer significant insights for ship-maintenance data governance. It is imperative to establish a data-cleansing methodology that integrates domain-specific physical knowledge. This will provide a solid and reliable data foundation for building high-precision predictive models that support practical operational and maintenance decision-making.
1.2. Research Motivation
The quality of ship-maintenance data directly determines the accuracy of maintenance-cost prediction and the reliability of navigation performance evaluation. With the pervasive adoption of IoT technologies in maritime operational systems, modern vessel sensor networks generate over 5TB of multi-source heterogeneous data daily, of which 12.7% constitutes anomalous data [7]. Such data anomalies not only incur substantial storage-resource inefficiencies but also undermine data value through both explicit and implicit pathways, ultimately inducing systemic deviations in critical decision-making processes. However, current research lacks engineering-operational definitions for anomalous ship-maintenance data, while conventional data-cleansing methodologies exhibit significant theoretical deficiencies and practical implementation barriers when confronting the multidimensional complexities inherent to maritime operating environments.
1.2.1. Engineering-Oriented Reengineering of Conventional Anomaly Detection Frameworks
Building upon the Hodge–Lehmann anomaly data theoretical framework, this study proposes an engineering-operational definition for ship-maintenance anomalies: a collection of nonconformant observations violating naval architectural constraints, deviating from historical statistical distributions, and compromising data relational integrity, induced by sensor drift, human–machine interface errors, or system integration flaws under specific operational environments and maintenance scenarios [8]. This definition encompasses four prototypical anomaly modalities, which will be explicated through Table 1′s marine information dataset.

Table 1.
Example of basic parameters for ships.
- Redundancy-Type Anomalies. These arise from spatiotemporal synchronization errors in multi-sensor systems or the simultaneous operation of parallel support systems. They typically manifest as duplicate work order records and redundant attribute fields. For instance, Data Rows 1 and 2 contain fully identical records for a -class vessel repair.
- Contradiction-Type Anomalies. These manifest as logical conflicts between hull physical parameters and fluid dynamics characteristics. Examples include combinations of vessel length, beam, and displacement that violate ship statics constraints, or main engine power and maximum speed deviating from theoretical calculation ranges. A typical case is Data Row 8, which records a -class vessel with a displacement of 8000 tons and a main engine power of 75,000 kW, yet lists a speed of 55 knots—far exceeding the established reasonable range (where vessels of comparable tonnage typically achieve speeds ≤30 knots). This necessitates verification for potential data-entry errors or sensor malfunction.
- Discrete-Type Anomalies. These exhibit abrupt, high-amplitude characteristics, typically manifesting as non-continuous, abnormal distributions in key parameters. For example, Data Row 3 records a -class vessel with a displacement of 32,000 tons and a length of 85 m—a combination far exceeding the reasonable dimensions for comparable vessels (where the actual displacement should be approximately 3200 tons).
- Missing-Type Anomalies. These present multimodal characteristics, including the absence of critical parameters and discontinuous maintenance records, as exemplified by Data Rows 4 and 6.
1.2.2. Multidimensional Challenges in Conventional Data Cleansing
The essence of data cleansing lies in transforming anomalies and refining the structure of datasets through systematic data-quality governance. This process reconstructs source data into high-quality, analytics-ready data assets. Contemporary shipboard equipment condition monitoring datasets exhibit inherent characteristics of multiparameter coupling and domain knowledge dependency, exposing significant limitations in conventional data-cleansing methods when confronting these operational complexities:
- Statistical Methodology Limitations: Conventional statistical approaches—including boxplot analysis and the three-sigma criterion—demonstrate diminishing efficacy when confronted with nonlinear interdependencies among multisource parameters, failing to detect latent anomalies due to their reliance on identical distribution assumptions. Yao et al. critically identified the inadequacy of conventional boxplot methods in complex marine engineering scenarios, pioneering a LOF-IDW hybrid methodology for integrated anomaly detection and rectification. This approach demonstrated a 27.6% average reduction in the data coefficient of variation post-cleansing through field validations on offshore platform monitoring systems [9]. In parallel, Zhu innovatively employed K-dimensional tree spatial indexing to characterize distributed photovoltaic plant topologies, synergizing enhanced three-sigma criteria to elevate high-reliability data ratios from 43.61% to 85.71% in grid-connected power quality analysis [10].
- Insufficient Sensitivity of Clustering Algorithms: Conventional clustering algorithms such as DBSCAN and K-means exhibit limited detection accuracy for anomalies in unevenly distributed density spaces, leading to erroneous cleansing of critical fault precursors. Song et al. enhanced DBSCAN density clustering through STL to decompose time-series trends and periodicity, achieving precision and recall rates of 0.91 and 0.81, respectively, for DO and pH anomaly detection in marine environmental monitoring [11]. In parallel, Han developed a hybrid data-cleansing strategy that integrates Tukey’s method with threshold constraints coupled with K-means clustering to optimize wind-speed-to-power characteristic curve fitting, resulting in an improved R2 value of 0.99 for cleansed datasets [12].
- Machine-Learning Models’ Disregard for Physical Constraints: While algorithms such as Isolation Forest (iForest) and Local Outlier Factor (LOF) demonstrate robust general-purpose anomaly detection capabilities, their lack of integration with domain-specific physical constraints remains a critical limitation. Liu et al. extracted four coarse-grained type-level features and three fine-grained method-level features, reframing software defect identification as an anomaly detection task using iForest. This approach achieved an average runtime of 21 min across five open-source software systems while reducing false positive rates by 75% [13]. Shen et al. further enhanced robustness through a soft-voting ensemble combining PCA-Kmeans, the Gaussian Mixture Model (GMM), and iForest, supplemented by a Gradient Boosting Decision-tree (GBDT)-based imputation model, attaining 99.1% precision and 95.9% recall [14]. However, these methods exhibit a fundamental flaw: their repair logic remains decoupled from equipment physics, risking physically implausible restoration outcomes under real-world operating conditions.
1.3. Research Innovations
This study addresses the complex challenge of multimodal anomaly data processing in ship-maintenance-cost prediction by proposing a technologically innovative framework with significant theoretical and practical contributions. The primary innovative achievements are manifested in four key aspects:
- Construction of a Physics-Driven Constraint Knowledge Base: This study pioneers the systematic encoding of ship hydrodynamics, structural mechanics, and maintenance operational protocols into a quantifiable constraint system. By establishing a multidimensional engineering–physical correlation network, we enable effective identification of contradiction-type anomalies while ensuring the cleansed data aligns with authentic vessel operating conditions.
- Design of a Feature-Weighted Isolation Forest Algorithm (W-iForest): We propose a dynamic weight allocation mechanism integrating rule-triggering frequency and expert knowledge to enhance the feature selection strategy of the iForest algorithm. By prioritizing the partitioning of highly sensitive parameters, this innovation significantly improves the detection efficiency for discrete-type anomalies.
- Development of a Genetic Algorithm-Ant Colony Optimization Collaborative Random Forest (GA-ACO-RF) Missing Data Imputation Model: This innovation synergizes Genetic Algorithms (GA) and Ant Colony Optimization (ACO) to dynamically adapt Random Forest (RF) hyperparameters. By leveraging GA to initialize ACO pheromone concentrations, we integrate GA’s global search capabilities with ACO’s local optimization strengths, effectively escaping local optima traps in high-dimensional missing data imputation.
- Establishment of a Multimodal Collaborative Cleansing Framework: We pioneer a three-stage closed-loop architecture: (1) Rule-Based Pre-Filtering, (2) W-iForest Anomaly Elimination, and (3) GA-ACO-RF Intelligent Imputation. This integrated framework achieves coordinated governance of contradiction-, discrete-, and missing-type anomalies, enabling generation of high-quality datasets with 88.2% physical compliance rates—a 25% improvement over conventional methods.
1.4. Research Structure
To achieve the aforementioned research objectives, the remainder of this paper is organized as follows:
- Section 2 comprehensively reviews advancements in data-cleansing methodologies, focusing on the evolutionary trajectories and existing bottlenecks of anomaly detection and imputation techniques.
- Section 3 proposes an innovative methodology framework, including (1) the construction of a marine engineering physical constraint knowledge base, (2) the design of the W-iForest anomaly detection algorithm, and (3) the development of the GA-ACO-RF missing value imputation model.
- Section 4 conducts empirical validation using multi-type vessel maintenance datasets, verifying model superiority through comparative experiments and ablation studies.
- Section 5 summarizes research findings and practical engineering applications, critically analyzes current limitations, and outlines future research directions.
2. Related Work
Under the backdrop of deep integration between artificial intelligence and big data technologies, data ecosystems are undergoing a significant transformation from single-structure formats to multimodal paradigms. Particularly with the proliferation of IoT technologies, multi-source heterogeneous data, including sensor time-series data and imaging data, have experienced exponential growth. Industry surveys indicate that data cleansing accounts for approximately 30% of total enterprise data governance costs [15], with data-quality issues emerging as a prominent bottleneck constraining model performance enhancement. This study systematically reviewed literature from 2017 to February 2025 using “data cleansing” and “data imputation” as dual core search terms across authoritative Chinese and English databases, including CNKI and Web of Science, ultimately selecting 98 academically representative research studies. The bibliometric analysis in Figure 1a demonstrates a marked year-on-year growth trend in data-cleansing research. Through constructing the co-word network mapping in Figure 1b for an in-depth analytical study of clusters in the literature, three evolutionary characteristics of data-cleansing technologies were revealed: (1) methodologically, a paradigm shift from traditional statistics to machine-learning/deep-learning integration; (2) application-wise, achieving deep adaptation from general-purpose data processing to vertical domain-specific implementations; and (3) technically, realizing transformative development from single-algorithm approaches to ensemble learning architectures. Taking wind turbine power-curve cleansing as a representative case, early-stage research predominantly employed traditional mathematical–statistical methods such as threshold-based approaches [16] and Interquartile Range (IQR) methods [17]. Contemporary studies have shifted toward intelligent algorithms, including iForest [18] and Graph Neural Networks (GNNs) [19], for constructing dynamic detection models. This chapter specifically addresses two critical challenges—outlier detection and missing value imputation—conducting a comprehensive analysis of their mathematical mechanisms, applicability boundaries, and performance thresholds, while systematically summarizing operational scenarios and inherent limitations across methodologies.
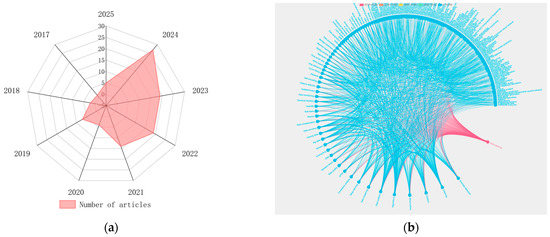
Figure 1.
Search results of the literature. (a) Annual publication statistics in the field of data cleaning from 2017 to 2025; the radar chart reflects the literature quantity from 2017 to 2025. (b) Research topic clustering map based on keyword co-occurrence; node size indicates keyword frequency, while line thickness represents co-occurrence strength.
2.1. Evolution and Comparative Analysis of Outlier Detection Techniques
As a pivotal research domain in data mining, outlier detection focuses on identifying anomalous observations that significantly deviate from conventional data patterns. Over decades of methodological evolution, this field has progressed through four distinct phases:
- Statistical Analysis-Based Detection Methods: Statistical detection methods establish threshold boundaries through the mathematical characterization of data distributions to quantitatively identify outliers. Classical algorithms include the three-sigma rule under Gaussian distribution assumptions, the IQR-based box plot method, and the extreme value theory-driven Grubbs’ test. These approaches demonstrate advantages in computational efficiency and low algorithmic complexity, making them particularly suitable for rapid cleansing of univariate datasets. Huang Guodong applied the three-sigma rule to cleanse univariate time-series data from water supply network pressure monitoring. By eliminating data points deviating beyond the mean range, an anomaly detection accuracy rate of 89% was achieved [20]. However, these limitations have become increasingly evident in complex industrial scenarios. First, algorithmic efficacy heavily relies on assumptions about data distribution patterns, leading to systematic misjudgments in non-Gaussian distributions. A representative case involves wind turbine operational data where Tip-speed Ratio (TSR) parameters typically exhibit multimodal mixture distribution characteristics. Under such conditions, the normality-assumption-based criterion erroneously flags 22–35% of operational mode transition points [21]. Second, traditional statistical methods fail to capture implicit correlations among multivariates. When processing strongly coupled multidimensional data, independent single-dimensional cleansing disrupts physical constraint relationships among parameters, resulting in the misclassification of normal operational fluctuations as anomalies. Empirical studies demonstrate that when cleansing 12-dimensional datasets from coal-fired power plant SCR denitrification systems, the false detection rate of box plot methods reaches 41.7%, significantly higher than association analysis-based machine-learning approaches [22].
- Density-Based Detection Methods: Density-based detection methods overcome the limitations of traditional statistical approaches reliant on global distribution assumptions by identifying anomalies through local neighborhood density variations. Current mainstream techniques primarily encompass two classical algorithms: DBSCAN and LOF. DBSCAN employs spatial density partitioning mechanisms, distinguishing core points, border points, and noise points, achieving anomaly localization through outlier detection in cluster-excluded discrete points. Cui Xiufang developed a density-reachable model with dynamic neighborhood parameters for maritime AIS data-cleansing requirements, successfully attaining 92.7% detection accuracy in berthing point identification and navigation trajectory anomaly detection [23]. LOF addresses anomaly detection challenges in non-uniform data distributions by calculating local density deviations between target points and their k-nearest neighbors. In water-quality monitoring, Chen innovatively integrated STL time-series decomposition with LOF algorithms, establishing a three-stage sensor noise filtration mechanism that achieved precise elimination of temporal anomalies [11]. The core advantage of these methods lies in their self-adaptive capability to identify sparse anomalies within locally dense regions without presupposing data distributions. Meng Lingwen successfully detected equipment anomalies under asynchronous operational conditions through density clustering in multi-parameter monitoring of power grid equipment [24]. Nevertheless, practical applications face significant challenges. DBSCAN exhibits parameter coupling effects between the neighborhood radius and the minimum points. Liu Jianghao’s cybersecurity intrusion detection study using the KDD CUP99 dataset demonstrated that optimal parameter combinations require determination through grid search optimization to address algorithmic sensitivity [25]. LOF confronts neighborhood-scale sensitivity, where k-value selection critically influences density calculation reliability. This necessitates cross-validation to identify optimal neighborhood scales, balancing the trade-off between detection sensitivity and false alarm rates.
- Machine-Learning-Based Anomaly Detection: This methodology achieves automated identification by establishing mapping relationships between data features and anomaly labels, broadly categorized into supervised and unsupervised learning paradigms. Within supervised learning frameworks, algorithms such as Support Vector Machines (SVM) and RF require comprehensively labeled training datasets to construct classification models. A representative application involves Han Honggui’s development of an enhanced SVM kernel function to construct a dissolved oxygen anomaly classifier for wastewater treatment processes, achieving a detection performance with an F1-score of 0.91 on industrial datasets [26]. Unsupervised methods, with iForest as a representative approach, enable rapid detection by constructing binary tree structures through random feature selection, leveraging anomalies’ susceptibility to isolation in feature spaces. Yang Haineng implemented this algorithm for power-curve cleansing in wind turbine SCADA systems, demonstrating a 40% improvement in computational efficiency compared to traditional IQR methods [27]. Current research demonstrates that these algorithms exhibit significant advantages in multi-source heterogeneous data-processing scenarios, such as multi-parameter monitoring of power grid equipment, with their detection accuracy and automation levels surpassing traditional threshold-based methods [28]. However, supervised learning confronts annotation cost challenges in domains like medical diagnostics, where data-labeling quality directly impacts model generalization capabilities [29]. While unsupervised methods reduce data dependency, they suffer from difficulties in tracing erroneous anomaly determinations. For instance, false elimination phenomena during SCADA system cleansing in wind power applications reveal how the black-box nature of decision-making logic impedes fault diagnosis implementation in industrial settings [30].
- Deep-Learning-Based Detection Methods: Deep-learning models demonstrate superior feature representation capabilities in complex scenarios through their deep neural architectures. Temporal models represented by the Long Short-Term Memory (LSTM) and Transformer architectures effectively capture temporal dependency features via gated mechanisms and attention networks. Xu Xiaogang’s developed Dual-Channel DLSTM achieved dynamic residual threshold optimization in steam turbine operational data prediction, constraining reconstruction errors within 0.5% [31]. For spatially correlated data, GNNs establish feature propagation paths through neighborhood information aggregation mechanisms. Li Li’s GCN-LSTM hybrid architecture, leveraging topological correlations among wind farm turbine clusters, accomplished wind speed anomaly cleansing with a 23% reduction in MAE [19]. Autoencoders (AEs) construct essential feature spaces via encoder–decoder frameworks. Zhao Dan employed Stacked Denoising Autoencoders (SDAEs) to process mine ventilation datasets, maintaining a 96% reconstruction accuracy under noise interference [32]. Such algorithms transcend the limitations of conventional approaches, demonstrating enhanced capabilities in processing high-dimensional unstructured data like images and texts while exhibiting distinct advantages in feature abstraction. Current research confronts two primary challenges: First, the heavy reliance on computational resources for model training, as evidenced by Liu Jianghao’s experiments revealing that DLSTM model training exceeds 12 h per session, with GPU memory consumption reaching 32GB [25]. Second, heightened sensitivity to data quality, with Peng Bo’s findings indicating reconstruction distortion in autoencoders when the signal-to-noise ratio falls below 15 dB, accompanied by an error propagation coefficient of 1.8 [33].
Based on the aforementioned research analysis, major algorithms in outlier mining exhibit significant diversity in technical characteristics and typical application scenarios, as detailed in Table 2.

Table 2.
Performance comparison of outlier mining algorithms.
2.2. Evolution and Comparison of Missing Value Imputation Techniques
Missing value handling techniques have evolved from statistical methods to machine-learning models, currently forming three primary methodological frameworks with significant differences in applicability and data adaptability:
- Traditional Imputation Methods: Traditional imputation methods are grounded in mathematical–statistical principles and primarily include univariate imputation and time-series interpolation. Univariate imputation fills missing values using central tendency metrics such as mean/median/mode. For instance, Liu Xin applied industry-standard temperature range mean imputation to blast-furnace molten iron temperature data with a missing rate <5%, effectively maintaining the stability of metallurgical process models [34]. Time-series interpolation encompasses linear interpolation, cubic spline interpolation, and ARIMA predictive imputation. Zhu Youchan employed cubic spline interpolation to restore 12 h data gaps caused by sensor failures in distribution network voltage sequences, achieving successful reconstruction [35]. These methods demonstrate advantages in terms of low computational complexity and applicability to small-scale structured data. However, they exhibit dual limitations: (1) The univariate processing paradigm neglects inter-feature correlations. When strong coupling relationships exist between photovoltaic power output and variables like irradiance and temperature, simple mean imputation introduces systematic bias [36]. (2) Sensitivity to non-random missing scenarios. Chen et al. demonstrated that traditional interpolation applied to continuous missing segments caused by sensor failures in water-quality monitoring generates spurious stationarity artifacts, leading to a 38% misjudgment rate in subsequent water-quality alert models [37].
- Statistical Model-Based Imputation Methods: Statistical modeling approaches enable multivariate inference of missing values by establishing data distribution assumptions. Multiple Imputation (MI) generates multiple complete datasets via Markov Chain Monte Carlo (MCMC) algorithms, reducing statistical inference uncertainty through imputation result integration. Jäger’s comparative experiments under Missing at Random (MAR) mechanisms revealed that MI achieves a 23.6% reduction in RMSE compared to five imputation methods (including K-means and RF), demonstrating superior accuracy [38]. Matrix Completion Methods (MCM) leverage low-rank matrix assumptions to recover missing values through nuclear norm minimization. Zhang innovatively combined sliding window mechanisms with MCM for real-time dynamic imputation of chemical process monitoring sensor data, achieving an 18.3% reduction in imputation error [39]. These methods’ principal advantage resides in effectively preserving datasets’ statistical properties, particularly suited for structured data types with defined characteristic patterns. In power load forecasting, Liu Qingchan’s application of MI methodology to handle temporal data gaps successfully maintained the load curve’s periodic characteristics [40]. However, two critical limitations must be acknowledged: (1) Sensitivity to missing data mechanisms. Maharana’s empirical analysis revealed that under Missing Not at Random (MNAR) conditions, MI suffers imputation accuracy degradation of up to 47% [41]. (2) Computational inefficiency in high-dimensional spaces. Gu Juping’s experimental observations indicated that matrix completion operations on 10,000-dimensional power grid datasets exceeded 24 h, severely constraining real-time processing capabilities [28].
- Machine-Learning-Based Imputation Methods: Machine-learning models with nonlinear mapping mechanisms provide innovative solutions for missing data problems. Ensemble learning approaches, notably RF and XGBoost, enhance prediction accuracy through collaborative multi-decision-tree modeling. Peng Bo’s IRF algorithm achieved breakthroughs in multivariate joint imputation for photovoltaic energy systems, elevating the coefficient of determination (R2) to 0.93, outperforming conventional methods [33]. Generative models like Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) produce realistic imputations by learning latent data distributions. Kiran Maharana’s VAE-based medical image restoration system attained a structural similarity index of 0.88 in reconstructing missing knee MRI regions, meeting clinical usability thresholds [41]. For temporal data characteristics, deep architectures such as LSTM and Transformer exhibit dynamic forecasting superiority. Wang Haining’s attention-guided LSTM achieved industry-leading performance in photovoltaic power output gap prediction with a MAPE of 2.1%, reducing errors by 47% compared to traditional time-series models [36]. These algorithms demonstrate exceptional performance in complex scenarios like smart grid systems. Liu Qingchan successfully implemented them for joint imputation of multi-source heterogeneous grid data, validating the algorithms’ capability to capture nonlinear correlations [40]. However, their double-edged nature requires prudent consideration. Mohammed’s research highlights that over-engineered architectures necessitate countermeasures like dropout mechanisms and regularization strategies to mitigate overfitting [42]. Côté warns that the black-box nature of generative models demands interpretability validation mechanisms when applied to regulated fields like finance and healthcare [29].
Based on the aforementioned analytical studies, Table 3 summarizes the technical characteristics and application scenarios of major missing value imputation algorithms.

Table 3.
Applicability comparison of missing value imputation techniques.
2.3. Limitations of Existing Research and Improvement Strategies
Data-cleansing technologies have undergone an evolutionary progression from statistical methods to machine learning and deep learning, with methodological frameworks demonstrating a critical paradigm shift from rule-driven systems to intelligent adaptive architectures. Outlier detection is transitioning from single-threshold determinations to multimodal anomaly recognition, while missing value imputation has advanced from simplistic filling to constraint-driven intelligent restoration. However, significant challenges persist when addressing the unique data characteristics of marine engineering applications: First, insufficient domain knowledge embedding prevails, where conventional methods lack systematic modeling frameworks for critical engineering physics constraints such as hull hydro-structural coupling effects and power system energy conservation principles. Second, real-time assurance mechanisms remain underdeveloped, as current knowledge-base constructions predominantly rely on static manual rules that impede rapid response capabilities under complex operational conditions. Third, inadequate processing capacity for high-dimensional dynamic data hinders adaptation to multi-parameter coupled evolution in next-generation vessel systems. To address these challenges, this study proposes a novel data-cleansing framework specifically designed for marine engineering datasets. The solution comprises three core innovations: (1) constructing a multi-physics-constrained knowledge base to achieve deep domain knowledge embedding, (2) developing the W-iForest algorithm to enhance anomaly detection accuracy, and (3) innovatively establishing a GA-ACO-RF algorithm for missing value compensation. The heuristic search mechanism significantly improves repair efficiency for complex missing patterns, providing a systematic solution to overcome existing technical bottlenecks.
3. Methodology
3.1. Multi-Dimensional Constraint-Based Rule Engine System
The rule base is constructed based on a ship lifecycle parameter system, with core data dimensions comprising (1) structural characteristic parameters: displacement, principal dimensions (length overall/beam/draft), construction costs; (2) dynamic performance parameters: prime mover power configuration, maximum service speed; (3) operational maintenance parameters: service lifespan, maintenance intervals, actual labor hours. Building upon this framework, six core cleansing rules have been established to systematically identify and eliminate data that violate physical operational principles or deviate from equipment performance specifications. This methodology effectively reduces contradiction-type anomalies, thereby enhancing the proportion of valid data within the original dataset.
3.1.1. Physics-Constrained Rule Base
The engineering relational constraint system for vessel characteristic variables is constructed based on multidimensional physical principles, integrating design specifications and operational maintenance data to establish a composite rule framework encompassing hydrodynamics, structural mechanics, and naval architecture. This rule base quantifies physical interrelationships among ship parameters to form a computable engineering constraint network, as detailed in Table 4.

Table 4.
Physics-constrained rule system for ships.
The displacement verification rule is derived from Archimedes’ principle and hull form design constraints regarding block coefficient. The lower limit of 0.6 corresponds to slender hull forms, while the upper limit of 0.85 accommodates full-form vessels, with a ±2% tolerance band addressing construction process variations [43]. The speed–power relationship rule characterizes the energy conversion mechanism in propulsion systems, revealing the cubic proportionality between speed and power consumption. The coefficient is determined by hull configuration characteristics (120–150 range), with a ≥15% power reserve ensuring operational redundancy for propulsion system safety. The length–beam ratio limit rule originates from the equilibrium between vessel stability and hydrodynamic efficiency, with a typical operational range of [3, 8]. The lower limit prevents seakeeping performance degradation caused by excessive rolling periods, while the upper threshold avoids structural integrity compromises from extreme slenderness ratios. An elastic buffer of ±0.2 accommodates stability compensation designs across diverse marine vessel types.
3.1.2. Operational-Constrained Rule Base
This knowledge base transforms tacit shipyard expertise into quantifiable models, with each rule grounded in industry standards and engineering practices, as detailed in Table 5.

Table 5.
Operational-constrained rule system for ships.
The man-hour efficiency rule is established in accordance with ship repair engineering labor hour standards, setting a maximum daily workload of 24 h per technician [44]. The component replacement rule adheres to ISO 14224:2016, implementing stratified safety coefficients: critical equipment κ = 0.9, auxiliary equipment κ = 0.8, non-critical equipment κ = 0.7. The maintenance-cost correlation rule employs a nonlinear cost escalation model: minor damage level , surface corrosion <5%; moderate damage level , structural deformation 5–15%; major damage level , functional impairment 16–30%; severe damage level , system failure >30%. The aging factor aligns with the 30-year design lifecycle mandated by IACS Unified Requirement Z10. When maintenance costs exceed 85% of new construction costs, automated equipment renewal protocols are triggered.
3.1.3. Rule Engine System
The Rule engine system originates from the inference mechanisms in expert systems, serving as a core component that decouples business logic from the application code through predefined semantic modules [45]. Its technical architecture comprises three critical dimensions: (1) the rule separation mechanism, which independently encapsulates business decision logic from programming code; (2) the dynamic execution framework, which supports real-time data input processing with rule interpretation and decision inference capabilities; and (3) the conflict resolution mechanism, which incorporates built-in rule prioritization and contradiction detection functions, while simultaneously being compatible with script-based rule definitions and embedded invocation in mainstream programming languages. This study establishes a dual-dimensional data-cleansing rule framework tailored to the critical characteristics of marine equipment data, with its technical implementation workflow illustrated in Figure 2. The process comprises four stages:
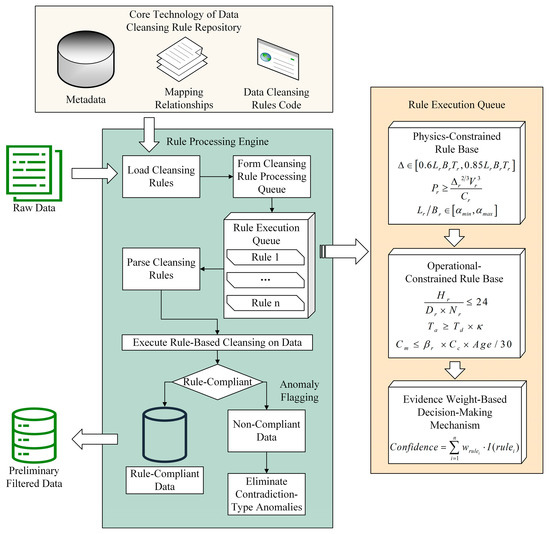
Figure 2.
Implementation flowchart of the ship-maintenance data cleaning rule base. Green boxes represent the rule processing engine, yellow boxes indicate the rule execution queue, and beige boxes denote the core technologies of the data cleaning rule base.
- Step 1: Data Dictionary Parsing. Decoding the field attributes and business semantics of raw data through a data dictionary, establishing a feature-rule mapping relationship matrix.
- Step 2: Rule Execution Queue Construction. Generating rule execution queues based on the mapping matrix, supporting real-time loading of rule definition files.
- Step 3: Sliding Window Processing. Implementing sequential scanning of data records using a window sliding mechanism, performing syntax validation, range detection, and logical verification operations.
- Step 4: Anomaly Handling. Eliminating identified conflicting anomalies and tagging them as missing values, ultimately generating a quality report containing cleansing metadata.
For multi-rule conflict resolution, the system employs an evidence-based weighting decision mechanism, as formalized in Equation (1):
where the weight coefficient is allocated based on rule type: 0.6 for physical constraint rules, and 0.4 for operational rules. When the composite confidence level exceeds the threshold of 0.7, the system automatically flags the data as suspicious and initiates manual verification procedures, while preserving original data provenance information for quality auditing purposes.
3.2. Feature-Weighted Isolation Forest Algorithm
The core mechanism of the iForest algorithm involves constructing random binary search trees to rapidly detect anomalies via significant differences in path lengths within tree structures. However, in marine-maintenance scenarios involving multidimensionally coupled engineering parameters (e.g., main engine power, displacement), traditional iForest exhibits inadequate feature discriminability. Current technological advancements in high-dimensional anomaly detection have evolved along dual methodological pathways: (1) The feature reduction approach, which employs manifold learning techniques like Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE) to achieve nonlinear mapping from high-dimensional spaces into lower-dimensional embeddings [46]. (2) The multidimensional detection approach, which directly processes raw feature spaces using density estimation methods such as LOF and DBSCAN. Given the significant physical interdependencies inherent in multi-sensor data from marine mechanical systems, where traditional dimensionality reduction methods risk distorting operational semantics, this study adopts the multidimensional detection pathway as the technological breakthrough. By leveraging rule-based constraints, we propose the W-iForest algorithm, which incorporates a feature weight allocation mechanism to prioritize critical parameter determination.
3.2.1. Isolation Forest Algorithm Principles
The iForest algorithm employs an ensemble learning framework that effectively mitigates the random deviations inherent in individual trees through a decision fusion mechanism that integrates multiple trees. Its core operational workflow comprises three pivotal components: isolation trees (iTrees), path length, and anomaly score [47].
- Definition: iTrees. An iTree, as the fundamental unit of the iForest, is a specialized decision tree based on a binary tree structure [48]. Node T within the tree is classified into two types: leaf nodes without child nodes and internal nodes containing two child nodes (, ). During initialization, the root node encompasses the entire training dataset. At each split, a feature dimension is randomly selected, and a split threshold is randomly chosen within the value range of dimension . The data in the current node are partitioned into the left subtree if , with the remaining data assigned to the right subtree . The partitioning process is recursively executed until it meets any of the following termination conditions: (1) a leaf node contains only one data instance, (2) the tree depth reaches a predefined maximum threshold, or (3) all samples in the current node share identical values across the selected feature dimensions. Normal samples, clustered in high-density regions, require multiple partitioning iterations for isolation, whereas anomalies—owing to their sparse distribution—are typically isolated rapidly.
- Definition: Path Length. The path length of a data sample is defined as the number of edges traversed from the root node to the leaf node during the tree traversal. This metric reflects the isolation difficulty of samples in the feature space, where anomalies exhibit significantly shorter path lengths than normal samples due to their sparse distribution.
- Definition: Anomaly Score. Based on binary search tree theory, the normalized path length for an -sample dataset can be calculated as shown in Equation (2).
- When approaches , approaches 0.5. The sample resides at the decision boundary between anomalies and normal data, making classification indeterminate.
- When approaches 0, approaches 1. The sample is identified as a significant anomaly.
- When approaches , approaches 0. The sample is classified as normal.
Figure 3a illustrates the computational architecture of the iForest algorithm, while Figure 3b demonstrates its isolation mechanism through a two-dimensional feature space example. During the initial partitioning phase, random hyperplanes divide the space into sub-regions. Through iterative execution of this process, anomaly point B—located in a low-density region—is isolated after only two partitioning steps, whereas normal point A—situated within a high-density cluster—requires four partitioning steps for isolation.
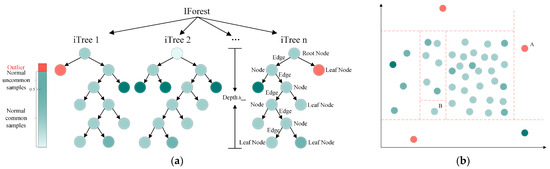
Figure 3.
iForest algorithm principles. (a) Architecture of the iForest algorithm. Randomly selects features to partition the space → recursively constructs isolation trees → outliers exhibit shorter paths (isolated with fewer splits). Normal points require more splits, and path length determines the anomaly score. (b) Demonstration of anomaly isolation in 2D feature space. Outlier B is isolated after only two splits (sparse region); normal point A requires four splits (dense cluster).
3.2.2. Enhanced Isolation Forest Algorithm
The traditional iForest algorithm employs uniform probability random feature selection for spatial partitioning. However, this mechanism exhibits significant limitations in marine-maintenance scenarios. As analyzed earlier, different maintenance data exhibit differentiated dependency characteristics on resource types, with specific resource utilization tendencies showing positive correlation to anomaly risks. When anomalies occur in high-dependency resources, not only does detection probability increase substantially, but the resulting service disruption impact becomes exponentially amplified. To address the mismatch between traditional algorithms’ feature selection mechanisms and operational characteristics in marine-maintenance scenarios, this study leverages the multi-dimensional constraint rule base established in Section 3.1. We propose a W-iForest algorithm that replaces the uniform probability distribution with a risk-prioritized weighted probability distribution. This innovation ensures that features with higher weights are selected for node splitting with probabilities positively correlated to their risk levels. The weight calculation model incorporates three core components: (1) Rule triggering frequency: A statistical analysis of feature-specific anomaly occurrence frequency within the rule base. Higher frequencies indicate stronger anomaly detection sensitivity for the corresponding feature. (2) Rule type weighting: The confidence disparity between physical constraint rules (weight = 0.6) and operational rules (weight = 0.4), as formalized in Equation (1), is mapped to feature importance. For instance, main engine power parameters receive significantly higher initial weights due to their association with high-confidence physical constraints. (3) Expert knowledge adjustment: critical parameters are assigned fixed expert weights (), while non-critical parameters receive , intensifying domain expertise guidance. Integrating these factors, the feature weight is computed via Equation (4):
where represents the total number of features, and denotes the empirical correction coefficient.
Let the feature set of samples be , where each feature corresponds to a weight (). A feature weighting matrix is constructed, and the feature importance metric is derived through normalization as Equation (5):
This weight metric reflects the features’ contribution to anomaly detection. After normalization, directly determines the selection probability () during node splitting, thereby prioritizing high-weight features.
The enhanced algorithm embeds rule-based knowledge into the iForest architecture through the following workflow, as depicted in Figure 4. The algorithm pseudocode is presented in Algorithms A1–A3 in Appendix A.
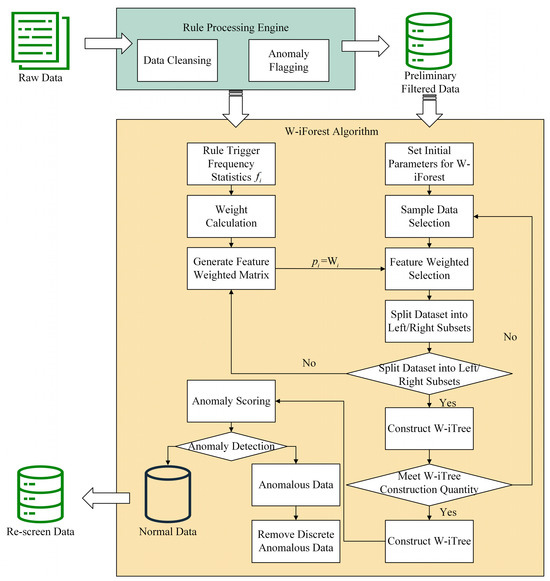
Figure 4.
W-iForest detection process. The yellow box indicates the dynamic weight calculation module, where feature selection probability is determined by normalized weights.
- Step 1: Establish a feature-to-rule trigger mapping matrix based on the rule execution workflow in Section 3.1.3, dynamically updating each feature’s anomaly trigger frequency .
- Step 2: Compute the feature weight matrix using Equation (4) and integrate it into the iForest model.
- Step 3: During the construction of each iTree, the probability of selecting a feature for node splitting is set as , ensuring priority partitioning of critical parameters.
- Step 4: Calculate anomaly scores via weighted path lengths (Equation (3)), then eliminate outliers by combining data validity and missingness criteria. Samples with scores >0.75 and missing data are replaced with zeros.
3.3. Genetic Algorithm–Ant Colony Optimization Collaborative Random Forest Algorithm
The missing data generated during outlier elimination can be categorized into three fundamental patterns based on distribution characteristics: random discrete missing, continuous sequential missing, and fixed-feature-dimensional missing. In practical engineering scenarios, these missing patterns typically coexist in hybrid forms, creating multidimensional composite missing data patterns [26]. Current research on feature-adaptive cleansing methods for such hybrid missing patterns remains insufficient, necessitating the development of an integrated processing framework. As a quintessential nonparametric regression prediction algorithm, RF achieves effective imputation of high-dimensional data through its ensemble decision-tree architecture. However, RF still encounters notable limitations in high-dimensional scenarios: (1) feature space expansion induces suboptimal node splits, (2) exponential growth of hyperparameter combinations, and (3) the greedy node-splitting strategy inadequately captures comprehensive feature interdependencies. To address these challenges in marine-maintenance data imputation, this study proposes a GA-ACO-RF hyperparameter optimization method. The GA method enables global exploration through selection, crossover, and mutation operations, where its population-based search mechanism achieves extensive coverage of the parameter space while mutation operators prevent premature convergence. ACO enhances local exploitation via pheromone-driven positive feedback mechanisms, intensively exploring high-quality solution regions through path reinforcement. Their synergistic integration establishes a two-phase optimization paradigm—“global screening + local refinement”—significantly enhancing the Random Forest algorithm performance.
3.3.1. Random Forest Regression Principles
The RF regression model is an ensemble architecture comprising regression trees, whose core philosophy lies in enhancing generalization capability through averaged predictions from multiple decision trees [47]. As illustrated in Figure 5, after the input dataset undergoes partitioning via the leaf nodes of individual regression trees, the model ultimately outputs the mean of predictions from all regression tree leaf nodes. The detailed implementation workflow of the RF regression model is as follows:
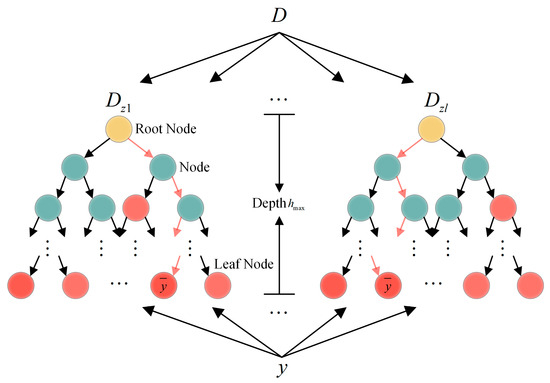
Figure 5.
Schematic diagram of RF regression model prediction principle. represents the structure of a single regression tree, denotes the tree depth, and the final output is the mean prediction of all trees. The yellow dot is the Root Node; the green dot is the Node; the red dot is the Red Node.
- Step 1: Bootstrap Sampling. The Bootstrap resampling method is employed to perform sampling with replacement from the training set . Each iteration extracts a subsample matrix with the same dimensions as the original dataset () to train the -th regression tree (), where denotes the number of features, and represents the number of data samples per feature.
- Step 2: Randomized Feature Space Partitioning. (1) Feature Randomization. At each non-leaf node of every decision tree, features () are randomly selected without replacement from the -dimensional feature space. (2) Optimal Split Point Selection. For each candidate feature, candidate split points are randomly selected to construct an -dimensional split point matrix . (3) Splitting Criterion Calculation. The Classification and Regression Tree (CART) algorithm’s squared error minimization criterion is applied to compute loss function values for all candidate split points.
In Equations (6) and (7), and represent the left and right subsets after splitting via , where and denote the sample counts of the respective subsets. The split point minimizing is selected for node partitioning. When , data are assigned to the left subtree; otherwise, they are assigned to the right subtree, generating new partitioned matrices and .
- Step 3: Decision-Tree Growth Control. The splitting process from Step 2 is repeated for each child node until any termination condition is met: (1) the node depth reaches a predefined maximum, (2) the node sample count falls below a set minimum, or (3) the squared error reduction within the node becomes smaller than a critical threshold.
- Step 4: Forest Ensemble Construction. Steps 1–3 are iteratively executed to generate structurally diverse regression trees. Each tree’s prediction is the mean value of training samples in its leaf node region. The final Random Forest output is the average of all tree predictions as Equation (8).
The convergence properties of RF models effectively suppress overfitting phenomena. Mathematically, it can be defined as an ensemble system comprising base classifiers , where is the input vector and is the output class. The margin function proposed by Breiman is defined as Equation (9).
where denotes the indicator function, and represents the averaging operator. The margin function quantifies the difference in confidence between the correct classification and the strongest incorrect classification. A larger margin value indicates higher classification reliability and reflects the model’s generalization capability.
The generalization error of the ensemble model is defined as Equation (10).
Based on the law of large numbers, Breiman proved that, as the number of decision trees , the generalization error converges to the following:
In Equation (11), denotes the distribution parameters of the decision trees. This convergence theorem demonstrates that, as the number of base classifiers increases, the generalization error asymptotically approaches a deterministic bound, providing a theoretical upper limit for predictive performance. When the ensemble size is sufficiently large, the model’s generalization error stabilizes, ensuring high prediction accuracy for new samples without overfitting to the training data.
The predictive performance of the RF regression model is highly dependent on the configuration of its key parameters [49]. These parameters typically include the number of decision trees (n_estimators), the maximum depth of each tree (max_depth), the minimum number of samples required to split an internal node (min_samples_split), and the minimum number of samples required to be at a leaf node (min_samples_leaf). Previous approaches often relied on empirical rules or default settings struggle to achieve optimal performance. Therefore, this study proposes an intelligent optimization strategy named GA-ACO to automatically identify the optimal combination of these parameters.
3.3.2. Enhanced Random Forest Algorithm
The GA simulates biological evolution to find optimal solutions. It treats potential parameter combinations as “individuals” within a population. This population evolves through cycles of fitness evaluation, the selection of high-performing individuals, crossovers to produce offspring, and low-probability mutation. This process ultimately yields high-performing parameter combinations [50]. Conversely, the ACO algorithm mimics the foraging behavior of ants. Ants deposit “pheromones” along paths while searching for food. Other ants are more likely to follow paths with higher pheromone concentrations, leading the colony to gradually discover the optimal path. In optimization problems, pheromones guide the algorithm to explore promising regions of the solution space [51]. This study integrates the strengths of both algorithms. Firstly, the GA performs a broad global search across the solution space, identifying a pool of promising parameter combinations. Secondly, information about these candidate solutions is transferred to the ACO algorithm. This guides the ACO to conduct a more refined, local search within the most promising regions, enhancing its ability to avoid becoming trapped in local optima [52].
The GA-ACO-RF algorithm workflow is illustrated in Figure 6, with the detailed procedure outlined below.
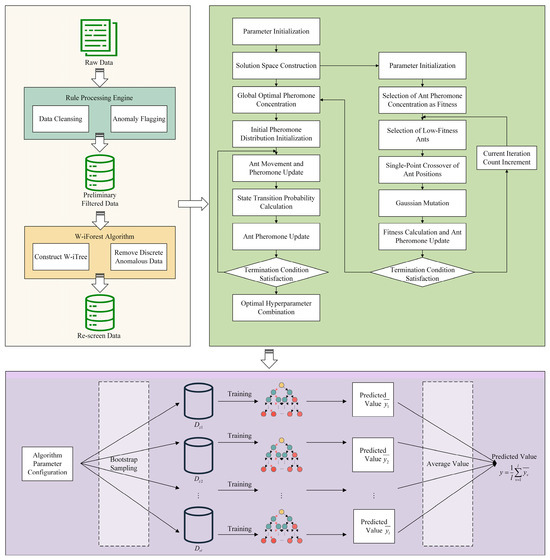
Figure 6.
Flowchart of the GA-ACO-RF algorithm. Yellow boxes represent the rule engine + W-iForest data cleaning steps, green boxes indicate GA global search + ACO local optimization, and pink boxes denote RF regression prediction for data imputation.
- Step 1: Parameter Initialization. Configure algorithm initialization parameters based on optimization problem characteristics. GA parameters: selection strategy, crossover probability , mutation probability , and maximum iterations . ACO parameters: initial pheromone concentration , ant colony size , pheromone evaporation coefficient , and objective function error threshold .
- Step 2: Fitness Function Design. Utilize pheromone concentration as the fitness evaluation metric for the genetic algorithm. The fitness function must satisfy the following: function outputs are non-negative and uniquely mapped, controllable time complexity, and strict alignment with optimization goals. The probability of the -th ant selecting element from set during path selection is determined by Equation (12). After all ants complete their path searches, individual fitness values are computed based on pheromone concentrations.
- Step 3: Solution Space Construction and Dynamic Pheromone Update. Initialize ant search paths and set a dynamic selection rate . Randomly select individuals to construct a candidate solution set. Perform local search optimization using the current optimal solution as the benchmark, conducting neighborhood searches via Equation (13):
The dynamic adjustment rule is defined as follows in Equation (14):
where , and the “+” operator is applied if ; otherwise, “−” is used.
Upon completing path traversal, update pheromone concentrations using Equation (15):
where denotes the pheromone increment on path by the -th ant.
- Step 4: Genetic Operation Optimization. Perform roulette wheel selection based on fitness values, employing a single-point crossover operator to exchange genetic material at randomly selected crossover points within the sorted population. Introduce Gaussian mutation operators to generate new individuals via Equations (16) and (17):
- Step 5: Iterative Convergence Check. Terminate and output the current global optimal solution if the maximum iteration count is reached; otherwise, return to Step 4 for further optimization.
- Step 6: Global Pheromone Update. Initialize the ACO algorithm’s pheromone distribution with the optimal concentrations derived from GA, enhancing population diversity.
- Step 7: State Transition Probability Calculation. Determine the transition probability for the -th ant moving from node to at time using Equation (18):
- Step 8: Iterative Pheromone Update. Dynamically adjust pheromone concentrations per Step 3 rules, establishing a positive feedback optimization loop.
- Step 9: Global Optimum Verification. Compare current and historical optimal solutions. Terminate if convergence criteria are satisfied; otherwise, repeat Steps 7–8.
- Step 10: Random Forest Model Training. Train the RF model using optimized hyperparameters (n_estimators, max_depth, min_samples_split, min_samples_leaf) with five-fold cross-validation for performance evaluation.
Leveraging ensemble learning principles, the RF regression algorithm is employed to perform joint imputation of missing data across multiple variables. This approach maximizes the preservation of the original data distribution characteristics while ensuring data completeness [53]. When a single feature is missing, the RF treats it as the prediction target and uses other complete features to estimate its value. When multiple features contain missing values simultaneously, the following “sequential imputation” strategy is implemented: The feature with the fewest missing data points is prioritized for imputation, while other missing values are temporarily assigned a placeholder value (e.g., zero). After filling this feature using RF prediction, the dataset is updated. The process then proceeds to impute the next feature with the lowest remaining missing-data rate. This cycle repeats iteratively until all missing values are filled. In the extreme scenario where all features are missing, a simple method (e.g., imputation using historical mean values) is first applied to preliminarily fill 1–2 key features. These preliminary imputed values are then leveraged to restart the RF model for more accurate secondary imputation. The algorithmic implementation is detailed in Algorithm A4 of Appendix A.
3.4. Hybrid Data-Cleansing Framework
In summary, the hybrid data-cleansing framework adopts a three-stage collaborative processing architecture, as illustrated in Figure 7. Stage 1 performs data validation against physical and operational rules, flagging or removing obviously erroneous data points. Stage 2 employs the W-iForest algorithm, enhanced by expert knowledge, to precisely identify and eliminate anomalies in the data. Stage 3 executes GA-ACO-RF missing value imputation, implementing the sequential imputation strategy to address remaining gaps following prior stages. Ultimately, this pipeline outputs a complete, cleansed dataset ready for subsequent analytical use.
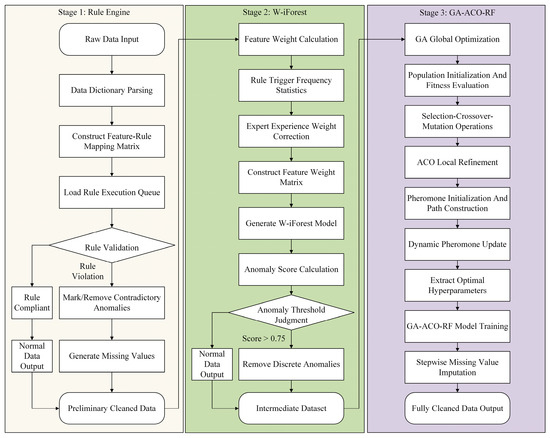
Figure 7.
Flowchart of the three-stage hybrid data-cleansing framework. This diagram illustrates the three-stage hybrid framework for ship-maintenance-cost prediction. The pipeline sequentially processes data through (1) a rule engine system identifying contradiction-type anomalies, (2) the W-iForest algorithm removing outlier-type anomalies, and (3) the GA-ACO-RF model imputing missing values, achieving comprehensive data governance.
4. Case Analysis and Discussion
4.1. Data Sources
A systematic data sampling template was designed (Table A1) to ensure methodological rigor. Through a six-month field investigation, the research team acquired 972 raw ship-maintenance datasets from seven ship repair yards, spanning the period 2010–2023. The sample encompasses primary vessel categories (e.g., bulk carriers, tankers, container ships), demonstrating significant industry representativeness. Following preliminary data processing, invalid records were excluded based on the following criteria: (1) records with over 50% missing values in critical variables, (2) records exhibiting manifest logical anomalies or physical-limit outliers, and (3) records where essential vessel attributes were entirely missing, precluding basic classification or analysis. This process eliminated 299 invalid records, resulting in 673 validated samples for subsequent analysis. Each data entry encompasses 13-dimensional engineering parameters: construction cost, displacement, length, beam, draft depth, maximum speed, main engine power, service duration, maintenance intervals, actual person-hours, damage coefficient, personnel count, and total maintenance cost. Notably, influenced by the completeness of original shipyard records, 10 parameters (excluding damage coefficient, personnel count, and total maintenance cost) exhibit varying degrees of data anomalies and missingness.
To address temporal characteristics in the data, this study employs the Producer Price Index (PPI) published by China’s National Bureau of Statistics (NBS) to perform inflation adjustments on multi-year cost data. This eliminates distortions caused by changing price levels across different years, ensuring cost data comparability. Using 2010 as the base year, a price adjustment model was constructed based on the NBS-released fixed-base PPI index (2010 = 100). First, annual price adjustment coefficients are calculated (Target Year PPI Index/Base Period PPI Index). These coefficients are then applied to deflate nominal maintenance costs across years, ultimately converting them into constant-price costs referenced to 2010. This standardization effectively unifies the valuation basis for multi-year cost data, eliminating inflationary distortions while simultaneously mitigating comparability issues stemming from accounting policy variations.
Through data visualization techniques, trend analysis was conducted on the raw dataset, with the variation patterns of 10 key variables illustrated in Figure 8. Preliminary analysis revealed significant data-quality issues: elevated missing data rates, pronounced noise interference, and excessive overall volatility. To address these challenges, systematic data-cleansing experiments were implemented for the 10 critical variables, with detailed methodological steps elaborated below.
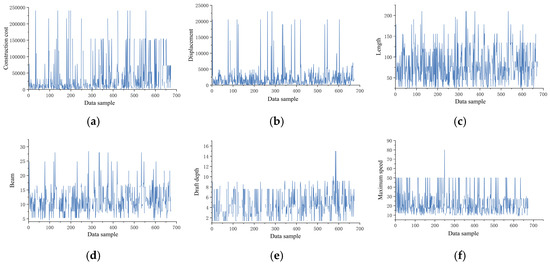
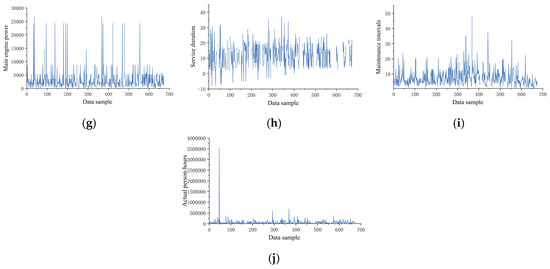
Figure 8.
Original data distribution curves of 10 variables, including construction costs: (a) construction costs, (b) displacement, (c) length, (d) beam, (e) draft depth, (f) maximum speed, (g) main engine power, (h) service duration, (i) maintenance intervals, and (j) actual person-hours.
4.2. Case Study
4.2.1. Outlier Detection
- Step 1: Rule Engine Preliminary Screening. Systematic cleansing and anomaly identification were performed on vessel maintenance data, with visualization results presented in Figure 9. Given the multidimensional characteristics of the dataset, the cleansing process focused on five core validation rules: displacement verification, speed–power relationship analysis, length–beam ratio constraints, person-hour efficiency evaluation, and cost correlation checks. Rule engine monitoring revealed that speed–power anomalies (38.64% triggering frequency) and displacement exceedances (34.86% triggering frequency) constituted the predominant anomaly types. Data provenance analysis identified two primary root causes of anomalies: (1) Missing principal dimension parameters. The absence of critical vessel principal dimensions prevented accurate calculation of displacement threshold ranges. Given that displacement serves as a key input variable for speed–power equations, such data anomalies triggered cascading effects across related parameters. (2) Propulsion system misreporting. Certain shipyards incorrectly reported “main engine power” as single-engine rated power rather than total vessel propulsion power, reflecting a systemic misunderstanding of powerplant specifications. Following multidimensional anomaly determination protocols, data instances violating ≥4 rules were classified as severe anomalies. Statistical analysis revealed 40 severe contradictory anomalies, accounting for 5.94% of the total dataset.
 Figure 9. Data cleaning effectiveness of the rule engine system: (a) ranking of the number of rule violations, (b) abnormal confidence distribution, and (c) severe anomaly distribution.
Figure 9. Data cleaning effectiveness of the rule engine system: (a) ranking of the number of rule violations, (b) abnormal confidence distribution, and (c) severe anomaly distribution. - Step 2: W-iForest Weighted Optimization. The W-iForest algorithm was applied for secondary data cleansing, utilizing a recursive spatial partitioning strategy to identify and eliminate discrete anomalies, thereby constructing a dataset containing missing values (null fields were temporarily populated with zeros). Based on cleansing results from the rule engine and domain expertise, six physical parameters—main engine power, maximum speed, length, beam, displacement, and draft depth—were identified as critical features and assigned an expert experience weight coefficient of 1, while all other parameters received a weight coefficient of 0.
- Step 3: Feature Weight Calculation. The feature weight for each variable is calculated via Equation (4), incorporating three key elements: (a) the frequency of anomaly triggers within the rule repository for each feature, (b) rule-type weighting factors (confidence level: 0.6 for physical constraint rules, 0.4 for operational rules), and (c) expert knowledge correction coefficients. To elucidate the weight allocation mechanism, consider a streamlined dataset example with three features: main engine power, vessel length, and maintenance cycle. Within the rule repository, their anomaly trigger frequencies are 12, 8, and 2 occurrences, respectively. Both engine power and vessel length are physical constraint rules (weight of 0.6), while the maintenance cycle is an operational rule (weight of 0.4), with expert correction coefficients uniformly set at 1.0. Unnormalized weights are calculated as follows: engine power is , vessel length is , and maintenance cycle is . Normalization yields final weights: engine power is , vessel length is , and maintenance cycle is . This demonstrates how physical parameters attain significantly higher weights due to both frequent rule triggering and higher rule-type weighting. Actual feature weight distributions for ship-maintenance data are presented in Table 6.
 Table 6. Feature weight allocation table of W-iForest algorithm.
Table 6. Feature weight allocation table of W-iForest algorithm. - Step 4: Anomaly Detection and Validation. By setting the anomaly threshold >0.75, the W-iForest algorithm detected 67 additional anomalous samples (9.95% of the total dataset), spanning 10 variables, including construction cost and actual person-hours. Post-cleansing via the rule base and W-iForest algorithm, the data distributions of all variables are visualized in Figure 10.
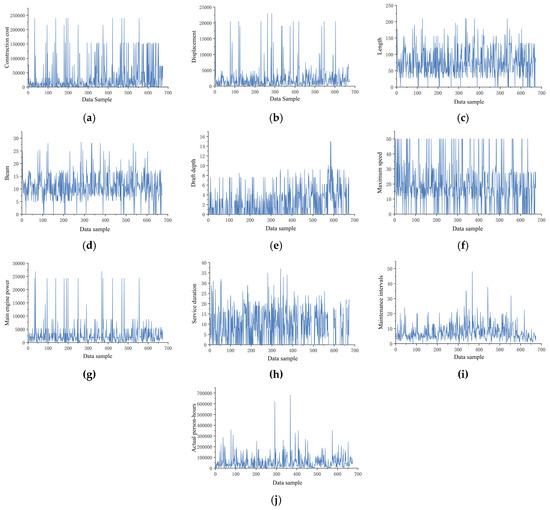 Figure 10. Distribution curves of cleaned data for 10 variables, including construction costs: (a) construction costs, (b) displacement, (c) length, (d) beam, (e) draft depth, (f) maximum speed, (g) main engine power, (h) service duration, (i) maintenance intervals, and (j) actual person-hours.
Figure 10. Distribution curves of cleaned data for 10 variables, including construction costs: (a) construction costs, (b) displacement, (c) length, (d) beam, (e) draft depth, (f) maximum speed, (g) main engine power, (h) service duration, (i) maintenance intervals, and (j) actual person-hours.
4.2.2. Missing Value Imputation
- Step 1: Missing Pattern Analysis. Using Python 3.12 64-bit, the missing values in the two-stage cleansed dataset were visualized. Figure 11 illustrates the quantity and distribution of missing values across variables. The parameters with the highest missing counts are draft depth (310 entries), in-service duration during maintenance (209 entries), construction cost (127 entries), maximum speed (120 entries), and main engine power (58 entries).
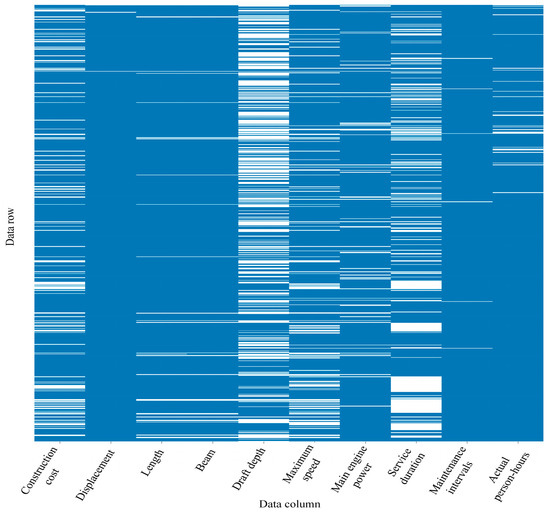 Figure 11. Distribution of missing values for each variable after cleaning. Draft depth (310 entries) and service duration during maintenance (209 entries) are the variables with the most severe missing data.
Figure 11. Distribution of missing values for each variable after cleaning. Draft depth (310 entries) and service duration during maintenance (209 entries) are the variables with the most severe missing data. - Step 2: GA-ACO-RF Collaborative Optimization. This study proposes a GA-ACO-RF imputation method that achieves high-precision missing data compensation through a multi-algorithm collaborative mechanism. GA achieves targeted propagation of high-quality genes through a high crossover probability () while maintaining population diversity with a mutation probability (); ACO employs a dynamic pheromone evaporation rate ( = 0.5) to autonomously adjust search directions, coupled with a heuristic weight factor ( = 2) to strengthen critical feature identification; RF suppresses overfitting via synergistic constraints (max_depth = 11 and min_samples_leaf = 1), while the parameter configuration n_estimators = 191 enhances computational efficiency without compromising model precision.
- Step 3: Hyperparameter Convergence Validation. The optimal parameter combination presented in Table 7 reveals the collaborative mechanism of multiple algorithms. The convergence curve shown in Figure 12 demonstrates that the algorithm reached the convergence threshold at 1029 iterations. At this point, the obtained hyperparameter combination achieves optimal imputation accuracy for the model.
 Table 7. Hyperparameter optimization results of GA-ACO-RF algorithm.
Table 7. Hyperparameter optimization results of GA-ACO-RF algorithm.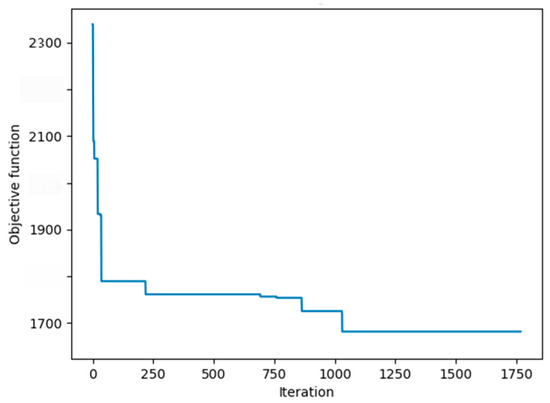 Figure 12. Convergence curve of GA-ACO-RF hyperparameter optimization. The convergence threshold was reached at 1029 iterations.
Figure 12. Convergence curve of GA-ACO-RF hyperparameter optimization. The convergence threshold was reached at 1029 iterations. - Step 4. Imputation Effectiveness and Limitations. Empirical analysis reveals that when fields with missing rates exceeding 25% (e.g., draft depth) and their correlated variables exhibit concurrent data gaps, the loss of nonlinear correlations among features compromises model inference capabilities. For imputing maintenance records of large vessels with a displacement of >20,000 tons, prediction errors significantly increase due to insufficient abnormal-condition samples, necessitating secondary validation. Post-imputation data distributions across all variables are visualized in Figure 13.
 Figure 13. Distribution curves of imputed data for 10 variables including construction costs: (a) construction costs, (b) displacement, (c) length, (d) beam, (e) draft depth, (f) maximum speed, (g) main engine power, (h) service duration, (i) maintenance intervals, and (j) actual person-hours.
Figure 13. Distribution curves of imputed data for 10 variables including construction costs: (a) construction costs, (b) displacement, (c) length, (d) beam, (e) draft depth, (f) maximum speed, (g) main engine power, (h) service duration, (i) maintenance intervals, and (j) actual person-hours.
4.3. Discussion and Analysis
This study selects total maintenance cost as the research focus due to its superior data completeness compared to other metrics. The effectiveness of the proposed methodology is validated through RF regression modeling. The experimental design employs a dual-validation framework comprising the following: (1) A comparative experiment, contrasting the predictive efficacy of traditional data-cleansing methods with the proposed innovative approach. (2) An ablation experiment, quantitatively evaluating each component’s contribution to maintenance-cost prediction by progressively removing elements of the data-cleansing framework. Employing a chronologically ordered data-partitioning strategy based on actual maintenance occurrence timestamps, with the first 80% of temporal data serving as the training set for model construction, while the remaining 20% is reserved as the test set for predictive performance validation. To comprehensively evaluate model performance, four primary metrics are proposed. Among these, RMSE and MAE serve as absolute error metrics where lower values denote superior predictive performance. MAPE achieves cross-scale comparability via relativization, while R2 statistically reveals model goodness-of-fit. The mathematical formulations for each metric are provided in Equations (19)–(22).
where denotes the total number of samples, represents the actual value, indicates the predicted value, and signifies the sample mean.
4.3.1. Comparative Analysis of Outlier Mining Algorithms
To address the quantitative evaluation requirements for multi-dimensional anomaly detection efficacy, this study employs the Rule Engine + W-iForest method as the core experimental group. Comparative analysis is conducted against six benchmark methods: Pure Rule Engine, Conventional iForest, DBSCAN clustering, 3 criterion, PCA-iForest hybrid method, and Z-score algorithm. Experimental evaluation utilizes five core metrics: number of detected anomalies, precision, recall, F1-score, and false positive rate. The assessment specifically examined each method’s anomaly identification sensitivity and discrimination accuracy in complex data scenarios, with particular focus on performance gains achieved by enhancing the rule engine with W-iForest. Comparative results are presented in Table 8.

Table 8.
Performance metrics comparison of outlier mining algorithms.
As evidenced in the table, the Rule Engine + W-iForest approach achieves optimal performance across all four core evaluation metrics, demonstrating significant advantages over the Pure Rule Engine method. The number of detected anomalies increased from 40 to 107, while recall improved from 60.0% to 95.3%, indicating enhanced capability to identify diverse and complex anomaly patterns while effectively overcoming the recall limitation inherent in pure rule-based systems. The F1-score shows a substantial 23.2 percentage-point improvement (from 70.6% to 93.8%), reflecting markedly enhanced overall detection capability. Crucially, precision increased from 85.0% to 92.5% while the false positive rate decreased from 15.0% to 7.5%, demonstrating that W-iForest not only strengthens anomaly capture capacity but also improves discrimination accuracy. Conventional iForest and PCA-iForest show sensitivity to high-dimensional data yet demonstrate elevated false detection rates without domain knowledge integration. DBSCAN and 3 Criterion deliver suboptimal performance (recall < 60%) in non-uniformly distributed data. An RF regression model was constructed using the cleansed sample dataset. The predicted values for the test set are visualized in Figure 14, while Table 9 quantitatively demonstrates the impact of different outlier processing algorithms on the final predictive model through four key evaluation metrics.
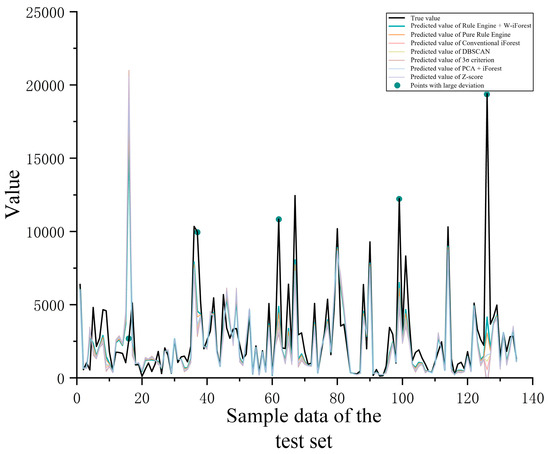
Figure 14.
Comparison of maintenance-cost predictions by different outlier mining algorithms.

Table 9.
Comparison of maintenance-cost prediction errors using different outlier mining algorithms.
Experimental data analysis demonstrates that the integrated Rule Engine + W-iForest approach significantly enhances predictive performance for total maintenance costs. Compared to the Pure Rule Engine method, this approach achieves substantial error reduction: the RMSE decreased from 2380.2 to 2253.5, MAE from 1145.3 to 1068.7, and MAPE from 45.2% to 41.1%. Crucially, the R2 increased from 0.3865 to 0.4233, indicating improved explanatory power for maintenance-cost variations. This superiority originates from its dual-stage processing mechanism: an initial screening of explicit anomalies through domain-specific rule bases, coupled with the capture of complex implicit noise via the adaptive-weight iForest algorithm. This framework effectively eliminates data contamination while maximally preserving critical feature information, thereby optimizing input quality for regression modeling. Cross-comparative analysis reveals that the Pure Rule Engine approach, which is reliant on expert-defined rigid constraints, demonstrates precise handling of known anomaly patterns but exhibits inadequate adaptability to nonlinear-correlated implicit noise. Traditional unsupervised methods (iForest, DBSCAN) suffer from premature deletion of valid samples or residual noise contamination due to the absence of physical mechanism guidance. Although the integrated PCA-iForest method alleviates the curse of dimensionality through feature reduction, its failure to incorporate domain knowledge constraints results in a lower R2 value (0.3278) compared to the hybrid method. Notably, the current optimal model’s R2 value (0.4233) indicates that the Random Forest regressor can explain approximately 42% of cost variation. While this outperforms benchmark methods, significant room for optimization remains.
While the prediction curves of all models in the figure demonstrate trend consistency, significant predictive deviations occur at six key inflection points. This phenomenon may stem from two primary causes: (1) inflection point samples exhibit extreme-value attributes or anomalous distribution characteristics in the original dataset, leading to differential outlier handling mechanisms across algorithms; and (2) complex collinearity relationships among multidimensional features potentially cause misidentification of key factors during feature screening phases.
4.3.2. Comparative Analysis of Missing Value Imputation Algorithms
To validate the data imputation performance of the GA-ACO-RF algorithm, this study designs the following comparative experiment. Using the dataset cleansed by the rule engine plus W-iForest method as the benchmark, six missing value processing approaches are implemented: mean imputation, KNN imputation, Multiple Imputation by Chained Equations (MICE), Conventional RF imputation, GA-RF imputation, and ACO-RF imputation. Within a unified evaluation framework, this study constructs an RF regression predictive model to analyze total maintenance costs. Through comparative analysis of the deviation between predicted values and ground truth (as detailed in Table 10) and predictive curve fitting performance (illustrated in Figure 15), a comprehensive assessment of different imputation algorithms’ efficacy is conducted.

Table 10.
Prediction accuracy comparison of maintenance costs under different imputation algorithms.
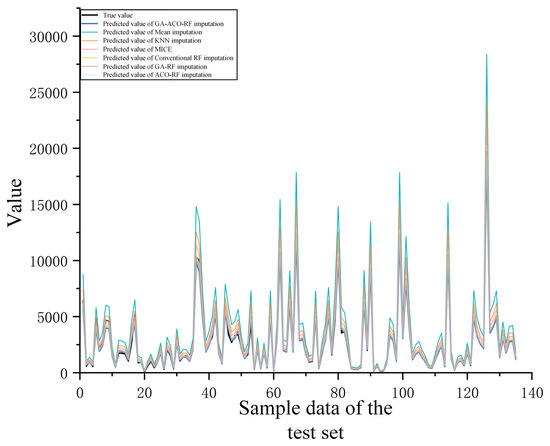
Figure 15.
Comparison of maintenance-cost predictions using different missing value imputation algorithms.
Experimental data indicate that compared to traditional imputation methods and enhanced RF imputation algorithms, the GA-ACO-RF algorithm achieves a closer approximation to ground truth values, demonstrating significant advantages in both precision and stability. Mean and KNN imputation neglect nonlinear feature correlations, while MICE multiple imputation is constrained by its linear assumptions, limiting its applicability in complex nonlinear datasets. Experimental results demonstrate that GA-ACO-RF achieves an RMSE of 1667.3, representing an approximately 29.1% error reduction compared to mean imputation. With R2 = 0.6714, the algorithm explains approximately 67% of maintenance-cost variance, significantly outperforming mean imputation (41%) and conventional RF imputation (63%). Although its MAPE of 28.3% shows a 12–15 percentage point improvement over the control groups, the absolute value remains elevated. This phenomenon may originate from the long-tailed distribution characteristics of maintenance costs and multicollinearity effects within the 12-dimensional feature space that impact prediction accuracy.
Based on the Python 3.12 64-bit simulation platform, RMSE curve simulations are conducted for four models—conventional RF, GA-RF, ACO-RF, and GA-ACO-RF—under equally configured structural parameters. As demonstrated in Figure 16, distinct convergence patterns emerge across the four models due to their unique optimization strategies. The conventional RF model maintains a static RMSE of 1850.2 throughout the process, reflecting its inherent limitation due to the absence of iterative optimization mechanisms. In contrast, the GA-RF model gradually converges to 1780.9 after approximately 793 iterations through global search operations, while the ACO-RF model achieves faster convergence to 1735.6 within 611 iterations by leveraging local path optimization. Most notably, the hybrid GA-ACO-RF model synthesizes both approaches, ultimately attaining the optimal RMSE of 1667.3 at 1029 iterations through synergistic dual-optimization mechanisms. From an algorithmic mechanism perspective, traditional RF captures data nonlinearities through feature importance evaluation (R2 = 0.6320), yet its hyperparameter sensitivity frequently induces local optima. The GA-RF approach optimizes feature subsets and tree structures via genetic selection, crossover, and mutation operations, reducing RMSE by 4.2% compared to conventional RF. ACO-RF employs a pheromone-guided path search strategy to dynamically adjust node-splitting parameters, effectively mitigating overfitting. The GA-ACO-RF framework synergizes the global exploration capabilities of GA with the local exploitation advantages of ACO. Through optimized population initialization and adaptive pheromone updating mechanisms, it achieves superior imputation accuracy. Notably, while the hybrid optimization strategy enhances performance, it increases computational complexity by approximately 40% compared to single-algorithm approaches. Implementation thus requires careful assessment of time cost acceptability within engineering decision-making cycles.
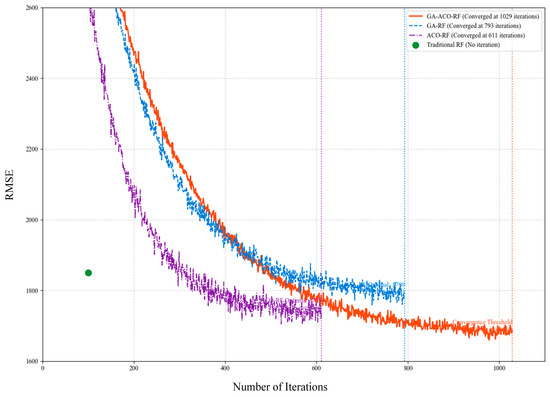
Figure 16.
Comparison of convergence curves for different RF algorithms.
4.3.3. Comparative Analysis of Data-Cleansing Algorithms
To validate the performance of the proposed hybrid data-cleansing framework integrating Rule Engine, W-iForest, and GA-ACO-RF algorithms, comparative experiments are conducted. Using the unprocessed raw dataset as the baseline, four conventional methods are implemented for data cleansing: Conventional iForest, Conventional RF, the K-means Algorithm, and the Mutual Information Algorithm. Subsequently, RF regression models are constructed to predict total maintenance costs using datasets cleansed by each respective method. A comprehensive comparative assessment of data-cleansing algorithm performance is achieved by evaluating key metrics between predicted and actual values. Quantitative results of these primary evaluation metrics are presented in Table 11, while Figure 17 visually contrasts maintenance-cost predictions generated from differently cleansed datasets.

Table 11.
Prediction accuracy comparison of maintenance costs under different data cleaning algorithms.
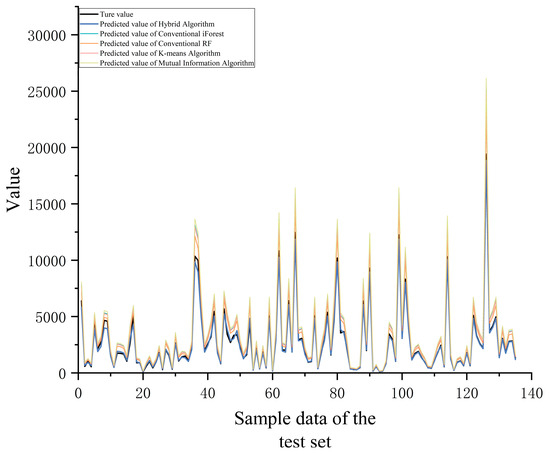
Figure 17.
Comparison of maintenance-cost predictions using different data cleaning algorithms.
The proposed hybrid algorithm comprehensively outperforms the optimal traditional methods across key metrics for maintenance-cost prediction. It achieves an RMSE of 1667.3 and an MAE of 697.9, representing reductions of 19.0% and 16.3%, respectively, compared to traditional approaches. Simultaneously, the algorithm attains a MAPE of 28.3% and an R2 of 0.6714, surpassing all benchmark methods. A particularly notable achievement is the algorithm’s 88.2% physical constraint compliance rate, ensuring data quality at the source level. This advantage directly correlates with enhanced prediction accuracy: the hybrid algorithm achieves a 27.8% lower RMSE compared to baseline methods like Mutual Information. Moreover, its MAPE is significantly lower than the >35% typically seen in conventional algorithms, while its R2 is markedly higher than the <0.6 commonly achieved by standard methods. In contrast, conventional methods exhibit notable limitations: iForest and RF demonstrate limited capability to incorporate complex domain rules, K-means shows poor scalability to high-dimensional anomalies, while Mutual Information lacks error correction functionality. Experiments confirm that our hybrid framework significantly enhances prediction accuracy while preserving data distribution integrity through the integration of rule-based constraints and intelligent algorithms. This approach delivers an efficient and robust solution for industrial data cleansing.
4.3.4. Ablation Study
To quantitatively assess the contribution of core components in the data-cleansing pipeline, this study designs a three-tier ablation experiment: (1) Base System: raw dataset; (2) Base + Anomaly Detection (AD): raw data cleansed by Rule Engine + W-iForest; and (3) Full System: AD enhanced with GA-ACO-RF imputation. Total maintenance costs are predicted using RF regression models. Table 12 documents the performance evolution across progressive component integration, while Figure 18 provides visual evidence of error distributions.

Table 12.
Comparison of ablation experiment results of data cleaning components.
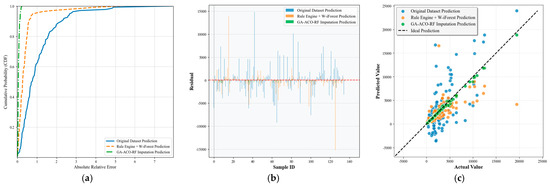
Figure 18.
Results of ablation experiments: (a) CDF curve graph, (b) residual comparison chart, and (c) scatter plot of predicted values.
As presented in the table, denotes the performance improvement magnitude of each component relative to the preceding stage. For both key metrics (RMSE and MAE), the Base System exhibits the poorest performance. Significant enhancements are achieved upon introducing the AD module and Full System. The ablation study further quantifies individual module contributions: (1) Removing AD causes severe performance degradation. RMSE surges from 1667.3 to 3371.1 (a 102.4% increase), while MAE rises by 234.7%. This conclusively demonstrates AD’s powerful noise-filtering capability. (2) The absence of the imputation component increases RMSE from 1667.3 to 2253.5 (35.1% rise) and MAE by 53.2%, confirming its critical role in ensuring data quality.
Error statistical analysis via the Cumulative Distribution Function (CDF), as shown in Figure 18a, further validates these findings. The CDF curve of GA-ACO-RF-imputed data exhibits a characteristic optimal profile, accumulating 90% of errors within the 0.2 interval on the x-axis. This validates the algorithm’s dual advantages in error control scope and distribution concentration. While the rule engine plus W-iForest-cleansed data maintains left-skewed characteristics, its box-plot distribution spanning the 0.2–0.75 interval expands by 37% compared to imputed data. The original dataset’s CDF curve demonstrates the slowest ascent and widest error range, exhibiting a distinct right-skewed distribution that indicates prediction errors dispersing across a broad interval. Results from Figure 18b,c demonstrate that the original dataset’s prediction residuals exhibit significant heteroscedasticity with high dispersion, reflecting the baseline model’s sensitivity to outliers and nonlinear relationships. After rule engine plus W-iForest cleansing, the residual range shows effective reduction but maintains a non-zero mean shift, revealing limitations in systemic bias correction through data-quality improvement. The GA-ACO-RF algorithm’s residuals converge markedly, with residual-fitted value scatter points evenly distributed along the zero line, validating the synergistic effects of hybrid optimization in feature space reconstruction and enhanced model generalization.
Experimental results demonstrate that the joint optimization of the W-iForest anomaly detection framework and GA-ACO-RF adaptive imputation mechanism elevates the model’s coefficient of determination on the test set by 37.3%. This dual enhancement in prediction accuracy and stability establishes a reliable data preprocessing paradigm for maintenance-cost forecasting of complex engineering equipment.
5. Conclusions
This study addresses the complexity of multimodal anomaly data governance in ship-maintenance-cost prediction by proposing a three-phase hybrid data-cleansing framework integrating physical constraints and intelligent optimization. Through rule base-driven pre-stage filtering, W-iForest algorithm-based anomaly detection and elimination, and GA-ACO-RF algorithm-based missing value compensation, synergistic governance of contradictory, discrete, and missing anomalies is achieved. Experimental results demonstrate that this method significantly enhances data quality in ship-maintenance datasets, achieving an 88.2% physical compliance rate and reducing the prediction model’s RMSE by 25% compared to conventional approaches, validating its efficacy and application potential in complex engineering scenarios. By significantly enhancing data quality and prediction accuracy, this framework produces more reliable maintenance-cost estimates. This enables fleet managers to formulate maintenance budgets with greater accuracy, effectively preventing resource wastage or budget overruns, thereby substantially reducing total lifecycle operation and maintenance costs. The primary mathematical symbols used in this paper and their definitions are detailed in Table A2 of Appendix C.
Notwithstanding these achievements, the study exhibits the following limitations: (1) Computational efficiency and scalability challenges. Multidimensional features in ship-maintenance data escalate computational complexity, particularly during GA-ACO-RF hyperparameter optimization, where convergence requires 1029 iterations; hence, prolonged iteration time impedes real-time decision-making. While validated on medium-scale datasets, the framework’s computational efficiency and feasibility in high-throughput industrial big data environments remain unverified. When processing larger datasets, the current implementation may encounter significant performance bottlenecks. Future work should explore distributed computing architectures, incremental learning strategies, or algorithmic simplifications to enhance scalability. (2) Adaptability to extreme missing data scenarios and domain generalization limitations. When missing rates exceed 25% for critical parameters (e.g., displacement, prime mover power), imputation errors increase substantially due to severed nonlinear inter-feature correlations, necessitating secondary manual verification. Furthermore, the method’s effectiveness relies heavily on modeling domain-specific rules and feature relationships within ship maintenance. This strong dependence on embedded domain knowledge significantly increases the difficulty and cost of adapting the framework to other industries or scenarios with divergent data characteristics. Enhancing its generalizability requires both validation across more diverse domains/datasets and the development of more universal rule representation/auto-adaptation mechanisms. (3) Model interpretability and potential expert bias. The RF regression’s coefficient of determination (R2 = 0.6714) indicates approximately 33% unexplained cost variance, requiring integration with deep-learning methods to excavate latent high-dimensional feature relationships. Simultaneously, incorporating expert knowledge to define feature weights within the W-iForest algorithm may introduce subjective expert preferences or domain-specific cognitive biases. This could potentially compromise the objectivity of model outcomes and their consistency across diverse operational scenarios.
Building upon this study’s achievements and limitations, future work will focus on the following directions to enhance framework capabilities and expand application boundaries: (1) Integrating deep learning to advance modeling capacity. Implement Transformer architectures to analyze temporal sensor data, enabling deeper exploration of complex nonlinear relationships and latent patterns within high-dimensional features. This integration aims to enhance prediction accuracy and feature interpretability. Concurrently, investigate synthetic data generation via VAE or GAN methods to expand training samples while ensuring privacy preservation. Such approaches will particularly strengthen model robustness in data-scarce scenarios, including extreme missing data conditions and rare failure modes. (2) Enhancing real-time processing capabilities and streaming data support. Develop a streaming data cleansing and prediction architecture to enable low-latency anomaly detection, missing value imputation, and preliminary cost estimation for real-time sensor monitoring data and online work order entries. This framework will address dynamic decision-making requirements. Concurrently, investigate lightweight models, online learning strategies, and incremental hyperparameter optimization methods to substantially reduce execution times for computationally intensive modules like GA-ACO-RF. These enhancements will significantly improve the framework’s practicality in resource-constrained edge devices or industrial settings requiring rapid response. (3) Automating domain rule selection and knowledge discovery. Leverage association rule mining and causal discovery algorithms to autonomously learn domain-specific constraints and feature relationships from cleansed data, minimizing dependence on manually defined expert rules. This approach enhances the framework’s adaptability and cross-domain transfer effectiveness. Furthermore, investigate meta-learning algorithms to enable automatic selection and configuration of optimal physical constraint sets and feature weight initialization strategies based on preliminary characteristics of new domain data. This capability will accelerate framework deployment in novel industries or application scenarios.
Author Contributions
Software, J.L. and Y.W.; data curation, K.L. and L.X.; Writing—original draft preparation, C.Z.; writing—review and editing, S.S. and L.X.; visualization, Y.W. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Foundation of China under Grant No. 19CGL073.
Data Availability Statement
The ship-maintenance datasets supporting this study were collected through six-month field investigations at multiple ship-maintenance facilities under non-disclosure agreements. While these data contain proprietary technical specifications and operational parameters, anonymized subsets may be made available upon formal request to the corresponding author, subject to approval by the participating maintenance contractors and compliance with institutional data governance protocols.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| W-iForest | Feature-Weighted Isolation Forest Algorithm |
| GA-ACO-RF | Genetic Algorithm–Ant Colony Optimization Collaborative Random Forest |
| RPD | Relative Percentage Difference |
| iForest | Isolation Forest |
| LOF | Local Outlier Factor |
| GMM | Gaussian Mixture Model |
| GBDT | Gradient Boosting Decision Tree |
| GA | Genetic Algorithms |
| ACO | Ant Colony Optimization |
| RF | Random Forest |
| IQR | Interquartile Range |
| GNNs | Graph Neural Networks |
| TSR | Tip-speed Ratio |
| SVM | Support Vector Machines |
| LSTM | Long Short-Term Memory |
| AEs | Autoencoders |
| SDAEs | Stacked Denoising Autoencoders |
| MI | Multiple Imputation |
| MCMC | Markov Chain Monte Carlo |
| MCM | Matrix Completion Methods |
| MAR | Missing at Random |
| MNAR | Missing Not at Random |
| GANs | Generative Adversarial Networks |
| VAEs | Variational Autoencoders |
| PCA | Principal Component Analysis |
| t-SNE | t-Distributed Stochastic Neighbor Embedding |
| CART | Classification and Regression Tree |
| PPI | Producer Price Index |
| MICE | Multiple Imputation by Chained Equations |
| CDF | Cumulative Distribution Function |
| AD | Anomaly Detection |
Appendix A
| Algorithm A1. iForest |
| Inputs:—feature weight matrix |
| Output: a set ofiTrees |
| 1: initialize Forest |
| 2: set height limit |
| 3: for to do |
| 4: ←sample |
| 5. Forest←ForestiTree |
| 6. end for |
| 7. return Forest |
| Algorithm A2. iTree |
| Inputs:—height limit |
| Output: an iTree |
| 1: if or then |
| 2: return LeafNode |
| 3: else |
| 4: # select feature based on weight distribution |
| 5. randomly select a feature from dimensions with probability distribution |
| 6. # randomly select split point within the range of feature |
| 7. uniformly sample between |
| 8. # split data into left/right subtrees |
| 9. |
| 10. |
| 11. return InternalNode |
| 12. end if |
| Algorithm A3. PathLength |
| Inputs:—an iTree |
| Output:—path length |
| 1: |
| 2: while tree is not a LeafNode |
| 3. . SplitFeature |
| 4. . SplitValue |
| 5. if |
| 6. |
| 7. else |
| 8. |
| 9. |
| 10. # adjust path length using harmonic number (Equation (2) in the document) |
| 11. |
| 12. return |
| 13. end if |
| Algorithm A4. GA-ACO-RF Imputation |
| Inputs: |
| features) |
| : RF hyperparameter search space (n_estimators, max_depth, ...) |
| genetic algorithm parameters (population size, generations, crossover rate, mutation rate |
| ant colony parameters (ants, pheromone decay |
| Output: |
| : imputed complete dataset |
| optimized RF hyperparameters |
| 1: initialization |
| 2: encode RF hyperparameters into chromosome structures (real-value encoding) |
| 3: generate initial GA population via random sampling |
| 4: GA Global Optimization Phase |
| 5. for to do |
| 6. fitness evaluation: |
| 7. for each chromosome in : |
| 8. train RF model with k-fold cross-validation |
| 9. compute fitness as on validation set |
| 10. selection: |
| 11. perform roulette wheel selection to retain elite individuals |
| 12. crossover: |
| 13. apply single-point crossover to generate offspring (probability ) |
| 14. Mutation: 15. introduce Gaussian noise to chromosomes (probability ) |
| 16. ACO Local Refinement Phase: |
| 17. map hyperparameter space to ACO path nodes |
| 18. initialize pheromone proportional to GA fitness values |
| 19. for each ant to do |
| 20. Path Construction: |
| 21. select hyperparameters via probabilistic rule (Equation (18)) |
| 22. Pheromone Update: |
| 23. update based on imputation performance (Equation (15)) |
| 24. Adaptive Reset: |
| 25. periodically reinitialize stagnant paths to avoid local optima |
| 26. Imputation with Optimized RF: |
| 27. extract optimal hyperparameters from ACO |
| 28. train GA-ACO-RF model |
| 29. for each missing feature in do |
| 30. set as target, train RF regressor on complete features |
| 31. predict missing values and update |
| 32. iterate until convergence (max iterations or error threshold) |
| 33. return , |
Appendix B

Table A1.
Sample table for ship-maintenance-cost data collection.
Table A1.
Sample table for ship-maintenance-cost data collection.
| Sample Table for Ship-Maintenance-Cost Data Collection | |||
|---|---|---|---|
| (1) Basic Vessel Info | |||
| Vessel Type | XXX | Vessel Model | XXX |
| Commissioning Date | XXX | Vessel Age (Years) | XXX |
| (2) Vessel Attributes | |||
| Construction Cost (CNY 10,000) | XXX | Displacement (Ton) | XXX |
| Length (m) | XXX | Beam (m) | XXX |
| Draft Depth (m) | XXX | Maximum Speed (Knots) | XXX |
| Propulsion System Type | XXX | Main Engine Power (KW) | XXX |
| (3) Contractor Details | |||
| Contractor Name | XXX | Frontline Technicians Count | XXX |
| Frontline Workforce Ratio (%) | XXX | Total Task Hours (Hours) | XXX |
| Fixed Assets Original Value (CNY 10,000 ) | XXX | Operating Revenue (CNY 10,000) | XXX |
| Operating Profit (CNY 10,000) | XXX | - | - |
| (4) Maintenance Costs | |||
| Direct Materials Cost (CNY 10,000) | XXX | Direct Labor Cost (CNY 10,000) | XXX |
| Manufacturing Overhead (CNY 10,000) | XXX | Specialized Expenses (CNY 10,000) | XXX |
| Period Costs (CNY 10,000) | XXX | Total Maintenance Cost (CNY 10,000) | XXX |
Appendix C

Table A2.
Symbol comparison table.
Table A2.
Symbol comparison table.
| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| Displacement (ton) | Expert experience weight | ||
| Length of ship (m) | Experience correction coefficient | ||
| Breadth of ship (m) | Standardized path length of iForest | ||
| Draft of ship (m) | Harmonic number of iForest | ||
| Main engine power (kW) | Euler’s constant | ||
| Maximum speed (kn) | Anomaly score of iForest | ||
| Ship type coefficient | Expected value of path length of sample in multiple iTrees | ||
| , | Minimum and maximum values of length–breadth ratio | Squared error loss function of CART algorithm | |
| Total maintenance person-hours (h) | , | Number of samples in left and right subsets after RF splitting | |
| Maintenance days | , | Means of left and right subsets after RF splitting | |
| Number of maintenance participants | , | Crossover rate and mutation rate of GA | |
| Actual replacement cycle | Maximum number of iterations of GA | ||
| Design life | Pheromone concentration of node j in ACO | ||
| Maintenance cost | Ant colony size of ACO | ||
| Construction cost | Pheromone evaporation coefficient of ACO | ||
| Safety coefficient for spare parts replacement | Pheromone increment of the k-th ant on path j | ||
| Damage coefficient of maintenance cost | Heuristic information of path i→j | ||
| Service life (years) | Transition probability from node i to node j for ant k at time t | ||
| Weight of rule i | Set of unexplored nodes accessible to ant k at node i | ||
| Weight of feature i | , | Weights of pheromone and heuristic factors in ACO | |
| Trigger frequency of rule |
References
- Golovan, A.; Mateichyk, V.; Gritsuk, I.; Lavrov, A.; Smieszek, M.; Honcharuk, I.; Volska, O. Enhancing Information Exchange in Ship Maintenance through Digital Twins and IoT: A Comprehensive Framework. Computers 2024, 13, 261. [Google Scholar] [CrossRef]
- Zhang, K.; Xi, P.; Liang, X.; Li, X. Decision-making Method and Application of Ship Maintenance Resource Allocation Based on ε-EGA Multi-criteria Adjustment. Oper. Res. Manag. Sci. 2023, 32, 53–60. [Google Scholar] [CrossRef]
- Ji, R.; Hou, H.; Sheng, G.; Zhang, L.; Shu, B.; Jiang, X. Data Quality Improvement Method for Power Equipment Condition Based on Stacked Denoising Autoencoders Improved by Particle Swarm Optimization. J. Shanghai Jiao Tong Univ. 2024. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.; Li, G.; Yao, B.; Wu, J. Short-term wind power prediction based on multidimensional data cleaning and feature reconfiguration. Appl. Energy 2021, 292, 116851. [Google Scholar] [CrossRef]
- Wang, D.; Li, S.; Fu, X. Short-Term Power Load Forecasting Based on Secondary Cleaning and CNN-BILSTM-Attention. Energies 2024, 17, 4142. [Google Scholar] [CrossRef]
- Shen, X.; Fu, X.; Zhou, C. A Combined Algorithm for Cleaning Abnormal Data of Wind Turbine Power Curve Based on Change Point Grouping Algorithm and Quartile Algorithm. IEEE Trans. Sustain. Energy 2019, 10, 46–54. [Google Scholar] [CrossRef]
- Brandis, V.A.; Menges, D.; Rasheed, A. Multi-Target Tracking for Autonomous Surface Vessels Using LiDAR and AIS Data Integration. Appl. Ocean Res. 2025, 154, 104348. [Google Scholar] [CrossRef]
- Deng, Y.; Li, Y.; Zhu, H.; Fan, S. Displacement Values Calculation Method for Ship Multi-Support Shafting Based on Transfer Learning. J. Mar. Sci. Eng. 2024, 12, 36. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, X.; Cui, W. A LOF-IDW based data cleaning method for quality assessment in intelligent com-paction of soils. Transp. Geotech. 2023, 42, 101101. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, X.; Wu, J.; Hu, S.; Wang, Y. A novel solar irradiance calculation method for distributed photo-voltaic power plants based on K-dimension tree and combined CNN-LSTM method. Comput. Electr. Eng. 2025, 122, 109990. [Google Scholar] [CrossRef]
- Song, C.; Cui, J.; Cui, Y.; Zhang, S.; Wu, C.; Qin, X.; Wu, Q.; Chi, S.; Yang, M.; Liu, J.; et al. Inte-grated STL-DBSCAN Algorithm for Online Hydrological and Water Quality Monitoring Data Cleaning. Environ. Ment. Model. Softw. 2025, 183, 106262. [Google Scholar] [CrossRef]
- Han, B.; Xie, H.; Shan, Y.; Liu, R.; Cao, S. Characteristic Curve Fitting Method of Wind Speed and Wind Tur-bine Output Based on Abnormal Data Cleaning. J. Phys. Conf. Ser. 2022, 2185, 012085. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, D.; Zhang, Y.; Wu, M. Configuration Type Identification Integrating Multi-Granularity Code Features and Isolation Forest Algorithm. Comput. Eng. Appl. 2024. Available online: https://link.cnki.net/urlid/11.2127.TP.20241120.1628.006 (accessed on 16 May 2025).
- Shen, L.; He, X.; Liu, M.; Qin, R.; Guo, C.; Meng, X.; Duan, R. A Flexible Ensemble Algorithm for Big Data Cleaning of PMUs. Front. Energy Res. 2021, 9, 695057. [Google Scholar] [CrossRef]
- Si, S.; Xiong, W.; Che, X. Data Quality Analysis and Improvement: A Case Study of a Bus Transportation System. Appl. Sci. 2023, 13, 11020. [Google Scholar] [CrossRef]
- Yin, Q.; Zhao, G. A Study on Data Cleaning for Energy Efficiency of Ships. J. Transp. Inf. Saf. 2017, 35, 68–73. [Google Scholar] [CrossRef]
- Feng, Z.; Zhu, S.; Zhao, Z.; Sun, M.; Dong, M.; Song, D. Comparative Study on Detection Methods of Wind Power Abnormal Data. Adv. Technol. Electr. Eng. Energy 2021, 40, 55–61. [Google Scholar] [CrossRef]
- Lai, G.; Liao, L.; Zhang, L.; Li, T. Wind Speed Power Data Cleaning Method for Wind Turbines Based on Fan Characteristics and Isolated Forests. J. Phys. Conf. Ser. 2023, 2427, 12001. [Google Scholar] [CrossRef]
- Li, L.; Liang, Y.; Lin, N.; Yan, J.; Meng, H.; Liu, Y. Data Cleaning Method Considering Temporal and Spatial Cor-relation for Measured Wind Speed of Wind Turbines. Acta Energiae Solaris Sin. 2024, 45, 461–469. [Google Scholar] [CrossRef]
- Huang, G.; Long, Z.; Zhu, Z.; Cheng, W. Monitoring Data Cleaning for Water Distribution System Based on Support Vector Machine. Water Wastewater Eng. 2022, 14, 124–129. [Google Scholar] [CrossRef]
- Mei, Y.; Li, X.; Hu, Z.; Yao, H.; Liu, D. Identification and Cleaning of Wind Power Data Methods Based on Control Principle of Wind Turbine Generator System. J. Chin. Soc. Power Eng. 2021, 41, 316–322, 329. [Google Scholar] [CrossRef]
- Xu, B. Parameter Correlation Based Parameter Abnormal Point Cleaning Method for Power Station. Autom. Electr. Power Syst. 2020, 44, 142–147. [Google Scholar] [CrossRef]
- Cui, X.; Lin, H.; An, N.; Wang, R. Ship Navigation Data Recognition Based on LOF-FCM Algorithm. Ship Eng. 2024, 46, 488–493. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, R.; Li, X.; Xi, Y. Cleaning Abnormal Status Data of Substation Equipment Based on Machine Learning. Proc. CSU-EPSA 2021, 33, 8. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, A.; Huang, Z.; Huang, D.; Chen, X. Dimension Reduction Optimization Analysis of CSE-CIC-IDS2018 Intrusion Detection Dataset Based on Machine Learning. Fire Control Command Control 2021, 46, 8. [Google Scholar] [CrossRef]
- Han, H.; Lu, S.; Wu, X.; Qiao, J. Abnormal Data Cleaning Method for Municipal Wastewater Treatment Based on Improved Support Vector Machine. J. Beijing Univ. Technol. 2021, 47, 1011–1020. [Google Scholar] [CrossRef]
- Yang, H.; Tang, J.; Shao, W.; Liu, B.; Chen, R. Wind Power Data Cleaning Method Based on Rule Base and PRRL Model. Acta Energiae Solaris Sin. 2024, 45, 416–425. [Google Scholar] [CrossRef]
- Gu, J.; Zhao, J.; Zhang, X.; Cheng, T.; Zhou, B.; Jiang, L. Research Review and Prospect of Data Cleaning for Multi-Parameter Monitoring Data of Power Equipment. High Volt. Eng. 2024, 50, 3403–3420. [Google Scholar] [CrossRef]
- Côté, P.O.; Nikanjam, A.; Ahmed, N.; Humeniuk, D.; Khomh, F. Data Cleaning and Machine Learning: A Systematic Literature Review. Autom. Softw. Eng. 2024, 31, 54. [Google Scholar] [CrossRef]
- Xia, Y.; Xia, H.; Feng, X. Research on SCADA Data Cleaning Method Based on Wind Power Curve. Renew. Energy Resour. 2022, 40, 1499–1504. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Z.; Wang, H. Turbine Data Cleaning Based on Deep LSTM. Therm. Power Gener. 2023, 52, 179–187. [Google Scholar] [CrossRef]
- Zhao, D.; Shen, Z.; Song, Z.; Xie, L.; Liu, B. Mine Airflow Speed Sensor Data Cleaning Model for Intelligent Ventilation. China Saf. Sci. J. 2023, 33, 56–62. [Google Scholar] [CrossRef]
- Peng, B.; Li, Y.; Gong, X. Improved K-Means Photovoltaic Energy Data Cleaning Method Based on Autoencoder. Comput. Sci. 2024, 51, 230700070-5. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.-J.; Shi, Q.; Zhou, L. Operation Parameters Optimization of Blast Furnaces Based on Data Mining and Cleaning. J. Northeast. Univ. Nat. Sci. 2020, 41, 1153–1160. [Google Scholar] [CrossRef]
- Zhu, Y.; Liang, W.; Wang, Y. Research on Data Cleaning and Fusion in Distribution Power Grid Based on Time Series Technology. Power Syst. Technol. 2021, 45, 2839–2846. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Fan, T.; Xie, X.; Ma, D. On Line Cleaning and Repairing Method of Photovoltaic System Data Acquisition. Acta Energiae Solaris Sin. 2022, 43, 57–65. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, P.; Liu, J.; Zheng, S.; Shan, Z.; Li, Z. An Adaptive Data Cleaning Framework: A Case Study of the Water Quality Monitoring System in China. Hydrol. Sci. J. 2022, 67, 1114–1129. [Google Scholar] [CrossRef]
- Jäger, S.; Allhorn, A.; Bießmann, F. A Benchmark for Data Imputation Methods. Front. Big Data 2021, 4, 693674. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, X.; Xia, L.; Tao, S.; Xiang, S. A Matrix Completion Method for Imputing Missing Values of Process Data. Processes 2024, 12, 659. [Google Scholar] [CrossRef]
- Liu, Q.; Zhong, Y.; Lin, C.; Li, T.; Yang, C.; Fu, Z.; Li, X. Electricity Consumption Data Cleansing and Imputation Based on Robust Nonnegative Matrix Factorization. Power Syst. Technol. 2024, 48, 2103–2112. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A Review: Data Pre-Processing and Data Augmentation Techniques. Glob. Transit. Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Mohammed, A.F.Y.; Sultan, S.M.; Lee, J.; Lim, S. Deep-Reinforcement-Learning-Based IoT Sensor Data Cleaning Framework for Enhanced Data Analytics. Sensors 2023, 23, 1791. [Google Scholar] [CrossRef] [PubMed]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F. Numerical Developments on the E-Motions Wave Energy Converter: Hull Design, Power Take-Off Tuning and Mooring System Configuration. Ocean. Eng. 2023, 280, 114596. [Google Scholar] [CrossRef]
- Song, M.; Shi, Q.; Zhang, F.; Wang, Y.; Li, L. Assessment of Rush Repair Capacity of Wartime Equipment Re-pair Institutions. J. Ordnance Equip. Eng. 2020, 41, 241–244. [Google Scholar] [CrossRef]
- Ge, C.; Gao, Y.; Miao, X.; Yao, B.; Wang, H. A Hybrid Data Cleaning Framework Using Markov Logic Net-works (Extended Abstract). In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering (ICDE), Chania, Greece, 19–22 April 2021; pp. 2344–2345. [Google Scholar] [CrossRef]
- Huang, G.; Zhao, X.; Lu, Q. Research on multi-source VOCs data cleaning method based on KPCA-IF-WRF model. J. Saf. Environ. 2022, 22, 3412–3423. [Google Scholar] [CrossRef]
- Li, X.; Liu, M.; Wang, K.; Liu, Z.; Li, G. Data Cleaning Method for the Process of Acid Production with Flue Gas Based on Improved Random Forest. Chin. J. Chem. Eng. 2023, 59, 72–84. [Google Scholar] [CrossRef]
- Li, M.; Su, M.; Zhang, B.; Yue, Y.; Wang, J.; Deng, Y. Research on a DBSCAN-IForest Optimisation-Based Anomaly Detection Algorithm for Underwater Terrain Data. Water 2025, 17, 626. [Google Scholar] [CrossRef]
- Saneep, K.; Sundareswaran, K.; Nayak, P.S.R.; Puthusserry, G.V. State of Charge Estimation of Lithium-Ion Batteries Using PSO Optimized Random Forest Algorithm and Performance Analysis. J. Energy Storage 2025, 114, 115879. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Z.; He, C.; Lin, X.; Li, C.; Huang, J. Research on Remaining Useful Life Prediction Method for Lithium-Ion Battery Based on Improved GA-ACO-BPNN Optimization Algorithm. Sustain. Energy Technol. Assess. 2025, 73, 104142. [Google Scholar] [CrossRef]
- Zheng, Y.; Lv, X.; Qian, L.; Liu, X. An Optimal BP Neural Network Track Prediction Method Based on a GA–ACO Hybrid Algorithm. J. Mar. Sci. Eng. 2022, 10, 1399. [Google Scholar] [CrossRef]
- He, G.; Du, Y.; Liang, Q.; Zhou, Z.; Shu, L. Modeling and Optimization Method of Laser Cladding Based on GA-ACO-RFR and GNSGA-II. Int. J. Precis. Eng. Manuf.-Green Technol. 2023, 10, 1207–1222. [Google Scholar] [CrossRef]
- Li, T.; Deng, L.; Mo, B.; Shi, F. Prediction of Cracks and Optimization of Process Parameters in Laser Cladding of Ni60 Based on GA-ACO-RFA. China Mech. Eng. 2024. Available online: https://link.cnki.net/urlid/42.1294.th.20240708.1823.012 (accessed on 20 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).