Parametric Effects of Mixing Channel Geometry on Entrainment Characteristics of Ejector in R410A Heat Pump Systems
Abstract
1. Introduction
2. Materials and Methods
- (1)
- Steady-state operating conditions;
- (2)
- The walls of the ejector are adiabatic and non-slipping;
- (3)
- Thermodynamic equilibrium between phases;
- (4)
- Equal velocity fields for liquid and vapor phases;
- (5)
- A uniform temperature distribution.
2.1. Governing Equations
2.2. Computational Technique
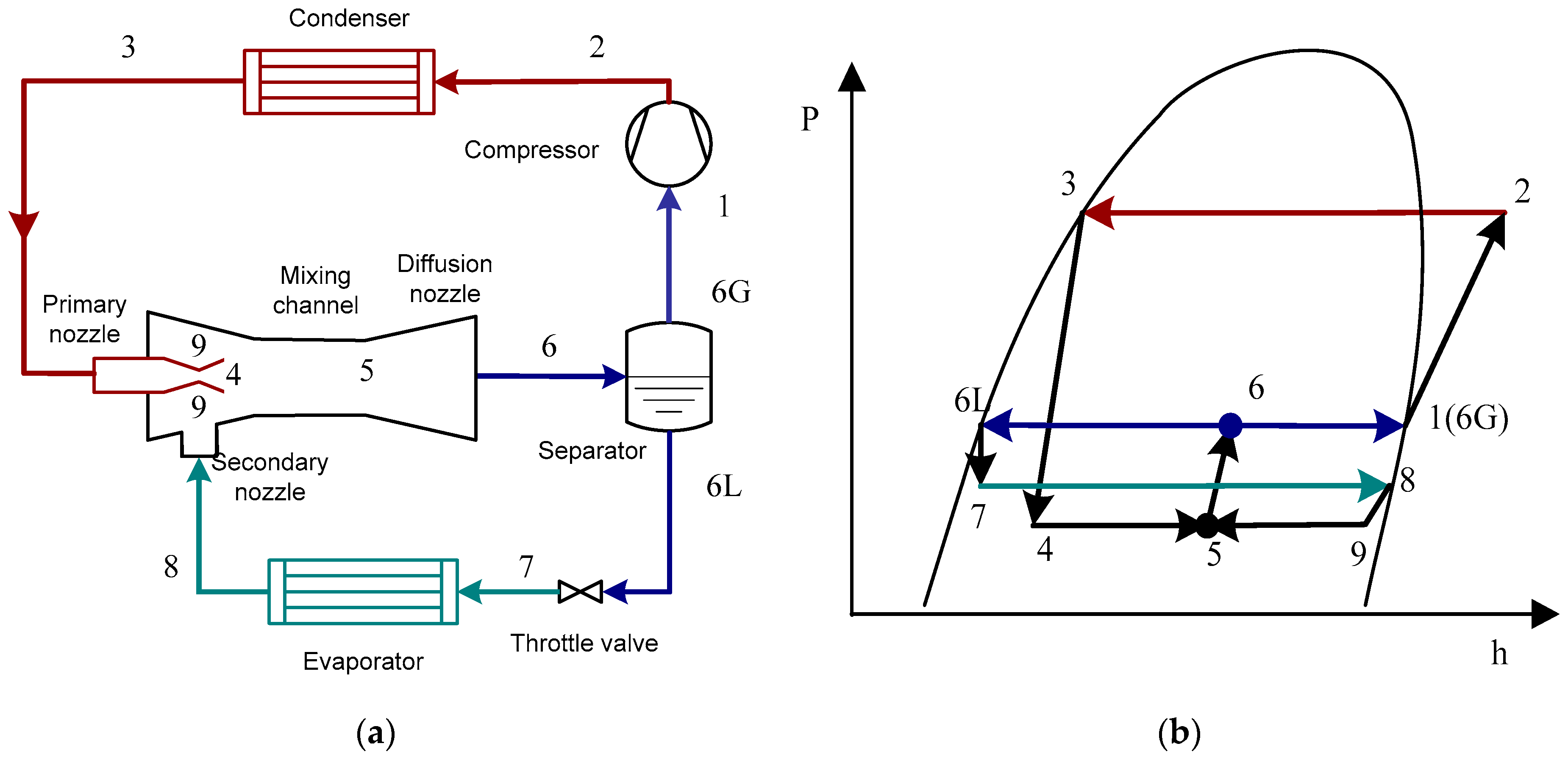
2.3. Geometry, Grid, and Boundary Conditions
- Primary inlet pressure: 2.13 MPa (subcooled liquid);
- Secondary inlet pressure: 0.75 MPa (saturated vapor);
- Discharge pressure: 0.85 MPa (two-phase mixture).
2.4. Model Validation
3. Results and Discussion
3.1. Ejector Flow Dynamics
3.2. Effect of Nozzle Exit Position
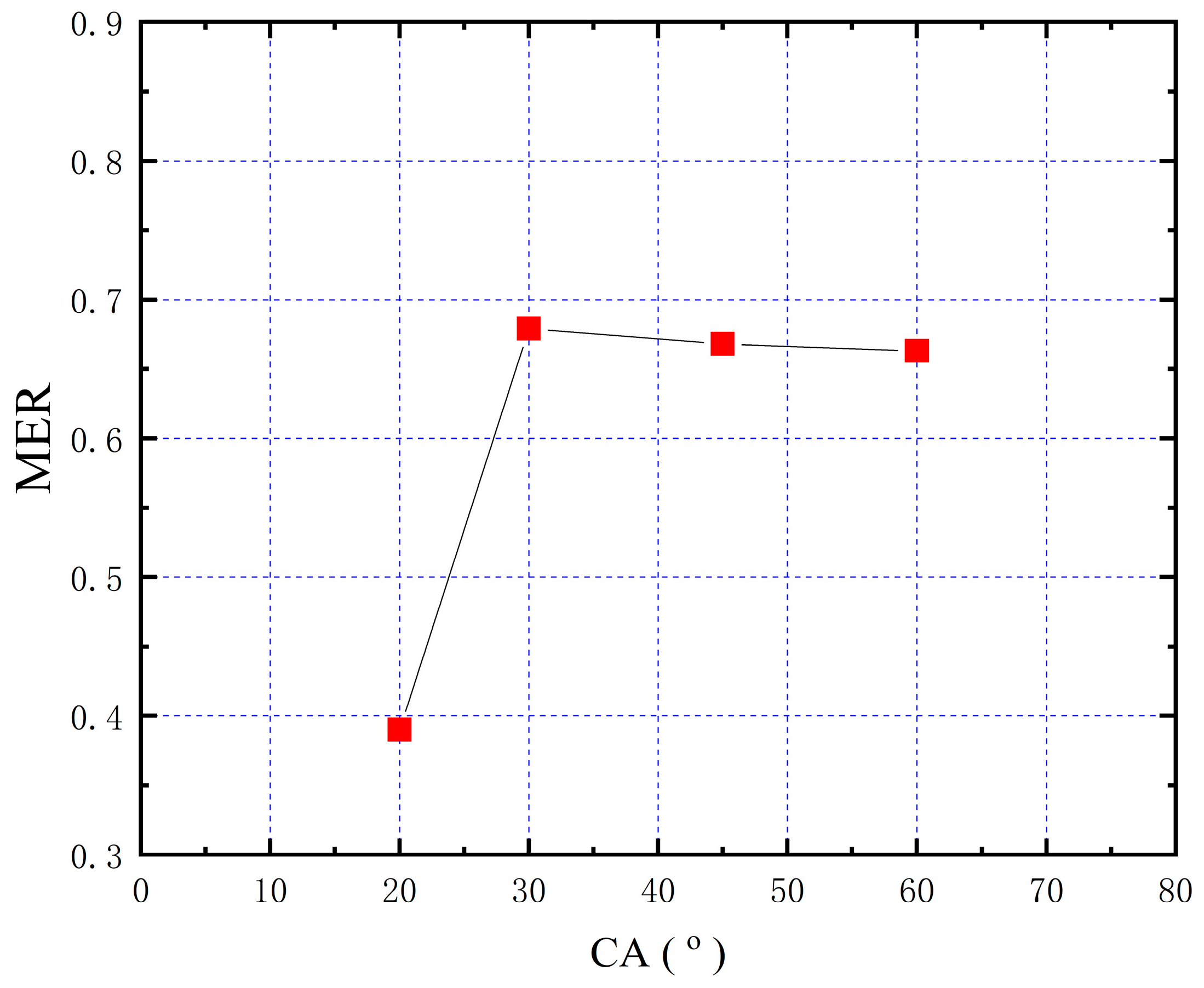
3.3. Effect of Pre-Mixing Channel Convergent Angle
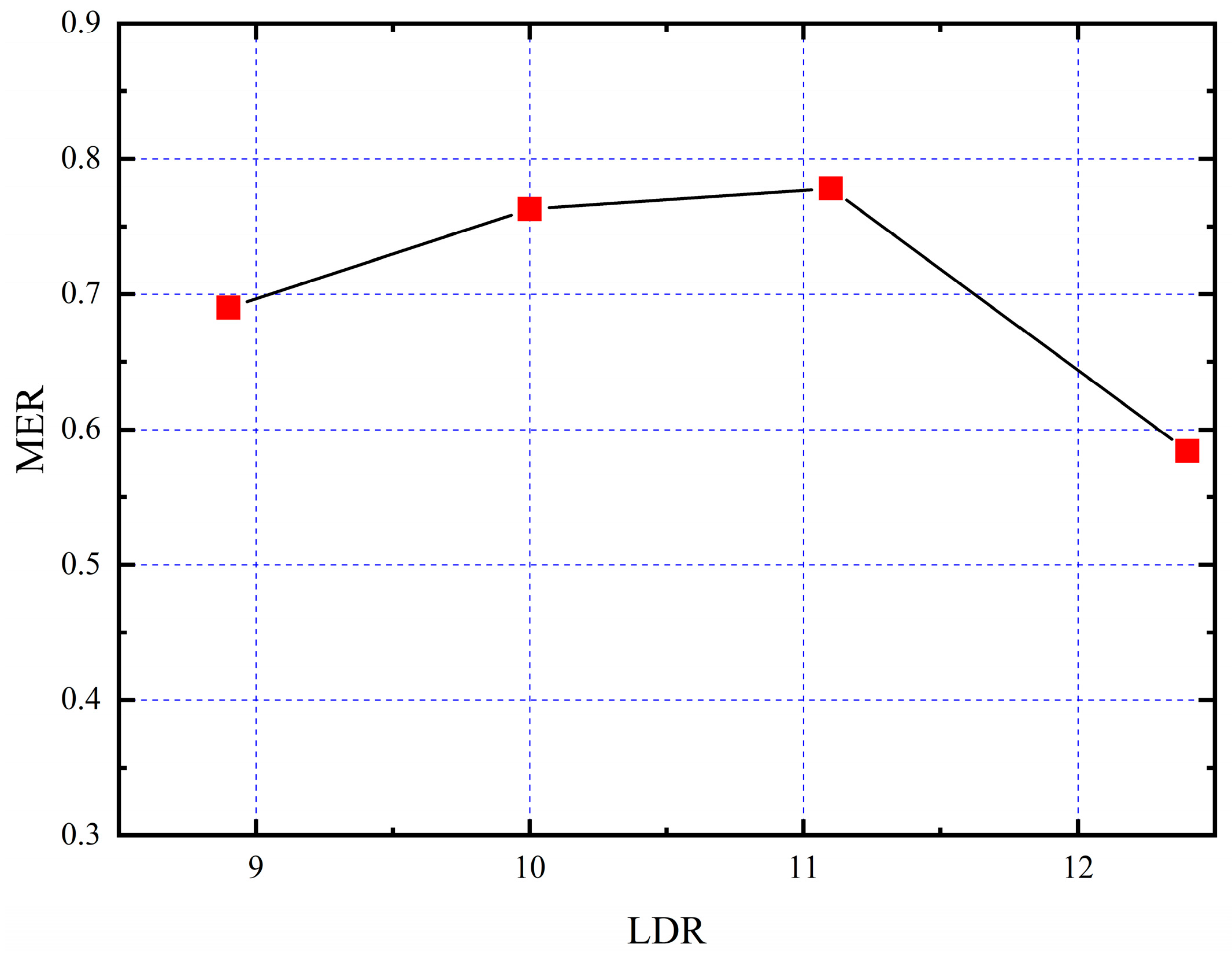
3.4. Effect of Diameter Ratio
3.5. Effect of Length-to-Diameter Ratio
3.6. Summary
4. Conclusions and Limitations
- (1)
- The CFD simulation results are basically consistent with the experimental data, with relative errors ranging from 8.3% to 17.1% for the primary MFR and −8.9% to 12.9% for the MER.
- (2)
- The primary nozzle position significantly influences the ejector entrainment performance, with an optimal NXP of 17 mm (≈3.5Dmix) maximizing the MER. Below this optimum, the MER increases gradually with the NXP, while exceeding it causes a sharp decline due to increased frictional losses.
- (3)
- The convergent angle (CA) exhibits a non-monotonic relationship with the MER, peaking at 30°. This optimum balances flow guidance and energy preservation, while larger angles induce vortex formation and efficiency degradation.
- (4)
- The diameter ratio (DDR = 6.4) and length-to-diameter ratio (LDR = 11.1) optimize momentum transfer while minimizing energy dissipation in the constant-area mixing channel.
- (1)
- The asymmetric attachment of the primary jet to the diffuser walls suggests inherent unsteadiness, consistent with prior LES studies of Venturi flows [49]. Steady-state simulations cannot resolve the following: transient vortex shedding from the primary nozzle, low-frequency oscillations in shear layer reattachment, and time-dependent momentum redistribution in the diffuser. The observed inherent unsteadiness in the ejector flow dynamics implies that practical systems may experience low-frequency oscillations in the MER and ejector efficiency reductions under off-design conditions.
- (2)
- The k-ε model employs Boussinesq’s eddy viscosity hypothesis, which assumes isotropic turbulence and a local equilibrium. These assumptions introduce some key limitations for ejector flows: anisotropy neglect means that it fails to capture strong streamline curvature in convergent/divergent sections and swirling flows from nozzle asymmetry; the overprediction of the eddy viscosity may result in the underestimation of the separation in diffuser regions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CA | Convergent angle of pre-mixing channel |
| COP | Coefficient of performance |
| DDR | Ratio between constant-area mixing channel diameter and primary nozzle throat diameter |
| LDR | Ratio between length and constant-area mixing channel diameter |
| MER | Mass entrained ratio |
| MFR | Mass flow rate, kg s−1 |
| NXP | Distance between primary nozzle outlet and constant-area mixing channel, mm |
| Variables | |
| cp | Specific heat, kJ kg−1 K−1 |
| Cμ | Turbulent viscosity coefficient |
| C1ε | Turbulent dissipation rate production term coefficient |
| C2ε | Turbulent dissipation rate dissipation term coefficient |
| C3ε | Buoyancy effect correction coefficient |
| D | Diameter, mm |
| h | Specific enthalpy, kJ kg−1 |
| H | Total enthalpy, kJ kg−1 |
| Gb | Generation of turbulence kinetic energy due to buoyancy |
| Gk | Generation of turbulence kinetic energy due to mean velocity gradients |
| k | Turbulence kinetic energy |
| ε | Rate of dissipation |
| λ | Effective thermal conductivity, W m−1 K−1 |
| L | Length, mm |
| p | Pressure, Pa |
| T | Temperature, K |
| U | Velocity vector, m s−1 |
| S | User-defined source term |
| x | Vapor mass fraction |
| YM | Contribution of fluctuating dilatation in compressible turbulence to overall dissipation rate |
| τ | Stress tensor, N m−2 |
| μ | Dynamic viscosity, Pa s |
| μt | Turbulent (or eddy) viscosity |
| Subscripts | |
| pn | Primary nozzle |
| dif | Diffuser |
| sn | Secondary nozzle |
| mix | Mixing channel |
| in | Inlet |
| out | Outlet |
References
- Zhang, Z.; Feng, X.; Tian, D.; Yang, J.; Chang, L. Progress in ejector-expansion vapor compression refrigeration and heat pump systems. Energ. Convers. Manage. 2020, 207, 112529. [Google Scholar] [CrossRef]
- Yang, T.; Yang, Y.; Zou, H.; Tian, C.; Butrymowicz, D. Comprehensive performance evaluation on a transcritical CO2 ejector-expansion heat pump system. Appl. Therm. Eng. 2024, 254, 123697. [Google Scholar] [CrossRef]
- Besagni, G. Ejectors on the cutting edge: The past, the present and the perspective. Energy 2019, 170, 998–1003. [Google Scholar] [CrossRef]
- Zou, L.; Yu, J. 4E assessment of ejector-enhanced R290 heat pump cycle with a sub-cooler for cold region applications. Energy 2024, 298, 131369. [Google Scholar] [CrossRef]
- Pottker, G.; Hrnjak, P. Ejector in R410A vapor compression systems with experimental quantification of two major mechanisms of performance improvement: Work recovery and liquid feeding. Int. J. Refrig. 2015, 50, 184–192. [Google Scholar] [CrossRef]
- Spitzenberger, J.; Mohammed, R.H.; Ismael, L.; Wang, P.; Ma, H.; Abu-Heiba, A.; Kowalski, S.; Nawaz, K. Experimental performance of ejector heat pump operating in the sub-critical mode. Energ. Convers. Manage. 2023, 278, 116724. [Google Scholar] [CrossRef]
- Fingas, R.; Haida, M.; Smolka, J.; Besagni, G.; Bodys, J.; Palacz, M.; Nowak, A.J. Experimental analysis of the air-to-water ejector-based R290 heat pump system for domestic application. Appl. Therm. Eng. 2024, 236, 121800. [Google Scholar] [CrossRef]
- Elbel, S. Historical and present developments of ejector refrigeration systems with emphasis on transcritical carbon dioxide air-conditioning applications. Int. J. Refrig. 2011, 34, 1545–1561. [Google Scholar] [CrossRef]
- Nakagawa, M.; Marasigan, A.R.; Matsukawa, T.; Kurashina, A. Experimental investigation on the effect of mixing length on the performance of two-phase ejector for CO2 refrigeration cycle with and without heat exchanger. Int. J. Refrig. 2011, 34, 1604–1613. [Google Scholar] [CrossRef]
- Yazdani, M.; Alahyari, A.A.; Radcliff, T.D. Numerical modeling of two-phase supersonic ejectors for work-recovery applications. Int. J. Heat Mass Tran. 2012, 55, 5744–5753. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A.; Andresen, T. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump. Int. J. Refrig. 2012, 35, 1617–1625. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Kus, W.; Fic, A.; Bulinski, Z.; Nowak, A.J.; Banasiak, K.; Hafner, A.; Cai, W. CFD-based shape optimisation of a CO2 two-phase ejector mixing section. Appl. Therm. Eng. 2016, 95, 62–65. [Google Scholar] [CrossRef]
- Dong, J.; Hu, Q.; Yu, M.; Han, Z.; Cui, W.; Liang, D.; Pan, X. Numerical investigation on the influence of mixing chamber length on steam ejector performance. Appl. Therm. Eng. 2020, 174, 115204. [Google Scholar] [CrossRef]
- Ameur, K.; Aidoun, Z. Two-phase ejector enhanced carbon dioxide transcritical heat pump for cold climate. Energ. Convers. Manage. 2021, 243, 1144. [Google Scholar] [CrossRef]
- Kakkirala, V.; Velayudhan Parvathy, C. Optimized mixing chamber length and diameter of a steam ejector for the application of gas turbine power plant: A computational approach. J. Therm. Anal. Calorim. 2022, 147, 8881–8894. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, Z.; Wu, Y.; Tian, D. A parametric study on the effect of mixing chamber for expansion work recovery CO2 ejector. J. Therm. Sci. 2022, 31, 1914–1927. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, M.S.; Kim, M.S. Experimental study on the improvement of CO2 air conditioning system performance using an ejector. Int. J. Refrig. 2011, 34, 1614–1625. [Google Scholar] [CrossRef]
- Liu, F.; Groll, E.A.; Ren, J. Comprehensive experimental performance analyses of an ejector expansion transcritical CO2 system. Appl. Therm. Eng. 2016, 98, 1061–1069. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y.; Groll, E.A. Performance enhancement of CO2 air conditioner with a controllable ejector. Int. J. Refrig. 2012, 35, 1604–1616. [Google Scholar] [CrossRef]
- Liu, F.; Groll, E.A.; Li, D. Investigation on performance of variable geometry ejectors for CO2 refrigeration cycles. Energy 2012, 45, 829–839. [Google Scholar] [CrossRef]
- Banasiak, K.; Palacz, M.; Hafner, A.; Buliński, Z.; Smołka, J.; Nowak, A.J.; Fic, A. A CFD-based investigation of the energy performance of two-phase R744 ejectors to recover the expansion work in refrigeration systems: An irreversibility analysis. Int. J. Refrig. 2014, 40, 328–337. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Nowak, A.J.; Banasiak, K.; Hafner, A. Shape optimisation of a two-phase ejector for CO2 refrigeration systems. Int. J. Refrig. 2017, 74, 212–223. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Yang, Y.; Jiang, P.-X. Flow visualization of supersonic two-phase transcritical flow of CO2 in an ejector of a refrigeration system. Int. J. Refrig. 2017, 74, 354–361. [Google Scholar] [CrossRef]
- Zheng, L.; Deng, J. Research on CO2 ejector component efficiencies by experiment measurement and distributed-parameter modeling. Energ. Convers. Manage. 2017, 142, 244–256. [Google Scholar] [CrossRef]
- Suo, J. Simulation and Experimental Study on Performance of Two-Stage Throttling Transcritical CO2 Ejector Refrigeration System. Master’s Thesis, Tianjin University of Commerce, Tianjin, China, 2018. [Google Scholar]
- Li, Y.; Deng, J. Numerical investigation on the performance of transcritical CO2 two-phase ejector with a novel non-equilibrium CFD model. Energy 2022, 238, 121995. [Google Scholar] [CrossRef]
- Li, Y.; Deng, J.; He, Y. Numerical study on the interaction of geometric parameters of a transcritical CO2 two-phase ejector using response surface methodology and genetic algorithm. Appl. Therm. Eng. 2022, 214, 118799. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, H.; Deng, J.; Wang, L.; Zhang, H. Performance improvement of CO2 two-phase ejector by combining CFD modeling, artificial neural network and genetic algorithm. Int. J. Refrig. 2023, 154, 151–167. [Google Scholar] [CrossRef]
- Yan, J.; Li, Z.; Zhang, H. Investigation on key geometries optimization and effect of variable operating conditions of a transcritical R744 two-phase ejector. Appl. Therm. Eng. 2023, 230, 120733. [Google Scholar] [CrossRef]
- Yu, M.; Zou, L.; Yu, J. Numerical investigation on the effect of area ratio on an adjustable ejector for heat pump dryer based on dynamic mesh. Energy 2024, 308, 132876. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Liu, X.; Shi, C. Jet performance exploration of an ejector for multi-parallel ejector air curtain. Int. Commun. Heat Mass Transf. 2025, 164, 108868. [Google Scholar] [CrossRef]
- Long, J.; Yu, B.; Wang, D.; Liu, C.; Shi, J.; Chen, J. A novel relaxation drift model for simulating liquid-vapor momentum non-equilibrium in two-phase ejectors. Case Stud. Therm. Eng. 2023, 52, 103758. [Google Scholar] [CrossRef]
- Hu, J.; Shi, J.; Liang, Y.; Yang, Z.; Chen, J. Numerical and experimental investigation on nozzle parameters for R410A ejector air conditioning system. Int. J. Refrig. 2014, 40, 338–346. [Google Scholar] [CrossRef]
- Yan, J.; Lin, C.; Cai, W.; Chen, H.; Wang, H. Experimental study on key geometric parameters of an R134A ejector cooling system. Int. J. Refrig. 2016, 67, 102–108. [Google Scholar] [CrossRef]
- Bilir Sag, N.; Ersoy, H.K. Experimental investigation on motive nozzle throat diameter for an ejector expansion refrigeration system. Energy Convers. Manag. 2016, 124, 1–12. [Google Scholar] [CrossRef]
- Huang, K.; Guo, X.; Zhang, P. Influence of Structural Parameters of Two-throat Nozzle Ejector on Performance of Two-phase Flow Ejector Refrigeration System. Energy Procedia 2017, 105, 5091–5097. [Google Scholar] [CrossRef]
- Jeon, Y.; Jung, J.; Kim, D.; Kim, S.; Kim, Y. Effects of ejector geometries on performance of ejector-expansion R410A air conditioner considering cooling seasonal performance factor. Appl. Energ. 2017, 205, 761–768. [Google Scholar] [CrossRef]
- Smolka, J.; Bulinski, Z.; Fic, A.; Nowak, A.J.; Banasiak, K.; Hafner, A. A computational model of a transcritical R744 ejector based on a homogeneous real fluid approach. Appl. Math Model 2013, 37, 1208–1224. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Fic, A.; Bulinski, Z.; Nowak, A.J.; Banasiak, K.; Hafner, A. Application range of the HEM approach for CO2 expansion inside two-phase ejectors for supermarket refrigeration systems. Int. J. Refrig. 2015, 59, 251–258. [Google Scholar] [CrossRef]
- Haida, M.; Smolka, J.; Hafner, A.; Palacz, M.; Banasiak, K.; Nowak, A.J. Modified homogeneous relaxation model for the R744 trans-critical flow in a two-phase ejector. Int. J. Refrig. 2018, 85, 314–333. [Google Scholar] [CrossRef]
- Lee, M.S.; Lee, H.; Hwang, Y.; Radermacher, R.; Jeong, H.-M. Optimization of two-phase R600a ejector geometries using a non-equilibrium CFD model. Appl. Therm. Eng. 2016, 109, 272–282. [Google Scholar] [CrossRef]
- Baek, S.; Ko, S.; Song, S.; Ryu, S. Numerical study of high-speed two-phase ejector performance with R134a refrigerant. Int. J. Heat Mass Tran. 2018, 126, 1071–1082. [Google Scholar] [CrossRef]
- Bai, T.; Lu, Y.; Wen, Z.; Yu, J. Numerical study on the structural optimization of R290 two-phase ejector with a non-equilibrium CFD model. Int. J. Refrig. 2025, 170, 287–301. [Google Scholar] [CrossRef]
- Ameur, K.; Aidoun, Z.; Ouzzane, M. Expansion of subcooled refrigerant in two-phase ejectors with no flux induction. Exp. Therm. Fluid Sci. 2017, 82, 424–432. [Google Scholar] [CrossRef]
- Lemmon, E.; Huber, M.; McLinden, M. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties—REFPROP, 9th ed.; Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Bodys, J.; Smolka, J.; Palacz, M.; Haida, M.; Banasiak, K.; Nowak, A.J. Effect of turbulence models and cavitation intensity on the motive and suction nozzle mass flow rate prediction during a non-equilibrium expansion process in the CO2 ejector. Appl. Therm. Eng. 2022, 201, 117743. [Google Scholar] [CrossRef]
- Li, C.; Liu, F.; He, M.; Liu, Y. Numerical study of a CO2 swirl ejector with lubricating oil. Int. J. Refrig. 2024, 165, 446–465. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, Y.; Li, C.; Zhang, F.; Jiang, P.X. Experimental investigation on the performance of transcritical CO2 ejector–expansion heat pump water heater system. Energ. Convers. Manage. 2018, 167, 147–155. [Google Scholar] [CrossRef]
- Semlitsch, B.; Laurendeau, E.; Mihəescu, M. Steady-State and Unsteady Simulations of a High Velocity Jet into a Venturi Shaped Pipe. In Proceedings of the 4th Joint US-European Fluids Engineering Summer Meeting, Chicago, IL, USA, 3–7 August 2014. [Google Scholar]
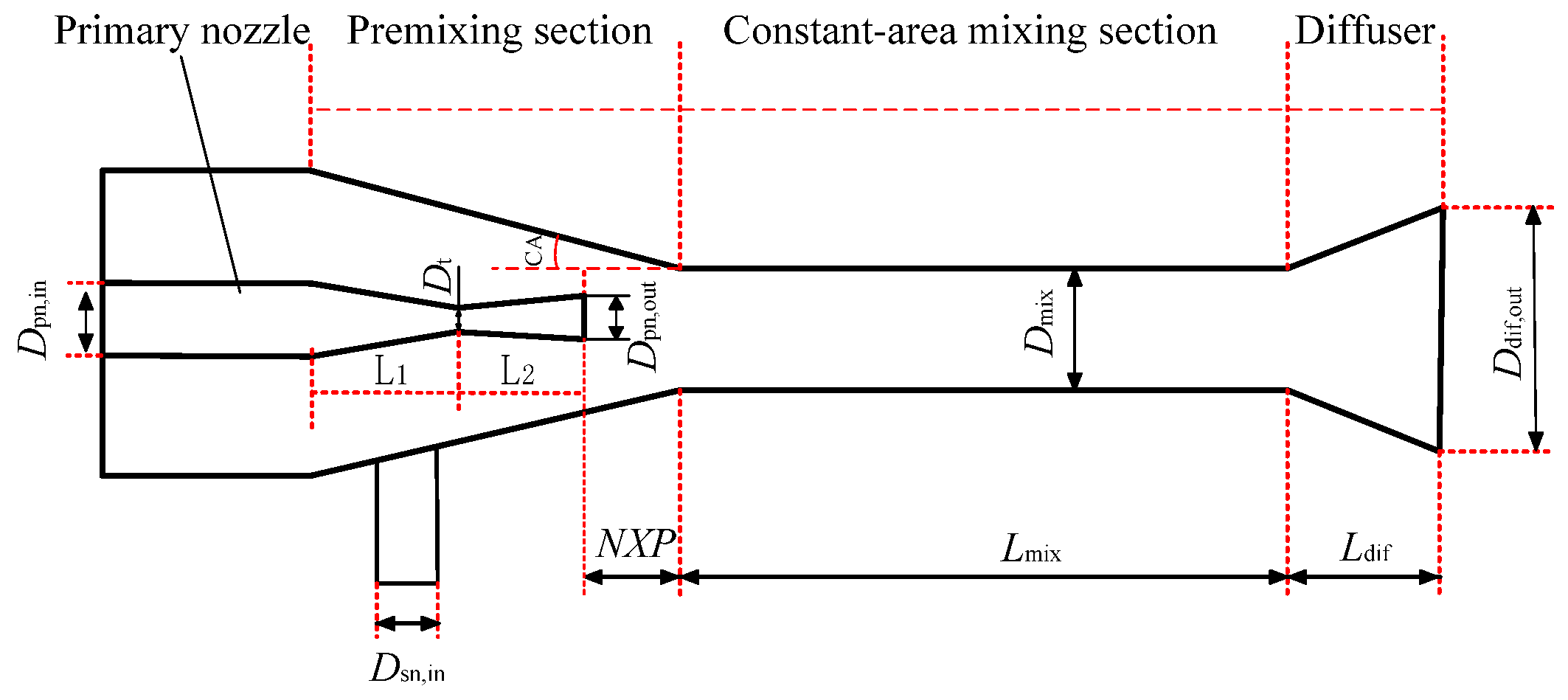










| Parameter | Size (mm) |
|---|---|
| Dpn,in | 10 |
| Dt | 0.7 |
| Dpn,out | 1.5 |
| Dmix | 5 |
| Ddif,out | 9.4 |
| Dsn,in | 6 |
| Lpn,d | 6 |
| Lmix | 50 |
| Ldif | 50 |
| Boundary Location | Condition Type |
|---|---|
| Primary inlet | Pressure—inlet/2.13 MPa |
| Secondary inlet | Pressure—inlet/0.75 MPa |
| Ejector exit | Pressure—outlet/0.85 MPa |
| All walls | Adiabatic, no slip |
| Reference | Working Fluid | Turbulence Model | Primary MFR Relative Error | Secondary MFR Relative Error |
|---|---|---|---|---|
| Li and Deng [26] | R744 | k-ε Realizable | −34.55–25.71% | −19.25–5.33% |
| Long et al. [32] | R744 | k-ω | N/A | −10–22% |
| Bai et al. [43] | R290 | k-ω SST | −12–12% | N/A |
| Bodys et al. [46] | R744 | k-ε Standard k-ε Realizable k-ω Standard k-kl-ω | 5–30% | 25–35% |
| Li et al. [47] | R744 | k-ε | −6.48–14.8% | −17.8–4.33% |
| NXP (mm) | CA (°) | DDR | LDR | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 | 15 | 17 | 19 | 20 | 30 | 45 | 60 | 5.0 | 5.7 | 6.4 | 7.1 | 8.9 | 10.0 | 11.1 | 12.4 | |
| MER | 0.62 | 0.71 | 0.77 | 0.64 | 0.39 | 0.68 | 0.66 | 0.66 | 0.58 | 0.66 | 0.70 | 0.62 | 0.69 | 0.69 | 0.76 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, Z.; Yang, M.; Chang, L.; Li, Y.; Zhang, Z. Parametric Effects of Mixing Channel Geometry on Entrainment Characteristics of Ejector in R410A Heat Pump Systems. Processes 2025, 13, 1933. https://doi.org/10.3390/pr13061933
Wang Y, Zhou Z, Yang M, Chang L, Li Y, Zhang Z. Parametric Effects of Mixing Channel Geometry on Entrainment Characteristics of Ejector in R410A Heat Pump Systems. Processes. 2025; 13(6):1933. https://doi.org/10.3390/pr13061933
Chicago/Turabian StyleWang, Yuying, Zhengdao Zhou, Meiyuan Yang, Li Chang, Yang Li, and Zhenying Zhang. 2025. "Parametric Effects of Mixing Channel Geometry on Entrainment Characteristics of Ejector in R410A Heat Pump Systems" Processes 13, no. 6: 1933. https://doi.org/10.3390/pr13061933
APA StyleWang, Y., Zhou, Z., Yang, M., Chang, L., Li, Y., & Zhang, Z. (2025). Parametric Effects of Mixing Channel Geometry on Entrainment Characteristics of Ejector in R410A Heat Pump Systems. Processes, 13(6), 1933. https://doi.org/10.3390/pr13061933







