Optimal Process Control for Rotor Speed Recovery and Secondary Frequency Drop Mitigation in Wind Turbine Frequency Regulation
Abstract
1. Introduction
2. Models and Characteristics of the System Frequency Response
2.1. Conventional System Frequency Response Model
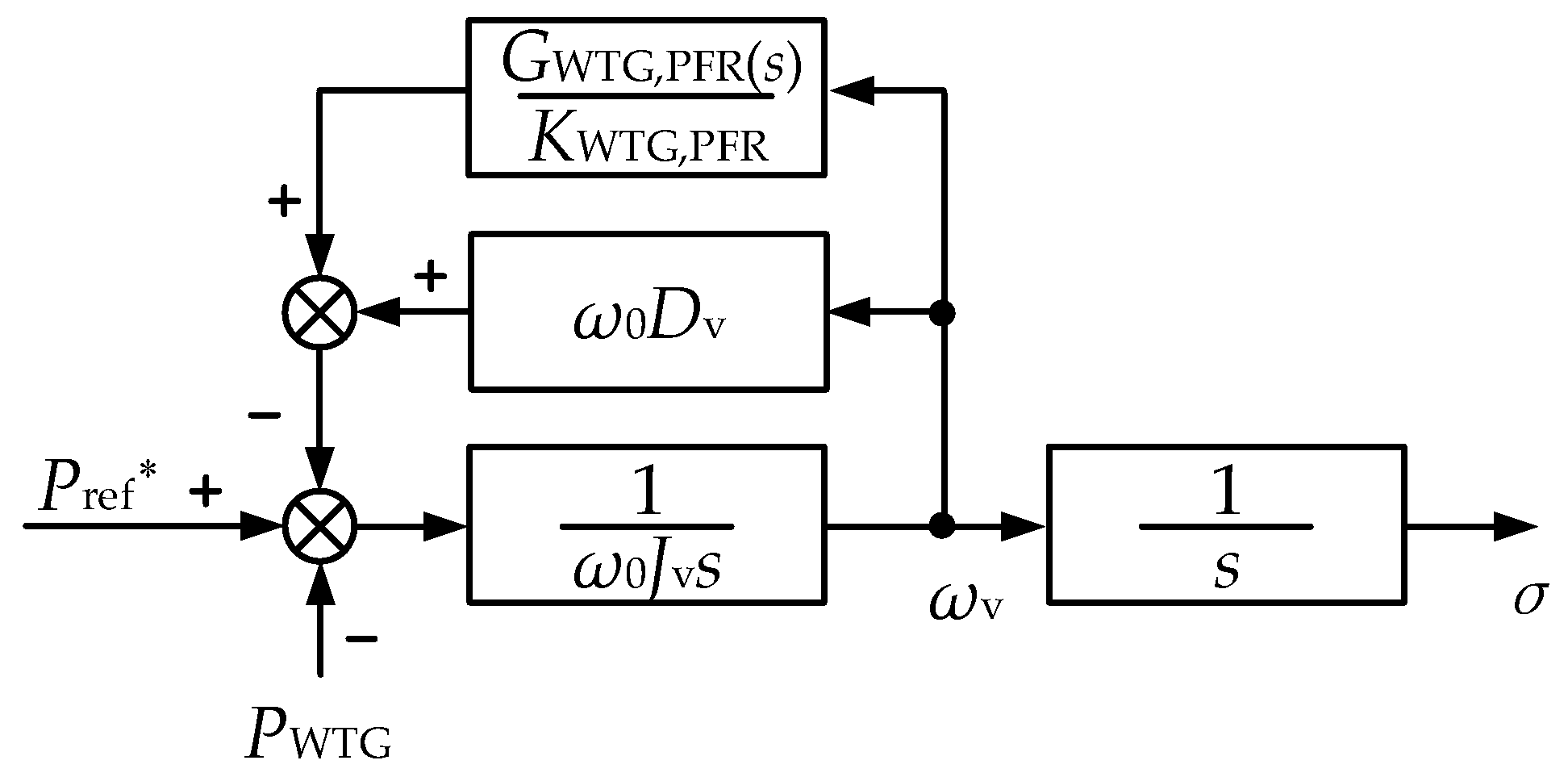
2.2. Windfarm Frequency Response Models
- (1)
- Rapid Power Response: The PFR power output of WTGs is unaffected by the turbine-governor inertia (in contrast to SGs), enabling near-instantaneous power injection during frequency deviations.
- (2)
- Aerodynamic Coupling: Increased active power output reduces the WTG rotor speed (governed by the turbine shaft dynamics in Equation (9)), thereby decreasing aerodynamic power (PA) and limiting sustained frequency regulation.
- (1)
- Thermal turbine PFR analogous scheme (excluding hysteresis compensation).
- (2)
- PFR power ramp-down scheme [27]. Considering the aerodynamic power reduction caused by rotor speed decline, the PFR power should progressively decrease with ωr. Due to the constraints of the transfer function in linear time-invariant (LTI) systems, ωr cannot be directly integrated into GWTG,PFR(s). A first-order high-pass filter block is implemented to emulate specific PFR power reduction dynamics associated with ωr.
2.3. System Frequency Response Characteristics
3. Segmented Wind Turbine Speed Recovery Strategy
3.1. Mechanism of SFD During Wind Turbine Speed Recovery
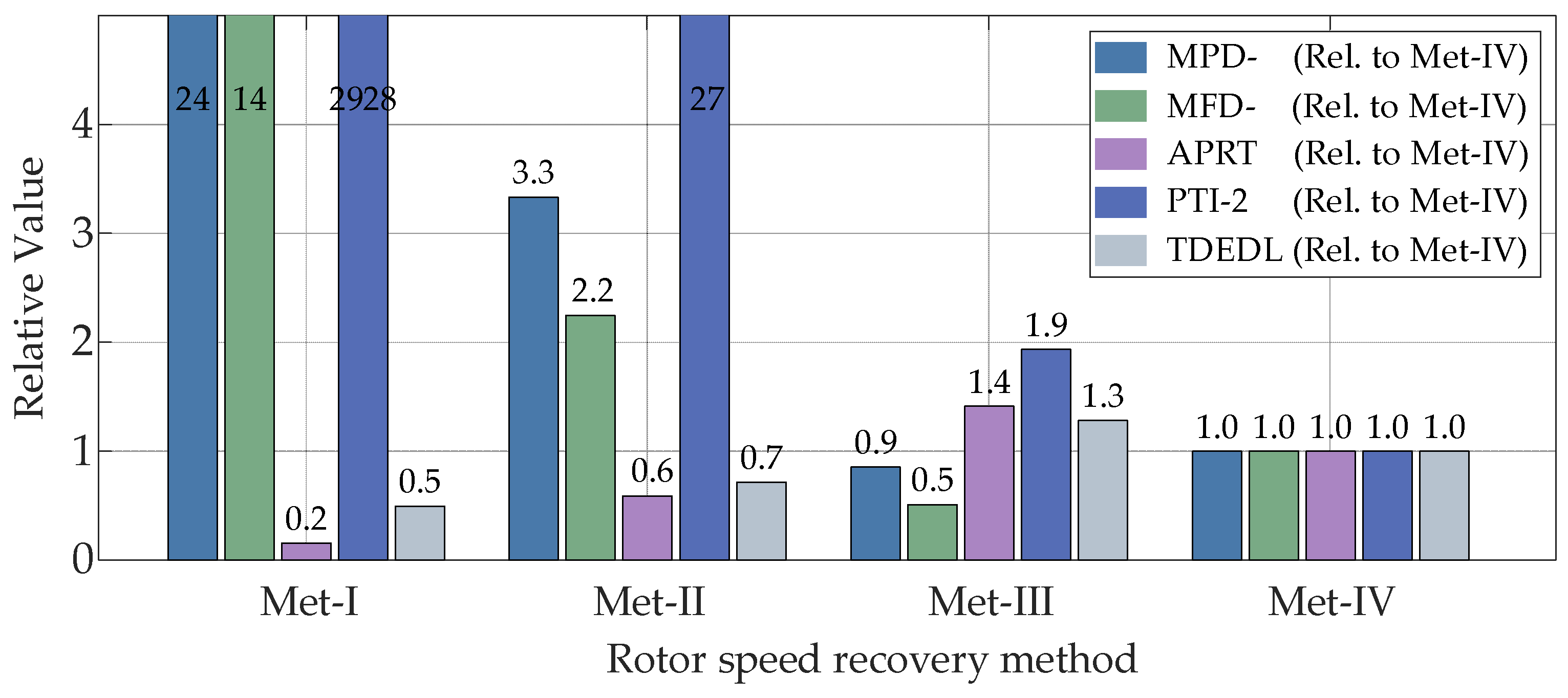
3.2. Evaluation Framework for Rotor Speed Recovery Performance
3.3. Design Principles of Segmented Rotor Speed Recovery
3.4. WTG Coordinated Control Strategy with Segmented Rotor Speed Recovery
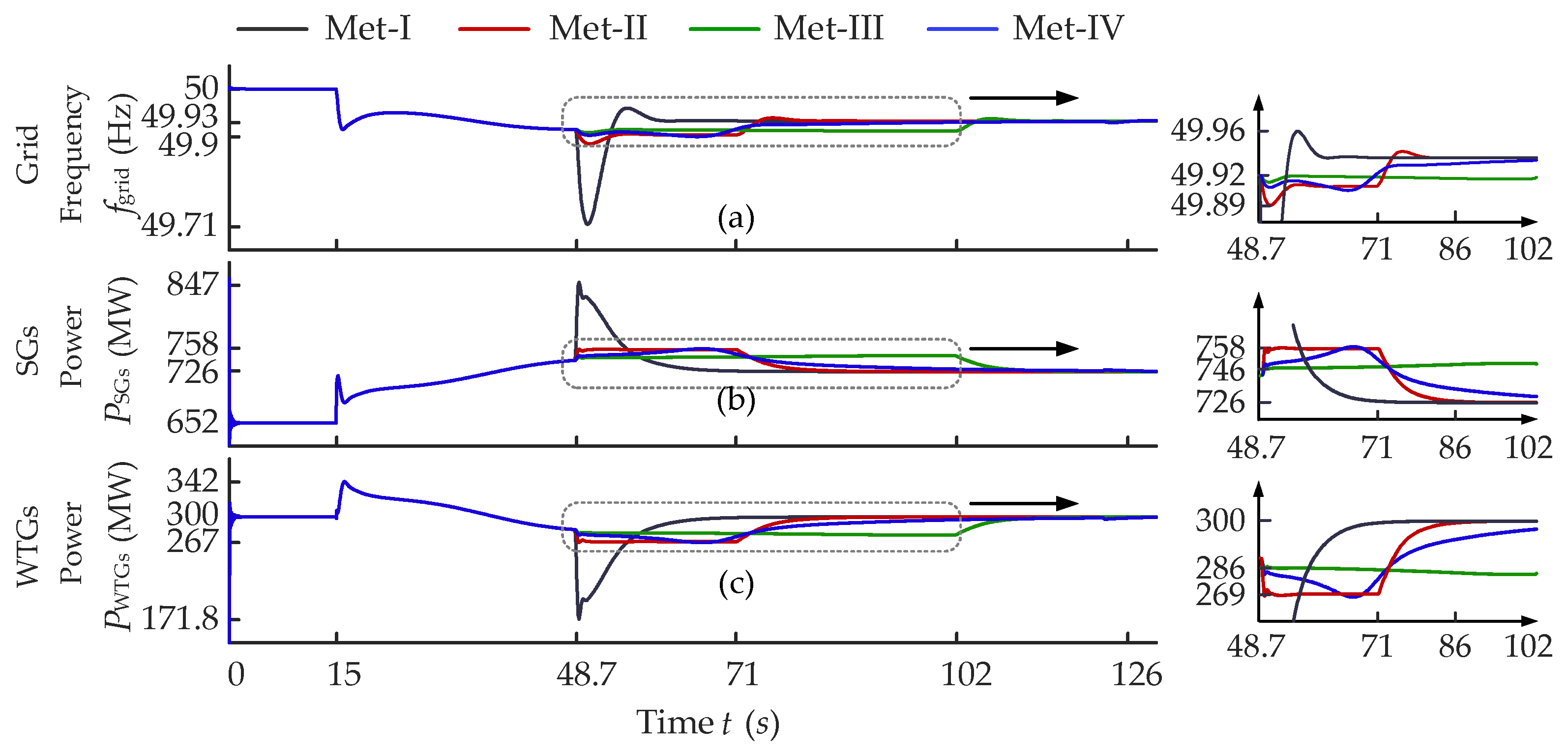
4. Case Studies
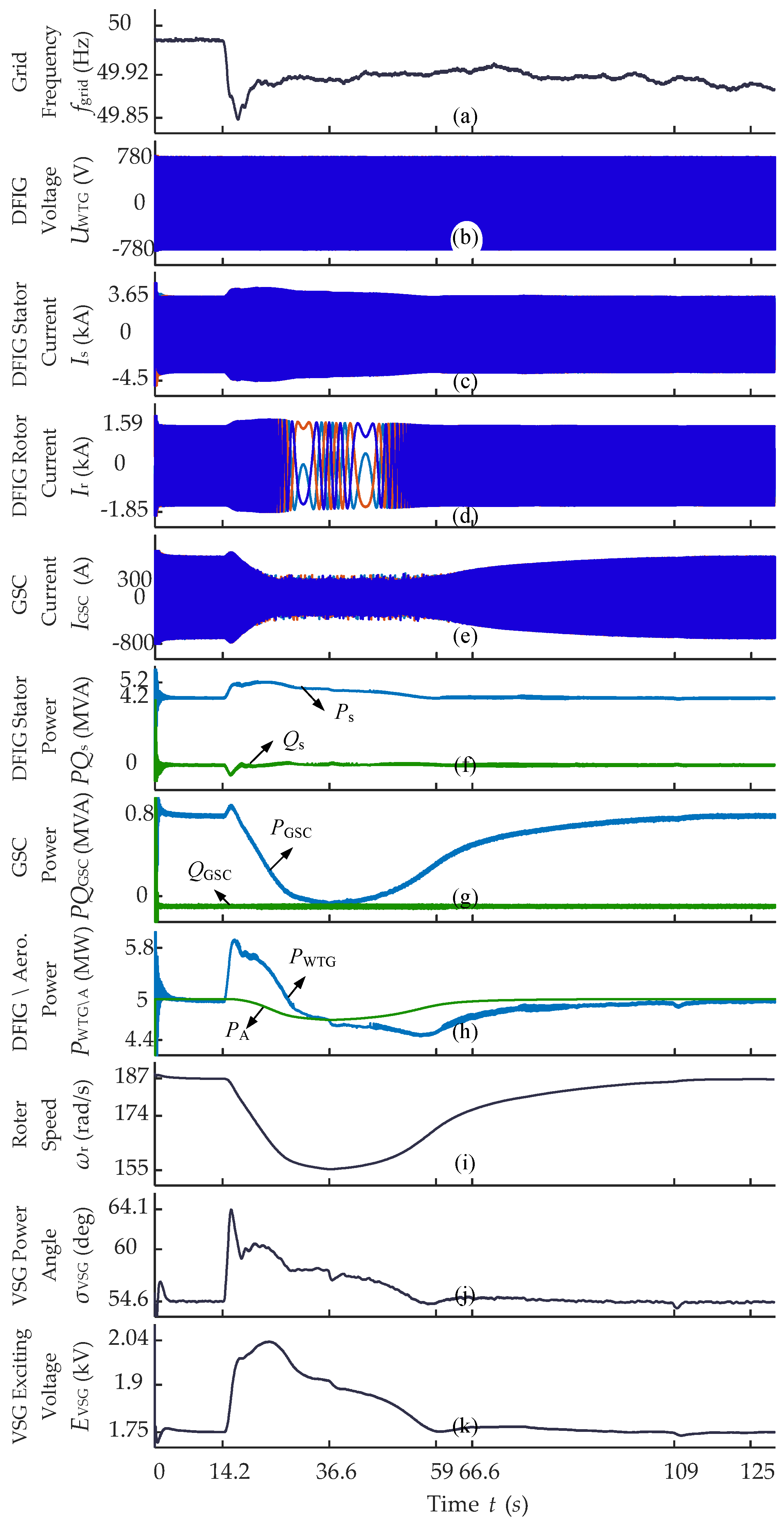
4.1. Grid Frequency Dip Operational Scenario
4.2. 10% Wind Power Penetration Scenario
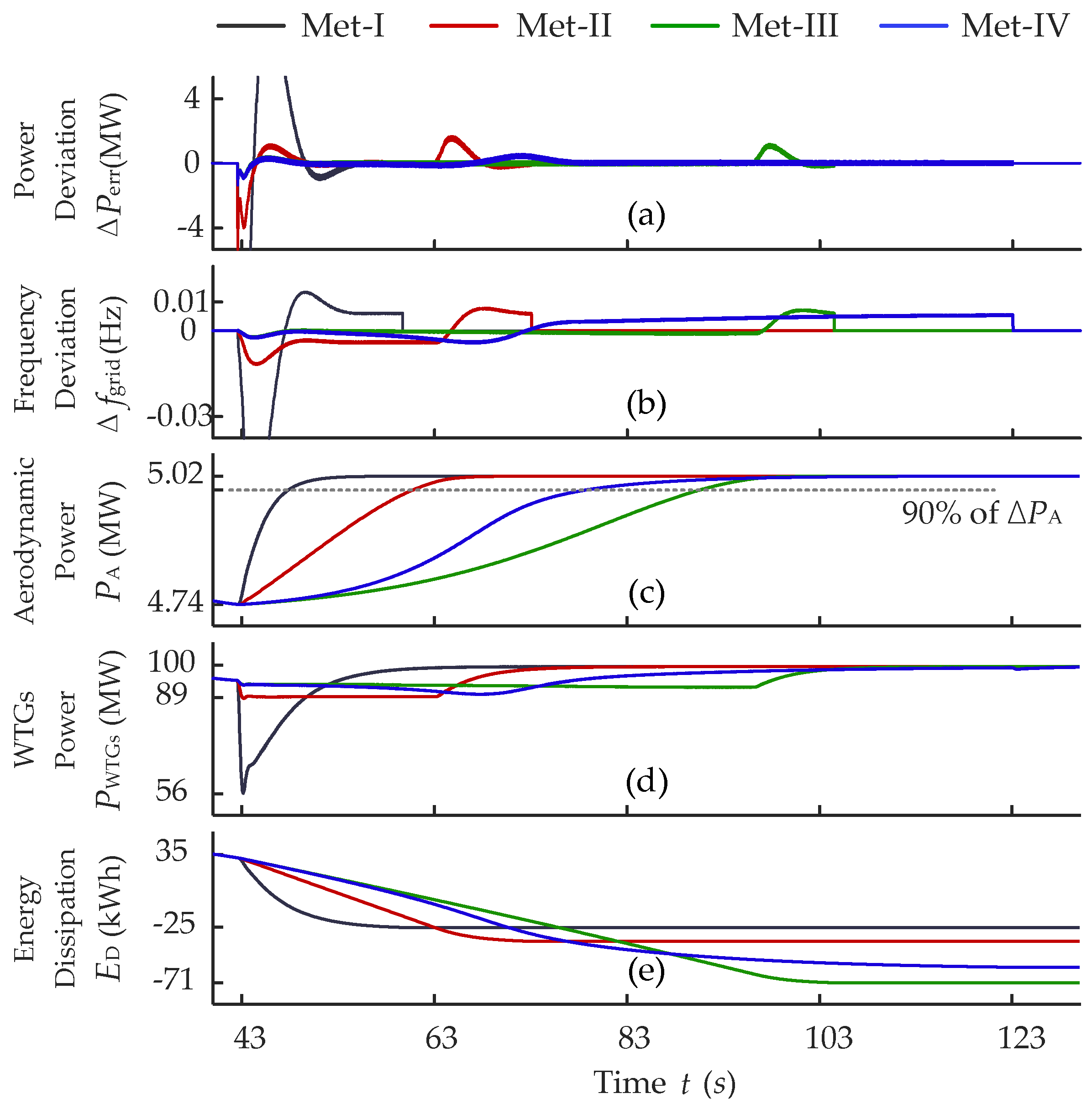
4.3. 30% Wind Power Penetration Scenario
5. Conclusions
- The segmented speed recovery control strategy innovatively utilizes aerodynamic power recovery status and WTG power recovery status, dividing the process into three sequential stages: aerodynamic power recovery stage, WTG power recovery stage, and final speed recovery stage. The proposed strategy employs stage-specific power control functions with differentiated objectives to achieve synergistic optimization of grid disturbance suppression and recovery rate acceleration, holistically improving the speed recovery process performance. Simulation results show that the proposed segmented SRS reduces aerodynamic power recovery time by 28.5% and minimizes power disturbance by 47.3% in a scenario with 30% wind power penetration.
- The speed recovery evaluation framework employs a five-dimensional system, encompassing maximum power deviation, aerodynamic power recovery duration, and power transient intensity, among other critical parameters, to quantify the recovery process performance. Under 10% and 30% wind power penetration level scenarios, the comparative evaluation of speed recovery strategies based on the proposed framework definitively validates the performance superiority of the segmented control strategy.
- The design of the segmented rotor speed recovery strategy in this study is based on the assumption that wind speed variations can be neglected over a time scale of seconds. However, in practical scenarios, fluctuations in wind speed during the rotor speed recovery process may affect the performance of the proposed strategy. Improving the adaptability of the strategy to wind speed variations will be an important direction for future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SRS | Speed Recovery Strategy |
| FR | Frequency regulation |
| PFR | Primary frequency regulation |
| SFR | System frequency response |
| SFD | Secondary frequency drop |
| WTG | Wind turbine generator |
| SG | Synchronous generator |
| GML | Grid-following |
| GFM | Grid-forming |
| VSG | Virtual synchronous generator |
| ESS | Energy storage system |
| MPPT | Maximum power point tracking |
| MPD- | Maximum power deviation, negative |
| MFD- | Maximum frequency deviation, negative |
| APRT | Aerodynamic power recovery time |
| PTI-2 | Power transient intensity, 2nd order |
| TDEDL | Transient dynamic energy dissipation loss |
References
- Zhuo, Z.; Du, E.; Zhang, N.; Nielsen, C.P.; Lu, X.; Xiao, J.; Wu, J.; Kang, C. Cost Increase in the Electricity Supply to Achieve Carbon Neutrality in China. Nat. Commun. 2022, 13, 3172. [Google Scholar] [CrossRef]
- Badesa, L.; Teng, F.; Strbac, G. Conditions for Regional Frequency Stability in Power System Scheduling—Part I: Theory. IEEE Trans. Power Syst. 2021, 36, 5558–5566. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Guo, L.; Li, X.; Liu, Y.; Wang, C. Towards wind farm droop-inertia feasible region assessment: A state space transformation approach considering power system dynamics. Sustain. Energy Technol. Assess. 2024, 71, 103961. [Google Scholar] [CrossRef]
- Lin, C.; Wu, Y. Coordinated Frequency Control Strategy for VSC-HVDC-Connected Wind Farm and Battery Energy Storage System. IEEE Trans. Ind. Appl. 2023, 59, 5314–5328. [Google Scholar] [CrossRef]
- Hu, Z.; Ren, Y.; Meng, Q.; Yun, P.; Fang, C.; Pan, Y. Improvement of Frequency Support for a DFIG Using a Virtual Synchronous Generator Strategy at Large Power Angles. Energies 2023, 16, 914. [Google Scholar] [CrossRef]
- Tafizare, E.; Rahimi, M. Grid-Following and Grid-Forming Control Modes of the Rotor and Grid Sides Converters for Seamless and Universal Operation of the Hybrid DFIG-Wind/Battery Energy Storage System in Grid-Connected and Stand-Alone Conditions. J. Energy Storage 2024, 104, 114623. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, J.; Hung, W.; Wang, C.; Zhang, X.; Bu, S.; Li, Q.; Urdal, H.; Booth, C. Synthetic Inertia Control Strategy for Doubly Fed Induction Generator Wind Turbine Generators Using Lithium-Ion Supercapacitors. IEEE Trans. Energy Convers. 2018, 33, 773–783. [Google Scholar] [CrossRef]
- Wang, S.; Tomsovic, K. A Novel Active Power Control Framework for Wind Turbine Generators to Improve Frequency Re-sponse. IEEE Trans. Power Syst. 2018, 33, 6579–6589. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, Z.; Fu, B.; Gong, S. Research on Frequency Control Method for Micro-Grid with a Hybrid Approach of FFR-OPPT and Pitch Angle of Wind Turbine. Int. J. Electr. Power Energy Syst. 2020, 127, 106670. [Google Scholar] [CrossRef]
- Ouyang, J.; Pang, M.; Li, M.; Zheng, D.; Tang, T.; Wang, W. Frequency control method based on the dynamic deloading of DFIGs for power systems with high-proportion wind energy. Int. J. Electr. Power Energy Syst. 2021, 128, 106764. [Google Scholar] [CrossRef]
- Ma, R.; Yuan, S.; Li, X.; Guan, S.; Yan, X.; Jia, J. Primary Frequency Regulation Strategy Based on Rotor Kinetic Energy of Double-Fed Induction Generator and Supercapacitor. Energies 2024, 17, 331. [Google Scholar] [CrossRef]
- Zhao, H.; Zong, Q.; Zhou, H.; Yao, W.; Sun, K.; Zhou, Y.; Wen, J. Frequency-Voltage Active Support Strategy for Hybrid Wind Farms Based on Grid-Following and Grid-Forming Hierarchical Subgroup Control. CSEE J. Power Energy Syst. 2025, 11, 1–13. [Google Scholar]
- Gao, X.; Wang, Z.; Ding, L.; Bao, W.; Wang, Z.; Hao, Q. A novel virtual synchronous generator control scheme of DFIG-based wind turbine generators based on the rotor current-induced electromotive force. Int. J. Electr. Power Energy Syst. 2024, 156, 109688. [Google Scholar] [CrossRef]
- Kheshti, M.; Ding, L.; Bao, W.; Yin, M.; Wu, Q.; Terzija, V. Toward Intelligent Inertial Frequency Participation of Wind Farms for the Grid Frequency Control. IEEE Trans. Ind. Inform. 2020, 16, 6772–6786. [Google Scholar] [CrossRef]
- Chung, Y.-K.; Wu, Y.-K. Novel Frequency Control Strategy by Wind Turbines Considering Wind Speed Fluctuations and Optimized Power Point Tracking. IEEE Trans. Ind. Appl. 2024, 60, 8191–8202. [Google Scholar] [CrossRef]
- Zhang, Z.; Kou, P.; Zhang, Y.; Liang, D. Coordinated Predictive Control of Offshore DC Collection Grid and Wind Turbines for Frequency Response: A Scheme Without Secondary Frequency Drop. IEEE Trans. Sustain. Energy 2023, 14, 1488–1503. [Google Scholar] [CrossRef]
- Kheshti, M.; Lin, S.; Zhao, X.; Ding, L.; Yin, M.; Terzija, V. Gaussian Distribution-Based Inertial Control of Wind Turbine Gen-erators for Fast Frequency Response in Low Inertia Systems. IEEE Trans. Sustain. Energy 2022, 13, 1641–1653. [Google Scholar] [CrossRef]
- Hu, Z.; Gao, B.; Xu, Z.; Jiang, S. Optimized Temporary Frequency Support for Wind Power Plants Con-sidering Expanded Operational Region of Wind Turbines. CSEE J. Power Energy Syst. 2025, 11, 1–14. [Google Scholar]
- Sun, M.; Sun, Y.; Chen, L.; Zou, Z.; Min, Y.; Liu, R.; Xu, F.; Wu, Y. Novel Temporary Frequency Support Control Strategy of Wind Turbine Generator Considering Coordination with Synchronous Generator. IEEE Trans. Sustain. Energy 2022, 13, 1011–1020. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, Y.; Li, Z.; Tao, J.; Wang, J. Fast Frequency Response Strategy for Wind-Storage Systems Based on Improved Torque Limit Control under Energy Perspective. J. Energy Storage 2025, 111, 115406. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, D.; Zou, X.; He, C.; Hu, J.; Kang, Y. Adaptive Temporary Frequency Support for DFIG-Based Wind Turbines. IEEE Trans. Energy Convers. 2023, 38, 1937–1949. [Google Scholar] [CrossRef]
- Yang, D.; Jin, Z.; Zheng, T.; Jin, E. An Adaptive Droop Control Strategy with Smooth Rotor Speed Recovery Capability for Type III Wind Turbine Generators. Int. J. Electr. Power Energy Syst. 2022, 135, 107532. [Google Scholar] [CrossRef]
- Tao Yukun, Y.F. Flexible Frequency Response Strategy for Wind Turbines Considering Secondary Frequency Drop and Ro-tational Speed Recovery. Autom. Electr. Power Syst. 2023, 48, 60–68. [Google Scholar]
- Gao, H.; Xin, H.; Huang, L.; Li, Z.; Huang, W.; Wu, C.; Ju, P. Common-Mode Frequency in Converter-Integrated Power Systems: Definition, Analysis, and Quantitative Evaluation. IEEE Trans. Power Syst. 2022, 37, 4846–4860. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Cui, H. Analytical Method to Aggregate Multi-Machine SFR Model with Applications in Power System Dynamic Studies. IEEE Trans. Power Syst. 2018, 33, 6355–6367. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, P.; Yang, Y.; Zhao, Z.; Lai, L.L. Fuzzy Adaptive Frequency Support Control Strategy for Wind Turbines With Improved Rotor Speed Recovery. IEEE Trans. Sustain. Energy 2024, 15, 1351–1364. [Google Scholar] [CrossRef]
- Yang, D.; Yan, G.-G.; Zheng, T.; Zhang, X.; Hua, L. Fast Frequency Response of a DFIG Based on Variable Power Point Tracking Control. IEEE Trans. Ind. Appl. 2022, 58, 5127–5135. [Google Scholar] [CrossRef]
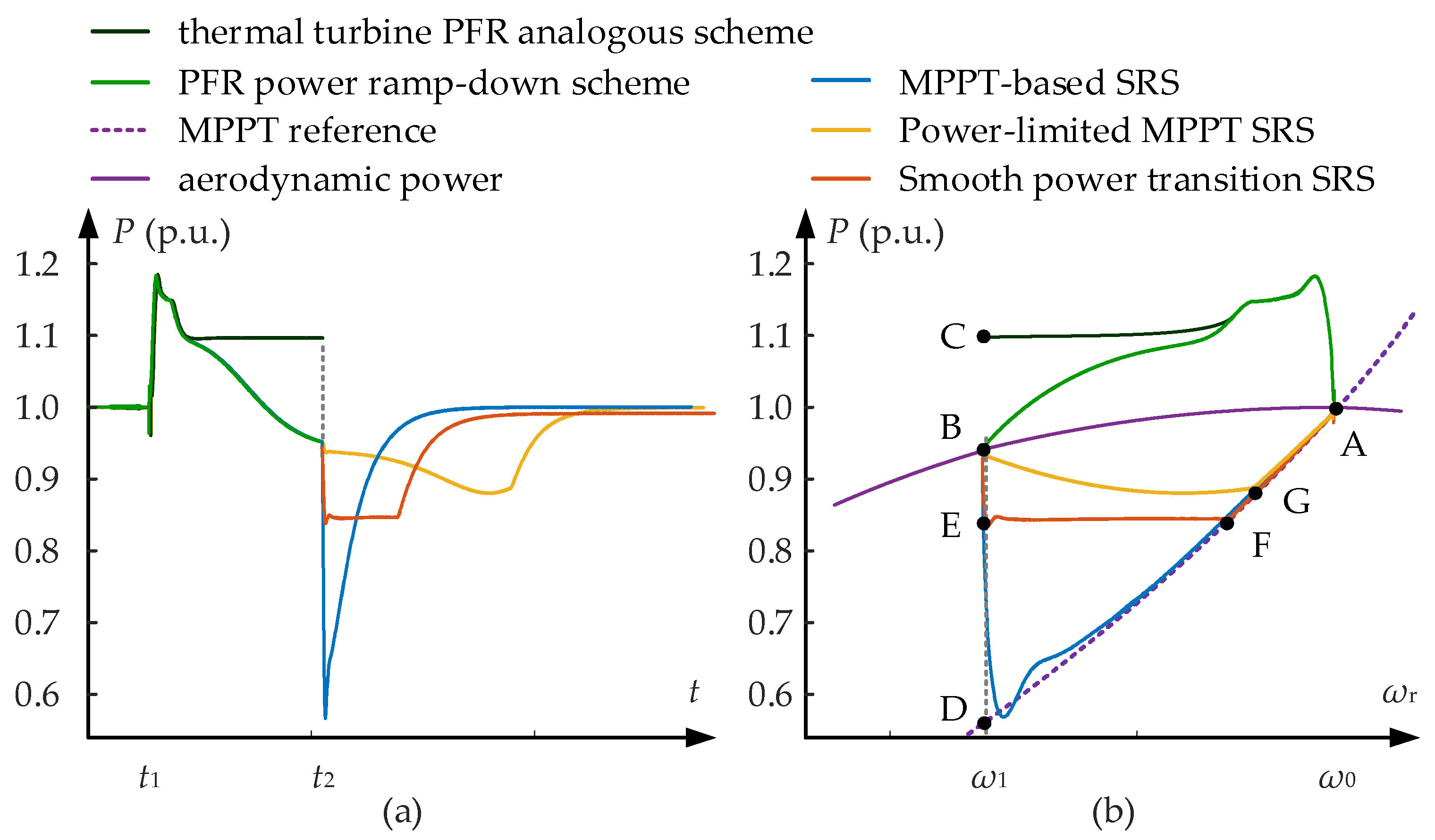










| Speed Recovery Strategy (SRS) | Trajectory in Figure 2b | Characteristic |
|---|---|---|
| MPPT-based SRS [17] | B→D→A | Fast rotor speed recovery; large power disturbances; high power ramp rate; high SFD induction risk |
| Power-limited MPPT SRS [18] | B→E→F→A | Moderate rotor speed recovery; moderate power disturbances; high power ramp rate; moderate SFD risk |
| Smooth power transition SRS [19] | B→G→A | Slow rotor speed recovery; mild power disturbances; low power ramp rate; low SFD risk |
| Parameter and Designation | Value |
|---|---|
| System-rated frequency fgrid | 50 Hz |
| SG G1/G2/G3 rated power | 400 MW |
| Load L1/L2/L3 rated power | 300/300/350 MW |
| Load disturbance Ld power | 50 MW |
| SG G1/G2/G3 speed regulation droop coefficient | 0.03 |
| Time constant of the governor system | 5 s |
| Wind farm-rated power | 100/300 MW (in 4.2/4.3) |
| DFIG-rated voltage UWTG | 950 V (line-to-line) |
| DFIG-rated power PWTG | 5 MW |
| Number of pole pairs np | 2 |
| Rated rotor speed ωr | 188 rad/s |
| DFIG stator-to-rotor turns ratio | 0.33 |
| Wind turbine inertia time constant HWTG | 5.2 s |
| Speed recovery control parameters k1~k2 (p.u.), k3~k4, δ | −0.75, 0.67, 0.3, 0.7, 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Hu, Z.; Zhao, Z.; Ren, Y. Optimal Process Control for Rotor Speed Recovery and Secondary Frequency Drop Mitigation in Wind Turbine Frequency Regulation. Processes 2025, 13, 1932. https://doi.org/10.3390/pr13061932
Yang L, Hu Z, Zhao Z, Ren Y. Optimal Process Control for Rotor Speed Recovery and Secondary Frequency Drop Mitigation in Wind Turbine Frequency Regulation. Processes. 2025; 13(6):1932. https://doi.org/10.3390/pr13061932
Chicago/Turabian StyleYang, Liqing, Zhishuai Hu, Zhenzhou Zhao, and Yongfeng Ren. 2025. "Optimal Process Control for Rotor Speed Recovery and Secondary Frequency Drop Mitigation in Wind Turbine Frequency Regulation" Processes 13, no. 6: 1932. https://doi.org/10.3390/pr13061932
APA StyleYang, L., Hu, Z., Zhao, Z., & Ren, Y. (2025). Optimal Process Control for Rotor Speed Recovery and Secondary Frequency Drop Mitigation in Wind Turbine Frequency Regulation. Processes, 13(6), 1932. https://doi.org/10.3390/pr13061932







