Research on the Real-Time Prediction of Wind Turbine Blade Icing Process Based on the MLP Neural Network Model and Meteorological Parameters
Abstract
1. Introduction
2. Implementation of CFD Simulation
2.1. Blade Element
2.2. Meteorological Conditions and Icing State Parameters
2.3. Assumptions
- (1)
- Three-dimensional and rotational effects on the icing process are neglected;
- (2)
- The icing process is studied based on blade elements, with no interaction between adjacent blade elements;
- (3)
- Water droplets are uniformly distributed in the air;
- (4)
- The blade surface is adiabatic.
2.4. Simulation Software and Basic Parameters
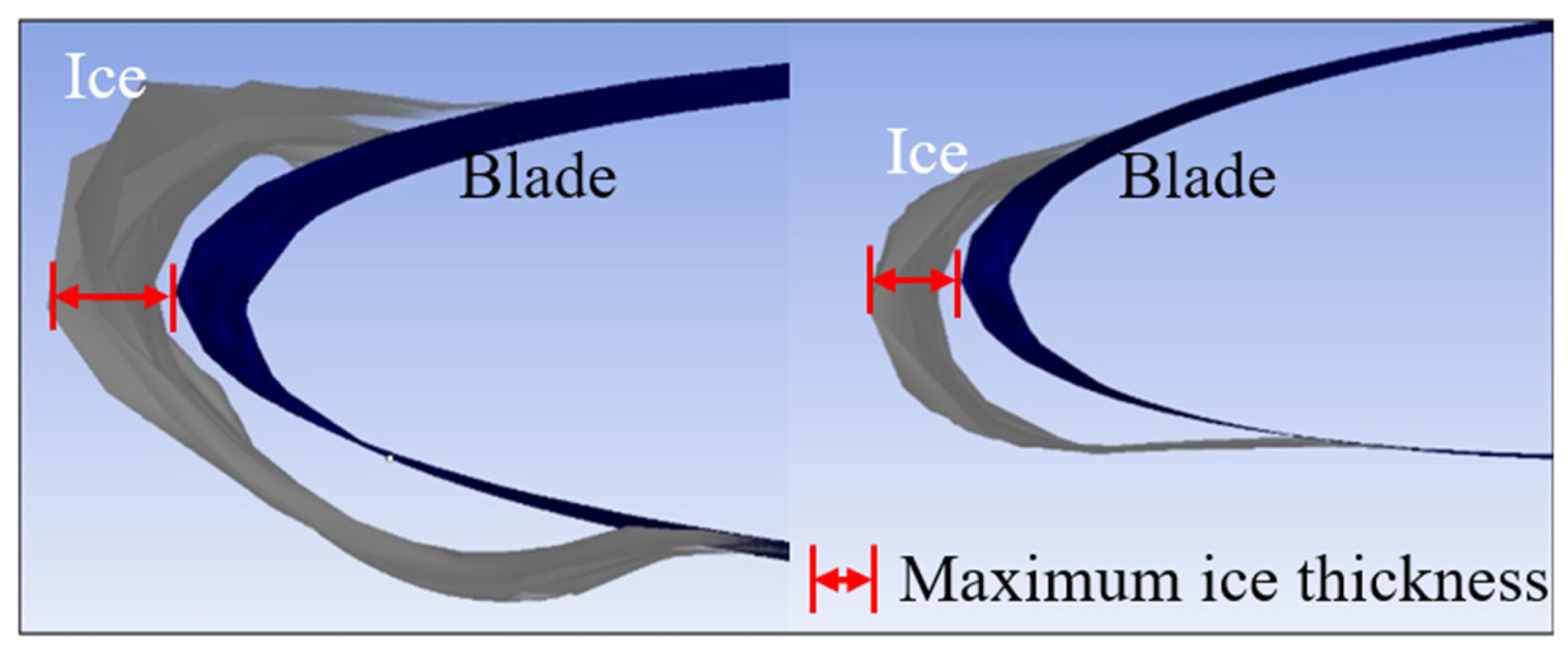
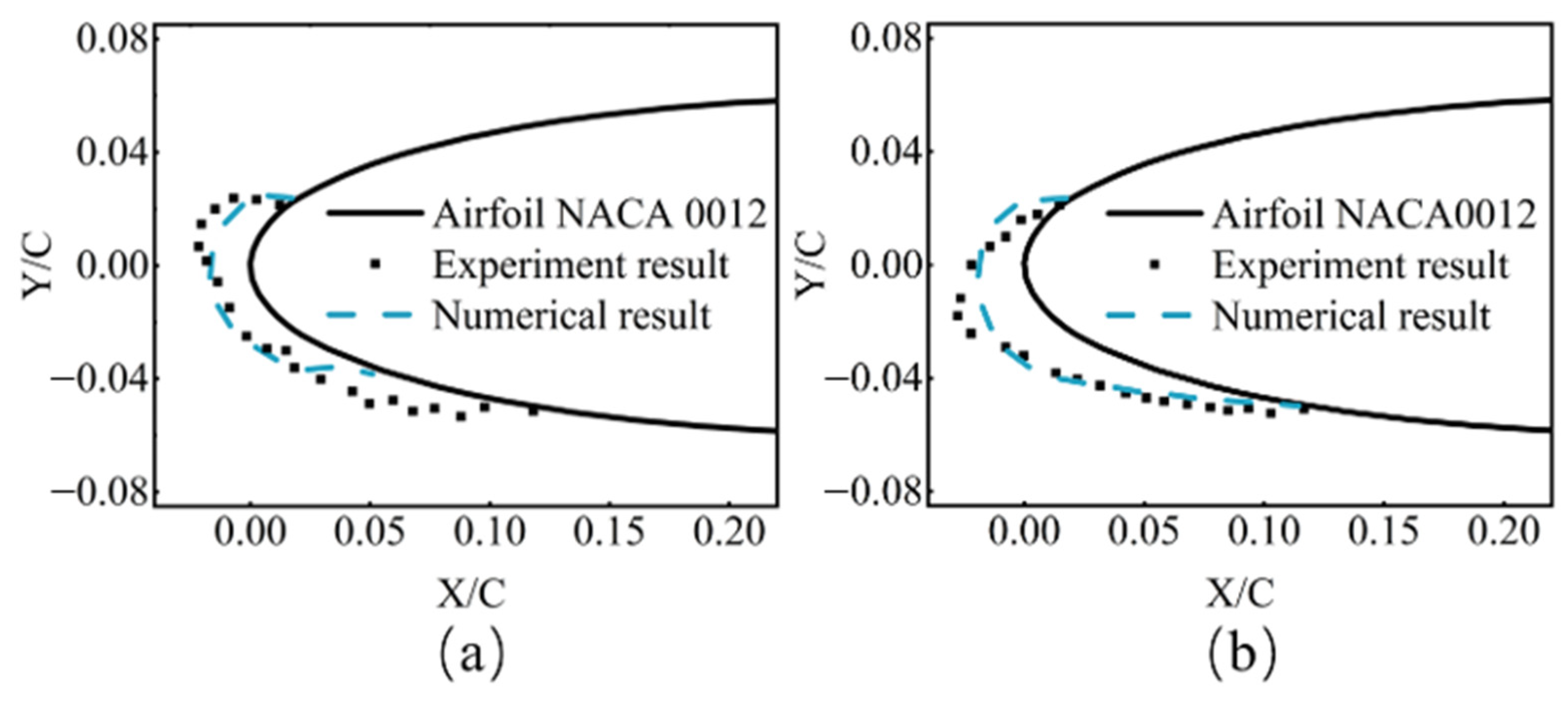
2.5. Simulation Verification
3. Implementation of MLP Model
3.1. Neural Network
3.2. Dataset and Dataset Division
3.3. Neural Network Structure Design
4. Results and Discussion
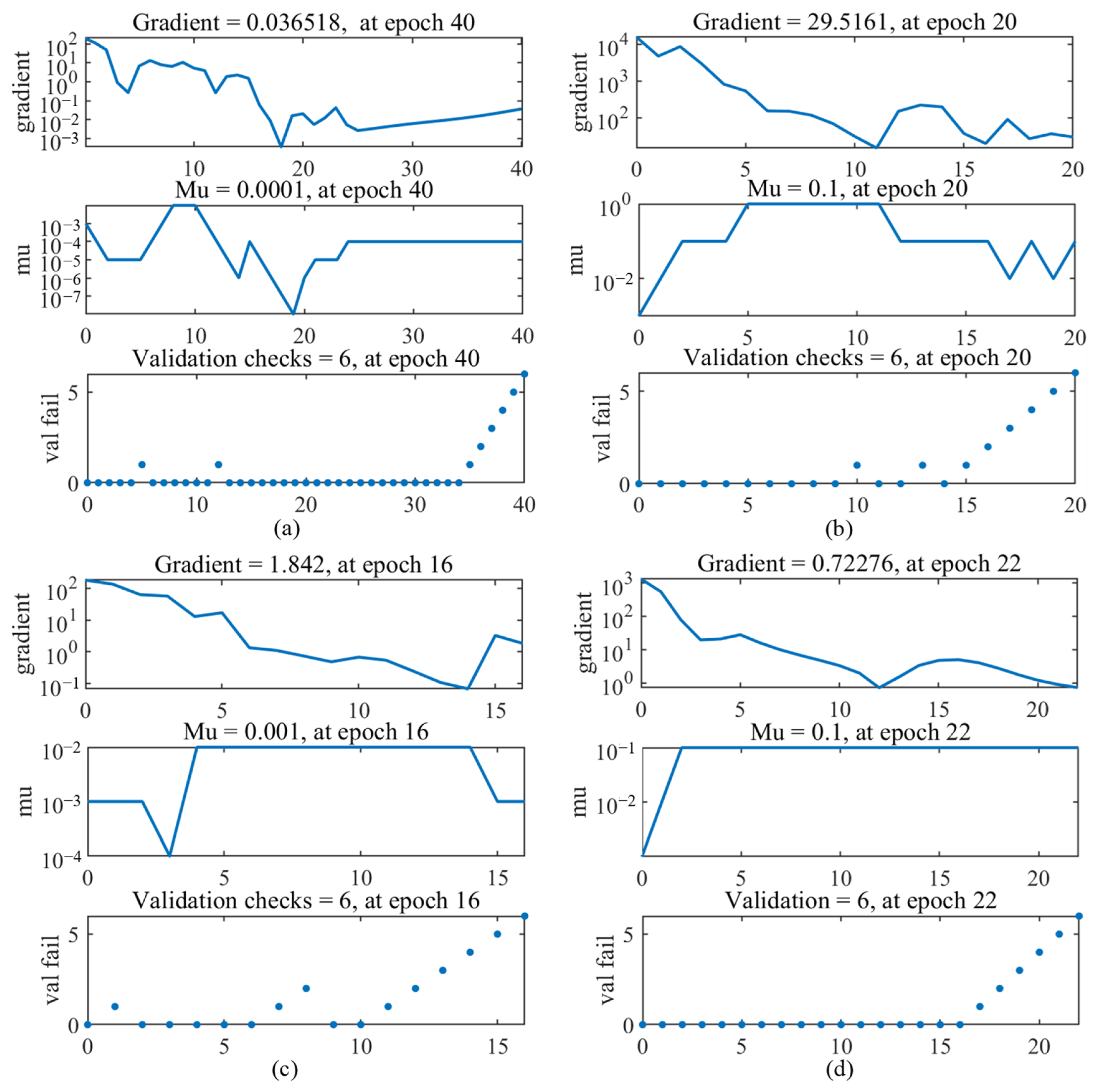
4.1. Final Model Configuration
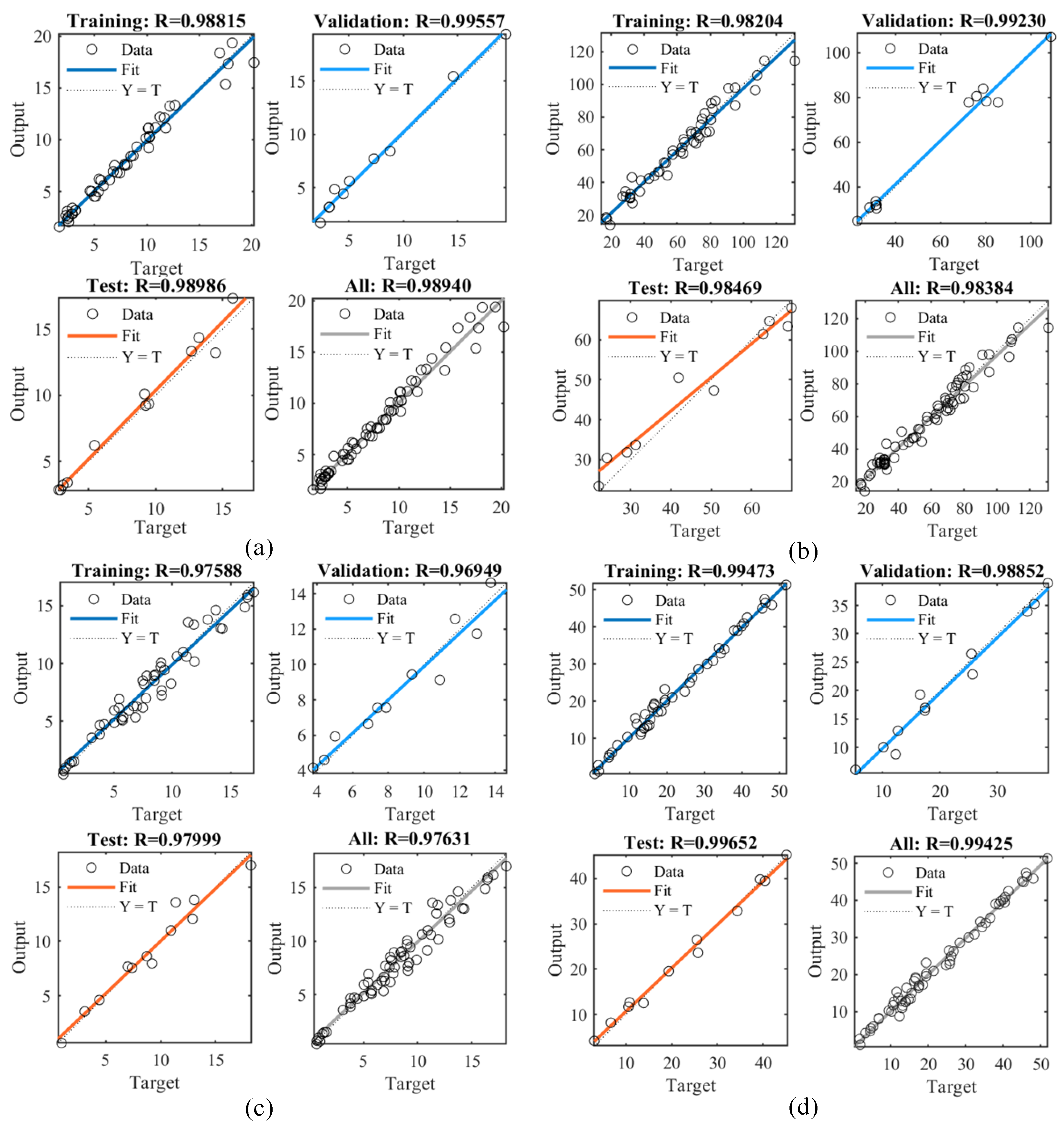
4.2. Model Performance Evaluation
4.3. Model Practicality
5. Conclusions
- (1)
- Compared with traditional numerical model prediction, this method can quickly predict the mass and thickness of icing based on icing conditions, improving computational efficiency.
- (2)
- The constructed MLP model demonstrates strong predictive accuracy, with MAPE values of 7.13% for rime ice mass prediction and 7.02% for rime ice thickness. For glaze ice, the MAPE values are 10.22% for mass and 9.42% for thickness, indicating reliable performance across different icing types.
- (3)
- With R2 values exceeding 0.95 for all models, the results confirm the MLP neural network’s suitability for accurately predicting the icing process. This high level of agreement between the predicted and actual values underscores the model’s robustness.
- (4)
- The MLP neural network’s method for predicting the icing process shows strong potential for application in wind farms. It enables the rapid forecasting of blade icing conditions while maintaining prediction accuracy, even under fluctuating climatic parameters. This capability is of particular value in dealing with the challenges that climate variability poses to wind power generation.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Number of hidden layer neurons |
| m | Number of input layer neurons |
| N | Total sample size |
| n | Number of output layer neurons |
| x | Input variable of the layer |
| Actual value of the i sample | |
| Predicted value of the i sample | |
| Mean of the actual value | |
| Mean of the predicted value | |
| α | Random constant |
| ANN | Artificial neural network |
| BP | Backpropagation |
| CFD | Computational Fluid Dynamics |
| DNN | Deep neural network |
| LM | Levenberg–Marquardt |
| LWC | Liquid water content |
| MAPE | Mean absolute percentage error |
| MLP | Multilayer Perceptron |
| MSE | Mean Squared Error |
| MVD | Median volume diameter |
| R | Pearson correlation coefficient |
| R2 | R-squared |
| SCG | Scaled Conjugate Gradient |
References
- Lamraoui, F.; Fortin, G.; Benoit, R.; Perron, J.; Masson, C. Atmospheric icing impact on wind turbine production. Cold Reg. Sci. Technol. 2014, 100, 36–49. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Pope, K.; Muzychka, Y.S. Effects of blade design on ice accretion for horizontal axis wind turbines. J. Wind Eng. Ind. Aerodyn. 2018, 173, 39–52. [Google Scholar] [CrossRef]
- Shu, L.; Li, H.; Hu, Q.; Jiang, X.; Qiu, G.; McClure, G.; Yang, H. Study of ice accretion feature and power characteristics of wind turbines at natural icing environment. Cold Reg. Sci. Technol. 2018, 147, 45–54. [Google Scholar] [CrossRef]
- Gao, L.; Dasari, T.; Hong, J. Wind farm icing loss forecast pertinent to winter extremes. Sustain. Energy Technol. Assess. 2022, 50, 101872. [Google Scholar] [CrossRef]
- Yirtici, O.; Tuncer, I.H. Aerodynamic shape optimization of wind turbine blades for minimizing power production losses due to icing. Cold Reg. Sci. Technol. 2021, 185, 103250. [Google Scholar] [CrossRef]
- Gao, L.; Liu, Y.; Ma, L.; Hu, H. A hybrid strategy combining minimized leading-edge electric-heating and superhydro-/ice-phobic surface coating for wind turbine icing mitigation. Renew. Energy 2019, 140, 943–956. [Google Scholar] [CrossRef]
- Wang, Z. Recent progress on ultrasonic de-icing technique used for wind power generation, high-voltage transmission line and aircraft. Energy Build. 2017, 140, 42–49. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, X.; Liu, Y.; Ren, J.; Yang, J.; Chen, N. Numerical investigation of dynamic icing of wind turbine blades under wind shear conditions. Renew. Energy 2024, 227, 120495. [Google Scholar] [CrossRef]
- Dalili, N.; Edrisy, A.; Carriveau, R. A review of surface engineering issues critical to wind turbine performance. Renew. Sustain. Energy Rev. 2009, 13, 428–438. [Google Scholar] [CrossRef]
- Ye, F.; Ezzat, A.A. Icing detection and prediction for wind turbines using multivariate sensor data and machine learning. Renew. Energy 2024, 231, 120879. [Google Scholar] [CrossRef]
- Hu, Q.; Xu, X.; Leng, D.; Shu, L.; Jiang, X.; Virk, M.; Yin, P. A method for measuring ice thickness of wind turbine blades based on edge detection. Cold Reg. Sci. Technol. 2021, 192, 103398. [Google Scholar] [CrossRef]
- Sirui, Y.; Mengjie, S.; Runmiao, G.; Jiwoong, B.; Xuan, Z.; Shiqiang, Z. A review of icing prediction techniques for four typical surfaces in low-temperature natural environments. Appl. Therm. Eng. 2024, 241, 122418. [Google Scholar] [CrossRef]
- Bose, N. Icing on a small horizontal-axis wind turbine—Part 1: Glaze ice profiles. J. Wind Eng. Ind. Aerodyn. 1992, 45, 75–85. [Google Scholar] [CrossRef]
- Fu, P.; Farzaneh, M. A CFD approach for modeling the rime-ice accretion process on a horizontal-axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2010, 98, 181–188. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J.; Schmitz, S. Scaled ice accretion experiments on a rotating wind turbine blade. J. Wind Eng. Ind. Aerodyn. 2012, 109, 55–67. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, X.; Liu, Y.; Ren, J.; Li, W.; Wang, Q.; Lai, Q. Simulation and analysis of wind turbine ice accretion under yaw condition via an Improved Multi-Shot Icing Computational Model. Renew. Energy 2020, 162, 1854–1873. [Google Scholar] [CrossRef]
- Chuang, Z.; Li, C.; Liu, S.; Li, X.; Li, Z.; Zhou, L. Numerical analysis of blade icing influence on the dynamic response of an integrated offshore wind turbine. Ocean Eng. 2022, 257, 111593. [Google Scholar] [CrossRef]
- Chuang, Z.; Yi, H.; Chang, X.; Liu, H.; Zhang, H.; Xia, L. Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions. J. Mar. Sci. Eng. 2023, 11, 1125. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Pope, K.; Naterer, G.F. Extended scaling approach for droplet flow and glaze ice accretion on a rotating wind turbine blade. J. Wind Eng. Ind. Aerodyn. 2023, 233, 105296. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Pope, K.; Naterer, G.F. Scaling formulation of multiphase flow and droplet trajectories with rime ice accretion on a rotating wind turbine blade. J. Wind Eng. Ind. Aerodyn. 2023, 232, 105247. [Google Scholar] [CrossRef]
- Cao, H.Q.; Bai, X.; Ma, X.D.; Yin, Q.; Yang, X.Y. Numerical Simulation of Icing on Nrel 5-MW Reference Offshore Wind Turbine Blades Under Different Icing Conditions. China Ocean Eng. 2022, 36, 767–780. [Google Scholar] [CrossRef]
- Shu, L.; Liang, J.; Hu, Q.; Jiang, X.; Ren, X.; Qiu, G. Study on small wind turbine icing and its performance. Cold Reg. Sci. Technol. 2017, 134, 11–19. [Google Scholar] [CrossRef]
- Li, T.; Xu, J.; Liu, Z.; Wang, D.; Tan, W. Detecting Icing on the Blades of a Wind Turbine Using a Deep Neural Network. CMES-Comput. Model. Eng. Sci. 2022, 134, 767–782. [Google Scholar] [CrossRef]
- Kreutz, M.; Ait Alla, A.; Lütjen, M.; Ohlendorf, J.H.; Freitag, M.; Thoben, K.D.; Zimnol, F.; Greulich, A. Ice prediction for wind turbine rotor blades with time series data and a deep learning approach. Cold Reg. Sci. Technol. 2023, 206, 103741. [Google Scholar] [CrossRef]
- LB Effects and Prevention Systems of Icing on Wind Turbines in Cold Climates; Mechanical Industry Press: Beijing, China, 2022.
- Guo, W.; Shen, H.; Li, Y.; Feng, F.; Tagawa, K. Wind tunnel tests of the rime icing characteristics of a straight-bladed vertical axis wind turbine. Renew. Energy 2021, 179, 116–132. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, T.; Li, X.; Li, Y. Effects of ambient temperature and wind speed on icing characteristics and anti-icing energy demand of a blade airfoil for wind turbine. Renew. Energy 2023, 217, 119135. [Google Scholar] [CrossRef]
- Homola, M.C.; Virk, M.S.; Wallenius, T.; Nicklasson, P.J.; Sundsbø, P.A. Effect of atmospheric temperature and droplet size variation on ice accretion of wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2010, 98, 724–729. [Google Scholar] [CrossRef]
- Li, Y.; Tagawa, K.; Feng, F.; Li, Q.; He, Q. A wind tunnel experimental study of icing on wind turbine blade airfoil. Energy Convers. Manag. 2014, 85, 591–595. [Google Scholar] [CrossRef]
- Lisheng, M.; He, S.; Yan, C.; Huanyu, D.; Xiaofeng, L. A numerical simulation of the distribution and the variation law of the liquid water content in icing wind tunnel. Appl. Therm. Eng. 2024, 236, 121539. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J.; Smith, E. An Experimental Correlation Between Rotor Test and Wind Tunnel Ice Shapes on NACA 0012 Airfoils2011; No. 2011-38-0092 SAE Technical Paper; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Emambocus, B.A.S.; Jasser, M.B.; Amphawan, A. A Survey on the Optimization of Artificial Neural Networks Using Swarm Intelligence Algorithms. IEEE Access 2023, 11, 1280–1294. [Google Scholar] [CrossRef]
- Cong, T.; Su, G.; Qiu, S.; Tian, W. Applications of ANNs in flow and heat transfer problems in nuclear engineering: A review work. Prog. Nucl. Energy 2013, 62, 54–71. [Google Scholar] [CrossRef]
- Ding, L. Human Knowledge in Constructing AI Systems—Neural Logic Networks Approach towards an Explainable AI. Procedia Comput. Sci. 2018, 126, 1561–1570. [Google Scholar] [CrossRef]
- Zarei, T.; Behyad, R. Predicting the water production of a solar seawater greenhouse desalination unit using multi-layer perceptron model. Sol. Energy 2019, 177, 595–603. [Google Scholar] [CrossRef]
- Tao, P.; Cheng, J.; Chen, L. Brain-inspired chaotic backpropagation for MLP. Neural Netw. 2022, 155, 1–13. [Google Scholar] [CrossRef]
- Hamed, M.M.; Khalafallah, M.G.; Hassanien, E.A. Prediction of wastewater treatment plant performance using artificial neural networks. Environ. Model. Softw. 2004, 19, 919–928. [Google Scholar] [CrossRef]
- Yuan, E. Artificial Neural Networks and Their Applications; Tsinghua University Press: Beijing, China, 1999. [Google Scholar]
- Hemmati-Sarapardeh, A.; Varamesh, A.; Husein, M.M.; Karan, K. On the evaluation of the viscosity of nanofluid systems: Modeling and data assessment. Renew. Sustain. Energy Rev. 2018, 81, 313–329. [Google Scholar] [CrossRef]
- Bayrak, G.; Yılmaz, A.; Çalışır, A. A new intelligent decision-maker method determining the optimal connection point and operating conditions of hydrogen energy-based DGs to the main grid. Int. J. Hydrogen Energy 2023, 48, 23168–23184. [Google Scholar] [CrossRef]









| Rime Ice | Glaze Ice | ||||||
|---|---|---|---|---|---|---|---|
| Temperature (°C) | LWC (g/m3) | Inflow Velocities (m/s) | Temperature (°C) | LWC (g/m3) | Inflow Velocities (m/s) | ||
| 1 | −15 | 0.90 | 50 | 1 | −7 | 1.0 | 60 |
| 2 | −12 | 1.20 | 30 | 2 | −5 | 2.5 | 20 |
| 3 | −16 | 0.45 | 40 | 3 | −10 | 3.5 | 80 |
| 4 | −17 | 1.20 | 70 | 4 | −9 | 4.5 | 90 |
| 5 | −13 | 0.45 | 50 | 5 | −3 | 2.0 | 60 |
| 6 | −19 | 0.90 | 70 | 6 | −5 | 2.0 | 80 |
| 7 | −13 | 0.90 | 90 | 7 | −2 | 2.0 | 50 |
| 8 | −13 | 1.50 | 80 | 8 | −2 | 5.0 | 70 |
| …… | …… | …… | …… | …… | …… | …… | …… |
| 81 | −15 | 0.60 | 80 | 81 | −2 | 1.0 | 10 |
| Algorithm | Neurons of Hidden Layer (Optimal) | Training Set | Validation Set | Test Set | |||
|---|---|---|---|---|---|---|---|
| MSE | R | MSE | R | MSE | R | ||
| LM | 1~5 (2) | 0.83411 | 0.98278 | 0.54557 | 0.98992 | 0.61996 | 0.98788 |
| LM | 6~10 (7) | 0.27298 | 0.99368 | 0.36988 | 0.99234 | 0.75867 | 0.98814 |
| LM | 11~15 (11) | 0.33202 | 0.99414 | 0.64000 | 0.98749 | 0.97475 | 0.98589 |
| SCG | 1~5 (1) | 1.60537 | 0.96734 | 0.70722 | 0.98676 | 1.57039 | 0.97123 |
| SCG | 6~10 (9) | 1.07933 | 0.97531 | 1.57133 | 0.96681 | 1.52062 | 0.96970 |
| SCG | 11~15 (11) | 1.04076 | 0.97580 | 1.38196 | 0.97597 | 1.36700 | 0.96722 |
| Algorithm | Neurons of Hidden Layer (Optimal) | Training Set | Validation Set | Test Set | |||
|---|---|---|---|---|---|---|---|
| MSE | R | MSE | R | MSE | R | ||
| LM | 1~5 (5) | 29.30641 | 0.98267 | 29.44242 | 0.97971 | 30.97942 | 0.97433 |
| LM | 6~10 (6) | 26.38219 | 0.98193 | 28.43736 | 0.98287 | 36.46518 | 0.97332 |
| LM | 11~15 (11) | 18.16991 | 0.98748 | 37.12486 | 0.96723 | 43.60025 | 0.97435 |
| SCG | 1~5 (1) | 54.77910 | 0.96212 | 59.44750 | 0.96000 | 42.13290 | 0.96724 |
| SCG | 6~10 (7) | 34.76492 | 0.97356 | 41.49538 | 0.97121 | 56.75743 | 0.97389 |
| SCG | 11~15 (12) | 40.30357 | 0.96970 | 44.65316 | 0.97107 | 47.28508 | 0.96563 |
| Algorithm | Neurons of Hidden Layer (Optimal) | Training Set | Validation Set | Test Set | |||
|---|---|---|---|---|---|---|---|
| MSE | R | MSE | R | MSE | R | ||
| LM | 1~5 (3) | 0.96700 | 0.97293 | 1.08500 | 0.96655 | 1.12500 | 0.96042 |
| LM | 6~10 (10) | 0.73346 | 0.98127 | 1.55606 | 0.96475 | 1.54762 | 0.94884 |
| LM | 11~15 (11) | 0.71901 | 0.98160 | 1.32484 | 0.96582 | 1.54757 | 0.94193 |
| SCG | 1~5 (3) | 1.91100 | 0.94508 | 1.58700 | 0.95240 | 2.02600 | 0.94549 |
| SCG | 6~10 (6) | 1.85511 | 0.94253 | 1.93382 | 0.93854 | 2.22085 | 0.95486 |
| SCG | 11~15 (11) | 1.56629 | 0.95334 | 1.81056 | 0.94540 | 2.35023 | 0.92321 |
| Algorithm | Neurons of Hidden Layer (Optimal) | Training Set | Validation Set | Test Set | |||
|---|---|---|---|---|---|---|---|
| MSE | R | MSE | R | MSE | R | ||
| LM | 1~5 (4) | 2.30446 | 0.99347 | 3.18796 | 0.99275 | 4.01227 | 0.98896 |
| LM | 6~10 (9) | 1.33831 | 0.99624 | 5.48801 | 0.98442 | 3.33344 | 0.99153 |
| LM | 11~15 (11) | 1.83584 | 0.99534 | 4.30354 | 0.98875 | 5.23997 | 0.98494 |
| SCG | 1~5 (3) | 9.92700 | 0.97381 | 9.44600 | 0.96896 | 10.9500 | 0.96690 |
| SCG | 6~10 (6) | 7.96202 | 0.97847 | 6.65297 | 0.98106 | 9.73238 | 0.97647 |
| SCG | 11~15 (11) | 4.80470 | 0.98628 | 6.42141 | 0.98145 | 11.6408 | 0.96594 |
| MSE | R2 | MAPE | |
|---|---|---|---|
| MLP for accretion mass of rime ice | 0.4488 | 0.9785 | 7.13% |
| MLP for maximum thickness of rime ice | 22.3434 | 0.9673 | 7.02% |
| MLP for accretion mass of glaze ice | 0.7974 | 0.9531 | 10.22% |
| MLP for maximum thickness of glaze ice | 2.0543 | 0.9885 | 9.42% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, N.; Cao, Q.; Zeng, Z.; Ma, K.; Zeng, S. Research on the Real-Time Prediction of Wind Turbine Blade Icing Process Based on the MLP Neural Network Model and Meteorological Parameters. Processes 2025, 13, 1910. https://doi.org/10.3390/pr13061910
Xie N, Cao Q, Zeng Z, Ma K, Zeng S. Research on the Real-Time Prediction of Wind Turbine Blade Icing Process Based on the MLP Neural Network Model and Meteorological Parameters. Processes. 2025; 13(6):1910. https://doi.org/10.3390/pr13061910
Chicago/Turabian StyleXie, Nan, Qingqing Cao, Zhixiang Zeng, Kebo Ma, and Sizhun Zeng. 2025. "Research on the Real-Time Prediction of Wind Turbine Blade Icing Process Based on the MLP Neural Network Model and Meteorological Parameters" Processes 13, no. 6: 1910. https://doi.org/10.3390/pr13061910
APA StyleXie, N., Cao, Q., Zeng, Z., Ma, K., & Zeng, S. (2025). Research on the Real-Time Prediction of Wind Turbine Blade Icing Process Based on the MLP Neural Network Model and Meteorological Parameters. Processes, 13(6), 1910. https://doi.org/10.3390/pr13061910






