Research on a Sand-Carrying Model of Horizontal Sections of Deep Coalbed Methane Wells
Abstract
1. Introduction
2. Theoretical Analysis
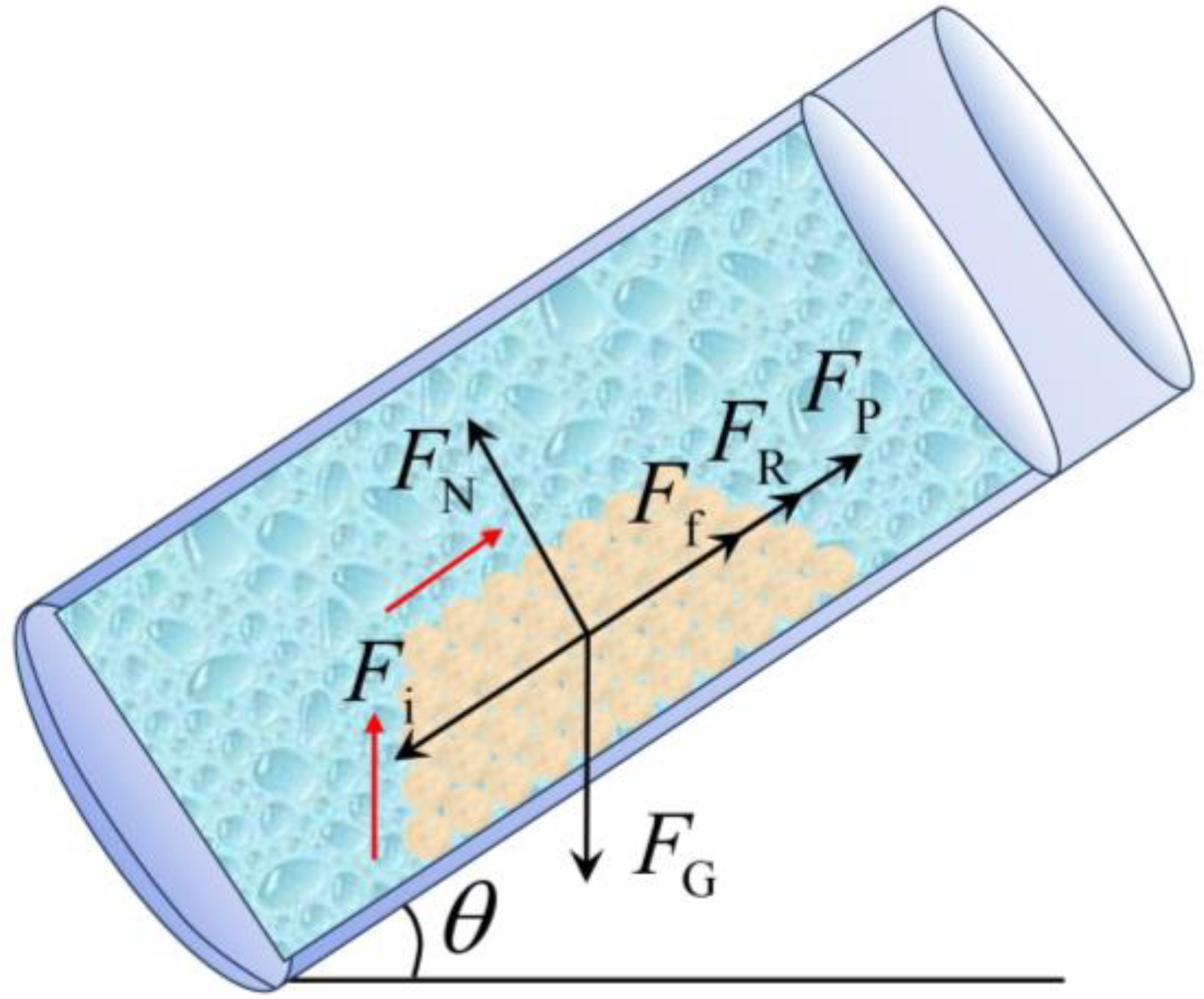
2.1. Sand Force Analysis
2.2. Establishment of the Critical Sand-Carrying Theoretical Model
3. Experimental System and Operating Conditions
3.1. Experimental Loop
3.2. Determination of the Experimental Scheme
3.3. Experimental Operation Conditions
4. Experimental Results and Discussion
4.1. Standard Deviation Analysis of Experimental Data
4.2. Analysis of Critical Flow State
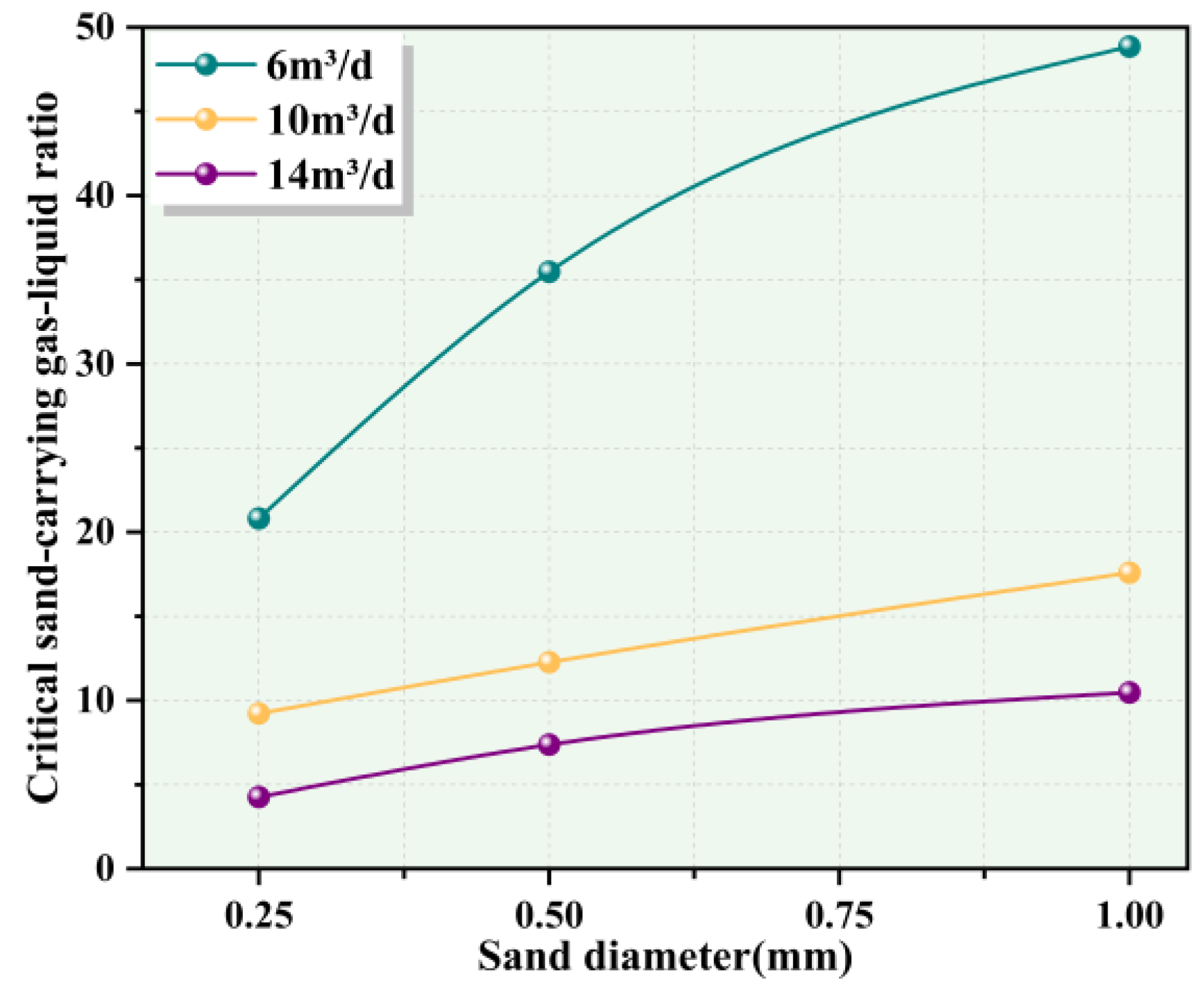
4.3. Effect of Different Water Flow Rates on Sand-Carrying
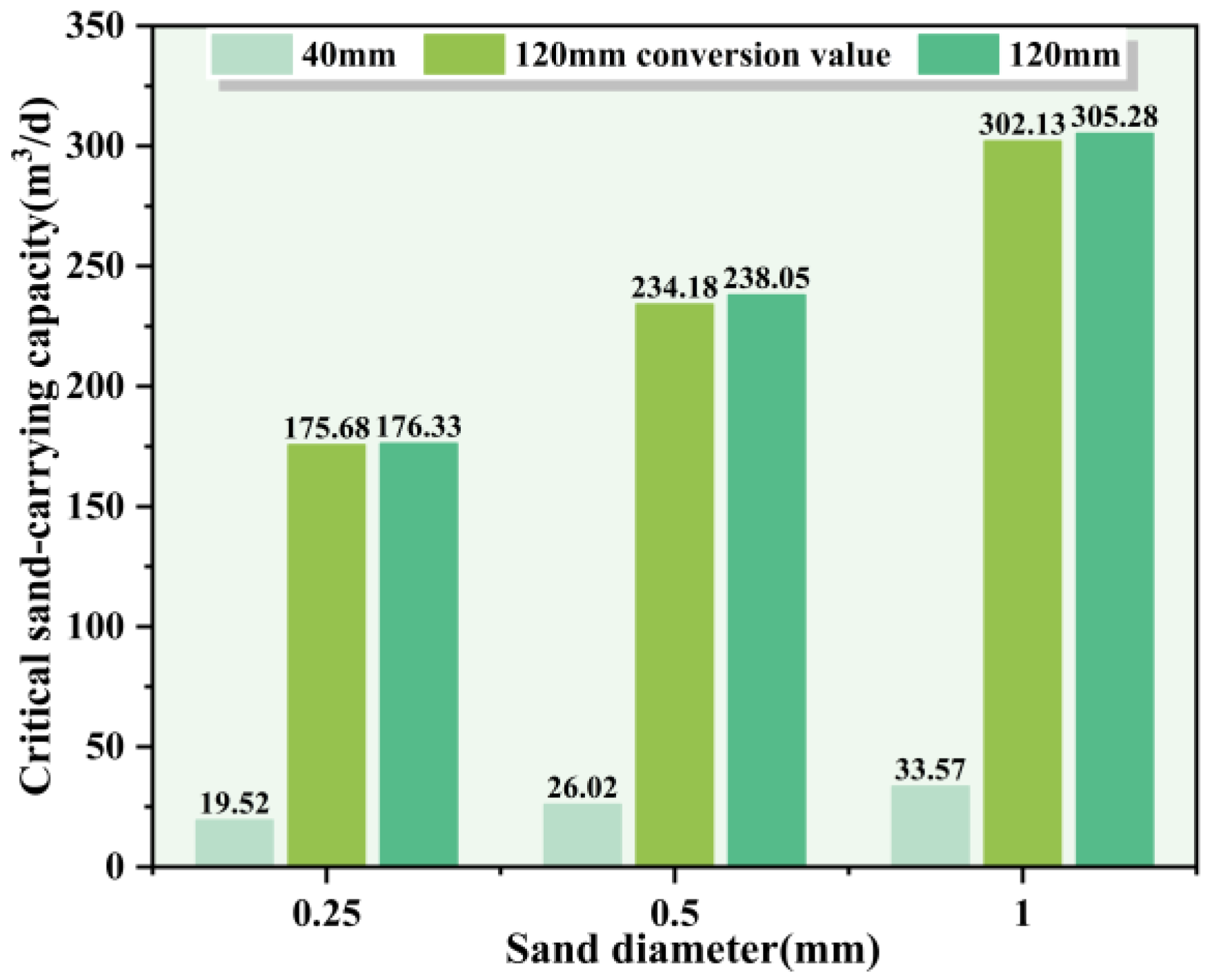
4.4. Effect of Different Sand Diameters on Sand-Carrying
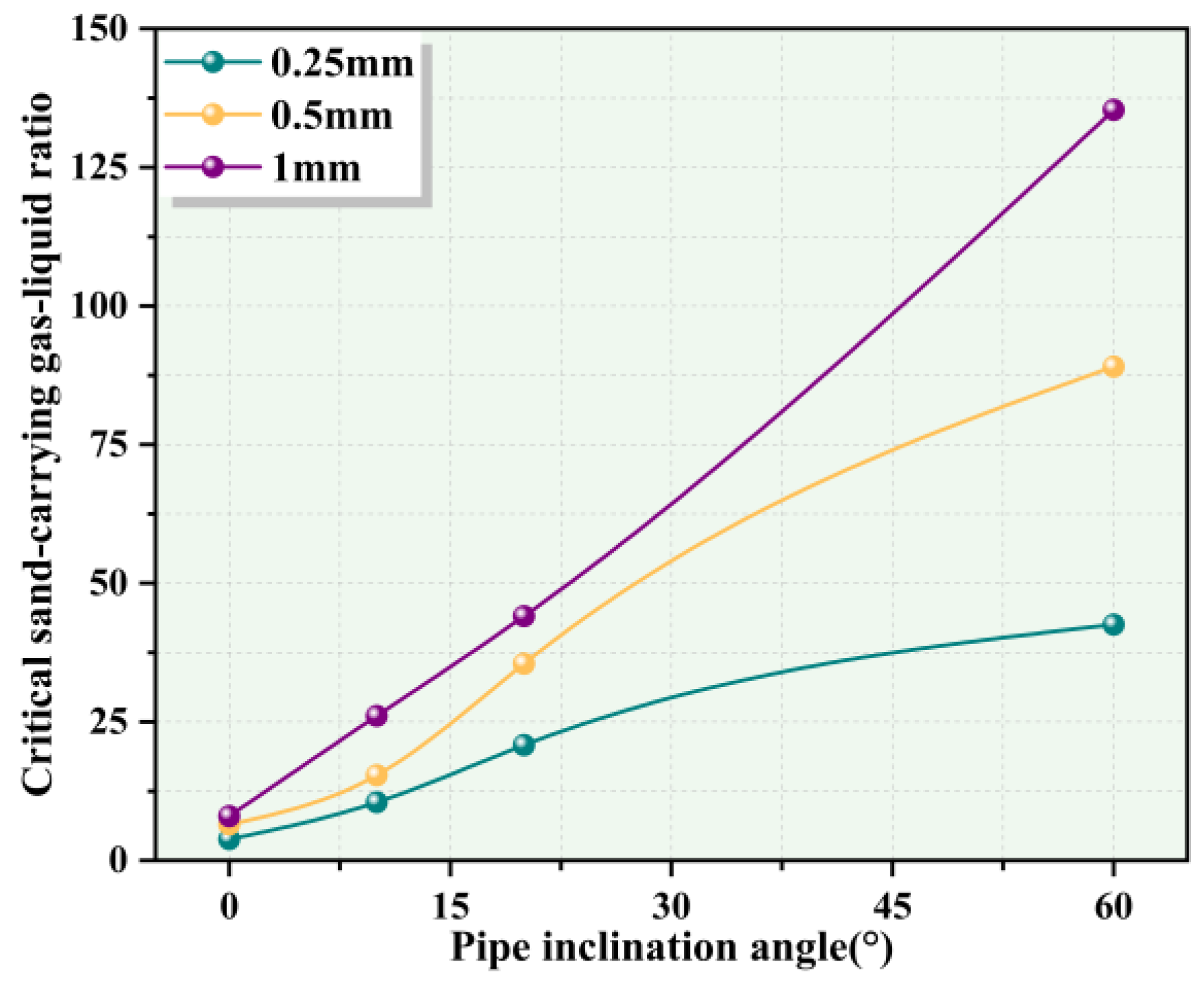
4.5. Effect of Different Inclination Angles on Sand-Carrying
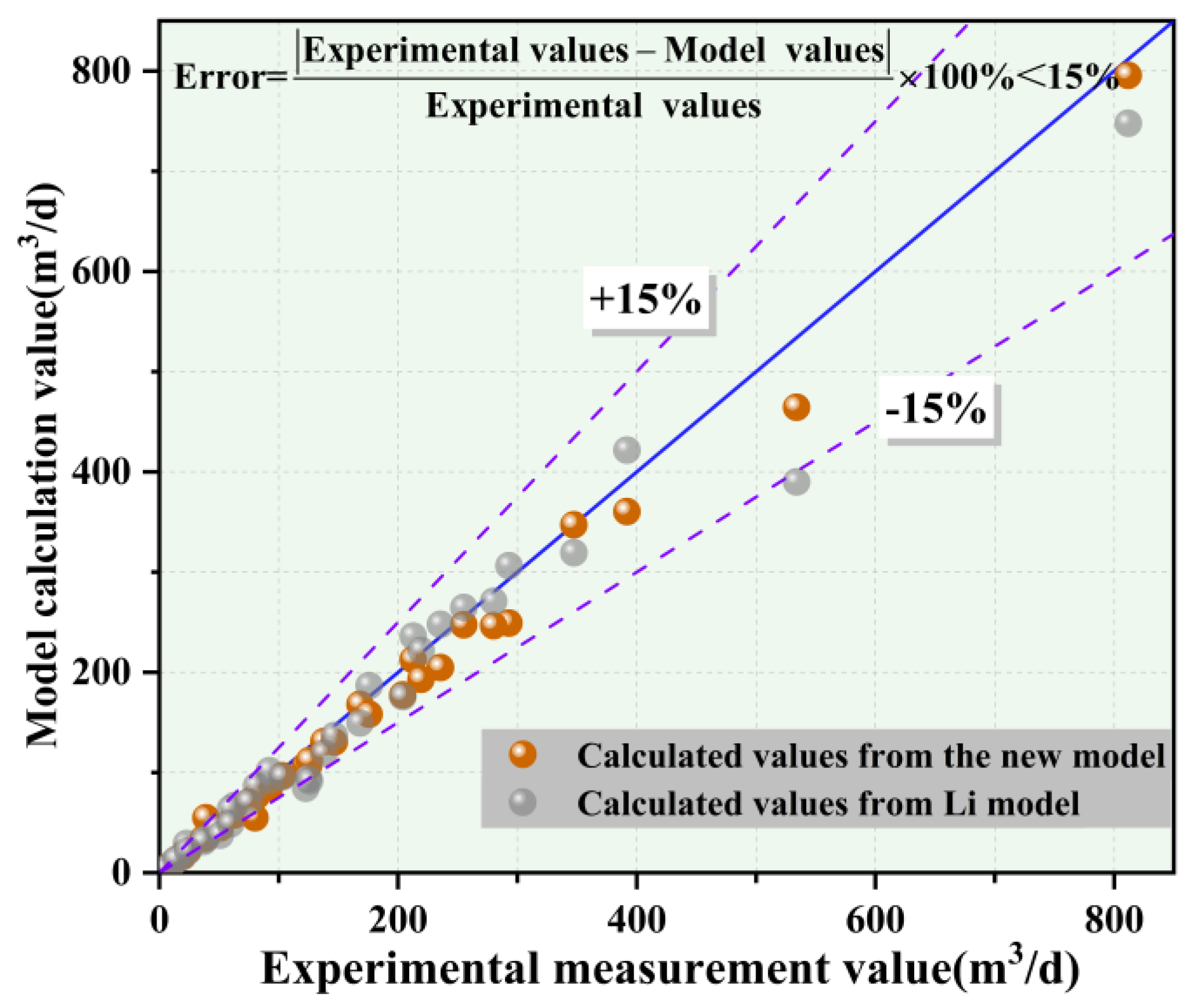
4.6. Error Analysis of the Critical Sand-Carrying Theoretical Model
5. Conclusions
- (1)
- Through the analysis of the stress on sand particles, a critical sand-carrying model of the horizontal section of deep coalbed methane wellbore based on gravity, buoyancy, resistance, and pressure difference was established.
- (2)
- Based on a large multiphase flow experimental platform, a sand-carrying experiment was conducted in the horizontal section of the wellbore, and the critical flow pattern in the test pipe was analyzed. As the pipe inclination angle increases, larger sand piles slide down more easily. The fluid shear force is not enough to lift all the sand particles, resulting in a stronger critical sand-carrying capacity.
- (3)
- In the experiments without water, the critical gas capacity exhibited a positive correlation with particle diameter. In tests involving water injection, when the pipe inclination remained constant, increasing the liquid flow rate led to a decrease in the required gas flow rate. Conversely, when the liquid flow rate was fixed, increasing the inclination angle resulted in a higher required gas flow rate. Both sand particle diameter and pipe inclination have a positive correlation with the critical sand-carrying capacity. As either parameter increases, the gas flow rate required for sand-carrying also increases, leading to a higher critical gas–liquid ratio.
- (4)
- The constructed model was verified using indoor test data. The results show that the deviation between the calculated values and the actual test results is within 15%, and the model has high accuracy, which provides a theoretical basis for the sand production in the horizontal section of deep coalbed methane wells.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, F.; Hou, W.; Xiong, X.; Xu, B.; Wu, P.; Wang, H.; Mao, D. The status and development strategy of coalbed methane industry in China. Pet. Explor. Dev. 2023, 50, 765–783. [Google Scholar] [CrossRef]
- Qin, Y.; Moore, T.A.; Shen, J.; Yang, Z.; Shen, Y.; Wang, G. Resources and geology of coalbed methane in China: A review. In Coal Geology of China; Routledge: Abingdon, UK, 2020; pp. 247–282. [Google Scholar]
- Li, H.; Wei, N.; Hu, H.; Ge, Z.; Jiang, L.; Liu, F.; Kvamme, B. The law of liquid-solid carrying in the wellbore of natural gas hydrate gas well under the condition of foam drainage gas recovery. Energies 2023, 16, 2414. [Google Scholar] [CrossRef]
- Ma, T.; Liu, J.; Fu, J.; Wu, B. Drilling and completion technologies of coalbed methane exploitation: An overview. Int. J. Coal Sci. Technol. 2022, 9, 68. [Google Scholar] [CrossRef]
- Moore, T.A. Coalbed methane: A review. Int. J. Coal Geol. 2012, 101, 36–81. [Google Scholar] [CrossRef]
- Huang, Q.; Li, M.; Huang, Y.; Zhang, A.; Lian, X.; Yan, Y.; Feng, X. Effect of inorganic salts in coal seams on the sand-carrying capacity of hydroxypropyl guar foam-fracturing fluid: An experimental study. Phys. Fluids 2023, 35, 093118. [Google Scholar] [CrossRef]
- Wei, G.; Wen, H.; Deng, J.; Ma, L.; Li, Z.; Lei, C.; Liu, Y. Liquid CO2 injection to enhance coalbed methane recovery: An experiment and in-situ application test. Fuel 2021, 284, 119043. [Google Scholar] [CrossRef]
- Turner, R.G.; Hubbard, M.G.; Dukler, A.E. Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells. J. Pet. Technol. 1969, 21, 1475–1482. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, M.; Dai, G. Motion of Solid Particles in a Vertically Upward Flow Field. J. China Univ. Pet. (Ed. Nat. Sci.) 1998, 22, 79. [Google Scholar]
- Li, M.-Z.; Wang, W.-Y.; He, Y.-F.; Yuan, M. Study on Sand-carrying in Vertical Wellbores. J. China Univ. Pet. (Ed. Nat. Sci.) 2000, 24, 33–35. [Google Scholar]
- Li, M.-Z.; Wang, W.-Y.; Zhao, G.-J. Research on Sand-carrying in Vertical Wellbores and Its Application in Oil Well Production. J. Exp. Mech. 2002, 17, 385–392. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, J.; Sun, F.; Zhou, J.; Liu, A. Experimental study on sand grain migration in wellbore. Acta Pet. Sin. 2006, 27, 130. [Google Scholar]
- Wen, J.; Xu, S. Local hydrodynamics in a gas-liquid-solid three-phase bubble column reactor. Chem. Eng. J. 1998, 70, 81–84. [Google Scholar]
- Mitra-Majumdar, D.; Farouk, B.; Shah, Y.T. Hydrodynamic modeling of three-phase flows through a vertical column. Chem. Eng. Sci. 1997, 52, 4485–4497. [Google Scholar] [CrossRef]
- Wen, J.P.; Huang, L.; Zhou, H.; Yu, B.T.; Hu, Z.D. The E/E/L Model and Simulation of Gas–Liquid–Solid Three-Phase Turbulent Flow. J. Chem. Ind. Eng. 2001, 52, 343. [Google Scholar]
- Zhou, G.M.; Feng, Y.R.; Xu, Z.H.; Li, X.F. Research on the Critical Sand Production Model for Gas Wells. Xinjiang Oil Gas 2003, 15, 57–59. [Google Scholar]
- Li, G.; Wang, X.; Xiao, X.Q.; Chen, J. Application of two-phase flow theory in gas well with sands. Fault-Block Oil Gas Field 2008, 15, 65–67. [Google Scholar]
- Xue, Z.Z. Theoretical and Experimental Research on Gas-Sand Two-Phase Flow in Natural Gas Production. Petrochem. Ind. Technol. 2016, 23, 201. [Google Scholar]
- Lin, L.; Lou, W.; Xie, J.; Li, L. Application Research on Critical Sand-carrying Parameters and Sand Production Prediction Models for Gas Wells. J. Chongqing Univ. Sci. Technol. (Nat. Sci. Ed.) 2015, 17, 65–68. [Google Scholar]
- Zhang, G.; Huang, X.; Yan, J.; Yi, L.; Wang, W.; Qu, X.; Sun, X. Research on the Minimum Sand-carrying Capability of Oil Wells in the Gu Dong Oilfield. J. Oil Gas Technol. 2001, 23, 33. [Google Scholar]
- Liu, A.P.; Deng, J.G. Research on the Minimum Sand-carrying Velocity of Low-Viscosity Liquid Flow in Vertical Wellbores. Oil Drill. Prod. Technol. 2007, 29, 31–33. [Google Scholar]
- Jiao, Y.H.; Deng, J.G.; Mou, S.B. Calculation of the Minimum Sand-carrying Velocity for Sand Production in Vertical Wellbores. West-China Explor. Eng. 2010, 22, 101–103. [Google Scholar]
- Wang, X.W.; Wang, J.; Wang, X. Laboratory Research on Gas Flow Sand-carrying Models in Vertical Gas Wells. China Pet. Chem. Stand. Qual. 2011, 31, 187–188. [Google Scholar]
- Dong, C.; Li, Y.; Zhang, Q.; Feng, S.; Zhang, L. Experimental study on sand-carrying mechanism and capacity evaluation in water-producing gas wells and its application in artificial lift optimization. In SPE Middle East Artificial Lift Conference and Exhibition; SPE: Richardson, TX, USA, 2014; p. SPE-173700. [Google Scholar]
- Dong, C.; Gao, K.; Wang PZhang, Q.; Cui, M.; Yao, F. Sand-carrying flow in low-viscosity wellbore fluid and characteristic flow velocities. Acta Pet. Sin. 2016, 37, 1280–1286. [Google Scholar]
- Zeng, S.R.; Dong, C.Y.; Wei, R.; Su, Y.; Wang, J.; Yan, Q.H. Comparing experiments and their matching application of the borehole critical sand-carrying velocity in the horizontal well with different pitching angles. Pet. Geol. Oilfield Dev. Daqing 2018, 37, 54–59. [Google Scholar]
- Deng, S.; Zhang, D.; Zhao, H.; Peng, H.; Wang, J.; Yan, X. A new method for calculating the minimum sand-carrying velocity in geothermal well production. Geothermics 2023, 114, 102811. [Google Scholar] [CrossRef]
- Han, H.; Shi, Z.; Zuo, W.; Wu, S.; Liu, Y.; Xie, K.; Long, L.; Mitri, H. Sand-Carrying Law and Influencing Factors in Complex Fractures of Nano-Clean Fracturing Fluid. Energies 2023, 16, 6056. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wang, F.; Wu, J.; Wang, Y. The Carrying Behavior of Water-Based Fracturing Fluid in Shale Reservoir Fractures and Molecular Dynamics of Sand-Carrying Mechanism. Processes 2024, 12, 2051. [Google Scholar] [CrossRef]
- Liu, S. Prediction of critical sand production concentration in reservoirs based on stationary bed theory in wellbore. Comp. Part. Mech. 2025, 1–17. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Wang, Z.; Zhang, M.; Liao, R. Study of sand particle transport characteristics and different critical velocities in sand-producing wells via indoor experiments. Sci. Rep. 2025, 15, 9707. [Google Scholar]
- Han, X.; Wu, J.; Ji, Y.; Liu, J.; Liu, Y.; Xie, B.; Chen, X.; Yin, H.; Liang, T. Impact of Viscoelasticity on Sand-Carrying Ability of Viscous Slickwater and Its Sand-Carrying Threshold in Hydraulic Fractures. Energies 2024, 17, 428. [Google Scholar] [CrossRef]
- Danielson, T.J. Sand transport modeling in multiphase pipelines. In Offshore Technology Conference; OTC: Houston, TX, USA, 2007; p. OTC-18691. [Google Scholar]
- Galindo, T. Sand Transport, Does Viscosity Matter? In SPE Liquids-Rich Basins Conference-North America; SPE: Richardson, TX, USA, 2019; p. D022S010R010. [Google Scholar]
- Abou-Kassem, A.J.; Sidahmed, A.; Kotb, O.; Haftani, M.; Nouri, A. Integrated wellbore-reservoir simulations to design sand retention tests for flowback scenarios in SAGD injection wells. J. Pet. Sci. Eng. 2022, 208, 109307. [Google Scholar] [CrossRef]
- Varkas, M.; Papamichos, E.; Berntsen, A.N. Experimental study of volumetric sand production with gas flow. Geoenergy Sci. Eng. 2024, 234, 212610. [Google Scholar] [CrossRef]
- Rowe, P.N.; Nienow, A.W. Minimum fluidisation velocity of multi-component particle mixtures. Chem. Eng. Sci. 1975, 30, 1365–1369. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.W.; Wang, J.; Zhou, B.; Yan, Q.H. Theoretical Model Analysis of Gas Flow Sand-carrying in Vertical Wellbores. J. Oil Gas Technol. 2011, 5, 274–276. [Google Scholar]
- JCGM 100:2008; JCGM, Evaluation of Measurement Data-Guide to the Expression of Uncertainty in Measurement. Guides in Metrology Committee: Paris, France, 2008.
- Gudala, M.; Naiya, T.K.; Govindarajan, S.K. Heavy oil-water dispersed flows in horizontal pipelines using bio-additives with energy analysis: Experimental and numerical investigations. J. Pet. Sci. Eng. 2022, 211, 110142. [Google Scholar] [CrossRef]
- Wang, G.; Liao, R.; Huang, L.; Xia, Q.; Zhang, M.; Lei, Y.; Wang, W. Study of the flow pattern and pressure drop law of the air-water-foam three-phase flow. Exp. Therm. Fluid Sci. 2024, 155, 111207. [Google Scholar] [CrossRef]
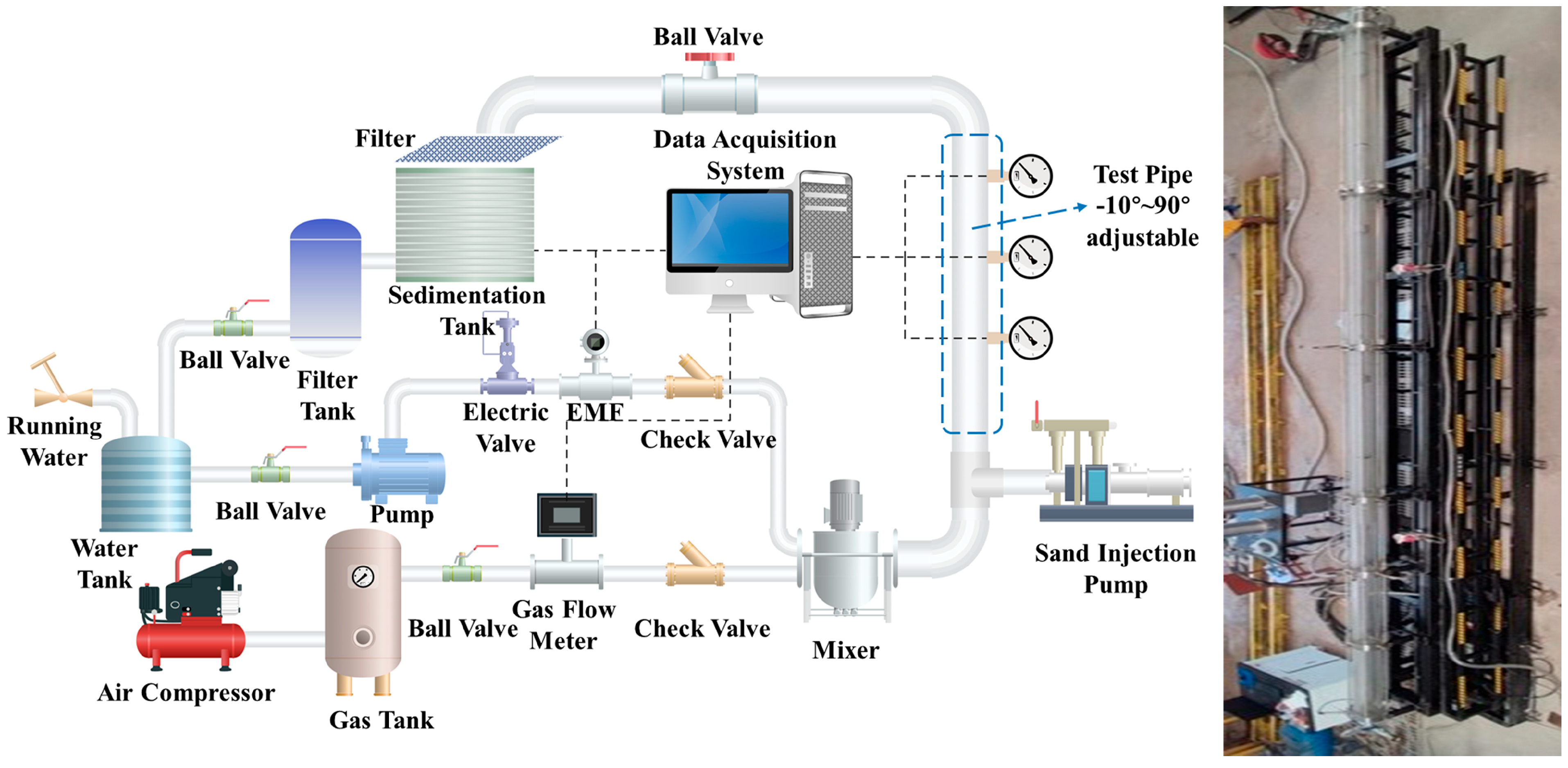





| System | Equipment Name | Working Conditions | Accuracy |
|---|---|---|---|
| Power systems | Single screw-rod air compressor (FHOGD-250) | Maximum displacement: 0.5787 m3/s; Working pressure range: 0~8 × 105 Pa. | |
| Centrifugal pumps (D620-35X10) | Maximum displacement: 0.0019 m3/s; Working pressure range: 0~8 × 105 Pa. | ||
| Sand Injection Pump (G/GH 6/4D) | Maximum displacement: 0.07 m3/s; Power range: 4~60 kW | ||
| Measurement systems | Gas phase flow meter (Proline mass 65) | Scale: 0~0.5787 m3/s | ±0.1% (FS) |
| Liquid flow meter (YK-LDF-DN10-B) | Scale: 0~0.002 m3/s | ±0.5% (FS) | |
| Differential pressure gauge (TCT-1206) | Scale: 0~2.5864 × 105 Pa | ±0.05% (FS) | |
| Manometer (Rosemount 3051S) | Scale: 0~1.2 × 107 Pa | ±0.1% (FS) | |
| High-speed camera (NEO 25M/C) | Maximum frame rate: 25,000 fps; Resolution: 1280 × 1024. |
| Number | Number of Sand Particles (Mesh) | Particle Size Range (mm) | Representative Particle Size (mm) | Material |
|---|---|---|---|---|
| S1 | 10~20 | 0.6~1.2 | 1 | Quartz sand |
| S2 | 20~40 | 0.4~0.6 | 0.5 | Quartz sand |
| S3 | 40~80 | 0.2~0.4 | 0.25 | Quartz sand |
| Particle Size (mm) | Liquid Flow (m3/d) | Critical Sand-Carrying Capacity (m3/d) | Ave. | SD | SE | ||||
|---|---|---|---|---|---|---|---|---|---|
| Exp. 1 | Exp. 2 | Exp. 3 | Exp. 4 | Exp. 5 | |||||
| 0.25 | 6 | 124.35 | 124.88 | 124.88 | 124.92 | 124.95 | 124.80 | 0.25 | 0.11 |
| 10 | 92.15 | 92.38 | 92.17 | 92.32 | 92.43 | 92.29 | 0.13 | 0.06 | |
| 14 | 59.68 | 59.83 | 59.74 | 59.62 | 59.73 | 59.72 | 0.08 | 0.03 | |
| 0.5 | 6 | 212.83 | 212.83 | 212.76 | 212.78 | 212.78 | 212.80 | 0.03 | 0.01 |
| 10 | 122.56 | 122.55 | 122.68 | 122.74 | 122.88 | 122.69 | 0.14 | 0.06 | |
| 14 | 102.95 | 103.15 | 103.15 | 103.26 | 103.26 | 103.15 | 0.13 | 0.06 | |
| 1 | 6 | 293.18 | 293.18 | 293.15 | 293.15 | 293.09 | 293.15 | 0.04 | 0.02 |
| 10 | 175.93 | 175.93 | 175.89 | 175.86 | 175.86 | 175.89 | 0.04 | 0.02 | |
| 14 | 146.33 | 146.58 | 146.58 | 146.64 | 146.73 | 146.57 | 0.15 | 0.07 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Qi, W.; Qi, W.; Hao, L.; Tang, A.; Yang, L.; Zhang, K.; Zhang, Y. Research on a Sand-Carrying Model of Horizontal Sections of Deep Coalbed Methane Wells. Processes 2025, 13, 1810. https://doi.org/10.3390/pr13061810
Sun L, Qi W, Qi W, Hao L, Tang A, Yang L, Zhang K, Zhang Y. Research on a Sand-Carrying Model of Horizontal Sections of Deep Coalbed Methane Wells. Processes. 2025; 13(6):1810. https://doi.org/10.3390/pr13061810
Chicago/Turabian StyleSun, Longfei, Weilin Qi, Wei Qi, Li Hao, Anda Tang, Lin Yang, Kang Zhang, and Yun Zhang. 2025. "Research on a Sand-Carrying Model of Horizontal Sections of Deep Coalbed Methane Wells" Processes 13, no. 6: 1810. https://doi.org/10.3390/pr13061810
APA StyleSun, L., Qi, W., Qi, W., Hao, L., Tang, A., Yang, L., Zhang, K., & Zhang, Y. (2025). Research on a Sand-Carrying Model of Horizontal Sections of Deep Coalbed Methane Wells. Processes, 13(6), 1810. https://doi.org/10.3390/pr13061810





