Adsorption Column Performance Analysis for Volatile Organic Compound (VOC) Emissions Abatement in the Pharma Industry
Abstract
1. Introduction
2. Dynamic Model Development
- Radial concentration and temperature gradients are negligible [10].
- The gas phase and adsorbent particles are in thermal equilibrium [10].
- Wall temperature is constant and equal to the ambient temperature [10].
- The ideal gas law applies and carrier gas adsorption is negligible [10].
- Adsorbent properties of beaded activated carbon (BAC) match those in [22].
- Initially (t = 0 s), the VOC adsorption column only contains carrier gas [9].
- Equilibrium obeys the Extended Langmuir model for mixtures [22].
Main Model Parameters and Case Studies
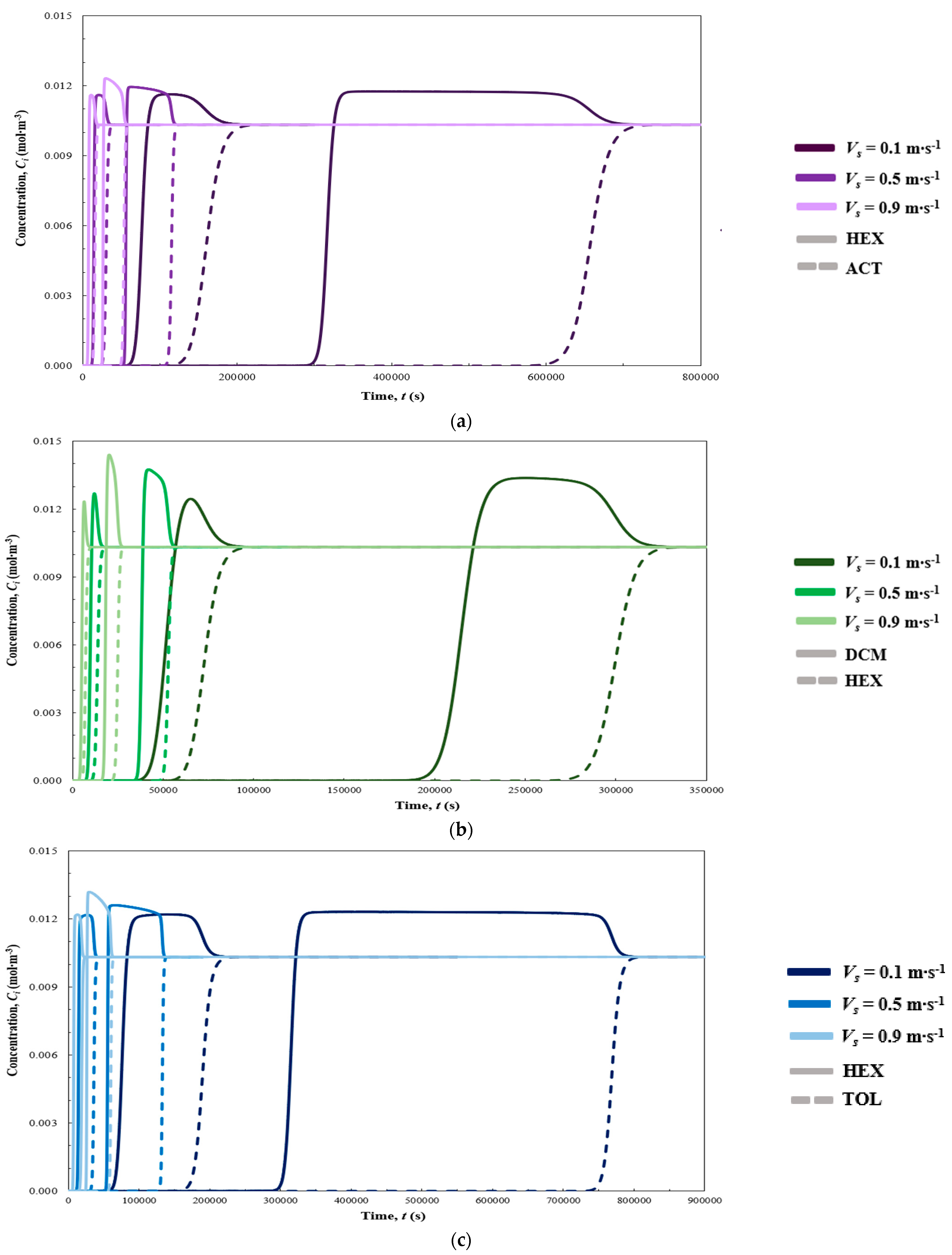
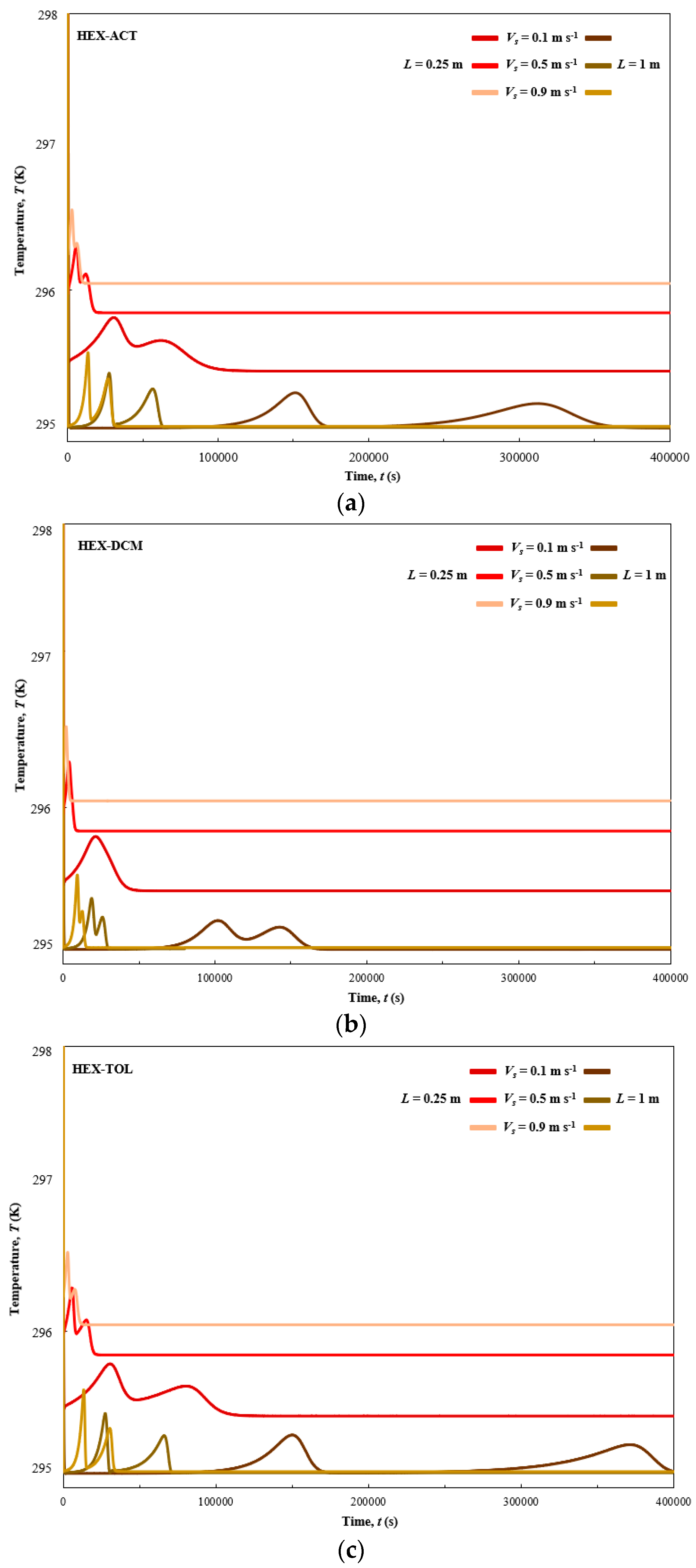

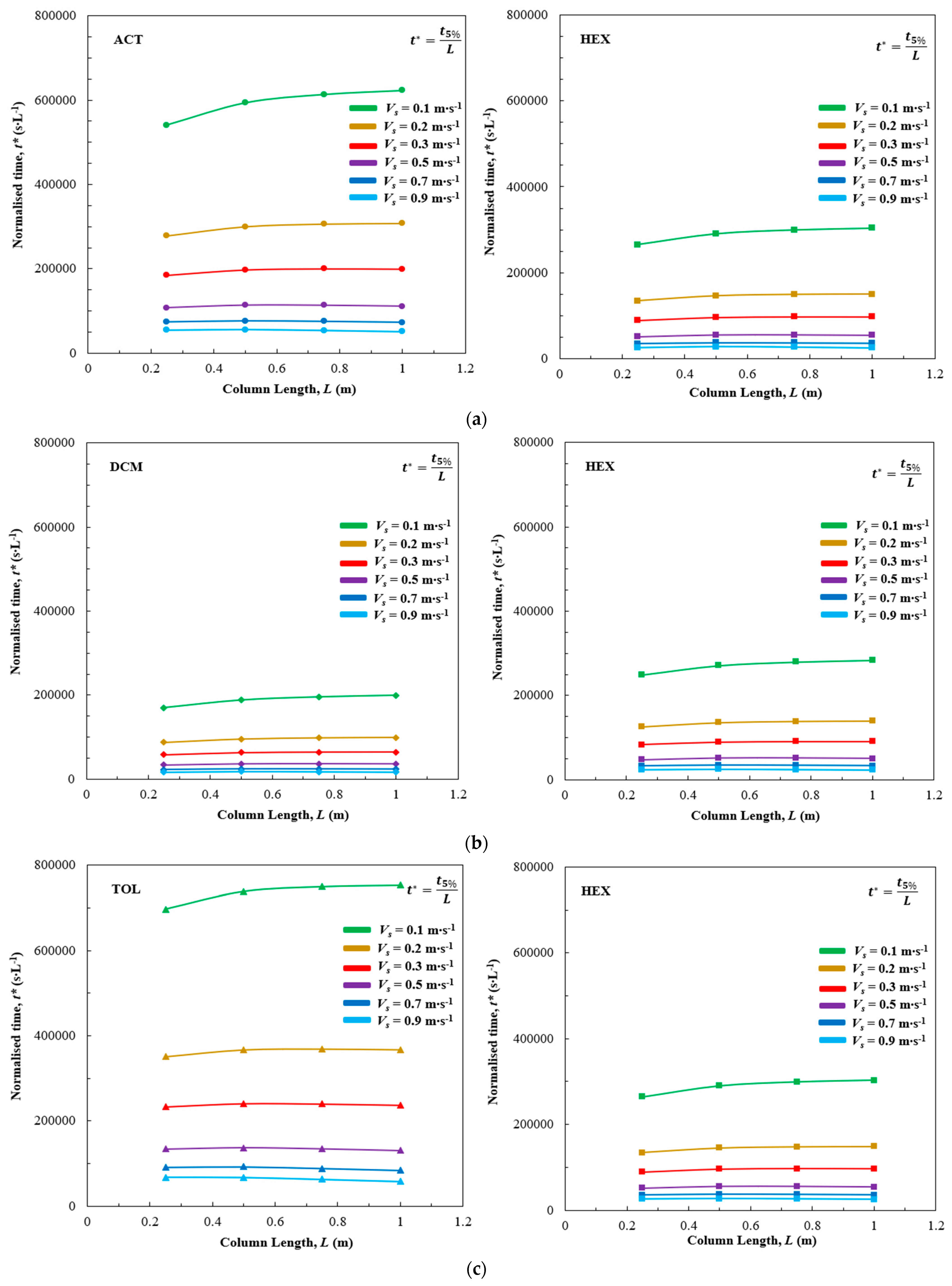
3. Results
3.1. Dynamic Simulation Results
3.2. Bed Design Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| bi | Langmuir affinity coefficient (m3 mol−1) |
| bo,i | pre-exponential Langmuir constant (m3 mol−1) |
| C | component gas phase VOC concentration (mol m−3) |
| C0,i | inlet concentration of i (mol m−3) |
| Cpg | specific heat capacity of gas (J kg−1 K−1) |
| Cpp | specific heat capacity of particle (J kg−1 K−1) |
| Cs0,i | adsorbed phase concentration at equilibrium with C0,i (mol m−3) |
| Ct | total gas phase VOC concentration (mol m−3) |
| D | bed inner diameter (m) |
| DAB,i | molecular diffusivity (m2 s−1) |
| Deff,i | effective diffusivity of i (m2 s−1) |
| Dk,i | Knudsen diffusivity (m2 s−1) |
| dlm | mean logarithmic column diameter (-) |
| dp | particle diameter (m) |
| Dz,i | axial dispersion coefficient (m2 s−1) |
| hint | internal heat transfer coefficient (W m−2 K−1) |
| ho | overall heat transfer coefficient (W m−2 K−1) |
| keff | effective thermal conductivity (W m−1 K−1) |
| kew | effective wall thermal conductivity (W m−1 K−1) |
| kez | effective axial thermal conductivity (W m−1 K−1) |
| kf,i | effective mass transfer coefficient of component i (m s−1) |
| kg | gas thermal conductivity (W m−1 K−1) |
| kLDF,i | LDF mass transfer coefficient (s−1) |
| kp | particle thermal conductivity (W m−1 K−1) |
| kw | wall thermal conductivity (W m−1 K−1) |
| L | bed length (m) |
| Mr | molecular weight (g mol−1) |
| P | pressure (atm only in Eq.(4)) / (Pa) |
| qi | adsorbed phase VOC concentration (mol m−3) |
| qe,i | equilibrium adsorption capacity of i (mol kg−1) |
| qρe,i | equilibrium adsorption capacity of i (mol m−3) |
| qm,i | maximum adsorption capacity of material for component i (mol kg−1) |
| R | column inner radius (m) |
| Rep | Reynolds number (adsorbent particle) |
| rp | average pore radius (1.1∙10−9 m) |
| Rp | particle radius (m) |
| SA | Surface area of adsorbent material (m2 g−1) |
| Sci | Schmidt number of i |
| Sh | Sherwood number (-) |
| T | temperature (K) |
| Tin | inlet temperature (K) |
| Tmax | maximum temperature (K) |
| Tw | wall temperature (K) |
| t5%,i | breakthrough onset time of component i (s) |
| t95%,i | breakthrough completion time of strongly adsorbing component i (s) |
| t105%,i | breakthrough completion time of weakly adsorbing component i (s) |
| t* | normalised time (s m−1) |
| duration of breakthrough for strongly adsorbing component (s) | |
| duration of breakthrough for weakly adsorbing component (s) | |
| u | interstitial velocity (m s−1) |
| Vpore | adsorbent pore volume (5.7∙10−4 m3 kg−1) |
| Vs | superficial velocity (m s−1) |
| x | wall thickness (m) |
| α0 | empirical mass diffusion correction factor (20) |
| ΔHad,i | heat of adsorption (J mol−1) |
| εb | bulk bed porosity (-) |
| εp | particle porosity (-) |
| μ | gas viscosity (Pa s) |
| ρb | bed density (kg m−3) |
| ρg | gas density (kg m−3) |
| ρp | particle density (kg m−3) |
| Σν | atomic diffusion volume (A: VOC, B: carrier) |
| τp | particle tortuosity (-) |
References
- Gonzalez Pena, O.I.; Lopez Zavala, M.A.; Cabral Ruelas, H. Pharmaceuticals market, consumption trends and disease incidence are not driving the pharmaceutical research on water and wastewater. Int. J. Environ. Res. Public Health 2021, 18, 2532. [Google Scholar] [CrossRef] [PubMed]
- David, J.C.; Constable, C.J.-G.; Henderson, R.K. Perspective on solvent use in the pharma industry. Org. Process Res. Dev. 2007, 11, 133–137. [Google Scholar] [CrossRef]
- Henderson, R.K.; Jiménez-González, C.; Constable, D.J.C.; Alston, S.R.; Inglis, G.G.A.; Fisher, G.; Sherwood, J.; Binks, S.P.; Curzons, A.D. Expanding GSK’s solvent selection guide—Embedding sustainability into solvent selection starting at medicinal chemistry. Green Chem. 2011, 13, 854–862. [Google Scholar] [CrossRef]
- Sheldon, R.A. The E factor: Fifteen years on. Green Chem. 2007, 9, 1273–1283. [Google Scholar] [CrossRef]
- UK Government, Department of Environment, Food & Rural Affairs. Emissions of Air Pollutants in The UK—Non-Methane Volatile Organic Compounds (NMVOCs). 2023. Available online: https://www.gov.uk/government/statistics/emissions-of-air-pollutants/emissions-of-air-pollutants-in-the-uk-non-methane-volatile-organic-compounds-nmvocs (accessed on 11 September 2023).
- Ma, J.W.; Li, L. VOC emitted by biopharmaceutical industries: Source profiles, health risks, and secondary pollution. J. Environ. Sci. 2024, 135, 570–584. [Google Scholar] [CrossRef] [PubMed]
- Simayi, M.; Shi, Y.Q.; Xi, Z.Y.; Ren, J.; Hini, G.; Xie, S.D. Emission trends of industrial VOCs in China since the clean air action and future reduction perspectives. Sci. Total Environ. 2022, 826, 153994. [Google Scholar] [CrossRef]
- Delage, F.P.P.; Le Cloirec, P. Mass transfer and warming during adsorption of high concentrations of VOCs on an activated carbon bed: Experimental and theoretical analysis. Environ. Sci. Technol. 2000, 34, 4816–4821. [Google Scholar] [CrossRef]
- Ruthven, D.M. Principles of Adsorption and Adsorption Processes; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1984. [Google Scholar]
- Suzuki, M. Adsorption Engineering; Elsevier Science Publishers: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Huang, H.; Haghighat, F.; Blondeau, P. Volatile organic compound (VOC) adsorption on material: Influence of gas phase concentration, relative humidity and VOC type. Indoor Air 2006, 16, 236–247. [Google Scholar] [CrossRef] [PubMed]
- Laskar, I.I.; Hashisho, Z.; Phillips, J.H.; Anderson, J.E.; Nichols, M. Modeling the effect of relative humidity on adsorption dynamics of volatile organic compound onto activated carbon. Environ. Sci. Technol. 2019, 53, 2647–2659. [Google Scholar] [CrossRef]
- Zheng, C.; Kang, K.; Xie, Y.C.; Yang, X.L.; Lan, L.; Song, H.; Han, H.; Bai, S.P. Dynamic adsorption behavior of 1.1.1.2-tetrafluoroethane (R134a) on activated carbon beds under different humidity and moisture levels. Sep. Purif. Technol. 2024, 329, 124851. [Google Scholar] [CrossRef]
- Cosnier, F.; Celzard, A.; Furdin, G.; Bégin, D.; Marêché, J.F. Influence of water on the dynamic adsorption of chlorinated VOCs on active carbon: Relative humidity of the gas phase versus pre-adsorbed water. Adsorpt. Sci. Technol. 2006, 24, 215–228. [Google Scholar] [CrossRef]
- Yao, X.L.; Liu, Y.; Li, T.; Zhang, T.T.; Li, H.L.; Wang, W.; Shen, X.B.; Qian, F.; Yao, Z.L. Adsorption behavior of multicomponent volatile organic compounds on a citric acid residue waste-based activated carbon: Experiment and molecular simulation. J. Hazard. Mater. 2020, 392, 122323. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Jiang, Y.; Zhang, Y.; Liu, S. Prediction of breakthrough curves for adsorption on activated carbon fibers in a fixed bed. Carbon 2004, 42, 3081–3085. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Zhu, J. Straw-based activated carbon: Optimization of the preparation procedure and performance of volatile organic compounds adsorption. Materials 2021, 14, 3284. [Google Scholar] [CrossRef]
- Fu, J.; Jin, C.; Zhang, J.; Wang, Z.; Wang, T.; Cheng, X.; Ma, C.; Chen, H. Pore structure and VOCs adsorption characteristics of activated coke powders derived via one-step rapid pyrolysis activation method. Asia-Pac. J. Chem. Eng. 2020, 15, e2503. [Google Scholar] [CrossRef]
- Xiao, J.S.; Peng, Y.Z.; Bénard, P.; Chahine, R. Thermal effects on breakthrough curves of pressure swing adsorption for hydrogen purification. Int. J. Hydrogen Energy 2016, 41, 8236–8245. [Google Scholar] [CrossRef]
- Jee, J.G.; Kim, M.B.; Lee, C.H. Adsorption characteristics of hydrogen mixtures in a layered bed: Binary, ternary, and five-component mixtures. Ind. Eng. Chem. Res. 2001, 40, 868–878. [Google Scholar] [CrossRef]
- Moe, W.M.; Collins, K.L.; Rhodes, J.D. Activated carbon load equalization of gas-phase toluene: Effect of cycle length and fraction of time in loading. Environ. Sci. Technol. 2007, 41, 5478–5484. [Google Scholar] [CrossRef]
- Tefera, D.T.; Lashaki, M.J.; Fayaz, M.; Hashisho, Z.; Philips, J.H.; Anderson, J.E.; Nichols, M. Two-dimensional modeling of volatile organic compounds adsorption onto beaded activated carbon. Environ. Sci. Technol. 2013, 47, 11700–11710. [Google Scholar] [CrossRef]
- Tefera, D.T.; Hashisho, Z.; Philips, J.H.; Anderson, J.E.; Nichols, M. Modeling competitive adsorption of mixtures of volatile organic compounds in a fixed-bed of beaded activated carbon. Environ. Sci. Technol. 2014, 48, 5108–5117. [Google Scholar] [CrossRef]
- Tzanakopoulou, V.E.; Pollitt, M.; Castro-Rodriguez, D.; Costa, A.; Gerogiorgis, D.I. Dynamic modelling, simulation and theoretical performance analysis of Volatile Organic Compound (VOC) abatement systems in the pharma industry. Comput. Chem. Eng. 2023, 174, 108248. [Google Scholar] [CrossRef]
- Tzanakopoulou, V.E.; Pollitt, M.; Castro-Rodriguez, D.; Gerogiorgis, D.I. Dynamic model validation and simulation of acetone–toluene and benzene–toluene systems for industrial Volatile Organic Compound (VOC) abatement. Ind. Eng. Chem. Res. 2024, 63, 7281–7299. [Google Scholar] [CrossRef] [PubMed]
- Tzanakopoulou, V.E.; Narasinghe, K.; Pollitt, M.; Castro-Rodriguez, D.; Gerogiorgis, D.I. Dynamic simulation and analysis of dichloromethane-acetone, dichloromethane-trichloromethane and dichloromethane-toluene VOC mixture abatement systems under transient feed conditions. Comput. Chem. Eng. 2024, 187, 108713. [Google Scholar] [CrossRef]
- Sircar, S.; Hufton, J.R. Why does the Linear Driving Force model for adsorption kinetics work? Adsorpt.-J. Int. Adsorpt. Soc. 2000, 6, 137–147. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. Investigating the validity of the Bosanquet formula for estimation of diffusivities in mesopores. Chem. Eng. Sci. 2012, 69, 684–688. [Google Scholar] [CrossRef]
- Knox, J.C.; Ebner, A.D.; LeVan, M.D.; Coker, R.F.; Ritter, J.A. Limitations of breakthrough curve analysis in fixed-bed adsorption. Ind. Eng. Chem. Res. 2016, 55, 4734–4748. [Google Scholar] [CrossRef]
- Giraudet, S.P.; Pré, P.; Le Cloirec, P. Modeling the temperature dependence of adsorption equilibirums of VOCs onto activated carbons. J. Environ. Eng. 2010, 136, 103–111. [Google Scholar] [CrossRef]
- Chuang, C.L.; Chiang, P.C.; Chang, E.E. Modeling VOCs adsorption onto activated carbon. Chemosphere 2003, 53, 17–27. [Google Scholar] [CrossRef]
- Shim, W.G.; Lee, J.W.; Moon, H. Equilibrium and fixed-bed adsorption of n-hexane on activated carbon. Sep. Sci. Technol. 2003, 38, 3905–3926. [Google Scholar] [CrossRef]
- Talmoudi, R.; AbdelJaoued, A.; Chahbani, M.H. Dynamic study of VSA and TSA processes for VOCs removal from air. Int. J. Chem. Eng. 2018, 2018, 2316827. [Google Scholar] [CrossRef]
- Angelopoulos, P.M.; Gerogiorgis, D.I.; Paspaliaris, I. Mathematical modeling and process simulation of perlite grain expansion in a vertical electrical furnace. Appl. Math. Model. 2014, 38, 1799–1822. [Google Scholar] [CrossRef]
- Akinlabi, C.O.; Gerogiorgis, D.I.; Georgiadis, M.C.; Pistikopoulos, E.N. Modelling, design and optimisation of a hybrid PSA-membrane gas separation process. Comput.-Aided Chem. Eng. 2007, 24, 363–370. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). Thermophysical Properties of Fluid Systems. 2023. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 11 September 2023).
- Coker, A.K. Physical Properties of Liquids and Gases. In Ludwig’s Applied Process Design for Chemical & Petrochemical Plants, 4th ed.; Coker, A.K., Ed.; Gulf Professional Publishing: Houston, TX, USA, 2007; pp. 103–132. [Google Scholar]
- Gerogiorgis, D.I.; Barton, P.I. Steady-state optimization of a continuous pharmaceutical process. Comput.-Aided Chem. Eng. 2009, 27, 927–932. [Google Scholar] [CrossRef]
- Kim, S.J.; Cho, S.Y.; Kim, T.Y. Adsorption of chlorinated volatile organic compounds in a fixed bed of activated carbon. Korean J. Chem. Eng. 2002, 19, 61–67. [Google Scholar] [CrossRef]
- Tsai, J.H.; Chiang, H.M.; Huang, G.Y.; Chiang, H.L. Adsorption characteristics of acetone, chloroform and acetonitrile on sludge-derived adsorbent, commercial granular activated carbon and activated carbon fibers. J. Hazard. Mater. 2008, 154, 1183–1191. [Google Scholar] [CrossRef]
- Yang, X.; Yi, H.H.; Tang, X.L.; Zhao, S.Z.; Yang, Z.Y.; Ma, Y.Q.; Feng, T.C.; Cui, X.X. Behaviors and kinetics of toluene adsorption-desorption on activated carbons with varying pore structure. J. Environ. Sci. 2018, 67, 104–114. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo, M.T.; Martínez de Yuso, A.; Rubio, B.; Pino, M.R. Conversion of almond shell to activated carbons: Methodical study of the chemical activation based on an experimental design and relationship with their characteristics. Biomass Bioenergy 2011, 35, 1235–1244. [Google Scholar] [CrossRef]
- Jolliffe, H.G.; Gerogiorgis, D.I. Technoeconomic optimisation and comparative environmental impact evaluation of continuous crystallisation and antisolvent selection for artemisinin recovery. Comput. Chem. Eng. 2017, 103, 218–232. [Google Scholar] [CrossRef]
- Jolliffe, H.G.; Gerogiorgis, D.I. Process modelling, design and technoeconomic evaluation for continuous paracetamol crystallisation. Comput. Chem. Eng. 2018, 118, 224–235. [Google Scholar] [CrossRef]

| System | C0,i (ppm) | Dz,i (m2 s−1) | ΔHad,i (J mol−1) | Tin (K) | L (m) | Vs (m s−1) | qm (mol kg−1) | εb | kLDF (s−1) | b0 (m3 mol−1) | Figures |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HEX-ACT | 250 | 0.68∙10−3 | 51,100 | 300 | 0.25, 1 | 0.1 | 7.060 | 0.38 | 8.45∙10−5 | 1.96∙10−8 | Figure 2 and Figure 3 |
| 250 | 0.52∙10−3 | 50,000 | 3.801 | 1.66∙10−4 | 2.35∙10−8 | ||||||
| HEX-ACT | 250 | 1.07∙10−3 | 51,100 | 300 | 0.25, 1 | 0.5 | 7.060 | 0.38 | 8.45∙10−5 | 1.96∙10−8 | Figure 2 and Figure 3 |
| 250 | 0.91∙10−3 | 50,000 | 3.801 | 1.66∙10−4 | 2.35∙10−8 | ||||||
| HEX-ACT | 250 | 1.47∙10−3 | 51,100 | 300 | 0.25, 1 | 0.9 | 7.060 | 0.38 | 8.45∙10−5 | 1.96∙10−8 | Figure 2 and Figure 3 |
| 250 | 1.31∙10−3 | 50,000 | 3.801 | 1.66∙10−4 | 2.35∙10−8 | ||||||
| HEX-DCM | 250 | 0.67∙10−3 | 40,000 | 300 | 0.25, 1 | 0.1 | 4.510 | 0.38 | 2.32∙10−4 | 7.41∙10−7 | Figure 2 and Figure 3 |
| 250 | 0.52∙10−3 | 50,000 | 3.801 | 1.55∙10−4 | 2.35∙10−8 | ||||||
| HEX-DCM | 250 | 1.07∙10−3 | 40,000 | 300 | 0.25, 1 | 0.5 | 4.510 | 0.38 | 2.32∙10−4 | 7.41∙10−7 | Figure 4 and Figure 5 |
| 250 | 0.91∙10−3 | 50,000 | 3.801 | 1.55∙10−4 | 2.35∙10−8 | ||||||
| HEX-DCM | 250 | 1.46∙10−3 | 40,000 | 300 | 0.25, 1 | 0.9 | 4.510 | 0.38 | 2.32∙10−4 | 7.41∙10−7 | Figure 4 and Figure 5 |
| 250 | 1.31∙10−3 | 50,000 | 3.801 | 1.55∙10−4 | 2.35∙10−8 | ||||||
| HEX-TOL | 250 | 0.54∙10−3 | 45,500 | 300 | 0.25, 1 | 0.1 | 4.610 | 0.38 | 5.36∙10−5 | 4.06∙10−7 | Figure 4 and Figure 5 |
| 250 | 0.52∙10−3 | 50,000 | 3.801 | 1.91∙10−4 | 2.35∙10−8 | ||||||
| HEX-TOL | 250 | 0.93∙10−3 | 45,500 | 300 | 0.25, 1 | 0.5 | 4.610 | 0.38 | 5.36∙10−5 | 4.06∙10−7 | Figure 4 and Figure 5 |
| 250 | 0.91∙10−3 | 50,000 | 3.801 | 1.91∙10−4 | 2.35∙10−8 | ||||||
| HEX-TOL | 250 | 1.33∙10−3 | 45,500 | 300 | 0.25, 1 | 0.9 | 4.610 | 0.38 | 5.36∙10−5 | 4.06∙10−7 | Figure 4 and Figure 5 |
| 250 | 1.31∙10−3 | 50,000 | 3.801 | 1.91∙10−4 | 2.35∙10−8 |
| System | C0,i (ppm) | ρb (kg m−3) | D (m) | Tin (K) | εp | dp (m) | Cpp (J kg−1 K−1) | Cpg (J kg−1 K−1) | kez (W m−1 K−1) | ho (W m−2 K−1) | hint (W m−2 K−1) | kw (W m−1 K−1) | x (m) | Figures |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HEX-ACT | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1014 | 0.13 | 9.05 | 9.05 | 14.2 | 0.001 | Figure 2 and Figure 3 |
| 250 | ||||||||||||||
| HEX-ACT | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1014 | 0.39 | 32.75 | 32.82 | 14.2 | 0.001 | Figure 2 and Figure 3 |
| 250 | ||||||||||||||
| HEX-ACT | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1014 | 0.66 | 52.33 | 52.52 | 14.2 | 0.001 | Figure 2 and Figure 3 |
| 250 | ||||||||||||||
| HEX-DCM | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1013 | 0.13 | 9.04 | 9.05 | 14.2 | 0.001 | Figure 2 and Figure 3 |
| 250 | ||||||||||||||
| HEX-DCM | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1013 | 0.39 | 32.74 | 32.81 | 14.2 | 0.001 | Figure 2 and Figure 3 |
| 250 | ||||||||||||||
| HEX-DCM | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1013 | 0.66 | 52.32 | 52.50 | 14.2 | 0.001 | Figure 4 and Figure 5 |
| 250 | ||||||||||||||
| HEX-TOL | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1014 | 0.13 | 9.06 | 9.06 | 14.2 | 0.001 | Figure 4 and Figure 5 |
| 250 | ||||||||||||||
| HEX-TOL | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1014 | 0.39 | 32.80 | 32.87 | 14.2 | 0.001 | Figure 4 and Figure 5 |
| 250 | ||||||||||||||
| HEX-TOL | 250 | 606 | 0.0152 | 300 | 0.56 | 0.00075 | 706.7 | 1014 | 0.66 | 52.41 | 52.60 | 14.2 | 0.001 | Figure 4 and Figure 5 |
| 250 |
| Vs (m s−1) | t5% (s) | t95% (s) | t105% (s) | (s) | (s) | Tmax (K) | ΔP (kPa) | Figure 2 and Figure 3 | |
|---|---|---|---|---|---|---|---|---|---|
| L = 0.25 m | |||||||||
| ACT | 0.1 | 135,185 | 186,806 | - | 51,622 | - | 295.80 | 0.91 | Figure 2a and Figure 3a |
| HEX | 66,240 | 82,722 | 167,489 | - | 101,249 | ||||
| ACT | 0.5 | 26,858 | 34,048 | - | 7190 | - | 296.33 | 6.26 | Figure 2a and Figure 3a |
| HEX | 12,801 | 15,504 | 31,357 | - | 18,556 | ||||
| ACT | 0.9 | 13,617 | 18,349 | - | 4732 | - | 296.58 | 15.15 | Figure 2a and Figure 3a |
| HEX | 6448 | 8292 | 16,517 | - | 10,069 | ||||
| L = 1 m | |||||||||
| ACT | 0.1 | 622,722 | 689,812 | - | 67,089 | - | 295.26 | 3.75 | Figure 2a and Figure 3a |
| HEX | 303,888 | 323,394 | 666,333 | - | 362,445 | ||||
| ACT | 0.5 | 111,102 | 118,558 | - | 7457 | - | 295.40 | 28.41 | Figure 2a and Figure 3a |
| HEX | 54,223 | 56,818 | 115,936 | - | 61,714 | ||||
| ACT | 0.9 | 50,841 | 55,686 | - | 4846 | - | 295.55 | 77.92 | Figure 2a and Figure 3a |
| HEX | 25,375 | 26,999 | 53,942 | - | 28,567 | ||||
| Vs (m s−1) | t5% (s) | t95% (s) | t105% (s) | (s) | (s) | Tmax (K) | ΔP (kPa) | Figure 2 and Figure 3 | |
|---|---|---|---|---|---|---|---|---|---|
| L = 0.25 m | |||||||||
| DCM | 0.1 | 42,484 | 55,960 | 80,433 | - | 37,949 | 295.80 | 0.93 | Figure 2b and Figure 3b |
| HEX | 62,155 | 84,074 | - | 21,919 | - | ||||
| DCM | 0.5 | 8404 | 10,517 | 14,999 | - | 6595 | 296.32 | 6.37 | Figure 2b and Figure 3b |
| HEX | 11,961 | 15,695 | - | 3734 | - | ||||
| DCM | 0.9 | 4243 | 5606 | 8039 | - | 3796 | 296.57 | 15.15 | Figure 2b and Figure 3b |
| HEX | 6018 | 8550 | - | 2532 | - | ||||
| L = 1 m | |||||||||
| DCM | 0.1 | 199,347 | 219,975 | 309,736 | - | 110,389 | 295.20 | 3.75 | Figure 2b and Figure 3b |
| HEX | 283,768 | 314,348 | - | 30,579 | - | ||||
| DCM | 0.5 | 36,236 | 38,780 | 54,261 | - | 18,025 | 295.36 | 28.41 | Figure 2b and Figure 3b |
| HEX | 50,523 | 54,470 | - | 3948 | - | ||||
| DCM | 0.9 | 17,133 | 18,586 | 25,943 | - | 8811 | 295.52 | 77.92 | Figure 2b and Figure 3b |
| HEX | 23,409 | 26,467 | - | 3059 | - | ||||
| Vs (m s−1) | t5% (s) | t95% (s) | t105% (s) | (s) | (s) | Tmax (K) | ΔP (kPa) | Figure 2 and Figure 3 | |
|---|---|---|---|---|---|---|---|---|---|
| L = 0.25 m | |||||||||
| TOL | 0.1 | 174,107 | 206,227 | - | 32,120 | - | 295.77 | 0.93 | Figure 2c and Figure 3c |
| HEX | 66,179 | 81,570 | 197,352 | - | 131,173 | ||||
| TOL | 0.5 | 33,483 | 38,827 | - | 5344 | - | 296.31 | 6.37 | Figure 2c and Figure 3c |
| HEX | 12,864 | 15,170 | 37,191 | - | 24,327 | ||||
| TOL | 0.9 | 16,902 | 20,982 | - | 4079 | - | 296.56 | 15.15 | Figure 2c and Figure 3c |
| HEX | 6505 | 8102 | 19,644 | - | 13,139 | ||||
| L = 1 m | |||||||||
| TOL | 0.1 | 752,898 | 784,410 | - | 31,512 | - | 295.27 | 3.75 | Figure 2c and Figure 3c |
| HEX | 302,704 | 320,280 | 775,966 | - | 473,262 | ||||
| TOL | 0.5 | 130,518 | 134,963 | - | 4445 | - | 295.42 | 28.41 | Figure 2c and Figure 3c |
| HEX | 53,973 | 56,165 | 133,890 | - | 79,917 | ||||
| TOL | 0.9 | 58,333 | 61,930 | - | 3597 | - | 295.59 | 77.92 | Figure 2c and Figure 3c |
| HEX | 25,170 | 26,488 | 60,772 | - | 35,602 | ||||
| t5% (s) | |||||||
|---|---|---|---|---|---|---|---|
| Vs (m s−1) | L (m) | HEX | ACT | HEX | DCM | HEX | TOL |
| 0.2 | 0.25 | 33,597 | 69,512 | 31,469 | 21,845 | 33,619 | 87,770 |
| 0.50 | 72,803 | 149,991 | 67,930 | 47,647 | 72,683 | 183,365 | |
| 0.75 | 111,529 | 229,683 | 104,243 | 73,573 | 111,228 | 276,469 | |
| 1 | 149,461 | 307,725 | 139,910 | 99,142 | 148,910 | 367,014 | |
| 0.3 | 0.25 | 22,161 | 46,164 | 20,741 | 14,503 | 22,228 | 58,203 |
| 0.50 | 47,818 | 98,816 | 44,587 | 31,444 | 47,801 | 120,317 | |
| 0.75 | 72,796 | 150,078 | 67,946 | 48,156 | 72,679 | 179,796 | |
| 1 | 96,970 | 199,526 | 90,643 | 64,544 | 96,557 | 236,853 | |
| 0.7 | 0.25 | 8726 | 18,384 | 8145 | 5738 | 8785 | 22,865 |
| 0.50 | 18,534 | 38,348 | 17,196 | 12,233 | 18,560 | 46,203 | |
| 0.75 | 27,520 | 56,359 | 25,515 | 18,312 | 27,459 | 66,563 | |
| 1 | 35,669 | 72,429 | 33,080 | 23,925 | 35,472 | 84,252 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzanakopoulou, V.E.; Pollitt, M.; Castro-Rodriguez, D.; Gerogiorgis, D.I. Adsorption Column Performance Analysis for Volatile Organic Compound (VOC) Emissions Abatement in the Pharma Industry. Processes 2025, 13, 1807. https://doi.org/10.3390/pr13061807
Tzanakopoulou VE, Pollitt M, Castro-Rodriguez D, Gerogiorgis DI. Adsorption Column Performance Analysis for Volatile Organic Compound (VOC) Emissions Abatement in the Pharma Industry. Processes. 2025; 13(6):1807. https://doi.org/10.3390/pr13061807
Chicago/Turabian StyleTzanakopoulou, Vasiliki E., Michael Pollitt, Daniel Castro-Rodriguez, and Dimitrios I. Gerogiorgis. 2025. "Adsorption Column Performance Analysis for Volatile Organic Compound (VOC) Emissions Abatement in the Pharma Industry" Processes 13, no. 6: 1807. https://doi.org/10.3390/pr13061807
APA StyleTzanakopoulou, V. E., Pollitt, M., Castro-Rodriguez, D., & Gerogiorgis, D. I. (2025). Adsorption Column Performance Analysis for Volatile Organic Compound (VOC) Emissions Abatement in the Pharma Industry. Processes, 13(6), 1807. https://doi.org/10.3390/pr13061807








