Abstract
The growing complexity of electrical infrastructure has elevated partial discharge (PD) detection to a crucial methodology for ensuring power system safety. Current PD pattern recognition approaches encounter persistent challenges in low-data scenarios, particularly regarding classification accuracy and model generalizability. This study develops a Firefly Algorithm with a Black Hole Mechanism-ResNet18 (FBH-ResNet18) framework that synergistically integrates the Firefly Algorithm with the Black Hole Mechanism (FBH algorithm) optimization with residual neural networks for PD signal classification using phase-resolved partial discharge (PRPD) mappings. A dedicated experimental platform first acquires PD signals through UHF sensors, which are subsequently converted into two-dimensional PRPD representations. The FBH algorithm systematically optimizes four key hyperparameters within the ResNet18 architecture during network training. The Black Hole Mechanism and improved population dynamics enhance optimization efficiency, resulting in more accurate hyperparameter tuning and improved model performance. Comparative evaluations demonstrate the enhanced performance of this parameter-optimized model against alternative configurations. Experimental results indicate that the improved ResNet18 achieves fast convergence and strong generalization on small-sample datasets, significantly enhancing recognition accuracy. During the first 80 generations of training, the classification accuracy reaches 89.11%, and in the final iteration, the model’s recognition accuracy increases to 92.55%, outperforming other models with accuracies generally below 90%. Additionally, the model shows excellent performance on the test set, with a loss function value of 0.250785, significantly lower than that of other models, indicating superior performance on small sample datasets. This research provides an effective solution for power cable fault diagnosis, offering high practical value.
1. Introduction
The power system, as a critical infrastructure supporting societal operations, plays a crucial role in ensuring the safety and stability of society. Power cables are essential for power transmission and distribution, offering compact size, high reliability, and resistance to external interference. They are widely used in urban power grids, industrial enterprises, and other areas. However, over time, power cables are subjected to various influences, including electrical, thermal, and mechanical stresses, and environmental factors, which degrade their insulation performance and lead to insulation deterioration. This not only affects the smooth operation of society but also poses a significant threat to personnel safety. According to reports [1], in 2022, the failure rate of 10kV distribution network cable lines in China was 1.43 failures per 100 km per year, which is considerably higher than the failure rates for transformers (0.15 failures per 100 units per year) and circuit breakers (0.17 failures per 100 units per year). Additionally, as most cables enter the later stages of their service life, it is likely that the failure rate of cables will increase in the future. Therefore, effective health monitoring of power cables is of great significance in improving the reliability and stability of power systems.
Insulation anomalies in operational cables frequently initiate electric field distortion and partial discharge (PD) phenomena [2], recognized as pivotal biomarkers for incipient fault risk assessment in power transmission systems. Contemporary PD detection systems bifurcate into offline inspection and online monitoring paradigms: offline modalities necessitate operational discontinuities, constraining their practical utility, whereas online alternatives facilitate uninterrupted insulation evaluation during live cable operation. The operational superiority of online systems—characterized by intelligent signal acquisition, continuous condition tracking, and diagnostic reliability—has driven their industrial proliferation [3]. Established online PD detection architectures principally integrate three methodologies: pulse current analysis method, ultra-high frequency (UHF) sensing technology, and ultrasonic wave detection [4]. Among these, UHF technology exhibits unparalleled sensitivity in weak PD signal acquisition and has been widely applied in practical engineering scenarios. For instance, researchers have proposed a real-time UHF-based online PD monitoring system capable of detecting partial discharge signals within gas-insulated switchgear (GIS) [5]. By integrating multiple sensor data streams, this system enables online condition assessment and early fault warning of GIS equipment. Additionally, a high-efficiency, portable system utilizing UHF-based dual-end PD detection and localization techniques has been developed for wind farm power cables [6]. This system can assess insulation conditions in real-time, rapidly identify potential failures, and ensure operational stability of the wind energy infrastructure. Furthermore, UHF sensing facilitates visualization through phase-correlated discharge representations, including PRPD (phase-resolved partial discharge) spectra [7] and PRPS (phase-resolved pulse sequence) matrices [8]. While recent advances exploit conventional PRPD signatures for discharge taxonomy, prevailing analytical frameworks—encompassing threshold-dependent detection, Gaussian statistical modeling, and wavelet-based signal decomposition—remain hampered by manual feature engineering requirements and suboptimal cross-domain adaptability, fundamentally limiting diagnostic throughput.
With the development of deep learning techniques, especially the widespread application of convolutional neural networks (CNNs) and recurrent neural networks (RNNs) in image classification, the performance of partial discharge pattern recognition has significantly improved. Ran Y. [9] proposed a partial discharge pattern recognition method based on PRPD and CNNs, which significantly improved recognition accuracy by improving CNN architecture and integrating multiple feature sets. Deng Y. [10] utilized multi-scale feature extraction and spatial interaction attention mechanisms to enhance the accuracy and efficiency of partial discharge pattern recognition. The model demonstrated excellent performance in handling complex partial discharge signals from power equipment, providing a new, efficient method for fault diagnosis and condition monitoring of electrical equipment. During the classification training process using neural networks, the settings of hyperparameters directly impact the final training results. Scholars have proposed various optimization algorithms for hyperparameter tuning. Guo Xingchao [11] suggested the use of Particle Swarm Optimization to optimize deep belief networks for identifying partial discharge characteristics in mining cables. Lei Zhipeng [12] proposed a target detection model based on the Transformer architecture, incorporating Bayesian optimization to improve convergence speed and accuracy for partial discharge type identification. Fei Z. [13] introduced an improved mantis optimization algorithm to optimize the biases and weights of backpropagation neural networks, verifying its effectiveness in identifying different types of partial discharge faults through simulation experiments. In studies by Srivastava R. [14] and Vigneshwaran B. [15], the Combined Sealion-Swarm Optimization Algorithm (CS-SOA) and Bayesian optimization algorithms were employed to optimize hyperparameters in convolutional neural networks. Zhaotao Yu [16] proposed an effective method for pipeline robot fault diagnosis based on Particle Swarm Optimization and ResNet (PSO-ResNet). Experimental results show that the PSO-ResNet model achieves superior diagnostic accuracy and adaptability compared to conventional approaches under varying working conditions and fault levels. Wang P. [17] developed a fault diagnosis approach for spent fuel cutting machines, integrating Bayesian optimization and a CBAM-enhanced ResNet model. The CBAM (Convolutional Block Attention Module) introduces both channel and spatial attention mechanisms to improve the extraction of fault features, while Bayesian optimization fine-tunes the network’s hyperparameters to enhance overall model performance. Additionally, some scholars have focused on partial discharge classification with small sample sizes. Jin H. [18] proposed a method combining Wasserstein GAN (WGAN) and Gradient Penalty (GP) to enhance partial discharge pattern recognition by generating synthetic samples to address the small-sample issue. Li S. [19] introduced a method based on a Convolutional Autoencoder-Assisted Classifier Generative Adversarial Network (CAE-ACGAN) and Residual Networks (ResNet) for partial discharge data augmentation and pattern recognition. This approach generates high-quality PRPD maps using CAE-ACGAN and performs classification using ResNet, yielding promising experimental results. Furthermore, Andreas Rauscher [20] suggested that optimizing network architectures and training strategies could significantly improve model performance under small-sample conditions. This is echoed by Tenbohlen S. [21] and Jung H. [22], who explored classification of overlapping partial discharge (PD) patterns and classification of phase-resolved partial discharge (PRPD) patterns using enhanced deep learning algorithms such as VGG and ResNet under limited data scenarios.
In summary, PRPD maps are commonly used in online partial discharge monitoring systems. However, obtaining large volumes of partial discharge data in actual power equipment operation is challenging. Additionally, feature extraction in traditional convolutional neural networks (CNNs) heavily depends on hyperparameter selection in fault type recognition. Manual hyperparameter tuning hinders effective feature extraction, particularly in small-sample classification, where generalization is poor and accuracy is limited. Furthermore, the Firefly Algorithm (FA), commonly used to optimize hyperparameters, suffers from several limitations, including slow convergence in high-dimensional spaces, premature stagnation in local optima, and insufficient adaptability to complex problem landscapes, all of which hinder its performance in small sample scenarios.
To address the limitations of the traditional Firefly Algorithm, this paper proposes an improved version that integrates Black Hole Mechanisms and enhanced population dynamics. The proposed FBH algorithm enhances convergence speed, global search ability, and parameter space exploration efficiency. By incorporating dynamic adjustments in the exploration and exploitation phases, the FBH algorithm effectively avoids local optima, ensuring a more robust optimization process. Compared to other metaheuristic-based optimization strategies such as Particle Swarm Optimization (PSO), Bayesian optimization (BO), and hybrid methods like CS-SOA, the FBH algorithm offers a unique advantage in balancing exploration and exploitation, especially under small-sample constraints. The introduction of the Black Hole Mechanism strengthens the global search behavior by guiding candidate solutions toward promising regions in the solution space, thereby mitigating the risk of premature convergence. This enhancement is particularly advantageous in small sample scenarios, where the traditional FA and other metaheuristics often struggle to maintain effective exploration of the solution space. In this model, the ResNet18 model serves as the fundamental neural network for pattern recognition and classification, and the FBH algorithm is used to optimize the hyperparameters, ensuring better feature extraction and improved performance in small sample datasets. Through this integration, our method aligns with current trends in optimization-driven neural architecture tuning while innovatively introducing black hole dynamics to overcome the inherent weaknesses of conventional approaches.
Based on the above background, this paper represents the relationship between the discharge phase and amplitude using two-dimensional PRPD maps and provides a detailed introduction. Using the established experimental platform and the collected data, a new partial discharge detection model is proposed for small sample PRPD maps. In the proposed model, the ResNet18 architecture is employed for pattern recognition and classification tasks, and the FBH algorithm is utilized to optimize the hyperparameters of the residual neural network. This integration improves feature extraction from small sample datasets, enhancing the generalization ability and classification accuracy. The effectiveness of the proposed model and algorithm is tested through experimental validation with the collected data. The structure of this paper is organized as follows: Section 2 introduces the platform and method for generating PRPD maps in the laboratory. Section 3 elaborates on the specific steps of using the improved residual network for partial discharge fault classification. Finally, the effectiveness of the FBH-ResNet18 model is verified through case studies and experimental analysis.
2. Experimental Generation of PRPD Maps and Pattern Recognition Methods
2.1. Test Platform of Partial Discharge
In this study, an experimental platform is built to simulate defects caused by partial discharge (PD) in cables under actual operating conditions. The wiring diagram for the partial discharge setup is shown in Figure 1 [23]. Sensor selection is critical in the process of collecting partial discharge data from power equipment. The High-Frequency Current Transformer (HFCT) selected for this experiment is the SH-JF-60 model, manufactured by Shanghai Jufeng Electric Automation Co., Ltd. (Shanghai, China). It features a 60 mm aperture, a frequency range [0.3–100 MHz], and a sensitivity of 0.1 pC. The BNC output interface is used for signal transmission. Installed on the grounding wire, the HFCT effectively detects ultra-high-frequency signals generated by the cable’s partial discharges. This sensor is known for its high sensitivity and strong anti-interference ability, ensuring accurate data collection in complex electromagnetic environments. For signal acquisition, a UHF sensor with a frequency range of 300 to 1500 MHz and a sensitivity of 10 pC is used to down-sample the signal to reduce the sampling rate of the data collected by the HFCT. This can help to filter out high-frequency noise and enhance the signal-to-noise ratio (SNR), improving the ability to process partial discharge characteristics in subsequent analysis steps.
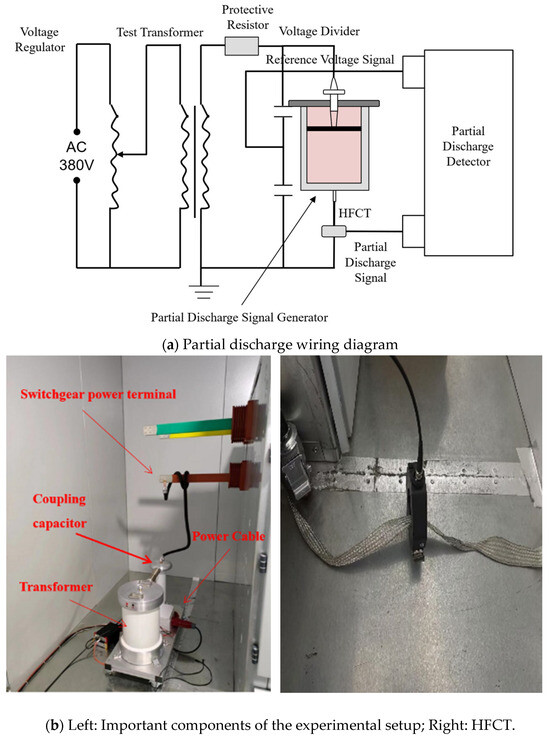
Figure 1.
Brief illustration of the experimental platform of partial discharge.
The experiment is conducted in a laboratory-simulated environment. The experimental platform includes a high-voltage power supply, a simulated cable, and defect models. Four typical defect types—corona discharge, gas gap discharge, floating discharge, and surface discharge—are used to simulate partial discharge scenarios occurring in actual cables and to collect corresponding PD signal data.
The phase-resolved partial discharge (PRPD) analysis method, which is widely recognized and used, is employed to process partial discharge signals [7]. PRPD is an important tool for analyzing partial discharge activities, as it provides a clear representation of the interrelationships between discharge frequency, quantity, and phase. PRPD maps exhibit distinct characteristics for different types of partial discharge, making them crucial for identifying early cable faults. For the detailed experimental steps and PRPD map generation methods, please refer to [23].
A total of 1426 PRPD maps were collected, with a resolution of 515 × 389. In these maps, the horizontal axis represents the normalized phase of a single cycle (0–360°), while the vertical axis indicates the amplitude range. The grid color intensity represents the frequency of occurrences within a specific amplitude range for each phase window. Figure 2 shows the PRPD maps for four types of partial discharge defects, as well as the one with no PD condition. To simulate a small sample scenario, 50 maps shown in Table 1 are randomly selected from each defect category for use in partial discharge pattern recognition. The selected dataset is then divided into a training set and a testing set at a ratio of 4:1 to ensure a fair evaluation of the model’s performance in limited-data conditions.
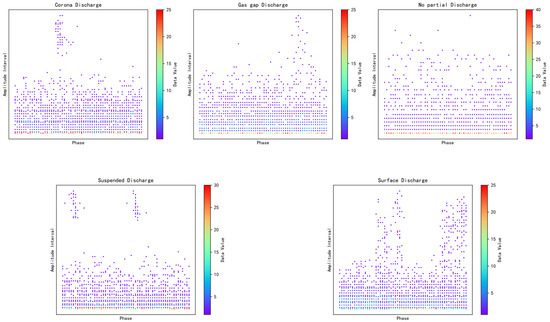
Figure 2.
PRPD maps of four partial discharge defects and the one with no partial discharge condition [23].

Table 1.
Number of PRPD maps for each defect type.
2.2. Residual Neural Network (ResNet)
It should be noted here that some typical discharges are difficult to obtain generally, and hence, sometimes, only small sample datasets can be obtained. However, small samples are prone to overfitting and degradation during the training of the models. Here, a residual neural network, proposed by He et al. [24], is employed to avoid the emergence of this circumstance. The residual unit, as shown in Figure 3, which is the fundamental building block of a residual neural network, mainly adds the output of the previous layer directly to the output of the current layer through an additional connection, serving as the input for the subsequent layer.
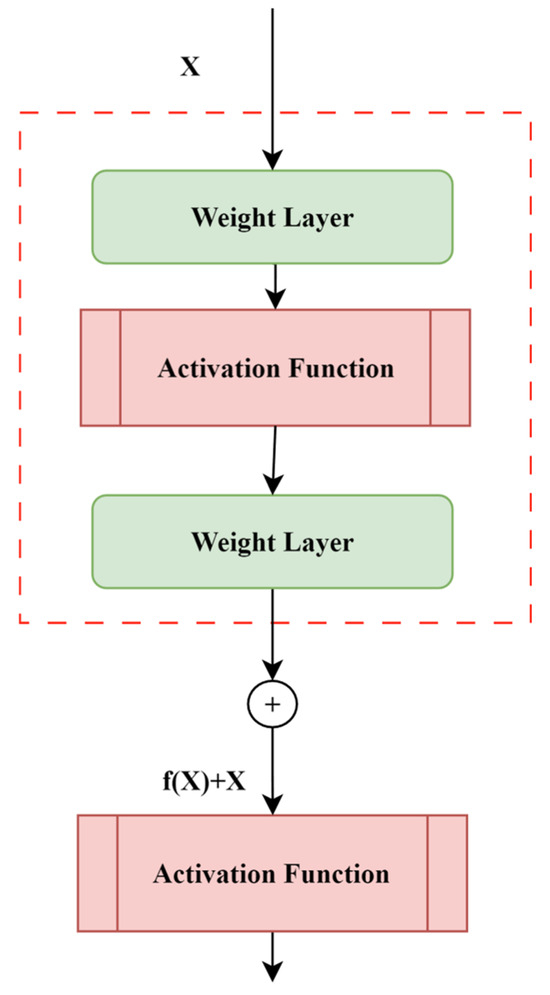
Figure 3.
Residual unit.
ResNet18 is a lightweight yet representative model in the residual network family, comprising an input layer, convolutional and pooling layers, fully connected layers, and an output layer. The architecture consists of 18 weighted layers, including 16 convolutional layers and 2 fully connected layers. In ResNet18, the convolutional layers are key for feature extraction, primarily using 3 × 3 convolutional kernels. These kernels effectively extract local features from images while reducing computational complexity and the number of parameters. In addition to the convolutional layers and residual units, the residual network also includes other components. For example, at the beginning of the network, there is a 7 × 7 convolutional layer to perform initial feature extraction, reducing image resolution rapidly, while increasing the number of feature channels. Furthermore, the network ends with fully connected layers that map the feature vectors to the final class space for classification tasks.
As a classic and efficient deep convolutional neural network model, ResNet performs excellently in general image classification and pattern recognition tasks. However, for small sample tasks, the initial hyperparameters of the network model are critical. Therefore, optimization algorithms are introduced to help extract good parameters for improved performance.
2.3. Improved Firefly Algorithm (FBH)
The Firefly Algorithm (FA) is a population-based heuristic optimization algorithm inspired by the behavior of fireflies in nature. Proposed by Yang in 2008 [25], it optimizes by simulating the flashing communication behavior between fireflies. The algorithm is simple to operate, converges quickly, and is highly adaptable. The implementation of the algorithm is based on three main assumptions: ① Fireflies are bisexual, meaning each firefly is attracted to others with higher light intensity. The attraction is proportional to the brightness and decreases with distance. The brightness of the firefly is influenced by the objective function.
Thus, the mathematical model of the firefly algorithm mainly includes three factors: brightness (I), attractiveness (β), and distance (r). The key steps of the algorithm are as follows:
- Brightness Calculation: Based on the inverse square law:
- 2.
- Attractiveness Calculation: The attractiveness at is , and at distance , it is given by:
- 3.
- Position Update: The distance between two fireflies and is:
Firefly i moves towards the brighter firefly j with the following update rule:
where α is a random step size, and is a random number between 0 and 1.
3. Introduction of the Black Hole Mechanism (BHM)
To further enhance the global search capability of the Firefly Algorithm and avoid premature convergence to local optima, the Black Hole Mechanism (BHM) is introduced. The BHM simulates the gravitational effect of a black hole, where a solution is “pulled” into the black hole once its fitness exceeds a certain threshold, and its position is reset. This mechanism helps to prevent the algorithm from getting trapped in local optima.
Dynamic Threshold Adjustment Strategy:
To better control the introduction of the Black Hole Mechanism, a dynamic threshold adjustment strategy is proposed. Specifically, as the number of iterations increases, the black hole threshold gradually decreases, ensuring that only solutions with significantly poor performance are “pulled” into the black hole during later iterations. This strategy maintains exploration while preventing premature convergence. The dynamic threshold formula is as follows:
To clarify the implementation of the BHM in the improved Firefly Algorithm, the detailed pseudocode of this mechanism is provided in Algorithm 1. The pseudocode outlines how each individual in the population is evaluated against the dynamically adjusted threshold. If its fitness is worse than the threshold, the individual is considered to have fallen into the black hole and is reinitialized within the search space to encourage exploration.
| Algorithm 1. Black Hole Mechanism (BHM) with Dynamic Threshold Pseudocode |
| Input: Population X = {x1, x2, …, xn}, max_iter, initial fitness list F0 |
| Output: Updated population X with BHM applied |
| 1: for iter = 1 to max_iter do |
| 2: Calculate threshold: |
| T_bh ← max(F0) × (0.8 − 0.5 × iter/max_iter) |
| 3: for each individual xi in X do |
| 4: Evaluate current fitness fi = Fitness(xi) |
| 5: if fi > T_bh then |
| 6: //Individual pulled into black hole |
| 7: xi ← Random Initialization ()//Reinitialize position |
| 8: end if |
| 9: end for |
| 10: end for |
3.1. Algorithm Testing
To accurately and efficiently evaluate the performance of the original Firefly Algorithm and the improved FBH algorithm, two common functions, Ackley and Rosenbrock, are selected for testing. The Ackley function is a widely used optimization test function, particularly in multidimensional optimization problems. Its characteristics make it an ideal choice for evaluating the performance of optimization algorithms in complex, multimodal problems. The Rosenbrock function, on the other hand, is a typical single-objective optimization problem, featuring multiple local optima and a flat global optimum, making it suitable for testing the global optimization capability of optimization algorithms.
Ackley Function:
Rosenbrock Function:
where
- is the dimension of the decision variables;
- is the value of the -th decision variable;
- is the base of the natural logarithm.
In this test experiment, the population size is set to 30, with iteration counts of 500 and 100, and parameters α = 0.5, , and . Additionally, to ensure fairness, both algorithms use the same initial population. The best fitness value in each generation is taken as the performance evaluation criterion, and the fitness change curve is plotted to compare the convergence speeds of the two algorithms.
Figure 4 presents the fitness evolution curves for two benchmark functions. Specifically, subfigures (a) and (b) illustrate the fitness variations of the original Firefly Algorithm and the improved FBH algorithm on the Ackley and Rosenbrock functions, respectively. It can be observed that the fitness of the FBH algorithm converges rapidly in the early stages, which is due to the introduction of the Black Hole Mechanism in the FBH algorithm’s iteration process. This mechanism increases the disturbance of particles in the search space, enabling the algorithm to find better solutions early on. Furthermore, the Black Hole Mechanism effectively prevents the algorithm from getting trapped in local optima by simulating the phenomenon of particles entering a black hole, demonstrating superior performance, especially on the Ackley function.
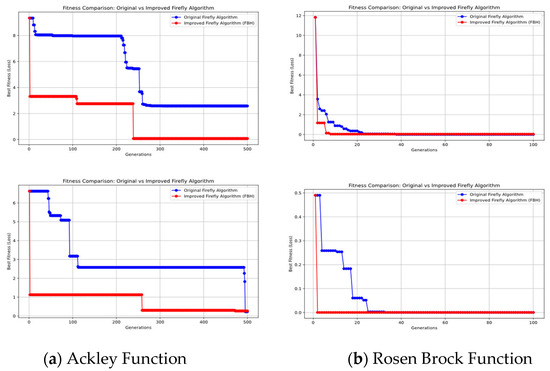
Figure 4.
Fitness variation curves of two test functions.
The results from both test functions show that the FBH algorithm, compared to the traditional Firefly Algorithm, exhibits stronger global search capabilities and faster convergence, particularly when optimizing complex functions with multiple local optima. The introduction of the Black Hole Mechanism significantly improves the overall performance of the algorithm, especially in multidimensional and high-complexity problems. The FBH algorithm is more effective at avoiding premature convergence, maintaining a good search diversity, and ultimately finding solutions closer to the global optimum.
Thus, the FBH algorithm not only achieves significant performance improvements but also exhibits stronger advantages in convergence rate and global search capability, making it particularly suitable for optimizing the hyperparameters of ResNet neural networks, which have complex structures and multiple local optima.
3.2. Partial Discharge Pattern Recognition Based on FBH-ResNet18
In the FBH-ResNet18 model, the Firefly Algorithm (FA) is innovatively combined with the Black Hole Mechanism (BHM) to optimize the hyperparameters of ResNet18. This study focuses on optimizing four key hyperparameters during the training process: learning rate, batch size, momentum, and weight decay coefficient. These parameters have a decisive impact on the training efficiency and performance of the model. However, determining their optimal combination is often challenging when using traditional methods such as grid search or random search. The Firefly Algorithm, inspired by the flashing behavior of fireflies and utilizing swarm intelligence, effectively finds the optimal hyperparameter combination through global search and local optimization. The addition of the Black Hole Mechanism further improves the algorithm’s ability to escape local optima, enhancing the global search capability. Specifically, the fitness value is determined by the loss function on the test set. This design helps in evaluating the model’s performance during the stages of training and avoids the issue of local optima, which can be caused by overfitting or underfitting.
The FBH algorithm iteratively guides the hyperparameters of ResNet18 to update in the direction that maximizes the fitness value, providing a better initialization for the model at the start of training. The Black Hole Mechanism introduces a dynamic threshold strategy, where solutions that exceed a certain fitness threshold are “pulled” into the black hole and reinitialized. This mechanism ensures that the optimization process avoids getting trapped in local optima by exploring the search space more effectively. This optimization strategy enhances the model’s convergence speed and recognition accuracy, especially in terms of its generalization ability on small sample datasets. The introduction of the Firefly Algorithm combined with the Black Hole Mechanism offers an efficient and robust solution for hyperparameter optimization. Its global search capability effectively circumvents the local optimum pitfalls of traditional methods, while the swarm intelligence mechanism enables rapid exploration of the parameter space. This novel approach, which integrates swarm intelligence and deep learning, not only improves model performance but also provides new research insights for solving similar small sample learning problems. The complete process of optimizing a residual convolutional neural network using the FBH algorithm is illustrated in Figure 5.
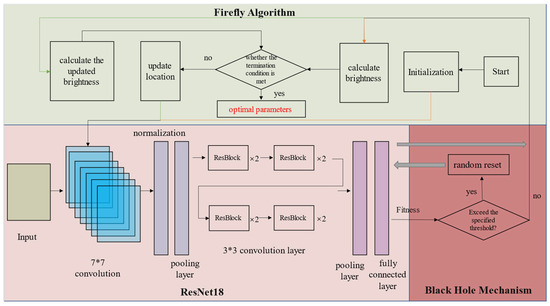
Figure 5.
FBH-ResNet18 model flowchart.
The specific process and parameters for optimizing ResNet18 using the improved Firefly Algorithm (FBH) are as follows:
① Set the range of hyperparameters to be optimized and algorithm parameters:
- Learning rate: (1 × 10−5, 1 × 10−2)
- Batch size: (4, 32)
- Momentum coefficient: (0.5, 0.999)
- Weight decay coefficient: (1 × 10−5,1 × 10−3)
- The update of the black hole threshold is referenced by Equation (6).
The number of the firefly population is set to 30, with a maximum number of iterations of 70, the update step size α = 0.5, and both the maximum attraction and light absorption coefficient γ are set to 1.0.
② Population Initialization: Randomly generate the hyperparameter combinations to initialize the positions of the fireflies, and input these into the ResNet18 neural network for training. Return the validation loss for each hyperparameter combination as the fitness value.
③ Evaluate the Black Hole Mechanism:
- After evaluating the fitness of each firefly, check if the firefly’s fitness is worse than the predefined black hole threshold.
- If a firefly’s fitness is worse than the predefined black hole threshold, replace it with a new random hyperparameter combination that is likely to improve performance.
- Recalculate the fitness value under the newly randomly generated hyperparameters.
④ Update the Optimal Solution: Record the current optimal hyperparameter combination. If the fitness of the current firefly is better than the historical optimal, update the optimal solution.
⑤ Update Firefly Positions: Update the positions (i.e., hyperparameter combinations) based on the attraction between fireflies.
- Attraction Calculation: Calculate the attraction by computing the distance and using Equation (3).
- Position Update: If the fitness of firefly is worse than firefly , firefly will move toward firefly . The position is updated using Equation (5), ensuring that the updated hyperparameter values remain within the predefined range.
⑥ Iterative Optimization: In each iteration, repeat the following steps:
- Evaluate the new firefly positions (i.e., hyperparameter combinations).
- Update the fitness values, repeat step ③, and record the optimal solution.
Output the optimal loss of the current iteration.
⑦ Check for Maximum Iteration: If the maximum iteration count is reached, stop the optimization process and output the final optimal hyperparameter combination and corresponding loss.
4. Case Study
4.1. Experimental Environment and Related Evaluation Indicators
This section conducts pattern recognition based on the previously generated PRPD maps and the FBH-ResNet18 neural network. The local discharge recognition performance of the improved residual neural network is compared with other neural network models under different parameters using relevant evaluation metrics. The FBH-ResNet18 model is implemented using Python toolkits under the PyTorch framework. The experiments are conducted in the PyCharm integrated development environment on a system running Windows 11 (64-bit), equipped with an Intel(R) Core(TM) i7-12700K processor and an NVIDIA GeForce RTX 3080 GPU. The programming environment is Python 3.12.9, and the PyTorch version used is 2.5.1 with CUDA 12.4 support.
To comprehensively evaluate the model’s recognition performance, this study primarily adopts accuracy and precision as performance metrics. Accuracy reflects the overall proportion of correctly classified samples, while precision measures the proportion of true positive predictions among all predicted positive instances. The mathematical definitions of these metrics are as follows:
where TP (True Positive) denotes the number of correctly identified positive cases, TN (True Negative) represents correctly identified negative cases, FP (False Positive) is the number of negative cases incorrectly classified as positive, and FN (False Negative) is the number of positive cases incorrectly classified as negative. These indicators provide valuable insights into the classification effectiveness and robustness of the FBH-ResNet18 model.
4.2. Comparison of Algorithm Optimization Results
The fitness function for optimizing the hyperparameters of the residual neural network using the improved Firefly Algorithm (FBH) is shown in Figure 6. As seen, the fitness function for FBH stabilizes rapidly, reaching an optimal or near-optimal hyperparameter configuration by approximately the 12th iteration. This quick stabilization in the early stages of training is a significant advantage of the FBH, demonstrating its efficiency in converging on a good solution.
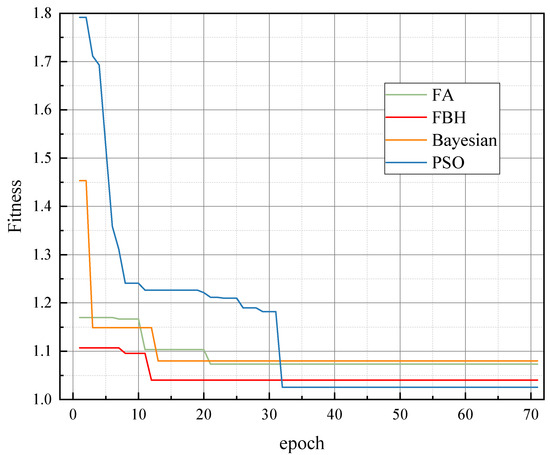
Figure 6.
Optimization of fitness functions for various algorithms.
For comparison, additional experiments were conducted using Bayesian optimization and Particle Swarm Optimization (PSO) to optimize the same neural network hyperparameters. Figure 6 clearly illustrates the convergence behavior of all tested optimization algorithms. In the initial training phases, the improved Firefly Algorithm (FBH) exhibits a notably faster convergence speed compared to Bayesian optimization, PSO, and the original Firefly Algorithm (FA). This rapid descent in fitness value in the early iterations suggests that FBH is more effective at quickly identifying promising regions of the hyperparameter space and escaping initial local optima. Furthermore, FBH achieves a consistently lower final fitness value than FA and Bayesian optimization, indicating that it finds better overall hyperparameter configurations.
While FBH demonstrates superior early convergence and a lower final fitness value compared to some other methods, it is also important to acknowledge its limitations. As observed in Figure 6, in the later stages of training, the PSO algorithm ultimately converges to a lower fitness value than FBH. This suggests that while FBH is excellent at rapidly finding good solutions and escaping early local optima, it may be more susceptible to getting trapped in local optima in the very late stages of optimization, compared to algorithms like PSO, which might explore the solution space more thoroughly over extended iterations.
For a comprehensive comparison, Table 2 presents six other experimental setups, including ResNet18_5, ResNet18_6, ResNet18_7, and ResNet18_8, which correspond to the hyperparameter settings optimized by the original Firefly Algorithm, the improved Firefly Algorithm, the Bayesian optimization Algorithm, and the Particle Swarm Optimization (PSO) Algorithm, respectively. These comprehensive experimental setups fully demonstrate the effectiveness and comparative performance of the proposed improved Firefly Algorithm.

Table 2.
Experimental parameter settings for five experimental groups.
4.3. Comparison of Improved Model and Original Model Performance
In this section, the improved FA-optimized ResNet18 model is compared with other residual models trained with random hyperparameters for partial discharge fault pattern recognition. The first comparison focuses on the difference in loss function convergence speeds.
The loss function curve relative to the number of iterations during the training process of different deep learning networks is shown in Figure 7. In the training set, the FBH-optimized improved ResNet18 model demonstrates robust performance. Compared to other models with initial losses greater than 1.70, the initial loss value (1.6845) is significantly smaller. Moreover, the loss function of the improved ResNet18 model decreases rapidly during the first 100 iterations. Afterward, the loss steadily declines, and the final training loss stabilizes at a lower level, indicating that the new model proposed in this paper has the advantages of a lower initial loss and faster convergence in the training set. In the test set, the loss function of the improved ResNet18 model decreases rapidly during the first 60 iterations, suggesting that the improved ResNet18 model has the advantage of fast and stable convergence in the early stages of training. In the middle of the training process, all models show a stable reduction in loss. After 100 iterations, the models approach stability. Upon completion of training, the FBH algorithm-optimized ResNet18 model achieves a final minimum loss of 0.250785, whereas the final loss values of the other models are 0.3075, 0.5149, 0.2736, 0.3459, 0.3040, and 0.30815, respectively. This indicates that the proposed improved algorithm can reduce the test set loss to some extent and has strong generalization capability.
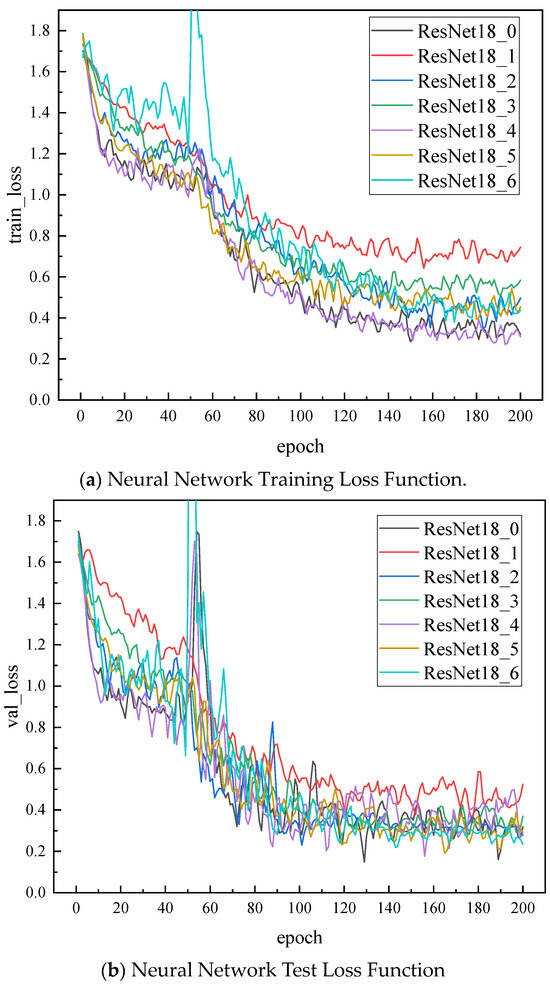
Figure 7.
Loss functions of various neural networks.
Similarly, Figure 8 shows the classification precision of partial discharge. The proposed improved residual network model starts with moderate precision in the early training stages, but compared to other models, it increases more rapidly in the first 80 iterations. By the 80th iteration, the precision reaches 89.11%, which is significantly higher than the second-best ResNet_5 at 81.97%. At the end of training, the improved model achieves a classification precision of 92.55%, still outperforming all other models. As training continues, the precision of convolutional neural networks tends to decrease slightly, which may be due to overfitting, as the experiments mainly focus on small samples. This suggests that increasing the number of iterations does not always lead to improved precision while sacrificing computational efficiency. The use of the improved ResNet18 model for small sample partial discharge pattern recognition offers faster convergence speed and higher precision.
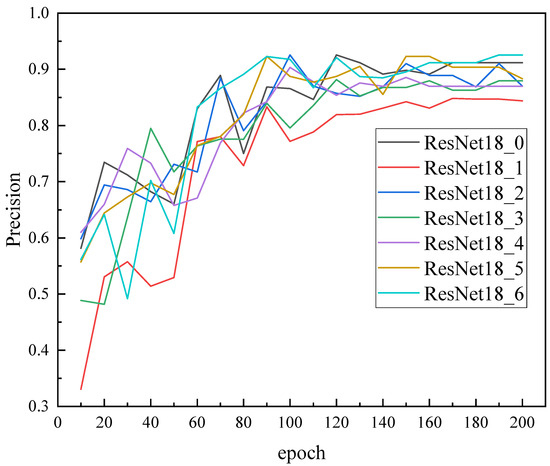
Figure 8.
Partial discharge classification precision curve.
Table 3 shows the recognition accuracy for each mode at the 200th generation under different parameters. Compared with other models, the FBH-optimized residual network achieves comparable or higher recognition accuracy across all modes, except for floating discharge, where it slightly trails Model 2. Specifically, the recognition accuracy for the no partial discharge and surface discharge types has reached 100%, and Model 6 outperforms the average recognition accuracy for all five discharge types by at least 2.5 percentage points. This fully demonstrates that the improved residual network model described in this paper has achieved significant results in partial discharge mode recognition, especially in needle discharge and surface discharge, with accuracy improvements of 6% and 5.14% compared to the average, respectively.

Table 3.
Recognition accuracy of each pattern type (%).
Figure 9 shows the partial discharge classification confusion matrix for the residual network model with five hyperparameter settings after 200 generations of training. Overall, the proposed improved ResNet18 model achieves the highest overall accuracy of 92%, significantly higher than the recognition accuracy of models with other parameter settings, such as Model 1 (82%) and Model 2 (86%). Furthermore, the improved residual network model demonstrates high accuracy in predicting each category. For example, the accuracy for predicting “no partial discharge” reaches 100%, indicating that the classification criteria for this category are very accurate with no misclassifications. This result highlights the advantage of parameter optimization, enabling the neural network to effectively capture key features of different partial discharge patterns. Additionally, although there are some misclassifications in the surface discharge category in Model 6, it can be said that the accuracy for each category remains relatively high, indicating that the model’s classification results are more balanced and possess strong generalization capability.
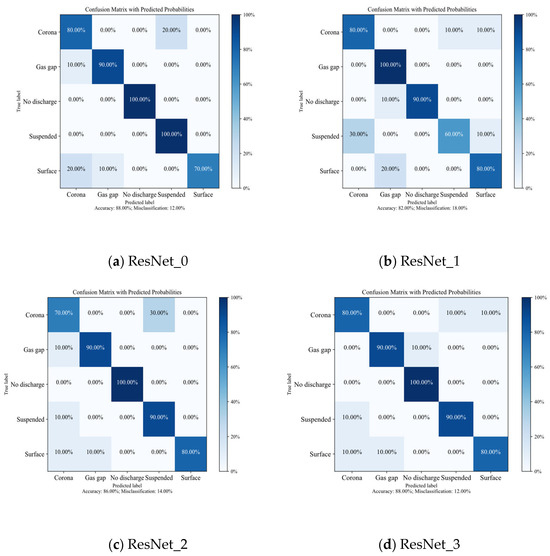
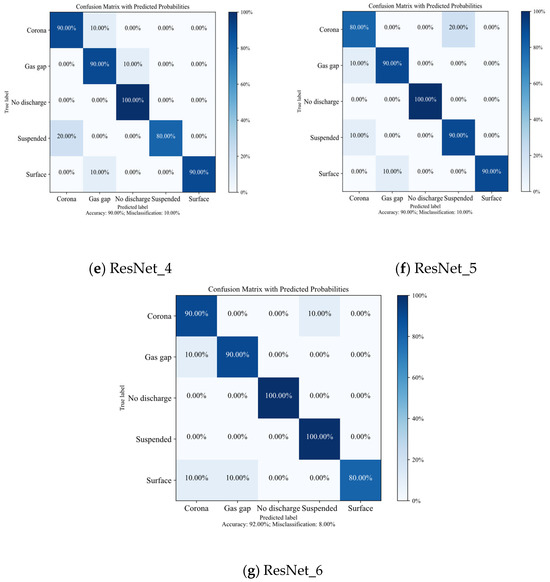
Figure 9.
Partial discharge classification confusion matrix under different parameters.
4.4. Comparison of Optimization Results from Different Algorithms
As shown in Figure 10, the ResNet18_6 model, optimized using the FBH algorithm, consistently demonstrates a more stable and rapid convergence to a lower training loss compared to ResNet18_7 (Bayesian optimization) and ResNet18_8 (PSO). In Figure 10a, the loss curve for ResNet18_6 exhibits a significantly smoother descent with fewer oscillations, indicating a more robust and efficient optimization process. This superior performance is further corroborated in Figure 10b, where ResNet18_6 maintains a lower loss value throughout the training epochs, even amidst the greater fluctuations observed in the other two models.
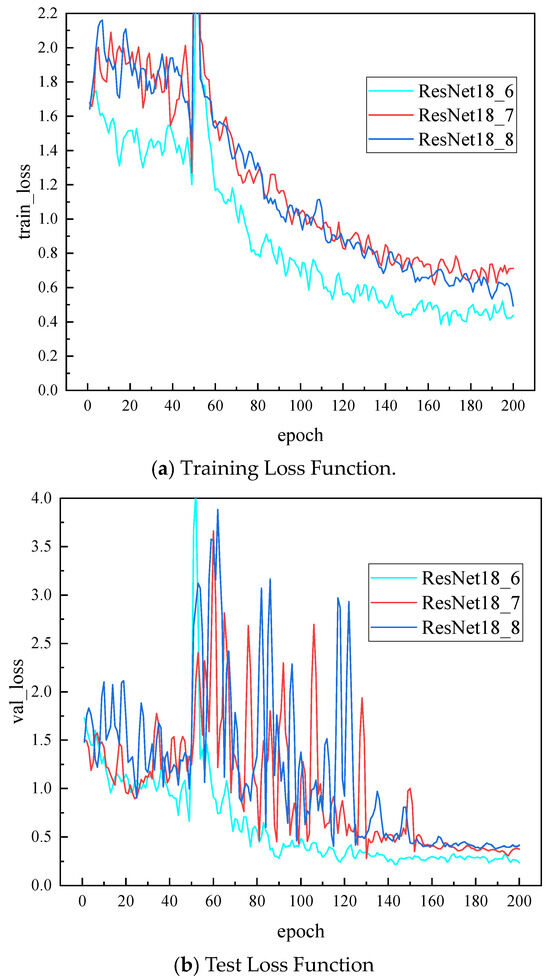
Figure 10.
Optimized network loss function.
Specifically, although ResNet18_6 begins with a slightly higher initial test loss (1.713905) compared to ResNet18_7 (1.505608) and ResNet18_8 (1.617132), it rapidly converges to a much lower final test loss (0.250785). This illustrates the model’s strong learning and generalization capabilities once properly optimized, despite a slightly less favorable starting point. Such an initial gap may suggest a relatively higher sensitivity to parameter initialization or the need for a longer warm-up period. Nonetheless, the final training loss for ResNet18_6 (0.420235) is substantially lower than that of ResNet18_7 (0.687216) and ResNet18_8 (0.501753), and the final test loss is also markedly lower than those of the other models. These results strongly support the effectiveness and superiority of the FBH algorithm in optimizing the ResNet18 architecture for partial discharge pattern recognition.
The performance of the optimized ResNet18 models is further evaluated by their precision curves and the time required for hyperparameter optimization, as presented in Figure 11 and Table 4, respectively.
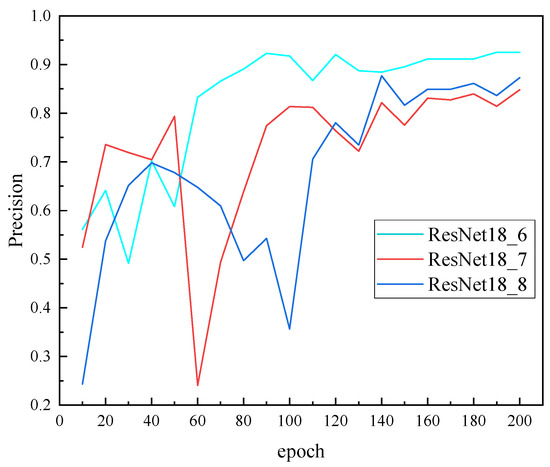
Figure 11.
Optimized network precision curve.

Table 4.
Comparison of optimization time for different algorithms.
As depicted in Figure 11, which illustrates the optimized network precision curve, ResNet18_6 (optimized by FBH) consistently achieves the highest precision throughout the training process compared to ResNet18_7 (Bayesian optimization) and ResNet18_8 (PSO). While all models show an increasing trend in precision, ResNet18_6 demonstrates a more rapid ascent and ultimately reaches and maintains a higher plateau of precision. Specifically, after 200 iterations, the final precision values for ResNet18_6, ResNet18_7, and ResNet18_8 are 0.9255, 0.8485, and 0.8731, respectively. This quantitative evidence further confirms ResNet18_6’s superior performance, indicating the FBH algorithm’s effectiveness in fine-tuning the ResNet18 architecture for more accurate partial discharge pattern recognition.
However, the enhanced performance of the FBH-optimized model comes with a consideration for computational resources, particularly in terms of optimization time. Table 4 provides a comparison of the optimization time for different algorithms. As shown in Table 4, the FBH algorithm required 28.13 h for optimization, which is longer than Bayesian optimization (7.75 h) but notably shorter than PSO (30.43 h) and comparable to FA (26.48 h). While the FBH algorithm demands a more extensive optimization period than Bayesian optimization, its investment in time yields significantly higher precision, as evidenced by Figure 11 and the reported final precision values. This trade-off between optimization time and achieved precision highlights that for critical applications demanding the highest accuracy in partial discharge pattern recognition, the FBH algorithm presents a compelling advantage despite its longer optimization duration. The superior precision achieved by ResNet18_6 ultimately translates to more reliable and robust diagnostic capabilities, justifying the increased computational effort for its hyperparameter tuning.
5. Conclusions
This study develops a Firefly Algorithm-optimized ResNet18 model for partial discharge pattern recognition, yielding four core findings:
(1) The optimized model demonstrates accelerated convergence with reduced initial loss values compared to baseline approaches, showing faster loss function reduction during early training phases.
(2) Achieving 92.55% classification accuracy, the model surpasses conventional models in both training efficiency and generalization ability, effectively addressing overfitting issues in small-sample scenarios.
(3) In specific discharge type analysis, accuracy improvements of 6% for needle discharge and 5.14% for surface discharge were observed, while maintaining consistent high performance across all defect categories.
(4) ResNet18_6 consistently demonstrated superior performance compared to Bayesian optimization (ResNet18_7) and Particle Swarm Optimization (PSO, ResNet18_8). It achieved significantly lower final training loss (0.420235) and test loss (0.250785), as well as a substantially higher final precision of 0.9255, outperforming ResNet18_7 (0.8485) and ResNet18_8 (0.8731).
These advancements establish a reliable solution for early insulation fault detection in power systems, particularly valuable for smart grid maintenance scenarios requiring robust pattern recognition with limited training data.
Nonetheless, the study has certain limitations. The FBH algorithm, although effective, imposes a higher computational cost, which could constrain its deployment in low-resource environments. Moreover, the current work focuses on a single-task optimization scenario using a specific dataset and model architecture. Broader evaluations across diverse data distributions or alternative deep learning models are required to further validate generalizability.
Future work will explore the applicability of the FBH algorithm in multi-objective optimization scenarios and other complex real-world tasks, such as fault localization, energy consumption forecasting, or condition-based maintenance. The hybrid nature of the FBH algorithm makes it a promising candidate for balancing competing objectives such as accuracy, time efficiency, and model complexity in broader industrial and engineering contexts.
Author Contributions
Conceptualization, Y.Y.; data curation, J.G.; formal analysis, T.L.; funding acquisition, Y.Y.; investigation, Y.Z. and Y.Y.; methodology, Z.J. and J.Z.; resources, Q.Z.; software, J.G.; supervision, J.Z.; validation, T.L.; visualization, Y.Z.; writing—original draft, Z.J.; writing—review and editing, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Grid Beijing Electric Power Company Science and Technology Program with Grant Number DCHA-KJ-24120301.
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of an ongoing study. Requests to access the datasets should be directed to zjrhust@gmail.com.
Acknowledgments
We would like to sincerely thank Deyou Wang and Jia Wang for their invaluable feedback and constructive suggestions during the preparation of this manuscript.
Conflicts of Interest
Authors Yuhai Yao, Jun Gu, and Tianle Li are employed by Beijing Dingcheng Hongan Technology Development Co., Ltd.; authors Ying Zhang and Qiao Zhao are employed by State Grid Beijing Electric Power Research Institute; Zihao Jia and Jingrui Zhang are partly employed by Nanjing Fuhua New Energy Technology Co., Ltd.; the authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- China National Energy Administration. 2022 Annual Report on National Electric Power Reliability; China National Energy Ad-ministration: Beijing, China, 2022. [Google Scholar]
- Fei, Z.; Li, Y.; Yang, S. Partial Discharge Pattern Recognition Based on an Ensembled Simple Convolutional Neural Network and a Quadratic Support Vector Machine. Energies 2024, 17, 2443. [Google Scholar] [CrossRef]
- Adamowicz, M.; Gulczyński, M.; Olesz, M. Diagnostyka off-line stanu izolacji uzwojeń silników 6 kV z wykorzystaniem obrazowania akustycznego wyładowań niezupełnych. Przegląd Elektrotech. 2024, 100, 60–67. [Google Scholar]
- Qi, B.; Li, C.; Hao, Z.; Geng, B.; Xu, D.; Liu, S.; Deng, C. Partial discharge detection for GIS: A comparison between UHF and acoustic methods. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–5. [Google Scholar]
- Sikorski, W.; Walczak, K.; Gil, W.; Szymczak, C. On-Line Partial Discharge Monitoring System for Power Transformers Based on the Simultaneous Detection of High Frequency, Ultra-High Frequency, and Acoustic Emission Signals. Energies 2020, 13, 3271. [Google Scholar] [CrossRef]
- Yan, Y.; Zhao, Y.; Zhao, K.; Trinchero, R.; Stievano, I.S.; Li, H. A high-efficiency portable system for insulation condition assessment of wind farm inter-array cables with double-sided partial discharge detection and localisation. IET Gener. Transm. Distrib. 2023, 17, 2523–2534. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Y.; Jia, Y.; Li, L. Parallel phase resolved partial discharge analysis for pattern recognition on massive PD data. Proc. CSEE 2016, 36, 1236–1244. [Google Scholar]
- Lu, J. Design of Live Detection System for Switchgear. Master’s thesis, North China Electric Power University, Beijing, China, 2015. [Google Scholar]
- Ran, Y. State Recognition of GIS Partial Discharge Based on PRPD and CNNs. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 94–98. [Google Scholar]
- Deng, Y.; Liu, J.; Zhu, K.; Xie, Q.; Liu, H. PMSNet: Multiscale Partial-Discharge Signal Feature Recognition Model via a Spatial Interaction Attention Mechanism. Sensors 2024, 24, 3342. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Jin, B. Research on Partial Discharge Feature Recognition of Mining Cables Based on PSO-DBN. Coal Technol. 2024, 43, 263–266. [Google Scholar]
- Lei, Z.; Peng, C.; Xu, Z.; Jiang, W.; Li, C.; Lin, L.; Peng, B. Multi-source Partial Discharge Recognition Method Based on Improved Deformable DETR Model and Its Application. Proc. CSEE 2024, 44, 6248–6260. [Google Scholar]
- Fei, Z.; Li, Y.; Yang, S. Pattern recognition of partial discharge faults in switchgear using a back propagation neural network optimized by an improved mantis search algorithm. Sensors 2024, 24, 3174. [Google Scholar] [CrossRef]
- Srivastava, R.; Avasthi, V. Deep convolutional neural network for partial discharge monitoring system. Adv. Eng. Softw. 2023, 180, 103407. [Google Scholar] [CrossRef]
- Vigneshwaran, B.; Iruthayarajan, M.W.; Maheswari, R.V. Recognition of shed damage on 11-kV polymer insulator using Bayesian optimized convolution neural network. Soft Comput. 2022, 26, 6857–6869. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, L.; Kim, J. The Performance Analysis of PSO-ResNet for the Fault Diagnosis of Vibration Signals Based on the Pipeline Robot. Sensors 2023, 23, 4289. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Chen, J.; Wang, Z.; Shao, W. Fault diagnosis for spent fuel shearing machines based on Bayesian optimization and CBAM-ResNet. Meas. Sci. Technol. 2023, 35, 025901. [Google Scholar] [CrossRef]
- Jin, H.; Gao, L.; Pan, J.; Zhang, C.; Zhang, H.; Wang, H. Enhancing partial discharge pattern recognition via WGAN-GP and inception-resnet-v2. Electr. Eng. 2024, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Wang, X.; Han, Y.; Feng, J.; Yin, Z.; Yang, J.; Luo, W.; Xie, J. Partial Discharge Data Enhancement and Pattern Recognition Method Based on a CAE-ACGAN and ResNet. Symmetry 2024, 17, 55. [Google Scholar] [CrossRef]
- Rauscher, A.; Kaiser, J.; Devaraju, M.; Endisch, C. Deep learning and data augmentation for partial discharge detection in electrical machines. Eng. Appl. Artif. Intell. 2024, 133, 108074. [Google Scholar] [CrossRef]
- Adam, B.; Tenbohlen, S. Classification of superimposed partial discharge patterns. Energies 2021, 14, 2144. [Google Scholar] [CrossRef]
- Jung, H.; Kim, Y.T.; Lee, S.K.; Ahn, J.H. Study on Deep-Learning Model for Phase Resolved Partial Discharge Pattern Classification Based on Convolutional Neural Network Algorithm. J. Electr. Eng. Technol. 2025, 20, 873–878. [Google Scholar] [CrossRef]
- Li, Y.; Gong, C.; Deng, T.; Jia, Z.; Wang, F.; Zhao, Q.; Zhang, J. Partial Discharge Pattern Recognition Based on Swin Transformer for Power Cable Fault Diagnosis in Modern Distribution Systems. Processes 2025, 13, 852. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).