Optimized Coordination of Distributed Energy Resources in Modern Distribution Networks Using a Hybrid Metaheuristic Approach
Abstract
1. Introduction
- A joint formulation focused on all DSR and SOP operations, allocative decisions of PV, and ESS management on the active power losses minimization and grid stability improvement.
- The framework incorporates time-dependent profiles for both load and renewable energy, enhancing the realism and effectiveness of decision-making processes.
- The proposed approach considers hard constraints for essential power system parameters such as radiality, voltage limits, state of charge (SOC) of ESS, and SOP capacity, yielding realistic and feasible estimations.
- To verify the strengths of the proposed framework, comprehensive simulations were conducted to achieve a 67.2% energy loss reduction in the full DER integration case, while guaranteeing a better solution quality and a superior computational performance than benchmark algorithms.
2. Problem Formulation
2.1. The Objective Function
2.2. Power Flow Constraints
2.2.1. Active Power Balance
2.2.2. Reactive Power Balance
2.2.3. Voltage Drop with Line Status
2.2.4. Conic Relaxation of Power Flow
2.2.5. Voltage Magnitude Limits
2.2.6. Dynamic Thermal Rating
2.2.7. Network Reconfiguration Constraints
- Radial Topology Requirement:
- Single Parent Node for Each Non-Substation Bus:
- Line Status Consistency:
2.2.8. Energy Storage System Constraints
- SOC Dynamics:
- Energy Capacity Limits:
- Charging and Discharging Power Bounds:
- Daily Energy Cycle:
2.2.9. Soft Open Point (SOP) Constraints
- Active Power Balance with Loss:
- Loss Quadratic Approximation:
- Reactive Power Support Limit:
- Converter Capacity:
- Reactive Power Bounds:
2.2.10. PV Integration Constraints
2.3. The Radiality Constraint Handling Method
2.4. The Proposed ESS Constraint Handling Method
2.4.1. ESS Parameter Initialization
- Capacity: Largest (in MWh) amount of energy that can be stored.
- Charge/Discharge Limits: Rated charge/discharge power of the ESS (MW).
- Efficiency: The efficiencies of charging and discharging, which represent energy losses during operation.
2.4.2. Mode Exclusivity and Power Limits
- Mode Exclusivity: An ESS unit cannot charge and discharge simultaneously. If both charging and discharging powers are non-zero, this method keeps the maximum absolute value and sets the other one to zero.
- 2.
- Power Limits: The charging and discharging powers are clamped to remain within their allowable limits.
2.4.3. State-of-Charge (SOC) Calculation
- and are the charging and discharging efficiencies, respectively.
- is the time step (1 h).
2.4.4. Cyclic Constraint Enforcement
- SOC Error Calculation: The difference between the final SOC and the initial SOC is computed for each ESS unit.
- 2.
- Adjustment Distribution: If the SOC error exceeds a predefined tolerance (e.g., 0.1%), the required energy adjustment is distributed evenly across all time steps.
- 3.
- Power Adjustment: The charging or discharging powers are adjusted at each time step to achieve the required energy adjustment while respecting the power limits and mode exclusivity constraints.
- 4.
- Iterative Refinement: The SOC trajectory is recalculated after each adjustment, and the process is repeated until the SOC error falls within the tolerance or the maximum number of iterations is reached.
2.4.5. Integration with Optimization
- During each iteration, the method is applied to every candidate solution to enforce ESS constraints.
- The fitness of each solution is evaluated after enforcing the constraints, ensuring that only feasible solutions are considered.
- The cyclic constraint is enforced iteratively, with adjustments made to the charging and discharging powers until the SOC at the end of the horizon matches the initial SOC.
- Radicality: Preserved through the fundamental loop technique and graph-theoretic checks (Section 2.3).
- ESS dynamics: Controlled by cyclic energy adjustments (Equations (29) and (30)), SOC bounds (Equation (13)), and mode exclusivity (charging/discharging cannot happen simultaneously, Equation (24)).
- Voltage/thermal limits: To ensure adherence to grid standards, they are enforced through penalization in the objective function (Equation (42)).
3. The Solution Algorithm
3.1. Introduction to the Cheetah Optimizer
- Search Strategy: This strategy mimics a scanning phase in hunting when cheetahs proactively explore their surroundings. Cheetah positions are randomly adjusted with the randomization parameter and the step size, which enables a wide exploration of the search space.
- Attack Strategy: During the attack phase, cheetahs zero in on their prey, moving back and forth in front of the target. The update method combines the current location of the cheetah and the prey location for improving the convergence capability towards finding optimal solutions of the algorithm.
- Sit-and-Wait Strategy: They tend to maintain their position as long as they are in danger of being spotted by prey. This helps prevent premature convergence, allowing the algorithm to explore multiple solutions through persistence of a portion of the population.
- Leave Prey And Go Home Strategy: This is employed when cheetahs become tired or could not hunt their prey which encourages exploration procedure in new areas which helps diversify some solution spaces and encourages finding of optimal solutions.
3.2. Overview of Grey Wolf Optimization
- Social hierarchy: Four roles that wolves fall in to—alpha, beta, delta, and omega. The alpha wolves are the ones in charge, and they lead the pack as the other wolves follow in order of social rank.
- Hunting mechanism: GWO exhibits a hunting mechanism that works through a natural balance between exploration and exploitation. By updating their positions according to the positions of the best found solutions (the alpha) and their own, the wolves form adaptive search dynamics.
3.3. The Proposed Hybrid CGWO Algorithm
3.3.1. Inspiration
3.3.2. Mathematical Formulation
- Population Initialization
- The Exploration Factor
- : Current iteration.
- : Maximum number of iterations.
- Cheetah Movement
- : Exploration coefficient.
- : Distance to the best solution.
- : Exploitation coefficient.
- : Random vectors in .
- Wolf Movement
- Fitness Evaluation
3.3.3. Algorithm Steps
- Provide the random initial population of cheetahs and wolves in search in feasible space.
- Objective Function: This is where one can evaluate the fitness of each candidate solution.
- Update Best Solution: is the fittest solution among all fitness values.
- Update Cheetah Movement: Update positions of cheetahs using cheetah movement Equation (33).
- Wolf Movement: Move the wolves using the wolf movement Equations (34)–(37)
- Update Exploration Factor: Linearly decrease the exploration factor (32).
- Termination: Repeat steps 2–6 until the maximum number of iterations is reached.
3.3.4. Advantages of the Proposed CGWO Algorithm
- Exploration and Exploitation: It balances exploration and exploitation globally and locally.
- Exploitation: The cheetah exploration characteristics make it less afraid of becoming trapped in local optima.
- Flexibility: It is easier to reconstruct the algorithm depending on the optimization problem and constraints.
- Exploration/Exploitation Balance: The exploration factor is deployed periodically, allowing the algorithm to dynamically balance the exploration and exploitation of solutions, maximizing the chance of finding high-quality solutions.
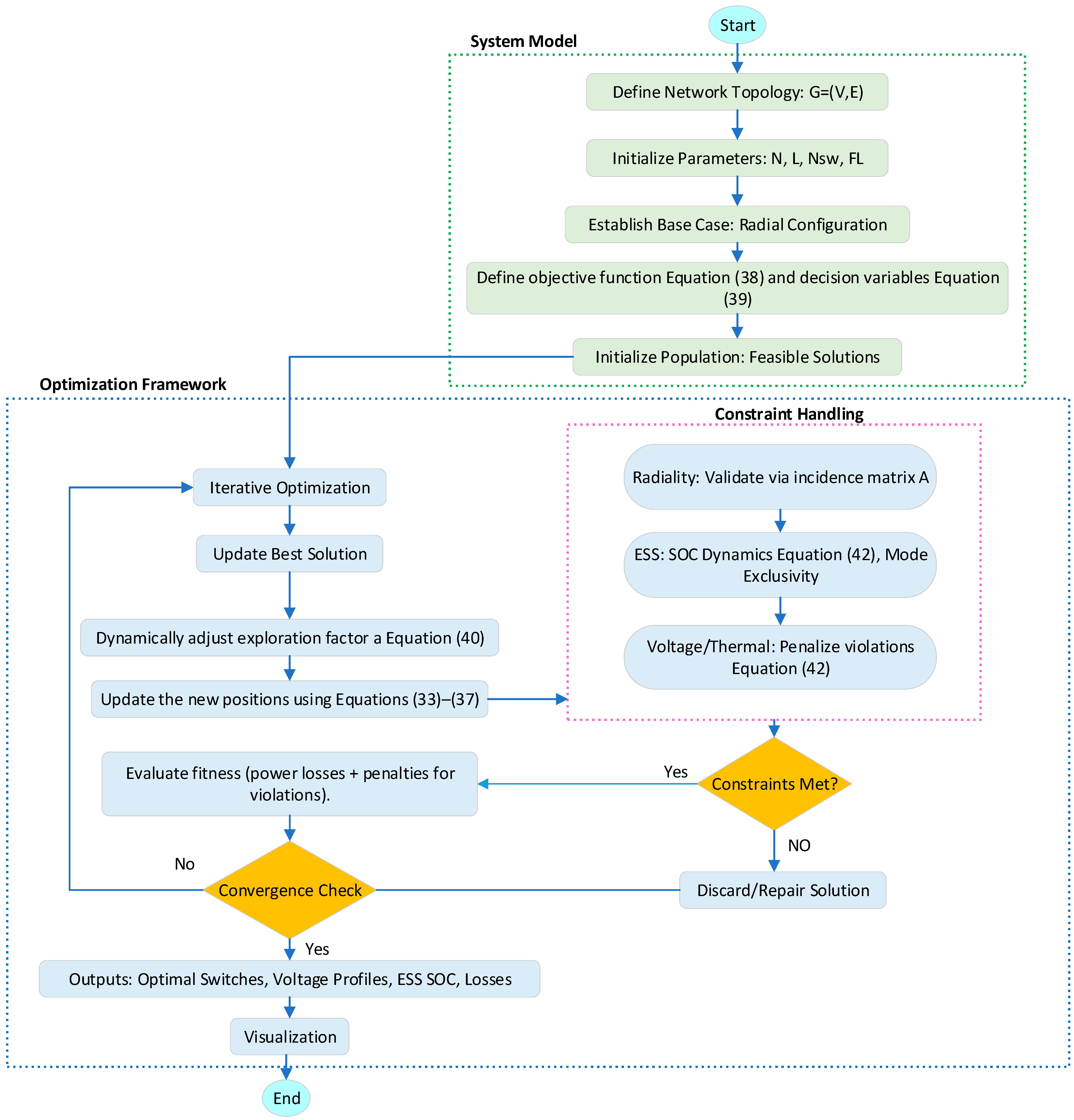
4. Implementation Procedure
4.1. System Modeling
- : Number of buses.
- : Number of branches.
- : Number of switches.
- : Fundamental loops, defined as sets of branches that can be opened to maintain radiality.
4.2. The Optimization Framework
- represents the active power loss at time ,
- is the penalty for voltage violations at time , and
- is the penalty for current violations at time .
Decision Variables
- : Switch locations to be open.
- : PV generation levels.
- and : ESS charging and discharging powers.
- and : SOP active and reactive powers.
4.3. Population Initialization
4.4. Iterative Optimization
4.5. Fitness Evaluation
4.6. Constraint Handling
4.6.1. The Radiality Constraint
4.6.2. ESS Constraints
- and : Charging and discharging efficiencies.
- : Time step (1 h).
4.6.3. Voltage and Thermal Constraints
4.7. Data Management
4.8. Result Analysis
- Optimal Switch Settings: The combination of open switches that minimize the total cost with radiality.
- Voltage Profiles: Min, max voltage at each bus over 24 h, within operational limits
- ESS SOC Trajectories: Charge level of ESS devices in response with time for showcasing energy management.
- Convergence Behavior: The progress of the best fitness value at every iteration, showing the convergence traits of the algorithm.
4.9. Visualization
- Convergence Curve: A graph depicting the optimal fitness value in iterations that illustrates the performance of the algorithm.
- Voltage Profile: A 24 h plot with the voltages observed at all busses (the bus voltage must be within the operational limits)
- ESS SOC Trajectories: A plot of the SOC of the ESS units over time, showing the charge and discharge of the storage.
5. Simulation Results
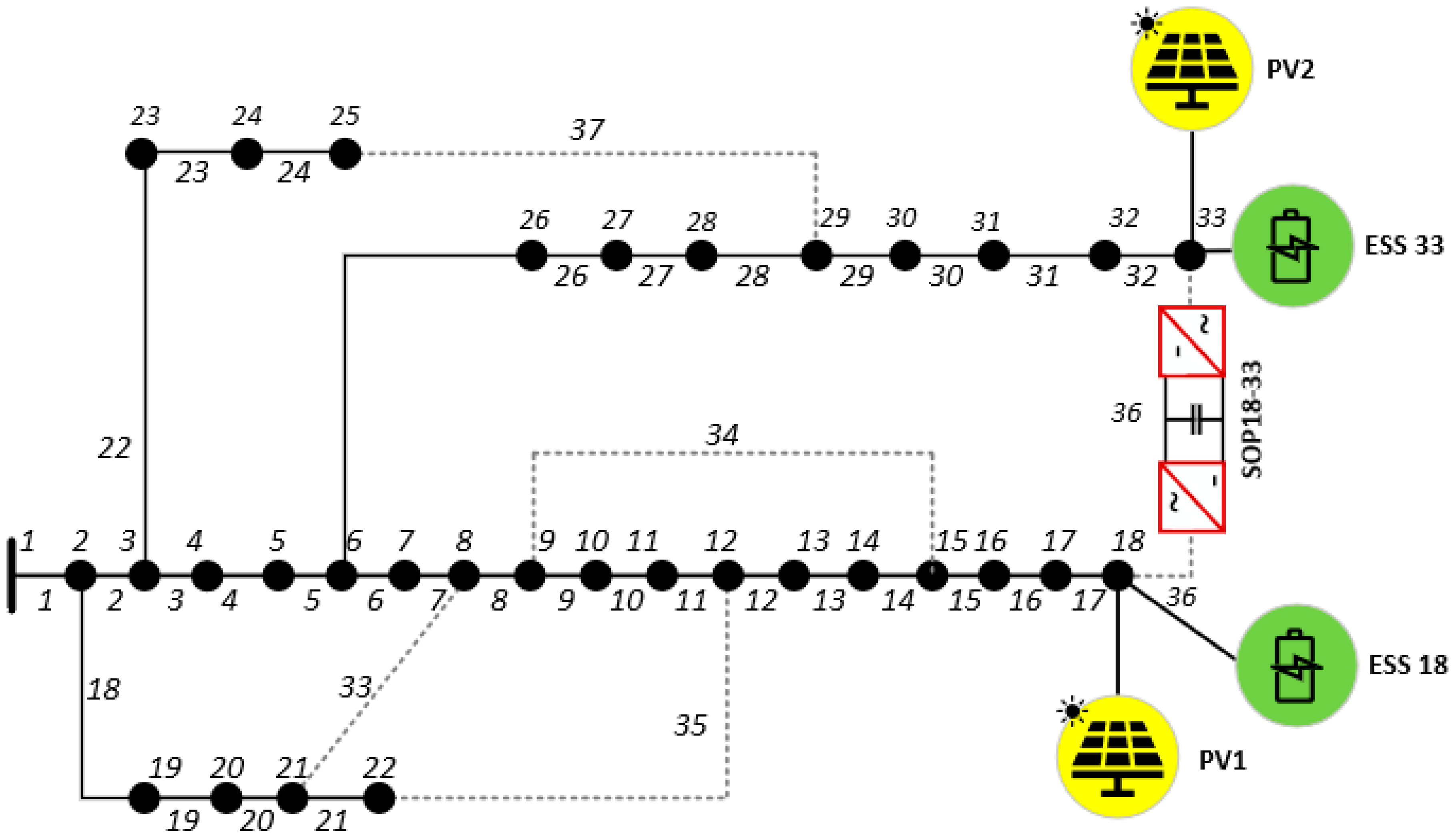
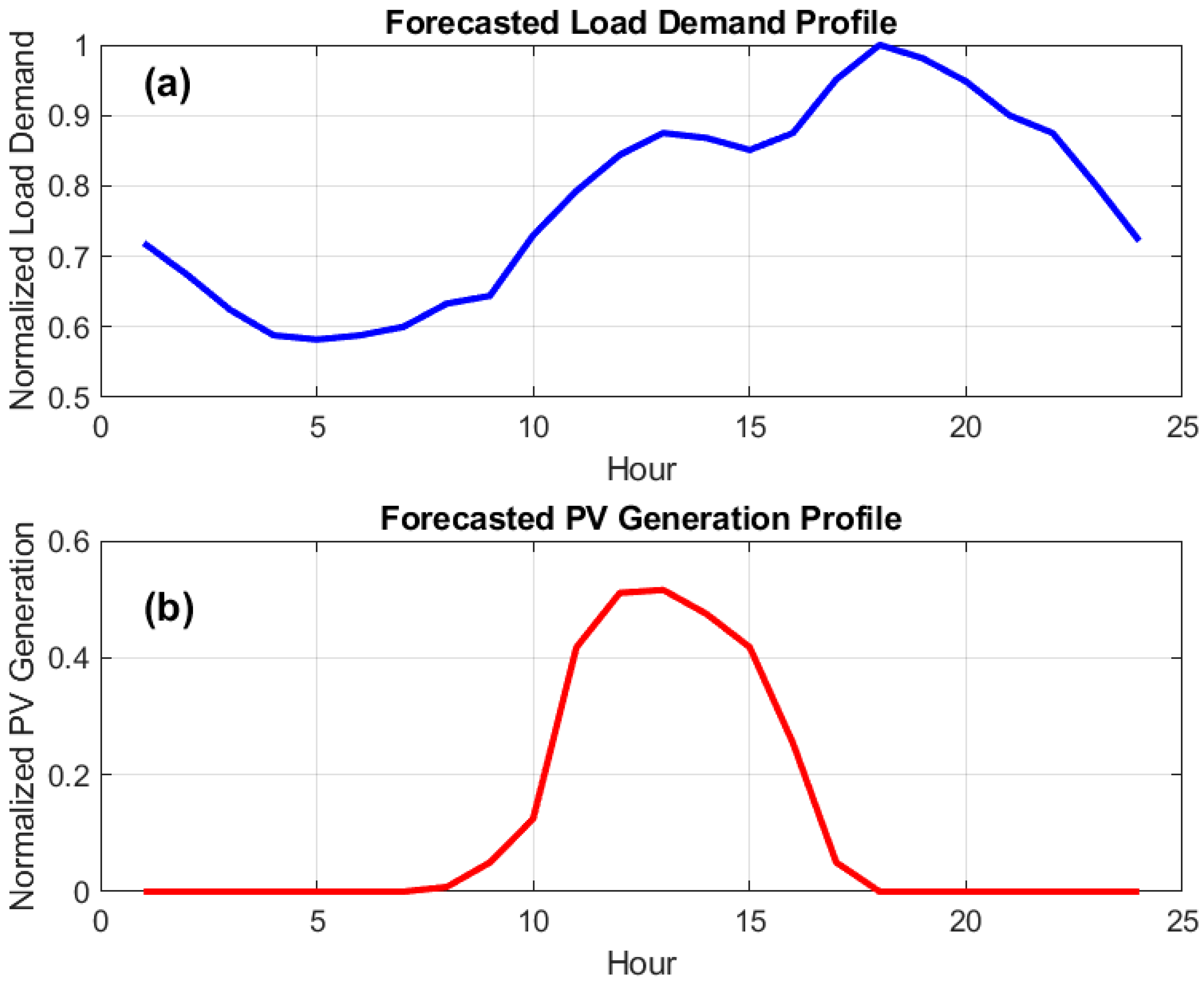
5.1. System Description and Input Data
5.2. Case Studies and Analysis
- Case 1 (Base Case): The system operates in its original configuration without reconfiguration or DER integration.
- Case 2 (DSR): The system is reconfigured by opening/closing switches to minimize power losses, without DER integration.
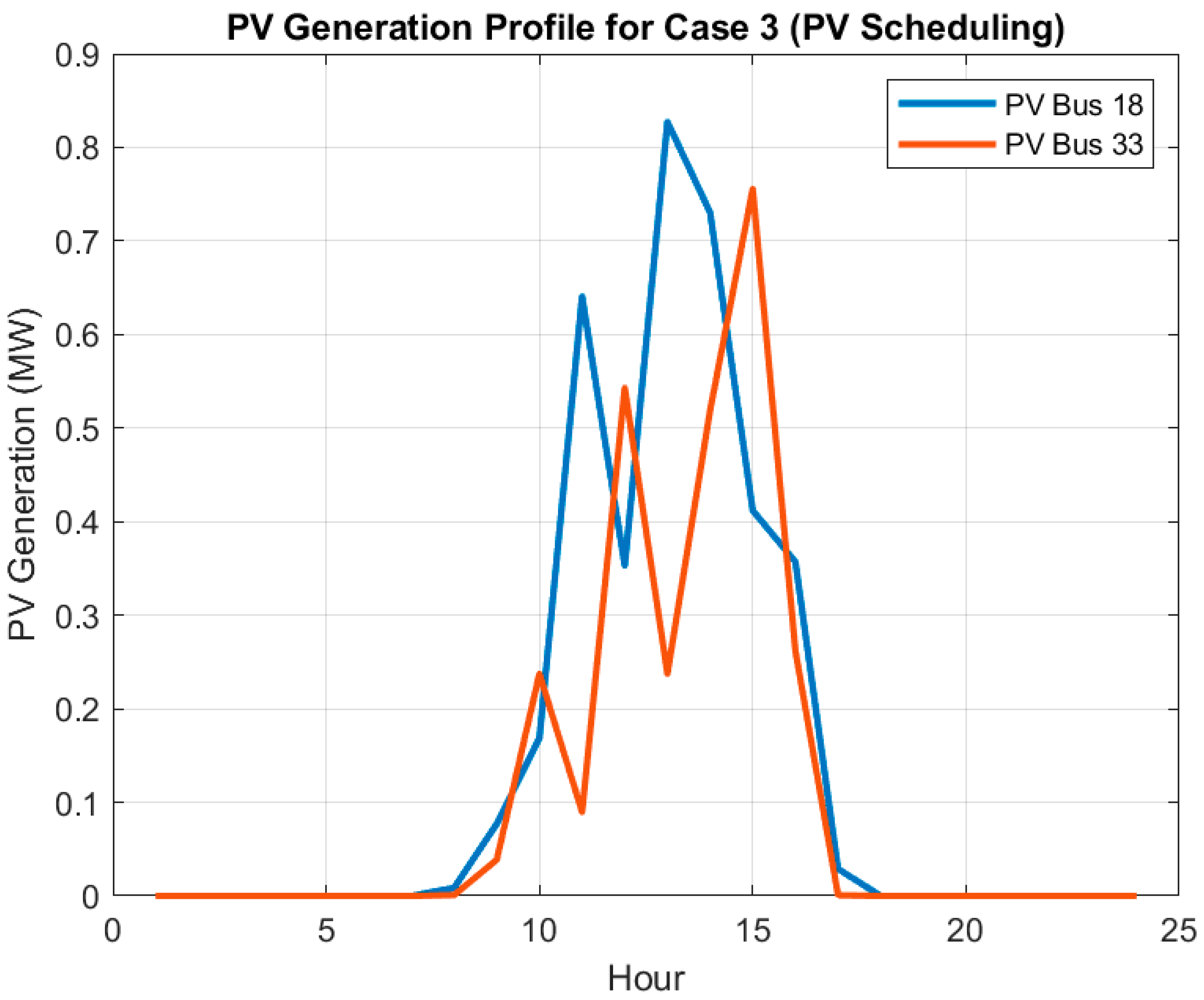
- Case 3 (PV Scheduling): PV generation is optimally scheduled to minimize power losses, without system reconfiguration or other DERs.
- Case 4 (SOP Scheduling): SOP power flow is optimized to minimize power losses, without system reconfiguration or other DERs.
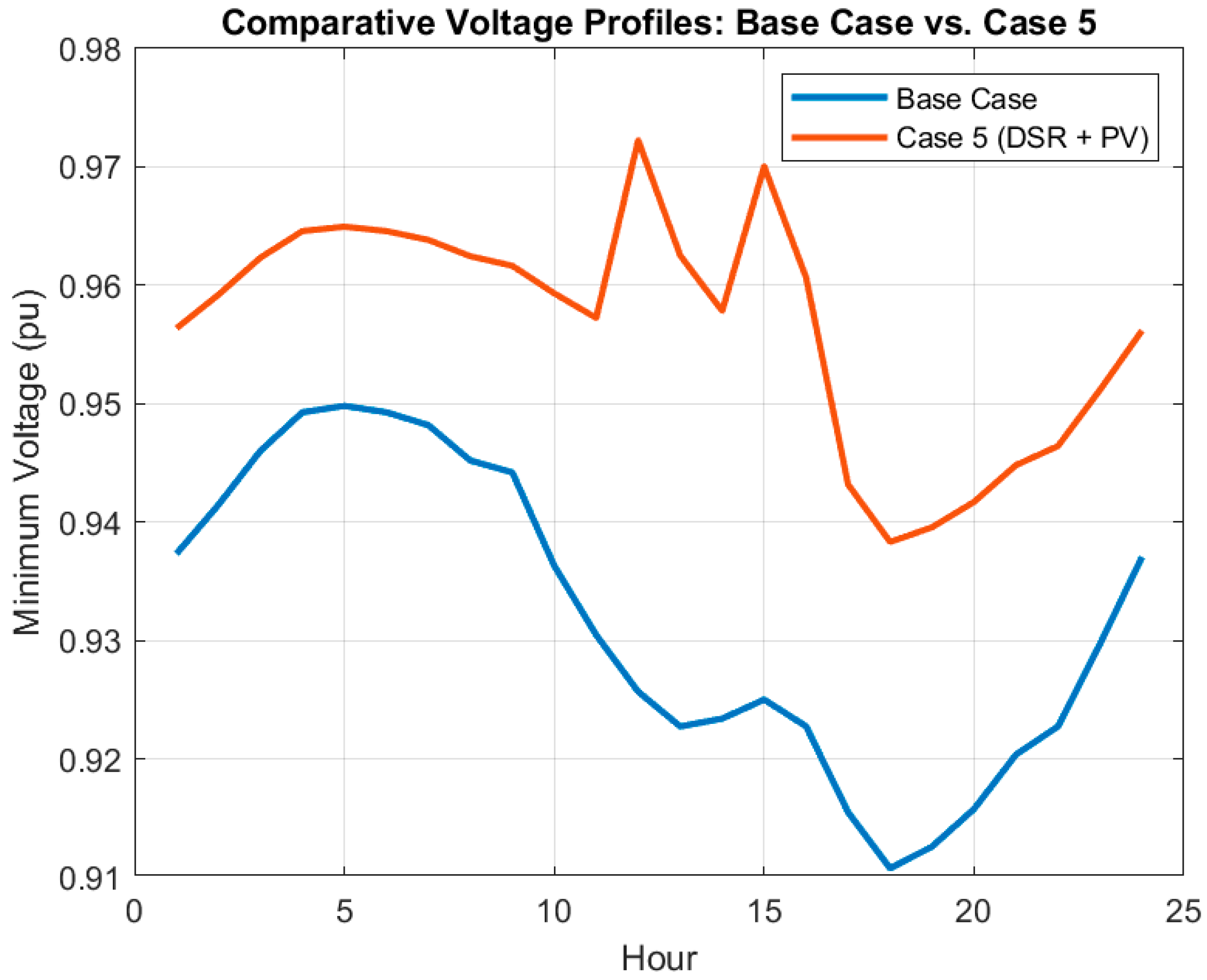
- Case 5 (DSR + PV Scheduling): The system is reconfigured, and PV generation is optimally scheduled to minimize power losses.
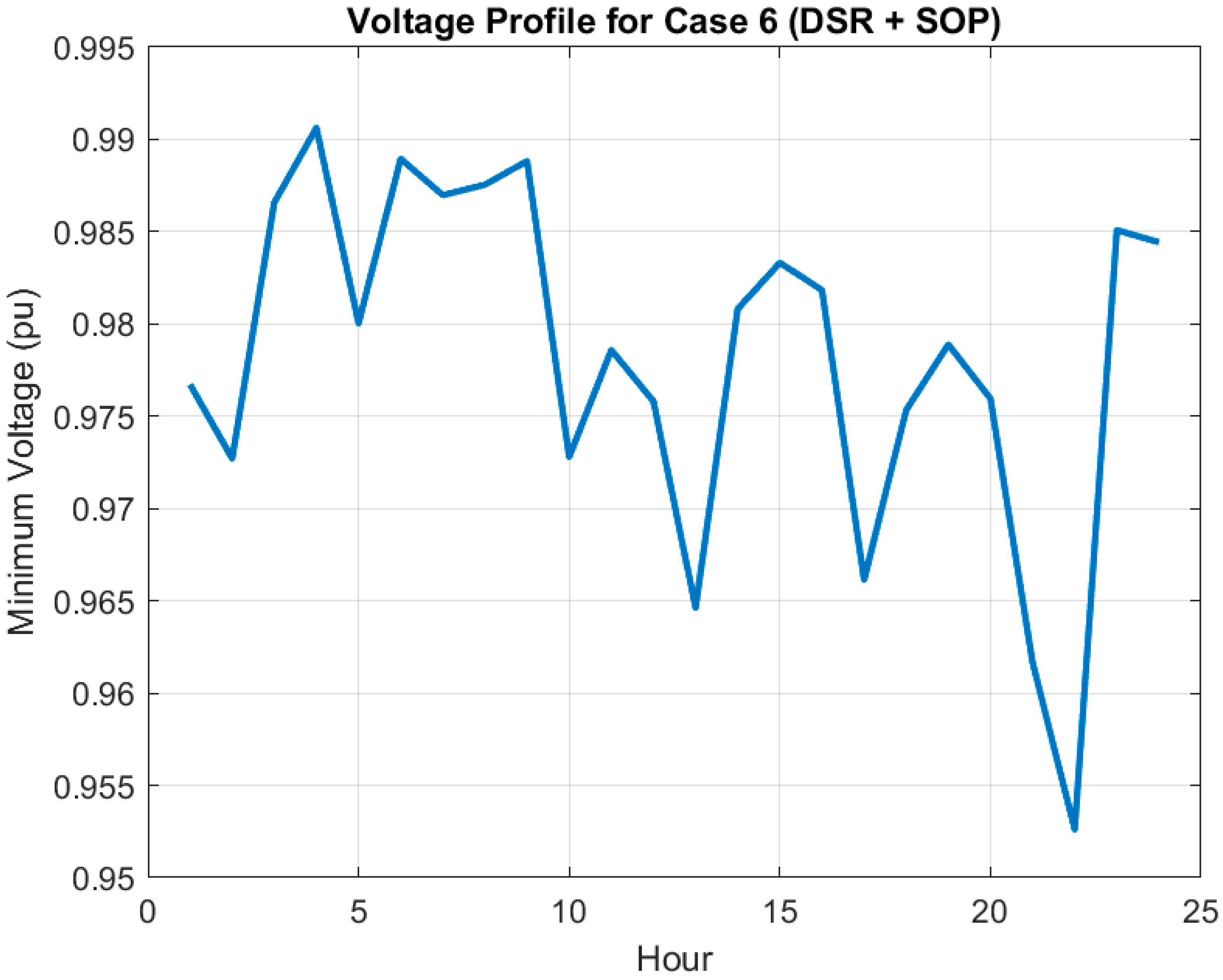
- Case 6 (DSR + SOP Scheduling): The system is reconfigured, and SOP power flow is optimized to minimize power losses.
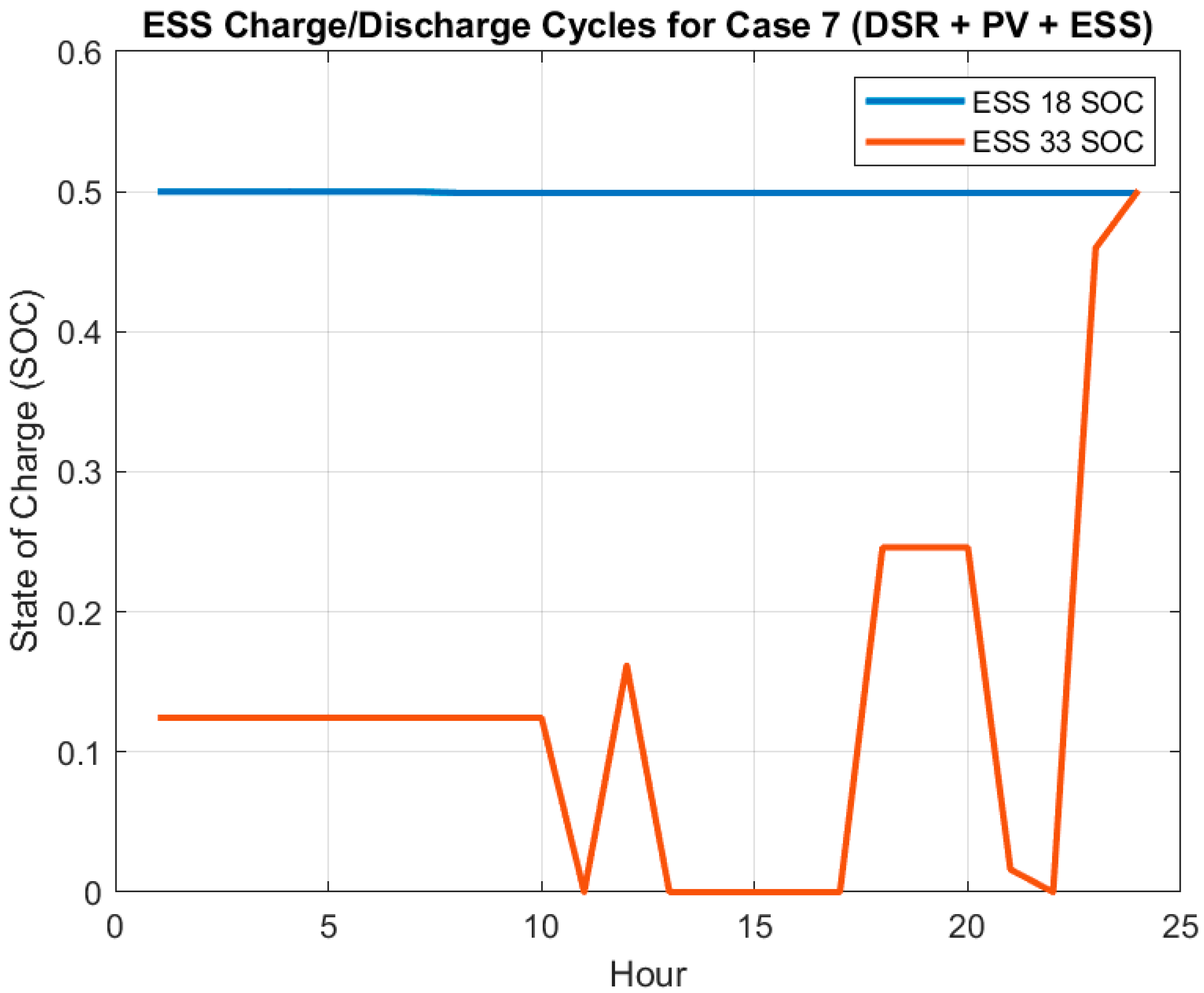
- Case 7 (DSR + PV + ESS): The system is reconfigured, and both PV generation and ESS operation are optimized.
- Case 8 (DSR + PV + ESS + SOP): The system is reconfigured, and PV generation, ESS operation, and SOP power flow are optimized simultaneously.
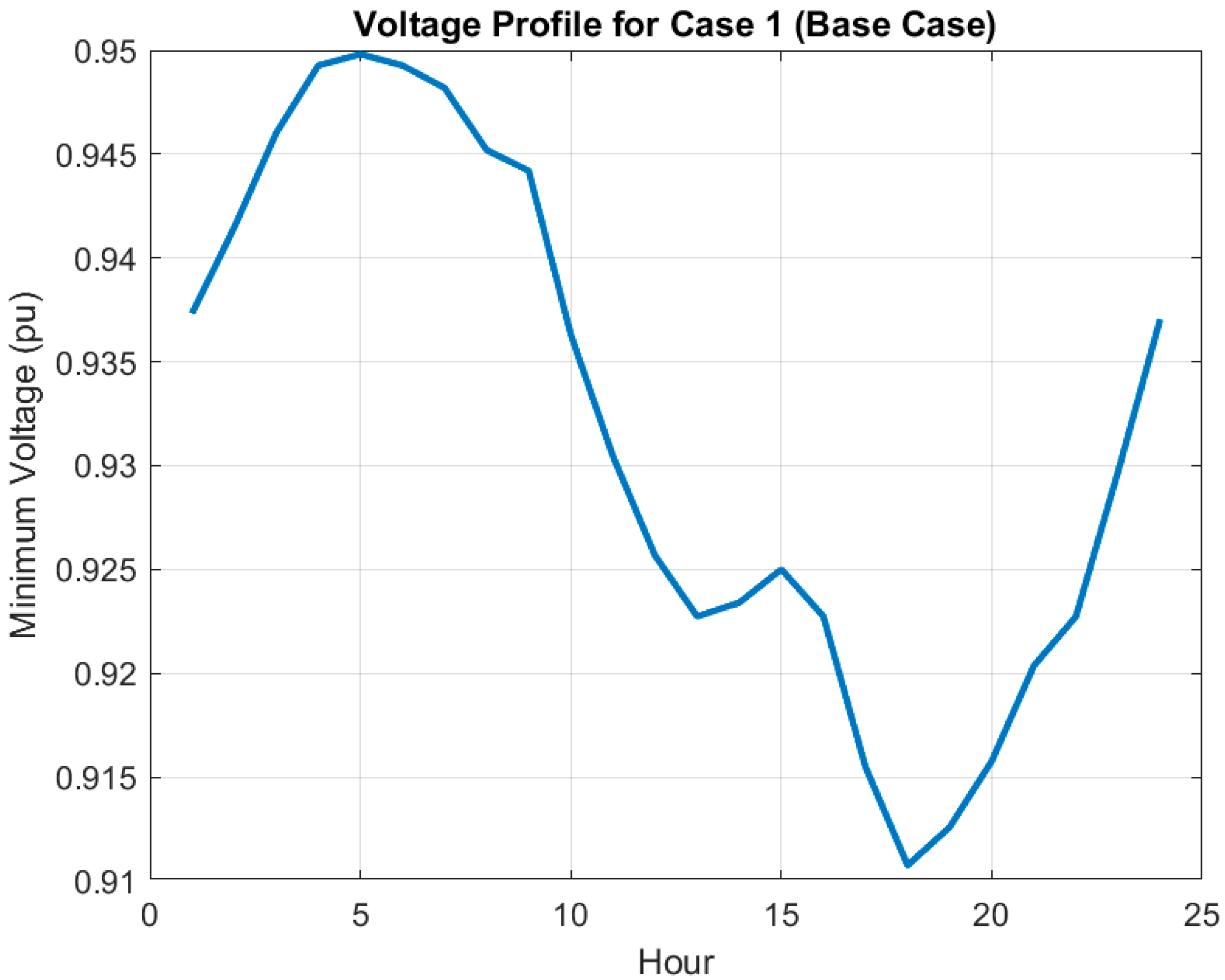
5.2.1. Case 1 (Base Case)
5.2.2. Case 2 (DSR)
5.2.3. Case 3 (PV Scheduling)
5.2.4. Example 4 (SOP Scheduling)
5.2.5. Case 5 (DSR + PV)
5.2.6. Case 6 (DSR + SOP)
5.2.7. Case 7 (DSR + PV + ESS)
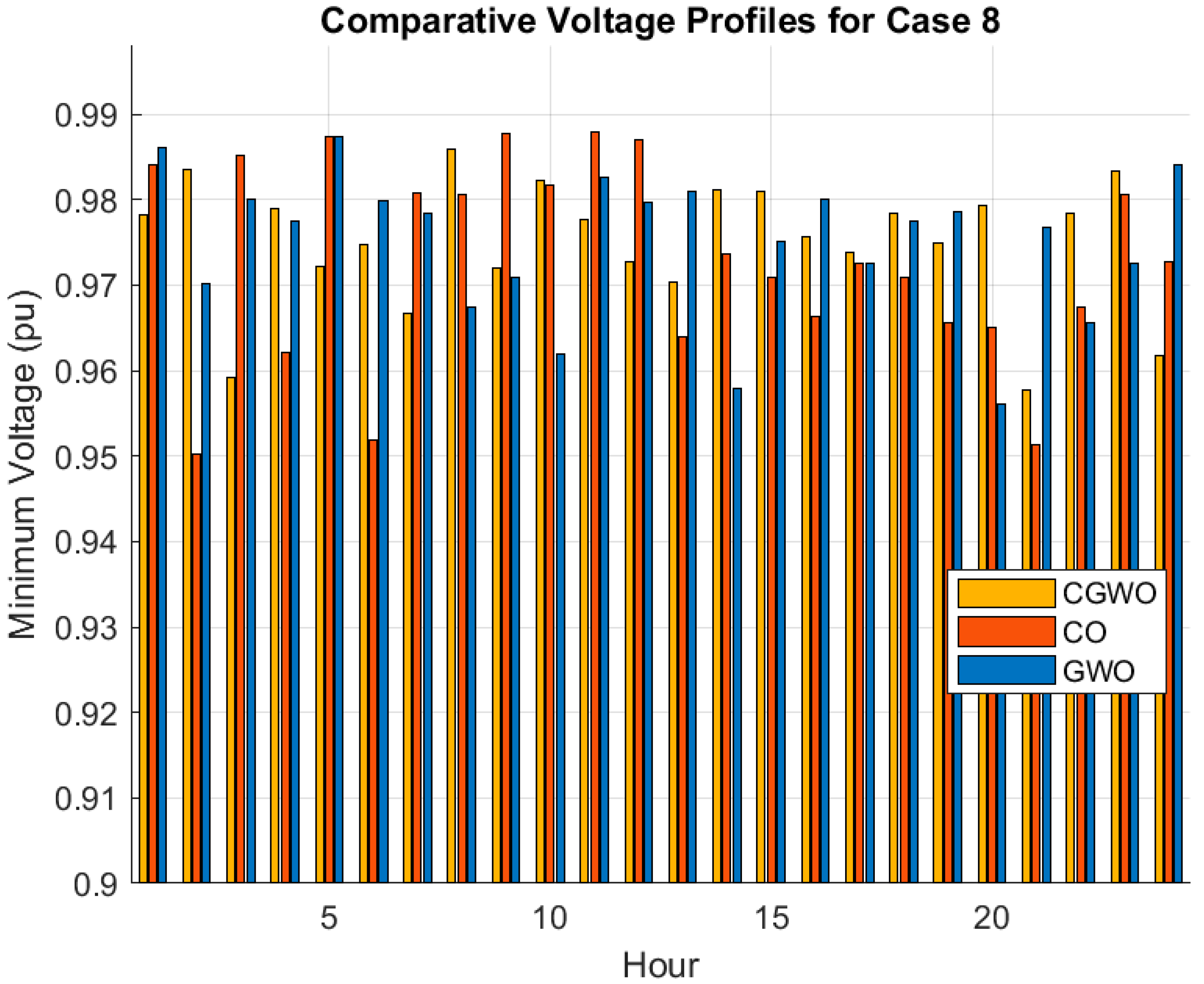
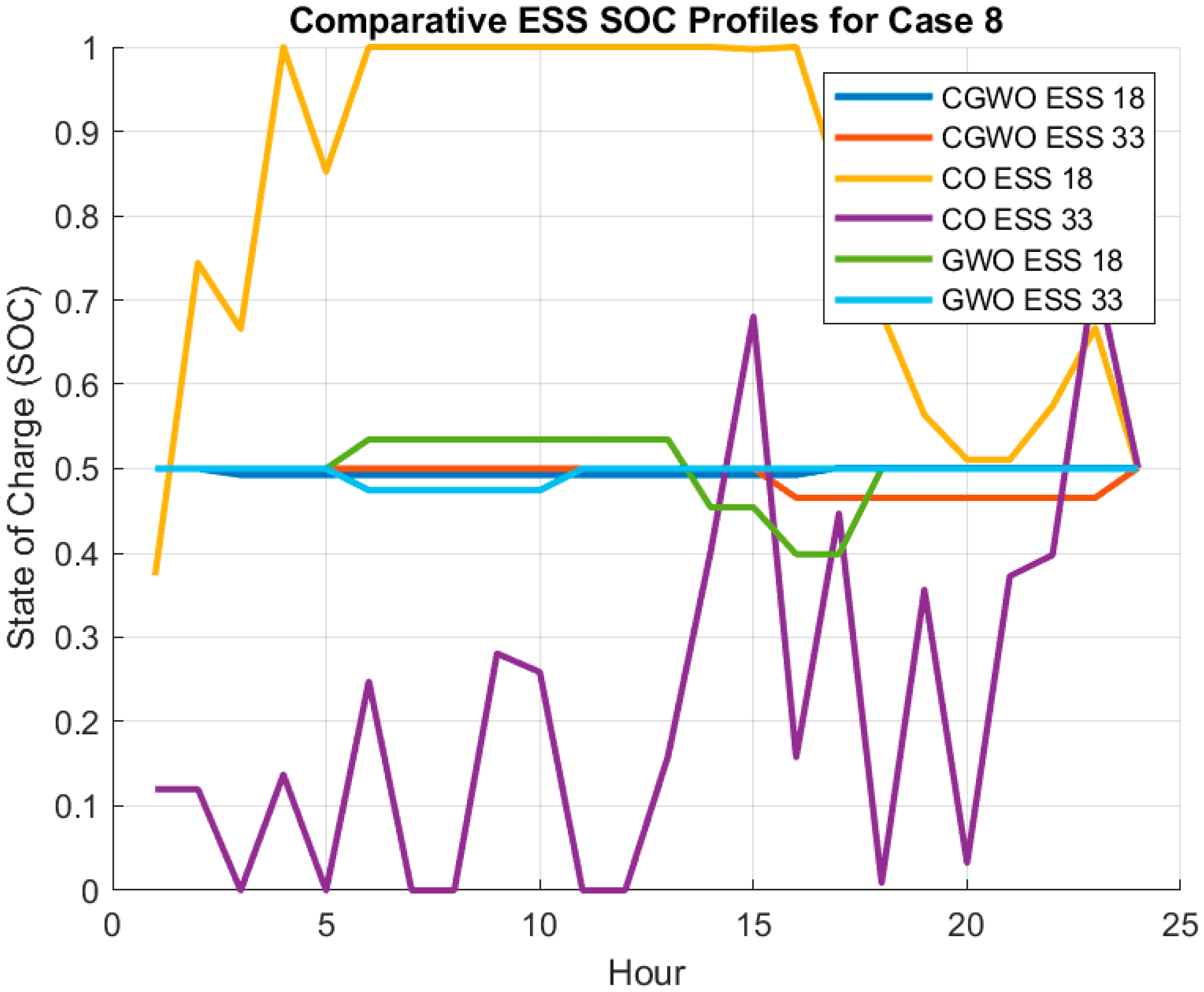
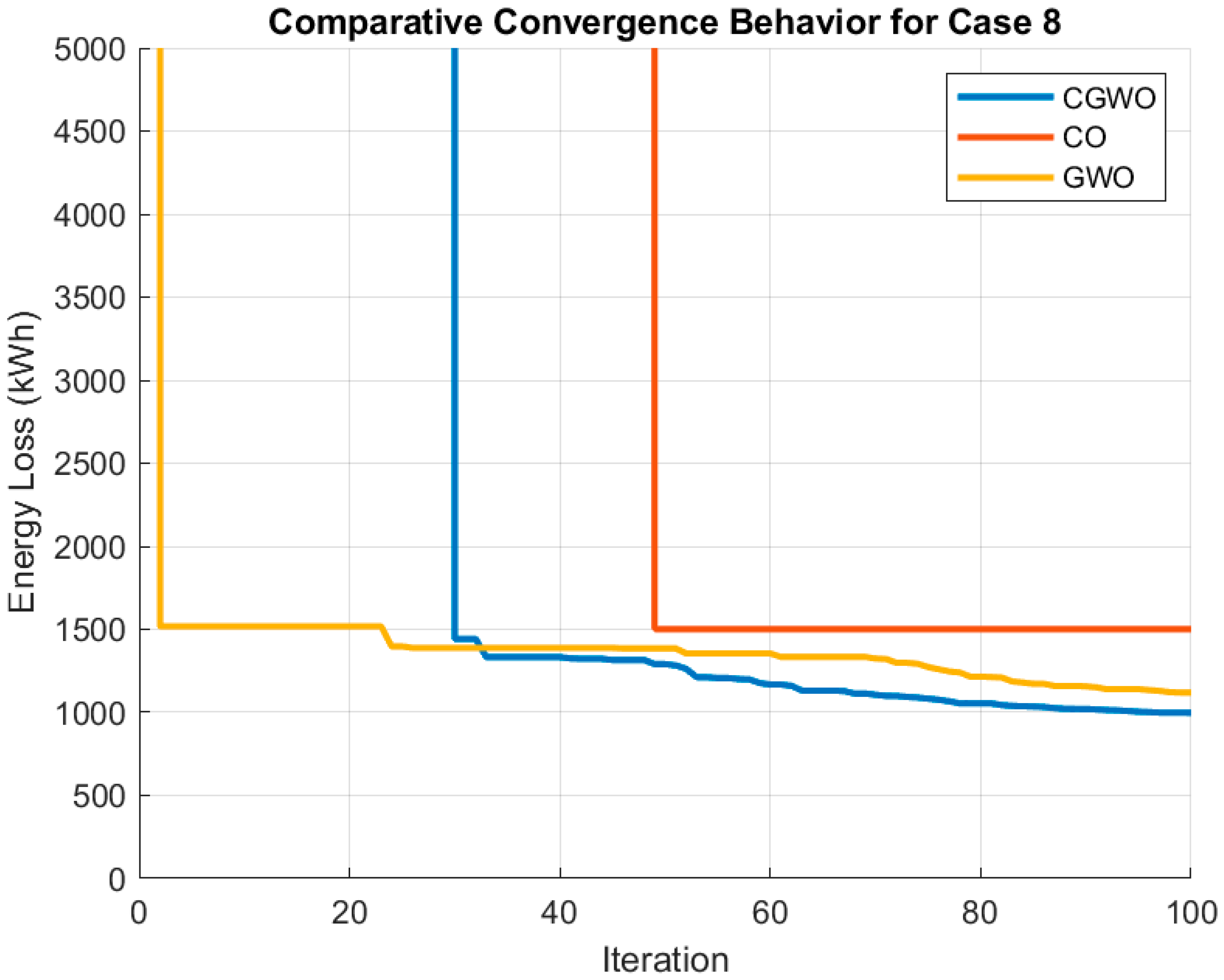
5.2.8. Case 8 (DSR + PV + ESS + SOP)
5.2.9. Computational and Operational Insights
- DSR has yielded a 29.8% loss reduction, but if SOP integration is performed alone, then it results in a 66.8% loss reduction, which indicates the major impact of SOP in minimizing losses or improving the voltage stability.
- ESS alone improves energy management and voltage profile, but needs to be paired with supporting technologies (e.g., SOPs) to reduce costs.
- The fully integrated DER (Case 8) shows the best results, with loss decreased by 67.2% and balanced ESS utilization.
5.3. Case 8—Comparison of Algorithms
5.3.1. Performance Overview
5.3.2. Convergence Behavior
5.3.3. Optimal Open Switch Locations
5.4. Discussion and Future Direction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohammedi, R.D.; Gozim, D.; Kouzou, A.; Mosbah, M.; Hafaifa, A.; Rodriguez, J.; Abdelrahem, M. Simultaneous Optimization of Network Reconfiguration and Soft Open Points Placement in Radial Distribution Systems Using a Lévy Flight-Based Improved Equilibrium Optimizer. Energies 2024, 17, 5911. [Google Scholar] [CrossRef]
- Saleh, A.A. Multi-Objective Optimal Probabilistic Planning in Distribution Systems Considering Load Growth. JES J. Eng. Sci. 2025, 53, 38–81. [Google Scholar] [CrossRef]
- Sadaoui, F.; Bouhadouza, B.; Hachemi, A.T. Optimal Reconfiguration of a Distribution Network Integrated Photovoltaic and Wind Systems Using Blood-Sucking Leech Optimizer. Stud. Eng. Exact Sci. 2024, 5, e11477. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Y.; Huang, Y. Optimal Configuration of Active Distribution Network Based on Soft Open Point. In Proceedings of the 2024 4th Power System and Green Energy Conference (PSGEC), Shanghai, China, 22–24 August 2024; pp. 1238–1242. [Google Scholar]
- Spampinato, C.; Valastro, S.; Calogero, G.; Smecca, E.; Mannino, G.; Arena, V.; Balestrini, R.; Sillo, F.; Ciná, L.; La Magna, A.; et al. Improved Radicchio Seedling Growth under CsPbI3 Perovskite Rooftop in a Laboratory-Scale Greenhouse for Agrivoltaics Application. Nat. Commun. 2025, 16, 2190. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Wang, B.; Sun, K. Stochastic Optimal Operation of SOP-Assisted Active Distribution Networks with High Penetration of Renewable Energy Sources. Sustainability 2024, 16, 5808. [Google Scholar] [CrossRef]
- Alrifaee, N.I.; Jama, M.A. A Survey of Recent Optimization Techniques in Power Distribution Network Reconfiguration. In Proceedings of the 2024 11th International Conference on Electrical and Electronics Engineering (ICEEE), Marmaris, Türkiye, 22–24 April 2024; pp. 232–238. [Google Scholar]
- Pawar, A.; Viral, R.K.; Bansal, M. A Novel Squirrel-Cat Optimization Based Optimal Expansion Planning for Distribution System. Sustain. Comput. Inform. Syst. 2024, 43, 101017. [Google Scholar] [CrossRef]
- Dehghany, N.; Asghari, R. Multi-Objective Optimal Reconfiguration of Distribution Networks Using a Novel Meta-Heuristic Algorithm. Int. J. Electr. Comput. Eng. 2024, 14, 3557–3569. [Google Scholar] [CrossRef]
- Duan, F.; Basem, A.; Jasim, D.J.; Belhaj, S.; Eslami, M.; Khajehzadeh, M.; Palani, S. A New Multi-Objective-Stochastic Framework for Reconfiguration and Wind Energy Resource Allocation in Distribution Network Incorporating Improved Dandelion Optimizer and Uncertainty. Sci. Rep. 2024, 14, 20857. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A. Optimal Allocation and Sizing of Distributed Generation in IEEE-85 BUS System Considering Various Load Models Using Multi-Objective Metaheuristic Algorithms. In Proceedings of the International Online Conference on Smart Grid Energy Systems and Control, Kurukshetra, India, 7–9 April 2023; Springer: New York, NY, USA; pp. 15–31. [Google Scholar]
- Kumar, G.; Sharma, K.; Sharma, K.; Dwivedi, S.P.; Shrivastava, A.; Bisht, Y.S. Optimizing Power Distribution Grids Using Particle Swarm Optimization Algorithm. In Proceedings of the 2024 4th International Conference on Innovative Practices in Technology and Management (ICIPTM), Noida, India, 21–23 February 2024; pp. 1–6. [Google Scholar]
- Xiong, M.; Yang, X.; Zhang, Y.; Wu, H.; Lin, Y.; Wang, G. Reactive Power Optimization in Active Distribution Systems with Soft Open Points Based on Deep Reinforcement Learning. Int. J. Electr. Power Energy Syst. 2024, 155, 109601. [Google Scholar] [CrossRef]
- Duan, F.; Eslami, M.; Khajehzadeh, M.; Basem, A.; Jasim, D.J.; Palani, S. Optimization of a Photovoltaic/Wind/Battery Energy-Based Microgrid in Distribution Network Using Machine Learning and Fuzzy Multi-Objective Improved Kepler Optimizer Algorithms. Sci. Rep. 2024, 14, 13354. [Google Scholar] [CrossRef]
- Elseify, M.A.; SeyyedAbbasi, A.; Domínguez-García, J.L.; Kamel, S. Probabilistic Optimal Planning of Multiple Photovoltaics and Battery Energy Storage Systems in Distribution Networks: A Boosted Equilibrium Optimizer with Time-Variant Load Models. J. Energy Storage 2023, 73, 108986. [Google Scholar] [CrossRef]
- Shobha, M.; Datta, B. Multi-Objective Hybrid Optimal Algorithm for Distribution System Feeder Reconfiguration. In Decarbonisation and Digitization of the Energy System; Kumar, A., Singh, S.N., Kumar, P., Eds.; Springer Nature: Singapore, 2024; pp. 217–225. [Google Scholar]
- Hou, T.; Li, L. Multi-Objective Optimization of Distribution Network System with Energy Storage and Distributed Photovoltaic Considering Static Voltage Stability. In Proceedings of the 2023 IEEE 4th China International Youth Conference on Electrical Engineering (CIYCEE), Chengdu, China, 8–10 December 2023; pp. 1–6. [Google Scholar]
- Najafi, M.; Miveh, M.R. Stochastic Optimal Reconfiguration and Placement of Photovoltaic Systems in Distribution Networks: A Real Case Study. Int. J. Energy Res. 2024, 2024, 1244075. [Google Scholar] [CrossRef]
- Salam, I.U.; Yousif, M.; Numan, M.; Zeb, K.; Billah, M. Optimizing Distributed Generation Placement and Sizing in Distribution Systems: A Multi-Objective Analysis of Power Losses, Reliability, and Operational Constraints. Energies 2023, 16, 5907. [Google Scholar] [CrossRef]
- Alwash, S.; Ibrahim, S.; Abed, A.M. Distribution System Reconfiguration with Soft Open Point for Power Loss Reduction in Distribution Systems Based on Hybrid Water Cycle Algorithm. Energies 2022, 16, 199. [Google Scholar] [CrossRef]
- Patari, N.; Venkataramanan, V.; Srivastava, A.; Molzahn, D.K.; Li, N.; Annaswamy, A. Distributed Optimization in Distribution Systems: Use Cases, Limitations, and Research Needs. IEEE Trans. Power Syst. 2021, 37, 3469–3481. [Google Scholar] [CrossRef]
- de Oliveira, R.; de Oliveira, L.W.; de Oliveira, E.J. Optimization Approach for Planning Soft Open Points in a MV-Distribution System to Maximize the Hosting Capacity. Energies 2023, 16, 1035. [Google Scholar] [CrossRef]
- Dai, B. Multi-Objective Optimization Model of Distribution Network Reconfiguration Considering Soft Open Point. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 468–472. [Google Scholar]
- Saaklayen, M.A.; Shabbir, M.N.S.K.; Liang, X.; Faried, S.O.; Janbakhsh, M. A Novel Methodology for Optimal Allocation and Sizing of Soft Open Points in Distribution Networks. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022; pp. 1–8. [Google Scholar]
- Alanazi, A.; Alanazi, M.; Abdelaziz, A.Y.; Kotb, H.; Milyani, A.H.; Azhari, A.A. Stochastic Allocation of Photovoltaic Energy Resources in Distribution Systems Considering Uncertainties Using New Improved Meta-Heuristic Algorithm. Processes 2022, 10, 2179. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T.; Viet Vo, C. Reconfiguration of Distribution Network Considering Photovoltaic System Placement Based on Metaheuristic Algorithms. In Advances in Artificial Intelligence for Renewable Energy Systems and Energy Autonomy; Springer: New York, NY, USA, 2023; pp. 135–156. [Google Scholar]
- Ntombela, M.; Kabeya, M.; Leoaneka, M.C. Artificial Intelligence Hybrid Algorithm for System Reconfiguration to Reduce Power Losses in the Distribution System. In Proceedings of the International Conference on Intelligent and Innovative Computing Applications, Balaclava, Mauritius, 8–9 December 2022; pp. 213–220. [Google Scholar]
- Morshed, K.A.; Ahmed, A. Optimal Planning of Multiple Renewable Energy-Integrated Distribution System with Uncertainties Using Artificial Hummingbird Algorithm. IEEE Access 2022, 10, 40716–40730. [Google Scholar]
- Chen, Y.; Yang, G.; Song, Z.; Sun, M.; Zhou, S. Optimal Configuration Method of Soft Open Point Considering Flexibility of Distribution System. In Proceedings of the 2022 IEEE 5th International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 18–20 November 2022; pp. 524–529. [Google Scholar]
- Farzamnia, A.; Marjani, S.; Galvani, S.; Kin, K.T.T. Optimal Allocation of Soft Open Point Devices in Renewable Energy Integrated Distribution Systems. IEEE Access 2022, 10, 9309–9320. [Google Scholar] [CrossRef]
- Souifi, H.; Abdallah, H.H. Optimal Distribution Network Reconfiguration Using Ant Lion Optimizer. In Proceedings of the 2022 IEEE 21st international Ccnference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2022; pp. 555–560. [Google Scholar]
- Nguyen, L.D.L.; Nguyen, P.K.; Vo, V.C.; Vo, N.D.; Nguyen, T.T.; Phan, T.M. Applications of Recent Metaheuristic Algorithms for Loss Reduction in Distribution Power Systems Considering Maximum Penetration of Photovoltaic Units. Int. Trans. Electr. Energy Syst. 2023, 2023, 9709608. [Google Scholar] [CrossRef]
- Leng, R.; Li, Z.; Xu, Y. A Comprehensive Literature Review for Optimal Planning of Distributed Energy Resources in Distribution Grids. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 1–5 November 2022; pp. 369–373. [Google Scholar]
- Mahdavi, M.; Alhelou, H.H.; Bagheri, A.; Djokic, S.Z.; Ramos, R.A.V. A Comprehensive Review of Metaheuristic Methods for the Reconfiguration of Electric Power Distribution Systems and Comparison with a Novel Approach Based on Efficient Genetic Algorithm. IEEE Access 2021, 9, 122872–122906. [Google Scholar] [CrossRef]
- Sadnan, R.; Dubey, A. Distributed Optimization in Distribution Systems with Grid-Forming and Grid-Supporting Inverters. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Rezaeian-Marjani, S.; Galvani, S.; Talavat, V. A Generalized Probabilistic Multi-objective Method for Optimal Allocation of Soft Open Point (SOP) in Distribution Networks. IET Renew. Power Gener. 2022, 16, 1046–1072. [Google Scholar] [CrossRef]
- Saedi, A.; Abu Hanifah, M.S.; Hela Ladin, H.; Yusoff, S.H. Optimal Distribution Network Reconfiguration Using Multi-Objective Cuckoo Search Algorithm. IIUM Eng. J. 2022, 23, 114–124. [Google Scholar] [CrossRef]
- Nkc, H.; Inkollu, S.R.; Patil, R.; Janamala, V. Aquila Optimizer Based Optimal Allocation of Soft Open Points for Multi Objective Operation in Electric Vehicles Integrated Active Distribution Networks. Int. J. Intell. Eng. Syst. 2022, 15, 269–278. [Google Scholar]
- Akbari, M.A.; Zare, M.; Azizipanah-Abarghooee, R.; Mirjalili, S.; Deriche, M. The Cheetah Optimizer: A Nature-Inspired Metaheuristic Algorithm for Large-Scale Optimization Problems. Sci. Rep. 2022, 12, 10953. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Mohamed, F.M.; Mekhamer, S.F.; Badr, M.A.L. Distribution System Reconfiguration Using a Modified Tabu Search Algorithm. Electr. Power Syst. Res. 2010, 80, 943–953. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Truong, A.V.; Phung, T.A. A Novel Method Based on Adaptive Cuckoo Search for Optimal Network Reconfiguration and Distributed Generation Allocation in Distribution Network. Int. J. Electr. Power Energy Syst. 2016, 78, 801–815. [Google Scholar] [CrossRef]
- Dolatdar, E.; Soleymani, S.; Mozafari, B. A New Distribution Network Reconfiguration Approach Using a Tree Model. World Acad. Sci. Eng. Technol. Int. J. Comput. Electr. Autom. Control Inf. Eng. 2009, 3, 2480–2487. [Google Scholar]





| Symbol | Definition | Unit |
|---|---|---|
| Set of time intervals | – | |
| Set of lines (branches) | – | |
| Set of buses (nodes) | – | |
| Set of substation nodes | – | |
| A | ||
| A2 | ||
| kW | ||
| kVAr | ||
| kW | ||
| kVAr | ||
| kW | ||
| kW | ||
| kVAr | ||
| kW | ||
| kW | ||
| kW | ||
| kVAr | ||
| p.u.2 | ||
| p.u. | ||
| (1 = closed, 0 = open) | – | |
| Element of bus-line incidence matrix | – | |
| Modified bus-line incidence matrix element | – | |
| kWh | ||
| ESS charging efficiency | – | |
| ESS discharging efficiency | – | |
| Rated apparent power capacity of SOP | kVA | |
| SOP loss coefficient | – |
| FL | Length of FL | Switches |
|---|---|---|
| 10 | 2, 3, 4, 5, 6, 7, 18, 19, 20, 33 | |
| 7 | 9, 10, 11, 12, 13, 14, 34 | |
| 15 | 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 18, 19, 20, 21, 35 | |
| 21 | 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 25, 26, 27, 28, 29, 30, 31, 32, 36 | |
| 11 | 3, 4, 5, 22, 23, 24, 25, 26, 27, 28, 37 |
| Case | Total Energy Loss (kWh) | Avg. Min Voltage (pu) | Avg. Voltage Deviation (pu) | Computation Time (s) | Optimal Switches | Avg. SOC ESS_18 | Avg. SOC ESS_33 |
|---|---|---|---|---|---|---|---|
| Case 1 (Base) | 3037.83 | 0.9317 | 0.0385 | 1.03 | [33–37] | 0 | 0 |
| Case 2 (DSR) | 2132.48 | 0.9551 | 0.0279 | 1430.70 | [4,6,14,21,36] | 0 | 0 |
| Case 3 (PV) | 2614.10 | 0.9412 | 0.0334 | 1579.72 | [33–37] | 0 | 0 |
| Case 4 (SOP) | 1008.17 | 0.9767 | 0.0130 | 1599.16 | [33–37] | 0 | 0 |
| Case 5 (DSR + PV) | 1894.03 | 0.9567 | 0.0241 | 1422.55 | [14,17,20,21,26] | 0 | 0 |
| Case 6 (DSR + SOP) | 1165.77 | 0.9782 | 0.0125 | 1431.38 | [6,7,9,23,36] | 0 | 0 |
| Case 7 (DSR + PV + ESS) | 1849.89 | 0.9572 | 0.0236 | 1410.67 | [7,11,34,36,37] | 0.4994 | 0.1301 |
| Case 8 (Full DER) | 997.41 | 0.9750 | 0.0134 | 1495.63 | [33–37] | 0.4961 | 0.4886 |
| Algorithm | CGWO | CO | GWO |
|---|---|---|---|
| Total Energy Loss (kWh) | 997.4129442 | 1501.317803 | 1119.312337 |
| Average Min.Voltage (pu) | 0.974981459 | 0.972809287 | 0.974975863 |
| Average Voltage Deviation (pu) | 0.013392952 | 0.012262379 | 0.013486971 |
| Computation Time (s) | 1495.62665 | 2114.623737 | 2103.772085 |
| Optimal Switches (open) | [33–37] | [3,20,26,34,36] | [33–37] |
| Average SOC of ESS at node 18 (MWh) | 0.496072178 | 0.811772588 | 0.499260108 |
| Average SOC of ESS at node 33 (MWh) | 0.488565063 | 0.225641089 | 0.494663891 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqahtani, M.; Alghamdi, A.S. Optimized Coordination of Distributed Energy Resources in Modern Distribution Networks Using a Hybrid Metaheuristic Approach. Processes 2025, 13, 1350. https://doi.org/10.3390/pr13051350
Alqahtani M, Alghamdi AS. Optimized Coordination of Distributed Energy Resources in Modern Distribution Networks Using a Hybrid Metaheuristic Approach. Processes. 2025; 13(5):1350. https://doi.org/10.3390/pr13051350
Chicago/Turabian StyleAlqahtani, Mohammed, and Ali S. Alghamdi. 2025. "Optimized Coordination of Distributed Energy Resources in Modern Distribution Networks Using a Hybrid Metaheuristic Approach" Processes 13, no. 5: 1350. https://doi.org/10.3390/pr13051350
APA StyleAlqahtani, M., & Alghamdi, A. S. (2025). Optimized Coordination of Distributed Energy Resources in Modern Distribution Networks Using a Hybrid Metaheuristic Approach. Processes, 13(5), 1350. https://doi.org/10.3390/pr13051350






