Research on the Degradation Model of a Smart Circuit Breaker Based on a Two-Stage Wiener Process
Abstract
1. Introduction
- (1)
- An in-depth study was conducted on the related degradation mechanisms, and its key functional modules are identified. Based on feature extraction and trend analysis of experimental data, the control circuit is found to exhibit a clear two-stage degradation pattern.
- (2)
- A degradation model based on a two-stage Wiener process is developed. By integrating the maximum likelihood estimation, the Schwarz information criterion, and reliability analysis, the turning point of performance degradation is accurately identified.
- (3)
- The quantile plot method is used to test the normality of degradation increments at different stages, and the reliability function along with the failure probability density function curve is obtained by extrapolating from the experimental data. The average service life of the control circuit under normal temperature conditions is predicted to be 178,100 h (20.3 years), and the turning point of degradation is estimated at 155,000 h (17.7 years).
2. Research on the Deterioration Process of the Control System in SCB
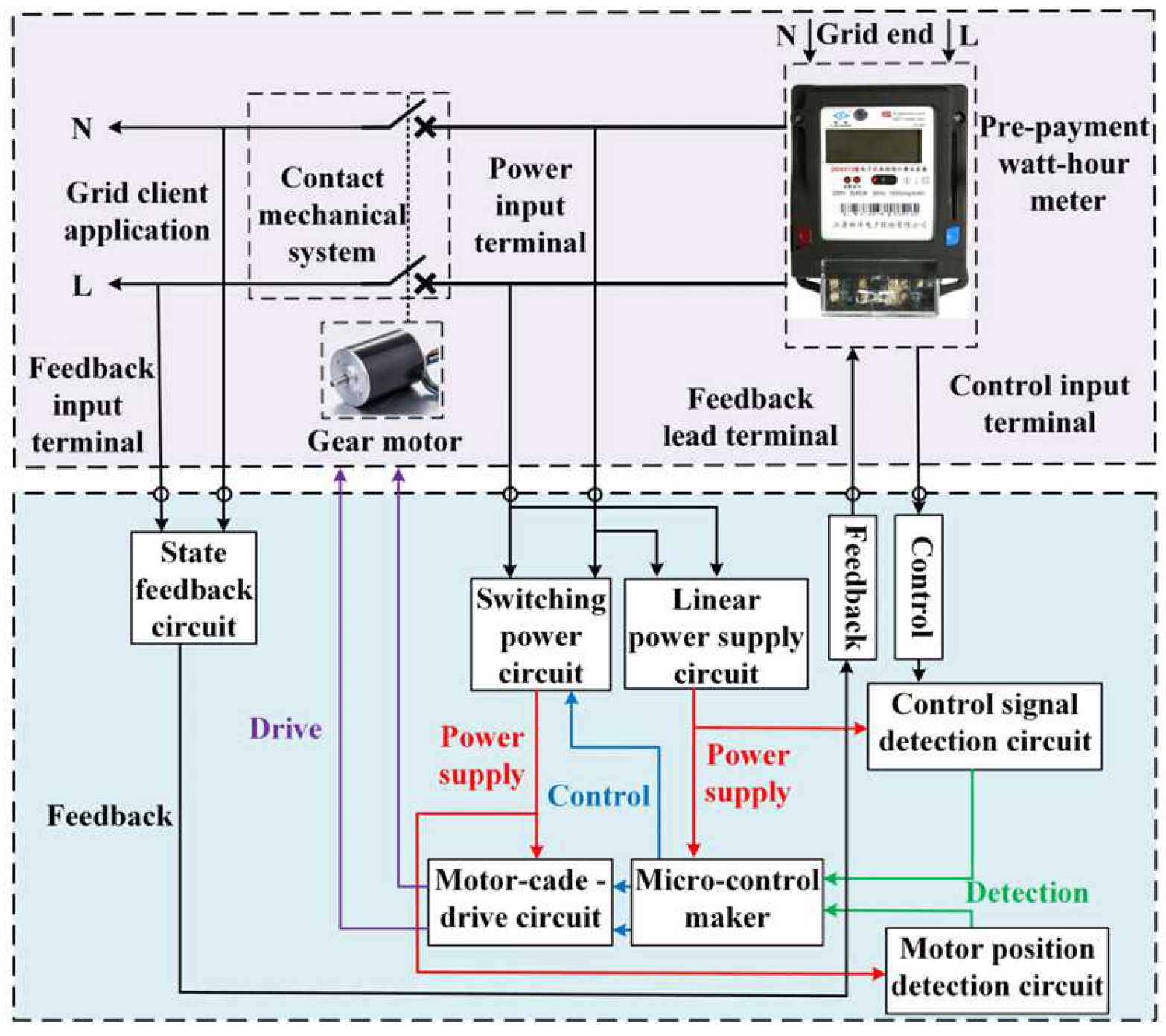
2.1. Study on the Functional Mechanism of the Control System
2.2. Determination of Key Modules
3. Accelerated Degradation Test Design and Characteristic Trend Analysis
3.1. Degradation State Monitoring Signal Selection
3.2. Accelerated Test Design
- (1)
- Stress Type and Levels in Accelerated Testing: Temperature is chosen as the sole accelerated stress factor. Typically, a single-stress temperature model requires test data at a minimum of three distinct temperature levels to enable an accurate parameter estimation. The temperature difference between adjacent levels is maintained at no less than 10 °C.
- (2)
- Determination of Sample Size for Accelerated Testing: Based on prior studies, a standard practice under single-temperature stress conditions is to include five samples per group. This approach minimizes the impact of individual variability on data interpretation and parameter estimation.
- (3)
- Accelerated Test Duration and Frequency: The test cycle is defined by taking into account changes in performance parameters, the overall testing workload, cost considerations, and the desired quantity of data. An initial inspection interval is established, and subsequent adjustments are made based on observed trends in performance degradation during testing.
- (1)
- At 25 °C, the initial values of key condition monitoring signals are recorded as the reference for the samples to evaluate performance degradation.
- (2)
- The samples are then sequentially subjected to cyclic accelerated aging tests under thermal stress conditions of 105 °C, 95 °C, and 85 °C.
- (3)
- Each test cycle lasts for 24 h. The process begins with the sample being stabilized at 25 °C for 0.5 h, followed by a temperature increase to the specified stress level over the next 0.5 h. The sample is then operated with one on–off switching cycle lasting 1 h. Afterward, the temperature is reduced back to 25 °C within 0.5 h. Following a 0.5 h hold at this temperature, the sample is removed for a measurement of its condition-monitoring parameters. This process is repeated for the next cycle.
- (4)
- Until all five samples under each stress fail, the test ends.
3.3. Experimental Data Feature Extraction and Trend Analysis
4. Two-Stage Wiener Process Degradation Model
4.1. Degradation Model Construction
4.2. Parameter Estimation and Turning Point Estimation
- (1)
- When tj < τ, the degradation process is in the first stage. The degradation increment Δxi obeys the inverse Gaussian distribution with drift parameter μ1 and diffusion parameter σ1. The likelihood function of the degradation process increment is as follows:
- (2)
- When τ < tj−1, the degradation process is in the second stage. The degradation increment Δxi obeys the inverse Gaussian distribution with drift parameter μ2 and diffusion parameter σ2. The likelihood function of the degradation process increment is as follows:
4.3. Reliability Estimation
4.4. Establishment of Residual Life Prediction Model
- (1)
- The failure of the product occurs in the first degradation stage, that is, tk < τ and th < τ. The degradation of the product can be regarded as a single-stage Wiener degradation process, and the probability density function of the residual life can be expressed as
- (2)
- When the product fails in the second degradation stage, that is, tk > τ and th > τ, and the product is reliable in the first degradation stage, the residual life probability density function can be expressed as
5. Life Prediction Degradation Model Test and Result Analysis
5.1. Degradation Model Test
5.2. Analysis of Life Prediction Results
6. Conclusions
- (1)
- The two-stage nonlinear degradation characteristics of the SCB. The distribution parameters and the ‘turning point’ of the degradation model are estimated using maximum likelihood estimation (MLE) and the Schwarz Information Criterion (SIC).
- (2)
- Reliability estimation and residual life are proposed as key reliability metrics for evaluating the performance decline in SCB. A degradation model, based on a two-stage Wiener process, is developed, and its accuracy is validated through a case analysis.
- (3)
- By applying the Arrhenius empirical acceleration model, the distribution parameters of the degradation model at room temperature are converted, yielding probability density function curves for reliability and residual life. The prediction results indicate that the average service life of the control circuit at room temperature is 178,100 h (20.3 years), with the degradation ‘turning point’ occurring at 155,000 h (17.7 years). This allows for a reliable evaluation of the decline in SCB performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Z.; Wang, Z. Analysis of Low Voltage Electrical Products and Market Development Status. Electr. Power Equip. 2008, 2, 104–107. [Google Scholar]
- Li, H.; Liu, D.; Yao, D.Y. Research on the development of China’s power system for the goal of carbon peak carbon neutrality. Chin. J. Electr. Eng. 2021, 41, 6245–6259. [Google Scholar]
- Fushun, N. Some understandings on fault prediction and health management technology. J. Instrum. 2018, 39, 1–14. [Google Scholar]
- Zhilin, D.; Feng, H.; Chunbo, Y.; Wu, W. A life prediction method for high-voltage thyristors based on Wiener process. J. Wuhan Univ. Eng. Ed. 2022, 55, 1044–1049. [Google Scholar]
- Xiaowei, X. Development of low-power control system for external circuit breaker of smart meter. Electr. Appl. Energy Effic. Manag. Technol. 2019, 23, 27–33. [Google Scholar]
- Jiaxing, H.; Meng, S.; Bo, J.; Jingyuan, L.; Xin, C. Two-phase degradation modeling and residual life prediction based on nonlinear wiener process. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021; IEEE: New York, NY, USA, 2021; pp. 1–8. [Google Scholar]
- Chen, X.; Liu, Z. Wiener process and extreme learning machine swarm based transfer learning for remaining useful life prediction of lithium battery. In Proceedings of the 2023 IEEE 16th International Conference on Electronic Measurement & Instruments (ICEMI), Harbin, China, 9–11 August 2023; IEEE: New York, NY, USA, 2023; pp. 1–10. [Google Scholar]
- Zhang, S.; Zhai, Q.; Shi, X.; Liu, X. A wiener process model with dynamic covariate for degradation modeling and remaining useful life prediction. IEEE Trans. Reliab. 2023, 72, 214–223. [Google Scholar] [CrossRef]
- Guobo, L. Research on the Residual Life Prediction Method of Equipment Based on Multi-Stage Wiener Process; Chongqing University: Chongqing, China, 2022. [Google Scholar]
- Guang, J. Reliability Technology Based on Degradation: Models, Methods and Applications, 1st ed.; National Defense Industry Press: Beijing, China, 2014; pp. 1–8. [Google Scholar]
- Pan, Z. Reliability Prediction Method and Software Implementation of Typical Airborne Electronic Equipment Based on Failure Physics and Fault Tree Analysis; Xidian University: Xi’an, China, 2020. [Google Scholar]
- Zhirong, L. Research on Reliability Modeling and Evaluation Method of Long Storage Equipment Based on Degradation Data; University of Electronic Science and Technology of China: Chengdu, China, 2020. [Google Scholar]
- Yang, S.; Xiang, D.; Bryant, A.; Mawby, P.; Ran, L.; Tavner, P. Condition monitoring for device reliability in power electronic converters: A review. IEEE Trans. Power Electron. 2010, 25, 2734–2752. [Google Scholar] [CrossRef]
- Junzuo, L. Research on Performance Degradation and Reliability Analysis of MEMS Accelerometer; University of Electronic Science and Technology of China: Chengdu, China, 2022. [Google Scholar]
- Jiang, L.; Hecheng, W.; Chen, Z. Reliability evaluation of long-life products based on semi-parametric degradation model. Syst. Eng. Electron. Technol. 2023, 45, 1893–1901. [Google Scholar]
- Rongbin, Y. Research on Service Reliability Evaluation Method of Photovoltaic Modules Based on Performance Degradation; South China University of Technology: Guangzhou, China, 2016. [Google Scholar]
- Yantian, T. Research on the Residual Life Prediction Method of Components Based on Wiener Process; North University of China: Taiyuan, China, 2023. [Google Scholar]
- Xuri, T.; Jikai, L.; Guangbin, L. Research on life estimation of photovoltaic DC circuit breaker based on grey prediction. Autom. Instrum. 2025, 46, 59–64. [Google Scholar]
- Nuoming, Y.; Ziran, W.; Zezhou, L.; Chenxi, W.; Guichu, W.; Yigang, L. Electrical life prediction method of DC circuit breaker based on residual network regression. Electr. Appl. Energy Effic. Manag. Technol. 2024, 10, 7–18. [Google Scholar]
- Wang, J.; Ma, X.; Zhao, Y.; Yang, L. A condition-based maintenance policy for two-stage continuous degradation considering inspection errors. In Proceedings of the 2023 5th International Conference on System Reliability and Safety Engineering (SRSE), Beijing, China, 20–23 October 2023; IEEE: New York, NY, USA, 2023; pp. 339–346. [Google Scholar]
- Zhao, X.; Yang, J.; Qin, Y. Optimal condition-based maintenance strategy via an availability-cost hybrid factor for a single-unit system during a two-stage failure process. IEEE Access 2021, 9, 45968–45977. [Google Scholar] [CrossRef]
- Zheng, R.; Zhou, Y.F.; Gu, L.; Zhang, Z. Joint optimization of lot sizing and condition-based maintenance for a production system using the proportional hazards model. Comput. Ind. Eng. 2021, 154, 107157. [Google Scholar] [CrossRef]
- Hangyu, L. Study on Arc Erosion Behavior and Mechanism of Silver-Based Contact Materials; University of Technology: Xi’an, China, 2022. [Google Scholar]
- Liu, Y.; Zhang, G.; Zhao, C.; Lei, S.; Qin, H.; Yang, J. Mechanical Condition Identification and Prediction of Spring Operating Mechanism of High Voltage Circuit Breaker. IEEE Access 2020, 8, 210328–210338. [Google Scholar] [CrossRef]
- Muratović, M.; Sokolija, K.; Kapetanović, M. Modelling of high voltage SF6 circuit breaker reliability based on Bayesian statistics. In Proceedings of the 2013 7th IEEE GCC Conference and Exhibition (GCC), Doha, Qatar, 17–20 November 2013; pp. 303–308. [Google Scholar]
- Zheng, X.; Cheng, Y. Research on Temperature Aging Life Equivalent Test Method of Press-Pack IGBTs Device Used in Circuit Breaker. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar]















| Time and Time Period | Meaning of Electrical Characteristics | |
|---|---|---|
| A | Open state | |
| B | a | Closing signal triggered |
| b | Switching power supply startup | |
| c-d | Motor start | |
| d-e | Motor unloaded | |
| f | The dynamic and static contacts start to make contact | |
| h-i | Motor braking | |
| j-k | Braking/precise positioning | |
| k | Close the switch in place | |
| l | Turn off the switch power supply | |
| C | Closed state | |
| Characteristic Parameter/V | Trend Score | Monotonicity Score | Robustness Score | Comprehensive Score |
|---|---|---|---|---|
| Peak-to-peak voltage at motor terminals | 0.836 | 0.329 | 0.992 | 0.715 |
| k | SIC(k) | k | SIC(k) | k | SIC(k) |
|---|---|---|---|---|---|
| 2 | 34.891 | 9 | 55.500 | 16 | 99.162 |
| 3 | 40.756 | 10 | 73.262 | 17 | 24.443 |
| 4 | 37.483 | 11 | 62.616 | 18 | 81.507 |
| 5 | 39.588 | 12 | 55.441 | 19 | 77.703 |
| 6 | 39.884 | 13 | 94.975 | 20 | 78.662 |
| 7 | 35.744 | 14 | 91.962 | 21 | 84.156 |
| 8 | 68.757 | 15 | 79.139 | 22 | 96.358 |
| Parameter | /h | |||||
|---|---|---|---|---|---|---|
| Temperature/°C | ||||||
| 105 | 3.38 × 10−3 | 3.47 × 10−2 | 1.26 × 10−2 | 3.59 × 10−2 | 410.60 | |
| 95 | 2.79 × 10−3 | 2.36 × 10−2 | 0.99 × 10−2 | 2.37 × 10−2 | 601.34 | |
| 85 | 1.82 × 10−3 | 1.76 × 10−2 | 0.67 × 10−2 | 1.26 × 10−2 | 916.51 | |
| Degradation Model | Input Data Volume | The Resources Used for Calculation | Subjective Risk | Mechanism Interpretability |
|---|---|---|---|---|
| Two-stage Wiener process model | moderate | moderate | small | large |
| Classical Wiener model [24] | small | small | small | moderate |
| Bayesian statistics [25] | mid | high | high | dependent on prior distribution selection |
| Finite element simulation model [26] | high | high | low | high |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Ren, J.; He, P.; Hou, L.; Wang, Y. Research on the Degradation Model of a Smart Circuit Breaker Based on a Two-Stage Wiener Process. Processes 2025, 13, 1719. https://doi.org/10.3390/pr13061719
Xie Z, Ren J, He P, Hou L, Wang Y. Research on the Degradation Model of a Smart Circuit Breaker Based on a Two-Stage Wiener Process. Processes. 2025; 13(6):1719. https://doi.org/10.3390/pr13061719
Chicago/Turabian StyleXie, Zhenhua, Jianmin Ren, Puquan He, Linming Hou, and Yao Wang. 2025. "Research on the Degradation Model of a Smart Circuit Breaker Based on a Two-Stage Wiener Process" Processes 13, no. 6: 1719. https://doi.org/10.3390/pr13061719
APA StyleXie, Z., Ren, J., He, P., Hou, L., & Wang, Y. (2025). Research on the Degradation Model of a Smart Circuit Breaker Based on a Two-Stage Wiener Process. Processes, 13(6), 1719. https://doi.org/10.3390/pr13061719







