Experimental Study on the Effect of Fractures on the Irreducible and Movable Water in Water-Bearing Tight Sandstone Gas Reservoirs
Abstract
1. Introduction
2. Experimental and Stimulation
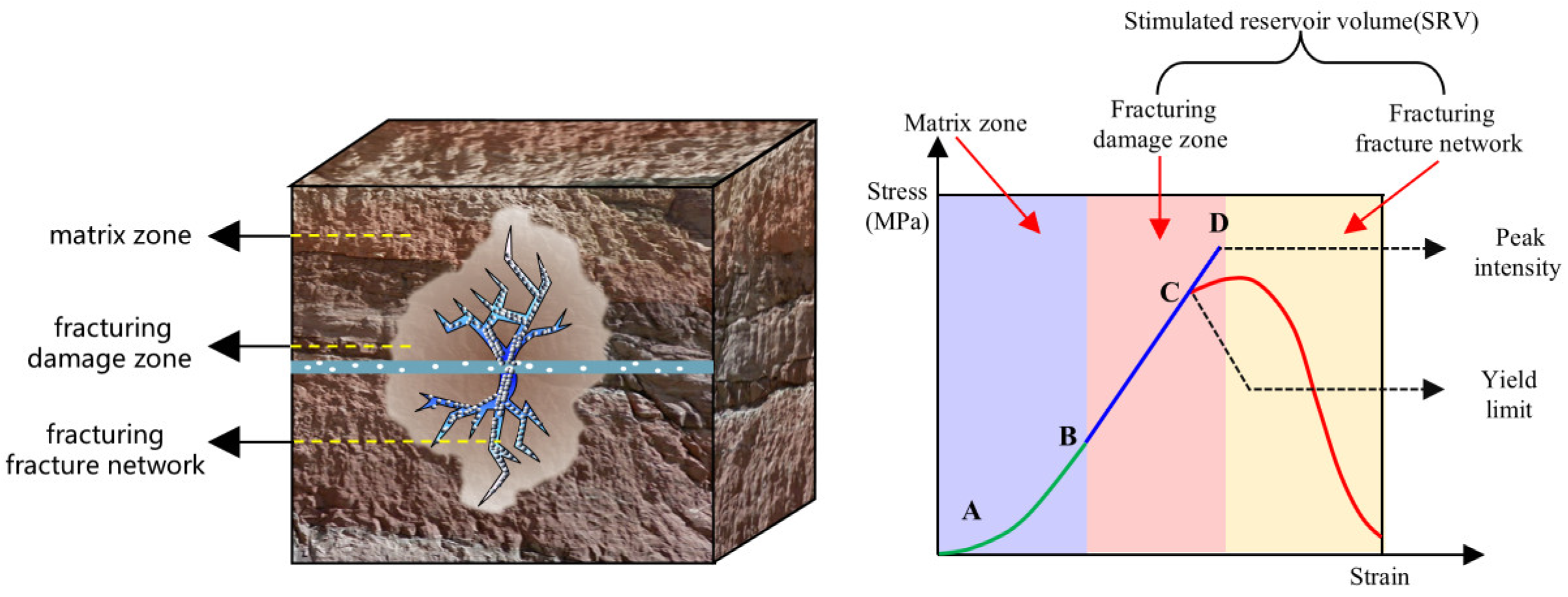
2.1. Physical Modeling of Fractures in Tight Gas Reservoirs
2.1.1. Similarity Criteria Parameters
- (1)
- A normal-pressure and isothermal system;
- (2)
- Immiscible gas–water flow governed by Darcy’s law;
- (3)
- Uniform thickness and homogeneous formation;
- (4)
- Isotropic porous medium exhibiting permeability;
- (5)
- Constant fluid viscosities under reservoir temperature;
- (6)
- Uniform initial saturation distribution.
2.1.2. Fractured Modeling
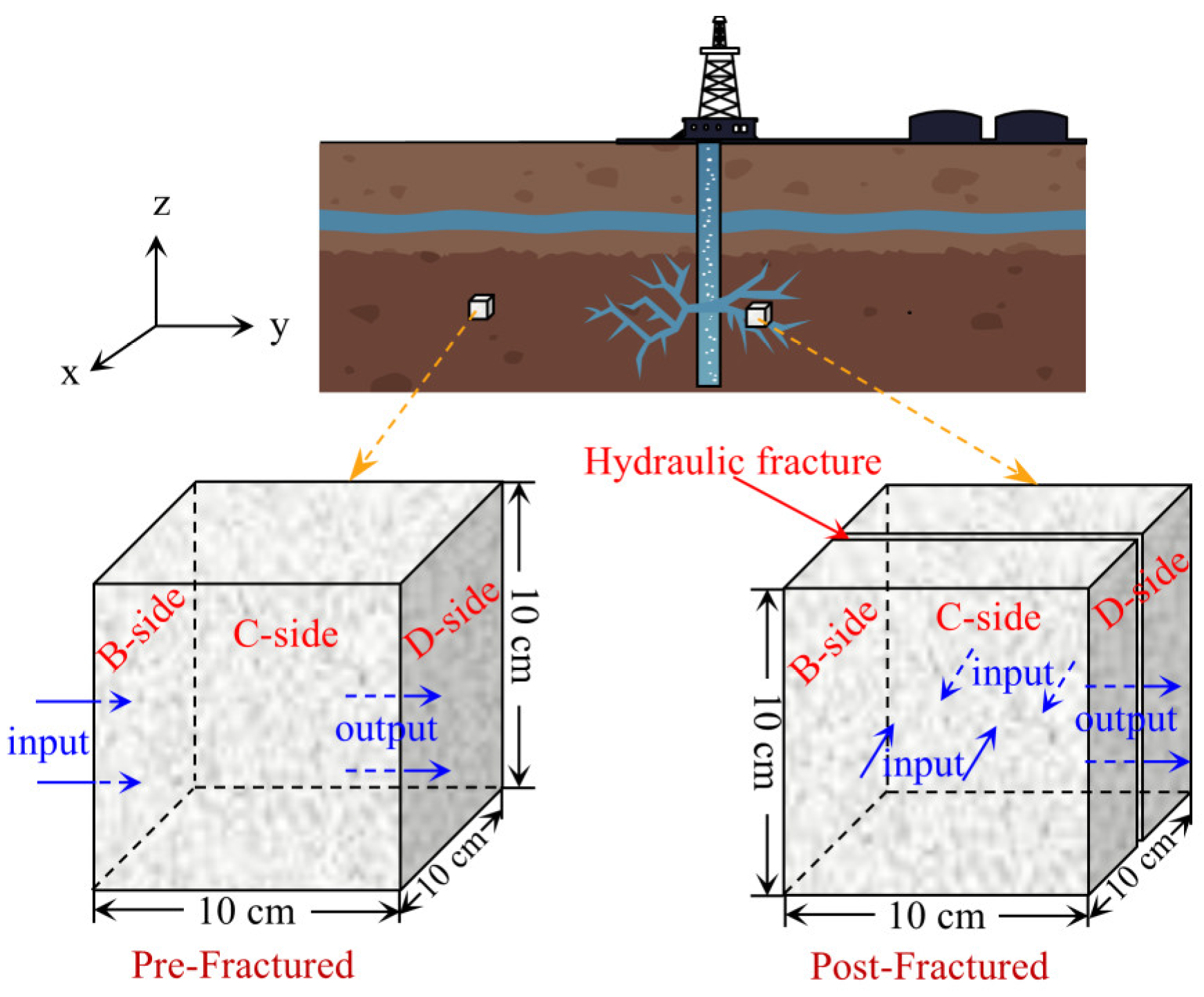
2.2. Waterflooding Experimental
2.2.1. Experimental Material
2.2.2. Experimental Method
- (1)
- Micro-CT test
- (2)
- NMR test
- (3)
- Threshold pressure gradient test
- (4)
- Irreducible water saturation at different pressure tests
- (5)
- Gas–water relative permeability test
- (6)
- Three-dimensional seepage experimental
2.2.3. Three-Dimensional Seepage Experimental Apparatus
2.2.4. Three-Dimensional Seepage Experimental Procedure
3. Results
3.1. Pore Structure Variations
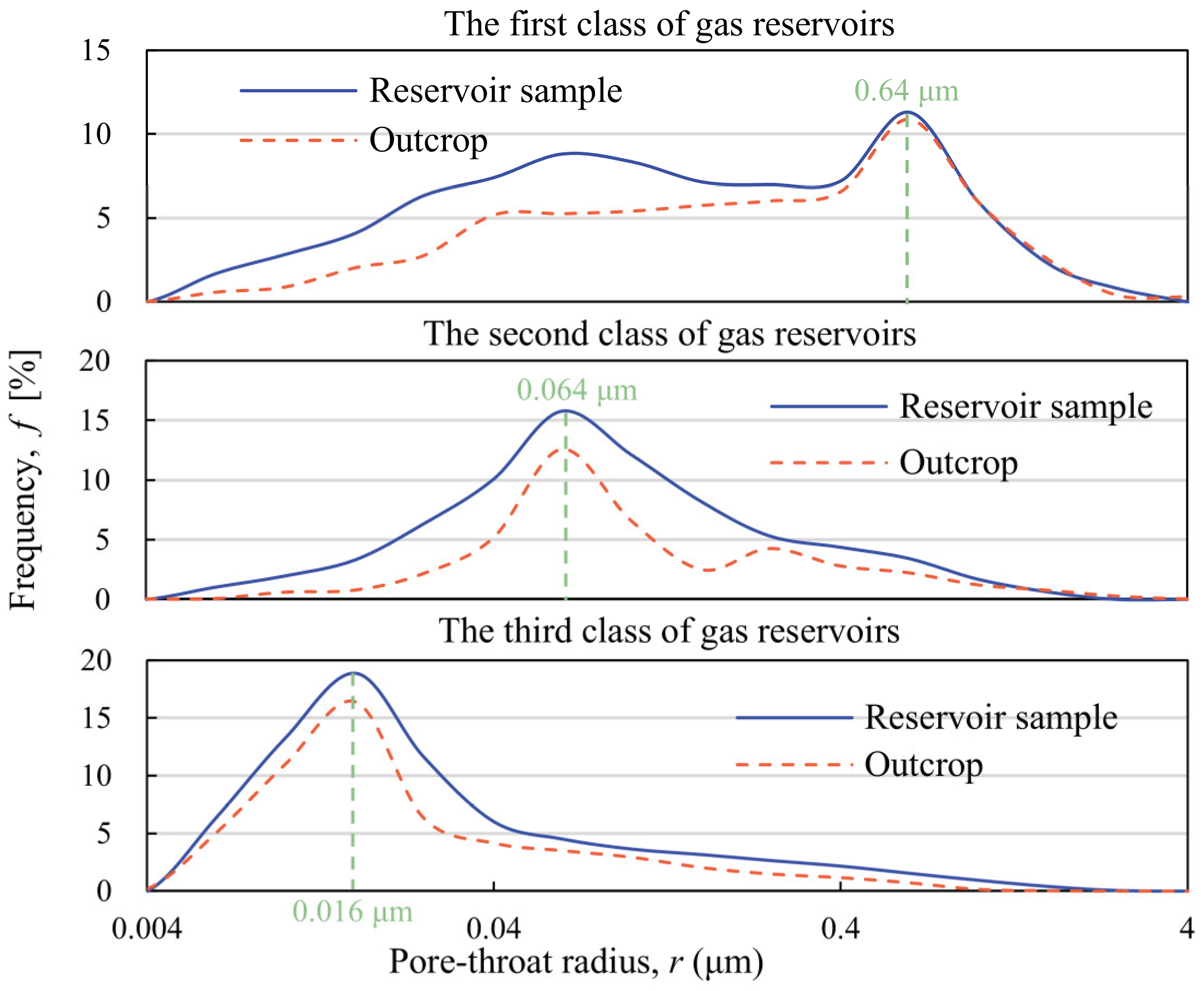
3.1.1. Micro-CT Test Results
3.1.2. NMR Test Results
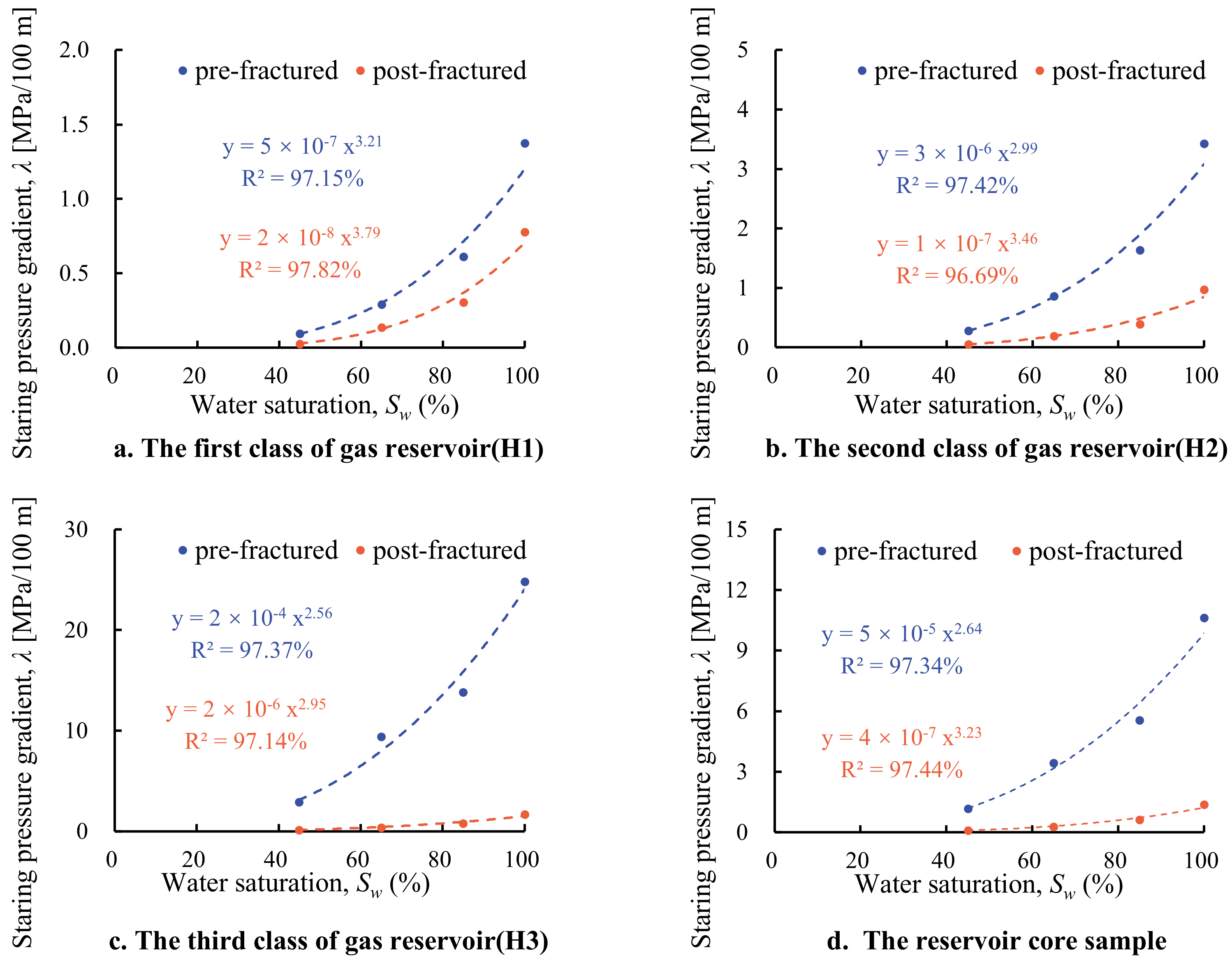
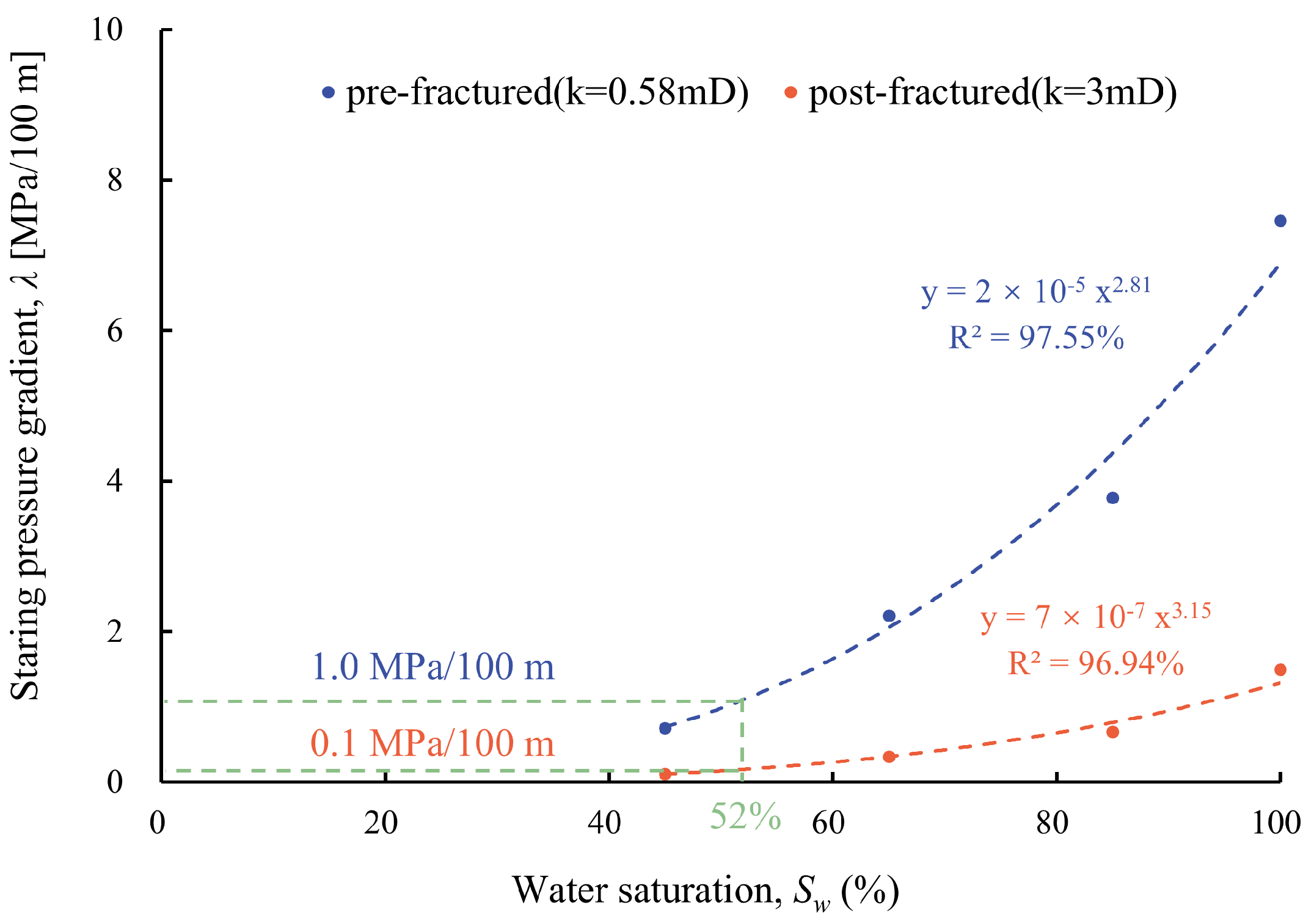
3.2. Threshold Pressure Gradient Variations
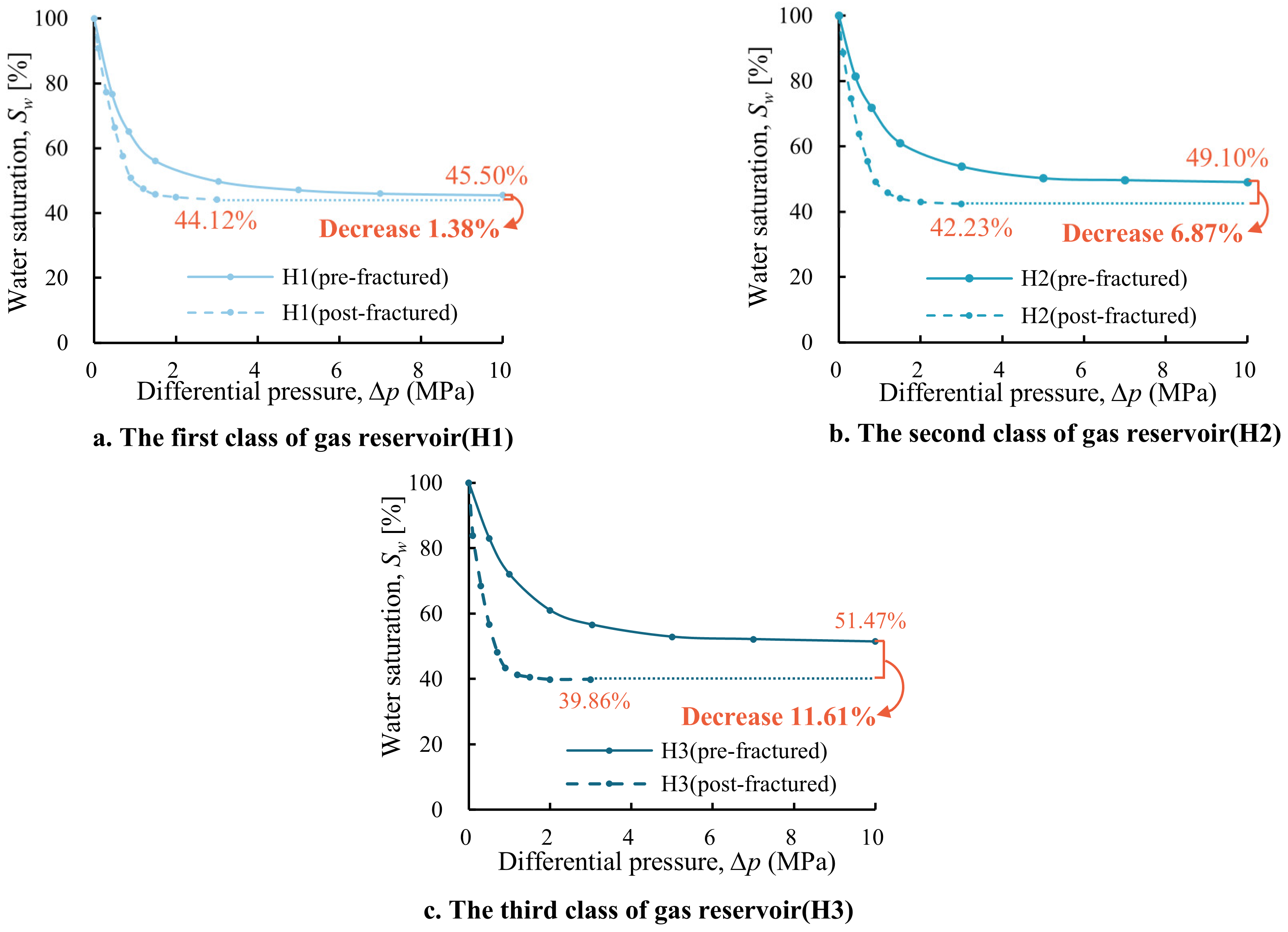
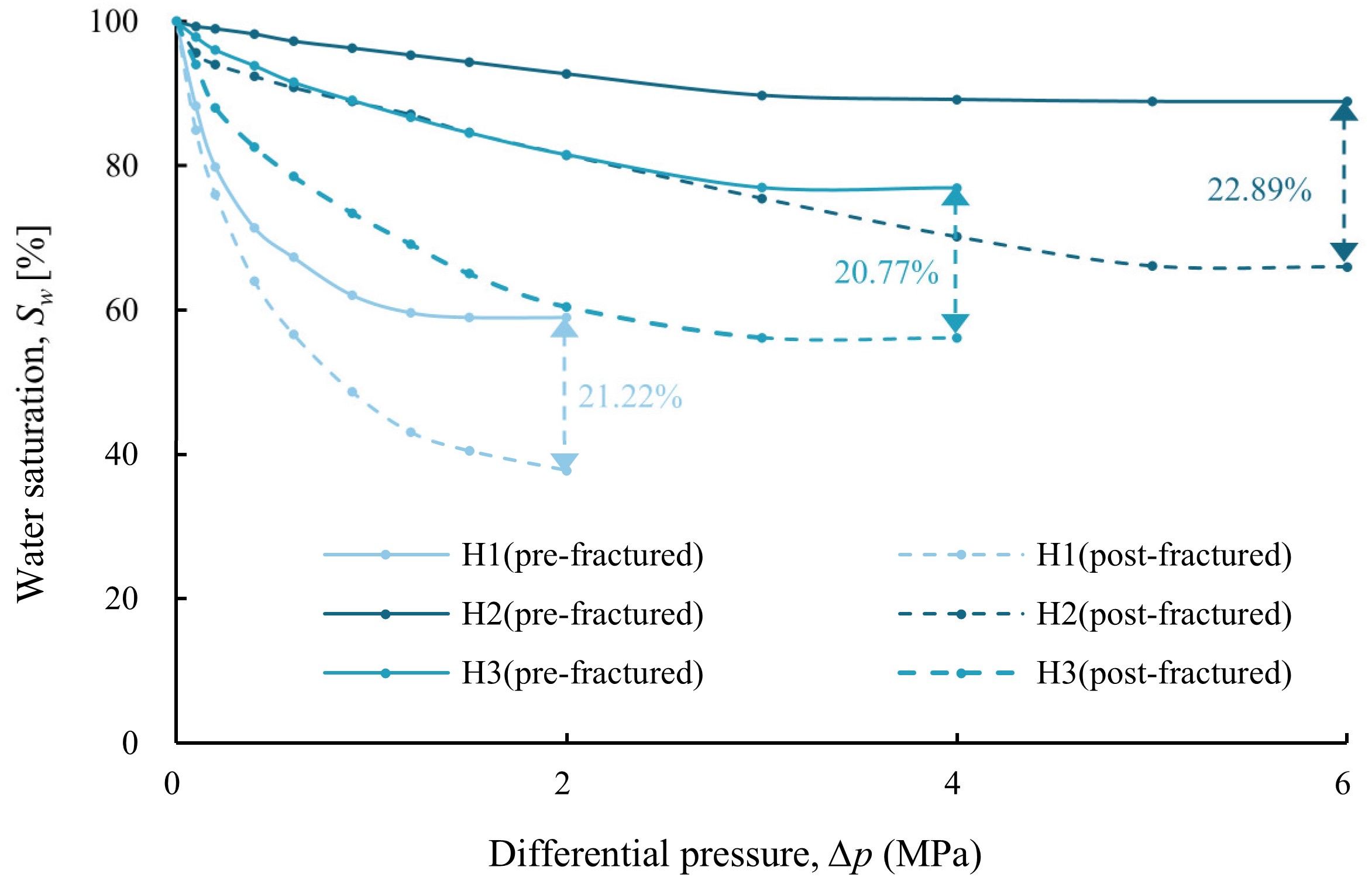
3.3. Transformation Relationship Between Irreducible and Mobile Water
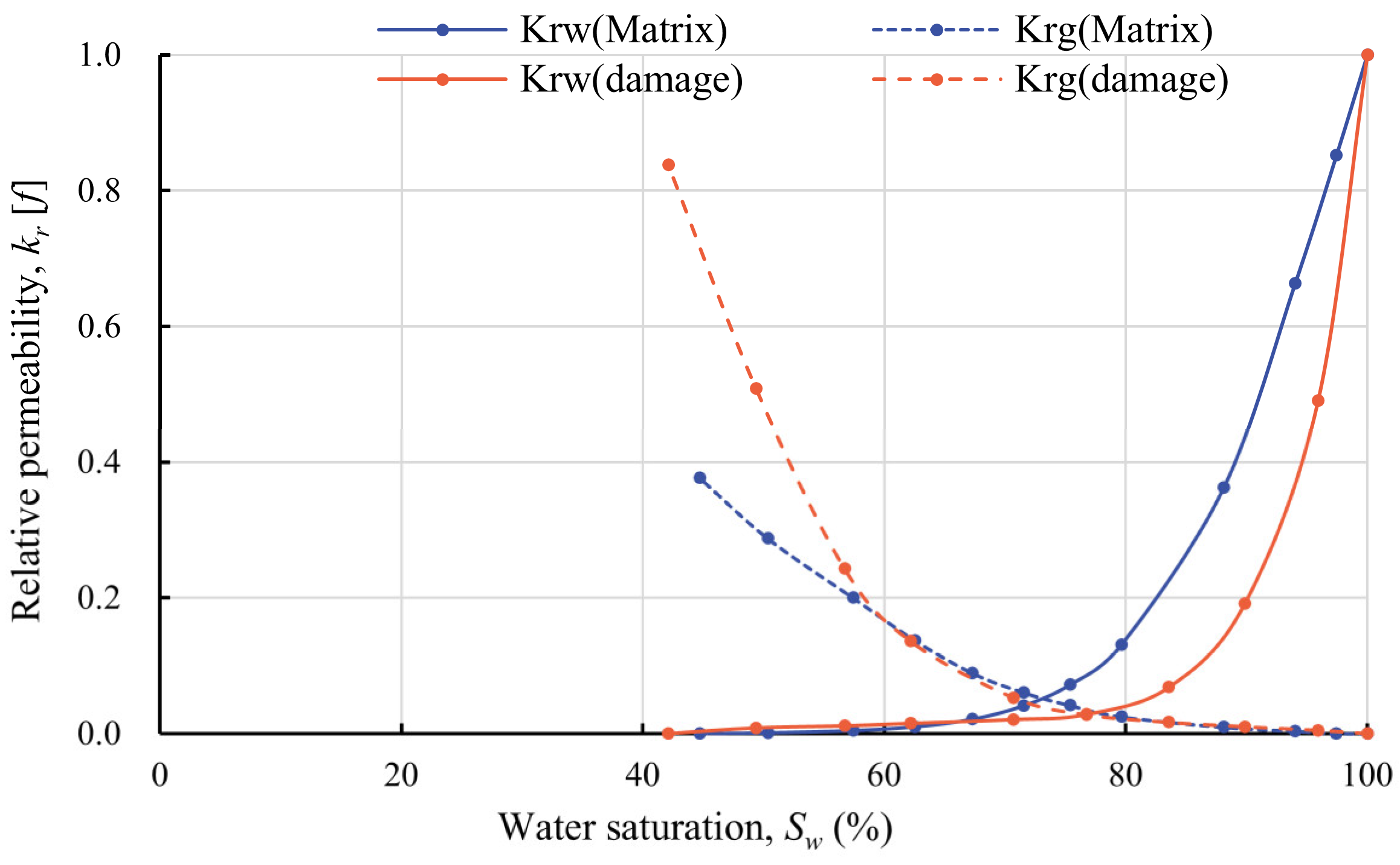
3.4. Gas–Water Flowability Variations
3.5. Quantification of Irreducible Water and Movable Water
4. Discussion
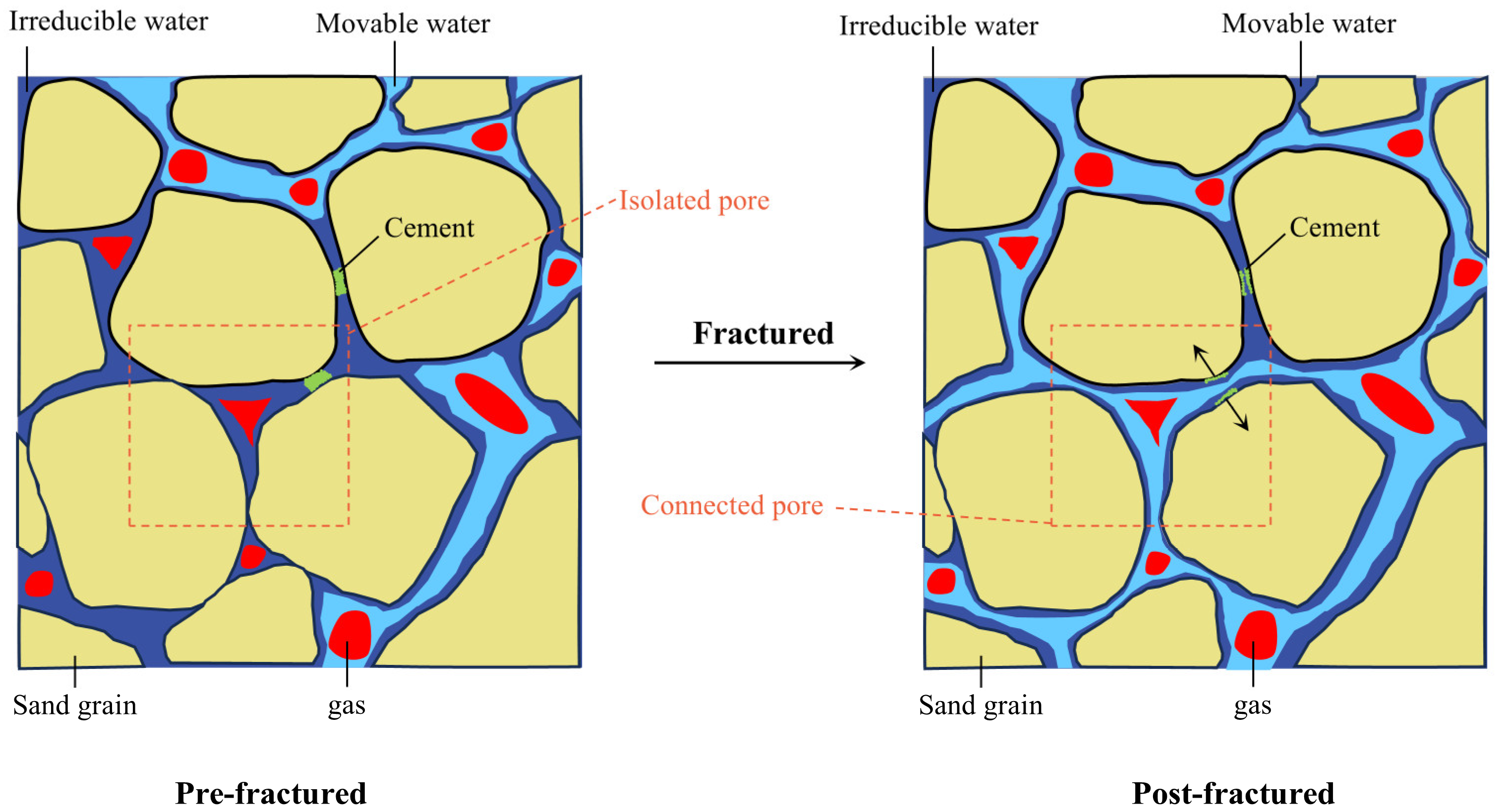
4.1. Flow Mechanism of Irreducible Water After the Change
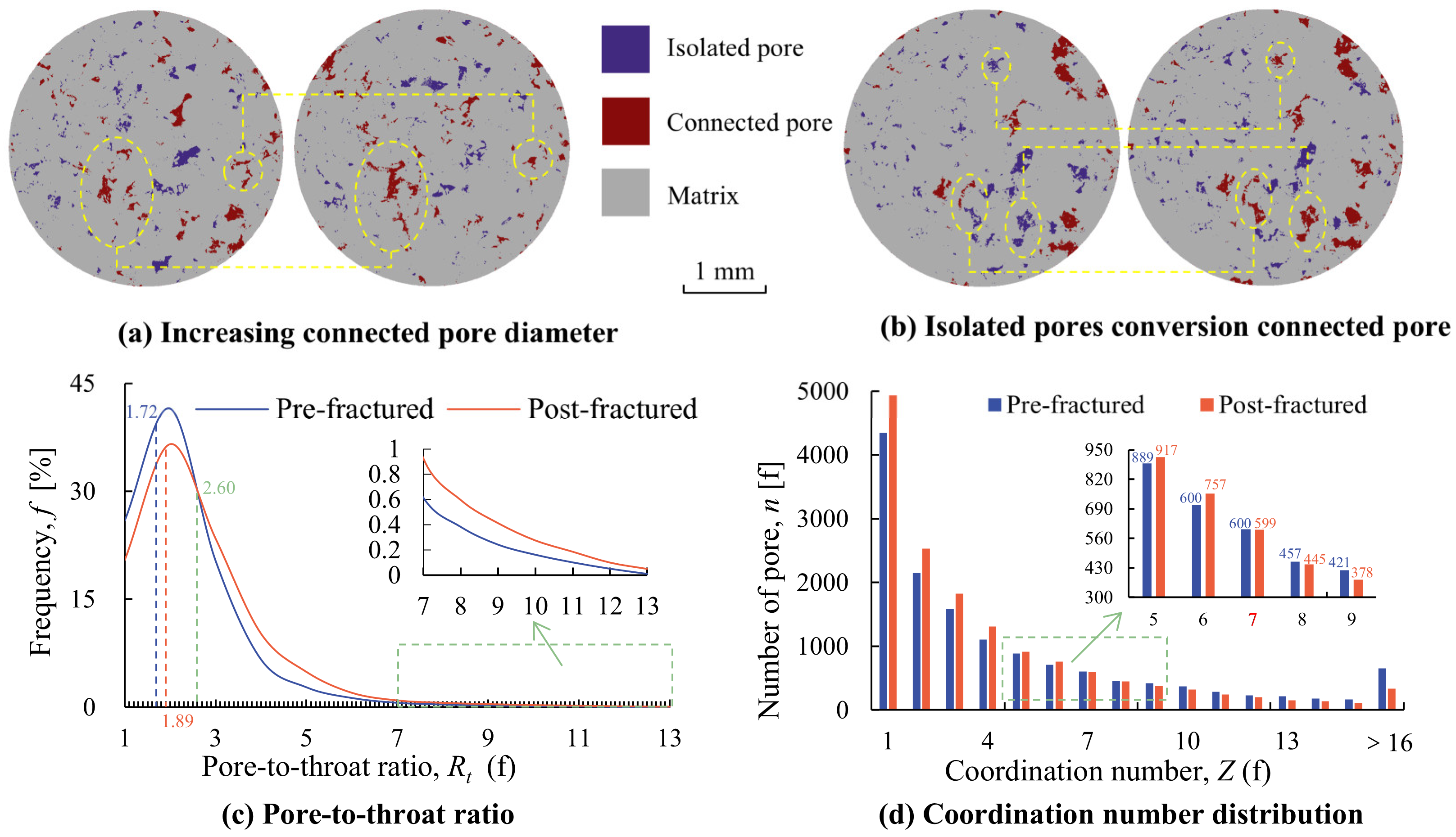
4.1.1. Pore Diameter Amplify
4.1.2. Isolated Pore Space Connected
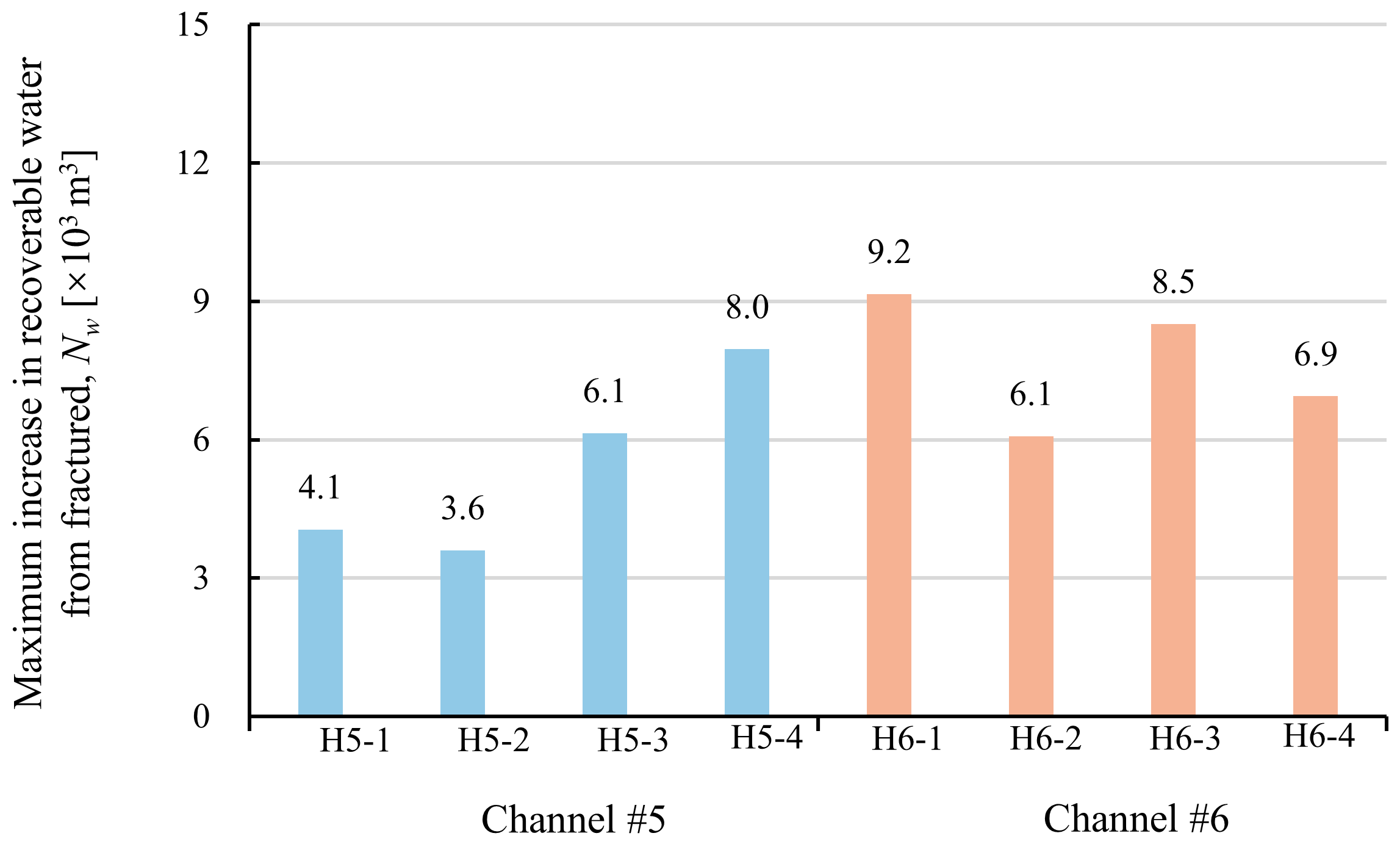
4.2. The Maximum Recoverable Water Increases from a Horizontal Well’s Hydraulic Fracturing
5. Conclusions
- (1)
- All three reservoir classes in the Dongsheng Gas Field, tight sandstone, exhibit a bimodal pore-throat distribution. The hydraulic fracturing process promotes significant modifications to the reservoir. This process reveals the creation of new seepage channels, increasing the diameter of the pore-throat connections and establishing links between isolated and connected pores. The conversion percentage from small to large pores in the three reservoir classes reached 12.4%, 17.0%, and 19.2%, respectively. This transformation achieves the capillary resistance, which causes 171% to 937% higher than that of pre-fractured matrix permeability.
- (2)
- The starting pressure gradient of water-bearing gas reservoirs increased with its rising water saturation, and this relationship can be described as a power function. After hydraulic fracturing stimulation, the starting pressure gradient of the gas reservoir decreased from 1 MPa/100 m to 0.1 MPa/100 m. The potential mechanisms underlying the reduction in starting pressure gradient on the gas–water flow include reduced capillary forces between fluid phases and the establishment of a continuous gas phase via bubble coalescence.
- (3)
- In damage zones, gas seepage primarily obeys Darcy flow. Pre-fracturing high capillary pressure causes irreducible saturation to decrease exponentially with rising pressure gradient, stabilizing after rapid attenuation. The lower irreducible saturation and a notable acceleration in water production rate may, therefore, be involved in their enhanced permeability and pore connectivity in hydraulic fracturing. In three classes of formations, the transformation of irreducible water to mobile water occurs at rates of 1.38%, 6.87%, and 11.61%. Fracture zones obey pipe flow (non-Darcy flow), which occurs, reaching 20.77% to 22.89% transform efficiency.
- (4)
- The relative permeability curves of gas and water phases in the matrix sample and damaged samples exhibit concave profiles. The water-phase permeability displays a rapid initial decline followed by a gradual reduction as water saturation decreases. Experiments performed in the damaged sample demonstrated enhanced gas–water flow capability, as evidenced by that of the matrix sample. In particular, the iso-permeability point shifts toward higher water saturation. The gas-phase relative permeability at irreducible water saturation is two times as high as that of the matrix sample.
- (5)
- The analysis of eight gas wells in the J30 well area of the Dongsheng Gas Field revealed that hydraulic fracturing increased water production by 3607 to 9163 m3. The results disclosed that hydraulic fracturing enhances initial water production rates and elevates water yields, which leads to a decrease in well performance. But this effect is only maintained during the first 3 to 6 months post-fracture. Despite this short-term water influx accelerating near-wellbore pressure depletion, we strongly suggest that it is critical to maintain the water–gas ratio (WGR) below 5 m3/104 m3 of gas in implementing an optimized production strategy. Such balanced production control ensures prolonged gas well stabilization.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, C.; Dong, D.; Wang, Y.; Li, X.; Huang, J.; Wang, S.; Guan, Q.; Zhang, C.; Wang, H.; Liu, H.; et al. Shale gas in China: Characteristics, challenges and prospects (II). Pet. Explor. Dev. 2016, 43, 182–196. [Google Scholar] [CrossRef]
- Burrows, L.C.; Haeri, F.; Cvetic, P.; Sanguinito, S.; Shi, F.; Tapriyal, D.; Goodman, A.; Enick, R.M. A literature review of CO2, natural gas, and water-based fluids for enhanced oil recovery in unconventional reservoirs. Energy Fuels 2020, 34, 5331–5380. [Google Scholar] [CrossRef]
- Yao, J.; Wang, C.; Huang, Z.; Zhou, X.; Li, J. Stress sensitivity of ultra-deep tight sandstone gas reservoirs based on microscopic ffuid-solid coupling. Nat. Gas Ind. 2024, 44, 45–55. [Google Scholar] [CrossRef]
- Meng, D.; Jia, A.; Ji, G.; He, D. Water and gas distribution and its controlling factors of large scale tight sand gas fields: A case study of western Sulige gas field, Ordos Basin, NW China. Pet. Explor. Dev. 2016, 43, 663–671. [Google Scholar] [CrossRef]
- Meng, D.; He, D.; Guo, Z.; Wang, G.; Ji, G.; Tang, H.; Zeng, Q. Dynamic analysis of high-water-cut tight sandstone gas reservoirs and study of water production splitting of gas wells: A case study on the Western Sulige Gas Field, Ordos Basin, NW China. Processes 2023, 11, 2093. [Google Scholar] [CrossRef]
- Pow, M.; Allan, V.; Mallmes, R.; Kantzas, A. Production of gas from tight naturally-fractured reservoirs with active water. In Proceedings of the 48th Annual Technical Meeting, Calgary, AB, Canada, 8–11 June 1997. [Google Scholar]
- Ghanbari, E.; Dehghanpour, H. The fate of fracturing water: A field and simulation study. Fuel 2016, 163, 282–294. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, R.; Shou, Q.; Zhao, J.; Zhang, Y. Analysis of atmospheric water locks and water lock solutions in tight sandstone gas reservoirs in the Ordos Basin. J. Phys. Conf. Ser. 2025, 2962, 012002. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y.; Wang, H.; Huang, L.; Liao, F.; Liu, Y.; Chen, Y. Study on the mechanism of water blocking in tight sandstone gas reservoirs based on centrifugal and nuclear magnetic resonance methods. Energies 2022, 15, 6680. [Google Scholar] [CrossRef]
- Khormali, A.; Ahmadi, S. Synergistic Effect Between Oleic Imidazoline and 2-Mercaptobenzimidazole for Increasing the Corrosion Inhibition Performance in Carbon Steel Samples. Iran. J. Chem. Chem. Eng. 2023, 42, 321–336. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Solano, N.; Bustin, R.M.; Bustin, A.M.M.; Chalmers, G.R.L.; He, L.; Melnichenko, Y.B.; Radliński, A.P.; Blach, T.P. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar] [CrossRef]
- Gao, H.; Li, H.A. Pore structure characterization, permeability evaluation and enhanced gas recovery techniques of tight gas sandstones. J. Nat. Gas Sci. Eng. 2016, 28, 536–547. [Google Scholar] [CrossRef]
- Wu, Y.; Tahmasebi, P.; Lin, C.; Zahid, M.A.; Dong, C.; Golab, A.N.; Ren, L. A comprehensive study on geometric, topological and fractal characterizations of pore systems in low-permeability reservoirs based on SEM, MICP, NMR, and X-ray CT experiments. Mar. Pet. Geol. 2019, 103, 12–28. [Google Scholar] [CrossRef]
- Xu, L.; Cai, M.; Dai, Z.; Zheng, Z.; Chen, W.; Yin, S.; Zhang, X.; Thanh, H.V.; Soltanian, M.R. Fractal and NMR based characterizations of multi-scale pore structure alterations in tight sandstones due to scCO2-water–rock interactions. Chem. Eng. J. 2025, 508, 160898. [Google Scholar] [CrossRef]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Nie, R.-S.; Zhou, J.; Chen, Z.; Liu, J.; Pan, Y. Pore structure characterization of tight sandstones via a novel integrated method: A case study of the Sulige gas field, Ordos Basin (Northern China). J. Asian Earth Sci. 2021, 213, 104739. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, C.; Ouyang, S.; Luo, B.; Zhao, D.; Sun, W.; Awan, R.S.; Lu, Z.; Li, G.; Zang, Q. Investigation of pore-throat structure and fractal characteristics of tight sandstones using HPMI, CRMI, and NMR methods: A case study of the lower Shihezi Formation in the Sulige area, Ordos Basin. J. Pet. Sci. Eng. 2022, 210, 110053. [Google Scholar] [CrossRef]
- Wang, W.; Lu, S.; Chen, X.; Li, X.; Li, J.; Tian, W. A new method for grading and assessing the potential of tight sand gas resources: A case study of the Lower Jurassic Shuixigou Group in the Turpan-Hami Basin, NW China. Pet. Explor. Dev. 2015, 42, 66–73. [Google Scholar] [CrossRef]
- Bo, N.; Dazhong, R.; Hu, W.; Hanpeng, Z.; Jianlin, G.; Ninghai, F.; Junjian, L.; Tian, L.; Qihui, L. Multi-scale combination characterization of micropore structure of tight sandstone gas reservoirs. Fault-Block Oil Gas Field 2024, 31, 35–41. [Google Scholar]
- Zhang, W.; Shi, Z.; Tian, Y. An improved method to characterize the pore-throat structures in tight sandstone reservoirs: Combined high-pressure and rate-controlled mercury injection techniques. Energy Explor. Exploit. 2020, 38, 014459872092072. [Google Scholar] [CrossRef]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.; Wang, X. Pore throat structure and fractal characteristics of tight oil sandstone: A case study in the Ordos Basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.; Fan, Z.; Chen, J.; Wang, S.; Zhou, Z.; Fan, X. Insight into the pore structure of tight sandstones using NMR and HPMI measurements. Energy Fuels 2016, 30, 10200–10214. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Z.; Sun, Z.; Cai, J.; Wang, L. Investigation on the pore structure and multifractal characteristics of tight oil reservoirs using NMR measurements: Permian Lucaogou Formation in Jimusaer Sag, Junggar Basin. Mar. Pet. Geol. 2017, 86, 1067–1081. [Google Scholar] [CrossRef]
- Dong, S.; Zeng, L.; Xu, C.; Dowd, P.; Gao, Z.; Mao, Z.; Wang, A. A novel method for extracting information on pores from cast thin-section images. Comput. Geosci. 2019, 130, 69–83. [Google Scholar] [CrossRef]
- Liu, D.; Sun, W.; Ren, D. Experimental investigation of pore structure and movable fluid traits in tight sandstone. Processes 2019, 7, 149. [Google Scholar] [CrossRef]
- Zafar, A.; Su, Y.-L.; Li, L.; Fu, J.-G.; Mehmood, A.; Ouyang, W.-P.; Zhang, M. Tight gas production model considering TPG as a function of pore pressure, permeability and water saturation. Pet. Sci. 2020, 17, 1356–1369. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Shen, W.; Gao, S.; Liu, H.; Ye, L.; Fang, F. Study of the effect of movable water saturation on gas production in tight sandstone gas reservoirs. Energies 2020, 13, 4645. [Google Scholar] [CrossRef]
- Zhu, W.; Zou, G.; Liu, Y.; Liu, W.; Pan, B. The influence of movable water on the gas-phase threshold pressure gradient in tight gas reservoirs. Energies 2022, 15, 5309. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Z.; Fu, S.; Li, A.; Zhong, J. Research on transformation of connate water to movable water in water-bearing tight gas reservoirs. Energies 2023, 16, 6961. [Google Scholar] [CrossRef]
- Xu, W.; Wu, C.; Guan, P.; Hu, F. Prediction of free water in the unconsolidated sandstone reservoir in the Quaternary gas field, Qaidam basin. Nat. Gas Geosci. 2012, 23, 952–955. [Google Scholar]
- Hu, Y.; Huayin, Z.; Yang, M.; Changmin, G.; Chunyan, J.; Xuan, X. The evaluation method for mobile water saturation of tight sandstone gas reservoir. Dev. Energy Sci. 2013, 2, 16–21. [Google Scholar]
- Ji, S. Movable Condition Research of Pore Water in Sulige Gas Field. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2015. [Google Scholar]
- Gao, S.; Hou, J.; Yang, H.; Xiong, W.; Hu, Z. Water production mechanism of Xujiahe low-permeability sandstone gas reservoirs in Middle Sichuan Basin. Nat. Gas Ind. 2012, 32, 40–42. [Google Scholar] [CrossRef]
- Ye, L.; Gao, S.; Yang, H.; Xiong, W.; Hu, Z.; Liu, H.; Du, S. Water production mechanism and development strategy of tight sandstone gas reservoirs. Nat. Gas Ind. 2015, 35, 41–46. [Google Scholar] [CrossRef]
- Liu, D.; Yue, X.; Hou, J.; Cao, J.; Wang, L. Experimental study of adsorbed water layer on solid particle surface. Acta Mineral. Sin. 2005, 25, 15–19. [Google Scholar] [CrossRef]
- Deng, Y.; Lu, Y.; Li, J.; REn, Z. Critical-flowing condition of inner-layer secondary-movable water in low-permeability gas reservoir. Nat. Gas Explor. Dev. 2011, 34, 36–38. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Z.; Ao, K.; Zhang, Y.; Wei, J. Manufacturing method of large-scale fractured porous media for experimental reservoir simulation. SPE J. 2013, 18, 1081–1091. [Google Scholar] [CrossRef]
- Cao, T.; Zhang, T.; Zhang, Y.; Wang, L. Physical simulation experiment of gas and water distribution during the accumulation of a tight sandstone gas reservoir. J. Chengdu Univ. Technol. Sci. Technol. Ed. 2024, 51, 60–75. [Google Scholar] [CrossRef]
- Awoleke, O.O.; Zhu, D.; Hill, A.D. New propped-fracture-conductivity models for tight gas sands. SPE J. 2016, 21, 1508–1517. [Google Scholar] [CrossRef]
- An, G.; Sun, H.; Ye, X.; Li, A.; Guo, W.; Fu, S.; Liu, S.; Zhu, Y.; Hu, Z. Research on the influence of sand-mud interlayer properties on the expansion of SAGD steam chamber. SPE J. 2024, 29, 3825–3843. [Google Scholar] [CrossRef]
- Jiao, C.; Liu, H.; Liu, P.; Gong, H. Similarity criterion of the physical simulating experiment for the development performances of low-permeability tight gas reservoirs. Pet. Geol. Oilfield Dev. Daqing 2019, 38, 156–161. [Google Scholar]
- Li, L.; Liu, W.; Zhang, Y.; Yao, C. Optimization of the fracturing operation parameters in Well Block Jin-58 of Dongsheng Gas Field. Pet. Geol. Oilfield Dev. Daqing 2020, 39, 48–55. [Google Scholar] [CrossRef]
- Bakarji, J.; Callaham, J.; Brunton, S.L.; Kutz, J.N. Dimensionally consistent learning with Buckingham Pi. Nat. Comput. Sci. 2022, 2, 834–844. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Heidaryan, E.; Moghadasi, J.; Rahimi, M. New correlations to predict natural gas viscosity and compressibility factor. J. Pet. Sci. Eng. 2010, 73, 67–72. [Google Scholar] [CrossRef]
- Zhang, W.; Mehrabian, A. Dimensionless solutions for the time-dependent and rate-dependent productivity index of wells in deformable reservoirs. SPE J. 2021, 26, 2814–2836. [Google Scholar] [CrossRef]
- Chen, D.; Wang, F.; Chen, H.; Wei, X.; Sun, S.; Zhu, S. Characterization of braided river reservoir architecture of the Upper Paleozoic He 8 member on Fugu Tianshengqiao outcrop, eastern Ordos Basin. Oil Gas Geol. 2019, 40, 335–345. [Google Scholar]
- Chen, A.; Chen, H.; Xiang, F.; Liu, W.; Hou, Z.; Shang, Y.; Ye, L.; Li, J. Sandstone characteristic and provenance analysis of the PermianShanxi Formation—Shangshihezi Formationinthe northeast of Ordos Basin China. J. Chengdu Univ. Technol. Sci. Technol. Ed. 2007, 34, 305–311. [Google Scholar]
- Xiao, D.; Lu, S.; Lu, Z.; Huang, W.; Gu, M. Combining nuclear magnetic resonance and rate-controlled porosimetry to probe the pore-throat structure of tight sandstone. Pet. Explor. Dev. 2016, 43, 961–970. [Google Scholar] [CrossRef]
- GB/T 21650.1; Pore Size Distribution and Porosity of Solid Materials by Mercury Porosimetry and Gas Adsorption. National Standardization Administration: Beijing, China, 2008.
- Tan, D.; Luo, L.; Tan, X.; Wang, J.; Gao, X.; Cao, T.; Zhou, H.; Zha, X. Diagenesis and reservoir formation effect of tight sandstone in lower Permian Shihezi formation, Dongsheng gasfield. Spec. Oil Gas Reserv. 2021, 28, 68–76. [Google Scholar] [CrossRef]
- Xu, W.; Li, L. Reservoir evaluation of the middle Permian lower Shihezi formation, Dongsheng gasfield, Ordos basin. Nat. Gas Explor. Dev. 2016, 39, 18–21,40. [Google Scholar]
- Song, X.; Gao, H.; Feng, C.; Yi, P.; Wang, C.; Li, T. Analysis of the influence of micro-pore structure on oil occurrence using nano-CT scanning and nuclear magnetic resonance technology: An example from Chang 8 tight sandstone reservoir, Jiyuan, Ordos Basin. Processes 2023, 11, 1127. [Google Scholar] [CrossRef]
- Feng, G.; Xie, H.; Meng, Q.; Wu, F.; Li, G. Advanced coal, petroleum, and natural gas exploration technology. Energies 2022, 15, 8976. [Google Scholar] [CrossRef]
- Wang, Y.; Long, Y.; Sun, Y.; Zhang, S.; Song, F.; Wang, X. Threshold pore pressure gradients in water-bearing tight sandstone gas reservoirs. Energies 2019, 12, 4578. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Y.; Li, J.; Chi, Y.; Li, J.; Fu, X. Stress sensitivity of tight reservoirs and its effect on oil saturation: A case study of Lower Cretaceous tight clastic reservoirs in the Hailar Basin, Northeast China. J. Pet. Sci. Eng. 2020, 184, 106484. [Google Scholar] [CrossRef]
- Mo, F.; Du, Z.; Peng, X.; Tang, Y.; Sun, H. Pore-scale analysis of flow resistance in tight sandstones and its relationship with permeability jail. J. Nat. Gas Sci. Eng. 2017, 44, 314–327. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, S.; Xiong, W.; Ye, L.; Liu, H.; Zhu, W.; Sun, X.; Li, X.; Zhu, W. An improved experimental procedure and mathematical model for determining gas-water relative permeability in tight sandstone gas reservoirs. Geoenergy Sci. Eng. 2023, 221, 211402. [Google Scholar] [CrossRef]
- Yu, Q.; Jia, Y.; Liu, P.; Hu, X.; Hao, S. Rate transient analysis methods for water-producing gas wells in tight reservoirs with mobile water. Energy Geosci. 2023, 5, 100251. [Google Scholar] [CrossRef]
- SY/T 5345; Test Method for Two Phase Relative Permeability in Rock. National Development and Reform Commission: Beijing, China, 2007.
- Li, Y.; Xiao, F.; Xu, W.; Wang, J. Performance evaluation on water-producing gas wells based on gas & water relative permeability curves: A case study of tight sandstone gas reservoirs in the Sulige gas field, Ordos Basin. Nat. Gas Ind. B 2016, 3, 52–58. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.; Zhu, G.; Dong, Y.; Danesh, N.N.; Chen, Z.; Zhang, T. Comparison of low-field NMR and microfocus X-ray computed tomography in fractal characterization of pores in artificial cores. Fuel 2017, 210, 217–226. [Google Scholar] [CrossRef]
- Jalali, M.; Gischig, V.; Doetsch, J.; Näf, R.; Krietsch, H.; Klepikova, M.; Amann, F.; Giardini, D. Transmissivity changes and microseismicity induced by small-scale hydraulic fracturing tests in crystalline rock. Geophys. Res. Lett. 2018, 45, 2265–2273. [Google Scholar] [CrossRef]
- Li, H.; Wang, D.; Gao, J.; Zhang, M.; Wang, Y.; Zhao, L.; Yang, Z. Role of saturation on elastic dispersion and attenuation of tight rocks: An experimental study. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018513. [Google Scholar] [CrossRef]
- Rao, Y.; Yang, Z.; Chang, L.; Zhang, Y.; Wu, Z.; Li, H. Influence of reservoir lithology on porous flow resistance of gas-bearing tight oil reservoirs and production forecast. J. Pet. Explor. Prod. Technol. 2022, 12, 409–419. [Google Scholar] [CrossRef]
- Ren, X.; Li, A.; Fu, S.; Tian, W. Influence of micro-pore structure in tight sandstone reservoir on the seepage and water-drive producing mechanism—A case study from Chang 6 reservoir in Huaqing area of Ordos basin. Energy Sci. Eng. 2019, 7, 741–753. [Google Scholar] [CrossRef]
- Lin, X.; Zeng, J.; Wang, J.; Huang, M. Natural Gas Reservoir Characteristics and Non-Darcy Flow in Low-Permeability Sandstone Reservoir of Sulige Gas Field, Ordos Basin. Energies 2020, 13, 1774. [Google Scholar] [CrossRef]
- Chao, Z.; Ma, G.; Hu, X.; Luo, G. Experimental research on stress-dependent permeability and porosity of compact sandstone with different moisture saturations. J. Nat. Gas Sci. Eng. 2020, 84, 103639. [Google Scholar] [CrossRef]
- Fatemi, S.M.; Sohrabi, M. Recovery mechanisms and relative permeability for gas/oil systems at near-miscible conditions: Effects of immobile water saturation, wettability, hysteresis, and permeability. Energy Fuels 2013, 27, 2376–2389. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, X.; Chen, J. Pore-scale hydraulic properties of virtual sandstone microstructures: Spatial variations and voxel scale effects. Arch. Civ. Mech. Eng. 2022, 23, 22. [Google Scholar] [CrossRef]
- Cui, Y.; Ming, J.; Shi, X.; Yang, W.; Zhang, Z.; Zhang, C. A new method for calculating reservoir core-bound water saturation using the cast thin section. Processes 2023, 11, 1397. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, G.; Liang, Q.; Chen, Q. Study on microscopic characteristics and rock mechanical properties of tight sandstone after acidification–supercritical CO2 composite action: Case study from Xujiahe Formation, China. Appl. Sci. 2024, 14, 4108. [Google Scholar] [CrossRef]
- He, X.; Wang, C.; Chang, B.; Cao, Z.; Tang, H. A dynamic reserve evaluation method for an ultra-deep fractured tight sandstone gas reservoir. Energies 2024, 17, 2648. [Google Scholar] [CrossRef]








| Number | Similarity Criteria | Similarity Properties | Uses | Physical Stimulate | Gas Reservoir |
|---|---|---|---|---|---|
| 1 | porosity | determining model porosity | 0.06–0.16 | 0.05–0.20 | |
| 2 | gas saturation similarity | determine model saturation | 0.50–0.60 | 0.50–0.60 | |
| 3 | gas compressibility similarity | determine model gas | 0.90–1.20 | 0.90~1.20 | |
| 4 | temperature similarity | determine model temperature | 1.43 | 1.43 | |
| 5 | geometric similarity | determine model size | 2 | 2 | |
| 6 | geometric similarity | determine model size | 1 | 0.4 | |
| 7 | dynamical similarity | determine modeled original pressure | 0.003 | 0.003 | |
| 8 | dynamical similarity | establish bottom-hole pressure conversion relationships | 0.1–10 | 0.1–10 | |
| 9 | kinematic similarity | determine model gas production rate | 0.1–0.3 | 0.1–0.5 | |
| 10 | degree of reserve recovery similarity | establish time conversion relationship | 0–0.95 | 0–1 |
| Parameters | Seepage Lengths | Width of Seepage Surface | Thicknesses | Absolute Open Flow Potential | Production Time |
|---|---|---|---|---|---|
| a (m) | b (m) | h (m) | q (×104 m3/d) | t (day) | |
| The gas reservoir conditions | 300 | 150 | 10 | 3.74 | / |
| The laboratory conditions | 0.1 | 0.1 | 0.1 | 1.44 | 0.0208 |
| Serial Number | Formation | Reservoir Classes | Edge Length l (cm) | Weights m (g) | Porosity ϕ (%) | Permeability k (mD) |
|---|---|---|---|---|---|---|
| H1 | Number 1 of the Shihezi Formation | I | 10.0 | 2289.00 | 15.53 | 2.466 |
| H2 | Number 1 of the Shihezi Formation | II | 10.0 | 2136.87 | 9.22 | 1.127 |
| H3 | Number 2 and 3 of the Shihezi Formation | III | 10.0 | 2397.90 | 6.06 | 0.206 |
| Serial Number | Reservoir Classes | Pre-Fractured | Post-Fractured | Permeability on Rate Multiplier Increase kc (%) | Change in Median Radius rc (μm) | ||
|---|---|---|---|---|---|---|---|
| Porosity ϕ (%) | Permeability k (mD) | Porosity ϕ (%) | Permeability k (mD) | ||||
| H1 | I | 15.53 | 2.466 | 16.08 | 4.229 | 171 | 0.97 |
| H2 | II | 9.22 | 1.127 | 9.84 | 3.378 | 300 | 0.19 |
| H3 | III | 6.06 | 0.206 | 6.59 | 1.924 | 934 | 0.05 |
| Sample | Irreducible Water Saturation Swi (%) | Relative Gas Phase Permeability at Irreducible Water Saturation krw(Swi) (f) | Water Saturation at the Isotonic Point Sw(krw = krg) (%) | Relative Permeability at the Isotonic Point kr(krw = krg) (f) |
|---|---|---|---|---|
| Matrix | 44.70 | 0.38 | 72.24 | 0.043 |
| Damage | 42.11 | 0.84 | 77.09 | 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, A.; Su, L.; Cao, G.; Luo, Z.; Yan, C.; Chen, Q. Experimental Study on the Effect of Fractures on the Irreducible and Movable Water in Water-Bearing Tight Sandstone Gas Reservoirs. Processes 2025, 13, 1685. https://doi.org/10.3390/pr13061685
Hu A, Su L, Cao G, Luo Z, Yan C, Chen Q. Experimental Study on the Effect of Fractures on the Irreducible and Movable Water in Water-Bearing Tight Sandstone Gas Reservoirs. Processes. 2025; 13(6):1685. https://doi.org/10.3390/pr13061685
Chicago/Turabian StyleHu, Aiguo, Li Su, Gang Cao, Zhuo Luo, Changhui Yan, and Qing Chen. 2025. "Experimental Study on the Effect of Fractures on the Irreducible and Movable Water in Water-Bearing Tight Sandstone Gas Reservoirs" Processes 13, no. 6: 1685. https://doi.org/10.3390/pr13061685
APA StyleHu, A., Su, L., Cao, G., Luo, Z., Yan, C., & Chen, Q. (2025). Experimental Study on the Effect of Fractures on the Irreducible and Movable Water in Water-Bearing Tight Sandstone Gas Reservoirs. Processes, 13(6), 1685. https://doi.org/10.3390/pr13061685






