Fuzzy Disturbance Observer-Based Adaptive Nonsingular Terminal Sliding Mode Control for Multi-Joint Robotic Manipulators

Abstract

This study proposes a novel fuzzy disturbance observer (FDO)-augmented adaptive nonsingular terminal sliding mode control (NTSMC) framework for multi-joint robotic manipulators, addressing critical challenges in trajectory tracking precision and disturbance rejection. Unlike conventional disturbance observers requiring prior knowledge of disturbance bounds, the proposed FDO leverages fuzzy logic principles to dynamically estimate composite disturbances—including unmodeled dynamics, parameter perturbations, and external torque variations—without restrictive assumptions about disturbance derivatives. The control architecture achieves rapid finite-time convergence by integrating the FDO with a singularity-free terminal sliding manifold and an adaptive exponential reaching law while significantly suppressing chattering effects. Rigorous Lyapunov stability analysis confirms the uniform ultimate boundedness of tracking errors and disturbance estimation residuals. Comparative simulations on a 2-DOF robotic arm demonstrate a 97.28% reduction in root mean square tracking errors compared to PD-based alternatives and a 73.73% improvement over a nonlinear disturbance observer-enhanced NTSMC. Experimental validation on a physical three-joint manipulator platform reveals that the proposed method reduces torque oscillations by 58% under step-type disturbances while maintaining sub-millimeter tracking accuracy. The framework eliminates reliance on exact system models, offering a generalized solution for industrial manipulators operating under complex dynamic uncertainties.

1. Introduction

The typical industrial robot comprises a series of servo joint motors and connecting rods arranged in series. The main advantage of this structure lies in the flexibility of the end effector and its relatively large working space, which enables it to be utilized for various processing operations in industrial production. However, the serial structure poses numerous challenges for the manipulation control. Multi-degree-of-freedom manipulators inherently exhibit nonlinear dynamics, strong coupling effects, and complex multi-input multi-output interactions. In actual applications, challenges also arise from time-varying payloads, joint friction uncertainties, and external perturbations, which significantly impede precise trajectory tracking and prompt recent advancements in robust control methodologies. Research into robot control methods has garnered increasing interest in recent years, resulting in the proposal of various control strategies.

Most classical PID controls can satisfy basic control requirements [1,2], but due to the nonlinearity and coupling of the manipulator itself, its effectiveness diminishes. The control accuracy of the PID is not satisfactory. Sliding mode control [3,4,5], rooted in variable structure control principles, forces system trajectories to follow predefined paths by dynamically adjusting the control structure, ultimately achieving the desired control goal. Owing to its insensitivity to parameter variations and external disturbances, sliding mode control inherently provides robust performance. To mitigate prolonged convergence and chattering in conventional sliding mode control, recent studies propose nonsingular terminal sliding mode controllers [6,7,8,9], which accelerate tracking convergence and improve precision.

The manipulator system is often subjected to various unknown disturbances during the movement process, including primarily unmodeled dynamic characteristics, parameter perturbations of the system, load changes, joint friction, etc. Such disturbances degrade the positional tracking performance of control systems, and estimation and compensation based on disturbance observers can significantly reduce the impact of the disturbances [10,11,12,13,14,15]. Extended state observers (ESO) and nonlinear disturbance observers (NDO) estimate disturbances by leveraging system output characteristics, and these estimates are integrated into feedback controllers to counteract disturbances. However, existing observer designs assume prior knowledge of disturbance bounds and their derivatives converging to zero over time, which limits practical applicability. While the design of these observers has been shown to address previous difficulties, from a control theory perspective, traditional approaches necessitate predefined bounds for external disturbances and parameter uncertainties, along with the assumption that disturbance derivatives asymptotically vanish—conditions rarely met in real-world scenarios. This implies that the interference is expected to weaken and eventually disappear, but this is not always the practice case. In such scenarios, the control system cannot converge and fails to achieve the desired control effect.

To overcome the above problems, this paper proposes a fuzzy disturbance observer (FDO)-augmented nonsingular terminal sliding mode control (NTSMC) framework. Unlike traditional disturbance observers that require prior knowledge of disturbance bounds, the proposed FDO leverages fuzzy logic principles to dynamically estimate composite disturbances—including unmodeled dynamics, parameter perturbations, and external torque variations—without relying on restrictive assumptions about disturbance derivatives. The universal approximation principle of fuzzy systems compensates for unknown system uncertainty, actuator failure, saturation, and interference, enhances the convergence rate of tracking errors, and eliminates singularity and chattering problems [16,17,18,19,20,21,22,23,24,25]. Lyapunov stability analysis confirms the global asymptotic convergence of the proposed method. The rest of this paper is arranged as follows: Section 2 introduces the dynamics model of the manipulator and expresses some reasonable assumptions. In Section 3 and Section 4, the FDO and nonsingular terminal sliding mode controller (NTSMC) are designed, respectively [17,26,27,28,29]. Section 5 proves its convergence and stability. Comparative simulations and real-world experiments are discussed in Section 6 and Section 7, with concluding remarks in Section 8.

2. Dynamic Model of the Manipulator

The dynamics equation of a multi-joint manipulator system is established using Lagrange dynamics. Considering the uncertainty, parameter change, and unknown disturbance of the model, the rigid body dynamics model can be expressed as

$$\left(M_0\left(q\right)+\Delta M\left(q\right)\right)\ddot{q}+\left(C_0\left(q,\dot{q}\right)\dot{q}+\Delta C\left(q,\dot{q}\right)\right)+\left(G_0\left(q\right)+\Delta G\left(q\right)\right)+d\left(t\right)=u$$

(1)

of which, $M_0\left(q\right)\in {ℝ}^{n\times n}$ represents the nominal value of the mass matrix, $C_0\left(q,\dot{q}\right)\in {ℝ}^{n\times 1}$ represents the nominal value of the centripetal force and Coriolis force matrix, and $G_0\left(q\right)\in {ℝ}^{n\times 1}$ is the nominal value of the gravity vector. $\Delta C$ and $\Delta G$ represent the unmodeled and parameter-perturbed parts, respectively. $q,\dot{q}, \mathrm{and} \ddot{q}$ correspond to the angular position, rotational speed, and acceleration of each joint within the manipulator’s kinematic framework, respectively. $u\in {ℝ}^{n\times 1}$ represents the joint driving torque vector, while $d\left(t\right)$ is the interference torque. Joint friction, modeling error, and external disturbance are the total disturbance $T_d$. Consequently, Equation (1) is further rewritten as

$$M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+G\left(q\right)+D\left(t\right)=u$$

(2)

where $D\left(t\right)=\left(\Delta M+\Delta C+\Delta G\right)+d\left(t\right)$ is the total interference. The manipulator model mentioned in the above formula possesses two fundamental mathematical characteristics: (1) $M\left(q\right)\in {ℝ}^{n\times n}$ is a positive definite symmetric matrix; (2) $\left(M-2C\right)$ is a skew-symmetric matrix. Considering the following control strategies, the following assumptions are made: (1) The joint’s angular states (position $q$ and velocity $\dot{q}$) are measurable with continuous and bounded characteristics under practical operating conditions; (2) The aggregate disturbance $T_d$, encompassing both internal and external uncertainties, remains bounded and exhibits continuous differentiability, and its upper bound is $T_d<\Gamma$. The desired trajectory for the manipulator’s joint angular configuration is mathematically formulated as a time-dependent reference signal, expressed by $q_d$, a second-order continuously differentiable function. The desired angular velocity and angular acceleration are ${\dot{q}}_d$ and ${\ddot{q}}_d$, respectively. The tracking error $e=q-q_d$ quantifies the deviation between actual and desired trajectories, while its temporal derivative $\dot{e}=\dot{q}-{\dot{q}}_d$ captures the rate of error variation. The controller’s primary goal is to enforce finite-time convergence of $e$ to a neighborhood of zero.

Let $x_1=q,x_2=\dot{q}$. The system state variable is taken as

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\ddot{q}=M^{-1}\left(q\right)u-M^{-1}\left(q\right)\left[C\left(q,\dot{q}\right)\dot{q}+G\left(q\right)\right]-M^{-1}\left(q\right)D\left(t\right)\end{array}\right.$$

(3)

To apply the fuzzy disturbance observer, let $M^{-1}\left(q\right)=b\left(x\right)$, $-M^{-1}\left(q\right)\cdot \left[C\left(q,\dot{q}\right)+G\left(q\right)\right]=f\left(x\right)$; then, the above formula can be written as follows:

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2\\ {\dot{x}}_2=f\left(x\right)+b\left(x\right)u+T_d\left(x,d\right)\end{array}\right.$$

(4)

where $T_d\left(x,d\right)=-M^{-1}\left(q\right)\cdot D\left(t\right)$ represents the cumulative effect of parametric variations and exogenous disturbances acting on the manipulator, which is robustly estimated via a fuzzy logic-based disturbance observer (FDO).

3. Fuzzy Disturbance Observer Design (FDO)

Fuzzy systems typically employ if-then rules, and in multi-input multi-output (MIMO) control architectures, the generalized dynamic representation can be expressed in the following state–space formulation:

$$\begin{gathered} If x_1 is A_1^j, x_2 is A_1^j,\dots ,x_n is A_n^j, \\ Then y_1 is B_1^j,y_2 is B_2^j,\dots ,y_m is B_m^j. \end{gathered}$$

(5)

where $x_i\left(i=1,2,\dots ,n\right)\in R^n$ is the system input, $y_i\left(i=1,2,\dots ,m\right)\in R^m$ is the system output, $A_i^j$ and $B_i^j$ are the fuzzy sets, and rule counts are denoted as $j=1,2,\dots ,M$.

The fuzzy system output, which uses a product inference machine, singleton fuzzifier, and centroid defuzzifier, can be expressed as Equation (6). The product inference machine combines the outputs of multiple fuzzy rules by multiplying them, enabling the system to aggregate information from different rules effectively. The singleton fuzzifier maps crisp input values to a single fuzzy set, simplifying the fuzzification process. Finally, the centroid defuzzifier converts the fuzzy output back to a crisp value by calculating the center of the area under the membership function curve, thus providing a single representative value for the output.

$$y\left(x\right)={\displaystyle \frac{{{\displaystyle \sum }}_{j=1}^M{\tilde{y}}_j\left({{\displaystyle \prod }}_{i=1}^n{\mu }_{A_j^i}\left(x_j\right)\right)}{{{\displaystyle \sum }}_{j=1}^M\left({{\displaystyle \prod }}_{i=1}^n{\mu }_{A_j^i}\left(x_j\right)\right)}}={\widehat{𝜛}}^T\xi \left(x\right)$$

(6)

Building upon the dynamic model in Equation (4), a fuzzy disturbance observer $T_d$ is synthesized to reconstruct unknown disturbances governed by the following differential equation:

$$\dot{\mu }=\sigma \left(x_2-\mu \right)-f\left(x\right)+b\left(x\right)u+\Omega (x,u|\widehat{𝜛})$$

(7)

Of which, $\Omega$ is the estimation of the unknown interference term $T_d$. $\varsigma =x_2-\mu$ is defined as the observation error value, so $\varsigma \to 0$ at that time can ensure the tracking of $\Omega$ to $T_d$. Then, Equation (7) can be expressed as the following Equation (8):

$$\dot{\varsigma }=-\sigma \varsigma +T_d-\Omega (x,u|\widehat{𝜛})$$

(8)

Let $x$ be a compact set $M_x$, and suppose that the optimal parameter vector ${\widehat{𝜛}}^{*}$ is located in the convex space $M_{𝜛}=\left\{𝜛\right|\parallel 𝜛\parallel \le m_{𝜛}\}$, where $m_{𝜛}$ is the parameter to be designed, and ${\widehat{𝜛}}^{*}$ is defined as

$${\widehat{𝜛}}^{\ast }={\arg }_{{\widehat{𝜛}}^{\ast }\in M_{\widehat{𝜛}}}^{\min }{[}_{x\in M_x}^{\sup }\left|T_d-\Omega (x,u|\widehat{𝜛})\right|]$$

(9)

of which sup is the minimum upper bound.

Assuming that the error term of interference observation is represented by $\epsilon (x|u)$ and its upper bound is $\parallel \epsilon \parallel \le \overline{\epsilon }$, then, by the universal approximation theorem, which asserts that fuzzy systems can approximate any continuous function over a compact domain to arbitrary accuracy, the unknown interference $T_d$ can be expressed as the sum of $\Omega$ and an error coefficient $\epsilon (x|u)$, namely

$$T_d=\Omega (x,u|{\widehat{𝜛}}^{*})+\epsilon \left(x,u\right)$$

(10)

The error term $\epsilon$ can be controlled by the number of if-then rules. Substitute Equation (10) and Equation (6) into Equation (8) to obtain the result:

$$\begin{array}{cc}\dot{\varsigma }=\hfill & -\sigma \varsigma +\Omega \left(x,u|{\widehat{𝜛}}^{*}\right)+\epsilon \left(x,u\right)-\Omega \left(x,u|\widehat{𝜛}\right)\hfill \\ & =-\sigma \varsigma +{\widehat{𝜛}}^{*T}\xi \left(x\right)-{\widehat{𝜛}}^T\xi \left(x\right)+\epsilon \left(x,u\right)\hfill \\ & =-\sigma \varsigma +{\widetilde{𝜛}}^T\xi \left(x\right)+\epsilon \left(x,u\right)\hfill \end{array}$$

(11)

where $\widetilde{𝜛}={\widehat{𝜛}}^{*}-\widehat{𝜛}$ is the parameter error. The optimal parameter ${\widehat{𝜛}}^{*}$ cannot be obtained by FDO, so $\widehat{𝜛}$ is estimated by designing an adaptive law, which is in the form of

$$\dot{\widehat{𝜛}}=\eta \varsigma \xi \left(x\right)$$

(12)

where $\eta$ is the standard number to be designed, then $\dot{\widetilde{𝜛}}=-\eta \varsigma \xi \left(x\right)$. In the following, it is rigorously demonstrated that the estimation error of the fuzzy disturbance observer converges to a uniformly ultimately bounded (UUB) region, and a candidate Lyapunov function, serving as a stability certificate, is constructed as $V={\displaystyle \frac{1}{2}}{\varsigma }^T\varsigma +{\displaystyle \frac{1}{2\eta }}{\widetilde{𝜛}}^T\widetilde{𝜛}$, and its derivative is obtained. Equations (11) and (12) are substituted into it to obtain

$$\begin{array}{l}\dot{V}={\displaystyle \frac{1}{2}}{\varsigma }^T\varsigma +{\displaystyle \frac{1}{2\eta }}{\widetilde{𝜛}}^T\widetilde{𝜛}\\ =\varsigma \dot{\varsigma }+{\displaystyle \frac{1}{\eta }}\left[{\displaystyle \frac{1}{\xi (x)}}(\dot{\varsigma }+\sigma \varsigma -\epsilon (x,u))\right]\cdot (-\eta \varsigma \xi (x))\\ =-\sigma {\varsigma }^2+\varsigma \epsilon (x,u)\\ =-{\displaystyle \frac{\sigma }{2}}{\varsigma }^2+{\displaystyle \frac{1}{2\sigma }}{\epsilon }^2(x,u)-{\left[\sqrt{{\displaystyle \frac{\sigma }{2}}}\varsigma -\sqrt{{\displaystyle \frac{1}{2\sigma }}}\epsilon (x,u)\right]}^2\\ \le -{\displaystyle \frac{\sigma }{2}}{\varsigma }^2+{\displaystyle \frac{1}{2\sigma }}{\epsilon }^2(x,u)\end{array}$$

(13)

From the above formula, when $\left|\varsigma \right|>{\displaystyle \frac{\epsilon }{\sigma }}$, $\dot{V}$ is negative definite. Since $\epsilon \left(x,u\right)$ can be arbitrarily small, there must be a value of $\epsilon$ that makes $\dot{V}<0$, so the error uniform boundedness of the fuzzy disturbance observer is proved.

4. Adaptive Terminal Sliding Mode Control Design

The nonsingular terminal sliding mode controller overcomes the singularity issue of the traditional terminal sliding mode controller and addresses the slow convergence speed when the error is small. In this paper, the controller is designed using the nonsingular terminal sliding mode method, and a novel adaptive exponential reaching law is employed to formulate the switching control term. This approach enhances the convergence speed of the system towards the sliding mode surface. An error system is established as follows:

$$\begin{gathered} \dot{e}=\dot{q}-{\dot{q}}_d \\ \ddot{e}=\ddot{q}-{\ddot{q}}_d \end{gathered}$$

(14)

Substitute this into Equation (4) to obtain:

$$\ddot{e}=f\left(x\right)+b\left(x\right)u+T_d\left(x,d\right)-{\ddot{q}}_d$$

(15)

For the above error system, the nonsingular terminal sliding mode surface is designed as follows:

$$s=e+{\alpha }^{-1}{e}^{g/h}+{\beta }^{-1}{\dot{e}}^{p/q}$$

(16)

of which $\alpha ,\beta \in R^{+}$, $g,h,p, \mathrm{and} q$ are positive odd numbers, and $1<p/q⟨2,g/h⟩p/q$. As shown in Equation (16), compared with the TSMC, since the index of $e_2$ is greater than 1, the negative index term caused by derivation is avoided. Moreover, the singularity problem is solved. Relative to a conventional nonsingular terminal SMC, the higher-order component ${\alpha }^{-1}{e}_1^{g/h}$ of error $e_1$ is added, so when the system state deviates significantly, the dominant higher-order error term $e_1$ enhances convergence speed. Near equilibrium, that is, $e_1<1$, the higher-order term becomes negligible, and its convergence speed is equivalent to the NTSMC. During sliding mode operation along the designed manifold, Equation (16) can be expressed as $e_2=-{\beta }^{q/p}{e}_1^{q/p}$ (ignoring the higher-order term of error $e_1$). At this time, the index of $e_1$ remains below unity, while the inverse error magnitude exceeds that of a linear sliding surface under identical conditions, thereby accelerating convergence. From Equation (16), the sliding function is formulated as $s$, while the equivalent control rate $u_{eq}$ is obtained by parallel vertical (15):

$$u_{eq}=-{\displaystyle \frac{1}{b\left(x\right)}}\left[\beta {\displaystyle \frac{q}{p}}{\dot{e}}^{2-{\displaystyle \frac{p}{q}}}\left(1+{\alpha }^{-1}{\displaystyle \frac{g}{h}}{e}^{{\displaystyle \frac{g}{h}}-1}\right)+f\left(x\right)+T_d\left(x,d\right)-{\ddot{q}}_d\right]$$

(17)

Replace the disturbance $T_d$ with the fuzzy disturbance observation value $\Omega$:

$$u_{eq}=-{\displaystyle \frac{1}{b\left(x\right)}}\left[\beta {\displaystyle \frac{q}{p}}{\dot{e}}^{2-p/q}\left(1+{\alpha }^{-1}{\displaystyle \frac{g}{h}}{e}^{g/h-1}\right)+f\left(x\right)+\Omega (x,u|{\widehat{𝜛}}^{*})+\epsilon \left(x,u\right)-{\ddot{q}}_d\right]$$

(18)

In the context of system (4), the switching control component of the sliding mode controller is designed using an exponential reaching strategy:

$$\dot{s}=-\epsilon \mathit{sgn}(x)-kx(k>0,\epsilon >0)$$

(19)

The reaching strategy comprises two components: an exponentially decaying term and a constant-velocity approaching term, and its coefficient k, ε has no self-adjusting function. Its convergence characteristics cannot achieve the best performance for different position state variables. While the switching control component guarantees sliding mode establishment, it simultaneously induces chattering effects within the system. This study introduces an adaptive variable-rate exponential reaching law to optimize convergence dynamics:

$$\dot{s}=-{\displaystyle \frac{\epsilon }{1+c{||e||}_1}}\mathit{sgn}(s)-\left(k+c{||e||}_1\right)s$$

(20)

Of which ${||x||}_1={{\displaystyle \sum }}_{i=1}^n\left|x_i\right|$ represents the first-order norm of the system’s state variable: $k>0,\epsilon >0,c>0,n>0$.

The proposed adaptive exponential law incorporates the first-order norm of state variables, dynamically tuning both exponential decay and constant-velocity approach rates based on the proximity to equilibrium. In the formula, the instantaneous solution of the exponential approach term is $s=s\left(0\right)e^{-\left(k+c{||x||}_1\right)t}$. When ${||x||}_1$ is large, and the exponential decay rate is much greater than that in Equation (19), the convergence time can be significantly shortened. At this time, the approach rate $\epsilon {\displaystyle \frac{1}{1+c{||x||}_1}}$ of the isokinetic approach term is far less than $\epsilon$ in Equation (19).

For small values of ${||x||}_1$, the adaptation gain $c$ is scaled according to the coefficient to shorten the sliding mode arrival time and reduce the system chattering. As the system stabilizes and the state variable $x$ asymptotically approaches zero, the adaptive law transitions to a standard exponential reaching mode. Using the reaching law to design a nonsingular terminal sliding mode controller, the switching control term $u_{sw}$ is derived as

$$u_{sw}=-{\displaystyle \frac{1}{b\left(x\right)}}\left[{\displaystyle \frac{\epsilon }{1+c{||e||}_1}}\mathit{sgn}(s)+\left(k+c{||x||}_1\right)s\right]$$

(21)

To sum up, the control law designed in this paper is as follows:

$$\begin{gathered} u=u_{eq}+u_{sw} \\ =-{\displaystyle \frac{1}{b\left(x\right)}}\left[\begin{array}{c}\beta {\displaystyle \frac{q}{p}}{\dot{e}}^{2-p/q}\left(1+{\alpha }^{-1}{\displaystyle \frac{g}{h}}{e}^{g/h-1}\right)+f\left(x\right)+\Omega (x,u|{\widehat{𝜛}}^{*})\\ +\epsilon \left(x,u\right)-{\ddot{q}}_d+{\displaystyle \frac{\epsilon }{1+c{||e||}_1}}\mathit{sgn}(s)+\left(k+c{||e||}_1\right)s\end{array}\right] \end{gathered}$$

(22)

The control system structure is shown in Figure 1:

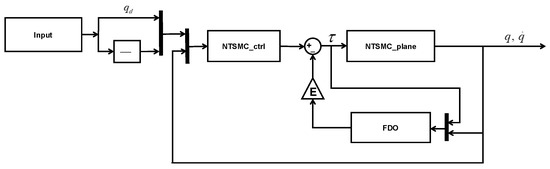
Figure 1. Control system structure.

5. Finite Time Convergence Analysis

Theorem 1. 

Applying the simplified dynamic model, Equation (4), the fuzzy interference disturbance observer, Equation (10), is integrated to estimate uncertainties, a nonsingular terminal sliding manifold (Equation (16)) is designed to eliminate singularities, convergence dynamics are governed by Equation (19), and control inputs defined in Equation (22) jointly ensure stability is chosen under specific parameter conditions for both controller and observer and sliding variables and estimation errors converge to zero within finite time.

Proof. 

Take the Lyapunov function:

$$V={\displaystyle \frac{1}{2}}{s}^{T}s$$

(23)

The derivative of $V,$ we calculate:

$$\begin{gathered} \dot{V}=s\dot{s}=s\left(\dot{e}+{\alpha }^{-1}{\displaystyle \frac{g}{h}}{e}^{{\displaystyle \frac{g}{h}}-1}\cdot \dot{e}+{\beta }^{-1}{\displaystyle \frac{p}{q}}{\dot{e}}^{p/q-1}\cdot \ddot{e}\right) \\ =s\left[\left(1+{\alpha }^{-1}{\displaystyle \frac{g}{h}}{e}^{g/h-1}\right)\dot{e}+{\beta }^{-1}{\displaystyle \frac{p}{q}}{\dot{e}}^{p/q-1}\left(f\left(x\right)+b\left(x\right)u+T_d\left(x,d\right)-{\ddot{q}}_d\right)\right] \end{gathered}$$

(24)

Substituting into Equation (22) gives the following:

$$\begin{gathered} \dot{V}=s\left[\left(1+{\alpha }^{-1}{\displaystyle \frac{g}{h}}{e}^{g/h-1}\right)\dot{e}+{\beta }^{-1}{\displaystyle \frac{p}{q}}{\dot{e}}^{p/q-1}\left(f\left(x\right)+b\left(x\right)u+T_d\left(x,d\right)-{\ddot{q}}_d\right)\right. \\ +{\beta }^{-1}{\displaystyle \frac{p}{q}}{\dot{e}}^{p/q-1}\left(\begin{array}{c}\beta {\displaystyle \frac{q}{p}}{\dot{e}}^{2-p/q}\left(1+{\alpha }^{-1}{\displaystyle \frac{g}{h}}{e}^{g/h-1}\right)+f\left(x\right)+\Omega (x,u|{\widehat{𝜛}}^{*})\\ +\epsilon \left(x,u\right)-{\ddot{q}}_d+{\displaystyle \frac{\epsilon }{1+c{e}_1}}\mathit{sgn}(s)+\left(k+c{||e||}_1\right)s\end{array}\right) \\ =-{\beta }^{-1}{\displaystyle \frac{p}{q}}{\dot{e}}^{p/q-1}\left({\displaystyle \frac{\epsilon }{1+c{||e||}_1}}\left|s\right|+\left(k+c{||e||}_1\right)s^2\right) \end{gathered}$$

(25)

From Equation (25), therefore, converges in finite time, i.e., converges to zero in finite time. □

6. Simulation Analysis

To verify the effectiveness of the above-proposed control strategy, the designed sliding mode control method is applied to the trajectory tracking problem of a 2-DOF rigid body robotic arm, and the simulation object of the robotic arm established is shown in Figure 2.

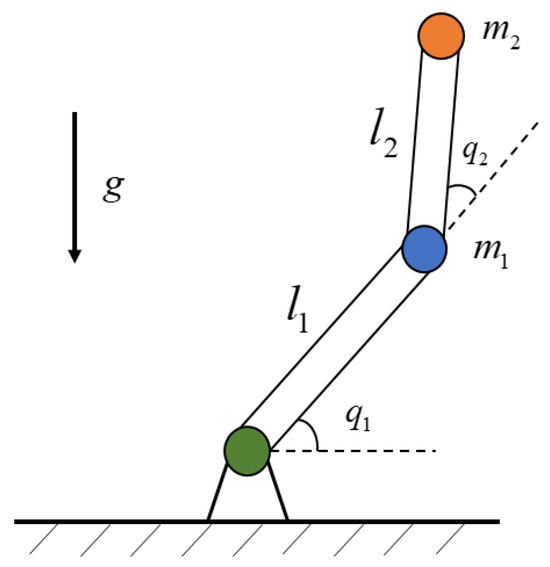
Figure 2. Schematic diagram of robotic arm (2-DOF).

In the figure, $l_1=1 \mathrm{m},l_2=0.8 \mathrm{m}$ is the length of the linkage of the robotic arm, $m_1=0.5 \mathrm{kg},m_2=1.5 \mathrm{kg}$ is the concentrated mass of the linkage and the load, and $J_1=5 \mathrm{kgm}, J_2=5 \mathrm{kgm}$ is the inertia of the linkage. Then, the parameter matrix of the robotic arm dynamics equation is as follows:

$$\begin{gathered} q=\left[\begin{array}{c}{q}_1\\ q_2\end{array}\right]\hspace{1em}\tau =\left[\begin{array}{c}{\tau }_1\\ {\tau }_2\end{array}\right] \\ M(q)=\left[\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right]\hspace{1em}C(q,\dot{q})=\left[\begin{array}{c}-m_2{l}_1{l}_2\sin (q_2){\dot{q}}_1^2-2m_2{l}_1{l}_2\sin (q_2){\dot{q}}_1{\dot{q}}_2\\ m_2{l}_1{l}_2\sin (q_2){\dot{q}}_2^2\end{array}\right] \\ G(q)=g\hspace{0.17em}\hspace{0.17em}\cdot \hspace{0.17em}\hspace{0.17em}\left[\begin{array}{c}(m_1+m_2)l_1\cos (q_2)+m_2{l}_2\cos (q_1+q_2)\\ m_2{l}_2\cos (q_1+q_2)\end{array}\right] \end{gathered}$$

(26)

Among them:

$$\begin{array}{c}{m}_{11}=\left(m_1+m_2\right)l_1^2+m_2{l}_2^2+2m_2{l}_1{l}_2\mathit{cos}(q_2)+J_1,\hfill \\ m_{12}=m_{21}=m_2{l}_2^2+m_2{l}_1{l}_2\mathit{cos}(q_2),\hfill \\ m_{22}=m_2{l}_2^2+J_2,\hfill \end{array}$$

(27)

Considering the joint friction, the two joint perturbation moments are designed as step-type square wave moments:

$$\rho \left(t\right)=\left[\begin{array}{c}{\rho }_1\\ {\rho }_2\end{array}\right]=\left[\begin{array}{c}{\eta }_{v1}{\dot{q}}_1+{\mu }_{c1}\mathit{sgn}({\dot{q}}_1)\\ {\eta }_{v2}{\dot{q}}_2+{\mu }_{c2}\mathit{sgn}({\dot{q}}_2)\end{array}\right]$$

(28)

The desired trajectory of the two joints is

$$q_d=\left[\begin{array}{c}{q}_{d1}\\ q_{d2}\end{array}\right]=\left[\begin{array}{c}\mathit{sin}(0.2\pi t)\\ \mathit{sin}(0.2\pi t)\end{array}\right]$$

(29)

The simulation model is constructed in MATLAB/SIMULINK, integrating the fuzzy disturbance observer (Equation (5)) and nonsingular terminal sliding mode controller (Equation (24)). The parameters are adjusted multiple times based on both theoretical and practical considerations. Key parameters include the fuzzy observer gain vector $r=250$ and a unit feed-forward matrix $E_2$. The feed-forward gain matrix is taken to be the unit array, the coefficient matrix for the nonsingular terminal sliding manifold $C_1=\left[\begin{array}{cc}0.9& 0\\ 0& 0.9\end{array}\right]$, $\beta =5,\alpha =3$, which is denoted by the controller as FDO-NTSMC. The simulation configuration employs the ode45 solver with a 10 s variable-step duration. Initial conditions include joint angles as $q_1=q_2=0.1$ and the joint angular velocity as ${\dot{q}}_1={\dot{q}}_2=0$.

To highlight the superiority of this designed controller system (FDO-NTSMC), it is compared with the nonsingular terminal sliding mode controller integrated with a nonlinear disturbance observer (NDO-NTSMC) and the conventional PD controller augmented by a fuzzy disturbance observer (FDO-PD), respectively, which are described as follows:

NDO-NTSMC: To evaluate disturbance estimation and chattering suppression via the fuzzy observer and to enhance trajectory tracking performance, a nonsingular terminal sliding mode controller is employed, whose controller output is

$$\tau ={\tau }_0+u_1+u_2$$

(30)

Among them:

$${\tau }_0=C\left(q,\dot{q}\right)+G\left(q\right)+M\left(q\right){\ddot{q}}_d$$

(31)

$$u_1=-{\displaystyle \frac{\alpha }{\beta }}M\left(q\right)C_1^{-1}diag\left({\dot{e}}^{2-\beta /\alpha }\right)$$

(32)

$$u_2=-\Gamma \cdot {\displaystyle \frac{{[s^T{C}_1\mathit{diag}\left({\dot{e}}^{\beta /\alpha -1}\right)M{(q)}^{-1}]}^T||s||}{{||s^T{C}_1\mathit{diag}\left({\dot{e}}^{\beta /\alpha -1}\right)M{(q)}^{-1}||}^2}}||\times C_1\mathit{diag}\left({\dot{e}}^{\beta /\alpha -1}\right)M{(q)}^{-1}||$$

(33)

FDO-PD: For comparison, to reflect the tracking effect of the nonsingular terminal sliding mode controller, the PD control law is taken as

$${\tau }_{PD}=\left[\begin{array}{c}{\tau }_{PD1}\\ {\tau }_{PD2}\end{array}\right]=\left[\begin{array}{c}{k}_P{e}_1+k_D{\dot{e}}_1\\ k_P{e}_2+k_D{\dot{e}}_2\end{array}\right]$$

(34)

where the proportional differential gains are $k_P=400 \mathrm{and} k_D=100$, respectively. The NDO control law is taken as Equation (5), and other parameters remain unchanged.

Comparative simulation results are summarized below: the observed values of FDO and NDO for square wave interference are shown in Figure 3, the effects of position tracking and velocity tracking are shown in Figure 4, the positional tracking error is shown in Figure 5, and the controller output torque is shown in Figure 6.

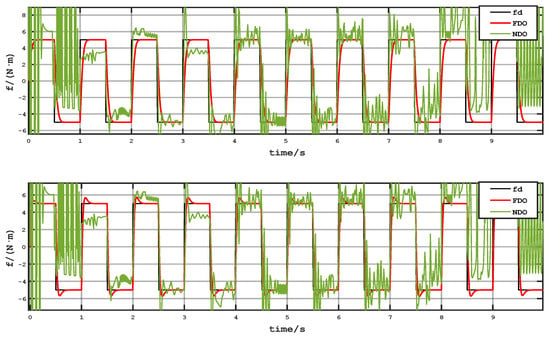
Figure 3. Effect of FDO and NDO observation.

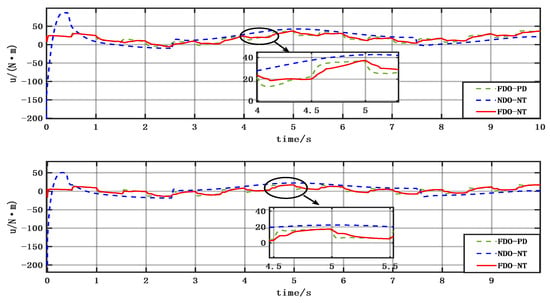
Figure 4. Controller output torque.

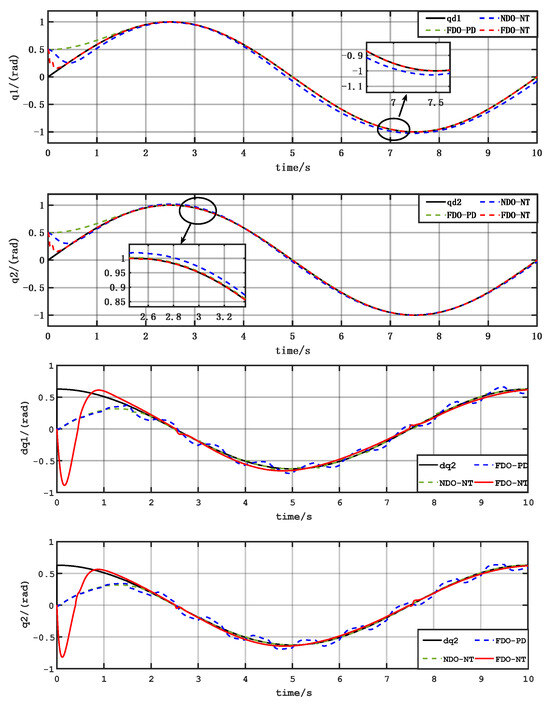
Figure 5. Trajectory tracking.

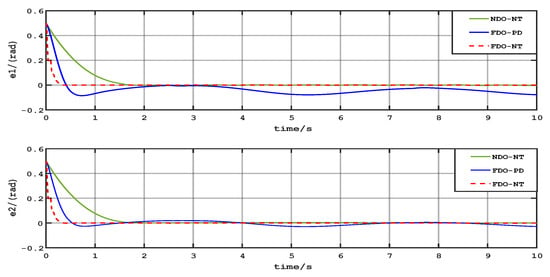
Figure 6. Tracking error.

Figure 3 demonstrates the fuzzy observer’s superior capability in tracking square-wave disturbances; the disturbance moment can be converged quickly after the sudden change, the output is smooth, and the overshoot is slight, while the output of the NDO observer is more jittery. The convergence of the early stage is slower, and only in the middle of the section can the approximate value of the disturbance moment and the value of the latter section be dispersed and not be converged, which indicates that the nonlinear disturbance observer only has an observation effect on the slow time-varying, small-amplitude disturbances and cannot play the role of observation for the large-scale, sudden change of disturbance.

Figure 4 compares the output torques of the three controllers, revealing that the FDO-NTSMC designed in this paper reacts quickly to the perturbations, such as changes in joint direction and adding interference moments, and has a smooth moment output. From the local zoomed-in diagram, when the direction of joint rotation changes, the output moment of the FDO-PD exhibits an obvious jitter vibration phenomenon. In contrast, the moment output by the FDO-NTSMC is relatively smooth, indicating that the addition of the interference observer can effectively reduce the system’s jitter vibration. The NDO-NTSMC experiences output saturation at the initial moment, while the FDO-NTSMC has a faster convergence speed and a minor output overshoot.

Trajectory tracking results indicate rapid convergence of the proposed FDO-NTSMC. Relative to the NDO-NTSMC, thanks to the better observation effect of the FDO on the interference, the robotic arm system for tracking the target trajectory of the interference resistance is better. After the FDO-PD controller was debugged multiple times to obtain the optimal gain values, there were still significant fluctuations after the system stabilized. In terms of the final tracking performance, the FDO-NTSMC showed better tracking results.

Figure 6 visually confirms the faster convergence of the FDO-NTSMC and minimizes the steady-state error compared to the other two controllers. The steady-state error is reduced by 40%, which effectively improves the system’s tracking accuracy. The disturbance torque is almost unaffected by the disturbance torque, which indicates that the control method has good robustness.

Root mean square error (RMS) is adopted to quantify control accuracy, defined as

$$E\left(e\right)={\left({\displaystyle \frac{1}{N}}{\displaystyle \sum }_{i=1}^n{e}_i^2\right)}^{1/2}$$

(35)

where $N$ is the sample count, and initial misalignment between the desired trajectory and robotic arm angles introduces significant error, impacting RMS calculations independently of the controller action. The error size is sampled from the seconds, and the total number of samples is 641. Table 1 summarizes the results, showing 97.28% and 98.28% reductions in RMS tracking errors for the FDO-NTSMC compared to the NDO-PD, and the mean square value decreases by 73.73% and 66.64%, respectively, compared with the NDO-NTSMC. From the above analysis, it can be concluded that the FDO-NTSMC can effectively reduce the tracking error and improve the tracking accuracy of the robotic arm on the target trajectory.

Table 1. Root mean square tracking errors for three controllers.

Controllers	Joint 1	Joint 2
FDO-NTSMC	0.000424	0.000424
FDO-PD	0.024595	0.015600
NDO-NTSMC	0.001614	0.001271

7. Experimental Analyses

Experimental validation on a physical robotic arm platform confirms the efficacy of the FDO-NTSMC. The experimental platform includes the host computer, the robotic arm body, and the driver. By writing the controller module in the host computer Simulink, the torque value is sent to the driver through the serial port. The driver converts the torque value into the current value and sends it to the joint motor through the CAN bus to drive the robot arm, while joint angles are measured by motor encoders and fed back to the controller at 3 ms intervals. Figure 7 is the system block diagram and the experimental setup is depicted in Figure 8.

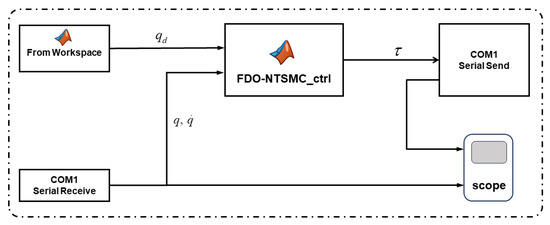
Figure 7. System block diagram.

Figure 8. Robotic arm experiment platform.

Robotic arm parameters: link masses are 2.5 kg, 2.9 kg, and 1.27 kg and lengths are(118 mm, 220 mm, and 240 mm, respectively, and only the first two joints are used in the experiment. A random initial point within the robotic arm’s workspace defines the desired trajectory. Kinematic inversion and polynomial interpolation generate desired joint trajectories, and the interpolation point information is sent to the controller once every 250 mm. The controller parameter selection is consistent with the simulation experiment, and the initial value of the angle of the two joints is 0. The experiment compares the FDO-NTSMC to the NTSMC and PD controllers and applies a step perturbation during the experiment with a size of 5 Nm and a duration of 0.5 s. The perturbation diagram is shown in Figure 3. In practical applications, high-frequency sampling feedback was implemented, and the physical experiment provided feedback at a frequency of 30 Hz. Figure 9 and Figure 10 present trajectory tracking results and the two joints control performance. The platform exhibits a 10 s startup latency. At 70 s, the trajectory errors of q1 and q2 are 0.227 rad and 0.154 rad, respectively. Take q2 as an example. At 70 s, the errors under the PD, FDO-NTSMC, and NTSMC are 0.097 rad, 0.033 rad, and 0.054 rad, respectively. The error under the FDO-NTSMC is the smallest.

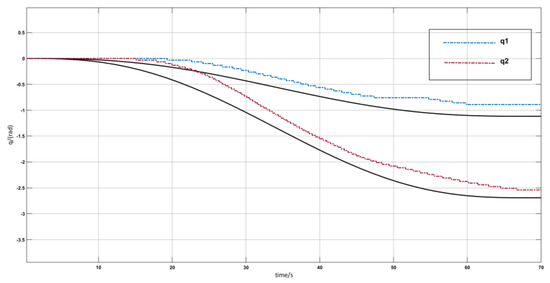
Figure 9. FDO-NTSMC trajectory tracking curve.

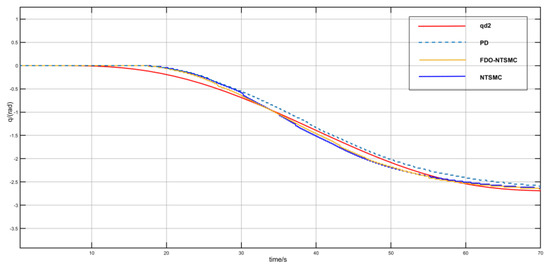
Figure 10. Joint two tracking effect.

By analyzing the experimental results, it can be seen that the FDO-NTSMC can effectively reduce the mean square error of angle tracking and improve tracking accuracy. The controller outputs of the FDO-NTSMC and NTSMC are shown in the following Figure 11:

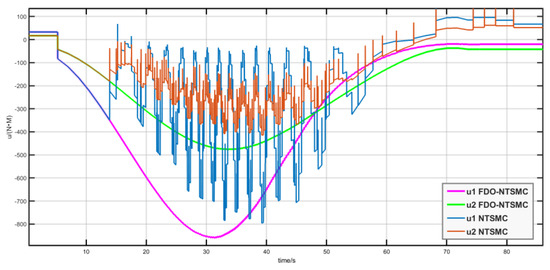
Figure 11. Controller output comparison.

The NTSMC has a large output jitter phenomenon, while the FDO-NTSMC output is smooth. Only the joint speed is larger when there is a certain jitter phenomenon, and the vibration amplitude is significantly smaller than the NTSMC. Test results show that in the face of the interference, the FDO-NTSMC relative to the NTSMC has obvious advantages. The control accuracy is higher, and it can inhibit the output jitter phenomenon, to achieve better experimental results.

8. Conclusions

A fuzzy observer-enhanced nonsingular terminal sliding mode controller is proposed for trajectory tracking, with Lyapunov stability rigorously analyzed. The algorithm improves its robustness to disturbances while ensuring the convergence of the sliding mode motion. The method approximates the internal and external disturbances of the system through a fuzzy system, gets rid of the dependence on specific model information, improves the control accuracy and disturbance resistance, reduces the output jitter of the controller, and adopts an improved nonsingular terminal sliding mode surface to enhance the speed of error convergence of the system state.

Simulations and experiments demonstrate the controller’s capability to estimate disturbances, suppress chattering, and enhance trajectory tracking speed and precision. The controller in this study is applicable to both two-degree-of-freedom and multi-degree-of-freedom robotic arms. Based on the disturbance assumptions set for the two joints in the two-degree-of-freedom case, it can be similarly applied to the other joints. In the future, methods to improve the fuzzy disturbance observer’s ability to handle discontinuous or non-stationary disturbances under extreme disturbance conditions can be explored.