Modular Multilevel Converter-Based Hybrid Energy Storage System Integrating Supercapacitors and Batteries with Hybrid Synchronous Control Strategy
Abstract
1. Introduction
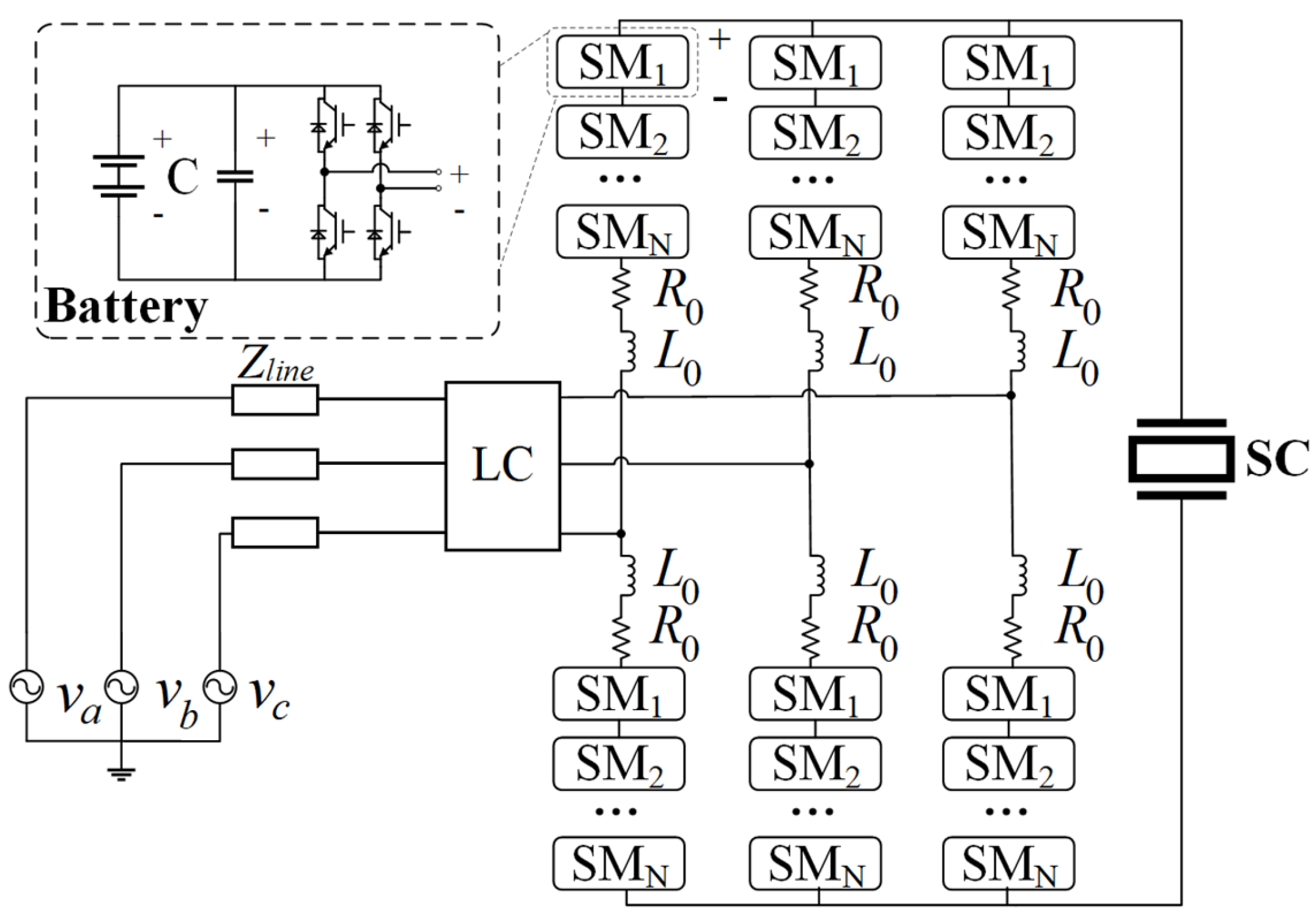
2. MMC-HESS Topology Working Principle
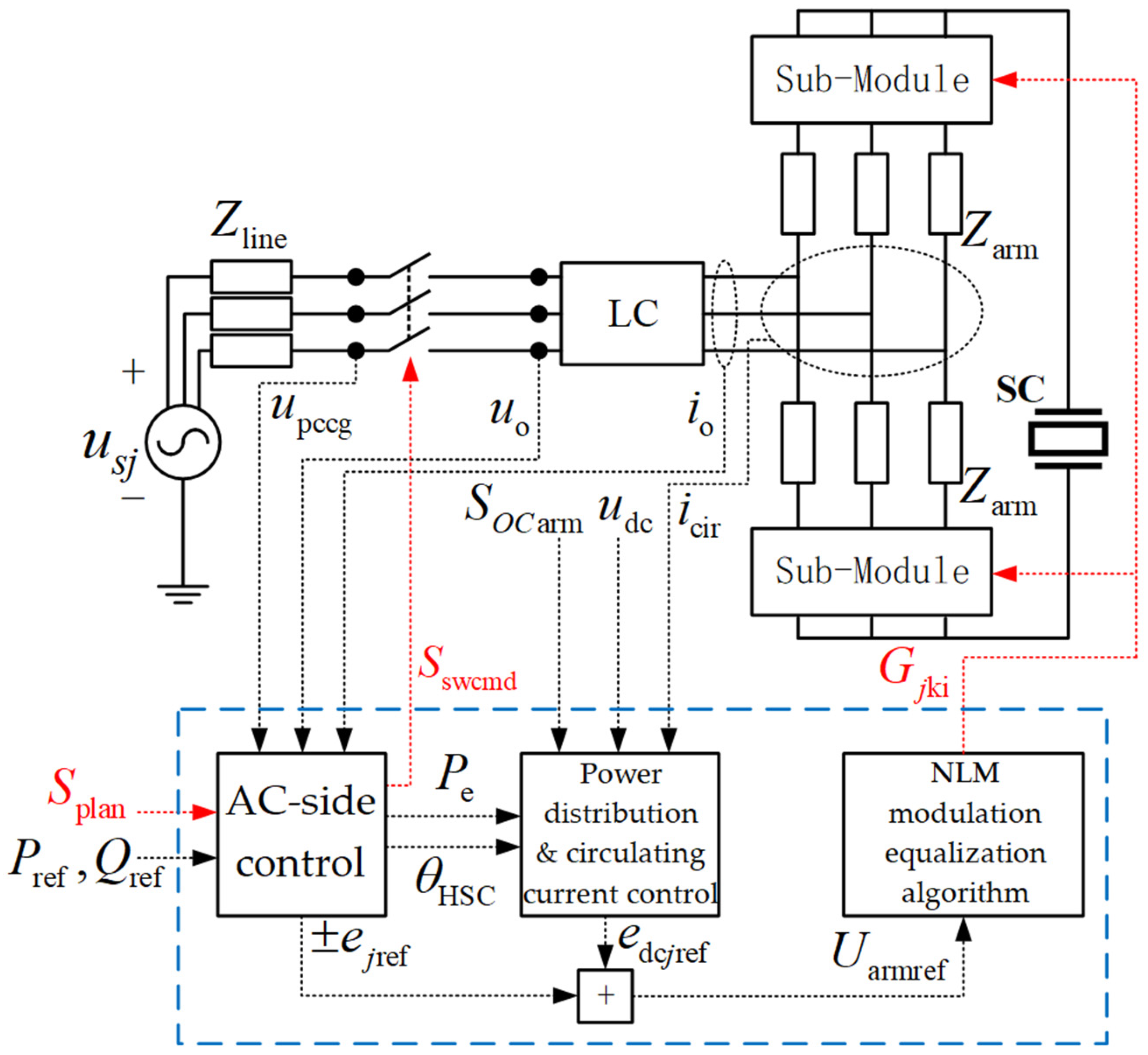
2.1. MMC-HESS Topology
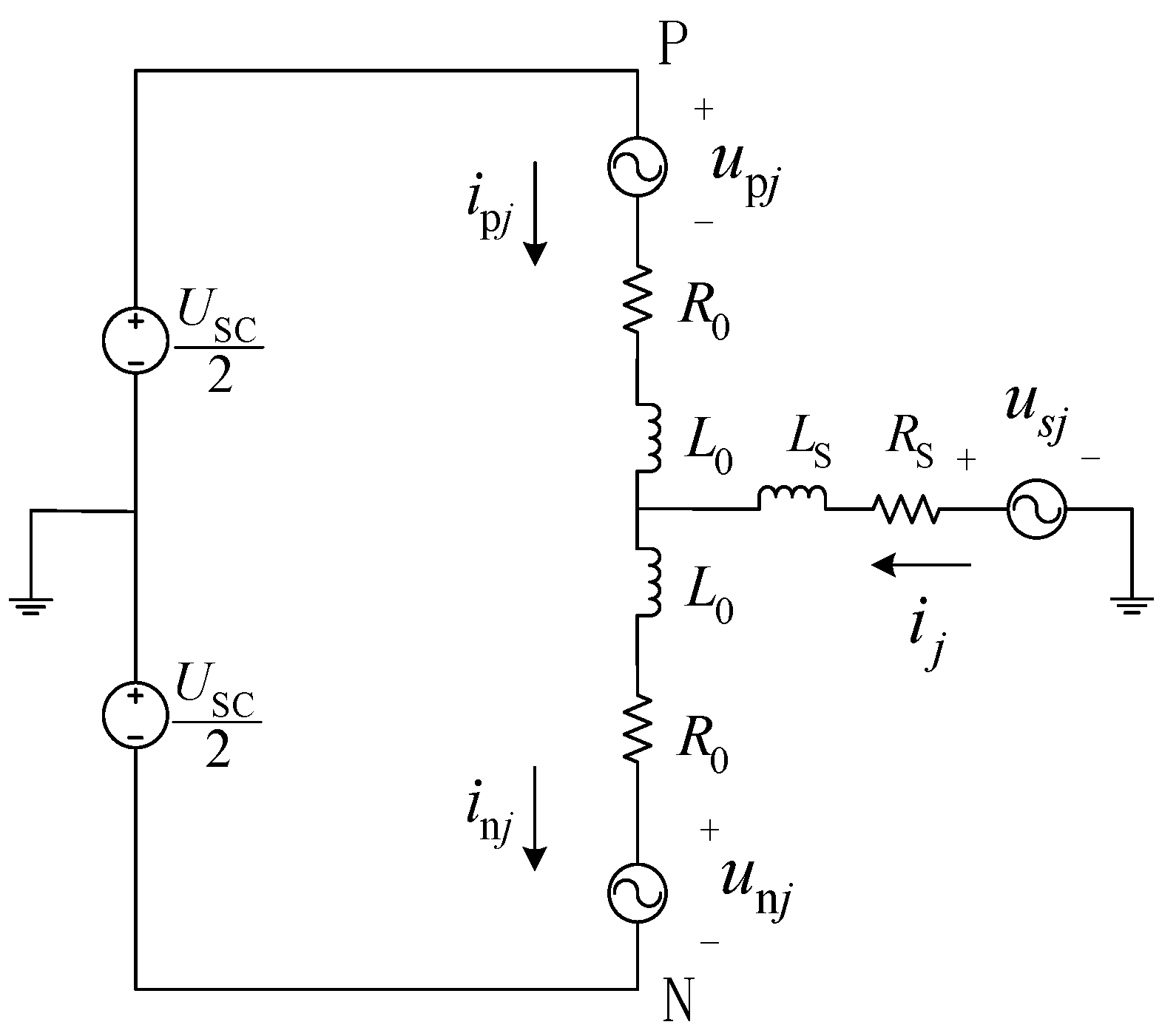
2.2. MMC-HESS Mathematical Model
2.3. Power Flow Characteristics
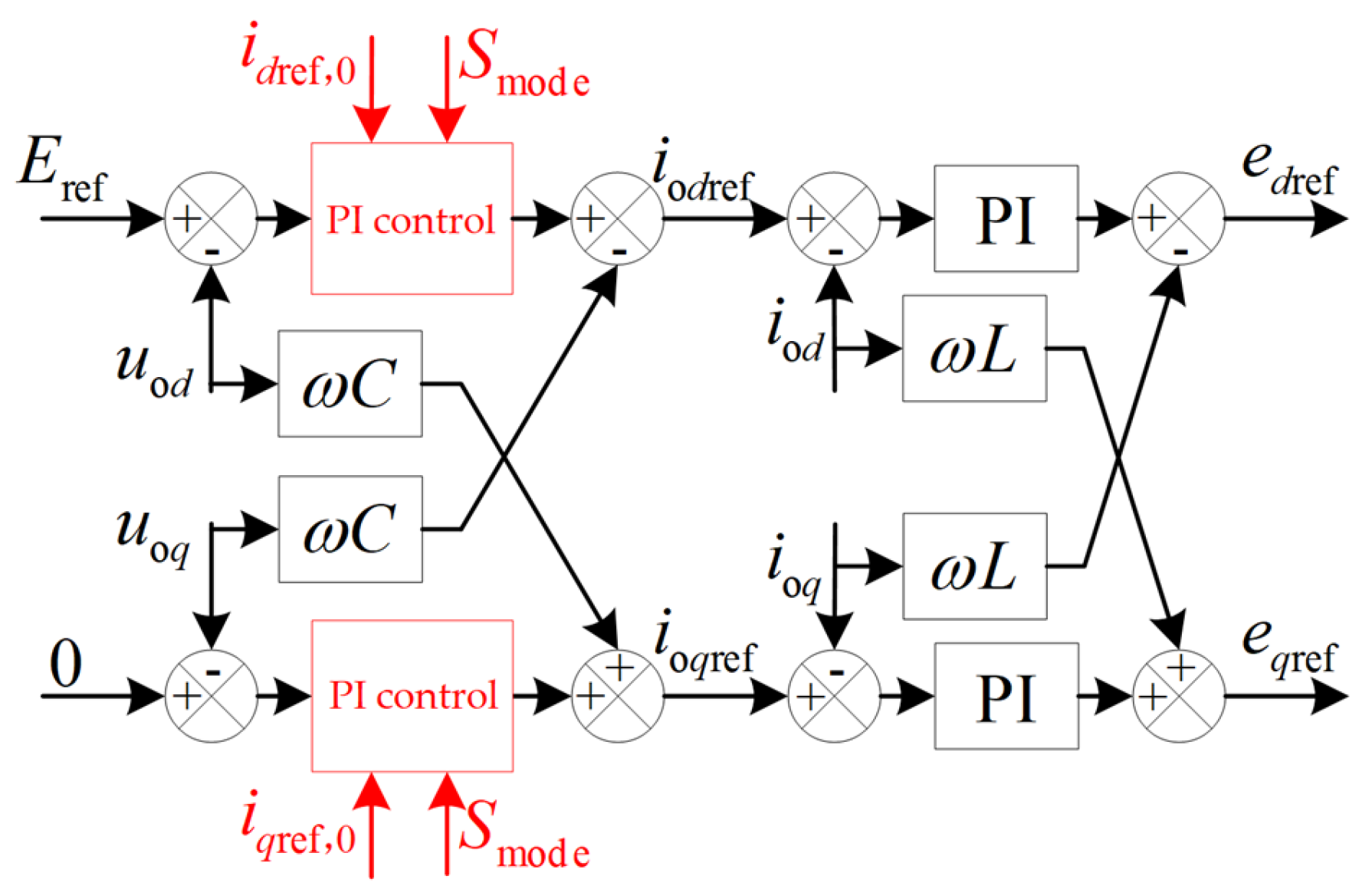
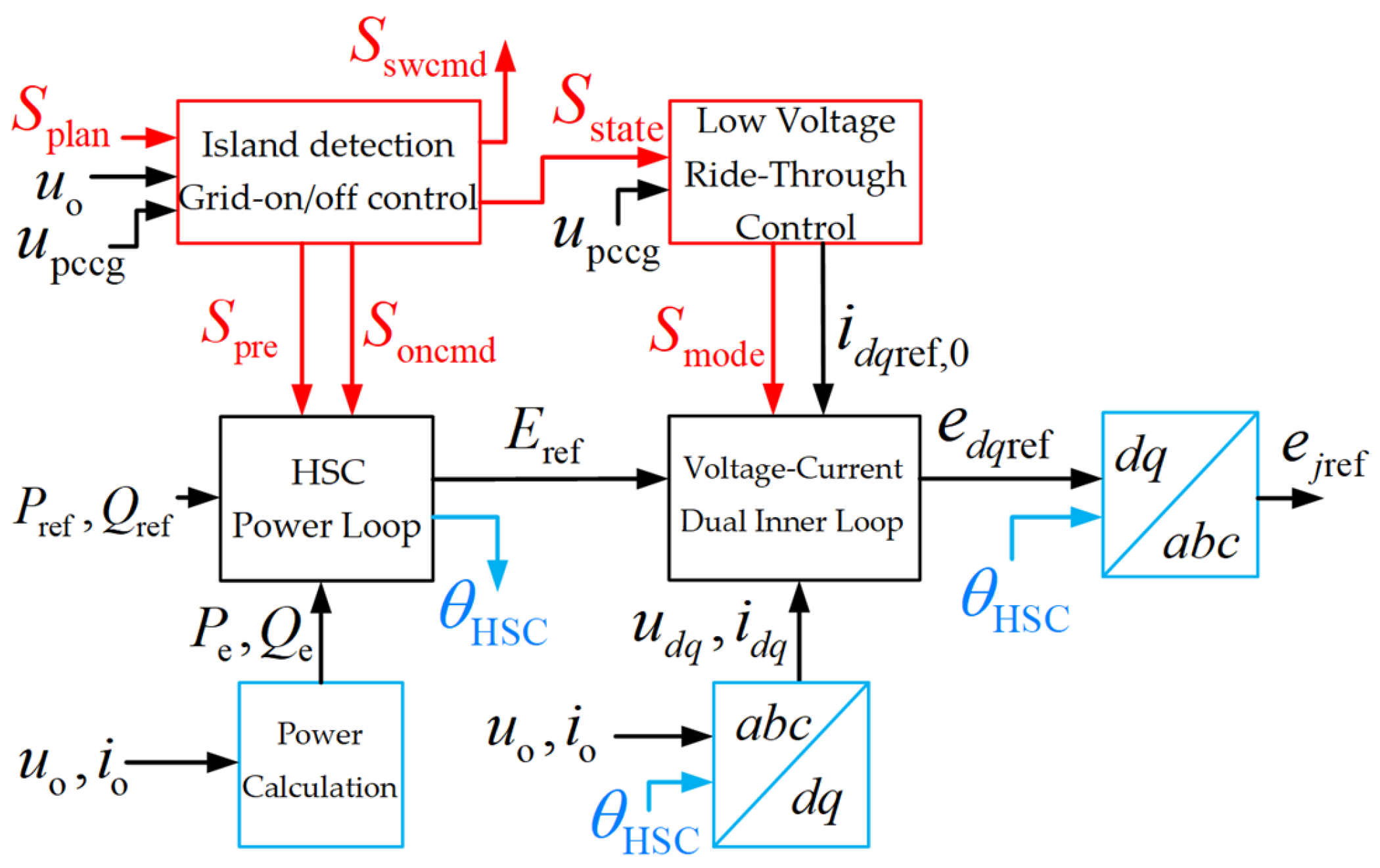
3. Hybrid Synchronous Control Strategy
3.1. AC-Side Control Strategy
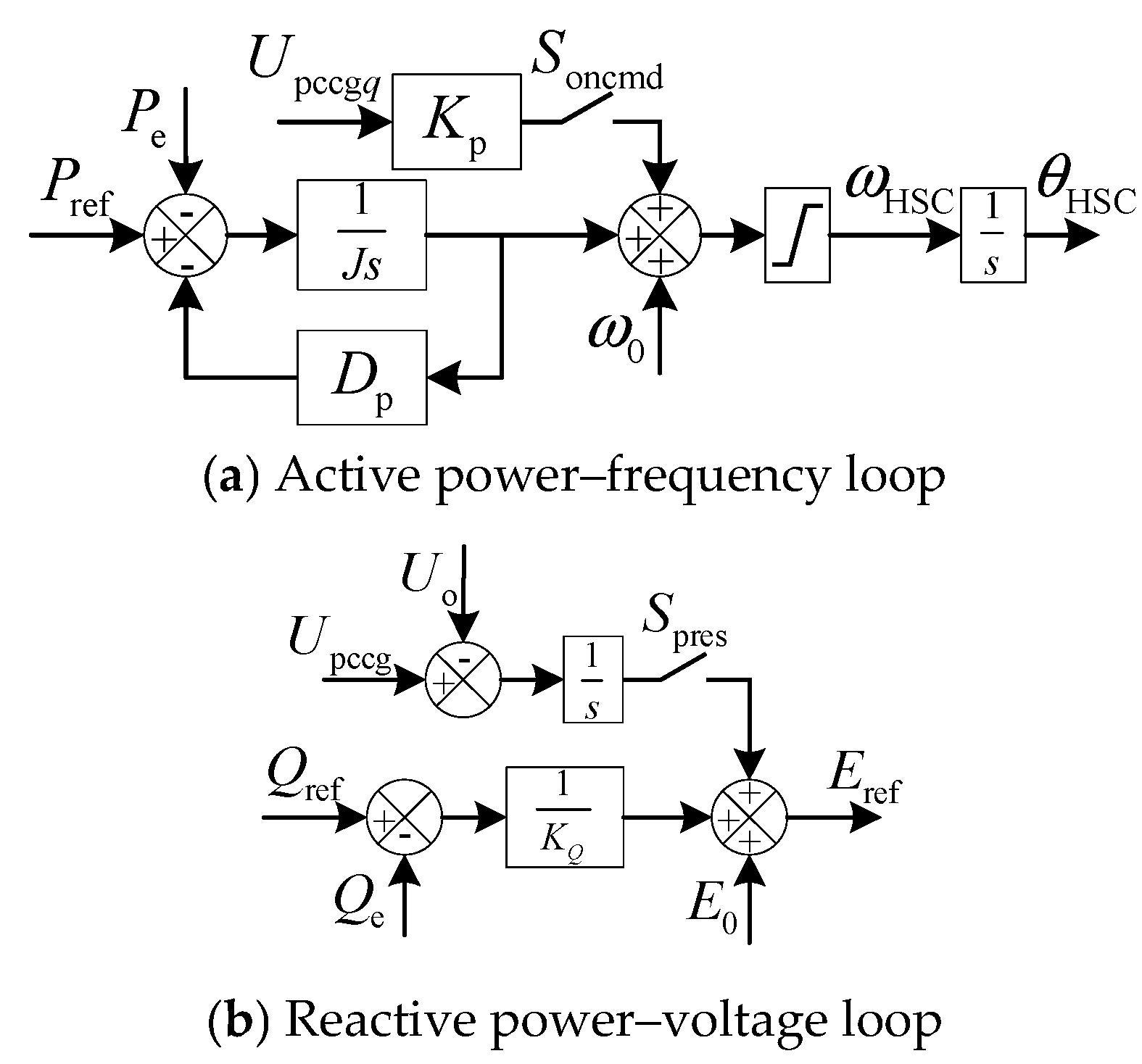
3.1.1. HSC Power Control Considering Both Grid-Connected and Off-Grid Modes
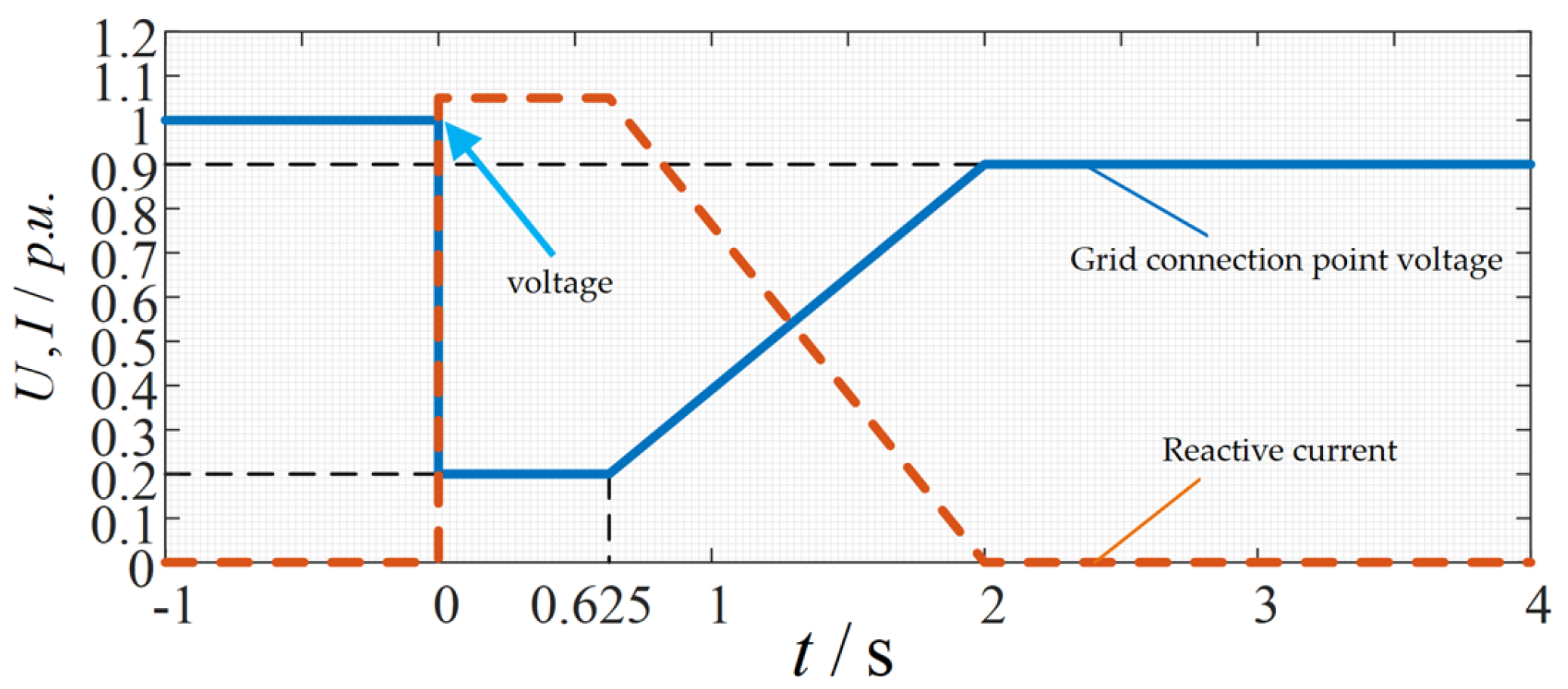
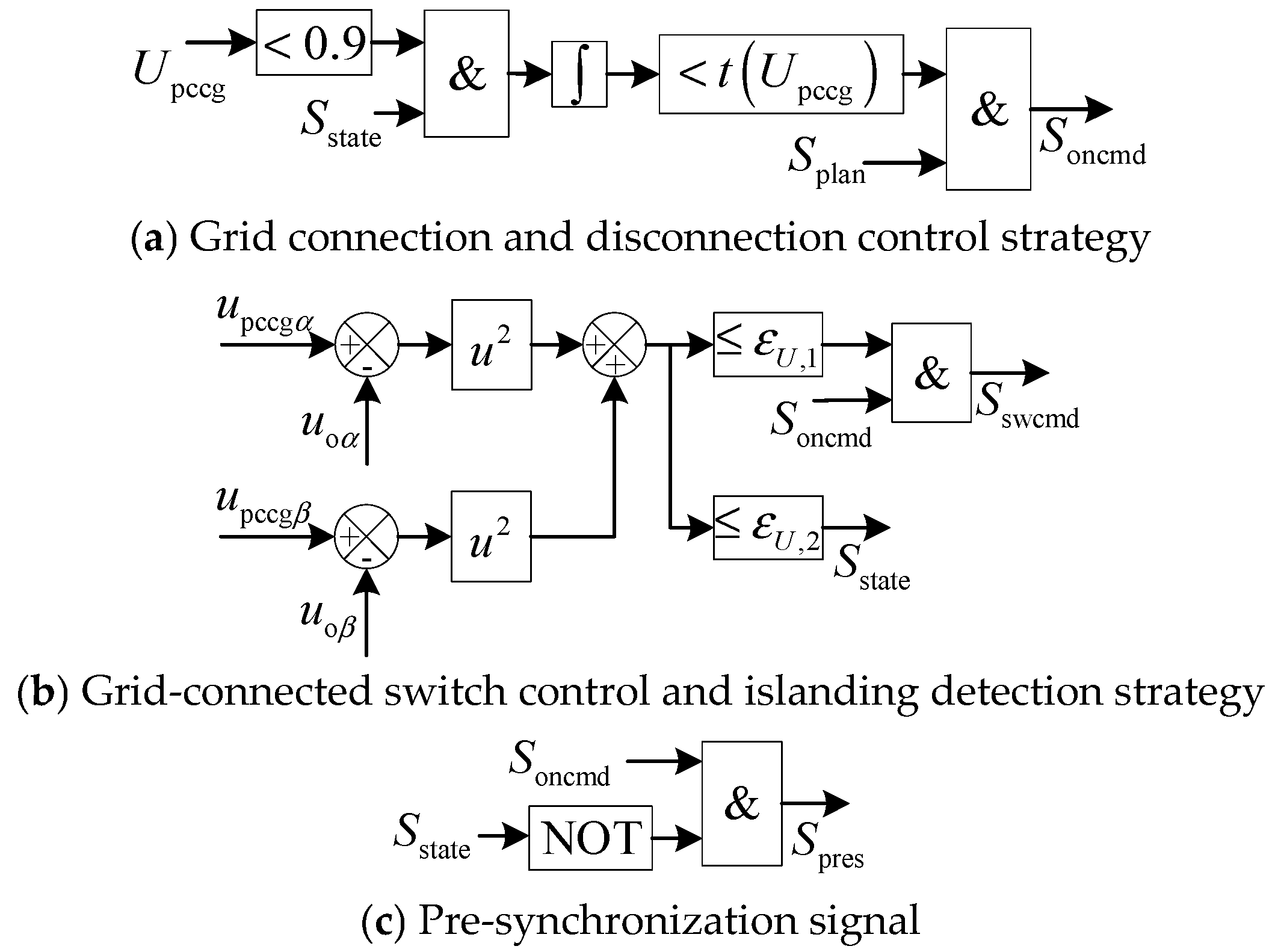
3.1.2. Low-Voltage Ride-Through Switching Strategy
3.1.3. Islanding Detection and Grid Connection/Island Operation Control
3.1.4. Overall AC-Side Control Model
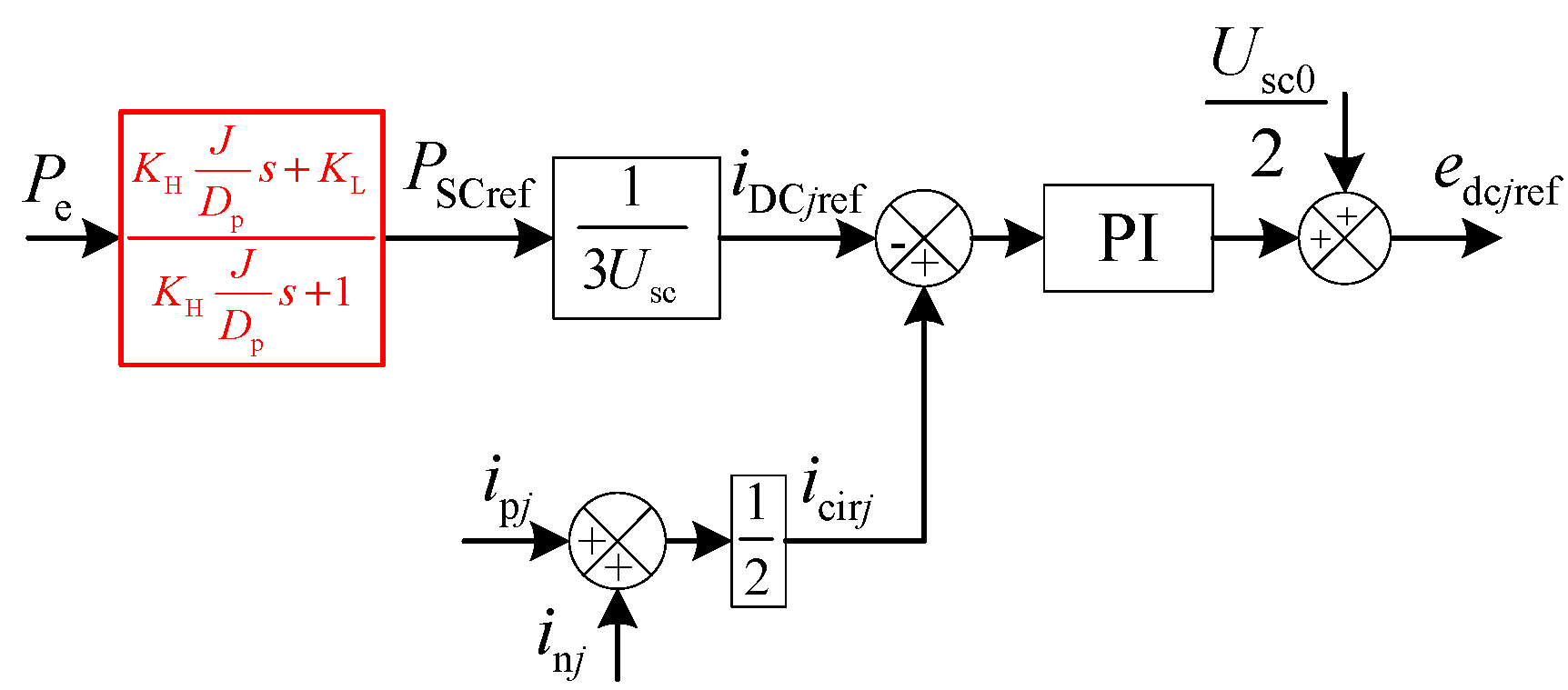
3.2. Supercapacitor Power Distribution Strategy
3.3. SOC Balancing Strategy
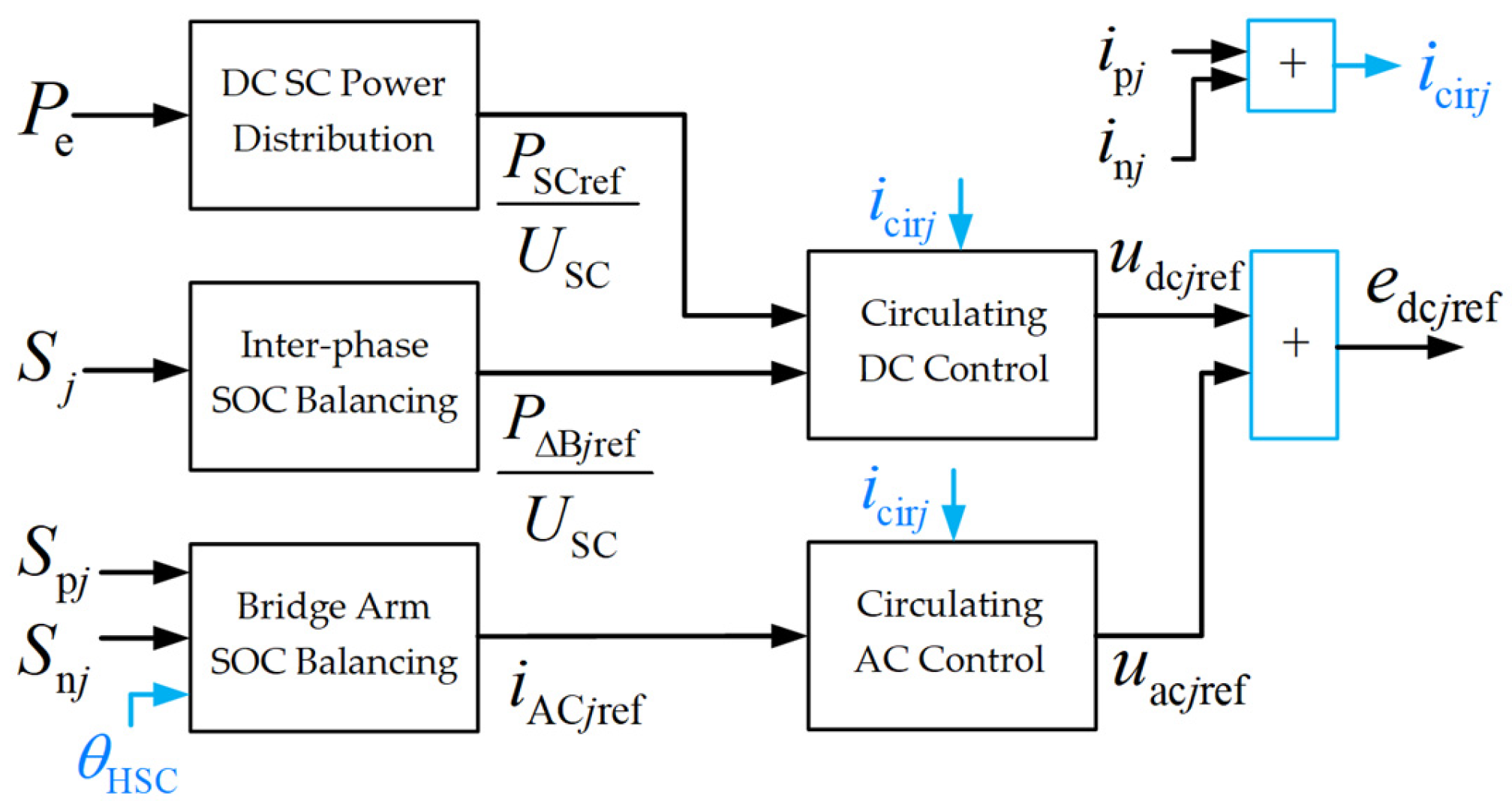
3.3.1. Bridge Arm SOC Balancing and Circulating Current Control
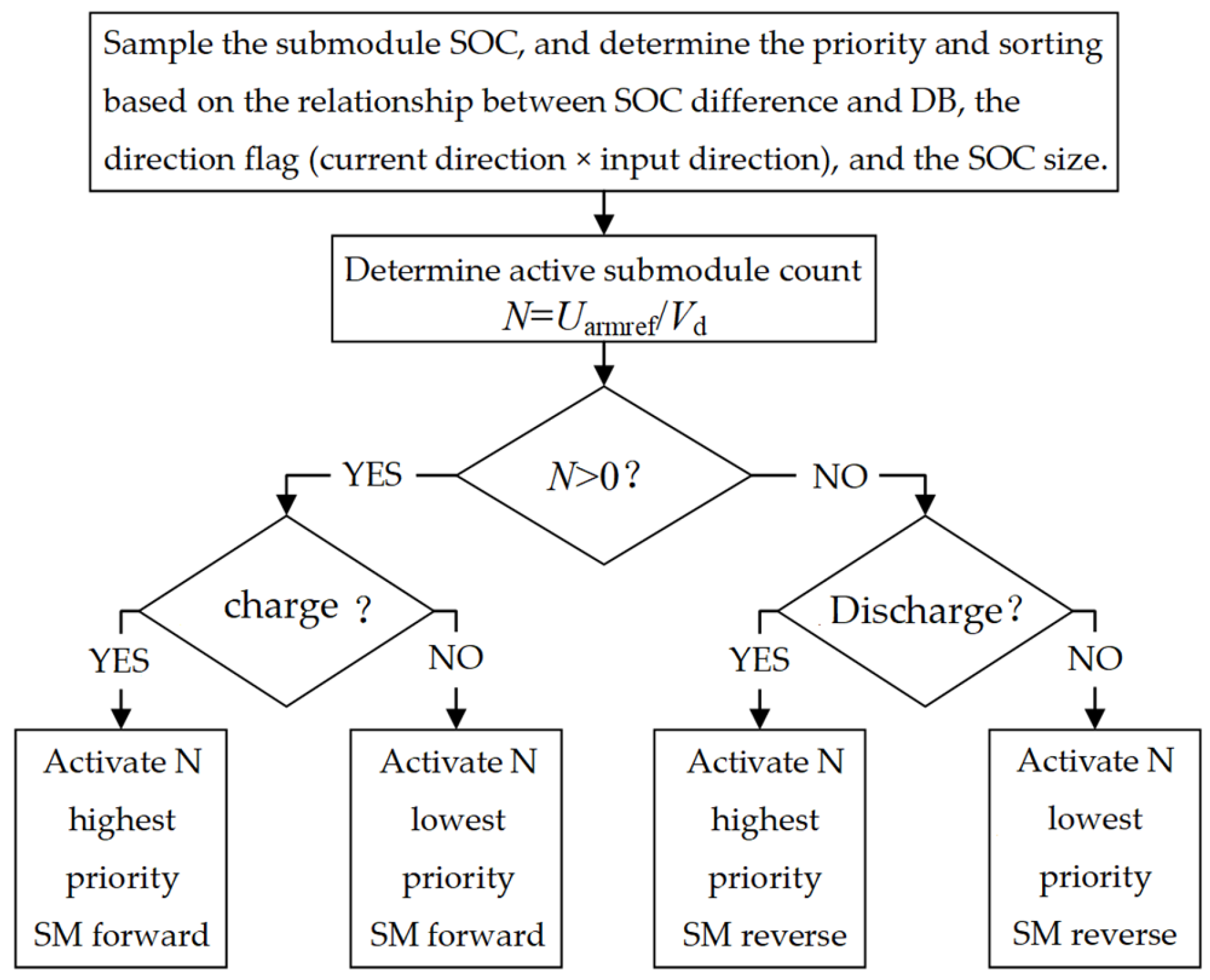
3.3.2. SOC Balancing and Voltage Modulation Within the Bridge Arm
3.4. Overall System Control Model
4. Discussion
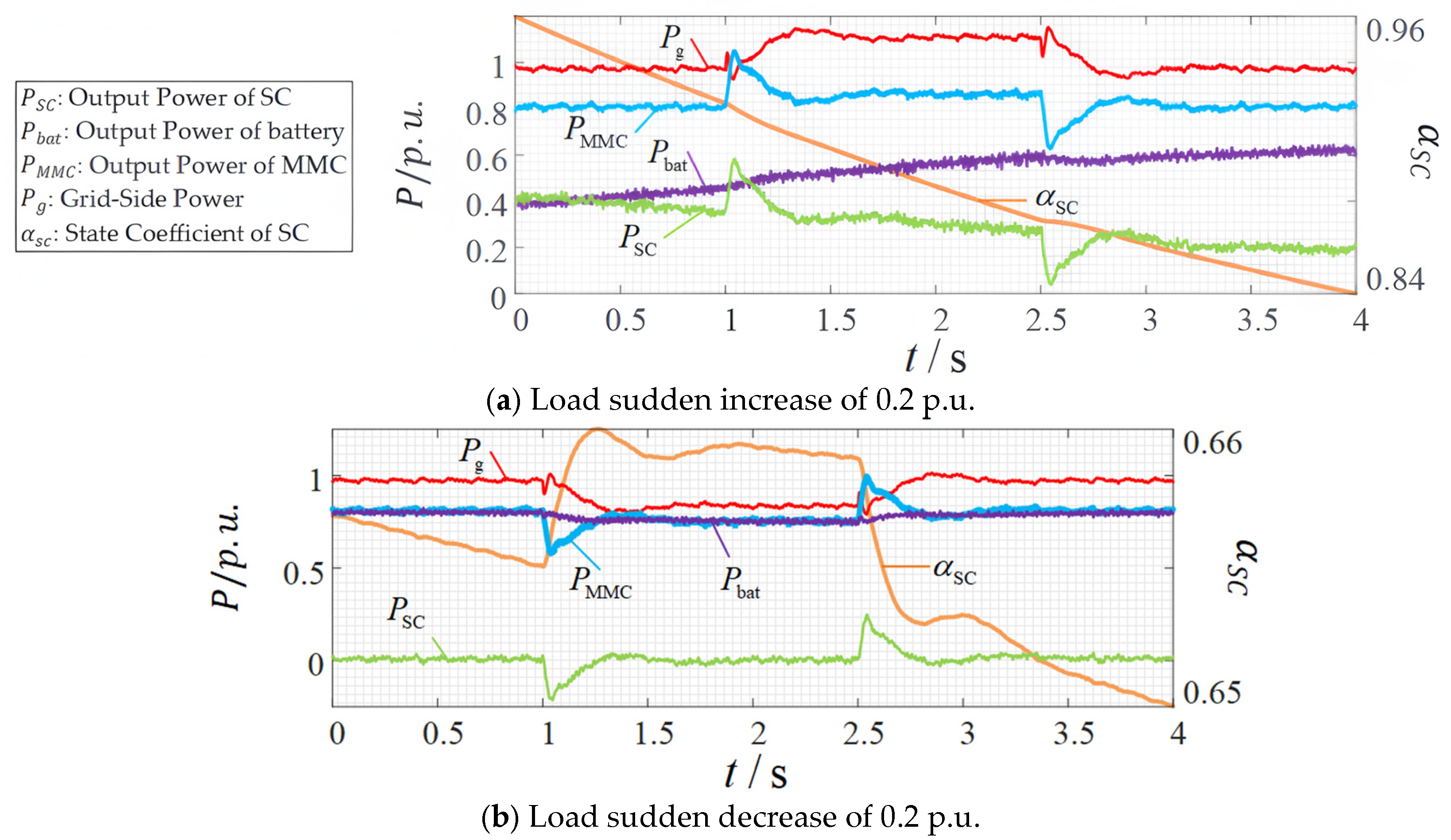
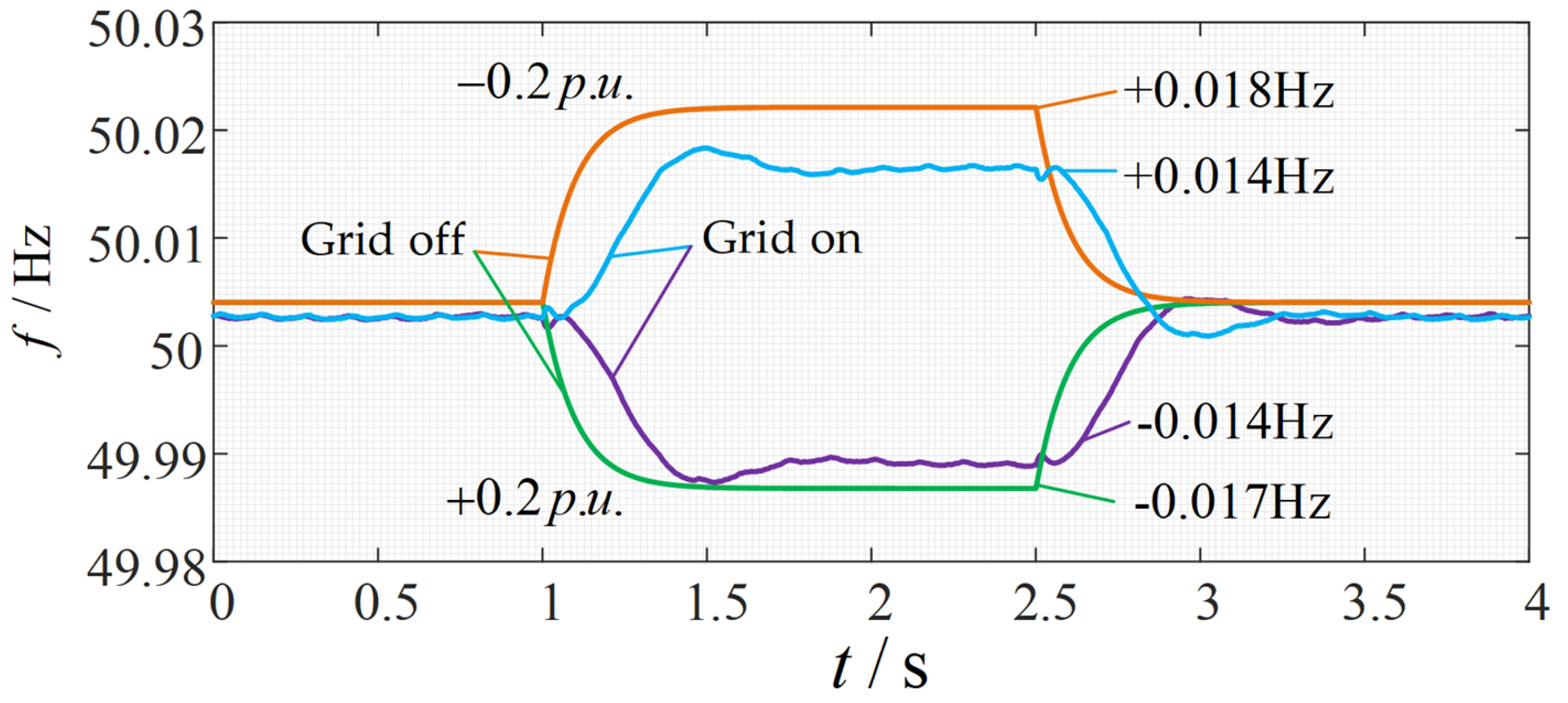
4.1. Inertia, Frequency Support, and Power Distribution
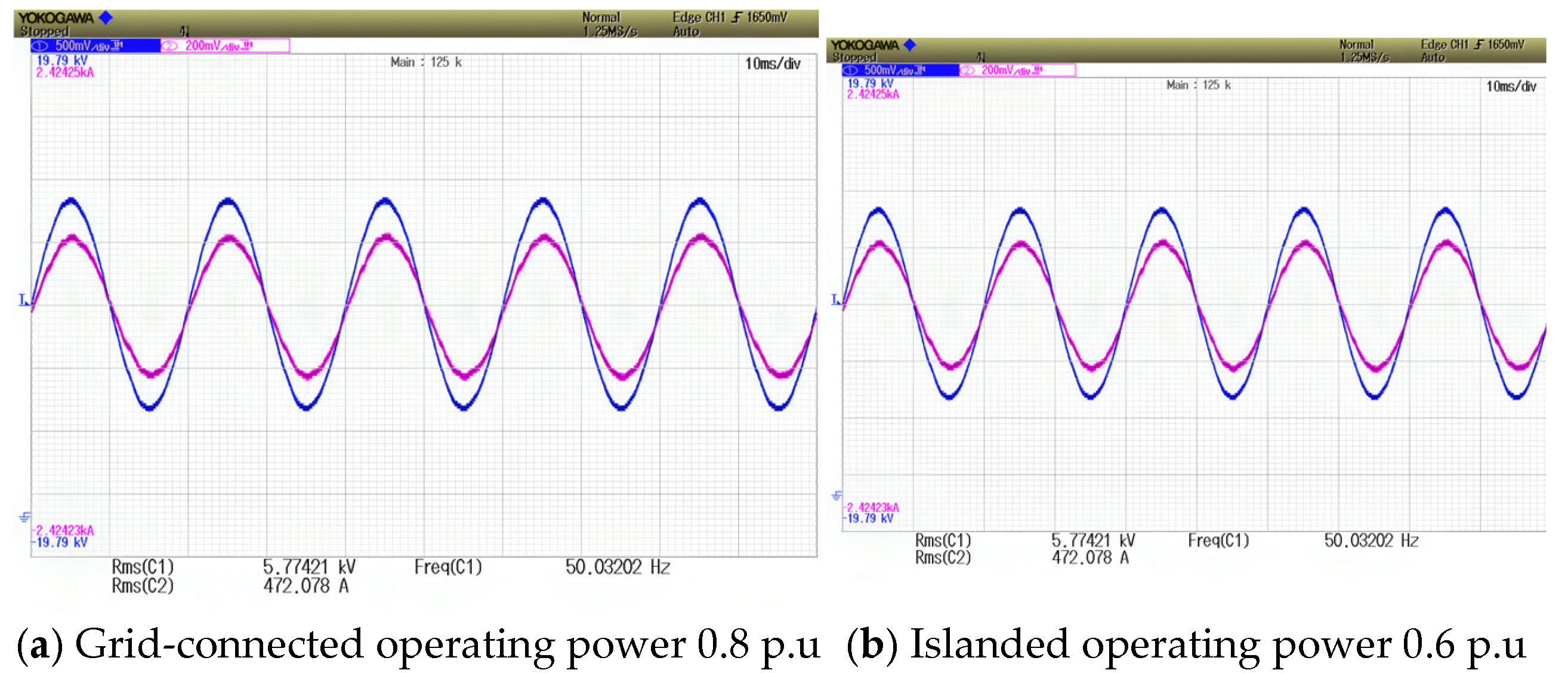
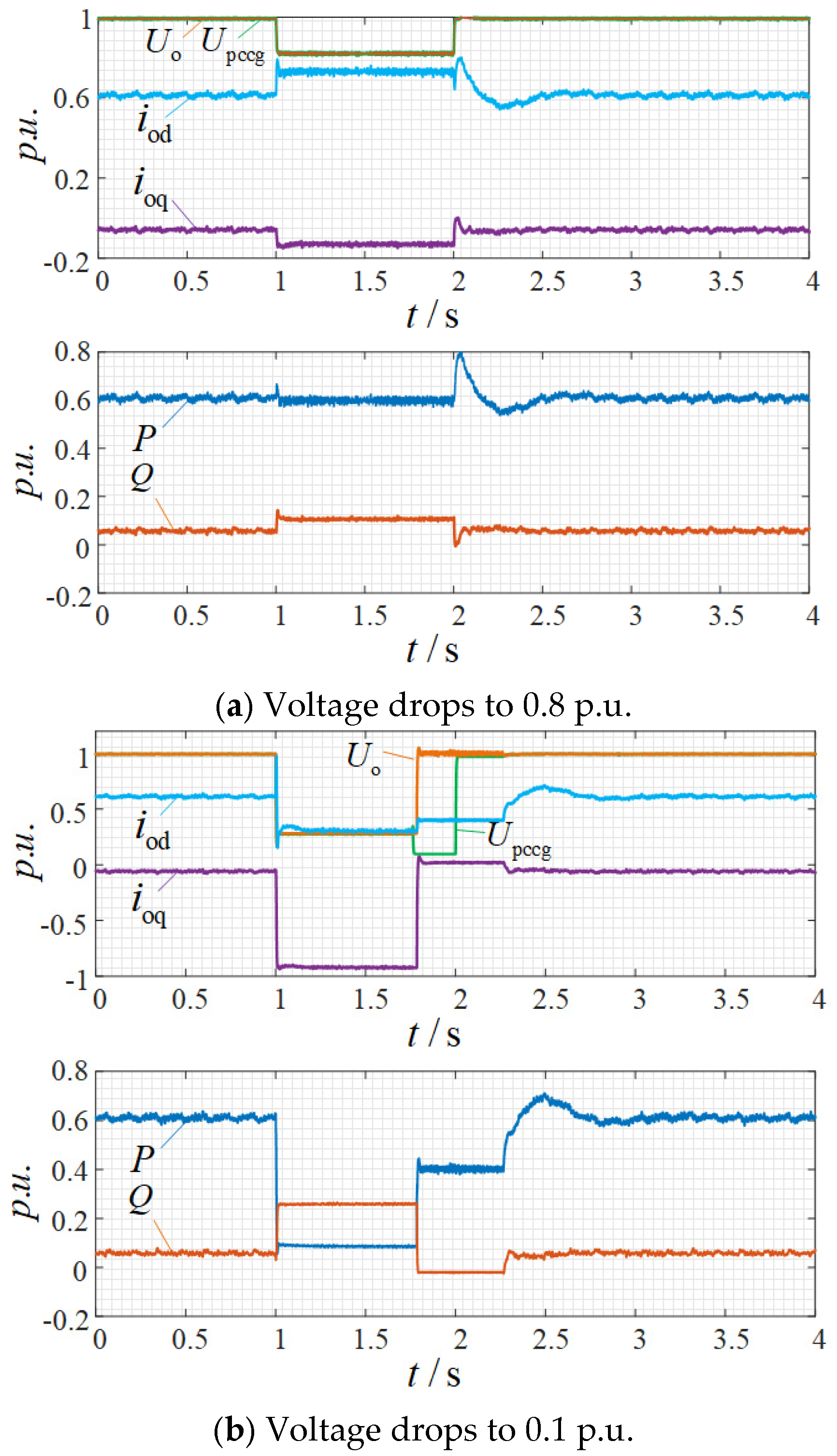
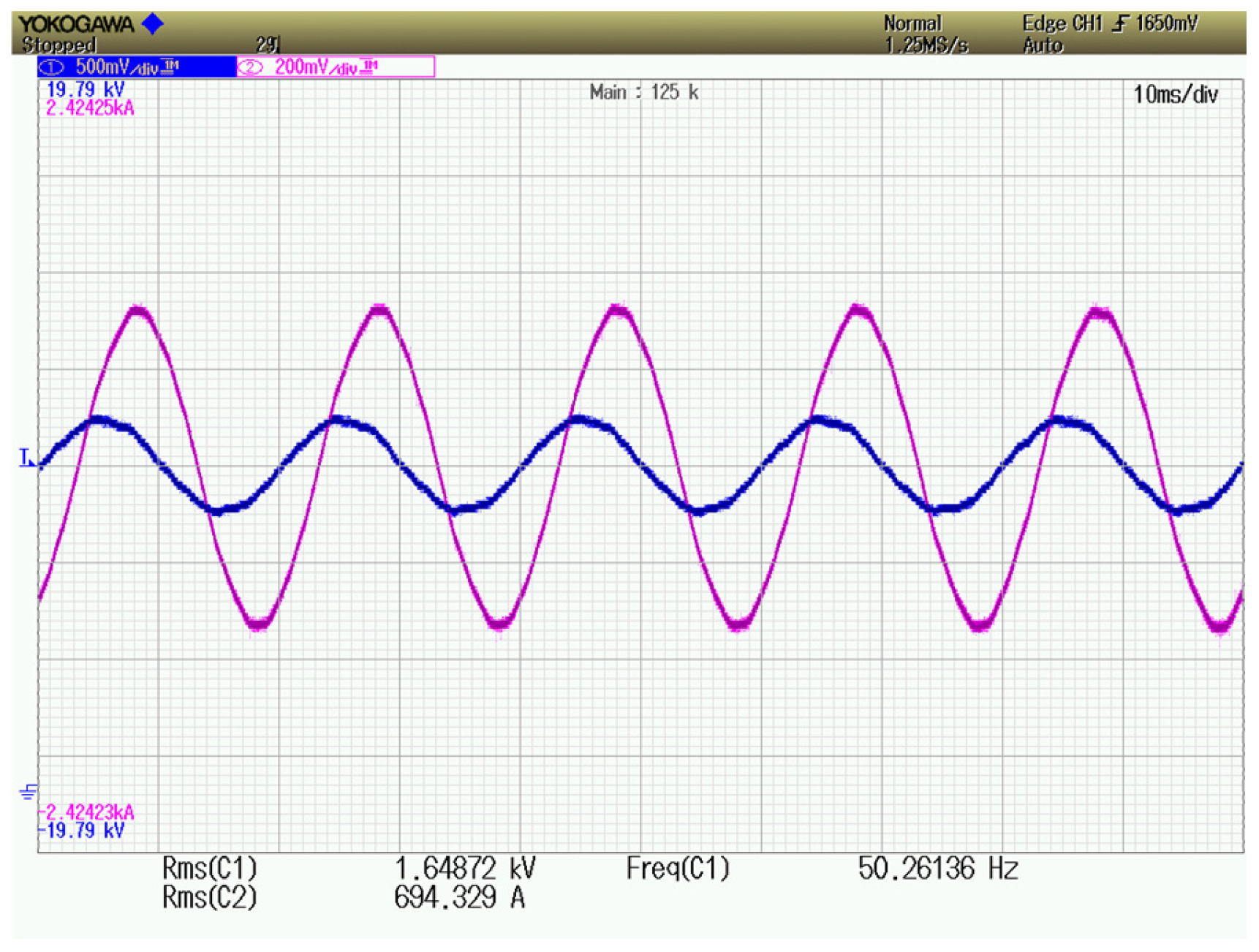
4.2. Low-Voltage Ride-Through and Grid Connection/Disconnection Switching
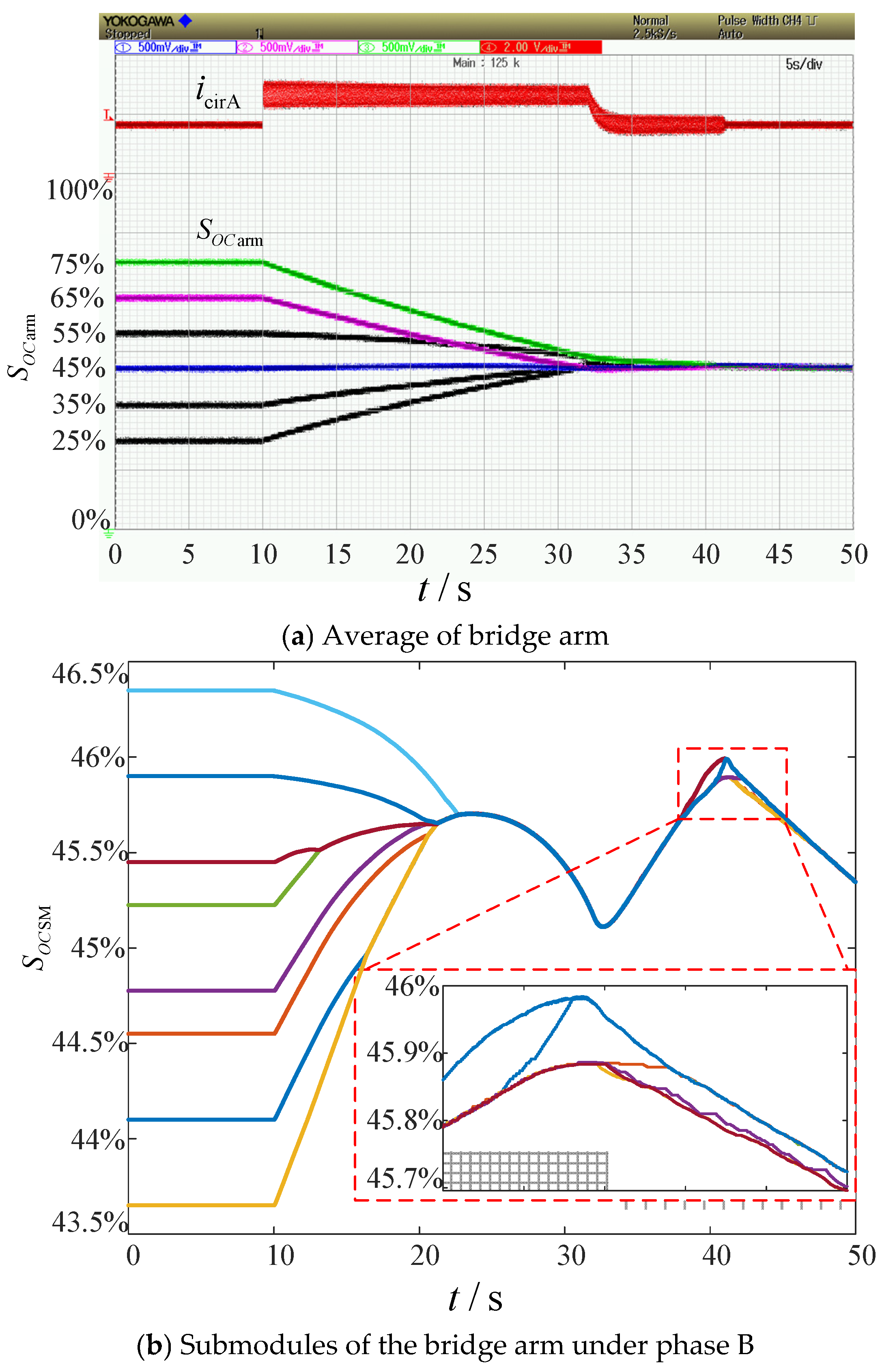
4.3. SOC Balancing Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Yang, Q.; Chen, Y.; Chen, X.; Wen, J. Optimal Parameters and Placement of Hybrid Energy Storage Systems for Frequency Stability Improvement. Prot. Control Mod. Power Syst. 2025, 10, 40–53. [Google Scholar] [CrossRef]
- Li, X.; Wang, S. Energy Management and Operational Control Methods for Grid Battery Energy Storage Systems. CSEE J. Power Energy Syst. 2021, 7, 1026–1040. [Google Scholar] [CrossRef]
- Xue, S.; Zeng, S.; Song, Y.; Hu, X.; Liang, J.; Qing, H. Adaptive Secondary Frequency Regulation Strategy for Energy Storage Based on Dynamic Primary Frequency Regulation. IEEE Trans. Power Deliv. 2024, 39, 3503–3513. [Google Scholar] [CrossRef]
- Cao, J.; Emadi, A. A New Battery/UltraCapacitor Hybrid Energy Storage System for Electric, Hybrid, and Plug-In Hybrid Electric Vehicles. IEEE Trans. Power Electron. 2012, 27, 122–132. [Google Scholar] [CrossRef]
- Hredzak, B.; Agelidis, V.G.; Jang, M. A Model Predictive Control System for a Hybrid Battery-Ultracapacitor Power Source. IEEE Trans. Power Electron. 2014, 29, 1469–1479. [Google Scholar] [CrossRef]
- Lukic, S.M.; Cao, J.; Bansal, R.C.; Rodriguez, F.; Emadi, A. Energy Storage Systems for Automotive Applications. IEEE Trans. Ind. Electron. 2008, 55, 2258–2267. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Z.; Wang, G.; Xu, Z. Modular Multilevel Converter with Embedded Energy Storage for Bidirectional Fault Isolation. IEEE Trans. Power Deliv. 2022, 37, 105–115. [Google Scholar] [CrossRef]
- Qiu, S.; Shi, B. An Enhanced Battery Interface of MMC-BESS. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019. [Google Scholar] [CrossRef]
- Zeng, W.; Li, R.; Huang, L.; Liu, C.; Cai, X. Approach to Inertial Compensation of HVdc Offshore Wind Farms by MMC With Ultracapacitor Energy Storage Integration. IEEE Trans. Ind. Electron. 2022, 69, 12988–12998. [Google Scholar] [CrossRef]
- Yu, X.; Wang, C.; Wang, Y.; Han, C. Arm Average Model and Operational Characteristics Analysis of MMC with Integrated Battery Energy Storage System. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 1426–1431. [Google Scholar] [CrossRef]
- Feng, G.; Ye, Y.; Sharma, R. A Modular Multilevel Converter Based Battery-Ultracapacitor Hybrid Energy Storage System for Photovoltaic Applications. In Proceedings of the 2015 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 10–13 March 2015. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, Y.; Yang, S.; Gao, F. A Modular Multilevel Converter-Based Grid-Tied Battery-Supercapacitor Hybrid Energy Storage System with Decoupled Power Control. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. Enhanced Virtual Synchronous Generator Control for Parallel Inverters in Microgrids. IEEE Trans. Smart Grid 2017, 8, 2268–2277. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive Virtual Inertia Control Strategy of VSG for Micro-Grid Based on Improved Bang-Bang Control Strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Ban, G.; Xu, Y.; Zhang, G.; Wu, Z.; Ma, X.; Yuan, X. Research on VSG Control Strategy for Improving Damping Performance of Weak Grid. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 1766–1771. [Google Scholar] [CrossRef]
- Yang, R.; Shi, G.; Zhang, C.; Li, G.; Cai, X. Internal Energy Based Grid-Forming Control for MMC-HVDC Systems with Wind Farm Integration. IEEE Trans. Ind. Appl. 2023, 59, 503–512. [Google Scholar] [CrossRef]
- Ji, K.; Pang, H.; Liu, S.; Tang, G. Impedance Analysis Considering Unstable Subsystem Poles for MMC-HVDC-Based Wind Farm Integration System. CSEE J. Power Energy Syst. 2022, 8, 634–639. [Google Scholar]
- Saeedifard, M.; Iravani, R. Dynamic Performance of a Modular Multilevel Back-to-Back HVDC System. IEEE Trans. Power Deliv. 2010, 25, 2903–2912. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Huang, X.; Deng, F. Control Strategy of Grid Forming MMC System for Grid Voltage Sag Ride Through. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 1133–1138. [Google Scholar] [CrossRef]
- Cai, W.; Hu, P.; Jiang, D.; Liang, Y. An MMC Based Hybrid Energy Storage System: Concept, Topology, and Control. In Proceedings of the 2020 IEEE 3rd Student Conference on Electrical Machines and Systems (SCEMS), Jinan, China, 4–6 December 2020; pp. 680–685. [Google Scholar] [CrossRef]
- Hu, P.; Teodorescu, R.; Guerrero, J.M. Negative-Sequence Second-Order Circulating Current Injection for Hybrid MMC Under Over-Modulation Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2508–2519. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, F.; Li, N. Control Strategy of MMC Battery Energy Storage System Under Asymmetrical Grid Voltage Condition. Chin. J. Electr. Eng. 2016, 2, 76–83. [Google Scholar] [CrossRef]
- Barresi, M.; De Simone, D.; Piegari, L. Direct State-of-Charge Balancing Control for Modular Multilevel Converter Integrating Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 733–746. [Google Scholar] [CrossRef]
- Hu, P.; Teodorescu, R.; Wang, S.; Li, S.; Guerrero, J.M. A Currentless Sorting and Selection-Based Capacitor-Voltage-Balancing Method for Modular Multilevel Converters. IEEE Trans. Power Electron. 2019, 34, 1022–1025. [Google Scholar] [CrossRef]
- Izadi, Y.; Beiranvand, R. A Comprehensive Review of Battery and Supercapacitor Cells Voltage-Equalizer Circuits. IEEE Trans. Power Electron. 2023, 38, 15671–15692. [Google Scholar] [CrossRef]
- Liu, T.; Wang, X. Physical Insight into Hybrid-Synchronization-Controlled Grid-Forming Inverters Under Large Disturbances. IEEE Trans. Power Electron. 2022, 37, 11475–11480. [Google Scholar] [CrossRef]


| Evaluation Metric | Topology 1 | Topology 2 | Topology 3 |
|---|---|---|---|
| Energy Utilization | High | Low | High |
| Dynamic Response Time | Slow | Medium | Fast |
| Power Distribution Efficiency | Low | Medium | High |
| SOC Balancing Complexity | High | Low | Low |
| Structure | Parameter | Label | Configuration | ||
|---|---|---|---|---|---|
| Grid | Voltage level/kV | Vbase | 10 | ||
| Rated frequency/Hz | f0 | 50 | |||
| Rated capacity/(MV·A) | Sbase | 10 | |||
| Line inductance (p.u.) | Ls | 0.2 | |||
| Line resistance (p.u.) | Rs | 0.002 | |||
| LC filter | Series inductance (p.u.) | Lf | 0.2 | ||
| Inductive parasitic resistance (p.u.) | Rf | 0.02 | |||
| Parallel capacitance (p.u.) | Cf | 0.02 | |||
| Parallel parasitic resistance (p.u.) | RCf | 0.1 | |||
| Bridge arm structure | Submodules per bridge arm | N | 8 | ||
| Bridge arm inductance/mH | L0 | 12 | |||
| Bridge arm resistance/Ω | R0 | 0.1 | |||
| SM internal capacitance/mF | C0 | 8.4 | |||
| Battery | Rated voltage/kV | VBr | 2.5 | ||
| Rated capacity/(A·h) | QBr | 20 | |||
| SOC Initial value/% | A phase | upper | SOCpa | 45 | |
| lower | SOCna | 47 | |||
| B phase | upper | SOCpb | 51 | ||
| lower | SOCnb | 49 | |||
| C phase | upper | SOCpc | 53 | ||
| lower | SOCnc | 55 | |||
| DC-side supercapacitor | Total series capacitance/F | CSC | 1 | ||
| Upper working voltage limit/kV | USCmax | 11 | |||
| Lower working voltage limit/kV | USCmin | 1 | |||
| HSC power loop | Virtual inertia (p.u.) | J | 2.5 | ||
| Damping coefficient (p.u.) | Dp | 100 | |||
| PLL component ratio coefficient (p.u.) | Kp | 10 | |||
| Voltage inner loop | Proportional coefficient (p.u.) | Kpv | 0.5 | ||
| Integral coefficient (p.u.) | Kiv | 500 | |||
| Current inner loop | Proportional coefficient (p.u.) | Kpi | 1 | ||
| Integral coefficient (p.u.) | Kii | 200 | |||
| SC power | High-frequency component compensation coefficient (p.u.) | KH | 5 | ||
| Low-frequency component compensation coefficient (p.u.) | KL0 | 0.5 | |||
| DC current loop | Proportional coefficient (p.u.) | KpDC | 0.5 | ||
| Integral coefficient (p.u.) | KiDC | 100 | |||
| SOC balance | Inter-phase SOC balancing coefficient (p.u.) | Kph | 50 | ||
| Bridge arm SOC balancing coefficient (p.u.) | Karm | 40 | |||
| DC component limit of circulating current (p.u.) | IDCcir_lim | 3 | |||
| AC component limit of circulating current (p.u.) | IACcir_lim | 2 | |||
| SOC dead zone/% | DB | 0.1 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, C.; Gou, J.; You, J.; Li, B.; Du, X.; Fu, Y.; Zhang, W.; Wang, X.; Shi, P. Modular Multilevel Converter-Based Hybrid Energy Storage System Integrating Supercapacitors and Batteries with Hybrid Synchronous Control Strategy. Processes 2025, 13, 1580. https://doi.org/10.3390/pr13051580
Yuan C, Gou J, You J, Li B, Du X, Fu Y, Zhang W, Wang X, Shi P. Modular Multilevel Converter-Based Hybrid Energy Storage System Integrating Supercapacitors and Batteries with Hybrid Synchronous Control Strategy. Processes. 2025; 13(5):1580. https://doi.org/10.3390/pr13051580
Chicago/Turabian StyleYuan, Chuan, Jing Gou, Jiao You, Bo Li, Xinwei Du, Yifeng Fu, Weixuan Zhang, Xi Wang, and Peng Shi. 2025. "Modular Multilevel Converter-Based Hybrid Energy Storage System Integrating Supercapacitors and Batteries with Hybrid Synchronous Control Strategy" Processes 13, no. 5: 1580. https://doi.org/10.3390/pr13051580
APA StyleYuan, C., Gou, J., You, J., Li, B., Du, X., Fu, Y., Zhang, W., Wang, X., & Shi, P. (2025). Modular Multilevel Converter-Based Hybrid Energy Storage System Integrating Supercapacitors and Batteries with Hybrid Synchronous Control Strategy. Processes, 13(5), 1580. https://doi.org/10.3390/pr13051580






