Abstract
This study addresses the assembly job shop scheduling problem (AJSSP) with parallel machines. In an assembly job shop, product structures are represented through hierarchical tree diagrams, where components and subassemblies are sequentially assembled to form the final product. A mixed-integer linear programming (MILP) model is formulated to minimize the total completion time. A dominance relations-based variable neighborhood search (DR-VNS) is proposed for solving AJSSP with parallel machines. The proposed approach integrates dominance relations among operations in the initialization phase and employs tailored neighborhood structures to address sequencing and assignment challenges, thereby enhancing the generation of neighboring solutions. Experimental studies conducted on test cases of varying scales and complexities demonstrate the effectiveness of the proposed algorithms in solving the AJSSP with parallel machines.
1. Introduction
Efficient scheduling has been extensively recognized as a crucial element in optimizing productivity across various industrial domains. The assembly job shop scheduling problem (AJSSP), which broadens the traditional job shop scheduling problem by integrating processing and assembly operations, has garnered research interest [1,2]. AJSSP can be classified into two categories. The first category allows for the machining of only the root components, excluding assemblies [3]. The second category permits the machining of both root components and assemblies [4], indicating that assemblies also require machining before the final product assembly. It is important to note that the current study focuses exclusively on the second category. Efficient scheduling has been extensively recognized as a crucial element in optimizing.
In an assembly job, higher-level items cannot be assembled until all preceding lower-level items are completed. Any operational delay may result in delays of the final assembly product. To reduce the delivery cycles and enhance production efficiency, parallel machines are utilized to perform the operations, particularly in complex production systems such as aero-engine assembly plants [5], liquid crystal display manufacturing [6], and printed circuit board production processes [7]. With the increase in levels of assembly, parameters like precedence relationships between components also increases, which makes assembly job shop scheduling with parallel machines very challenging.
Meta-heuristic methods have been extensively utilized to tackle the assembly job shop scheduling problem [8]. Among these methods, the variable neighborhood search (VNS) algorithm efficiently generates high-quality approximate solutions for complex combinatorial problems through its systematic neighborhood changes and perturbation operations; it has demonstrated widespread application in real-world production scheduling problems [9]. A high-quality initial solution can significantly enhance search efficiency, while the variable neighborhood structure effectively prevents the solution from becoming trapped in local optima.
This paper presents a dominance relations-based variable neighborhood search for the AJSSP with parallel machines. The main contributions are summarized as follows:
- (1)
- An MILP model is developed for AJSSP with parallel machines to describe production constraints.
- (2)
- A novel dominance relations-based variable neighborhood search (DR-VNS) algorithm is developed. The proposed methodology establishes dominance relations between overlapping operations, which are subsequently integrated into a locally optimal sequencing procedure to generate high-quality initial solutions. These solutions are then refined through an advanced variable neighborhood search mechanism.
- (3)
- Extensive computational experiments on test cases and comparisons with meta-heuristic algorithms are conducted, demonstrating the superiority of the proposed DR-VNS.
The remainder of this paper is organized as follows. Previous research on AJSSP is reviewed in Section 2. The assembly job shop scheduling problem with parallel machines is described in Section 3. Dominance relations, which form the basis for the locally optimal sequencing procedure, are presented in Section 4. The dominance relations-based variable neighborhood search (DR-VNS) is presented in Section 5, while its performance evaluation is detailed in Section 6. Finally, conclusions and suggestions for future research are provided in Section 7.
2. Literature Review
Research on the AJSSP began in the 1960s [10], with early studies primarily focusing on developing scheduling rules. Siegel [11] found that the total work remaining (TWKR) priority rule was predominantly the best rule with respect to mean lead time. Reeja and Rajendran [12] introduced two novel priority rules: Operation Synchronization Data (OSD) and an enhanced variant of Operation Due Date (ODD). Empirical analyses demonstrate that the TWKR/OSD combination outperforms alternative approaches in terms of both average flow duration and staging delay metrics. Additional dispatching rules for dynamic assembly job shops, incorporating weighted considerations for work holding, earliness, tardiness, and flowtime, have also been proposed [13]. Xie et al. [14,15] developed a set of scheduling rules based on the product processing tree, demonstrating enhanced operational parallelism and reduced total processing time.
Given the combinatorial explosion nature of scheduling problems, some other research studies focus on developing efficient heuristic and meta-heuristic algorithms capable of generating feasible solutions within practical computational times. Pathumnakul and Egbelu [16] examined weighted early completion penalties in AJSSP, proposing a decomposition heuristic based on local optimality principles. Zou et al. [17] developed an evolutionary computation-based optimization algorithm featuring three innovative components: an advanced initial solution generator, a level barrier-based crossover operator, and a corresponding mutation operator. Zhang et al. [18] proposed an efficient distributed ant colony optimization (ACO) methodology for multi-objective production scheduling in flexible job shops with assembly processes. Zhu et al. [19] studied the flexible job shop scheduling problem with job precedence constraints arising from multi-level assembly production. A novel shuffled cellular evolutionary gray wolf optimizer (SCEGWO) was developed, featuring triple-vector encoding and cellular neighborhood evolution to efficiently explore the complex solution space. Cheng et al. [20] addressed an AJSSP with material integrity and sequential constraints (AJSSP-IS), proposing a lexicographical MILP model for small-scale optimization and an enhanced simulated annealing algorithm (ESA) with assembly-driven initialization and two-stage decoding to minimize both completion time and inventory levels efficiently. Zheng et al. [21] studied the robust AJSSP under uncertain setup and processing times by proposing a data-driven framework that combines kernel density estimation for uncertainty quantification with a customized discrete particle swarm optimization (PSO) algorithm to optimize schedule robustness through interval-based scheduling methods.
The literature reveals the limited exploration of AJSSP with parallel machine configurations, despite their prevalence in large-scale, complex product assembly. Jiang and Wang [22] investigated the aero-engine assembly workshop problem under uncertain assembly times. Operations are processed by parallel work groups, where the number of workers per group is adjustable. Wan and Yan [23] investigated an integrated assembly job shop scheduling and workforce reconfiguration problem in knowledgeable manufacturing, developing a heuristic algorithm with backward insertion search and dominance-based optimization to minimize total costs. However, the allocation of operations to parallel machines is conducted randomly. Hao et al. [24] introduced a two-stage assembly scheduling problem with nested operations for rocket tank welding, aiming to minimize both makespan and average passage time through a logistic-based improved genetic algorithm (LBIGA) and backward computation heuristics.
VNS is a metaheuristic widely applied to combinatorial optimization problems in recent years [25,26]. It integrates several desirable metaheuristic properties, including simplicity, efficiency, effectiveness, and generality [9,27]. This study introduces a dominance relations-based variable neighborhood search for AJSSP. Dominance relations between operations are derived and applied to a locally optimal sequencing procedure, which optimizes both the sequence and assignment of operations on parallel machines. Following this, an initial schedule is generated and refined using a VNS algorithm. Four types of neighborhood structures are employed to guide the refinement process.
3. Problem Formulation
We consider an assembly job shop system comprising multiple workstations. Each workstation j (j = 1, 2, …, m) comprises functionally identical machines. Each product follows a tree-structured precedence hierarchy, where components and subassemblies—each associated with a distinct set of operations—are assembled into the final product. Each operation may have several predecessors but only one successor. Higher-level subassemblies cannot begin assembly until all predecessor operations are completed. Thus, delays in any operation propagate to the final product.
This paper addresses AJSSP with parallel machines, aiming to minimize total completion time. The solution consists of two key components: (1) assigning operations to parallel machines and (2) scheduling the operations for processing.
The basic assumptions are as follows:
- (1)
- The assembling structures of all products are known and must be followed.
- (2)
- All machines and products are available at time zero.
- (3)
- No operation is allowed to be pre-empted.
- (4)
- Each machine processes at most one operation simultaneously.
- (5)
- Each operation can be performed by at most one machine at a time.
- (6)
- Operations cannot be processed until all its preceding operations have been completed.
- (7)
- All operation processing times are predetermined and known.To formalize the model, we introduce the following notations, as shown in Table 1.
 Table 1. List of notations.
Table 1. List of notations.
The mathematical model for AJSSP is as follows:
The objective function (1) minimizes the total completion time; constraint (2) enforces non-pre-emptive operation processing; constraint (3) maintains precedence relationships based on the product structure, where denotes the start time of the successor to operation k of product i; constraint (4) expresses the fact that the start time of each operation must be positive; constraints (5) and (6) ensure that each machine can process only one operation simultaneously; constraint (7) means that each operation cannot be assigned to another machine once it starts; and constraints (8) and (9) define the 0–1 integer variables.
4. Dominance Relations of Operations
In this section, dominance relations between two operations that conflict on a machine are presented. Consider the tree structure of products in Figure 1, where nodes on product trees are expressed as operation index-workstation-processing time. For example, 1-1-3 denotes operation 1 performed on workstation 1, with a processing time of 3.
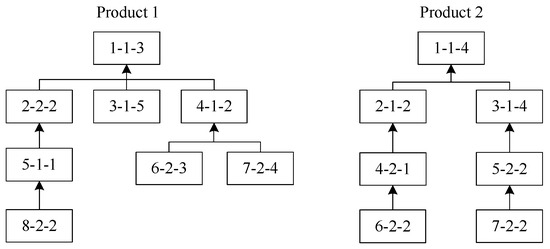
Figure 1.
Tree structure of products.
Consider the scheduling of products shown in Figure 1. First, an ideal schedule is generated where each operation completes precisely when its successor begins (see Figure 2). This ideal schedule assumes that each product is processed in isolation, disregarding all other products [16]. These individual ideal schedules are then superimposed to create a combined schedule for all products. However, this merged schedule typically becomes infeasible due to operation overlaps.
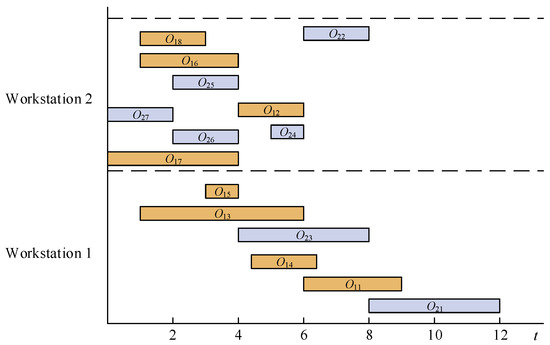
Figure 2.
An ideal schedule.
To resolve this infeasibility, we develop two fundamental definitions and establish corresponding sequencing propositions that guarantee solution feasibility through local optimization.
Let denote the set of preceding operations of , and represent its immediate successor operation. Let represent the earliest available time of the assigned machine for .
Definition 1.
The earliest start time of is defined as : if the set of predecessors is non-empty, then ; otherwise, .
Definition 2.
The latest completion time of is defined as : .
To resolve operation overlaps, operations may be shifted leftward or rightward. Left-shifting of cannot be earlier than its start time , while right-shifting delays its successor’s start time, potentially increasing the final product’s completion time. Presented below are two locally optimal sequencing propositions to address these overlap issues.
Proposition 1.
For two overlapping operations and satisfying > −− and > −−, if / - > 1, then sequence is optimal with start times = and = + ; otherwise, is optimal with start times = + and = .
Proof of Proposition 1.
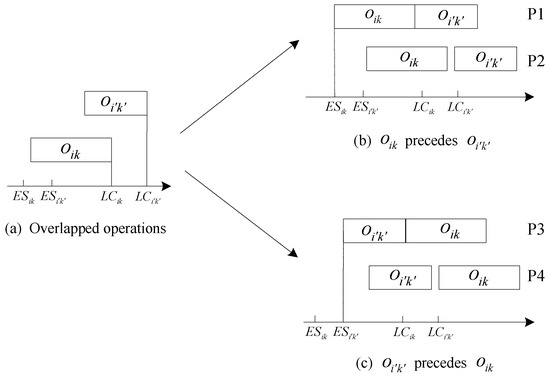
For two overlapping operations and that satisfy > −− and > −−, the relative positions of and are shown in Figure 3.

Figure 3.
The positions of operation sequences.
If precedes , two relative configurations (P1 and P2) exist, as shown in Figure 3b. In the P1 → P2 transition, both operations exceed their latest completion time, thereby increasing total completion time. Consequently, configuration P1 achieves the minimum completion time. Conversely, if precedes , configuration P3 achieves the minimum completion time, as shown in Figure 3c. Thus, the minimum completion time occurs exclusively at either P1 or P3.
The completion time increments for P1 and P3 are
If / > 1, we derive < . P1 achieves the minimum completion time, and the start times are = and = + , respectively. Otherwise, if / ⩽ 1, then we have ≥ . P3 achieves the minimum completion time, with start times = + and = . □
Proposition 2.
For two overlapping operations and satisfying ⩽ −−, is optimal with start times = and = + .
The proof of Proposition 2 is analogous to that of Proposition 1.
5. A Dominance Relations-Based Variable Neighborhood Search
A dominance relations-based variable neighborhood search is proposed to solve the AJSSP with parallel machines. The scheduling optimization is implemented in two steps: (1) a locally optimal sequencing procedure is used to determine the assignment and sequence of the operations, generating an initial schedule; and (2) a variable neighborhood search is developed to further optimize the assignment and sequence of operations.
5.1. Locally Optimal Sequence of Operations
A locally optimal sequencing procedure is proposed to simultaneously optimize operation scheduling and assignment. Operations are selected based on dominance relations in Section 4 and assigned to machines offering the earliest start times within their workstations.
The following additional notations are employed in this procedure.
| Notation | Description |
| P | Set of unscheduled operations |
| Sequence matrix of operations | |
| Dominance matrix | |
| Assignment matrix of operations | |
| Earliest start time of the machine l at workstation j |
The main steps of the locally optimal sequencing procedure (Algorithm 1) are as follows.
| Algorithm 1 Locally optimal sequencing procedure |
|
Output: Output an initial sequence of operations and assignment of operations . |
5.2. Variable Neighborhood Search
VNS is a well-known local search method for solving combinatorial and optimization problems. The fundamental paradigm involves systematic neighborhood changes during the search process. The initialization, encoding and decoding, neighborhood structures, and local search method are explained as follows:
- (1)
- Initial solution
An initial solution consists of a sequence of operations and an assignment of operations , obtained using the Algorithm 1 as described in Section 5.1.
- (2)
- Encoding and decoding
Each solution is encoded as a matrix by a , where L denotes the total number of operations. The first row contains temporal priority values, establishing the processing order. The higher its priority value, the earlier the operation starts. The second row contains the indices of parallel machines for the associated operations.
To demonstrate the solution encoding, we examine products (Figure 1) with two workstations, each of which contains two identical machines, numbered as 1–4 in sequence.
Assume that the initial schedule comprises the operation sequence → → → → → → → → → → → → → → with machine assignments 4 → 3 → 4 → 3 → 2 → 1 → 4 → 4 → 3 → 4 → 2 → 3 → 2 → 1 → 2. Thus, the matrix encoding for this solution can be seen in Figure 4.

Figure 4.
Encoding.
The decoding process employs the zero in-degree topological sort algorithm to derive a feasible operation sequence [5]. From the candidate set of unscheduled operations, the operation with maximal priority value is selected while satisfying all precedence constraints. The machine assignment vector is directly extracted from the solution matrix’s second row.
- (3)
- Neighborhood structures
Four types of neighborhood structures are employed, as shown in Figure 5.
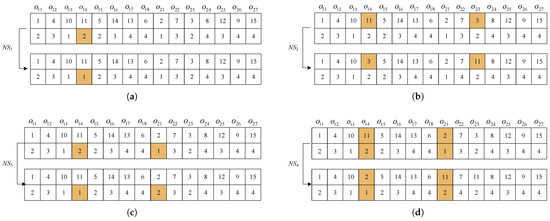
Figure 5.
(a) Neighborhood structure . (b) Neighborhood structure . (c) Neighborhood structure . (d) Neighborhood structure .
: Machine Reassignment. For a selected operation , modify its machine assignment. This changes the assignment of the operation.
: Priority Transposition. For operations and performed on the same machine, exchange their priority. This changes the sequence of the operations.
: Machine Exchange. For operations and performed by different machines at the same workstation, swap their machine assignments. This changes the assignment of operation.
: Composite Move. For operations and performed by different machines at the same workstation, swap both their priorities and machine assignment. This changes both the sequence and assignment of operations.
- (4)
- Local search
The VNS incorporates a threshold accepting method [28] to navigate the solution space through the four defined neighborhood structures (–). This approach systematically balances intensification and diversification during the search process.
5.3. The Framework of the DR-VNS
The framework of DR-VNS integrates dominance relations into variable neighborhood search. Algorithm 2 presents the pseudo-code implementation of the DR-VNS method.
| Algorithm 2 Dominance Relations-based Variable Neighborhood Search (DR-VNS) |
|
Output: Output the sequence of operations and assignment of operations . |
6. Numerical Experiments
This section presents two sets of numerical experiments that test the following: (1) the effectiveness of the propositions proposed in Section 4 and (2) the effectiveness of the proposed DR-VNS in Section 5.
To evaluate the effectiveness of the dominance relations established in Propositions 1 and 2 and the DR-VNS algorithm, a set of instances covering diverse problem scales and structural configurations were generated. Three classes of product structures were implemented: single-level structures (S1), two-level structures (S2), and three-level structures (S3) [11]. Table 2 provides the specific parameter settings for generating those instances, a total number of instances was generated with different scales for production configurations. Each combination was executed for 10 independent replications, yielding 540 total experimental runs.

Table 2.
Parameter settings for generating instances.
All experiments were conducted on Windows 10 with an Intel Core i7-7300HQ 2.5 GHz processor (Lenovo, Beijing, China) with 8 GB of RAM. All algorithms were implemented in Matlab.
6.1. The Effectiveness of Proposed Propositions
The proposed Propositions 1 and 2 in Section 4 were tested for sequencing operations to minimize the total completion time, and the procedure was referred to as H(DR).
While dispatching rules can effectively determine operation sequences, they lack the capability to allocate operations to parallel machines. In this section, we conducted a comparative analysis by substituting our dominance relations in Algorithm 1 with five well-established dispatching rules.
A famous simple dispatching rule, SPT (shortest processing time), is reported to be an effective rule in minimizing the mean flowtime. Hence, we used them to replace the proposed dominance relations in Algorithm 1. The procedures are referred to as H(SPT).
Dispatching rule OSD (operation synchronization date) and TWKR-OSD perform well in terms of minimizing the mean, maximum, and standard deviations in flowtime [11]; hence, we will use them to replace the proposed dominance relations in Section 4. The procedures are referred to as H(OSD) and H(TWKR-OSD), respectively.
Dispatching rules LFT-ECT (latest finish time–earliest completion time) and EFT-ECT (earliest finish time–earliest completion time) perform well in scheduling operations with weighted mean flowtime [13]. The procedures are referred to as H(ECT-LFT) and H (EFT-ECT), respectively.
The results of the proposed propositions and the five dispatching rules are summarized in Table 3 and Table 4. A Wilcoxon signed-rank test () was conducted to evaluate statistical differences in the results. The symbols ‘+’, ‘−’, and ‘=’ denote the cases where DR-VNS outperforms, underperforms or shows no statistically significant difference compared to the competing algorithm, respectively.

Table 3.
Comparison results of the six dispatching rules (b = 2).

Table 4.
Comparison results of the six dispatching rules (b = 3).
The results indicate that H(DR) and H(OSD) consistently outperform other rules in minimizing the total completion time in all cases, regardless of the product structure levels or number of parallel machines. The performances of H(EFT-ECT), H(LFT-ECT), and H(TWKR-OSD) are slightly inferior, while the H(SPT) performs poorly in minimizing the total completion time.
Figure 6 and Figure 7 illustrate the total completion times of the dispatching rules for different levels of product structures and varying numbers of workstations, respectively. The results clearly show that the DR rule performs well. Comparing H(OSD) with H(DR) reveals a similar trend, but the latter is better at saving the total completion time by 5.97% on average.
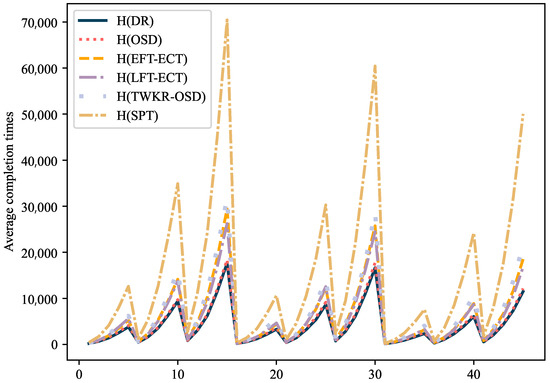
Figure 6.
Total completion times of dispatching rules on different levels of product structures.
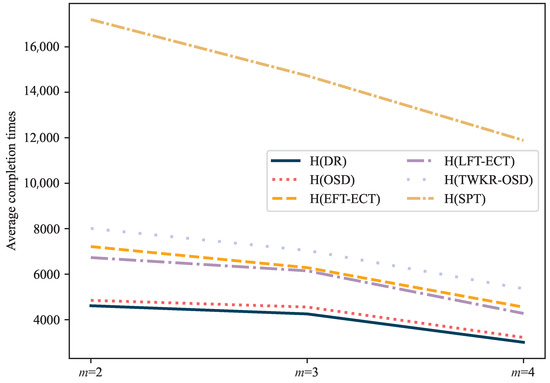
Figure 7.
Average completion times with different numbers of parallel machines.
6.2. The Effectiveness of DR-VNS
To assess the performance of our DR-VNS algorithm, we conducted comparative evaluations against three state-of-the-art heuristics: (1) backward insertion search (BIS) [23], which serves as an alternative to VNS; (2) simple genetic algorithm (SGA) as a baseline evolutionary method; and (3) an improved genetic algorithm (IGA) enhanced with dominance relations-based chromosome initialization. For the genetic parameter, the crossover and mutation rates were set to 0.9 and 0.4, respectively. A partially matched crossover (PMX) and an order-based mutation operator, both specifically selected for their demonstrated effectiveness in solving order-based scheduling problems [29], was employed here.
The average objective value and wall clock times (WCTs in seconds) for the various algorithms were recorded. The test results are summarized in Table 5 and Table 6.

Table 5.
Comparison results of the five algorithms (b = 2).

Table 6.
Comparison results of the four algorithms (b = 3).
The performances of the different algorithms were compared based on the improvement rate (), computed as follows:
where is the objective value obtained by H(DR), and is the average objective value of the compared algorithm.
Higher IR values indicate better performance. The results demonstrate that the proposed DR-VNS outperforms the other algorithms, with an average IR of 6.50%. In comparison, the IR values for BIS, IGA, and VNS were 3.09%, 0.27%, and 0.4%, respectively. While both DR-VNS and BIS leverage identical dominance relations for operation sequencing, their respective optimization mechanisms—variable neighborhood search versus backward insertion search—yield significantly different outcomes. Notably, DR-VNS provides an additional 2.09% average cost reduction compared to BIS, conclusively demonstrating the enhanced optimization capability of our VNS implementation.
The average IR across varying problem scales and product structures is presented in Figure 8. DR-VNS emerged as the top-performing algorithm, achieving average IR values of 6.64%, 7.29%, and 4.75% for product structures S1, S2, and S3, respectively. All algorithms exhibited decreasing IR values as problem complexity increases.
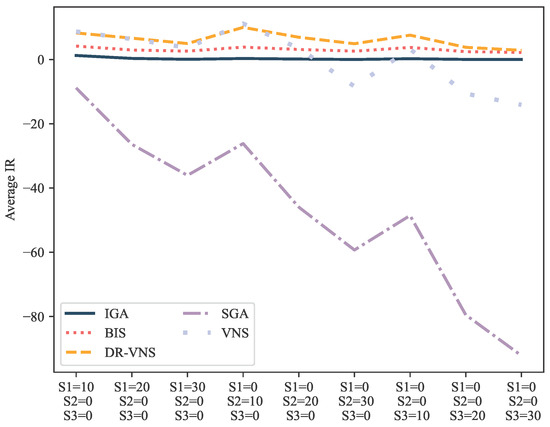
Figure 8.
The average IR across varying problem scales and product structures.
Among the compared methods, DR-VNS demonstrated superior performance with average IR values of 8.63%, 5.80%, and 4.26% for problem sizes of 10, 20, and 30 products, respectively, while BIS showed moderately lower performance with corresponding IR values of 3.93%, 2.86%, and 2.48%. The SGA proved ineffective in minimizing total completion time. While VNS achieved comparable results to DR-VNS for small-scale problems (n = 10) with an IR of 7.72%, its performance deteriorated significantly for larger problems (n = 30), yielding a negative IR of −6.27% that was substantially worse than our proposed H(DR) method.
7. Conclusions
In this paper, a solution to the assembly job shop scheduling problem with the consideration of minimizing the total completion time is presented. Two locally optimal sequencing propositions were proposed and applied in the development of a locally optimal sequencing procedure. The relative performance of this procedure and the proposed DR-VNS was thoroughly analyzed. Experimental results demonstrate the effectiveness of both the proposed locally optimal sequencing propositions and the heuristic, showing that they perform exceptionally well across different numbers of products, parallel machines, and product structures. This demonstrates their effectiveness and promise in solving the AJSSP with parallel machines.
For future research, the development of an enhanced locally optimal sequencing procedure that integrates multiple metaheuristics could be further explored. This would help overcome the short-sighted nature of the current sequencing procedure, potentially leading to even more efficient solutions.
Author Contributions
Conceptualization, X.W. and T.J.; methodology, X.W. and T.J.; software, X.W.; validation, X.W.; formal analysis, X.W. and T.J.; investigation, X.W. and T.J.; resources, X.W. and T.J.; data curation, X.W.; writing—original draft preparation, X.W.; writing—review and editing, X.W.; visualization, T.J.; supervision, T.J.; project administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Natural Science Foundation of the Jiangsu Higher Education Institutions of China under grant 21KJB630011.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shi, F.; Zhao, S.; Meng, Y. Hybrid algorithm based on improved extended shifting bottleneck procedure and GA for assembly job shop scheduling problem. Int. J. Prod. Res. 2020, 58, 2604–2625. [Google Scholar] [CrossRef]
- Abbaas, O.; Ventura, J.A. A multi-agent resource bidding algorithm for order acceptance and assembly job shop scheduling. Int. J. Prod. Res. 2024, 62, 4856–4883. [Google Scholar] [CrossRef]
- Talens, C.; Perez-Gonzalez, P.; Fernandez-Viagas, V.; Framinan, J.M. New hard benchmark for the 2-stage multi-machine assembly scheduling problem: Design and computational evaluation. Comput. Oper. Res. 2021, 158, 107364. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Z.; Zhang, G.; Huang, Z. Multi-objective evolutionary algorithm based flexible assembly job-shop rescheduling with component sharing for order insertion. Comput. Oper. Res. 2024, 169, 106744. [Google Scholar] [CrossRef]
- Yan, H.S.; Wan, X.Q. Self-reconfiguration and rescheduling of aero-engine assembly shop with rework disruption in knowledgeable manufacturing environment. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 237, 1230–1240. [Google Scholar] [CrossRef]
- Ho, J.W.; Huang, Y.S.; Fu, C.T. Dispatching problems for parallel machines in the TFT-LCD assembly process. Int. Trans. Oper. Res. 2021, 28, 2715–2732. [Google Scholar] [CrossRef]
- Qiu, J.; Liu, J.; Peng, C.; Chen, Q. A novel predictive–reactive scheduling method for parallel batch processor lot-sizing and scheduling with sequence-dependent setup time. Comput. Ind. Eng. 2024, 189, 109985. [Google Scholar] [CrossRef]
- Ba, Z.; Yuan, Y.; Liu, J. A modified memetic algorithm with multi-operation precise joint movement neighbourhood structure for the assembly job shop scheduling problem. Int. J. Prod. Res. 2024, 62, 6292–6324. [Google Scholar] [CrossRef]
- Brandimarte, P.; Fadda, E. A reduced variable neighborhood search for the just in time job shop scheduling problem with sequence dependent setup times. Comput. Oper. Res. 2024, 167, 106634. [Google Scholar] [CrossRef]
- Maxwell, W.L.; Mehra, M. Multiple-factor rules for sequencing with assembly constraints. Nav. Res. Logist. Q. 1968, 15, 241–254. [Google Scholar] [CrossRef]
- Siegel, G.B. An Investigation of Jobshop Scheduling for Jobs with Assembly Constraints; Cornell University: Ithaca, NY, USA, 1971. [Google Scholar]
- Reeja, M.K.; Rajendran, C. Dispatching rules for scheduling in assembly jobshop-part 1. Int. J. Prod. Res. 2000, 38, 2051–2066. [Google Scholar] [CrossRef]
- Natarajan, K.; Mohanasundaram, K.M.; Shoban Babu, B.; Suresh, K.; Raj, A.A.D.; Rajendran, C. Performance evaluation of priority dispatching rules in multi-level assembly job shops with jobs having weights for flowtime and tardiness. Int. J. Adv. Manuf. Technol. 2007, 31, 751–761. [Google Scholar] [CrossRef]
- Xie, Z.; Zhou, W.; Wang, J. Resource cooperative integrated scheduling algorithm based on sub-tree cycle decomposition of process tree. J. Mech. Eng. 2022, 58, 228–239. [Google Scholar]
- Xie, Z.; Zhou, W.; Wang, J. Resource cooperative integrated scheduling algorithm considering hierarchical scheduling order. Comput. Integr. Manuf. Syst. 2022, 28, 3391–3402. [Google Scholar]
- Pathumnakul, S.; Egbelu, P.J. An algorithm for minimizing weighted earliness penalty in assembly job shops. Int. J. Prod. Econ. 2006, 103, 230–245. [Google Scholar] [CrossRef]
- Zou, P.; Rajora, M.; Liang, S.Y. A new algorithm based on evolutionary computation for hierarchically coupled constraint optimization: Methodology and application to assembly job-shop scheduling. J. Sched. 2018, 21, 545–563. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zhang, B.; Wang, S. Multi-objective optimisation in flexible assembly job shop scheduling using a distributed ant colony system. Eur. J. Oper. Res. 2020, 283, 441–460. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Cao, D.; Li, M. A shuffled cellular evolutionary grey wolf optimizer for flexible job shop scheduling problem with tree-structure job precedence constraints. Appl. Soft Comput. 2022, 125, 109235. [Google Scholar] [CrossRef]
- Cheng, L.; Tang, Q.; Zhang, L.; Li, Z. Inventory and total completion time minimization for assembly job shop scheduling considering material integrity and assembly sequential constraint. J. Manuf. Syst. 2022, 65, 660–672. [Google Scholar] [CrossRef]
- Zheng, P.; Zhang, P.; Wang, M.; Zhang, J. A data-driven robust scheduling method integrating particle swarm optimization algorithm with kernel-based estimation. Appl. Sci. 2021, 11, 5333. [Google Scholar] [CrossRef]
- Jiang, T.H.; Wang, H.X. Study on the self-evolution problem of an aircraft-engine assembly workshop with uncertain number of assembly times. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1418–1428. [Google Scholar] [CrossRef]
- Wan, X.Q.; Yan, H.S. Integrated scheduling and self-reconfiguration for assembly job shop in knowledgeable manufacturing. Int. J. Prod. Res. 2015, 53, 1746–1760. [Google Scholar] [CrossRef]
- Hao, H.; Zhu, H.; Shen, L.; Zhen, G.; Chen, Z. Research on assembly scheduling problem with nested operations. Comput. Oper. Res. 2023, 175, 108830. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, C.; Fan, J.; Li, X.; Gao, L. A genetic algorithm with critical path-based variable neighborhood search for distributed assembly job shop scheduling problem. Swarm Evol. Comput. 2024, 85, 101485. [Google Scholar] [CrossRef]
- Lu, X.; Lu, C. Mixed-production flexible assembly job shop scheduling considering parallel assembly sequence variations under dual-resource constraints using multi-objective hybrid memetic algorithm. Comput. Oper. Res. 2025, 176, 106932. [Google Scholar] [CrossRef]
- Ma, X.; Bi, L.; Jiao, X.; Wang, J. An efficient and improved coronavirus herd immunity algorithm using knowledge-driven variable neighborhood search for flexible job-shop scheduling problems. Processes 2023, 11, 1826. [Google Scholar] [CrossRef]
- Adibi, M.A.; Shahrabi, J. A clustering-based modified variable neighborhood search algorithm for a dynamic job shop scheduling problem. Int. J. Adv. Manuf. Technol. 2014, 70, 1955–1961. [Google Scholar] [CrossRef]
- Ryu, M.; Ahn, K.I.; Lee, K. Finding effective item assignment plans with weighted item associations using a hybrid genetic algorithm. Appl. Sci. 2021, 11, 2209. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).