Abstract
Load frequency control (LFC) is essential for maintaining the stability of power systems subjected to load variations and renewable energy disturbances. This paper presents two advanced Proportional–Integral–Derivative–Acceleration (PIDA) controllers optimized using hybrid techniques: Teaching–Learning-Based Optimization combined with transit search (PIDA-TLBO-TS) and with Exponential Distribution Optimization (PIDA-TLBO-EDO). The proposed hybrid optimization approaches integrate global exploration and local exploitation capabilities to achieve near-global optimal solutions with superior convergence performance. Three test scenarios are studied to assess controller performance: a load disturbance in area 1, a disturbance in area 2, and a disturbance introduced by stochastic wave energy input. In each case, the proposed hybrid controllers are benchmarked against the conventional TLBO-based PIDA controller available in the literature. Simulation results confirm that the hybrid PIDA-TLBO-EDO controller consistently outperforms the alternatives in terms of peak-to-peak oscillation, root mean square (RMS) error, settling time, and overshoot. Specifically, it achieves a 0.49% to 15% reduction in peak-to-peak oscillations and a 2.5% to 18% improvement in RMS error, along with a 10.27% improvement in tie-line power deviation and a 15.38% reduction in frequency oscillations under wave energy disturbances. Moreover, the PIDA structure, enhanced by its acceleration term, contributes to better dynamic response compared to traditional controller designs. The results highlight the effectiveness and robustness of the proposed hybrid controllers in damping oscillations and maintaining system stability, particularly in modern power systems with high levels of renewable energy integration. This study emphasizes the potential of combining complementary optimization techniques to enhance LFC system performance under diverse and challenging conditions.
1. Introduction
One of the most critical issues in maintaining system frequency under various types of disturbance is load frequency control (LFC). Previous literature commonly used the two-area system, with each area having its own controller [1] to improve the transient performance of the system. The deviation in the tie-line power and the system frequency is calculated through the error in the area control (ACE). Equation (1) describes the error in a multi-area system [1].
where Pij is the power through the tie line and Bi is the biassing coefficient of the frequency of area “i”.
The literature has mostly used optimization-based controllers to enhance the transient response of the system. The authors of [1] used a hybrid partial swarm-based PI controller to reduce the index of performance (μ) given by Equation (2):
where a, b, and c are constants and |∆fi|, |∆fj|, and |∆Pt| represent changes in the frequency of area “i”, changes in the frequency of area ii, and the power through the tie, respectively. The results showed a large improvement in the system damping by using the PI controller. The authors of [2,3] discussed the importance of renewable energy and LFC challenges. Renewable energy sources (RESs) like solar and wind are critical for creating sustainable power systems, but their unpredictable and variable nature poses significant challenges. These fluctuations can upset the balance between electricity supply and demand, causing frequency instability in the power grid. Load frequency control (LFC) plays a vital role in maintaining this balance by adjusting generator output to match changing loads, keeping the system frequency stable (typically at 50 Hz or 60 Hz). Traditional LFC methods, originally designed for consistent fossil fuel-based generation, struggle to cope with the rapid changes introduced by RESs. As renewable energy use increases, advanced LFC strategies become essential to avoid issues like blackouts or equipment damage. The authors also made an evolution of LFC models and advanced techniques. LFC models have evolved from simple single-area systems to complex multi-area and deregulated setups, where coordination between regions and contractual agreements adds further complexity [2,4]. To manage RES variability, modern techniques include optimization algorithms, artificial intelligence like machine learning for predictive control, and energy storage systems, including batteries and FACTS devices. These innovations allow the grid to respond swiftly to fluctuations, with storage systems absorbing excess energy when RES output is high and supplying it during low-output periods. In microgrids, which often depend heavily on RESs, fast and tailored LFC strategies are particularly important to ensure stability in these smaller, localized networks [2,5]. Finally, the authors of [2] investigated future directions and research needs. The future of LFC in RES-integrated power systems hinges on improving grid resilience against disruptions, such as sudden drops in renewable output or cyberattacks. Research is needed to develop adaptive control methods that adjust dynamically to real-time conditions and to create scalable solutions for both large-scale grids and microgrids. As global adoption of RESs accelerates, ongoing innovation is critical to keep power systems stable and reliable during the shift to cleaner energy. These advancements will help ensure that the integration of renewable sources strengthens, rather than undermines, the performance of modern power grids. Different researchers studied the LFC with several controllers and optimizations methods. The authors of [6] introduced a new strategy for load frequency control (LFC) in power systems that rely heavily on renewable energy sources, such as wind and solar power. Renewable energy can make maintaining a stable frequency challenging because its output fluctuates. To address this, the authors propose using an advanced PIλ(1 + PDF) controller, a type of control system fine-tuned with the Zebra Optimization Algorithm (ZOA) to keep the frequency steady. They also combine this controller with a hybrid energy storage system, which includes a Vanadium Redox Flow Battery (VRFB) and superconducting magnetic energy storage (SMES), to smooth out power variations. Additionally, an IPFC-FACTS device (Interline Power Flow Controller—Flexible AC Transmission System) is used to improve power flow management across the system. The approach was tested on a four-area power system, where it successfully reduced frequency deviations and enhanced stability under different operating conditions. The authors of [7] introduce a method for automatic generation control (AGC) in a three-area interconnected power system, utilizing fuzzy logic controllers (FLCs) and superconducting magnetic energy storage (SMES) units. The system comprises two steam turbines and one hydro turbine, facing frequency deviations and tie-line power fluctuations due to unpredictable load changes. The proposed fuzzy PI-type controller outperforms traditional PI controllers by reducing settling time and overshoot, while SMES units enhance stability by rapidly managing energy during load disturbances. Simulations conducted using MATLAB R2021a demonstrate that integrating FLCs with SMES units significantly improves the system’s dynamic performance compared to conventional approaches. Other researchers explored load frequency control (LFC) in a two-area interconnected power system using a fuzzy gain scheduling PI (FGPI) controller. It aims to maintain stable frequency and tie-line power flow despite load disturbances. The proposed FGPI controller adjusts proportional and integral gains dynamically using seven fuzzy rules, outperforming conventional PI controllers and other fuzzy methods like those by Chang and Akalın. Simulations show it achieves shorter settling times and comparable overshoots, offering a simple, effective solution for reliable power system performance without requiring detailed system parameter knowledge [8]. The authors of [9] proposed an optimized control system for photovoltaic (PV) systems under partial shading (PS) conditions using the emperor penguin optimizer (EPO) algorithm. The EPO optimizes the initial duty cycle of the boost converter and tunes the gains of the PI controller and second-order amplifier (SOA) to maximize power extraction from PV arrays. The system’s performance is compared with the cuttlefish algorithm (CFA) and particle swarm optimization (PSO) across various PS scenarios. Results from MATLAB/SIMULINK simulations show that EPO enhances power harvesting, reduces oscillations, and ensures robustness under dynamic irradiance changes, outperforming CFA and offering a simpler alternative to PSO. The authors of [10] investigated load frequency control (LFC) in single- and two-area power systems using PI, PID, fuzzy logic (FLC), and fuzzy-tuned PI (FTPI) controllers. This addresses frequency deviations caused by varying load demands. Simulations show that the conventional PI controller effectively minimizes frequency deviation, while the FTPI controller excels in reducing settling time. By dynamically adjusting PI gains with fuzzy logic based on error signals, the FTPI achieves a balanced response with minimal frequency deviation and faster stabilization compared to other controllers. The authors of [11] proposed a Bacteria Foraging Optimization Algorithm (BFOA) to tune PI controllers for load frequency control (LFC) in a two-area interconnected power system. The BFOA optimizes controller parameters to minimize frequency deviations and tie-line power oscillations, using an integral of time multiplied by absolute error (ITAE) objective function. Simulation results demonstrate that the BFOA-tuned PI controller outperforms conventional PI controllers and genetic algorithm (GA)-tuned controllers, offering superior damping, reduced settling time, and robustness across various operating conditions and parameter variations. The authors of [12] explored the use of an Artificial Neural Network (ANN) controller for automatic generation control (AGC) in a four-area interconnected power system, comprising three steam turbine areas with reheat effects and one hydro turbine area with generation rate constraints. The ANN, utilizing a back propagation-through-time algorithm, controls all areas simultaneously to manage frequency and tie-line power deviations caused by load perturbations. Simulation results show that the ANN controller outperforms conventional integral controllers, achieving faster settling times and better dynamic response under various load conditions. The authors of [13] presented a robust PID controller optimized using the Imperialist Competitive Algorithm (ICA) for load frequency control (LFC) in a three-area power system. The controller addresses load disturbances—small, rapid load changes—using a first-order low-pass filter to enhance stability. The ICA tunes the PID parameters to minimize frequency deviations and tie-line power oscillations across a wide range of load changes, considering turbine nonlinearities. MATLAB/SIMULINK simulations of a three-area system show that the proposed PID controller outperforms genetic algorithm (GA)- and Neural Network-optimized PI controllers, offering faster response, reduced overshoot, and improved dynamic performance. The authors of [14] investigated automatic generation control (AGC) in interconnected thermal systems with two equal areas, three unequal areas, and five unequal areas, each equipped with single reheat turbines and generation rate constraints of 3% per minute. It introduces a novel Integral–Double Derivative (IDD) controller and compares its performance with classical controllers (I, PI, ID, PID). Controller gains for the two-area system are optimized classically, while the Bacterial Foraging (BF) technique is used to simultaneously optimize gains and governor speed regulation parameters in the multi-area systems. Results show that the IDD controller outperforms others, offering superior dynamic response. Sensitivity analysis confirms its robustness to changes in loading, system parameters, and step-load perturbations. Other researchers introduced a novel robust PID controller for automatic generation control (AGC) in hydro turbine power systems. Utilizing the Nichols chart, the controller ensures the open-loop frequency response aligns with a specified ellipse, enhancing overshoot control, stability, and system dynamics. Tested on a multimachine hydro-power system, the proposed PID controller outperforms conventional PI controllers and another PID design using the QFT method, demonstrating improved damping and robustness across a wide range of operating conditions. By eliminating the transient droop compensator, it achieves faster dynamic responses. Other controllers with PSO, harmony search, the cuttlefish algorithm, emperor penguin optimizers, and fuzzy logic are presented in [15,16,17] and proved their superiority through their low settling time and overshoot. The authors of [18] improved the two-area system by using the fuzzy gain controller. The authors of [19] used an integral derivative differential evaluation-based technique and proved its validation through comparison with other optimization techniques. An adaptive PID weighted particle swarm-based technique is presented in [20], proving its superiority over GA and PSO optimizations. The nonlinearity in the governor is taken into consideration in [21] by using the differential evolution technique. The Laurent series expands the controller transfer function in [22]. The two-area system is improved by using the firefly technique in [23]. The authors of [24,25] used gravitational search and differential evaluation techniques. Three areas of fuzzy PID-PSO-based techniques are presented in [26]. At the same time, Kharitonov’s theorem and the locus of stability boundary dampen the oscillation in the LFC system [27]. Combined thermal and PV generators are presented in [28]. Conventional PID is presented in [29]. The tilt integral derivative is presented in [30], and its validation is proven through comparison with conventional controllers. A fractional controller based in flower pollination is used in [31] to enhance the AGC system. Double derivative-based PID, cascaded PD, and a PID BAT technique-based controller with two degrees of freedom based on the Cuckoo search technique and PIDA-TLBO are presented in [32,33] to enhance the LFC performance under different disturbances. The authors of [34] studied different schemes of LFC with integrated wind generators. The authors of [35] proposed a detailed analysis of the LFC event triggered using the Lyapunov functional. This proved the reliability of the system by applying the proposed controller to the IEEE 39 bus system. Other authors have studied the LFC adaptive controller based on the scale of a microgrid [36]. The authors of [37] proposed a novel load frequency control (LFC) strategy for modern power systems by integrating Proportional–Integral–Derivative (PID) controllers with the Gray Wolf Optimizer (GWO) algorithm. Addressing the increasing complexity of multi-area power systems, including configurations with thermal, hydro, and wind energy sources, the study presents two simulation cases to evaluate system response to load disturbances and renewable variability. The results demonstrate that GWO-optimized PID controllers significantly enhance frequency stability, reduce oscillations, and achieve faster recovery times compared to traditional methods. The authors of [38] introduced a novel low-delay dynamic event-triggered mechanism (DETM) and integrate it with a distributed model predictive control (DMPC) strategy to enhance load frequency control (LFC) in virtual power plants (VPPs) operating under a cloud-edge-terminal framework. By incorporating an adaptive adjustment variable and a dynamic variable into the DETM, the method effectively manages data packet transmissions, significantly reducing communication delays and network congestion. The proposed event-based DMPC framework allows edge-based controllers to independently process control actions, minimizing latency compared to traditional centralized approaches. Extensive case studies on a two-area power system demonstrate the proposed algorithm’s superiority in reducing average triggering rates, data processing time, and communication overhead, while maintaining robust control performance. The authors of [39] explored the enhancement of load frequency control (LFC) in a two-area interconnected power system using superconducting magnetic energy storage (SMES). The system comprises diverse energy sources—hydroelectric and thermal (steam) power plants in area 1, and a gas power plant in area 2—modeled via state-space equations representing a fifteenth-order dynamic system. By integrating SMES, which leverages superconducting coils to store energy in a magnetic field with rapid charge–discharge capabilities, the study demonstrates significant improvements in frequency stability. MATLAB simulations reveal that SMES reduces frequency deviations, dampens power oscillations, and shortens recovery times following disturbances, such as sudden load changes, compared to a system without SMES. The authors of [40] presented a novel Lyrebird Optimization Algorithm (LOA), inspired by the behavioral strategies of lyrebirds, to optimize the parameters of a Proportional–Integral–Derivative controller with a filter (PIDn) for enhanced load frequency control (LFC) in a two-area interconnected power system comprising non-reheat thermal stations. The study incorporates generation rate constraints (GRCs) and evaluates the LOA-PIDn approach through simulations across three disturbance scenarios, comparing its performance against established methods such as Ziegler–Nichols (ZN), the genetic algorithm (GA), the Bacteria Foraging Optimization Algorithm (BFOA), the Firefly Algorithm (FA), and others. The results highlight the LOA’s superiority, achieving a lower integral of time multiplied by absolute error (ITAE) and faster settling times for frequency deviations and tie-line power variances, thus improving system stability and reliability.
In this article, PIDA hybrid TLBO-TS-based and PIDA hybrid TLBO-EDO-based methods are presented in each area of the two LFC systems. Three cases are studied; the first is a disturbance in area 1. The second case is a disturbance in area 2. The third case is a disturbance of renewable energy through wave energy. In each case, the presented controller is compared to the PIDA-TLBO base presented in the literature. The main contribution of this paper lies in the integration of two optimization techniques, one characterized by strong exploration capabilities and the other by effective exploitation. This hybrid approach ensures convergence toward a near-global optimal solution and demonstrates superior performance compared to individual optimization methods reported in the literature. Additionally, the PIDA controller, enhanced by its acceleration term, outperforms the conventional controller in terms of overall system performance.
The main contributions of this paper are as follows:
- Developed a hybrid optimization approach that integrates techniques with strong exploration (global search) and exploitation (local refinement) capabilities.
- Introduced this hybrid optimization to tune PIDA controllers for load frequency control (LFC) systems.
- Demonstrated that the hybrid methods ensure convergence toward near-global optimal solutions.
- Showed that the proposed hybrid controllers achieve better system performance compared to individual optimization methods from the literature through three distinct disturbance scenarios, including renewable energy disturbance.
- Highlighted the advantage of the PIDA controller structure, specifically the acceleration term, in enhancing overall system performance over conventional controllers.
This paper is organized as follows: Section 1 introduces the importance of LFC and reviews existing literature on optimization-based controllers. Section 2 details the proposed hybrid optimization techniques, TS and EDO, along with the TLBO algorithm. Section 3 describes the system under study, including the two-area power system model. Section 4 presents the mathematical formulation of the PIDA controller. Section 5 defines the objective function used for optimization. Section 6 models the wave energy disturbance. Section 7 provides simulation results and statistical analysis for three case studies, comparing the performance of the proposed controllers. Section 8 provides the results discussion. Finally, Section 9 concludes the paper by summarizing the findings and highlighting the potential of the proposed controllers in improving LFC performance in modern power systems.
2. Optimization Techniques
This article uses two hybrid techniques to tune the LFC controller parameters. The first is a hybrid TLBO-TS, and the second is a hybrid TLBO-EDO. In the hybrid method, TLBO is first used to tune the controller; after that, the results with ±10% are used as a search range for the TS and EDO to select suitable gains.
2.1. Transit Search (TS)
The TS algorithm mainly consists of five phases: the galaxy phase, transit phase, planet phase, neighbor phase, and exploitation phase. The galaxy phase involves choosing a galaxy and determining the best number of the star’s host. The transit phase involves detecting any reduction in the received lights, determining the distance between the telescope and the stars, and finally finding the new brightness of the stars. The planet phase involves defining the observed planet’s location and keeping it as the best location for the host star. The neighbor phase involves following all steps for the neighbor planet, as in the planet phase. The exploitation phase involves determining the best planet after neglecting the noise. The flowchart of the TS is shown in Figure 1 [41,42].

Figure 1.
Flowchart of the TS optimization algorithm.
2.2. Exponential Distribution (EDO)
This method depends on a certain probability distribution function (PDF) to obtain the time taken to the event occurrence. In its exploration phase, it depends on key factors such as the mean, variance, and memoryless property to update the solutions. In the exploration phase, the EDO is developed using the initial population to take two random parameters. The EDO flowchart is shown in Figure 2 [43].
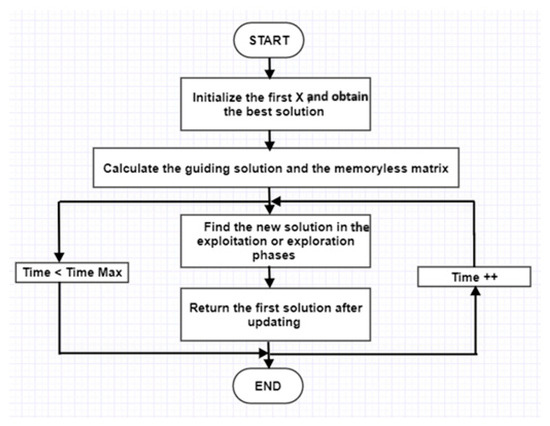
Figure 2.
EDO algorithm flowchart. “Time ++” means increment the time counter by 1.
2.3. Teaching–Learning-Based Optimization (TLBO)
Rao [44] proposed the TLBO optimization method in 2011. It was based on the interaction between students and a teacher. TLBO is based on several steps, such as initializing the parameters, and then the learner is modified by calculating the solution array. These steps are repeated till the stopping criteria are reached, as shown in Figure 3.

Figure 3.
TLBO algorithm flowchart.
3. System Under Study
In this article, the two systems presented in [33] are used to validate the proposed LFC systems, as shown in Figure 4.
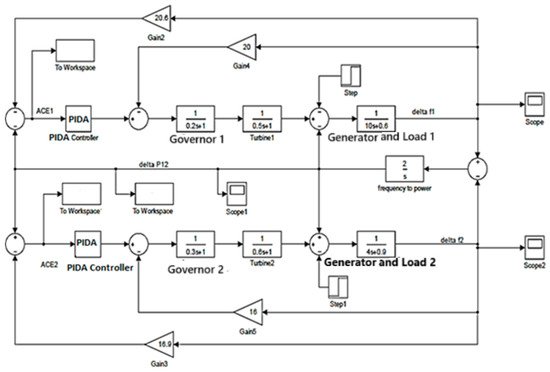
Figure 4.
The system under study.
The model parameters are as follows:
- The system speed regulation is 0.05 for area 1 and 0.0625 for area 2.
- The sensitive frequency coefficient is 0.6 for area 1 and 0.9 for area 2.
- The inertia coefficients are 5 and 4 for area 1 and area 2, respectively.
- The time constants of the governor are 0.2 and 0.3, respectively.
- The time constants of the turbines are 0.5 and 0.6 for areas 1 and 2, respectively.
4. PIDA Controller
The PIDA controller is the same as the PID controller, with an additional acceleration block. The acceleration block enhances the performance of the system by decreasing the transient time and damping the oscillations. The PIDA controller is mathematically expressed in the time domain by Equation (3) and in the Laplace domain by Equation (4) [45]:
where U(t) and e(t) are the system output and error, respectively. Kp, Ki, Kd, and Ka are the proportional, integral, derivative, and acceleration blocks, respectively.
where a and b are time constants.
5. Objective Function
The objective function is the sum of square input errors to the system controller. This objective function aims to minimize both the errors in the frequencies of the two areas simultaneously. Equation (5) presents the objective function [33].
where T is the MATLAB time of simulation.
6. Wave Modeling
Different disturbances are used in this article; one is the wave energy disturbance, one of the most promising renewable energy sources. The Archimedes converting system with a linear PM synchronous machine (LSG) is used in the article [46,47]. The equations of the system are as follows [46,48].
7. Simulation Results
7.1. Case 1
A step input disturbance of 1% load change is applied to the first area of the system. At the same time, the second area is free of disturbance. The parameters of the LFC controller in both areas with TLBO hybrid EDO and TLBO hybrid TS are shown in Table 1 and Table 2, respectively. The changes in area frequencies and in the tie power are shown in Figure 5, Figure 6 and Figure 7.

Table 1.
PIDA parameters with TLBO hybrid EDO case 1.

Table 2.
PIDA parameters with TLBO hybrid TS case 1.

Figure 5.
Delta F1 case 1.

Figure 6.
Delta F2 case 1.
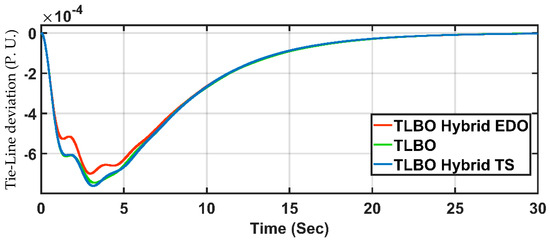
Figure 7.
Tie-line power deviation case 1.
From Table 3, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO Hybrid TS-based method by 0.49% and the PIDA TLBO-based method [33] by 0.49%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 7.62% and the PIDA TLBO-based RMS [33] by 7.71%, with almost the same STD in all methods.

Table 3.
The statistical parameters of area 1 frequency case 1.
From Table 4, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO hybrid TS-based method by 2.43% and the PIDA TLBO-based method [33] by 3.65%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 6.09% and the PIDA TLBO-based RMS [33] by 6.74%, with almost the same STD in all methods.

Table 4.
The statistical parameters of area 2 frequency case 1.
From Table 5, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO Hybrid TS-based method by 10.14% and the PIDA TLBO-based method [33] by 7.25%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 6.47% and the PIDA TLBO-based RMS [33] by 6.24%, with almost the same STD in all methods.

Table 5.
The statistical parameters of tie-line power case 1.
7.2. Case 2
A step input disturbance of 1% load change is applied to the second area of the system. At the same time, the first area is free of disturbance. The parameters of the LFC controller in both areas with TLBO hybrid EDO and TLBO hybrid TS are shown in Table 6 and Table 7, respectively. The changes in area frequencies and in the tie power are shown in Figure 8, Figure 9 and Figure 10.

Table 6.
PIDA parameters with TLBO hybrid EDO case 2.

Table 7.
PIDA parameters with TLBO hybrid TS case 2.

Figure 8.
Delta F1 case 2.

Figure 9.
Delta F2 case 2.
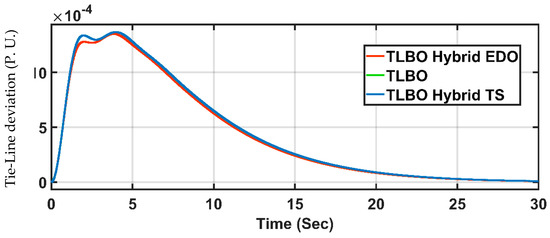
Figure 10.
The tie-line power deviation, case 2.
The results of case 2 are shown in Figure 8, Figure 9 and Figure 10, and the statistical analysis is presented in Table 8, Table 9 and Table 10.

Table 8.
The statistical parameters of area 1 frequency case 2.

Table 9.
The statistical parameters of area 2 frequency case 2.

Table 10.
The statistical parameters of tie-line power case 2.
From Table 8, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO hybrid TS-based method by 5.38% and the PIDA TLBO-based method [33] by 5.38%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 2.61% and the PIDA TLBO-based RMS [33] by 2.58%, with almost the same STD in all methods.
From Table 9, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO hybrid TS-based method by 5.75% and the PIDA TLBO-based method [33] by 5.75%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 3.52% and the PIDA TLBO-based RMS [33] by 3.57%, with almost the same STD in all methods.
From Table 10, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO hybrid TS-based method by 0.74% and the PIDA TLBO-based method [33] by 0.74%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 2.47% and the PIDA TLBO-based RMS [33] by 2.44%, with almost the same STD in all methods.
7.3. Case 3
A wave disturbance is applied to the first area of the system. At the same time, a step input disturbance is applied to the second area. The results of case 3 are shown in Figure 11, Figure 12 and Figure 13, and the statistical analysis is presented in Table 11, Table 12 and Table 13. The changes in area frequencies and in the tie power are shown in Figure 11, Figure 12 and Figure 13.
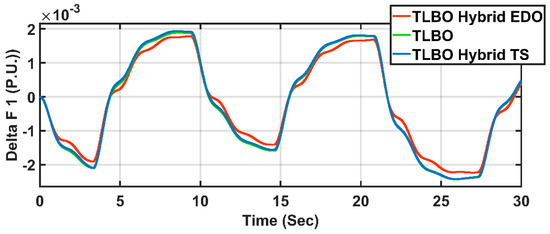
Figure 11.
Delta F1 case 3.
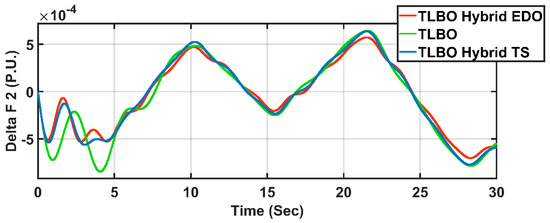
Figure 12.
Delta F2 case 3.

Figure 13.
The tie-line power deviation, case 3.

Table 11.
The statistical parameters of area 1 frequency case 3.

Table 12.
The statistical parameters of area 2 frequency case 3.

Table 13.
The statistical parameters of tie-line power case 3.
From Table 11, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO hybrid TS-based method by 5.55% and the PIDA TLBO-based method [33] by 8.34%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 15.38% and the PIDA TLBO-based RMS [33] by 15.38%, with almost the same STD in all methods.
From Table 12, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO hybrid TS-based method by 9.4% and the PIDA TLBO-based method [33] by 15.38%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 9.38% and the PIDA TLBO-based RMS [33] by 18.19%, with almost the same STD in all methods.
From Table 13, it is clear that the PIDA TLBO hybrid EDO-based method has better oscillation and overshoot, where the peak-to-peak oscillation is better than the PIDA TLBO hybrid TS-based method by 10.27% and the PIDA TLBO-based method [33] by 11.64%. Moreover, the PIDA TLBO hybrid EDO-based RMS is better than the PIDA TLBO hybrid TS-based RMS by 10.52% and the PIDA TLBO-based RMS [33] by 12.28%, with almost the same STD in all methods.
8. Discussion
The analysis of the three cases demonstrates the superior performance of the PIDA TLBO hybrid EDO-based method over both the PIDA TLBO hybrid TS-based and the baseline PIDA TLBO-based [33] methods across multiple metrics. In case 1, the EDO-based approach consistently outperformed others, achieving peak-to-peak oscillation improvements ranging from 0.49% to 10.14% and RMS reductions of 6.09% to 7.71%, with negligible differences in standard deviation (STD) across all methods. Case 2 showed similar trends, though with smaller margins, where the EDO-based method improved peak-to-peak oscillations by 0.74% to 5.75% and RMS by 2.44% to 3.57%, again maintaining a comparable STD. Case 3 exhibited the most significant enhancements, particularly in RMS, with reductions of up to 18.19% and peak-to-peak oscillation improvements ranging from 5.55% to 15.38%, while the STD remained consistent. These results collectively highlight the EDO-based method’s robustness in minimizing oscillations and overshoot, with case 3 showing the most pronounced benefits, likely due to its specific system dynamics. The consistent STD across methods suggests that the EDO-based approach achieves these improvements without compromising stability, making it a promising choice for optimizing control performance in the tested scenarios.
9. Conclusions
This paper presents a PIDA controller to enhance the performance of the load frequency control (LFC) system. Two relatively recent optimization techniques are employed to tune the PIDA controller: a hybrid TLBO-TS approach and a hybrid TLBO-EDO approach. The LFC system is evaluated under various disturbance scenarios. Three cases are investigated: the first two involve load changes in different areas, while the third considers a wave energy disturbance. The results indicate that the PIDA controller tuned using the hybrid TLBO-EDO method achieves superior performance in terms of peak-to-peak oscillation and RMS values, with improvements of approximately 0.49–10% and 2.5–15%, respectively, compared to the hybrid TLBO-TS approach, and about 0.49–15% and 2.5–18%, respectively, compared to the standard TLBO-based PIDA controller. It is recommended that future works study the LFC with accurate battery modeling (charge–discharge dynamics, aging, and degradation effects). Also, it is recommended that the proposed controllers be implemented on a Real-Time Digital Simulator (RTDS) platform, which will enable hardware-in-the-loop testing under conditions closely resembling real power system environments.
Author Contributions
Conceptualization, A.M.S.; Methodology, A.M.S.; Software, M.A.A.; Validation, S.F.M.; Formal analysis, H.K.; Writing—original draft, A.M.S., M.A.A. and S.F.M.; Writing—review & editing, H.K., M.A.I. and A.M.; Supervision, A.M.; Funding acquisition, M.A.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| The damping factor of the hydraulic system | |
| The constant of the spring | |
| v | The linear speed of the LSG rotor |
| Electromagnetic force | |
| The floater force | |
| , | The currents and voltages of the stator |
| The inductance of the stator | |
| The stator resistance | |
| The PM flux | |
| λ | Pole width |
References
- Saiuree, R.; Reddy, K. A comprehensive review of load frequency control of decentralized networks. In Proceedings of the 2025 33rd Southern African Universities Power Engineering Conference (SAUPEC), Centurion, South Africa, 29–30 January 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 1–6. [Google Scholar]
- Masikana, S.B.; Sharma, G.; Sharma, S. Renewable energy sources integrated load frequency control of power system: A review. e-Prime—Adv. Electr. Eng. Electron. Energy 2024, 8, 100605. [Google Scholar] [CrossRef]
- Biswas, S.; Roy, P.K.; Chatterjee, K. FACTS-based 3DOF-PID controller for LFC of renewable power system under deregulation using GOA. IETE J. Res. 2023, 69, 1486–1499. [Google Scholar] [CrossRef]
- Singh, V.P.; Waghmare, A.V.; Meena, V.P.; Benedetto, F.; Varshney, T. Rank exponent method based optimal control of AGC for two-area interconnected power systems. IEEE Access 2024, 12, 35571–35585. [Google Scholar]
- Peddakapu, K.; Mohamed, M.R.; Srinivasarao, P.; Arya, Y. Assessment of energy storage and renewable energy sources-based two-area microgrid system using optimized fractional order controllers. J. Energy Storage 2024, 86, 111191. [Google Scholar] [CrossRef]
- Khan, I.A.; Mokhlis, H.; Mansor, N.N.; Illias, H.A.; Daraz, A.; Ramasamy, A.K.; Marsadek, M.; Afzal, A.R. Load frequency control in power systems with high renewable energy penetration: A strategy employing PIλ (1 + PDF) controller, hybrid energy storage, and IPFC-FACTS. Alex. Eng. J. 2024, 106, 337–366. [Google Scholar] [CrossRef]
- Demiroren, A.; Yesil, E. Automatic generation control with fuzzy logic controllers in the power system including SMES units. Electr. Power Energy Syst. 2024, 26, 291–305. [Google Scholar] [CrossRef]
- Cam, E.; Kocaarslan, I. Load frequency control in two area power systems using fuzzy logic controller. Energy Convers. Manag. 2005, 46, 233–243. [Google Scholar] [CrossRef]
- Sameh, M.A.; Marei, M.I.; Badr, M.A.; Attia, M.A. An optimized PV control system based on the Emperor Penguin Optimizer. Energies 2021, 14, 751. [Google Scholar] [CrossRef]
- Thenmalar, K. Fuzzy logic based load frequency control of power system. Mater. Today Proc. 2021, 45, 8170–8175. [Google Scholar]
- Ali, E.S.; Abd-Elazim, S.M. Bacteria foraging optimization algorithm based load frequency controller for interconnected power system. Electr. Power Energy Syst. 2011, 33, 633–638. [Google Scholar] [CrossRef]
- Zeynelgil, H.L.; Demiroren, A.; Sengor, N.S. The application of ANN technique to automatic generation control for multi area system. Electr. Power Energy Syst. 2002, 24, 345–354. [Google Scholar] [CrossRef]
- Shabani, H.; Vahidi, B.; Ebrahimpour, M. A robust PID controller based on imperialist competitive algorithm for load-frequency control of power systems. ISA Trans. 2012, 52, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Saikia, L.C.; Nanda, J.; Mishra, S. Performance comparison of several classical controllers in AGC for multi-area interconnected thermal system. Electr. Power Energy Syst. 2011, 33, 394–401. [Google Scholar] [CrossRef]
- Mokhtar, M.; Marei, M.I.; El-Sattar, A.A. Improved Current Sharing Techniques for DC Microgrids. Electr. Power Compon. Syst. 2018, 46, 757–767. [Google Scholar] [CrossRef]
- Sameh, M.A.; Attia, M.A.; Marei, M.I.; Badr, M.A. Enhancing the Performance of Photovoltaic Systems under Partial Shading Conditions Using Cuttlefish Algorithm. In Proceedings of the IEEE Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019. [Google Scholar]
- Sameh, M.A.; Badr, M.A.; Badr, M.A.L.; Marei, M.I.; Attia, M.A. Optimized PIA Controller for Photovoltaic System Using Hybrid Particle Swarm Optimization and Cuttlefish Algorithm. In Proceedings of the IEEE Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 1102–1108. [Google Scholar]
- Juang, C.-F.; Lu, C.-F. Power system load frequency control by genetic fuzzy gain scheduling controller. J. Chin. Inst. Eng. 2011, 28, 1013–1018. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Biswal, A.; Sekhar, G.C. Design and analysis of tilt integral derivative controller with filter for load frequency control of multi-area interconnected power systems. ISA Trans. 2016, 61, 251–264. [Google Scholar] [CrossRef] [PubMed]
- Sharifi, A.; Sabahi, K.; Shoorehdeli, M.A.; Nekoui, M.; Teshnehlab, M. Load Frequency Control in Interconnected Power System using Multi-Objective PID Controller. In Proceedings of the IEEE Conference on Soft Computing in Industrial Applications, Muroran, Japan, 25–27 June 2008; pp. 25–27. [Google Scholar]
- Mohanty, B.; Panda, S.; Hota, P.K. Differential evolution algorithm based automatic generation control for interconnected power systems with non-linearity. Alex. Eng. J. 2014, 53, 537–552. [Google Scholar] [CrossRef]
- Padhan, D.G.; Majhi, S. A new control scheme for PID load frequency controller of single-area and multi-area power systems. ISA Trans. 2013, 52, 242–251. [Google Scholar] [CrossRef]
- Padhan, S.; Sahu, R.K.; Panda, S. Application of firefly algorithm for load frequency control of multi-area interconnected power system. Electr. Power Compon. Syst. 2014, 42, 1419–1430. [Google Scholar] [CrossRef]
- Rout, U.K.; Sahu, R.K.; Panda, S. Design and analysis of differential evolution algorithm based automatic generation control for interconnected power system. Ain Shams Eng. J. 2013, 4, 409–421. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Padhan, S. Optimal gravitational search algorithm for automatic generation control of interconnected power systems. Ain Shams Eng. J. 2014, 5, 721–733. [Google Scholar] [CrossRef]
- Shayeghi, H.; Jalili, A.; Shayanfar, H. Multi-stage fuzzy load frequency control using PSO. Energy Convers. Manag. 2008, 49, 2570–2580. [Google Scholar] [CrossRef]
- Saxena, S.; Hote, Y.V. Decentralized PID load frequency control for perturbed multi-area power systems. Electr. Power Energy Syst. 2016, 81, 405–415. [Google Scholar] [CrossRef]
- Abd-Elazim, S.M.; Ali, E.S. Load frequency controller design of a two-area system composing of PV grid and thermal generator via firefly algorithm. Neural Comput. Applic 2016, 30, 607–616. [Google Scholar] [CrossRef]
- Shankar, G.; Mukherjee, V. Quasi oppositional harmony search algorithm based controller tuning for load frequency control of multi-source multi-area power system. Electr. Power Energy Syst. 2016, 75, 289–302. [Google Scholar] [CrossRef]
- Topno, P.N.; Chanana, S. Non-integer order control for LFC problem of two-area thermal power system with GRC. In Proceedings of the International Conference on Innovations in Electrical, Electronics, Instrumentation and Media Technology (ICEEIMT), Coimbatore, India, 3–4 February 2017. [Google Scholar]
- Debbarma, S.; Dutta, A. Utilizing Electric Vehicles for LFC in Restructured Power Systems Using Fractional Order Controller. IEEE Trans. Smart Grid 2017, 8, 2554–2564. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Multi-verse optimisation: A novel method for solution of load frequency control problem in power system. IET Gener. Transm. Distrib. 2017, 11, 3601–3611. [Google Scholar] [CrossRef]
- Mostafa Elsaied, M.; Abdallah Attia, M.; Abdelhamed Mostafa, M.; Fouad Mekhamer, S. Application of different optimization techniques to load frequency control with WECS in a multi-area system. Electr. Power Compon. Syst. 2018, 46, 739–756. [Google Scholar] [CrossRef]
- Asghar, R.; Fulginei, F.R.; Wadood, H.; Saeed, S. A Review of Load Frequency Control Schemes Deployed for Wind-Integrated Power Systems. Sustainability 2023, 15, 8380. [Google Scholar] [CrossRef]
- Huang, T.; Lv, X. Load Frequency Control of Power System Based on Improved AFSA-PSO Event-triggering Scheme. Front. Energy Res. 2023, 11, 1235467. [Google Scholar] [CrossRef]
- Abubakr, H.; Guerrero, J.M.; Vasquez, J.C.; Mohamed, T.H.; Mahmoud, K.; Darwish, M.M.F.; Dahab, Y.A. Adaptive LFC incorporating modified virtual rotor to regulate frequency and tie-line power flow in multi-area microgrids. IEEE Access 2022, 10, 33248–33268. [Google Scholar] [CrossRef]
- Tuan, D.H.; Tran, D.T.; Thanh, V.N.N.; Van Huynh, V. Load Frequency Control Based on Gray Wolf Optimizer Algorithm for Modern Power Systems. Energies 2025, 18, 815. [Google Scholar] [CrossRef]
- Kang, K.; Shi, N.; Cai, S.; Zhang, L.; Shao, X.; Cao, H.; Fei, M.; Zhou, S.; Wan, X. Distributed model predictive load frequency control for virtual power plants with novel event-based low-delay technique under cloud-edge-terminal framework. Energies 2025, 18, 1380. [Google Scholar] [CrossRef]
- Shahgholian, G.; Fathollahi, A. Advancing Load Frequency Control in Multi-Resource Energy Systems Through Superconducting Magnetic Energy Storage. AppliedMath 2025, 5, 1. [Google Scholar] [CrossRef]
- El-Rifaie, A.M. A Novel Lyrebird Optimization Algorithm for Enhanced Generation Rate-Constrained Load Frequency Control in Multi-Area Power Systems with Proportional Integral Derivative Controllers. Processes 2025, 13, 949. [Google Scholar] [CrossRef]
- Mirrashid, M.; Naderpour, H. Transit search: An optimization algorithm based on exoplanet exploration. Results Control Optim. 2022, 7, 100127. [Google Scholar] [CrossRef]
- Haswell, C.A. Transiting Exoplanets; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Shawqran, A.M.; El-Marhomy, A.; Attia, M.A.; Kamh, M.Z. Novel blade angle controllers techniques based on heuristics algorithms. Ain Shams Eng. J. 2022, 13, 101782. [Google Scholar] [CrossRef]
- Ahn, S.; Haas, K.A.; Neary, V.S. Dominant Wave Energy Systems and Conditional Wave Resource Characterization for Coastal Waters of the United States. Energies 2020, 13, 3041. [Google Scholar] [CrossRef]
- Marei, M.I.; Mokhtar, M.; El-Sattar, A.A. MPPT strategy based on speed control for AWS-based wave energy conversion system. Renew. Energy 2015, 83, 305–317. [Google Scholar] [CrossRef]
- Mokhtar, M.; Marei, M.I.; Sameh, M.A.; Attia, M.A. An adaptive load frequency control for power systems with renewable energy sources. Energies 2022, 15, 573. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).