Effect of Precipitated Bubbles on the Behavior of Gas–Liquid Two-Phase Flow in Ruhrstahl Heraeus Refining
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Principles
2.1.1. Geometric Similarity
2.1.2. Dynamic Similarity
2.1.3. Precipitated Bubble Similarity Criteria
2.1.4. Vacuum Degree Similarity
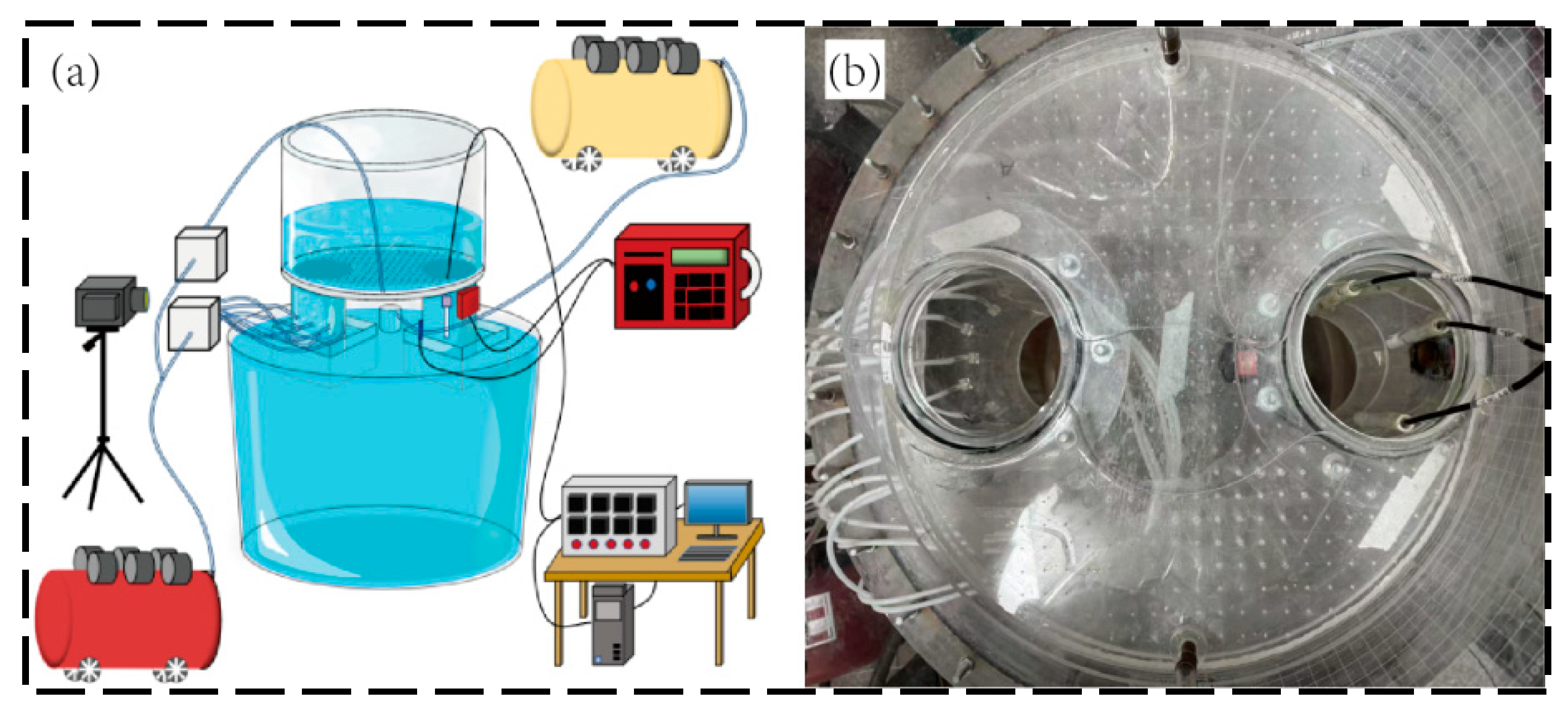
2.2. Experimental Setup
2.3. Experimental Measurement Methods
- (1)
- Circulation flow
- (2)
- Mixing time
- (3)
- Vacuum chamber dwell time
- (4)
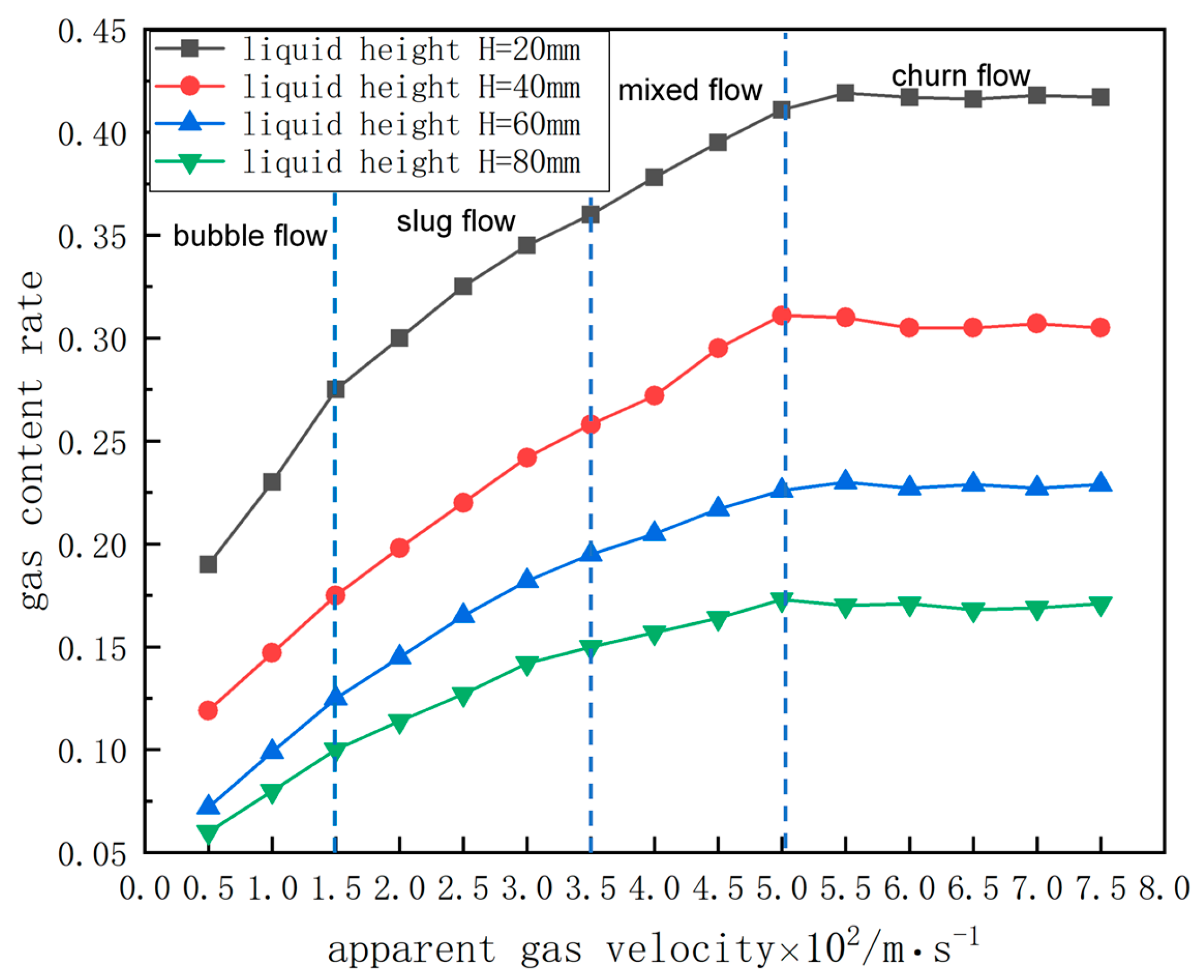
- Gas content
2.4. Experimental Program
3. Results
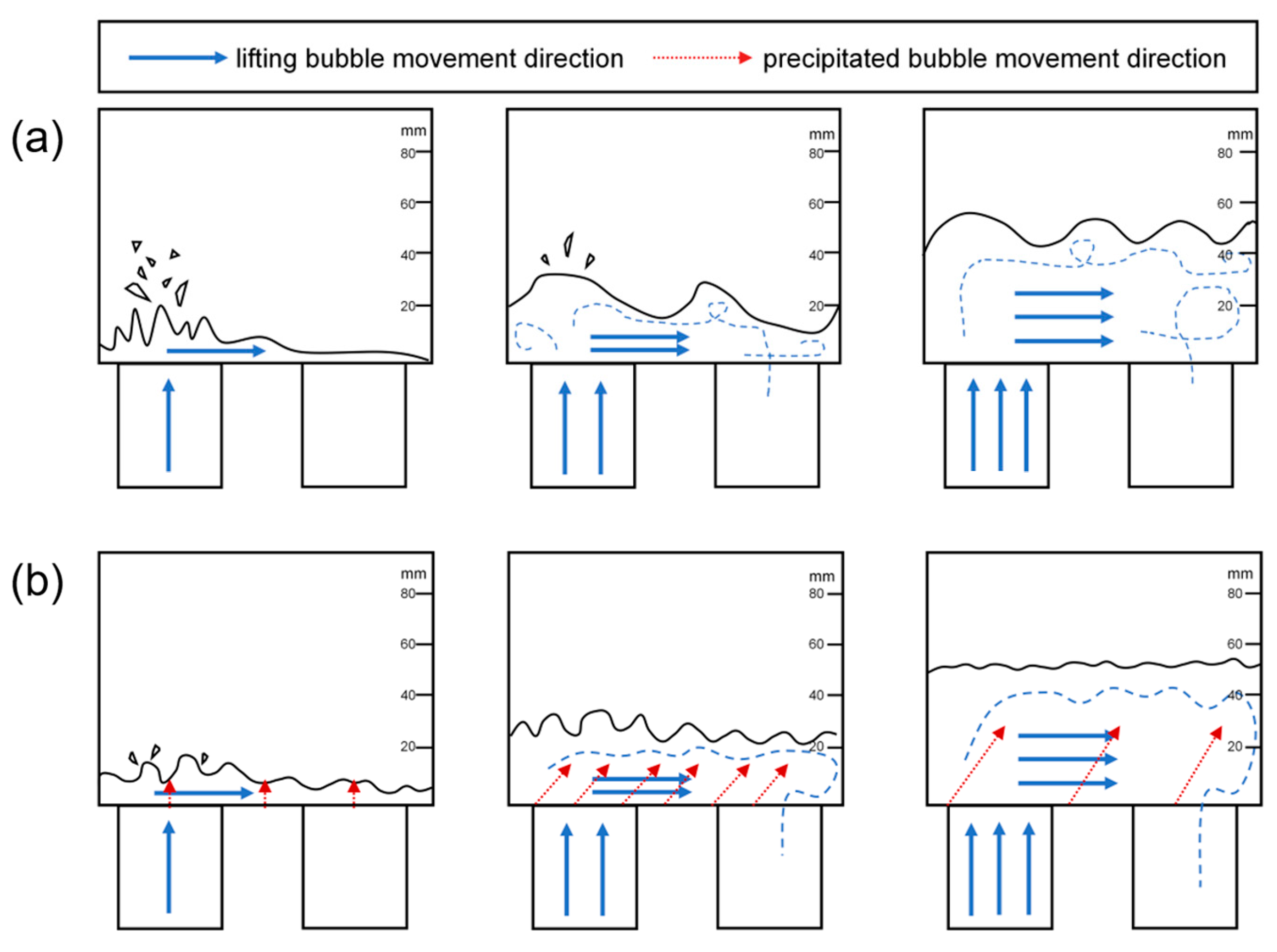
3.1. Analysis of Gas–Liquid Two-Phase Flow in the Rising Tube Under the Influence of Precipitated Bubbles
3.2. Analysis of Gas–Liquid Two-Phase Flow in a Vacuum Chamber Under the Influence of Precipitated Bubbles
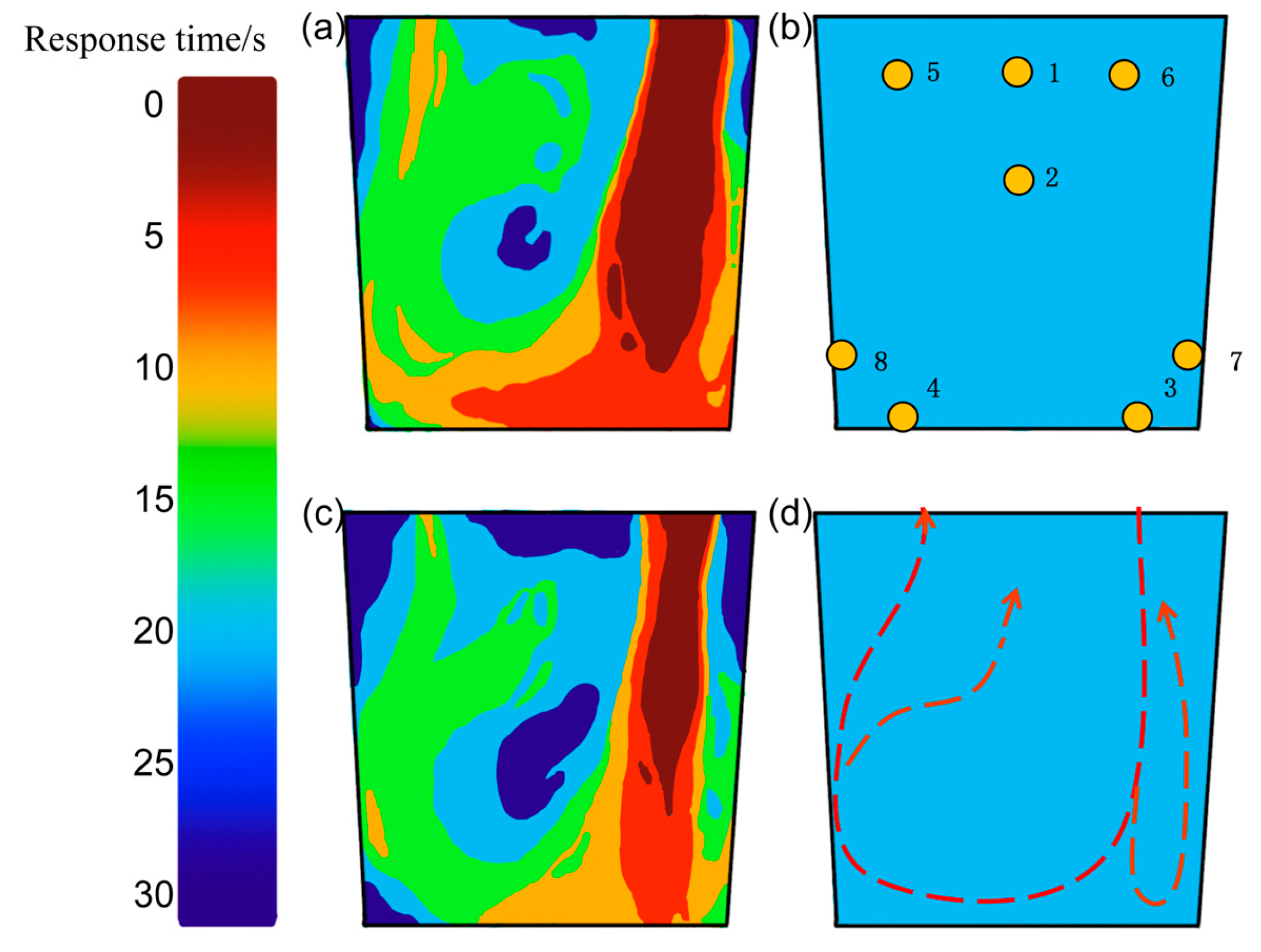
3.3. Analysis of Molten Steel Flow Behavior in the Ladle Under the Influence of Precipitated Bubbles
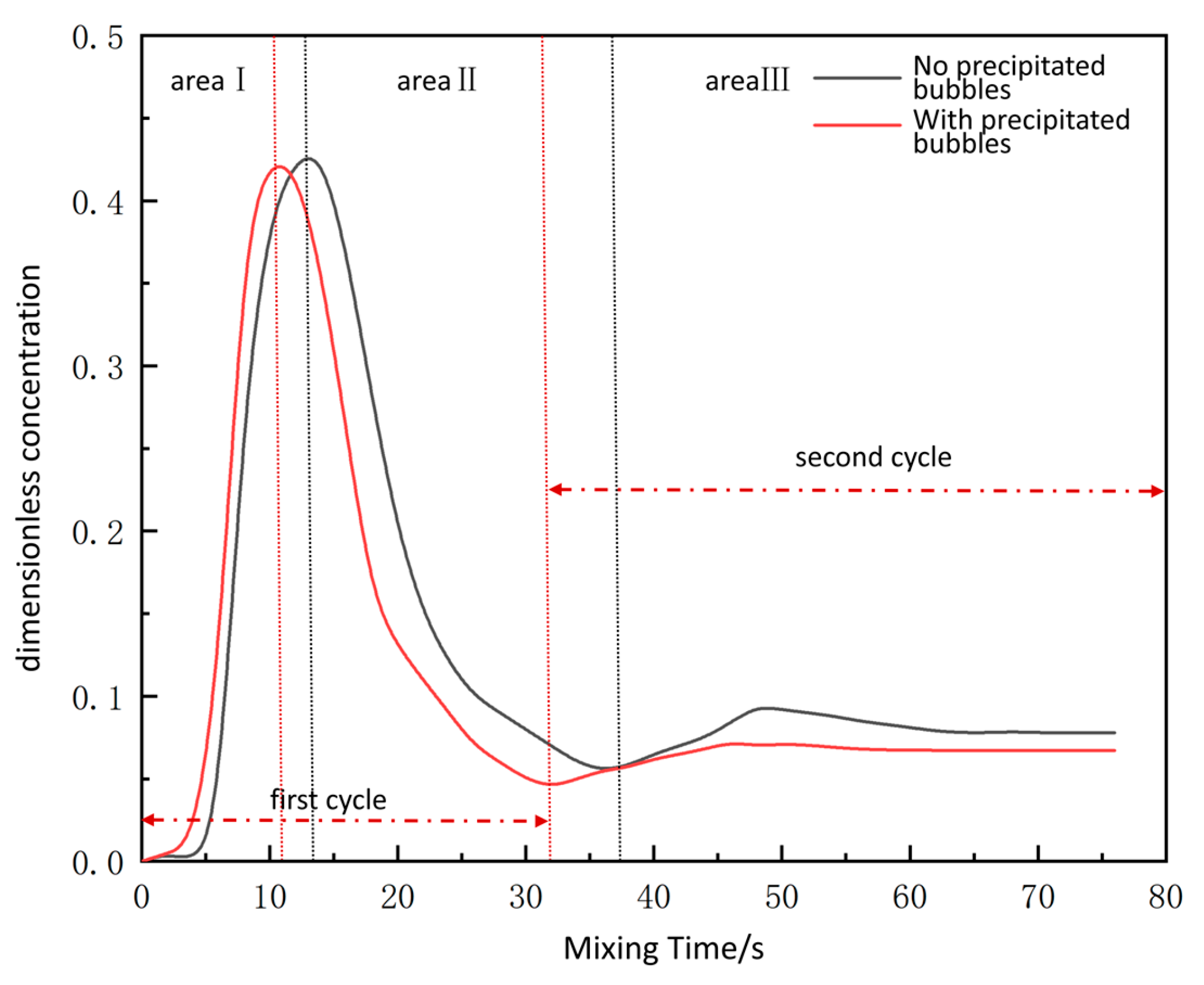
3.4. Analysis of Evaluation Indicators Under the Influence of Precipitated Bubbles
4. Conclusions
- (1)
- In order to ensure the similarity of fluid flow behavior under the influence of precipitation bubbles, the effects of surface tension, inertial force, buoyancy, and gravity are taken into account to obtain quasi-numbers that reflect the similarity of the phenomena of the precipitated bubbles:
- (2)
- In the first 2 min of decarburization, the liquid steel only exists in the rising tube, and the bubbles mainly exhibit a small ellipsoidal adhesion rise, representing a bubble flow. At a decarburization time of 2 min, the liquid steel experiences the lowering of the vacuum, the lifting volume of gas increases, and the bubbles elongate into a bullet-shaped or plug-shaped morphology, representing a slug flow. After a decarburization time of 3–4 min, the small bubbles grow quickly and become large bubbles, and the big bubbles rise. In this process, the liquid pressure is reduced, the large bubbles appear broken, and the bubble flow is difficult to stabilize, representing a mixed flow. After a decarbonization time of 5 min, the bubble collision and bursting in the vacuum chamber is more intense, with a large number of bubbles in the liquid in a torn net-like structure, representing a churn flow. Future research should combine numerical simulations of bubble dynamics with experimental results from water models to validate these findings.
- (3)
- Without precipitated bubbles an under the maximum spatter height of 40 mm, the average fluctuation amplitude of the whole decarburization process is 25 mm; under the influence of precipitated bubbles, the liquid surface spattering inside the vacuum chamber decreases, the fluctuation frequency increases, the fluctuation amplitude decreases, the maximum spatter height decreases to 18 mm, the average fluctuation amplitude of the whole decarburization process decreases to 10 mm, and the fluctuation frequency increases. When the spattering is serious, the same amount of liquid steel need to be processed several times, easily leading to cold steel. Precipitated bubbles move in the liquid steel flow direction, accelerate the liquid steel flow rate, and reduce the eddy current in the vacuum chamber, and because the liquid steel in the vacuum chamber remains too long, the liquid steel content of carbon and oxygen elements that reduce the difficulty of decarburization will increase. The residence time in the vacuum chamber should not be too long. And this increases the concentration gradient between the ladle and the vacuum chamber, accelerates the mixing of the liquid steel in the ladle, improves the mixing, and reduces the volume of the dead zone by 50%.
- (4)
- Throughout the decarburization process, the precipitated bubbles were positively correlated with the increase in circulation flow rate and the decrease in mixing time, with a maximum increase of 42% and 28%, respectively, and the difference first showed the trend of increasing and then decreasing with the change in decarburization time, reaching the maximum circulation flow rate and the shortest of mixing time when decarburization was performed for 6 min. The vacuum chamber residence time increased with the rise of the liquid surface height to reach a stable trend, and the increase in precipitated bubbles in the liquid steel and the vacuum chamber residence time were negatively correlated. As decarburization proceeded, the gas content decreased overall, and the gas content was relatively higher at each decarburization time influenced by the precipitated bubbles, especially between 3 and 5 min, when decarburization mainly occurs. The impact of precipitated bubbles on the gas–liquid two-phase flow in RH reactors cannot be overlooked. In the actual production process of industrial RH refining units, operators can slightly reduce the flow rate of the lift gas during periods of intense decarburization reactions to ensure the efficient operation of the refining system. Future industrial experiments should continue to optimize gas injection practices for further improvement.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- She, C.; Peng, K.; Sun, Y.; Ren, Y.; Zhang, L. Kinetic Model of Desulfurization During RH Refining Process. Metall. Mater. Trans. B 2024, 55, 92–104. [Google Scholar] [CrossRef]
- Xu, Z.; Ouyang, X.; Chen, C.; Li, Y.; Wang, T.; Ren, R.; Yang, M.; Zhao, Y.; Xue, L.; Wang, J. Numerical Simulation of the Density Effect on the Macroscopic Transport Process of Tracer in the Ruhrstahl–Heraeus (RH) Vacuum Degasser. Sustainability 2024, 16, 3923. [Google Scholar] [CrossRef]
- Liu, Z.; Lou, W.; Zhu, M. Numerical Analysis of Fluid Flow and Powder Transport Characteristics of RH-Degasser Ladle Bottom Powder Injection (RH-PBI) Process. Metall. Mater. Trans. B 2024, 55, 418–430. [Google Scholar] [CrossRef]
- Mukherjee, D.; Shukla, A.K.; Senk, D.G. Cold Model-Based Investigations to Study the Effects of Operational and Nonoperational Parameters on the Ruhrstahl–Heraeus Degassing Process. Metall. Mater. Trans. B 2017, 48, 763–771. [Google Scholar] [CrossRef]
- Dong, J.; Feng, C.; Zhu, R.; Wei, G.; Jiang, J.; Chen, S. Simulation and Application of Ruhrstahl–Heraeus (RH) Reactor with Bottom-Blowing. Metall. Mater. Trans. B 2021, 52, 2127–2138. [Google Scholar] [CrossRef]
- Heijnen, J.; Hols, J.; van der Lans, R.; van Leeuwen, H.; Mulder, A.; Weltevrede, R. A simple hydrodynamic model for the liquid circulation velocity in a full-scale two- and three-phase internal airlift reactor operating in the gas recirculation regime. Chem. Eng. Sci. 1997, 52, 2527–2540. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, G.; Wang, Q.; Li, S.; Dai, W. Mathematical model for decarburization of ultra-low carbon steel during RH treatment. Ironmak. Steelmak. 2020, 47, 655–664. [Google Scholar] [CrossRef]
- Iguchi, M.; Kawabata, H.; Nakajima, K.; Morita, Z.-I. Measurement of bubble characteristics in a molten iron bath at 1600 °C using an electroresistivity probe. Metall. Mater. Trans. B 1995, 26, 67–74. [Google Scholar] [CrossRef]
- Park, Y.-G.; Doo, W.-C.; Yi, K.-W.; An, S.-B. Numerical Calculation of Circulation Flow Rate in the Degassing Rheinstahl-Heraeus Process. ISIJ Int. 2000, 40, 749–755. [Google Scholar] [CrossRef]
- Takahashi, M.; Matsumoto, H.; Saito, T. Mechanism of Decarburization in RH Degasser. ISIJ Int. 1995, 35, 1452–1458. [Google Scholar] [CrossRef]
- Kuwabara, T.; Umezawa, K.; Mori, K.; Watanabe, H. Investigation of Decarburization Behavior in RH-reactor and Its Operation Improvement. Trans. Iron Steel Inst. Jpn. 1998, 28, 305–314. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Kishimoto, Y.; Sakuraya, T.; Fujii, T.; Aratani, M.; Nishikawa, H. Effect of Refining Conditions for Ultra Low Carbon Steel on Decarburization Reaction in RH Degasser. ISIJ Int. 1992, 32, 126–135. [Google Scholar] [CrossRef]
- He, Q.; Yao, T.-L.; Liu, L.; Li, X.-C.; Ni, B.; Li, L.-F. An experimental study on RH vacuum chamber with a weir. J. Iron Steel Res. Int. 2023, 30, 1929–1938. [Google Scholar] [CrossRef]
- Wang, J.; Ni, P.; Chen, C.; Ersson, M.; Li, Y. Effect of gas blowing nozzle angle on multiphase flow and mass transfer during RH refining process. Int. J. Miner. Metall. Mater. 2023, 30, 844–856. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, M.; Zhao, J.; Yao, C.; Xing, L.; Ai, X. Coordinated control of decarbonization efficiency and oxygen absorption rate in Ruhrstahl–Heraeus degasser based on mechanism model and BP neural network. J. Iron Steel Res. Int. 2025, 32, 606–618. [Google Scholar] [CrossRef]
- Chen, G.; He, S. Prediction of liquid circulation flow rate in RH degasser: Improvement of decarburization at low atmospheric pressure. J. Iron Steel Res. Int. 2024, 31, 1661–1667. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.; He, Y.; Zhou, C.; Yuan, B.; Zhang, M.; Barati, M. Study of Dispersed Micro-bubbles and Improved Inclusion Removal in Ruhrstahl–Heraeus (RH) Refining with Argon Injection Through Down Leg. Metall. Mater. Trans. B 2023, 54, 2347–2359. [Google Scholar] [CrossRef]
- Al-Masry, W. Influence of Gas Separator and Scale-up on the Hydrodynamics of External Loop Circulating Bubble Columns. Chem. Eng. Res. Des. 2004, 82, 381–389. [Google Scholar] [CrossRef]
- Castillejos, A.H.; Brimacombe, J.K. Measurement of physical characteristics of bubbles in gas-liquid plumes: Part I. An improved electroresistivity probe technique. Metall. Trans. B 1987, 18, 649–658. [Google Scholar] [CrossRef]
- Coulaloglou, C.; Tavlarides, L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Friedlander, S.K.; Marlow, W.H. Smoke, Dust and Haze: Fundamentals of Aerosol Behavior; Oxford University Press: New York, NY, USA, 1977; Volume 30, p. 58. [Google Scholar]
- Ramírez-López, A. Analysis of Mixing Efficiency in a Stirred Reactor Using Computational Fluid Dynamics. Symmetry 2024, 16, 237. [Google Scholar] [CrossRef]
- Kim, T.S.; Yang, J.; Park, J.H. Effect of Physicochemical Properties of Slag on the Removal Rate of Alumina Inclusions in the Ruhrstahl–Heraeus (RH) Refining Conditions. Metall. Mater. Trans. B 2022, 53, 2523–2533. [Google Scholar] [CrossRef]
- Zhang, L.; Jing, X.; Xu, Z.; Cai, K. Mathematical Model of Decarburization of Ultra-LowCarbon Steel during RH Treatment. Int. J. Miner. Metall. Mater. 1997, 5, 19–23. [Google Scholar]
- Zhu, B.; Liu, Q.; Kong, M.; Yang, J.; Li, D.; Chattopadhyay, K. Effect of Interphase Forces on Gas–Liquid Multiphase Flow in RH Degasser. Metall. Mater. Trans. B 2017, 48, 2620–2630. [Google Scholar] [CrossRef]
- Li, Y.H. Study on Fast Decarburization of Ruhrstahl-Hereaeusand Hydrodynamics in an External Loop Airlift Reactor. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2015. [Google Scholar]
- Chen, G.; He, S. Circulation flow rate and decarburization in the RH degasser under low atmospheric pressure. Vacuum 2018, 153, 132–138. [Google Scholar] [CrossRef]
- Liu, C. Investigation on Multiphase Fluid Flow, Mixing and Decarburization During RH Vacuum Refining Process. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2021. [Google Scholar]
- Yuan, J.D. Numerical Simulation Study on Gas-liquid Circulating Flow at Different Side-injecting Conditions in RH Refining System. Spec. Steel 2023, 44, 1–7. [Google Scholar]
- Peng, K.; Liu, C.; Zhang, L.; Sun, Y. Numerical Simulation of Decarburization Reaction with Oxygen Blowing During RH Refining Process. Metall. Mater. Trans. B 2022, 53, 2004–2017. [Google Scholar] [CrossRef]
- Zhu, H.W. Study on Bubble Evolution and Turbulent Behavior of Liquid Level in RH Vacuum Chamber. Master’s Thesis, Taiyuan University of Science and Technology, Taiyuan, China, 2022. [Google Scholar]
- Dong, C. Research on Gas-Liquid Two Phase Flow Behavior in RH Reactor. Master’s Thesis, Taiyuan University of Science and Technology, Taiyuan, China, 2021. [Google Scholar]
- Liu, W.P. Physical modeling of the influence of RH process parameters on the mixingeffect of molten steel. Steelmaking 2025, 41, 45–52. [Google Scholar]
- Jin, Y. Physical simulation of RH refining bottomblowing process optimization. China Metall. 2019, 29, 17–21. [Google Scholar]
- Ai, X.G. A Study on Water Model for Circulation Flow Rate Optimizationin RH Degassing Refining. Spec. Steel 2009, 30, 1–3. [Google Scholar]






| RH Prototype Steel Handling Capacity (t) | Geometric Similarity Ratio of Physical Models λ | References |
|---|---|---|
| 300 | 1/6 | Yihong Li [26] |
| 300 | 1/6 | Hongwei Zhu [31] |
| 300 | 1/6 | Chao Dong [32] |
| 210 | 1/5 | Wenping Liu [33] |
| 150 | 1/4 | Yu Jin [34] |
| 70 | 1/3.27 | Xingang Ai [35] |
| Materialistic | Density (Kg/m3) | Dynamic Viscosity (Kg/m·s) | Kinematic Viscosity (m2/s) | Surface Tension (N/m) |
|---|---|---|---|---|
| Liquid steel (1600 °C) | 7000 | 0.0064 | 0.913 × 10−4 | 1.6 |
| Water (20 °C) | 1000 | 0.001 | 1 × 10−6 | 0.073 |
| Parameter Name | Prototype Size (mm) | Model Size (mm) |
|---|---|---|
| Ladle depth | 4200 | 1050 |
| Diameter of the top of the ladle | 3920 | 980 |
| Diameter of the bottom of the ladle | 3638 | 909.5 |
| Steel liquid filling depth | 3915 | 978.75 |
| Vacuum chamber diameter | 2524 | 631 |
| Immersion tube inner diameter | 750 | 187.5 |
| Immersion tube outer diameter | 1500 | 375 |
| Immersion tube length | 1650 | 412.5 |
| Similarity Criteria | Expression | Definition |
|---|---|---|
| Modified Froude number | Ratio of inertial force to gravitational force | |
| Weber number | Ratio of gas–liquid interfacial tension to gravitational force | |
| Galileo number | Ratio of gravitational force to viscous force | |
| Grashof number | Ratio of buoyancy force to viscous force |
| Carbon Reduction Time (min) | Prototypical Reaction Carbon Content/% | Prototype Volume of Precipitated CO/m3 | Prototype Flow Rate of Precipitated CO (L/min) | Model Flow Rate of Precipitated CO (L/min) |
|---|---|---|---|---|
| 2 | 0.000641 | 3.589 | 3589.265 | 3.949 |
| 3 | 0.007358 | 41.207 | 41,207.393 | 45.342 |
| 4 | 0.006641 | 37.192 | 37,192.606 | 40.924 |
| 5 | 0.004126 | 23.108 | 23,108.559 | 25.427 |
| 6 | 0.001873 | 10.491 | 10,491.440 | 11.544 |
| 7 | 0.003151 | 17.648 | 17,648.084 | 19.419 |
| 8 | 0.000348 | 1.951 | 1951.915 | 2.147 |
| Decarbonization Time (min) | Lift Gas Flow Rate (m3/h) | Degree of Vacuum (kPa) | Vacuum Chamber Liquid Level Height (mm) |
|---|---|---|---|
| 0–2 | 160 | >20 | 0 |
| 2–4 | 180 | 20~5.5 | 0–170 |
| 4–18 | 220 | 5.5~0.02 | 170–250 |
| 18–vacuum breaking | 150 | <0.02 | 250 |
| Scheme Number | Model Rise Tube Bubble Precipitation Amount (L/min) | Model Vacuum Chamber Bubble Precipitation Amount (L/min) | Lift Gas Volume (L/min) | Vacuum Chamber Liquid Level Height (mm) |
|---|---|---|---|---|
| 1 | 1.1 | 1.97 | 33 | 13 |
| 2 | 13.6 | 22.67 | 37 | 48 |
| 3 | 12.2 | 20.46 | 37 | 60 |
| 4 | 7.6 | 12.71 | 45 | 66 |
| 5 | 3.4 | 5.77 | 45 | 72 |
| 6 | 4.2 | 9.7 | 45 | 73 |
| 7 | 0.6 | 1.07 | 45 | 74 |
| Gas–Liquid Two-Phase Flow Pattern | Feature |
|---|---|
| Bubble flow | The gas phase is dispersed as discrete small bubbles in the continuous liquid phase, with nearly spherical shapes. |
| Slug flow | The gas phase forms elongated gas bullets (analogous to pistons) enshrouded in a liquid film, with liquid slugs separating the gas bullets. |
| Mixed flow | The mixture state is complex, potentially containing multiple flow patterns, and represents a transitional flow regime. |
| Churn flow | Following the rupture of gas bullets, a highly disturbed mixed flow pattern emerges, characterized by an unstable gas–liquid interface and the fragmentation of the liquid phase into chunks or droplets. |
| Decarbonization Time (min) | Bubble Size (mm) | Eo | Re | Bubble Shape |
|---|---|---|---|---|
| 2 | 6–8 | 3.5–6.6 | 3.5–5.3 | Near-spherical/ellipsoidal |
| 4 | 8–23 | 10.3–92.1 | 6.9–23.1 | Cap |
| 6 | 17–39 | 39.9–125.2 | 12.7–37.3 | Cap/irregular morphology |
| 8 | 20–43 | 44.1–156.2 | 16.2–40.1 | Irregular morphology |
| Molten Steel Flow Pattern in the Vacuum Chamber | Feature |
|---|---|
| Boiling flow pattern | At the outlet of the rising pipe, there is intense turbulence of bubbles, accompanied by a large number of droplet splashes. |
| Transitional flow pattern | At the riser outlet, the turbulence of the molten steel diminishes, internal fluctuations intensify, and droplet splashing decreases. |
| Fluctuating flow pattern | Droplet splashing disappears, accompanied by severe fluctuations of molten steel in the vacuum chamber. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Chen, Z.; Tian, Y.; Wang, D.; He, Y.; Hua, C.; Ren, Z.; Zhang, P. Effect of Precipitated Bubbles on the Behavior of Gas–Liquid Two-Phase Flow in Ruhrstahl Heraeus Refining. Processes 2025, 13, 1484. https://doi.org/10.3390/pr13051484
Li Y, Chen Z, Tian Y, Wang D, He Y, Hua C, Ren Z, Zhang P. Effect of Precipitated Bubbles on the Behavior of Gas–Liquid Two-Phase Flow in Ruhrstahl Heraeus Refining. Processes. 2025; 13(5):1484. https://doi.org/10.3390/pr13051484
Chicago/Turabian StyleLi, Yihong, Zongyi Chen, Yan Tian, Dong Wang, Yibo He, Chengjian Hua, Zhifeng Ren, and Pengju Zhang. 2025. "Effect of Precipitated Bubbles on the Behavior of Gas–Liquid Two-Phase Flow in Ruhrstahl Heraeus Refining" Processes 13, no. 5: 1484. https://doi.org/10.3390/pr13051484
APA StyleLi, Y., Chen, Z., Tian, Y., Wang, D., He, Y., Hua, C., Ren, Z., & Zhang, P. (2025). Effect of Precipitated Bubbles on the Behavior of Gas–Liquid Two-Phase Flow in Ruhrstahl Heraeus Refining. Processes, 13(5), 1484. https://doi.org/10.3390/pr13051484






