A Generic Fracture Conductivity Model for Partially Propped Fracture Networks with Proppant Embedment and Proppant Pack Deformation
Abstract
1. Introduction
2. Model Development
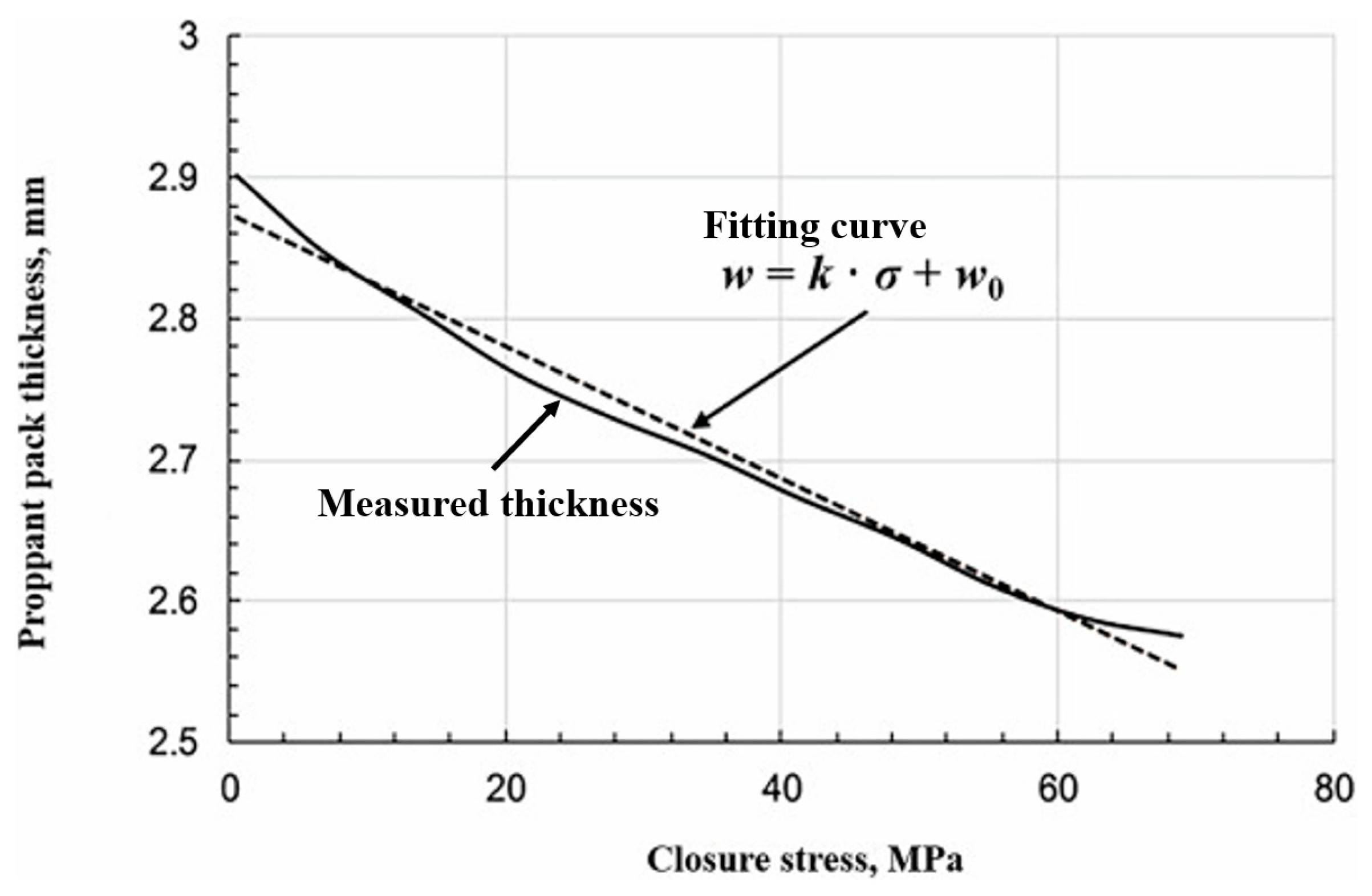
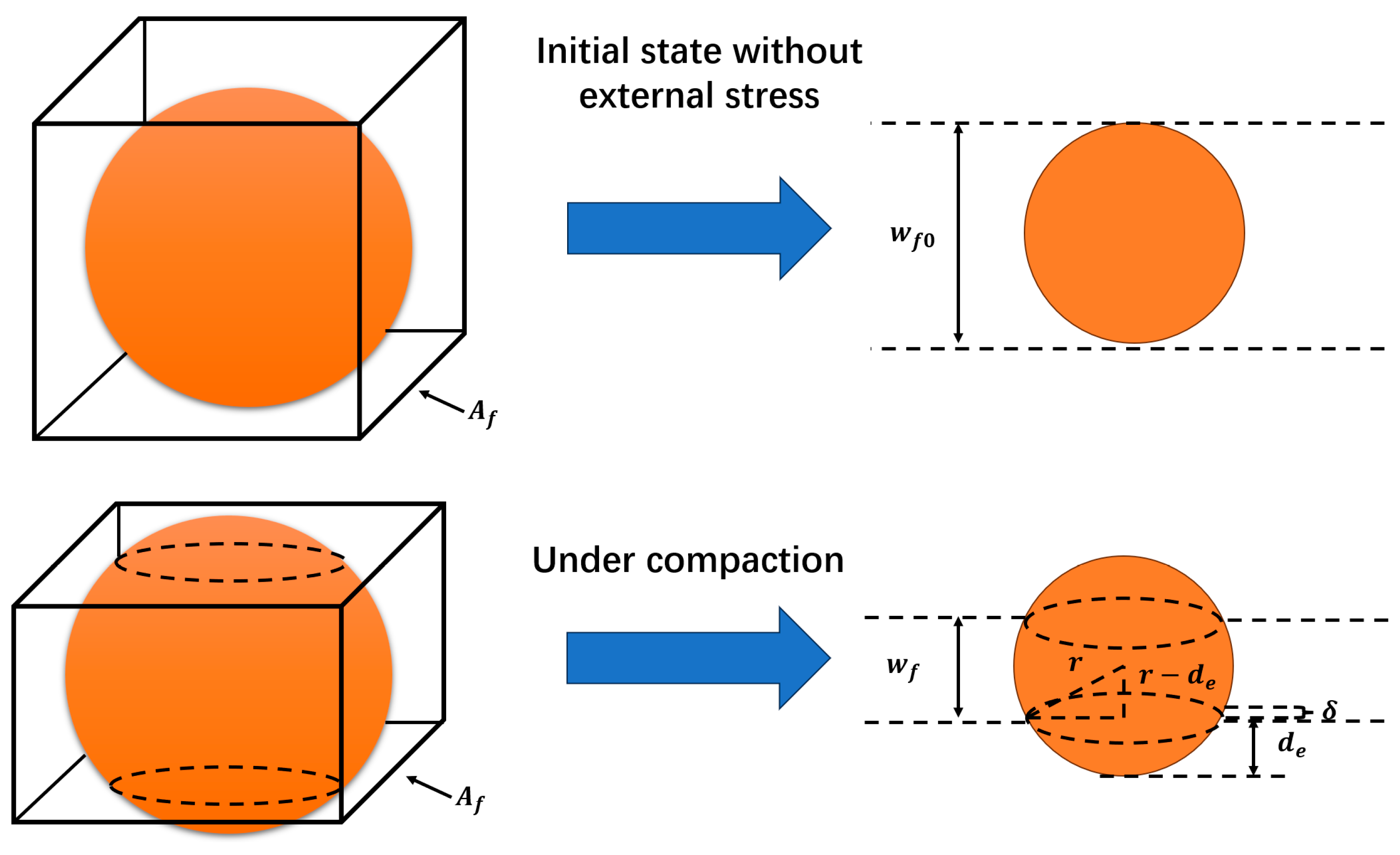
2.1. Dynamic Propped Fracture Width Model
2.2. Propped Fracture Permeability Model
2.3. Dynamic Unpropped Fracture Width Model
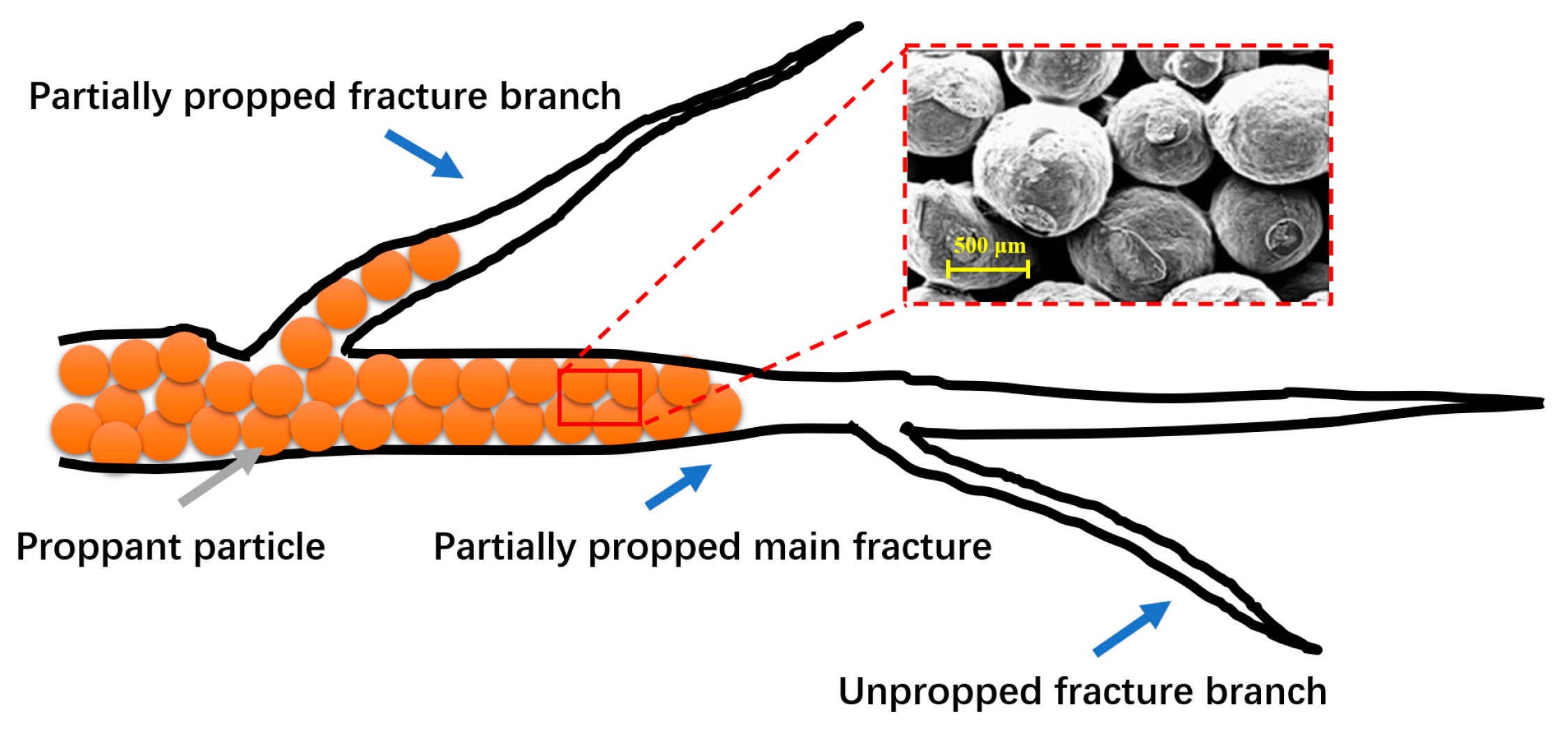
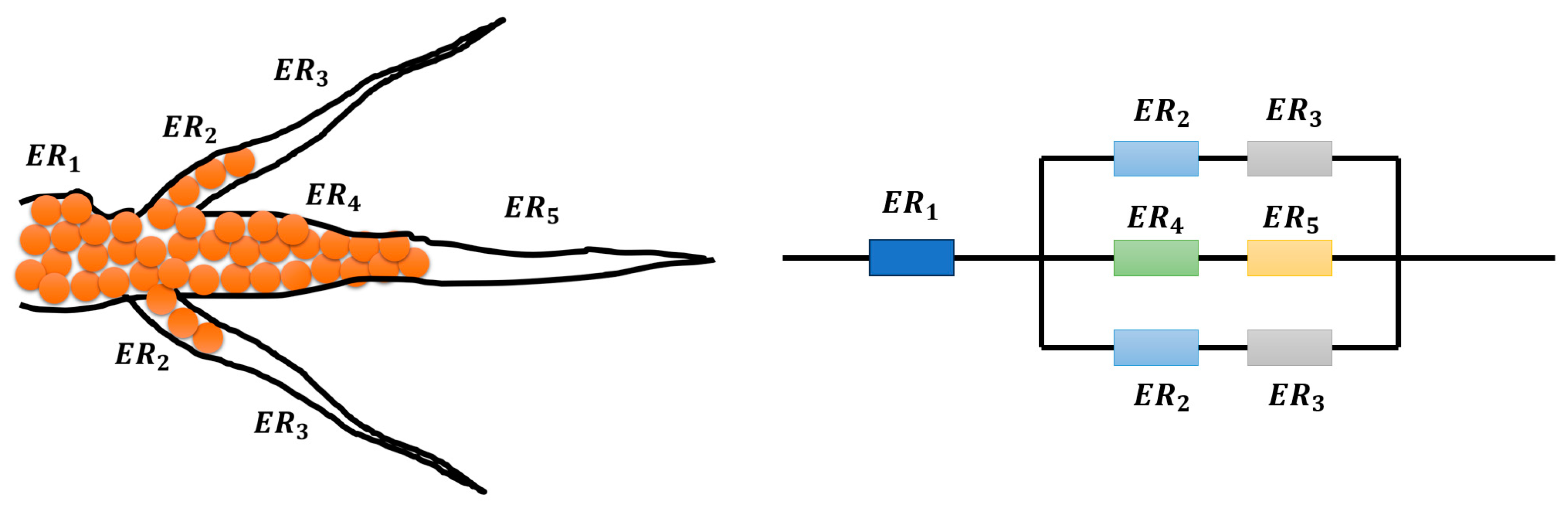
2.4. Partially Propped Fracture Network Conductivity Model
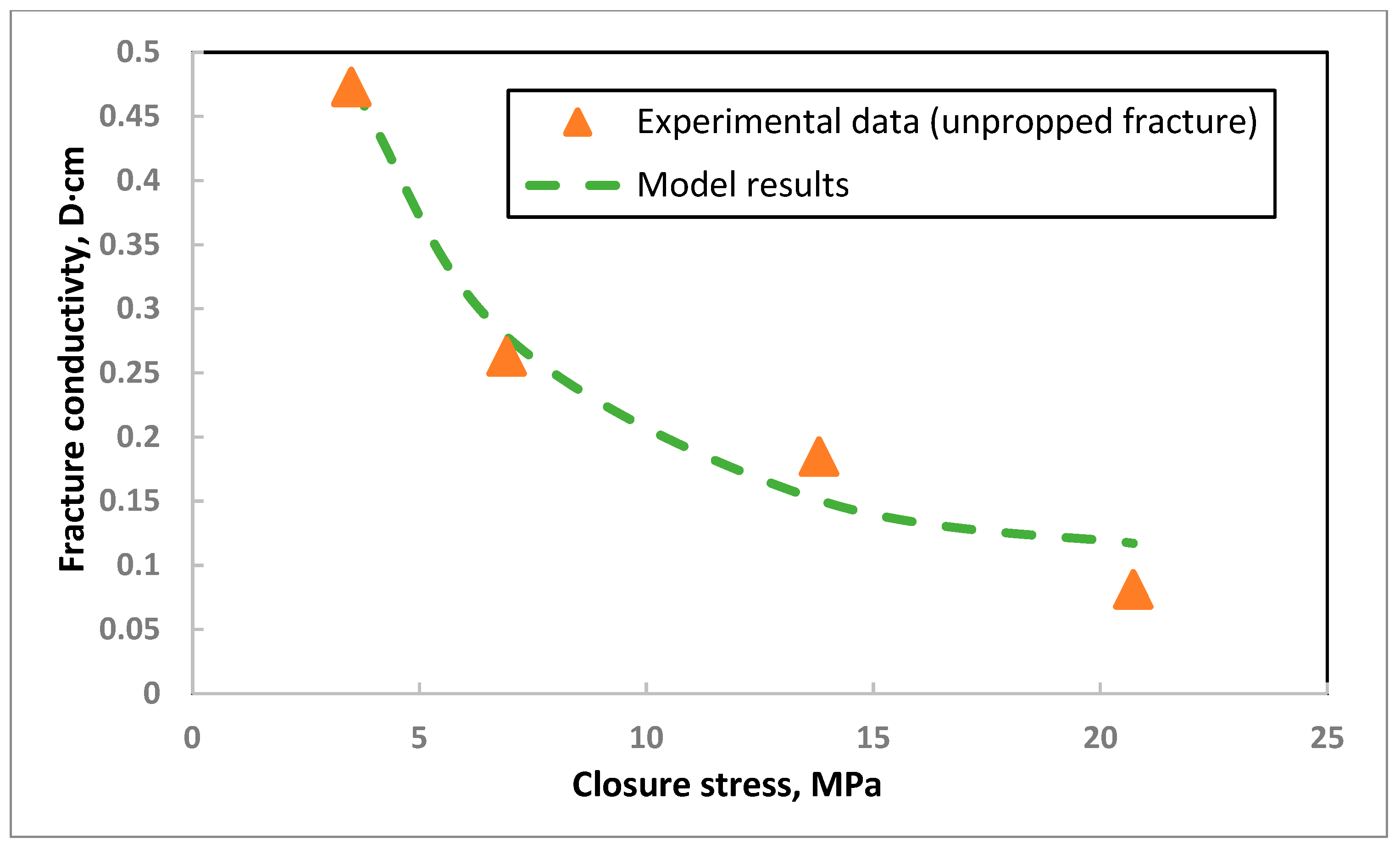
3. Model Validation
4. Results and Discussion
4.1. The Impacts of the Proppant Pack Compressibility
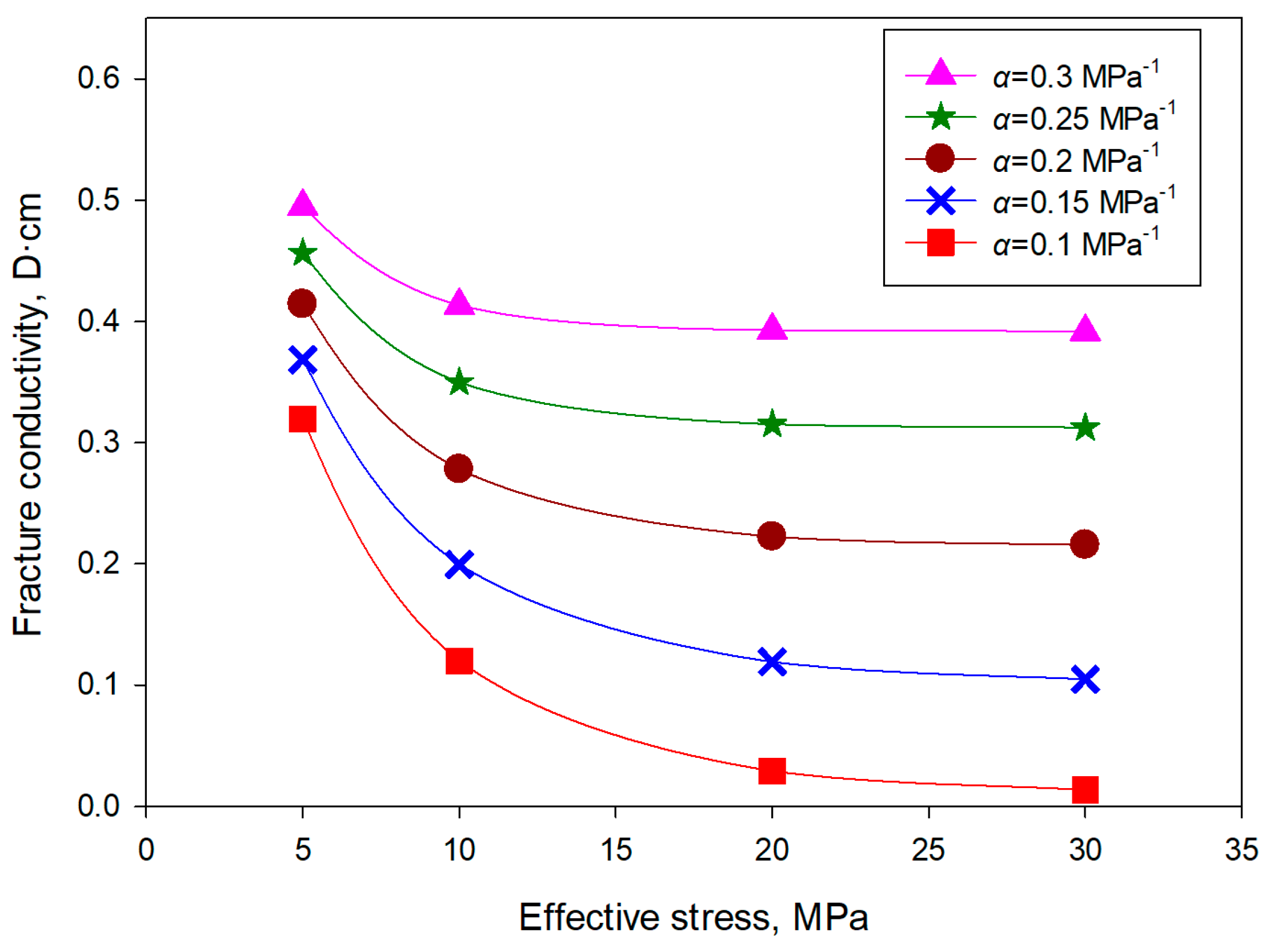
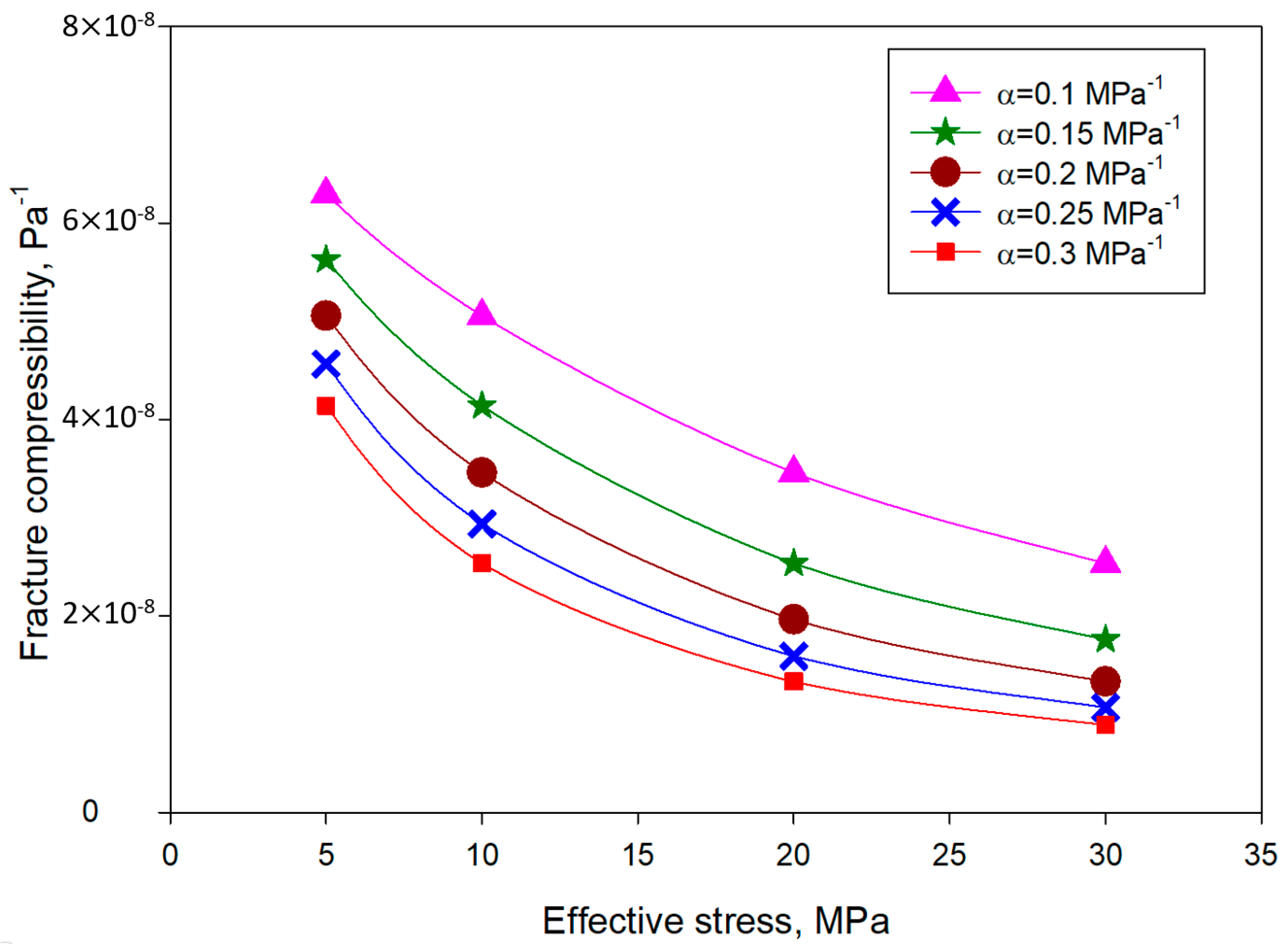
4.2. The Impacts of the Rate at Which the Compressibility Decreased for Unpropped Fractures
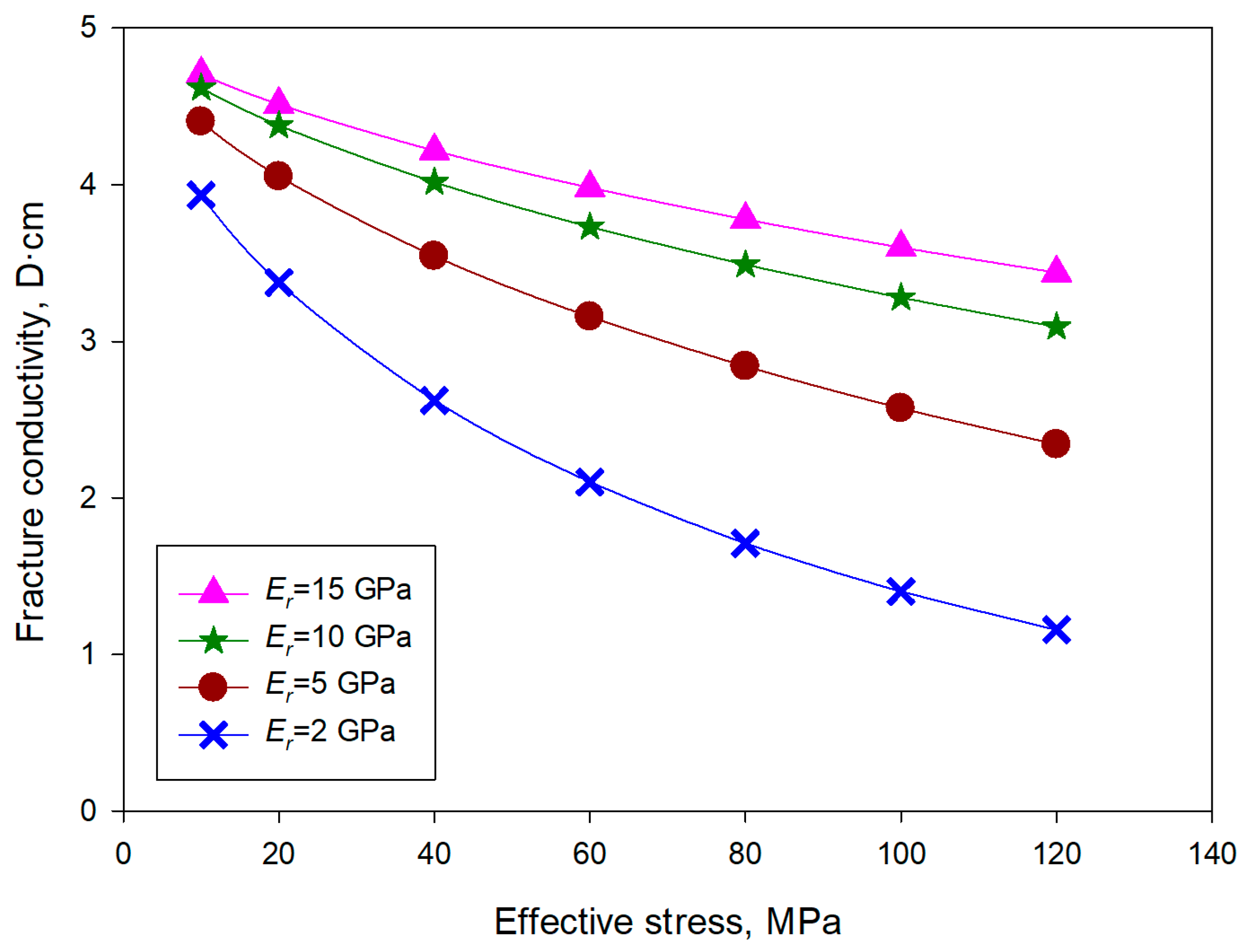
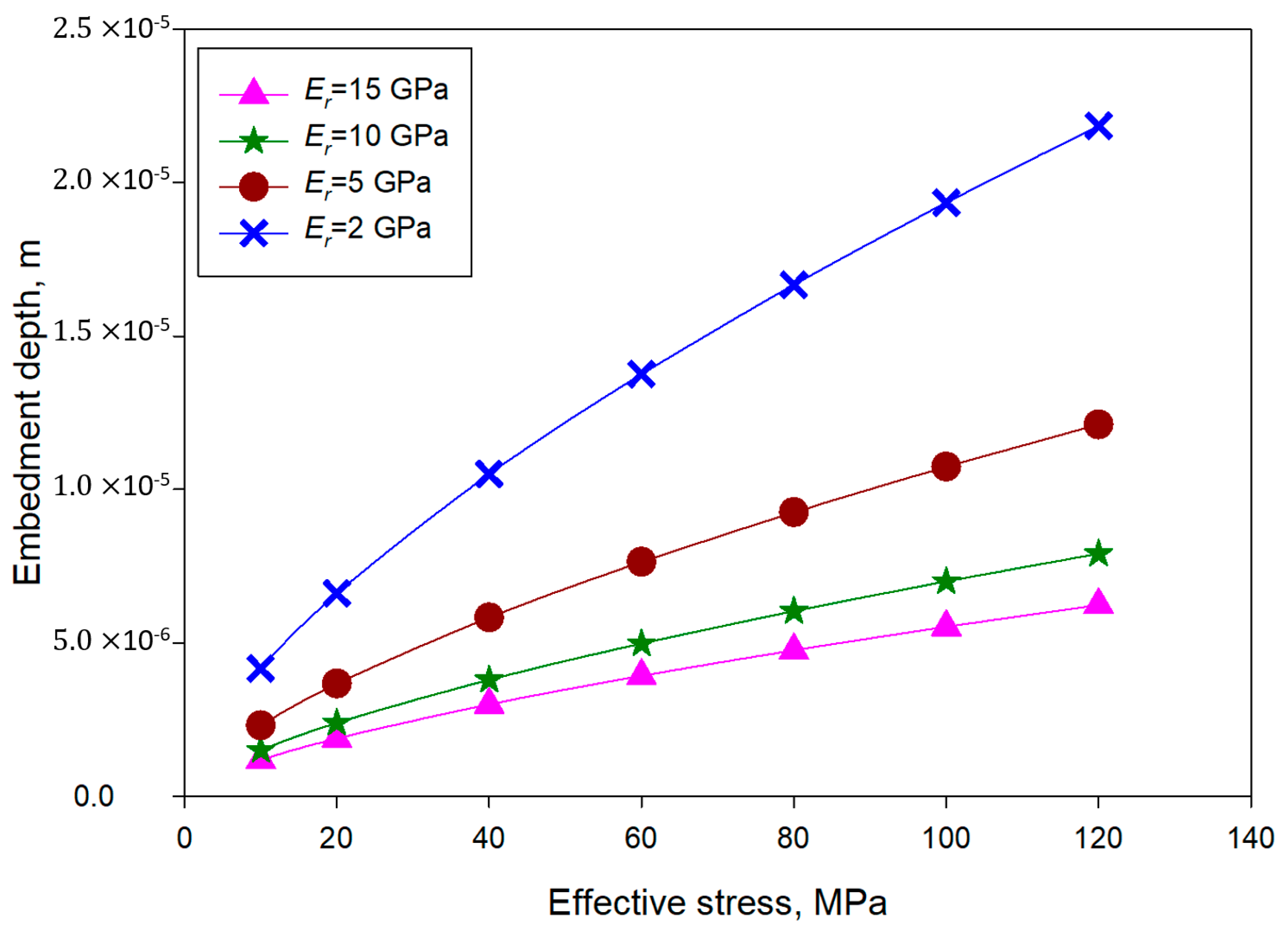
4.3. Impacts of Fracture Surface Elastic Modulus on Fracture Conductivity
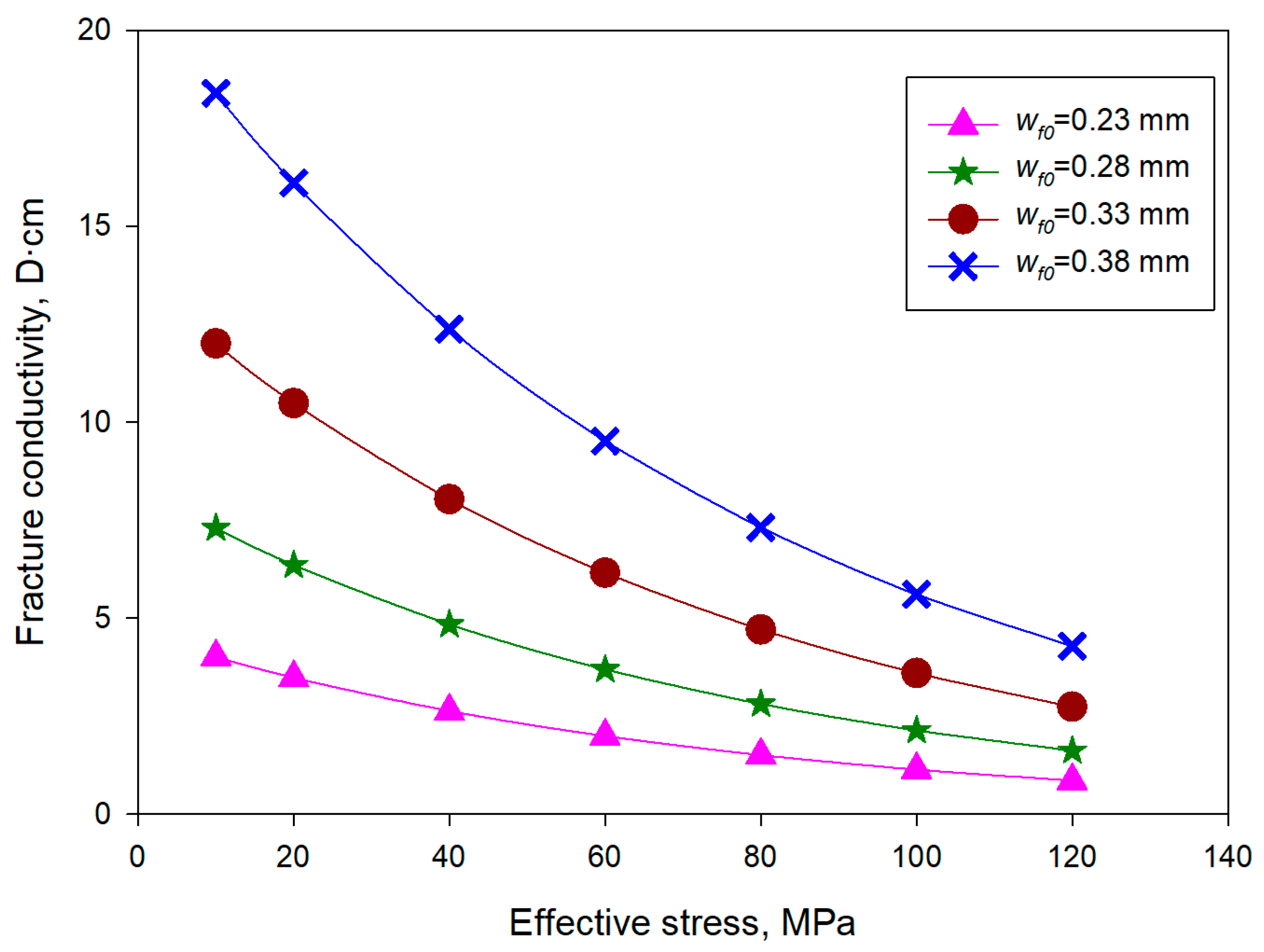
4.4. Impacts of Propped Fracture’s Initial Aperture
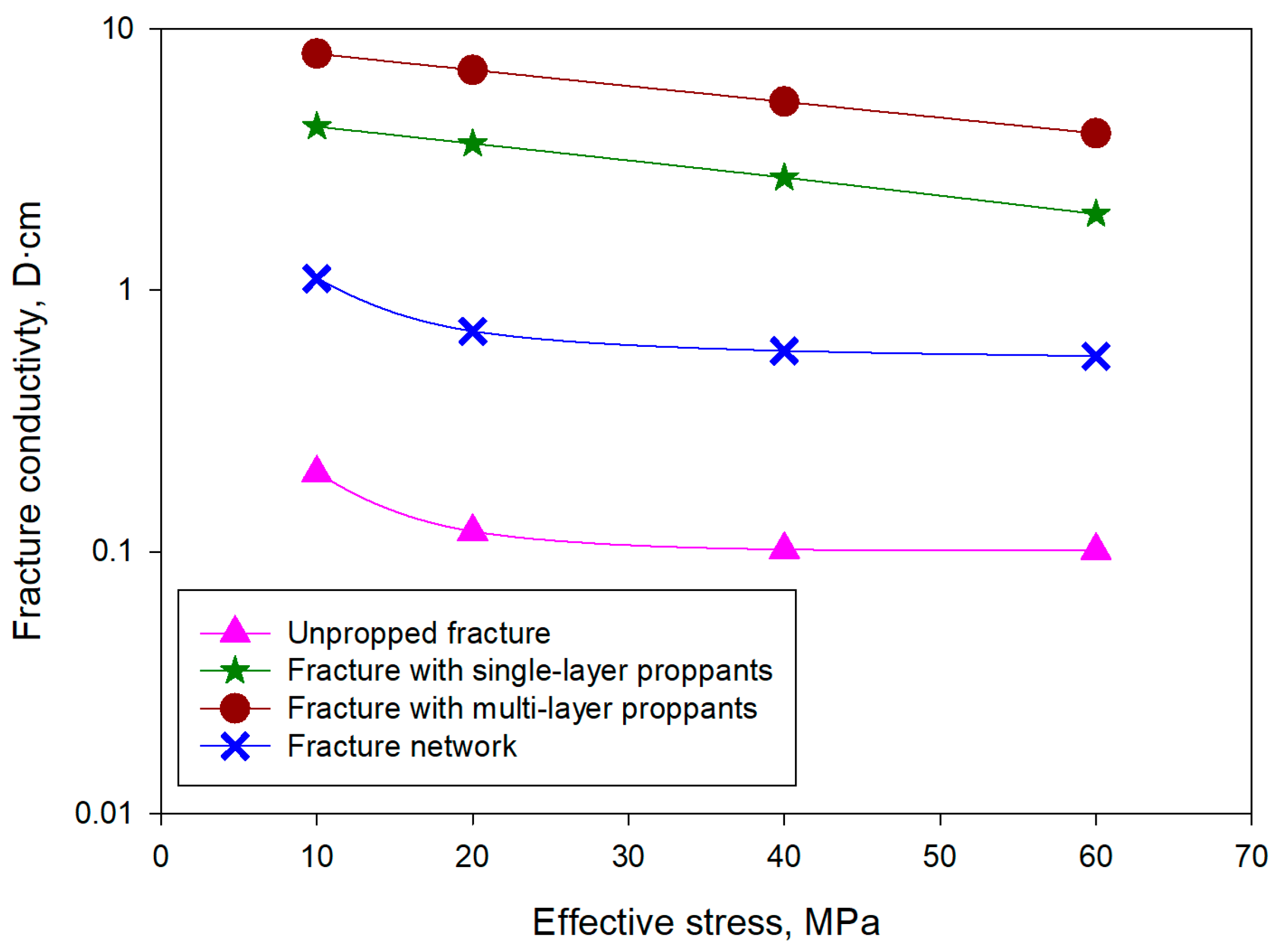
4.5. The Evolution of the Overall Fracture Network Conductivity
5. Conclusions
- (1)
- The proppant pack compressibility mainly controlled the porosity of the proppant pack and hence its permeability. An increase in the proppant pack compressibility substantially impaired the conductivity, especially under high-stress conditions. When the compressibility was larger than 0.05 MPa−1, the conductivity was significantly reduced under an effective stress of 80 MPa or larger.
- (2)
- The unpropped fracture compressibility changed with the effective stress. With an increase in the compressibility reduction rate, the fracture conductivity reduction slowed down as the effective stress increased. When the rate of decrease reached 0.3 MPa−1, the unpropped fracture conductivity was relatively stable, with the effective stress changing from 10 to 30 MPa.
- (3)
- The fracture surface elastic modulus of single-layer propped fractures mainly influenced the proppant embedment depth. As a result, it dominated the fracture width and propped segment porosity. With a decrease in the elastic modulus from 15 GPa to 10 GPa, the conductivity evolution curves only slightly moved down. As the modulus was decreased to 5 GPa, a significant conductivity reduction and substantial embedment depth increment could be observed.
- (4)
- A larger initial propped fracture aperture led to a higher fracture conductivity under the same stress conditions. The initial propped fracture aperture is crucial for shallow unconventional reservoirs as the conductivity difference at different initial apertures is more noticeable under low in situ stress conditions. However, this parameter is less important for deep unconventional formations because the high in situ stress narrows the conductivity differences among cases with different initial fracture apertures.
- (5)
- The overall fracture network conductivity was heavily influenced by the proportion of unpropped fracture segments. The fracture network conductivity was close to the unpropped fracture segment’s conductivity, even though the unpropped section length was half of the fracture network length. The shape of the fracture network conductivity evolution curve changed from that of the unpropped fracture conductivity curve to that of the propped fracture conductivity curve as the unpropped length proportion decreased from 45.5% to 9.1%. Achieving high proppant placement efficiency is vital for achieving overall high conductivity for a fracture network.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Danso, D.K.; Negash, B.M.; Ahmed, T.Y.; Yekeen, N.; Ganat, T.A.O. Recent advances in multifunctional proppant technology and increased well output with micro and nano proppants. J. Pet. Sci. Eng. 2021, 196, 108026. [Google Scholar] [CrossRef]
- Wu, W.; Sharma, M.M. A model for the conductivity and compliance of unpropped and natural fractures. SPE J. 2017, 22, 1893–1914. [Google Scholar] [CrossRef]
- Neto, L.B.; Khanna, A.; Kotousov, A. Conductivity and performance of hydraulic fractures partially filled with compressible proppant packs. Int. J. Rock Mech. Min. Sci. 2015, 74, 1–9. [Google Scholar] [CrossRef]
- Zuo, L.; Li, X.; Han, Z.; You, Q.; Liu, X. Numerical Simulation of Proppant Transport in Major and Branching Fractures Based on CFD-DEM. ACS Omega 2024, 9, 13163–13171. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Cao, H.; Wu, J.; Wang, F.; Wang, Y. The Crack Propagation Behaviour of CO2 Fracturing Fluid in Unconventional Low Permeability Reservoirs: Factor Analysis and Mechanism Revelation. Processes 2025, 13, 159. [Google Scholar] [CrossRef]
- Barboza, B.R.; Chen, B.; Li, C. A review on proppant transport modelling. J. Pet. Sci. Eng. 2021, 204, 108753. [Google Scholar] [CrossRef]
- Guerra, J.; Zhu, D.; Hill, A.D. Impairment of fracture conductivity in the eagle ford shale formation. SPE Prod. Oper. 2018, 33, 637–653. [Google Scholar] [CrossRef]
- Shamsi, M.M.M.; Nia, S.F.; Jessen, K. Dynamic conductivity of proppant-filled fractures. J. Pet. Sci. Eng. 2017, 151, 183–193. [Google Scholar] [CrossRef]
- Mittal, A.; Rai, C.S.; Sondergeld, C.H. Proppant-conductivity testing under simulated reservoir conditions: Impact of crushing, embedment, and diagenesis on long-term production in shales. SPE J. 2018, 23, 1304–1315. [Google Scholar] [CrossRef]
- Liu, Y.X.; Zhou, H.Y.; Guo, J.C.; Zhang, Q.; Chen, C. Controlling factors of fracture aperture reduction based on experimental study using proppant pack apparent Young’s modulus. J. Pet. Sci. Eng. 2022, 208, 109506. [Google Scholar] [CrossRef]
- Geng, S.; Wang, Q.; Zhu, R.; Li, C. Experimental and numerical investigation of Non-Darcy flow in propped hydraulic fractures: Identification and characterization. Gas Sci. Eng. 2024, 121, 205171. [Google Scholar] [CrossRef]
- Van der Vlis, A.C.; Haafkens, R.; Schipper, B.A.; Visser, W. Criteria for proppant placement and fracture conductivity. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 28 September–1 October 1975; SPE: Calgary, AB, Canada, 1975. [Google Scholar]
- Volk, L.J.; Raible, C.J.; Carroll, H.B.; Spears, J.S. Embedment of high strength proppant into low-permeability reservoir rock. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 27–29 May 1981; SPE: Calgary, AB, Canada, 1981. [Google Scholar]
- Li, K.; Gao, Y.; Lyu, Y.; Man, W. New Mathematical Models for Calculating Proppant Embedment and Fracture Conductivity. SPE J. 2015, 20, 496–507. [Google Scholar] [CrossRef]
- Awoleke, O.O.; Zhu, D.; Hill, A.D. New propped-fracture-conductivity models for tight gas sands. SPE J. 2016, 21, 1508–1517. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, D.; Hill, A.D. Water-induced damage to propped-fracture conductivity in shale formations. SPE Prod. Oper. 2016, 31, 147–156. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.P.; Feng, Y.; Wang, H.; Zhang, L.; McLennan, J.D. Modeling of fracture width and conductivity in channel fracturing with nonlinear proppant-pillar deformation. SPE J. 2019, 24, 1288–1308. [Google Scholar] [CrossRef]
- Liu, Y.; Mu, S.; Guo, J.; Chen, C.; Wang, S. Model for fracture conductivity considering particle size distribution in a proppant monolayer. J. Nat. Gas Sci. Eng. 2021, 95, 104188. [Google Scholar] [CrossRef]
- Liu, Y.; Mu, S.; Guo, J.; Yang, X.; Chen, C.; Liu, H. Analytical model for fracture conductivity with multiple particle sizes and creep deformation. J. Nat. Gas Sci. Eng. 2022, 102, 104607. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhou, S.; Li, B.; Pan, Z.; Liu, D.; Yan, D. Integrating embedment and creep behavior for multisize proppant in shale: Conceptual model and validation. SPE J. 2023, 28, 3389–3408. [Google Scholar] [CrossRef]
- Teng, B.; Li, H.; Yu, H. A novel analytical fracture-permeability model dependent on both fracture width and proppant-pack properties. SPE J. 2020, 25, 3031–3050. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, H.; Li, T.; Wang, Y.; Ren, F.; Ma, G. Evaluation of geothermal development considering proppant embedment in hydraulic fractures. Renew. Energy 2020, 153, 985–997. [Google Scholar] [CrossRef]
- Kohshour, I.O.; Leshchyshyn, T.; Munro, J.; Yorro, M.C.; Adejumo, A.T.; Ahmed, U.; Barati, R.; Kugler, I.; Reynolds, M.; Cullen, M.; et al. Examination of water management challenges and solutions in shale resource development-could waterless fracturing technologies work? In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, URTEC, San Antonio, TX, USA, 1–3 August 2016.
- Xu, J.; Ding, Y.; Yang, L.; Liu, Z.; Gao, R.; Yang, H.; Wang, Z. Effect of proppant deformation and embedment on fracture conductivity after fracturing fluid loss. J. Nat. Gas Sci. Eng. 2019, 71, 102986. [Google Scholar]
- Li, J.; Li, B.; Lu, J.; Duan, S.; Gao, Z. Evolution of fracture permeability and its compressibility in proppant-supported shale. J. Nat. Gas Sci. Eng. 2022, 105, 104713. [Google Scholar]
- Reiss, L.H. The Reservoir Engineering Aspects of Fractured Formations; Editions Technip: Paris, France, 1980. [Google Scholar]
- Xu, Y.; Ezulike, O.; Dehghanpour, H. Estimating compressibility of complex fracture networks in unconventional reservoirs. Int. J. Rock Mech. Min. Sci. 2020, 127, 104186. [Google Scholar]
- Cui, X.; Bustin, R.M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams. AAPG Bull. 2005, 89, 1181–1202. [Google Scholar] [CrossRef]
- McKee, C.R.; Bumb, A.C.; Koenig, R.A. Stress-dependent permeability and porosity of coal and other geologic formations. SPE Form. Eval. 1988, 3, 81–91. [Google Scholar] [CrossRef]
- Zeng, F.; Peng, F.; Guo, J.; Rui, Z.; Xiang, J. Gas mass transport model for microfractures considering the dynamic variation of width in shale reservoirs. SPE Reserv. Eval. Eng. 2019, 22, 1265–1281. [Google Scholar] [CrossRef]
- Ji, G.; Chen, S.; Zhou, T.; Huang, Z.; Li, F. A new method of predicting network fracture conductivity based on the similitude principle of water and electricity. Phys. Fluids 2021, 33, 116605. [Google Scholar] [CrossRef]
- Guo, J.; Ren, J.; Wang, S.; Chen, C.; Lai, J.; Gou, B. Comprehensive study of fracture flow characteristic and feasibility of hybrid volume stimulation technique in tight fractured carbonate gas reservoir. J. Pet. Sci. Eng. 2019, 174, 362–373. [Google Scholar] [CrossRef]
- Zhang, J.; Kamenov, A.; Zhu, D.; Hill, A.D. Laboratory Measurement of Hydraulic Fracture Conductivities in the Barnett Shale. SPE Prod. Oper. 2014, 29, 216–227. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Feng, X.T.; Connell, L.D. Laboratory study of proppant on shale fracture permeability and compressibility. Fuel 2018, 222, 83–97. [Google Scholar] [CrossRef]
- Chen, T.; Fu, Y.; Feng, X.T.; Tan, Y.; Cui, G.; Elsworth, D.; Pan, Z. Gas permeability and fracture compressibility for proppant-supported shale fractures under high stress. J. Nat. Gas Sci. Eng. 2021, 95, 104157. [Google Scholar] [CrossRef]
- Tang, J.; Zhu, J.; Shao, T.; Wang, J.; Jiang, Y. A coal permeability model with variable fracture compressibility considering triaxial strain condition. Nat. Resour. Res. 2021, 30, 1577–1595. [Google Scholar] [CrossRef]
- Ding, M.; He, M. Effect of water-induced rock softening on rock anisotropy during drilling process. Rock Mech. Rock Eng. 2024, 57, 8193–8214. [Google Scholar] [CrossRef]
- Pouraskarparast, Z.; Aghaei, H.; Colombera, L.; Masoero, E.; Ghaedi, M. Fracture aperture: A review on fundamental concepts, estimation methods, applications, and research gaps. Mar. Pet. Geol. 2024, 164, 106818. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, G.; Zhao, Y.; Jia, X.; Zhi, Z.; Wang, Q.; Zeng, J.; Xu, S.; Lu, C. A Generic Fracture Conductivity Model for Partially Propped Fracture Networks with Proppant Embedment and Proppant Pack Deformation. Processes 2025, 13, 1462. https://doi.org/10.3390/pr13051462
Shao G, Zhao Y, Jia X, Zhi Z, Wang Q, Zeng J, Xu S, Lu C. A Generic Fracture Conductivity Model for Partially Propped Fracture Networks with Proppant Embedment and Proppant Pack Deformation. Processes. 2025; 13(5):1462. https://doi.org/10.3390/pr13051462
Chicago/Turabian StyleShao, Guolin, Yizhong Zhao, Xiaodong Jia, Zhaoyang Zhi, Qijing Wang, Jie Zeng, Shiqian Xu, and Cong Lu. 2025. "A Generic Fracture Conductivity Model for Partially Propped Fracture Networks with Proppant Embedment and Proppant Pack Deformation" Processes 13, no. 5: 1462. https://doi.org/10.3390/pr13051462
APA StyleShao, G., Zhao, Y., Jia, X., Zhi, Z., Wang, Q., Zeng, J., Xu, S., & Lu, C. (2025). A Generic Fracture Conductivity Model for Partially Propped Fracture Networks with Proppant Embedment and Proppant Pack Deformation. Processes, 13(5), 1462. https://doi.org/10.3390/pr13051462







