Evaluation of the Effectiveness of Anti-Turbulence Additives in the Transportation of High-Viscosity Oil at Low Ambient Temperatures

Abstract

This article investigates the effectiveness of using anti-turbulence additives (ATAs) to reduce hydraulic resistance during the pipeline transportation of high-viscosity oil. This study focuses on analyzing the impact of ATA dosage on the pressure loss and oil flow rate under turbulent flow conditions. Experiments demonstrated that a 40 g/t ATA concentration reduces hydraulic resistance by 25.1–36.7%, increasing pipeline throughput by ~60% (from 179.9 t/h to 289.8 t/h). This efficiency eliminates the need for constructing additional pumping stations, reducing capital costs by an estimated USD 5–7 million per 100 km of pipeline. Graphs confirm a nonlinear relationship between ATA dosage and pressure loss reduction, with optimal efficiency observed at 40 g/t. The findings emphasize the need for developing a comprehensive model that accounts for the physicochemical properties of the oil and additives, as well as the influence of flow parameters. These results provide a foundation for further research and the industrial application of ATA.

1. Introduction

Currently, companies in the fuel and energy sector are focusing on optimizing existing technological processes [1,2,3]. Various methods are employed to enhance the energy efficiency of oil pipeline transportation [4,5]. The main methods are oil heating at pumping stations or during transportation, oil treatment with ultrasonic or electromagnetic waves, and mixing. These achieve efficiency with less viscous oil, oil transport in the form of emulsion with water, and the use of various additives. Each of these methods has its own advantages and disadvantages. For the main pipelines, the most common is the use of anti-turbulence additives (ATAs), which reduce hydraulic resistance in pipelines [6,7,8].

Frictional head losses are the primary factor affecting energy efficiency in pipeline transportation. Reducing frictional losses decreases energy consumption by 15–20% in pumping systems (Burger et al., 1982) [9], prolongs pipeline service life by mitigating erosion (Litvinenko et al., 2020) [10], and reduces CO₂ emissions by ~12% per ton of transported oil (Fetisov et al., 2023) [11]. Frictional head losses arise due to internal friction forces between the layers of the moving fluid [12,13]. During pumping, mechanical energy from the organized motion is dissipated and converted into the chaotic motion of fluid particles. In turbulent flow conditions, energy is further dissipated into vortex flows, pulsations, and thermal energy within the fluid itself. Vortex flows increase mechanical stress on pipe walls, while thermal dissipation raises oil temperature by 2–4 °C [11,14].

Anti-turbulence additives reduce the proportion of dissipated energy. This effect is achieved due to the high-molecular structure of ATA suspensions (gels), which integrate into the flow and suppress pulsations in the near-wall region, significantly reducing hydraulic resistance by up to 60% [15,16,17].

The ability of certain substances to reduce hydraulic resistance in turbulent fluid flows was first observed and described in the 1940s by the British scientist Benjamin Toms [18]. Based on laboratory tests, he concluded that the hydraulic friction coefficient could be reduced by approximately twofold through the introduction of a low-concentration polymethyl methacrylate polymer into a turbulent flow of monochlorobenzene. This phenomenon was later named Tom’s effect [19,20].

ATAs were first used on an industrial scale in 1979 in the Trans-Alaska Pipeline System. This application increased the pipeline’s capacity from 1.45 million barrels per day to 2.1 million barrels per day by significantly reducing hydraulic resistance by nearly twofold [9].

This efficiency eliminated the need to construct two additional pumping stations. In the USSR, the first industrial trials of ATAs were conducted in 1985 [10]. On the final section of the Lisichansk–Tikhoretsk trunk pipeline, a hydraulic efficiency improvement of 24% was achieved with the use of additives [21].

Currently, anti-turbulence additives are actively used for hydrocarbon transportation through pipelines both in the Russian Federation and worldwide [22,23,24]. Significant research is underway to develop new materials that reduce hydraulic resistance [25,26,27]. The mechanism of action of additives is very complex. Additives that show high efficiency in scientific research can have a negative effect on operating pipelines. The action of an additive depends, to a large extent, on the composition of the oil it uses to pump. For this reason, determining the effectiveness of new additives requires expensive industrial tests on existing pipelines.

The scientific novelty of the research consists of a complex analysis of the influence of the concentration of anti-turbulent additives on hydraulic resistance during the transportation of viscous oil in conditions of low temperatures.

In this regard, one of the key tasks in the development of an oil transport is to develop a calculation methodology that allows for the accurate determination of the effectiveness of anti-turbulence additives. Within the framework of this article, it is necessary to analyze the existing dependencies, which are used to determine the coefficient of hydraulic resistance in oil transport through the main pipelines, taking into account the influence of additive efficiency, to carry out pilot tests to determine the efficiency of ATA on the operating main oil pipeline, and to show how much the stated theoretical efficiency of the additive can differ from the actual one, which can be obtained only by conducting research on the operating oil pipelines [28].

2. Theory of Calculation of the Hydraulic Resistance Coefficient When Using Anti-Turbulent Additives

The calculation of hydraulic resistance during the flow of oil in pipelines with anti-turbulence additives (ATAs) is a complex task [29]. This complexity arises from the multitude of formulas describing the dependence of hydraulic resistance on the Reynolds number, additive concentration, relative roughness, other auxiliary parameters, and the coefficients determined experimentally.

To compute the hydraulic resistance coefficient for Newtonian oil flow without additives, the Prandtl–Kármán (or Blasius) formula is typically used [30]:

$$\sqrt{{\displaystyle \frac{1}{\lambda }}}=4.0{\log }_{10}Re\sqrt{\lambda }-0.4,$$

(1)

where Re—Reynolds number.

In [31], Equation (1) was modified to account for the influence of additives on oil transportation:

$$\sqrt{{\displaystyle \frac{1}{\lambda }}}=\left(4.0+\delta \right){\log }_{10}Re\sqrt{\lambda }-0.4-\delta {\log }_{10}\sqrt{2}d{W}^o,$$

(2)

where $\delta$ and $W^o$ are empirical parameters of the polymer additive.

In the same study, a formula was presented to determine hydraulic resistance in the asymptotic flow regime, where the friction coefficient becomes nearly independent of the polymer used:

$$\sqrt{{\displaystyle \frac{1}{\lambda }}}=19.0{\log }_{10}Re\sqrt{\lambda }-32.4.$$

(3)

Professor M.V. Lurie [31] proposed a modification of the semi-empirical shear turbulence theory by T. von Kármán through the introduction of additional boundary conditions. As a result, the following equation was derived:

$$\sqrt{{\displaystyle \frac{8}{\lambda }}}={\displaystyle \frac{1}{\kappa }}\left(\ln {\displaystyle \frac{k\left(\theta \right)·\kappa ·Re\sqrt{\frac{\lambda }{8}}}{1+a\left(\theta \right)·\epsilon ·Re\sqrt{\frac{\lambda }{8}}}}-{\displaystyle \frac{137}{60}}\right)$$

(4)

where $\theta$—additive concentration; $k\left(\theta \right)$ and $a\left(\theta \right)$—constants, depending on the additive concentration and reflecting the peculiarities of interaction of the turbulent flow wall layer with the internal surface of the pipeline (determined experimentally for each ATA); $\epsilon$—roughness; $\kappa$—Karman constant.

This method for determining the hydraulic resistance coefficient effectively characterizes the influence of surface-type ATAs on the transported hydrocarbon. By emphasizing boundary conditions, it specifically describes the near-wall region, where the primary effect of anti-turbulence additives is observed.

In the works of A.M. Nechval and V.I. Muratova [32], a formula for determining the hydraulic resistance coefficient was proposed based on Altschul’s universal logarithmic equation:

$${\lambda }_f={\displaystyle \frac{1.6364}{{\left\{\ln \left[1+A_1\left(C\right)\right]·W_f\right\}}^2}}$$

(5)

$$W_f={\displaystyle \frac{Re}{{Re}_f·\frac{0.1·k_3}{D}+7}}$$

(6)

where $D$—pipeline diameter, m; ${Re}_f$—Reynolds number for fluid flow with the additive; $A_1\left(C\right)={\displaystyle \frac{1}{W}}·exp\left[\ln W·{\left(1-{\displaystyle \frac{\psi \left(C\right)}{100}}\right)}^{-0.5}\right]-1$—mixed friction parameter, which is determined from the condition of equal flow rates and a known value of the required hydraulic efficiency of the turbulent additive $\psi \left(C\right)={\displaystyle \frac{C}{k_0+k_{1}C+k_2{C}^2}}$ ($k_0,k_1,k_2$—parameters determined empirically).

Thus, this formula allows the determination of the hydraulic resistance coefficient during the transportation of hydrocarbons with ATAs, relying exclusively on the results of experimental trials for specific ATA grades.

Nechval and Muratova [33,34] also noted that introducing the correction factor $A_1\left(C\right)$ enables the determination of the hydraulic resistance coefficient λ for two friction zones—Blasius (hydraulically smooth pipes) and Altschul’s mixed friction zone—with the relative error not exceeding 4%.

Chernikin A.V. and Chernikin V.A. [35,36] proposed a method for determining the hydraulic resistance coefficient using the formula

$$\lambda =0.11·{\left[{\displaystyle \frac{\alpha +\epsilon +X^{1.4}}{115X+1+Y}}\right]}^{0.25},$$

(7)

where $\alpha ={\displaystyle \frac{68}{Re}};$ $\epsilon ={\displaystyle \frac{k}{D}};$ $X={\left(28\alpha \right)}^{10}$; $Y=A{C}^p{\epsilon }^q$; $C$—additive concentration; $A,p,q$—constant for a particular brand of ATAs.

This formula transitions to the universal equation proposed earlier by A.V. Chernikin [37] for calculating any flow regime when the ATA is absent (C = 0):

$$\lambda =0.11·{\left[{\displaystyle \frac{\alpha +\epsilon +X^{1.4}}{115X+1}}\right]}^{0.25}.$$

(8)

The universal formula aligns with well-known equations for specific flow regimes. However, to describe the behavior of the friction coefficient when the ATA is used, variable Y is introduced in Equation (1). Its value is determined through the mathematical processing of experimental data for a specific ATA. The authors applied this analysis to the ATA “Neccad-447”, achieving an average deviation of results by 6% [38].

In the modern scientific literature, dependencies have been proposed that allow taking into account the influence of the ATA using empirical coefficients, for example, in [39]

$${\lambda }^{-1/2}=\left({\displaystyle \frac{4}{n^{0.75}}}+\xi \right)log\left[Re{·\lambda }^{(1-n/2)}\right]-{\displaystyle \frac{0.4}{n^{1.2}}}-2.1\xi ,$$

(9)

where $n$—flow behavior index in the power law; $\xi$—empirical coefficient.

This formula is supported by experimental studies of ATA efficiency depending on fluid properties and flow characteristics. But its application is based on a large number of preliminary experiments that would allow the determination of empirical coefficients.

In [40], when applying multiple regression analysis, the dependence of the

$$\lambda =exp\left(a_1+a_{2}C+a_3{C}^2+a_4{C}^3+{\displaystyle \frac{a_5+a_{6}C+a_7{C}^2}{Re}}\right),$$

(10)

where $C$ is polymer concentration (wppm); $a_1, a_2, a_3, a_4, a_5, a_6, a_7$—constants.

Formula (10) takes into account the dependence of the hydraulic coefficient of resistance on the Reynolds number, but for its use, it is necessary to determine a large number of experimental coefficients, which complicates its use.

Based on the analysis of hydraulic resistance calculation methods, it can be concluded that the complexity of determining the hydraulic resistance coefficient in oil pipeline transportation with the ATA lies in accounting for the additive’s influence on oil viscosity, density, and flow characteristics. A comprehensive model is required to consider the interaction between the oil and additive, as well as potential nonlinear effects arising under various operating conditions.

The theoretical description of Tom’s effect remains a challenging task, with no consensus or universally accepted formula for accurately describing this phenomenon. Researchers worldwide continue to accumulate experimental data on this effect and propose mathematical models to describe it [41].

3. Hydraulic Calculation Based on Additive Efficiency Data

Theoretical hydraulic calculation is carried out before pilot tests to obtain the values of pressure loss and flow variation based on the characteristics of ATA.

The study of the additive effect on hydraulic resistance is determined on the oil pipeline, the scheme of which is shown in Figure 1, and the main parameters are shown in

Table 1. Main characteristics of the pipeline.

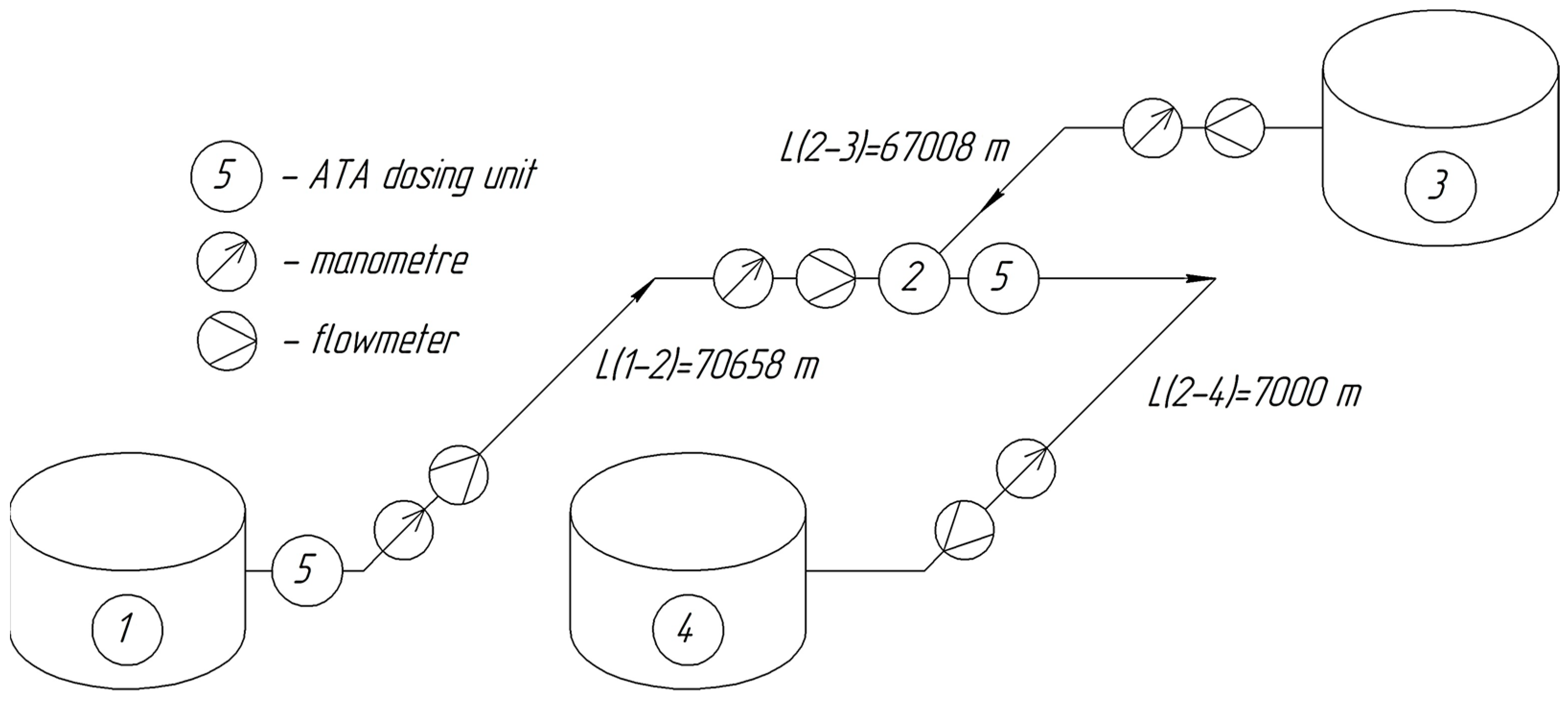
Pipe Section	Length, m	External Diameter, m	Internal Diameter, m	Volume, m3
1-2	70,658	0.325	0.309	5296
2-3	67,008	0.325	0.305	4893
2-4	7000	0.325	0.309	524

.

The diagram in Figure 1 represents a section of a gas main, the main line of which 1-4 has a length of 77,658 m. At point 2, there is an oil quantity and quality measurement unit. At this point, the interfield oil pipeline 3-2 with an internal diameter of 0.305 m is connected to the main pipeline 1-4 through a T-pipe.

Hydraulic Calculation Methodology

The calculated average oil flow temperature was determined by the formula [42]

$$t={\displaystyle \frac{\left(t_1+t_2\right)}{2}},$$

(11)

where $t_1 \mathrm{a}\mathrm{n}\mathrm{d} t_2$—oil temperatures at the beginning and end of the pipeline, respectively, °C.

The values of the oil density at the corresponding temperatures in the pipeline were determined by the formula [42]

$${\rho }_t={\rho }_{20}-\xi \left(t-20\right),$$

(12)

where $t$—oil temperature, °C; ${\rho }_{20}$—oil density at 20 °C, $\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$; $\xi$—temperature correction, $\mathrm{k}\mathrm{g}/({\mathrm{m}}^3·°\mathrm{C})$.

The initial and final head is determined by the formula

$$H={\displaystyle \frac{P}{\rho g}}.$$

(13)

When constructing the pressure (hydraulic) characteristic of the oil pipeline, the total head losses in the oil pipeline were determined by the formula

$$H=h_{\tau }+∆Z+h,$$

(14)

where $h_{\tau }$—friction head losses, m; $h$—head transferred to the end of the pipeline, m; $∆Z$—difference between the geodetic elevations of the end and the beginning of the pipeline, m.

Friction head losses were calculated by the Darcy–Weisbach formula [43]:

$$h_{\tau }=\lambda {\displaystyle \frac{L}{D}}{\displaystyle \frac{w^2}{2g}},$$

(15)

where $w={\displaystyle \frac{4Q_h}{3600\pi D^2}}$—average flow velocity, $\mathrm{m}/\mathrm{s}$; $Q_h={\displaystyle \frac{M}{24·{\rho }_t·{10}^{-3}}}$—hourly volumetric flow rate, ${\mathrm{m}}^3/\mathrm{h}$; $M$—expenditure, $\mathrm{t}/\mathrm{d}$; ${\rho }_t$—density at design temperature, $\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$.

The Reynolds number was calculated by the formula [44]

$$Re={\displaystyle \frac{wD}{\nu }},$$

(16)

where $\nu$—kinematic viscosity of oil at design temperature, ${\mathrm{m}}^2/\mathrm{s}$.

The coefficient of hydraulic resistance, depending on the mode of fluid flow in the pipeline, was calculated according to the following formulas:

(a) for the laminar regime at numbers $Re<2300$ by the Stokes formula [45]

$$\lambda ={\displaystyle \frac{64}{Re}}.$$

(17)

(b) at Reynolds numbers $2300<Re<{\displaystyle \frac{10D}{{\mathsf{\Delta }}_e}}$, i.e., the turbulent flow regime located in the zone of hydraulically smooth pipes according to the Blasius formula [46]

$$\lambda ={\displaystyle \frac{0.3164}{{Re}^{0.25}}}.$$

(18)

where ${\mathsf{\Delta }}_e$—equivalent roughness coefficient, m.

(c) at Reynolds numbers ${\displaystyle \frac{10D}{{\mathsf{\Delta }}_e}}<Re<{\displaystyle \frac{500D}{{\mathsf{\Delta }}_e}}$, i.e., the turbulent flow regime located in the region of mixed friction by the universal Altschul formula [47]

$$\lambda =0.11{\left({\displaystyle \frac{68}{Re}}+{\displaystyle \frac{{\mathsf{\Delta }}_e}{d}}\right)}^{0.25},$$

(19)

When determining the hydraulic resistance coefficient of turbulent oil flow with the anti-turbulent additive, the following expression was used [48]:

$${\lambda }_f=\left[1-DR\right]{\lambda }_0,$$

(20)

where ${\lambda }_f \mathrm{a}\mathrm{n}\mathrm{d} {\lambda }_0$—hydraulic resistance coefficients at oil flow with and without the additive, accordingly, $DR$—theoretical value of drag reduction.

The results of the calculation carried out according to formulas 9-18 are presented in

Table 2. Results of hydraulic calculation.

№	Dosage of Additive, g/t	Flow Rate, t/h	Inlet Pressure, kgf/cm2	Pressure Loss ΔP, kgf/cm2	Theoretical Value of Drag Reduction, %	Hydraulic Resistance Coefficient
Pipe section 1-2
1	Without ATA	179.9	54.4	24.0	-	0.0340
2	40	289.8	57.8	26.2	36	0.0218
3	50	289.7	60.4	26.8	41	0.0201
4	60	289.8	63.0	27.1	45	0.0187
Pipe section 2-4
1	Without ATA	179.9	54.4	24.0	-	0.0340
2	40	289.8	57.8	26.2	36	0.0218
3	50	289.7	60.4	26.8	41	0.0201
4	60	289.8	63.0	27.1	45	0.0187

, and the processing of the results is presented in Figure 2.

The polynomial trend reflects saturation effects at higher ATA concentrations, where additive aggregation limits further drag reduction.

According to the hydraulic calculation, it can be concluded that the use of ATAs can significantly reduce the energy costs of pumping oil. However, to determine the actual values of hydraulic resistance reduction and pressure loss reduction, it is necessary to carry out experimental studies. The aim of this study is to establish the true value of the anti-turbulence additive’s effectiveness by means of pilot testing under real pipeline operating conditions.

4. Pilot Testing of an Anti-Turbulence Additive

The effectiveness of anti-turbulence additives depends on the rheological properties of the oil and the physicochemical characteristics of the additive. The physicochemical properties of the oil and additive are presented in

Table 3. Physicochemical properties of oil.

Name of Parameter	Value
Temperature at the beginning of the section, °C	30
Temperature at the end of the section, °C	22
Paraffin content, %	2.62
Density, kg/m3	873
Kinematic viscosity (at 20 °C)	36.7 mm2/s
Water content, %	0.1

and

Table 4. Physicochemical properties of the additive.

Name of Parameter	Value
Appearance	White-colored suspension
Viscosity at 20 °C, mPa∙s	167
Viscosity at −40 °C, mPa∙s	1015.8
Density at 20 °C, kg/m3	876
Solidification temperature, °C	Less than −50
Particulate matter content, %	37.8

.

The investigated oil belongs to the class of viscous (≥30 mm²/s) heavy (871–895 kg/m³) oil. At 22 °C, it exhibits Newtonian properties.

Industrial tests were carried out on the main oil pipeline, the scheme of which is shown in Figure 1. The main objective of the industrial trial was to evaluate the actual effectiveness of an anti-turbulence additive in improving the flow characteristics of a high-viscosity oil pipeline. This study focused on three concentrations of the additive, 40 g/t, 50 g/t, and 60 g/t, and analyzed their effects on key operating parameters such as pressure drop, flow rate, and pipeline performance.

The tests were carried out on an operating pipeline with a known diameter, length, and capacity. The anti-turbulence additive was a polymer-based compound designed to reduce energy losses due to turbulence and improve flow efficiency.

The pipeline was divided into three segments for the trials, with each segment representing a distinct set of operational parameters (e.g., terrain, temperature variation, and flow rate). Baseline data, including flow rate and pressure drop, were collected prior to the additive injection.

A specialized injection system was installed to ensure the precise dosing of the additive at each concentration. The system included flow meters, pressure gauges, and sampling ports for real-time monitoring.

The trial evaluated the additive at concentrations of 40 g/t, 50 g/t, and 60 g/t. Each concentration was tested over a 24-h period to account for variations in operational conditions. The trial considered external factors such as ambient temperature and oil viscosity, which could influence the effectiveness of the additive.

The pilot trial included the following stages:

• Preparing the dosing equipment to ensure safe and uninterrupted operation during the trial.
• Injecting the anti-turbulence additive at a concentration of 40 g/t at the injection point.
• Filling the pipeline with oil and bringing the system to steady-state operation.
• Increasing the oil flow rate through the pipeline while maintaining steady-state conditions.
• Recording pressure and flow rate measurements over 24 h of pipeline operation under the dosing conditions of 40 g/t of additive.
• Reducing the flow rate to the initial values.
• Repeating steps 2-6 for additive concentrations of 50 g/t and 60 g/t.
• Stopping the injection of the additive into the pipeline.
• Processing the obtained results.

The trial aimed to establish a clear correlation between additive concentration and pipeline performance improvements. The results guided recommendations for routine additive use in similar pipeline systems and provided valuable insights into scaling up the technology for broader applications in the oil and gas sector.

5. Results and Discussion

The effectiveness of the additive is determined based on the experimental data on pressure losses and flow rates and is calculated using the following formula [49]:

$$DR=\left(1-{\displaystyle \frac{{∆P}_f·Q_0^2}{{∆P}_0·Q_f^2}}\right)·100\%,$$

(21)

where ${∆P}_f$—pressure losses with the additive, kg/cm²;

$Q_0$—volumetric flow rate without the additive, m³/h;

${∆P}_0$—pressure losses without the additive, kg/cm²;

$Q_f$—volumetric flow rate with the additive, m³/h.

Pressure losses can be determined by the formula [50]

$$∆P=P_1-P_2-g\left({\rho }_2{Z}_2-{\rho }_1{Z}_1\right),$$

(22)

where $P_1$—inlet pressure, Pa;

$P_2$—pressure at the end of the pipeline, Pa;

${\rho }_1$ and ${\rho }_2$—oil density at the beginning and end of the pipeline, kg/m³;

$Z_1$ and $Z_2$—geodetic elevations at the beginning and end of the pipeline route, m.

Since the pipeline, where the research was carried out, does not change its design position, the part of the equation that takes into account the geodetic mark can be neglected, and the pressure change can be determined by the formula

$$∆P=P_1-P_2.$$

(23)

The tests included different concentrations of the ATA (40, 50, and 60 g/t) across two pipeline sections. The findings are summarized in

Table 5. Results for section 1-2.

№	Dosage of Additive, g/t	Flow Rate, t/h	Inlet Pressure, kgf/cm2	Outlet Pressure, kgf/cm2	Pressure Loss ΔP, kgf/cm2
1	Without ATA	179.9	54.4	30.4	24.0
2	40	289.8	63.0	35.9	27.1
3	50	289.7	60.4	33.6	26.8
4	60	289.8	57.8	31.8	26.2

and

Table 6. Results for section 2-4.

№	Dosage of Additive, g/t	Flow Rate, t/h	Inlet Pressure, kgf/cm2	Outlet Pressure, kgf/cm2	Pressure Loss ΔP, kgf/cm2
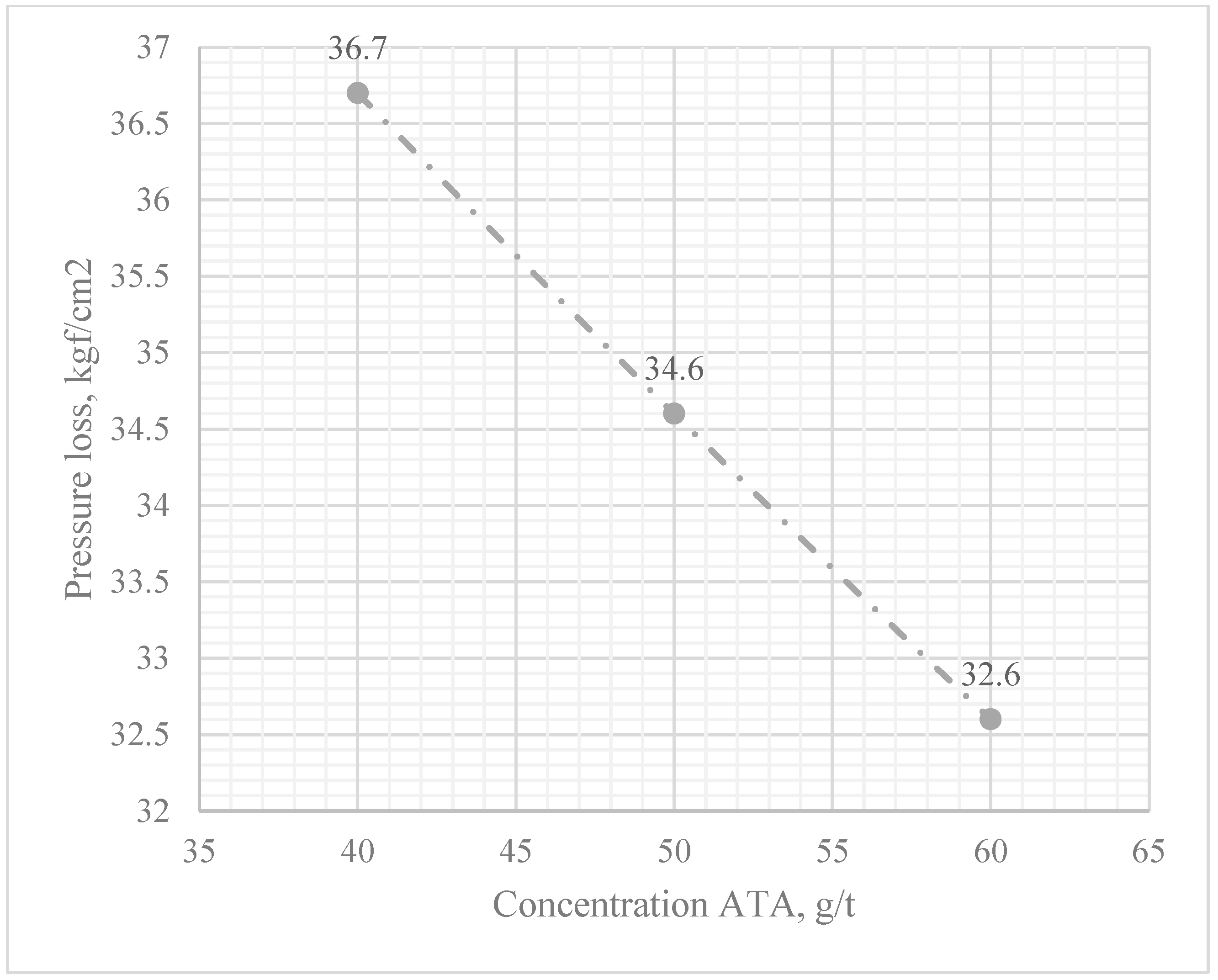
1	Without ATA	198.4	37.8	4.4	33.4
2	40	305.4	39.5	2.8	36.7
3	50	307.5	41.4	6.8	34.6
4	60	307.4	43.8	11.2	32.6

.

The dependency of pressure losses on additive concentration is shown in Figure 3 and Figure 4.

From the obtained experimental values by formula (6), the values of the efficiency of the application of the anti-turbulence additive were calculated (

Table 7. ATA effectiveness based on the results of the pilot test.

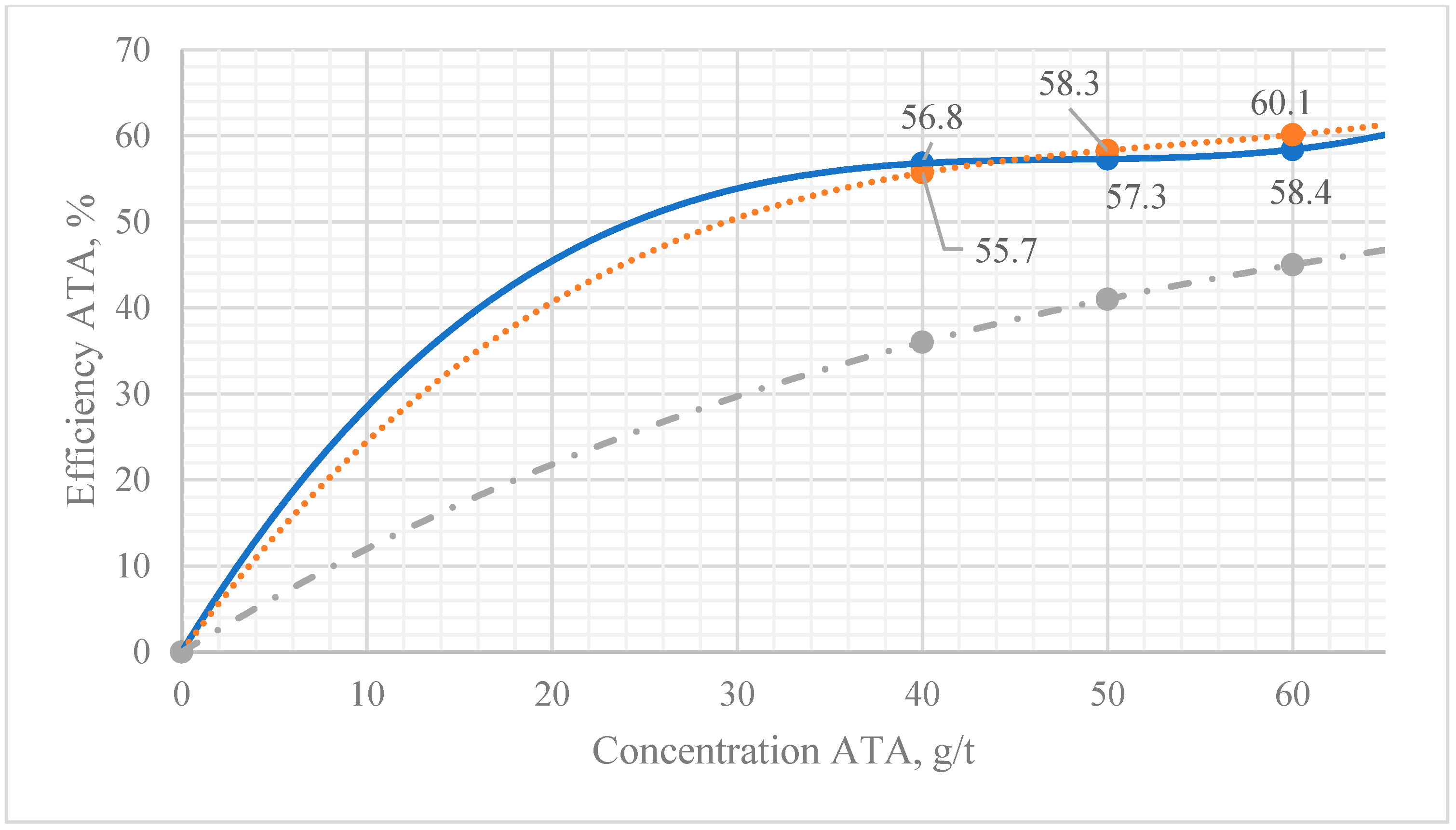
№	Dosage of Additive, g/t	ATA Effectiveness, % (Section 1-2)	ATA Effectiveness, % (Section 2-4)	Calculated ATA Effectiveness, %
1	40	55.7	56.8	36
2	50	57.3	58.3	41
3	60	58.4	60.1	45

).

Graphically, the experimental data on the effectiveness of ATA use are presented in Figure 5. The blue line on the graph is a polynomial approximation and extrapolation of the values of anti-turbulence additive efficiency obtained during pilot tests onto the 70 km length pipeline section 1-2. The red dotted line is a polynomial approximation and extrapolation of the values of anti-turbulence additive efficiency obtained during pilot tests onto the 7 km length pipeline section 2-4. And the dashed line is a line of the calculated value of the efficiency of the ATA based on the manufacturer’s data.

ATA effectiveness: Experimental results reveal that increasing the dosage of ATA from 40 to 60 g/t yields minimal growth in effectiveness, leveling off at approximately 58%.

Table 8. Deviations of experimental results.

№	Dosage of Additive, g/t	Deviation of ATA Effectiveness, % (Section 1-2)	Deviation of ATA Effectiveness, % (Section 2-4)
1	40	36.7	33.6
2	50	27.9	29.7
3	60	22.3	25.1

presents the values of the deviations of the experimentally obtained values of ATA efficiency from the theoretical ones based on Table 7. The deviation of ATA $\epsilon$ efficiency was calculated according to the formula

$$\epsilon ={\displaystyle \frac{{DR}_{ex}-{DR}_{calc}}{{DR}_{ex}}}·100\%,$$

(24)

where ${DR}_{ex}$—experimental ATA effectiveness, ${DR}_{calc}$—calculated ATA effectiveness.

Calculation of deviations: Experimentally determined effectiveness values deviate from calculated ones by 22.3–36.7%, underscoring the complexity of selecting a hydraulic calculation method. Factors include the following:

• interaction of the additive with the specific oil composition [50];
• changing flow conditions [50];
• polymer degradation [51];
• inaccuracies in computational models [52].

Theoretical models often do not take into account specific oil characteristics (viscosity, paraffin content, water content, impurities) that strongly influence additive performance under real conditions. In actual operation, the flow parameters—velocity, temperature gradient along the pipeline, hydraulic regime—vary and may differ from the conditions assumed in the calculations and the aggregation and dispersion of the additive in the flow stream. While theory often assumes a perfect distribution of the additive over the flow cross-section, in practice, polymer particles may aggregate or be unevenly distributed [52]. In a real pipeline, the additive can degrade mechanically due to shear stresses, cavitation, or turbulence, which reduces its effectiveness compared to the design. Theoretical formulas simplify the real picture, often using averaged or empirical coefficients that do not take into account the specific interactions between the additive and the oil in different temperature and hydraulic regimes.

6. Conclusions

A nonlinear relationship between ATA dosage and pressure loss reduction has been experimentally established, and the economic effect of their application has been quantitatively evaluated. On the basis of the conducted experimental studies on the influence of an anti-turbulent additive with the parameters presented in Table 3 and Table 4 on the process of pumping high-viscosity oil, it can be noticed that with the growth of ATA dosage from 40 to 60 g/t, its efficiency grows insignificantly and reaches an efficiency plateau at approximately 58%. However, the decision on the materiality of differences in dosages in this range should be made on the basis of the results of a feasibility study for a particular oil pipeline.

It can also be concluded that the effect of hydraulic resistance reduction when this ATA is introduced into the flow is quite significant, indicating the additive’s potential for further industrial application.

The experimental study of the ATA application has confirmed that a competent choice of additive allows for an increase in oil pipeline throughput up to 55%, which allows for a significant reduction in pumping costs.

Within the scope of this study, the dependencies used to determine the hydraulic resistance coefficient in oil transportation through trunk pipelines were analyzed, considering the impact of additive efficiency. The literature review confirmed that the topic remains relevant from the early days of Tom’s effect research to the present. Scientists are trying to determine the most optimal formula, which would take into account the properties of oil and additives. But it is impossible to obtain an accurate determination of the reduction in hydraulic resistance without conducting industrial tests.

The experimental–industrial tests conducted to determine the effectiveness of the ATA on the operating main oil pipeline demonstrated the extent to which the theoretical effectiveness of the additive may differ from its actual performance. This is influenced by a large number of factors. Further research in this direction should be aimed at investigating the mechanism of Tom’s effect influence on the pumped liquid. In the future, it is necessary to determine how the rheological properties of the fluid affect the change in ATA efficiency.