A Generalized Model for Estimating the Viscosity of Crude Oil
Abstract
1. Introduction
2. Experimental Data
2.1. Data Sources
2.2. Sensitivity Analyses
3. Results and Discussion
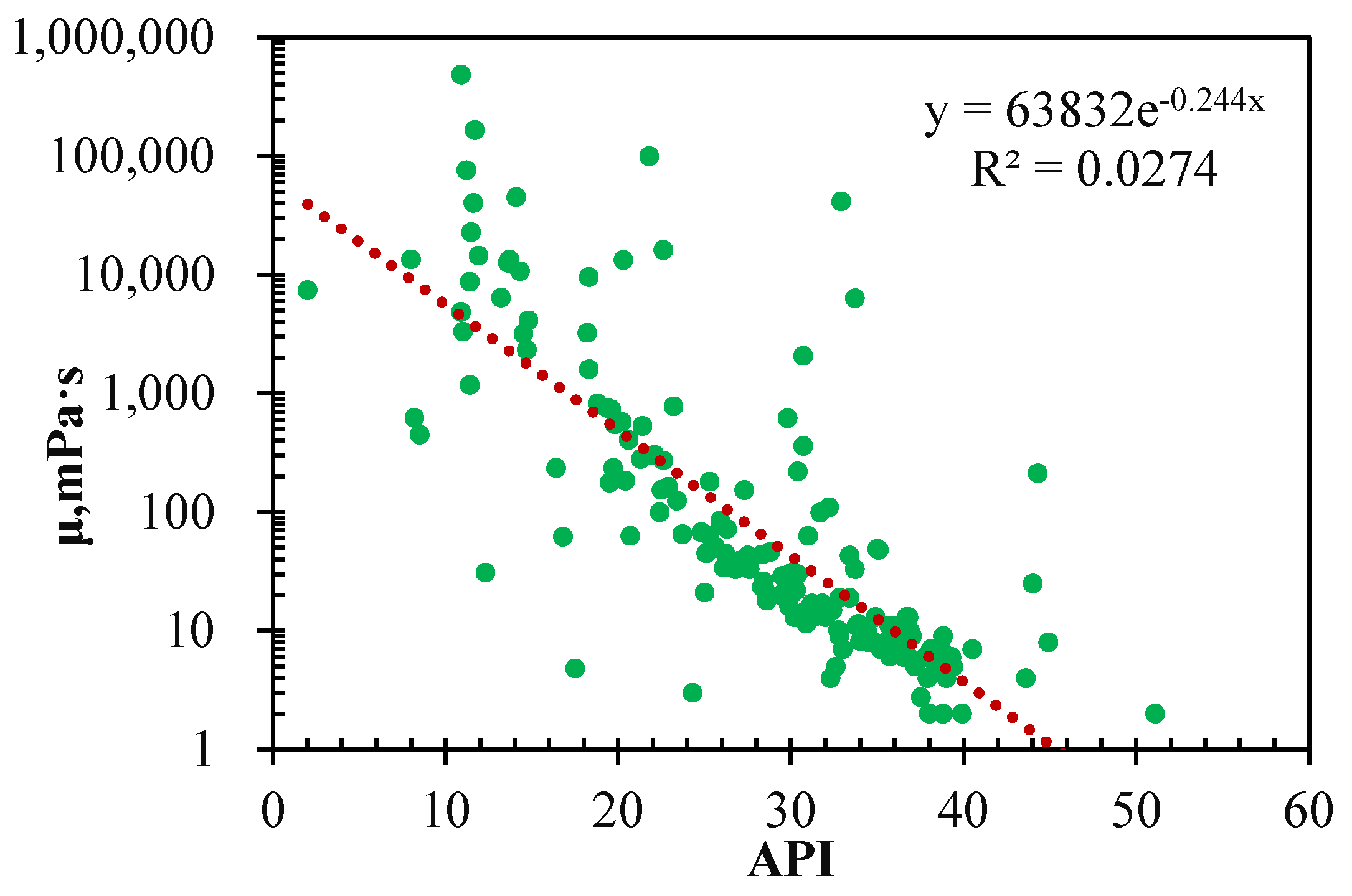
3.1. Description and Analysis of Existing Viscosity Empirical Models
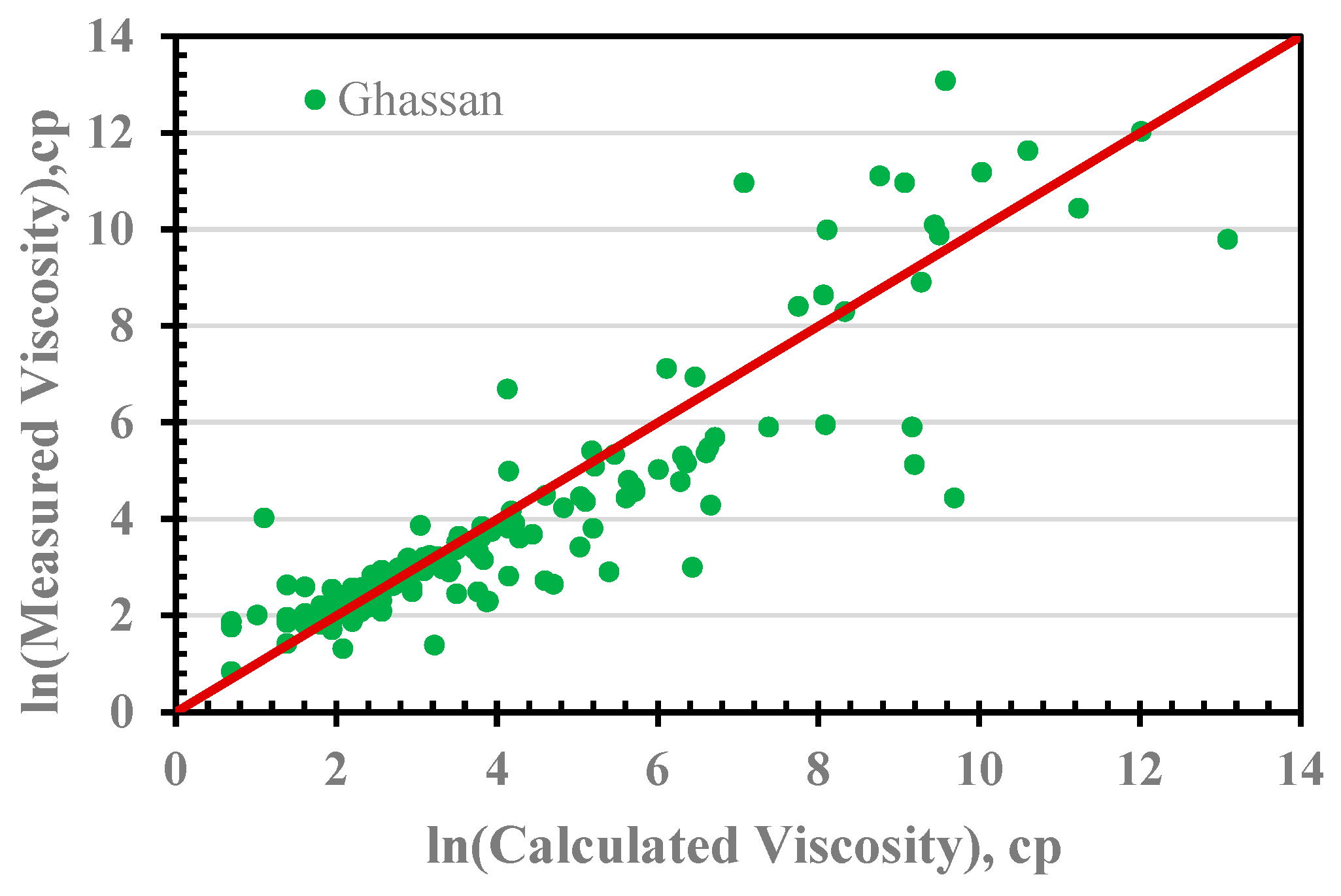
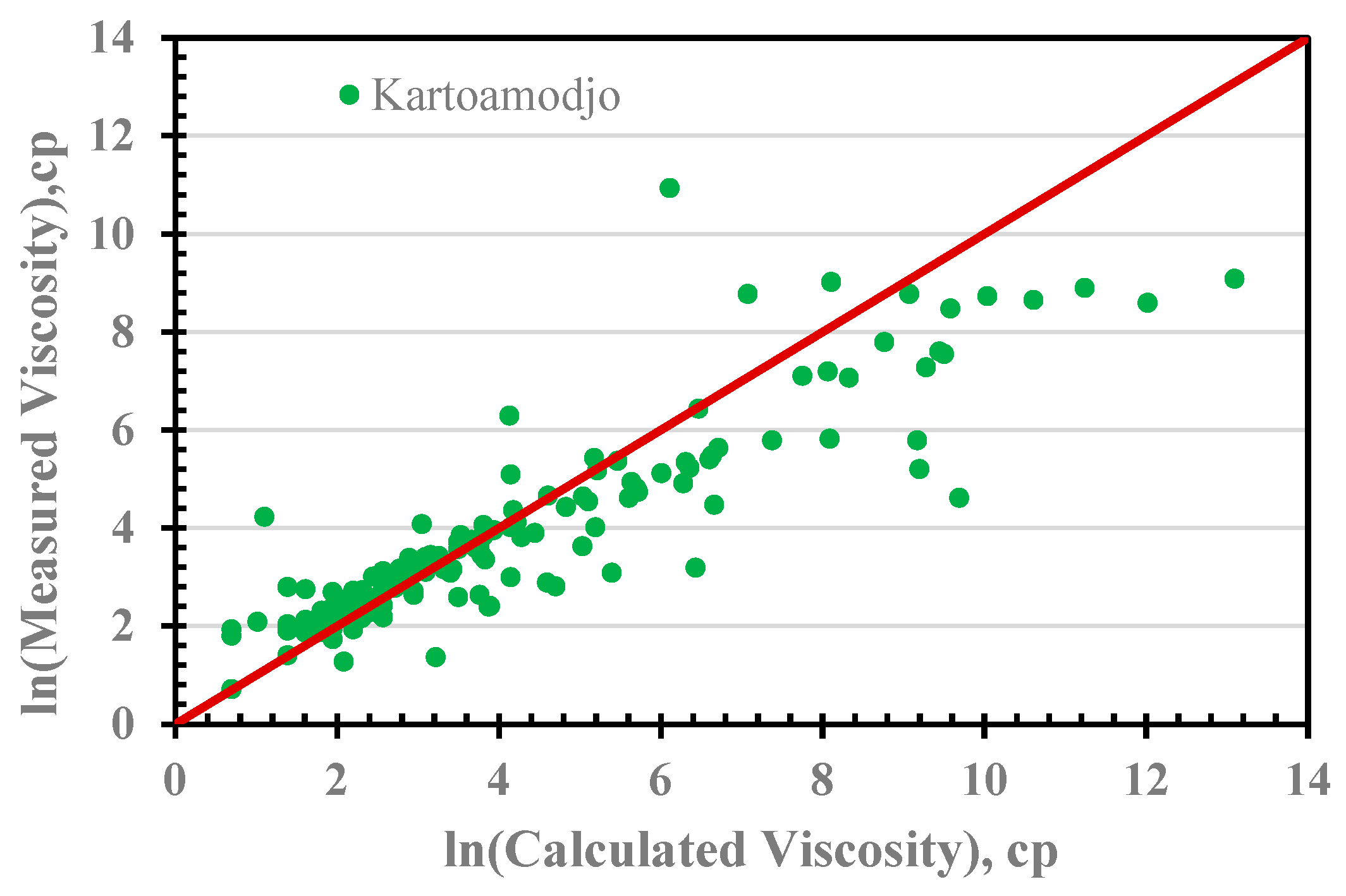
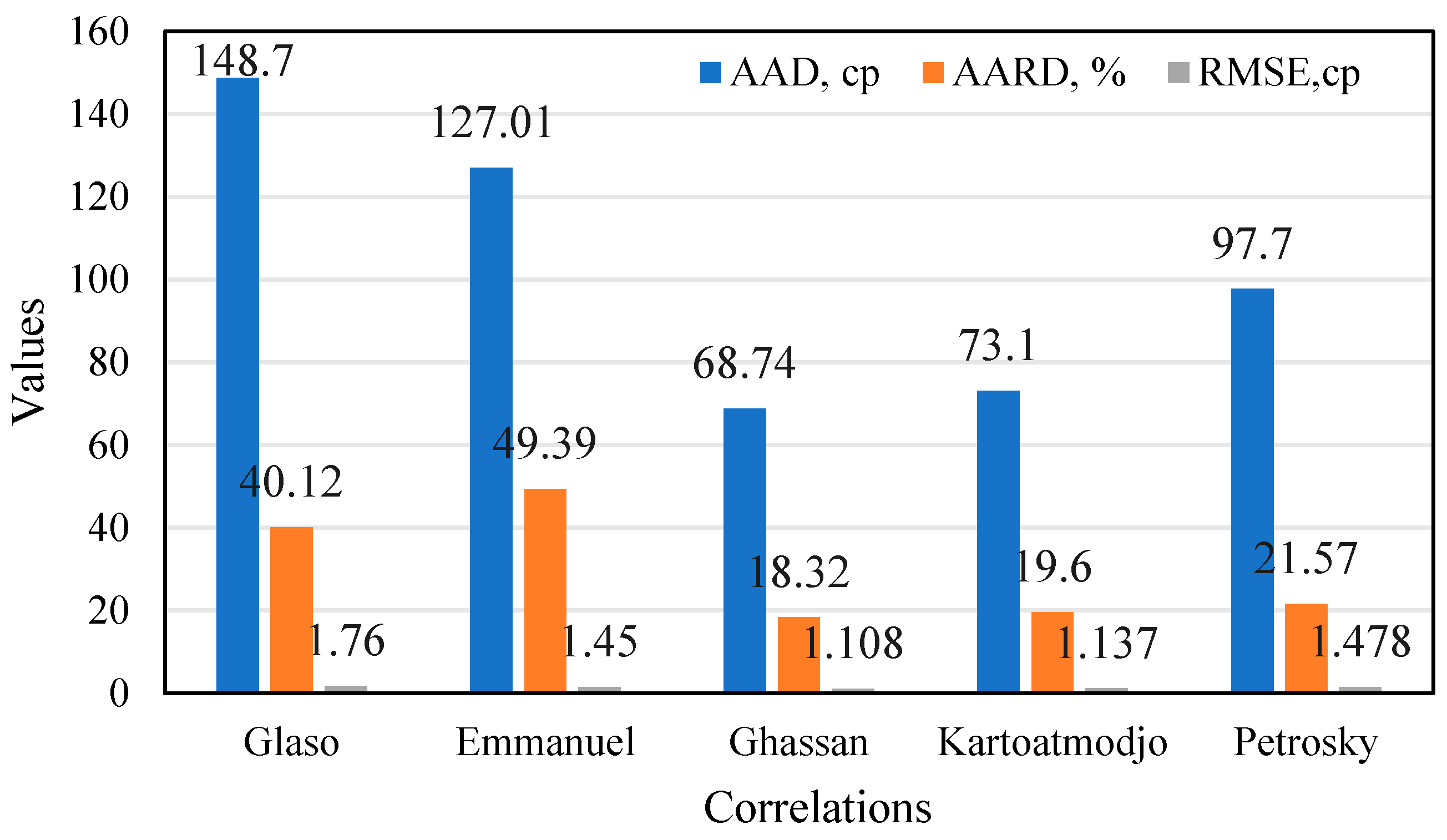
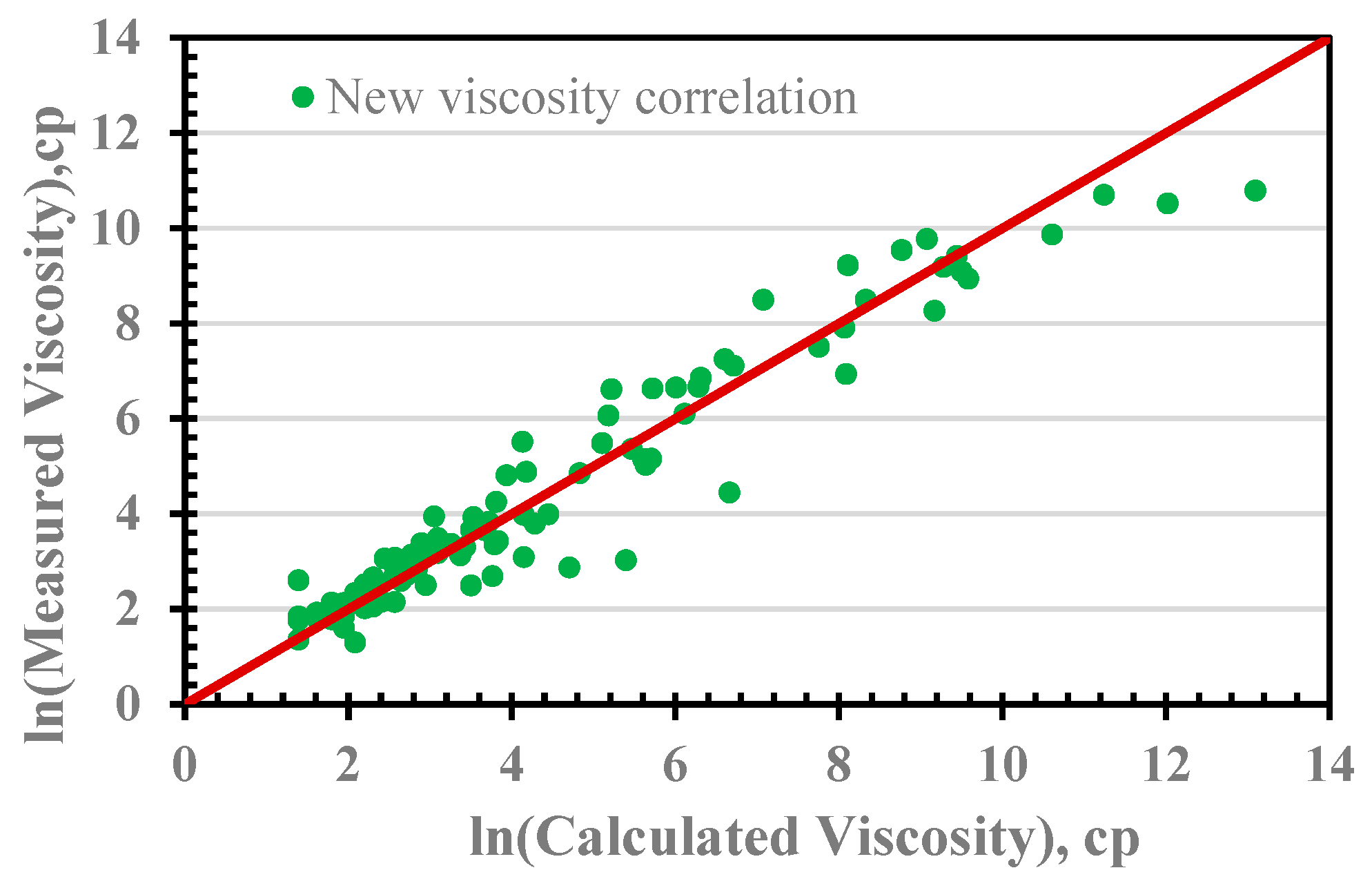
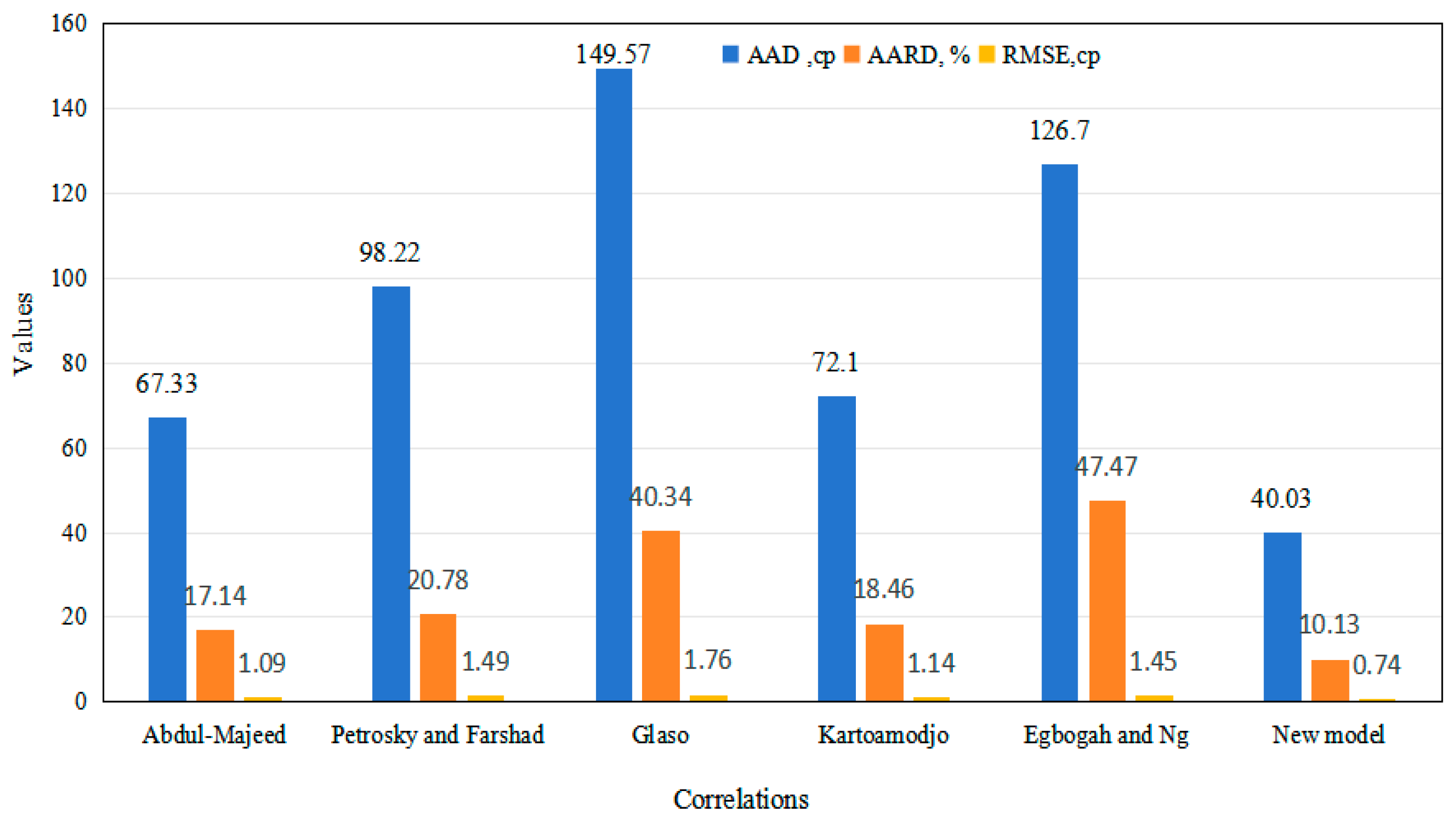
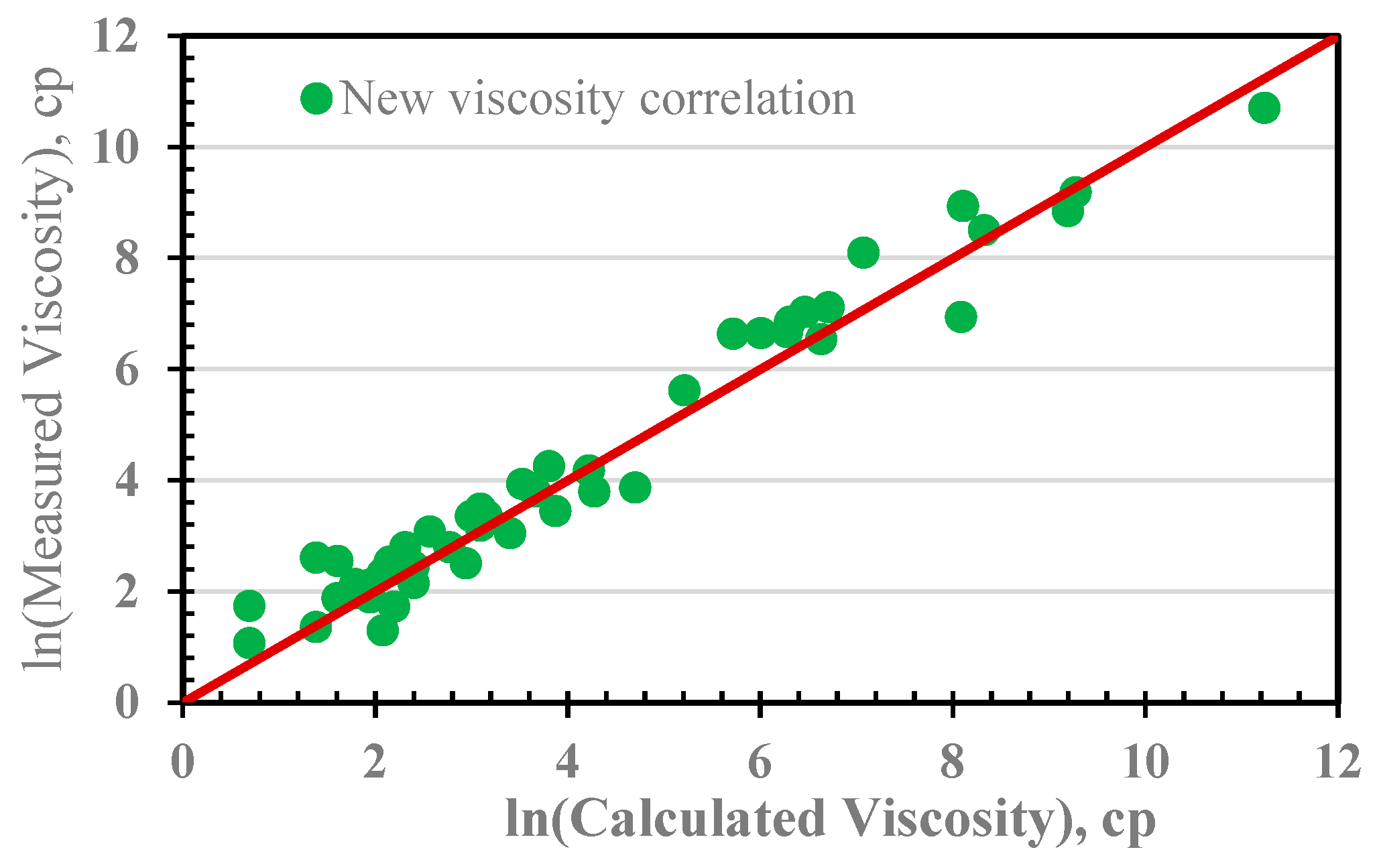
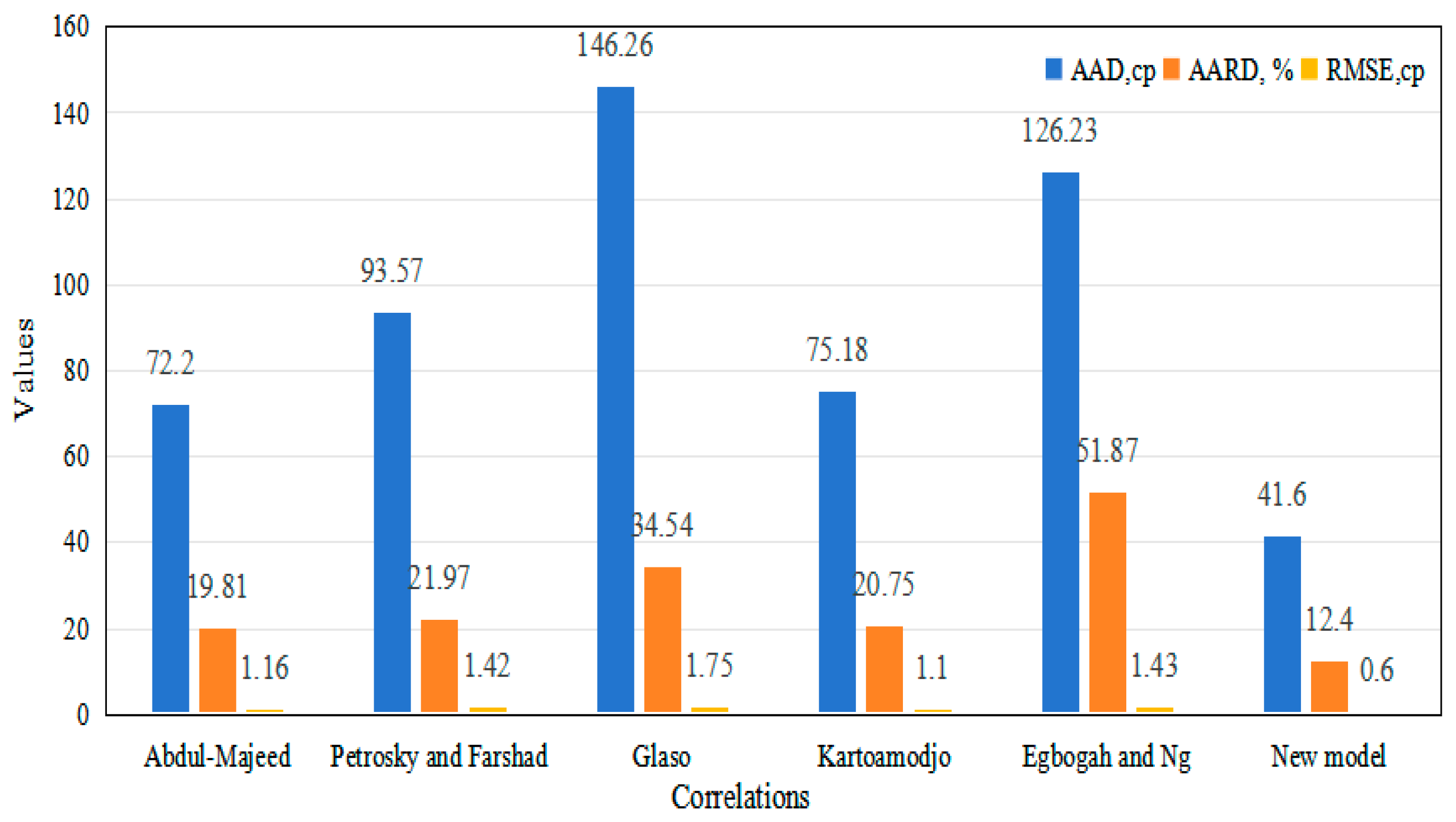
3.2. Graphical and Statistical Error Analysis
3.3. Establishing a New Unified Crude Oil Viscosity Model
| A = 17.93 | B = −0.06 | C = −185,096 |
| D = −0.73 | E = −0.018 | F = 0.702 |
| G = 1.77 | H = 0.13 | I = −1.48 |
| J = 0.13 | K = −0.03 |
3.4. Evaluation of New Model
3.5. Model Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| API gravity | American Petroleum Institute |
| Sa | Saturated, wt% |
| Ar | Aromatics, wt% |
| T | Temperature, °F |
| Re | Resins, wt% |
| Asp | Asphaltene, wt% |
| AAD | Average absolute deviation, cp |
| AARD | Average absolute relative deviation, % |
| RMSE | Root Mean Square Error, cp |
| μexp,i | Experimental value of dynamic viscosity, cp |
| μpre,i | Predicted value of dynamic viscosity, cp |
| LM | Levenberg–Marquardt |
| UGO | Universal global optimization |
| PSO | Particle swarm optimization |
| GA | Genetic algorithm |
| SA | Simulated annealing |
| ρOpertemp. | Oil density at operating temperature, gm/cc |
| SGc7+ | Specific gravity of C7+ components |
| MWci | Molecular weight of component Ci |
| μod | Dead oil viscosity, cp |
| C4, C5, C6, A, B...I | Empirical parameters |
| c1, c2 | Acceleration constant |
| r1, r2 | Random factor |
| Pbest | Best position |
| gbest | Particle table |
| v | Particle velocity |
| LUGO | UGO objective functions |
| Lm | LM objective functions |
| α | Regularization term |
References
- Abedini, R.; Abedini, A.; Eslami, Y.N. A new correlation for prediction of under saturated oil viscosity. Pet. Coal 2010, 52, 50–55. [Google Scholar]
- Daniyar, B.; Gaukhar, R.; Dinara, T. Comparison of measured and calculated high-viscosity crude oil temperature values in a pipeline during continuous pumping and shutdown modes. Int. J. Thermofluids 2024, 24, 100950. [Google Scholar]
- Osamah, A.; Mohammad, J.; Abullhaq, A.M.H. Heavy oil viscosity and density prediction at normal and elevated temperatures. J. Pet. Explor. Prod. Technol. 2016, 6, 253–263. [Google Scholar] [CrossRef]
- Alhamd, S.J.; Rashid, F.L.; Al-Obaidi, M.A.; Aldami, A.K. Unveiling crude oil viscosity and rheological Properties: An experimental comparison of Nano silica and Nano Molybdenum disulfide in Bazargan Oilfield. Fuel 2024, 381, 133698. [Google Scholar] [CrossRef]
- Nabeel, A.R.; Gholamreza, V.N.; Ibrahim, A.; Amin, F. A new correlation for prediction of viscosities of Omani Fahud-field crude oils. Adv. Model. Fluid Dyn. 2012, 293–300. [Google Scholar] [CrossRef][Green Version]
- Zhao, Q.; Shi, Q.; AlHammadi, A.A. Viscosity Modeling of Heavy Crude Oil Using the Friction TheoryCombined with PC-SAFT. Energy Fuels 2023, 37, 10248–10256. [Google Scholar] [CrossRef]
- Beggs, H.D.; Robinson, J.R. Estimating the Viscosity of Crude Oil Systems. J. Pet. Technol. 1975, 27, 1140–1141. [Google Scholar] [CrossRef]
- Standing, M.B. Volumetric and Phase Behavior of Oil Filed Hydrocarbon Systems; Society of Petroleum Engineers: Richardson, TX, USA, 1977. [Google Scholar]
- Emmanuel, O.E.; Jack, T.N. An improved temperature-viscosity correlation for crude oil systems. J. Pet. Sci. Eng. 1990, 4, 197–200. [Google Scholar]
- Ghassan, H.A.M.; Riadh, R.K.; Naeema, H.S. New correlation for estimating the viscosity of undersaturated crude oils. J. Can. Pet. Technol. 1990, 29, 80–85. [Google Scholar] [CrossRef]
- Kartoatmodjo, T.; Schmidt, Z. Large data bank improves crude physical property correlations. Oil Gas J. 1994, 92, 51–55. [Google Scholar]
- Petrosky, G.E.; Farshad, F.F. Viscosity correlation for Gulf of Mexico crude oil. In Proceedings of the SPE Production Operations Symposium Oklahoma, Oklahoma City, OK, USA, 2–4 April 1995; pp. 249–258. [Google Scholar]
- Bennison, T. Prediction of Heavy Oil Viscosity. Presented at the 1998 IBC Heavy Oil Field Development Conference, London, UK, 2–4 December 1998. [Google Scholar]
- Elsharkawy, A.M.; Gharbi, R.B.C. Compressing classical and neural regression techniques in modeling crude oil. Adv. Eng. Softw. 2001, 32, 215–224. [Google Scholar] [CrossRef]
- Hossain, M.S.; Sarica, C.; Zhang, H.Q.; Rhyne, L.; Greenhill, K.L. Assessment and development of heavy-oil viscosity correlations. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium, Calgary, AB, Canada, 1–3 November 2005; pp. 1–9. [Google Scholar]
- Alomair, O.; Elsharkawy, A.; Alkandari, H. Viscosity predictions of Kuwaiti heavy crudes at elevated temperatures. In Proceedings of the SPE Heavy Oil Conference and Exhibition, Kuwait city, Kuwait, 12–14 December 2011; pp. 1–18. [Google Scholar] [CrossRef]
- Felipe, S.M.; Gabriela, S.R.; Jorge, A.; Gustavo, M. Comparison of correlations based on API gravity for predicting viscosity of crude oils. Fuel 2014, 138, 193–199. [Google Scholar]
- Mansour, E.M.; Desouky, S.M.; Aily, M.E.; Helmi, M.E. The effect of asphaltene content on predicting heavy dead oils viscosity: Experimental and modeling study. Fuel 2018, 212, 405–411. [Google Scholar] [CrossRef]
- Abdulrahim, K.; Osamah, A.; Adel, E. Measurements and predictions of Middle Eastern heavy crude oil viscosity using compositional data. J. Pet. Sci. Eng. 2019, 173, 990–1004. [Google Scholar]
- Hénaut, I.; Barré, L.; Argillier, J.F.; Brucy, F.; Bouchard, R. Rheological and structural properties of heavy crude oils in relation with their asphaltenes content. In Proceedings of the SPE International Symposium on Oilfield Chemistry, Houston, TX, USA, 13–16 February 2001. [Google Scholar] [CrossRef]
- Sunil, L.K.; Selim, G.S. Asphaltenes: The cholesterol of petroleum. In Proceedings of the Middle East Oil Show, Manama, Bahrain, 11–14 March 1995. [Google Scholar] [CrossRef]
- Mohammad, T.; Sai, R.P.; Vahid, T.; Mahmoud, R.P.; Walter, G.C. Understanding the polydisperse behavior of asphaltenes during precipitation. Fuel 2014, 117, 206–217. [Google Scholar]
- James, H.G.; James, H.H.; Mark, J.K.; David, G. Petroleum refining technology and economics. In Petroleum Engineering Book; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar] [CrossRef]
- Argillier, J.F.; Barre, L.; Brucy, F.; Dournaux, J.L.; Hénaut, I.; Bouchard, B. Influence of Asphaltenes Content and Dilution on Heavy Oil Rheology. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium, Porlamar, Venezuela, 12–14 March 2001. [Google Scholar] [CrossRef]
- Amy, H.; Eun-Jae, S.; Matthew, W.L.; Andrew, M.H.; Mike, B. Correlating the chemical and physical properties of a set of heavy oils from around the world. Fuel 2008, 87, 3065–3070. [Google Scholar]
- Mahdi, G.; Mohammad-Javad, S.; Ahmad, R.S.A. Effects of Asphaltene Content and Temperature on Viscosity of Iranian Heavy Crude Oil: Experimental and Modeling Study. Energy Fuels 2013, 27, 7217–7232. [Google Scholar]
- Lilian, P.; Lia, B.S.B.; Nelson, O.R. Role of Asphaltenes and Additives on the Viscosity and Microscopic Structure of Heavy Crude Oils. Energy Fuels 2016, 30, 3644–3651. [Google Scholar]
- Speight, J.G. The Chemistry and Technology of Petroleum; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Pierre, C.; Barré, L.; Pina, A.; Moan, M. Composition and Heavy Oil Rheology. Oil Gas Sci. Technol. 2004, 59, 489–501. [Google Scholar] [CrossRef]
- Luo, P.; Gu, Y. Effects of asphaltene content on the heavy oil viscosity at different temperatures. Fuel 2007, 86, 1069–1078. [Google Scholar] [CrossRef]
- Sheu, E.Y.; De-Tar, M.M.; Storm, D.A. Rheological properties of vacuum residue fractions in organic solvents. Fuel 1991, 70, 1151–1156. [Google Scholar] [CrossRef]
- Hernández, M.E.; Vives, M.T.; Jean, P. Relationships among viscosity, composition, and temperature for two groups of heavy crudes from the Eastern Venezuelan Basin. Org. Geochem. 1983, 4, 173–178. [Google Scholar] [CrossRef]
- Rashid, S.A.; Omar, H.; Sabah, A.A. New correlating parameter for the viscosity of heavy crude oils. Energy Fuels 2006, 20, 2586–2592. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Rodionova, G.; Simon, S.; Ilyin, O.; Arinina, M.P.; Kulichikhin, V.G.; Sjöblom, J. Some Compositional Viscosity Correlations for Crude Oils from Russia and Norway. Energy Fuels 2016, 30, 9322–9328. [Google Scholar] [CrossRef]
- Fan, T.; Wang, J.; Jill, S.B. Evaluating Crude Oils by SARA Analysis. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 13–17 April 2002. [Google Scholar] [CrossRef]
- Argillier, J.-F.; Coustet, C.; Henaut, I. Heavy oil rheology as a function of asphaltene and resin content and temperature. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium and International Well Technology Conference, Calgary, AB, Canada, 4–7 November 2002. [Google Scholar] [CrossRef]
- Yisa, A. Mathematical modelling of oil viscosity at bubble point pressure and dead oil viscosity of Nigerian crude. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 5–7 August 2019. [Google Scholar] [CrossRef]
- Izmailov, A.F.; Solodov, M.V.; Uskov, E.I. A globally convergent Levenberg–Marquardt method for equality-constrained optimization. Comput. Optim. Appl. 2019, 72, 215–239. [Google Scholar] [CrossRef]
- Fischer, A.; Izmailov, A.F.; Solodov, M.V. The Levenberg–Marquardt method: An overview of modern convergence theories and more. Comput. Optim. Appl. 2024, 89, 33–67. [Google Scholar] [CrossRef]







| Author | Year | Correlation |
|---|---|---|
| Beggs and Robinson [7] | 1975 | |
| Standing [8] | 1977 | |
| Glaso [9] | 1980 | |
| Emmanuel and Jack [9] | 1990 | |
| Ghassan et al. [10] | 1990 | |
| Kartoamodjo and Schmidt [11] | 1994 | |
| Petrosky and Farshad [12] | 1995 | |
| Bennison [13] | 1998 | |
| Elsharkawy and Gharbi [14] | 2001 | |
| Hossain et al. [15] | 2005 | |
| Alomair et al. [16] | 2011 | |
| Felipe et al. [17] | 2014 | |
| Mansour [18] | 2018 | |
| Abbulrahim et al. [19] | 2019 |
| Property | Mean | Std | Min | Max | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| API gravity (°) | 27.69 | 7.95 | 8 | 44.9 | −0.51 | 0.01 |
| Saturates (wt%) | 54.94 | 16.56 | 14 | 88 | −0.46 | −0.42 |
| Aromatics (wt%) | 30.1 | 9.51 | 11 | 63 | 0.76 | 1.67 |
| Resins (wt%) | 10.44 | 6.09 | 1 | 31 | 1.23 | 1.14 |
| Asphaltene (wt%) | 6.38 | 5.67 | 0.15 | 26 | 1.78 | 3.28 |
| Viscosity (cp) | 445.84 | 1601.92 | 4 | 485,500 | 5.95 | 41.04 |
| Item | Function | R2 |
|---|---|---|
| Viscosity vs. API gravity | 0.6878 | |
| Viscosity vs. saturate | 0.5629 | |
| Viscosity vs. aromatic | 0.1857 | |
| Viscosity vs. resin | 0.538 | |
| Viscosity vs. asphaltene | 0.5882 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Jiang, T.; Li, Y. A Generalized Model for Estimating the Viscosity of Crude Oil. Processes 2025, 13, 1433. https://doi.org/10.3390/pr13051433
Gao X, Jiang T, Li Y. A Generalized Model for Estimating the Viscosity of Crude Oil. Processes. 2025; 13(5):1433. https://doi.org/10.3390/pr13051433
Chicago/Turabian StyleGao, Xiaodong, Tianwen Jiang, and Yang Li. 2025. "A Generalized Model for Estimating the Viscosity of Crude Oil" Processes 13, no. 5: 1433. https://doi.org/10.3390/pr13051433
APA StyleGao, X., Jiang, T., & Li, Y. (2025). A Generalized Model for Estimating the Viscosity of Crude Oil. Processes, 13(5), 1433. https://doi.org/10.3390/pr13051433







