Statistical Damage Constitutive Model for Mudstone Based on Triaxial Compression Tests
Abstract
1. Introduction
2. Tests and Methods
2.1. Material and Mineral Analysis
2.2. Test Setup and Test Program
3. Mathematical Modeling and Validation of Stress–Strain in Mudstone Damage
3.1. Mudstone Damage Mechanism Analysis
3.2. Statistical Microscopic Damage Mechanics Modeling
3.3. Model Parameter Determination
3.4. Model Validation
4. Results and Discussion
4.1. Results of Mechanical Characterization of Mudstone
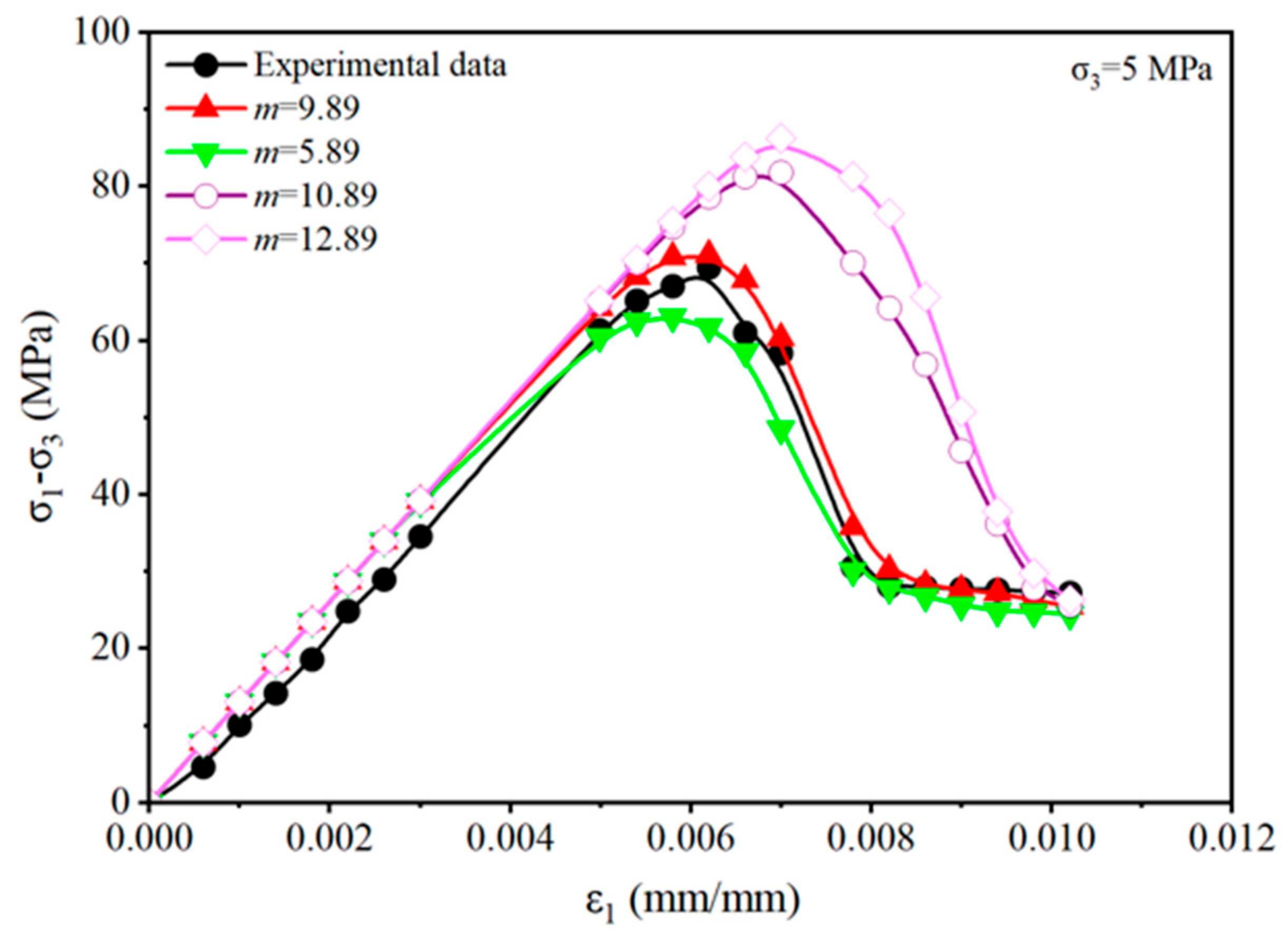
4.2. Parameter Sensitivity Analysis
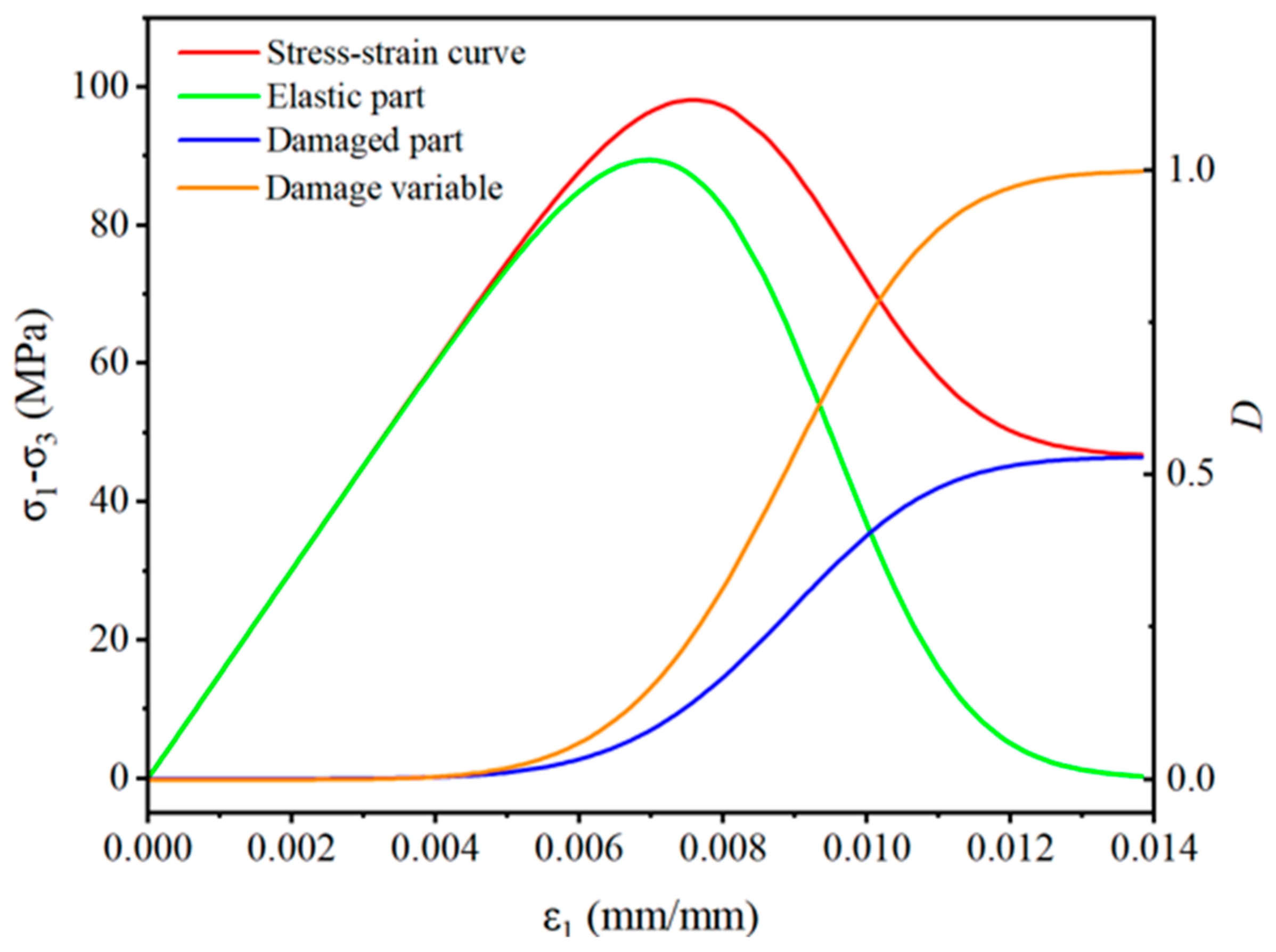
4.3. Damage Evolution Analysis
5. Conclusions
- (1)
- Mudstone’s stress–strain curve has clear stage features; as peripheral pressure rises, the material’s peak and residual strengths considerably increase, and its elastic modulus also rises.
- (2)
- The validity of the developed model is confirmed by comparing and analyzing the constructed mudstone statistical damage model with the test findings. It is also possible to anticipate the stress–strain response under various peripheral pressures using the constructed mudstone damage constitutive model. This is crucial for comprehending and forecasting mudstone behavior in real-world engineering applications.
- (3)
- The sensitivity analysis validates the impact of the model parameters on the mudstone damage characteristics. The microstructural characteristics of mudstone are closely related to the parameter ε0, whereas the macroscopic deformation strength of mudstone is primarily reflected by the parameter m.
- (4)
- A new tool for comprehending and forecasting the mechanical behavior of mudstone under intricate stress situations is provided by the statistical damage ontology model of mudstone that was suggested in this study. To confirm and broaden the model’s applicability, future research can investigate its application to different kinds of rocks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| C | A constant of integration | f(p) | Probability density distribution function |
| D | The damage variable | m | Mechanical properties of mudstone |
| Ded | Environmental damage and its variable | p | Randomly distributed variable |
| Dnd | Natural damage and its variable | Greek letter | |
| Dsd | Stress damage and its variable | ε1 | The axial strain |
| E | The modulus of elasticity | ε0 | Mechanical properties of mudstone |
| N | The sum of all the microelements | ε1 | The peak point strain |
| ND | The number of damaged microelements | σ1 | The axial load |
| Vd | The total amount of damaged rock units | σi | The apparent stress |
| Vud | The volume of undamaged rock units | σie | The effective stress |
References
- Guan, Q.S. Casing milling and fishing technology of directional borehole in mudstone formation in underground coal mine. Saf. Coal Mines 2021, 52, 152–155. [Google Scholar] [CrossRef]
- Xiao, D.; Fu, W.; Wu, Q.; Sun, R.; Huang, F.; Tan, S.; Zhang, Y.; Fang, X. Drilling fluid for mudstone in wulonggou mine of qinghai province. Explor. Eng. (Rock Soil Drill. Tunneling) 2019, 46, 45–50. [Google Scholar]
- Guo, Z.; Wang, Q.; Yin, S.; Kuai, X.; Yan, D.; Li, M.; Qu, Y. The creep compaction behavior of crushed mudstones under the step loading in underground mining. Int. J. Coal Sci. Technol. 2019, 6, 408–418. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, K.; Cui, S.; Yao, J.; Wu, Y.; Sepehrnoori, K.; Jia, C. Numerical Simulation of Reactive Flow in Fractured Vuggy Carbonate Reservoirs Considering Hydro-Mechanical-Chemical Coupling Effects. SPE J. 2025, 30, 853–874. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Chen, C.; Kong, L.; Wang, G. Engineering geology of residual soil derived from mudstone in zimbabwe. Eng. Geol. 2020, 277, 105785. [Google Scholar] [CrossRef]
- Wu, L.Z.; Li, S.H.; Sun, P.; Huang, R.Q.; Li, B. Shear creep tests on fissured mudstone and an improved time-dependent model. Pure Appl. Geophys. 2019, 176, 4797–4808. [Google Scholar] [CrossRef]
- Douma, L.A.N.R.; Dautriat, J.; Sarout, J.; Dewhurst, D.N.; Barnhoorn, A. Impact of water saturation on the elastic anisotropy of the whitby mudstone, united kingdom. Geophysics 2020, 85, MR57–MR72. [Google Scholar] [CrossRef]
- Li, S.N.; Liu, X.X.; Li, Y.; Wang, W.W.; Zhou, Y.M. Study on the deformation characteristics and damage evolution law of the progressive failure process of carbonaceous mudstone. China J. Highw. Transp. 2022, 35, 99–107. [Google Scholar] [CrossRef]
- Jing, H.; Yin, Q.; Yang, S.; Chen, W. Micro-mesoscopic creep damage evolution and failure mechanism of sandy mudstone. Int. J. Geomech. 2021, 21, 04021010. [Google Scholar] [CrossRef]
- Bai, W.; Lu, X.; Guan, J.; Huang, S.; Yuan, C.; Xu, C. Stress–strain behavior of FRC in uniaxial tension based on mesoscopic damage model. Crystals 2021, 11, 689. [Google Scholar] [CrossRef]
- Kang, G.; Yang, Z.; Chen, P.; Liu, R.; Ning, Y.; Pang, S. Mechanical behavior simulation of particulate-filled composite at meso-scale by numerical manifold method. Int. J. Mech. Sci. 2021, 213, 106846. [Google Scholar] [CrossRef]
- Rinker-Schaeffer, C.W.; O’Keefe, J.P.; Welch, D.R.; Theodorescu, D. Metastasis suppressor proteins: Discovery, molecular mechanisms, and clinical application. Clin. Cancer Res. 2006, 12, 3882–3889. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Guo, W.; Wu, S.; Chu, J. An experimental approach for determination of the weibull homogeneity index of rock or rock-like materials. Acta Geotech. 2019, 15, 375–391. [Google Scholar] [CrossRef]
- Jiang, H.P.; Jiang, A.N.; Yang, X.R. Statistical damage constitutive model of high temperature rock based on weibull distribution and its verification. DOAJ (DOAJ Dir. Open Access J.) 2021, 42, 1894–1902. [Google Scholar] [CrossRef]
- Yang, B.; Qin, S.; Xue, L.; Chen, H. The reasonable range limit of the shape parameter in the weibull distribution for describing the brittle failure behavior of rocks. Rock Mech. Rock Eng. 2021, 54, 3359–3367. [Google Scholar] [CrossRef]
- Lisjak, A.; Liu, Q.; Zhao, Q.; Mahabadi, O.K.; Grasselli, G. Numerical simulation of acoustic emission in brittle rocks by two-dimensional finite-discrete element analysis. Geophys. J. Int. 2014, 196, 1263. [Google Scholar] [CrossRef]
- Ren, C.; Yu, J.; Liu, S.; Yao, W.; Zhu, Y.; Liu, X. A plastic strain-induced damage model of porous rock suitable for different stress paths. Rock Mech. Rock Eng. 2022, 55, 1887–1906. [Google Scholar] [CrossRef]
- Ma, Q.; Tan, Y.; Liu, X.; Gu, Q.; Li, X. Effect of coal thicknesses on energy evolution characteristics of roof rock-coal-floor rock sandwich composite structure and its damage constitutive model. Compos. Part B Eng. 2020, 198, 108086. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, J.; Ren, Y.; Liang, C.; Liao, Y. Study on very long-term creep tests and nonlinear creep-damage constitutive model of salt rock. Int. J. Rock Mech. Min. Sci. (1997) 2021, 146, 104873. [Google Scholar] [CrossRef]
- Yang, C.; Zhou, K.; Xiong, X.; Deng, H.; Pan, Z. Experimental investigation on rock mechanical properties and infrared radiation characteristics with freeze-thaw cycle treatment. Cold Reg. Sci. Technol. 2021, 183, 103232. [Google Scholar] [CrossRef]
- Zhang, H.; Meng, X.; Yang, G. A study on mechanical properties and damage model of rock subjected to freeze-thaw cycles and confining pressure. Cold Reg. Sci. Technol. 2020, 174, 103056. [Google Scholar] [CrossRef]
- Zhu, T.; Chen, J.; Huang, D.; Luo, Y.; Li, Y.; Xu, L. A DEM-based approach for modeling the damage of rock under freeze–thaw cycles. Rock Mech. Rock Eng. 2021, 54, 2843–2858. [Google Scholar] [CrossRef]
- Tang, Y.; Okubo, S.; Xu, J.; Peng, S. Progressive failure behaviors and crack evolution of rocks under triaxial compression by 3d digital image correlation. Eng. Geol. 2019, 249, 172–185. [Google Scholar] [CrossRef]
- Sun, X.; Li, X.; Zheng, B.; He, J.; Mao, T. Study on the progressive fracturing in soil and rock mixture under uniaxial compression conditions by CT scanning. Eng. Geol. 2020, 279, 105884. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, H.; Liu, X. Rock damage constitutive model based on the modified logistic equation under freeze–thaw and load conditions. J. Cold Reg. Eng. 2021, 35, 04021016. [Google Scholar] [CrossRef]
- Li, Y.; Jia, D.; Rui, Z.; Peng, J.; Fu, C.; Zhang, J. Evaluation method of rock brittleness based on statistical constitutive relations for rock damage. J. Pet. Sci. Eng. 2017, 153, 123–132. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F. A review of experimental and theoretical research on the deformation and failure behavior of rocks subjected to cyclic loading. J. Rock Mech. Geotech. Eng. 2021, 13, 1203–1230. [Google Scholar] [CrossRef]
- Wang, C.; He, B.; Hou, X.; Li, J.; Liu, L. Stress–energy mechanism for rock failure evolution based on damage mechanics in hard rock. Rock Mech. Rock Eng. 2019, 53, 1021–1037. [Google Scholar] [CrossRef]

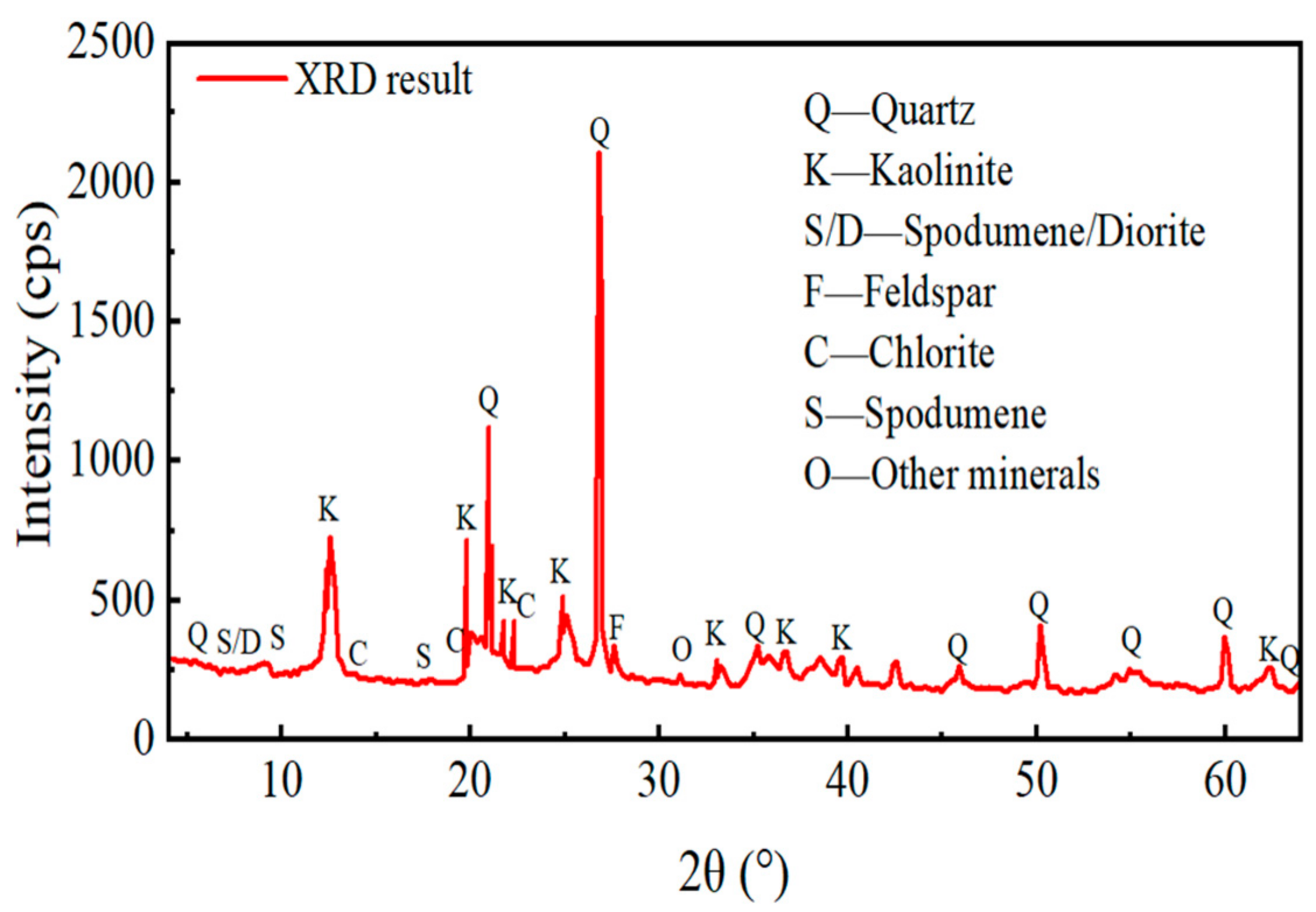
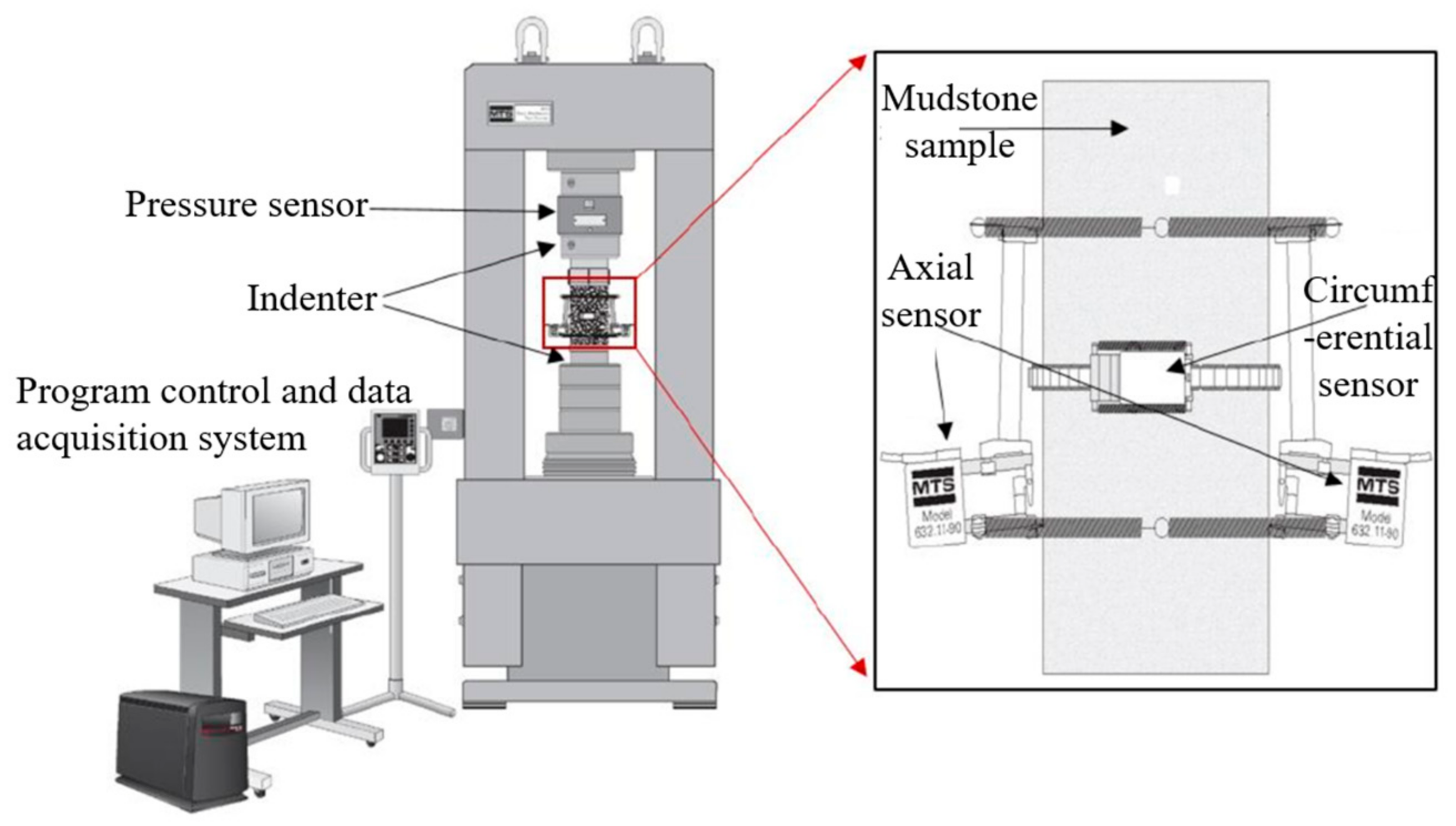


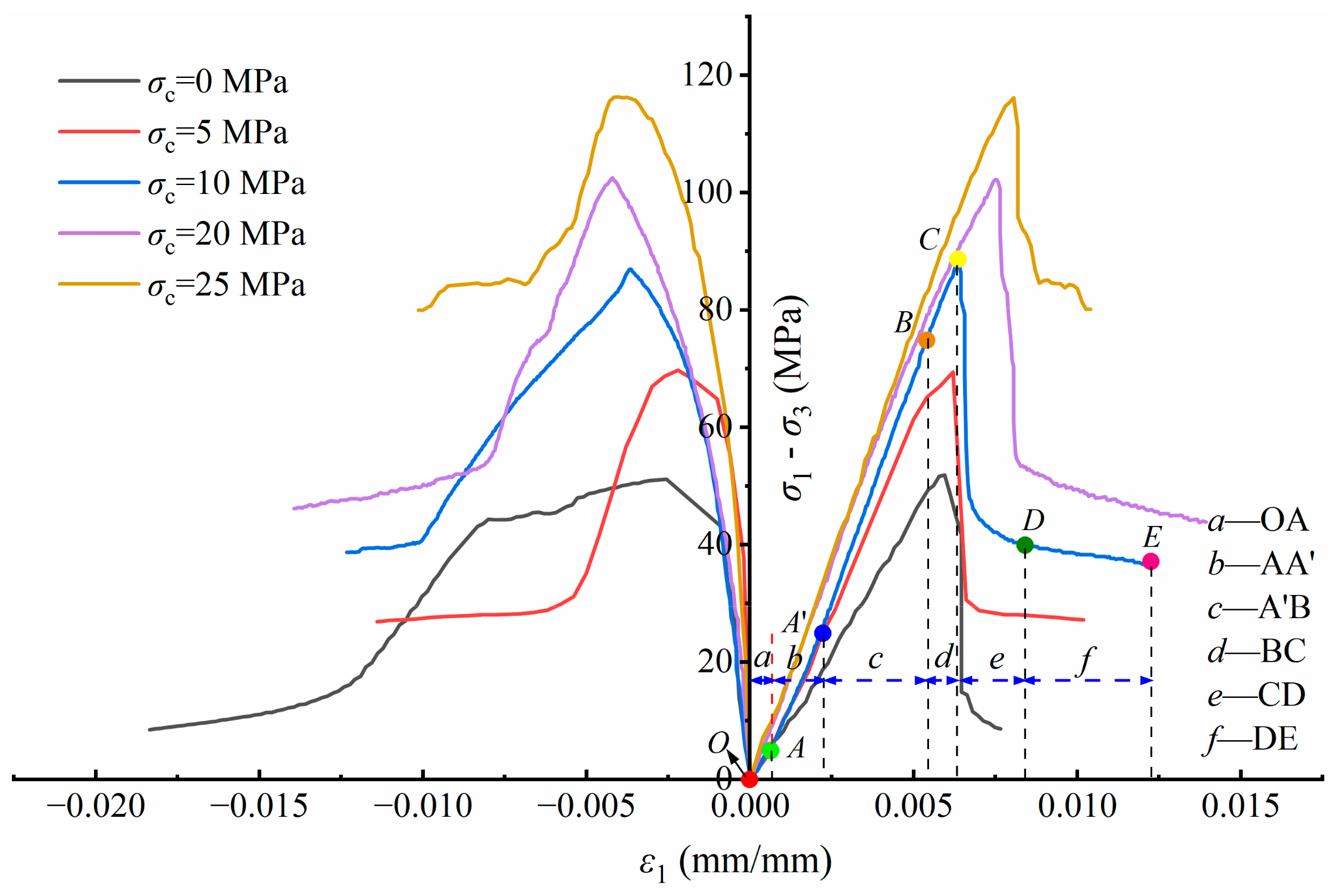
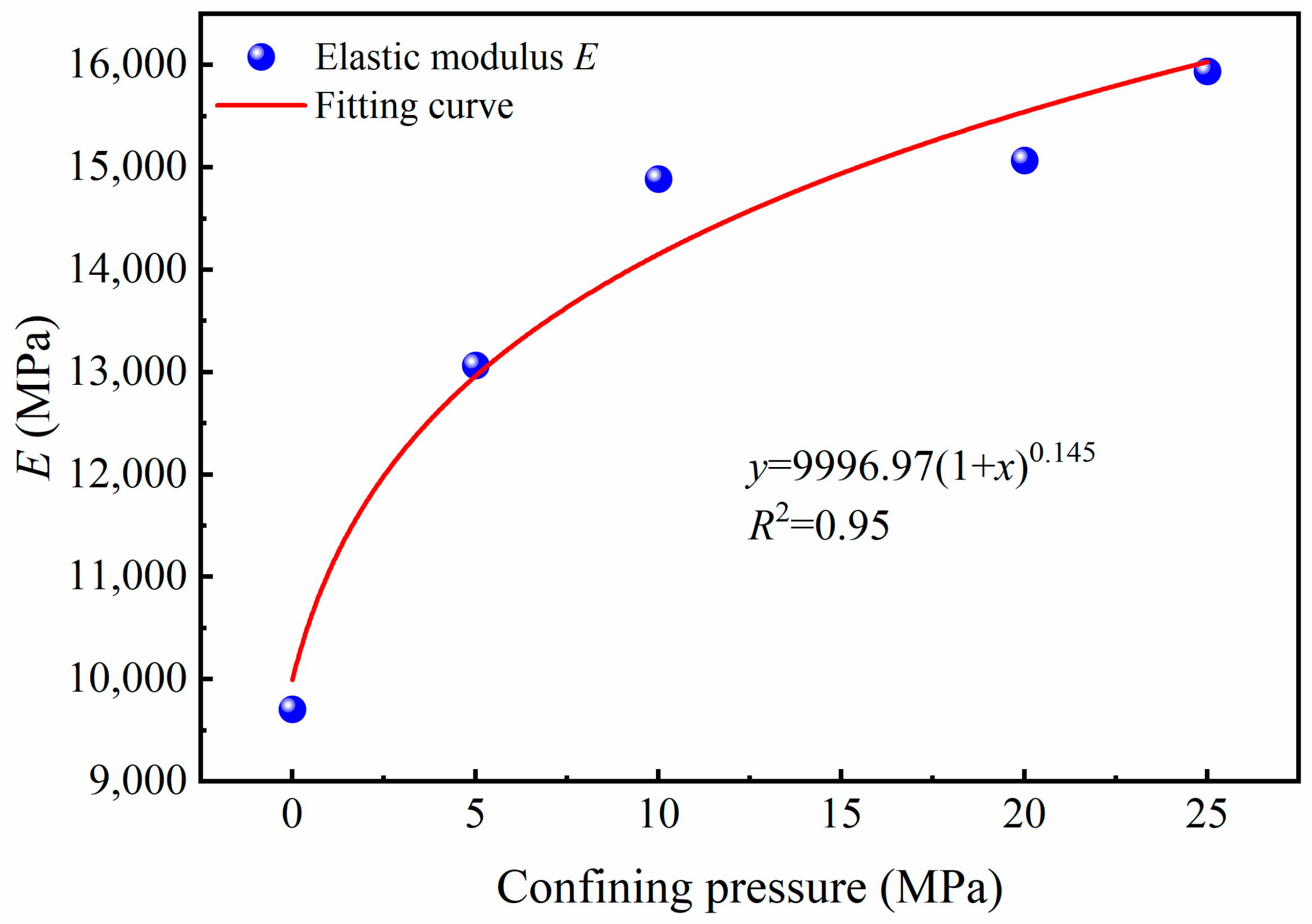

| Mudstone | ρ (g/cm3) | φ (%) | w (%) | d (mm) | h (mm) |
|---|---|---|---|---|---|
| Average value | 2.13 | 10.23 | 1.35 | 50.02 | 100.01 |
| σ3 (MPa) | Parameter | |||
|---|---|---|---|---|
| E (MPa) | (σ1 − σ3)r (MPa) | m | ε0 | |
| 0 | 9709.34 | 12.25 | 13.72 | 0.0077 |
| 5 | 13,067.58 | 27.65 | 9.89 | 0.0088 |
| 10 | 14,888.26 | 37.38 | 8.68 | 0.0092 |
| 20 | 15,068.65 | 46.55 | 6.38 | 0.0119 |
| 25 | 15,939.62 | 81.63 | 4.89 | 0.0137 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, L.; Ren, S.; Li, X.; Liu, M.; Long, K. Statistical Damage Constitutive Model for Mudstone Based on Triaxial Compression Tests. Processes 2025, 13, 864. https://doi.org/10.3390/pr13030864
Liu Y, Chen L, Ren S, Li X, Liu M, Long K. Statistical Damage Constitutive Model for Mudstone Based on Triaxial Compression Tests. Processes. 2025; 13(3):864. https://doi.org/10.3390/pr13030864
Chicago/Turabian StyleLiu, Yuanjie, Lichuan Chen, Shicong Ren, Xiujun Li, Mengjiao Liu, and Kun Long. 2025. "Statistical Damage Constitutive Model for Mudstone Based on Triaxial Compression Tests" Processes 13, no. 3: 864. https://doi.org/10.3390/pr13030864
APA StyleLiu, Y., Chen, L., Ren, S., Li, X., Liu, M., & Long, K. (2025). Statistical Damage Constitutive Model for Mudstone Based on Triaxial Compression Tests. Processes, 13(3), 864. https://doi.org/10.3390/pr13030864





