The Optimal Configuration of Energy Storage Capacity Based on the NSGA-II Algorithm and Electrochemical Energy Storage Operational Modes

Abstract

Due to the intermittency and volatility of renewable energy generation, the safe and stable operation of the power system is affected, leading to issues such as frequency deviations in the grid and voltage exceeding limits during grid connection. Therefore, energy storage is required to smooth out the fluctuations of renewable energy and facilitate its absorption. This paper studies the capacity optimization allocation of electrochemical energy storage on the new energy side and establishes the capacity optimization allocation model on the basis of fully considering the operation mode of electrochemical energy storage. Aiming at maximum net benefit and minimum grid-connected fluctuation, the model considers the constraints of energy storage capacity and power upper and lower limits, charge and discharge power constraints and state of charge constraints, and adopts the NSGA-II method (Non-dominated Sorting Genetic Algorithm II) to solve it. The example analysis shows that the energy storage configuration scheme can take into account the effect of smoothing fluctuation and economy by adopting the strategy proposed in this paper, ensuring the maximum life of energy storage based on the electrochemical energy storage operation mode. It is verified that the proposed strategy can increase the life of energy storage by 3 times.

1. Introduction

Due to the intermittency and volatility of renewable energy sources, such as wind and photovoltaic power, the integration of these generation units into the grid poses significant burdens on the power grid. Energy storage systems can enhance the reliability and stability of new power systems, serving as an important means to address the challenges faced by these systems. However, with the frequent charging and discharging of energy storage, the degradation of batteries gradually increases, making the capacity configuration of energy storage systems with consideration for their lifespan a significant research topic [1].

At present, there are many studies on capacity optimization configuration of new energy storage to reduce new energy fluctuations, most of which consider the goal of minimum comprehensive cost and the index of grid-connected volatility. As shown in [2], using the minimization of grid-connected volatility as the objective function, this study focuses on allocating different power components to various types of energy storage to determine the rated capacity and power of mixed energy storage. As optimized in [3], with the objective function of maximizing system net profit, a capacity allocation model considering wind power smoothing has been established. Reference [4] established a hybrid energy storage capacity configuration model of a wind-storage–hydrogen–gas turbine to smooth wind power fluctuations. Reference [5] proposed a capacity optimization allocation method for a hybrid energy storage system based on quadratic decomposition and established a hybrid energy storage capacity optimization allocation model to smooth wind power fluctuations.

The aforementioned literature [2,3,4,5] established single-layer configuration models, which have shortcomings in system operation optimization, while a two-layer model can achieve multi-objective collaborative optimization. Reference [6] established a two-layer configuration model aiming at the minimum fluctuation of grid-connected wind power, the minimum fluctuation of hybrid energy storage, and the best charging and discharging effect of hybrid energy storage. Reference [7] proposed a double-layer optimal configuration model of photovoltaic- and hydrogen-energy-storage-assisted peak regulation, which takes into account both wave smoothing and peak regulation, and effectively reduces the impact of photovoltaic fluctuations on the distribution network. A two-layer configuration model was established with the objective function of minimizing daily operating costs and minimizing wind power fluctuations [8]. Reference [9] established a two-layer configuration model aiming at maximizing energy storage operation benefits, compensating wind power prediction bias and smoothing wind power fluctuations, and optimized the charge and discharge strategy of energy storage in the inner layer.

Some scholars also considered the life of electrochemical energy storage for capacity allocation. Reference [1] proposed a multi-objective battery energy storage capacity optimization configuration model that comprehensively considered economic cost, life span, and attenuation index. Reference [10] built a composite energy storage capacity configuration model with the goal of maximizing the net benefit of life cycles, which can effectively smooth wind power fluctuations. Reference [11] regulated the battery cycle life by limiting the number of daily cycles and restricted the battery service life to a fixed number of years for capacity configuration. Reference [12] established a battery life model and proposed an energy storage capacity allocation method that considered the service life and cost constraints of energy storage batteries. Reference [13] established the energy storage life model, comprehensive cost model, and unbalance degree optimization model, and built a multi-objective optimization model of energy storage capacity allocation. A battery life loss model was constructed, and a dual-layer optimal configuration method of hybrid electric/thermal energy storage was proposed considering battery life loss [14].

From the aforementioned literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14], it is evident that some studies have considered the lifespan of batteries; however, there has been no examination of the operating modes of electrochemical energy storage. This paper proposes a dual-layer capacity configuration method that takes into account the operating modes of electrochemical energy storage. The proposed strategy considers the lifespan of electrochemical energy storage and can generate additional benefits, which have not been addressed in the previous literature. The upper model of this paper aims to maximize comprehensive benefits and minimize grid fluctuation volatility, optimizing the capacity of the energy storage system, while the lower layer seeks to minimize the grid fluctuation indicators for various scenarios, optimizing the operation of the energy storage. Finally, an example analysis shows that the strategy proposed in this paper can improve the service life of energy storage and generate additional benefits, and the two-layer model in this paper can obtain better results than the single-layer model.

2. Electrochemical Energy Storage to Smooth the New Energy Fluctuation Strategy

2.1. Power Decomposition

In this paper, the VMD (Variational Mode Decomposition) [15] method is used to process the wind–photovoltaic joint output, which is decomposed into K eigenmode functions, with different center frequencies of each component and the minimum estimated bandwidth sum of all components. Compared with the traditional empirical mode decomposition method, the components obtained by VMD have the advantages of high precision and less aliasing.

By using the VMD method, the wind–photovoltaic joint output can be decomposed into IMF components with different frequencies. This paper proposes to determine the boundary frequency between different types of components, and then, based on the center frequency of each component, divide the IMF components obtained after VMD processing wind–photovoltaic combined output into three categories: high frequency, medium frequency, and low frequency, and select the reference power of hybrid energy storage according to different operating conditions.

2.2. Charge–Discharge Strategy for Electrochemical Energy Storage

Because electrochemical energy storage has the ability to adjust quickly, its dynamic response speed is on the order of seconds, making it suitable for smoothing out high-frequency fluctuation components. At the same time, this paper considers the operational mode of electrochemical energy storage, employing a one charge and two discharge operation strategy for power adjustment. This approach fulfills the objective of dampening fluctuations in energy storage and prevents frequent charging and discharging of the batteries, thereby extending their service life.

In this paper, high-frequency components are selected as the calming target of electrochemical energy storage, and the expression is as follows:

$$P_{ba,ref}=-P_{unit,h}$$

(1)

where $P_{ba,ref}$ is output for the target of electrochemical energy storage; $P_{unit,h}$ is the high-frequency component after decomposition.

3. Two-Layer Optimal Configuration Model

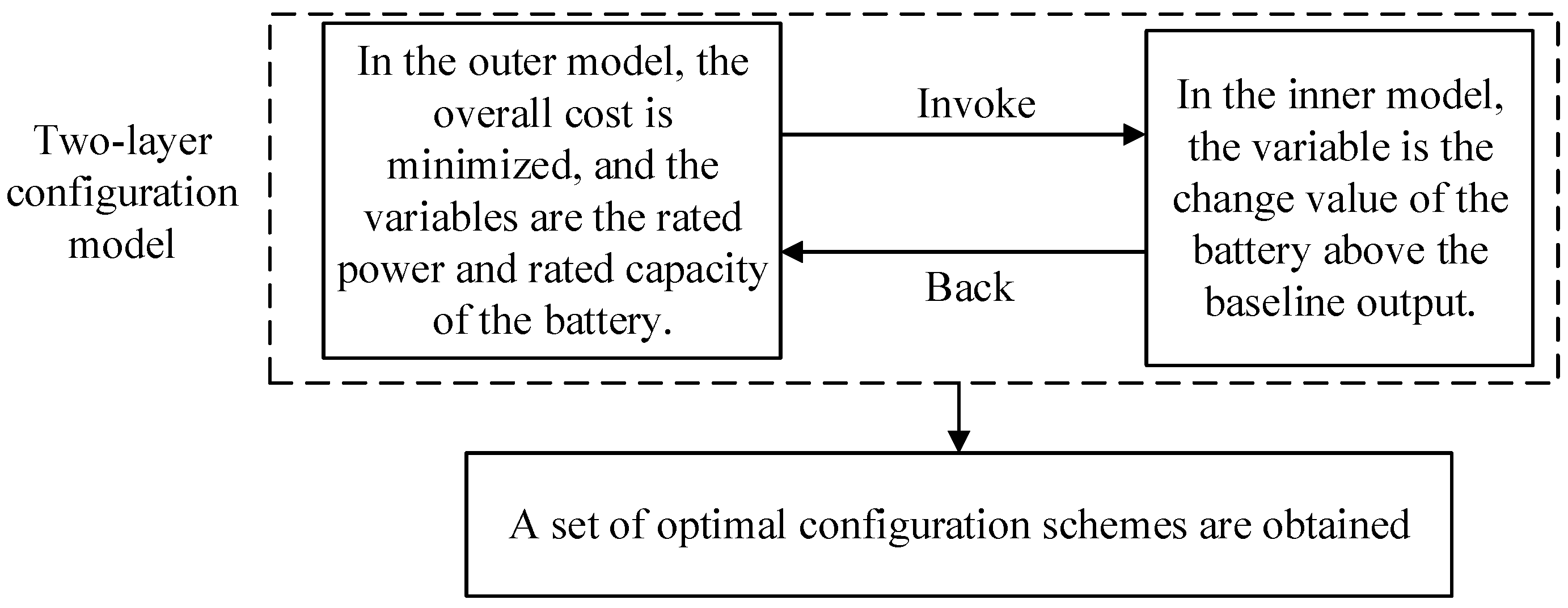
This article adopts a two-layer decision-making model to optimize energy storage configuration considering operational issues. The outer layer is a multi-objective optimization problem, where the variables are the capacity and rated power of the electrochemical energy storage configuration, and the objective functions are the cost and volatility of energy storage. The inner layer considers the operation of energy storage, with the variable being the output adjusted from the planned output to track the grid-connected reference power.

The architecture diagram of the two-layer model is shown in Figure 1:

The outer layer outputs the energy storage capacity and power to the inner layer for calculation. The inner layer calculates the corresponding charge and discharge power based on the given parameters, computes the adaptive value, and returns it to the outer layer. Due to the difficulty in obtaining an absolutely optimal solution, this paper assumes that a cyclical process of the two-level model for a certain number of iterations is sufficient to consider the optimal solution achieved.

3.1. Electrochemical Energy Storage Capacity Optimization Model

3.1.1. Inner-Layer Model

The optimization of the inner-layer model for energy storage operations is based on the operational mode of one charge and two discharges. Power adjustments are made on the basis of the reference power to achieve the goal of reducing fluctuations.

Objective Function

The power of the link deviates from the plan, which will affect the security and stability of the power grid. Therefore, the goal of the inner model is set as the minimum deviation between the actual output of the wind–photovoltaic system and the planned output. In order to measure the degree of deviation between the actual output and the planned output of the combined system, the output deviation coefficient is defined as follows:

$$D={\displaystyle \frac{1}{T}}\sum _{t=1}^T{\left({\displaystyle \frac{P_{unit,t}-P_{ref}}{P_{wsu}}}\right)}^2$$

(2)

where $P_{unit}$ is the actual output power of the combined system; $P_{ref}$ is the grid-connected reference power of the combined system, which is obtained by decomposing the wind-view output data through VMD; $P_{wsu}$ is the average output power of the combined system. The sampling interval $∆t$ = 1 min for electrochemical energy storage, so t is 1440.

The inner layer aims to minimize the output deviation index of the combined system, so as to meet the goal of reducing the grid-connected fluctuation of energy storage.

Constraint Condition

During the operation of the inner layer, the energy storage needs to be constrained to some extent, including the constraint of electrochemical energy storage power and the constraint of charged state.

(1)

Electrochemical energy storage power constraints

At any time, the output of the energy storage needs to be within the limited range of the rated power.

$$-P_B\le P_{bat}\le P_B$$

(3)

(2)

Constraints on charging status

At any given time, the amount of energy stored should conform to the equation constraint of charge and discharge, and the SOC (State of Charge) should be in a safe state to reduce life loss.

$$SOC(t+1)=SOC\left(t\right)+P_c\left(t\right){\eta }_c\Delta t-P_d\Delta t/{\eta }_d$$

(4)

$${SOC}_{min}\le SOC\left(t\right)\le {SOC}_{max}$$

(5)

$$SOC\left(T\right)\approx SOC\left(1\right)$$

(6)

3.1.2. Outer-Layer Optimization Model

In the outer model, the capacity of the electrochemical energy storage is configured, and the rated capacity and power of the energy storage are calculated. Considering economic efficiency and reliability, the objective is to maximize overall benefits while minimizing grid-connected volatility.

The multi-objective formula is shown in the equation:

$$\left\{\begin{array}{c}{f}_1=maxW\\ f_2=min\delta \end{array}\right.$$

(7)

Net Benefit

Considering the environmental performance of batteries, this paper adopts lithium batteries. Taking into account the total life cycle cost of energy storage and the revenue from the difference in peak and valley electricity prices, the target function considered in this paper is the total life cycle cost minus the revenue from the difference in peak and valley electricity prices, expressed by the following formula:

$$maxW=W_{dp}-C_{inv}-C_{op}-C_{loss}$$

(8)

(1)

Initial construction cost

$$C_{inv}=C_P{P}_B+C_E{E}_B$$

(9)

where $C_{inv}$ is the initial construction cost; $C_P$ and $C_E$ are unit power cost and unit capacity cost of energy storage. $P_B$ and $E_B$ indicate the rated power and rated capacity of the energy storage.

(2)

Operation and maintenance costs

$$C_{op}=\left(C_K{P}_B+C_V{E}_B\right)F$$

(10)

$$F={\displaystyle \frac{r{\left(1+r\right)}^Y}{{\left(1+r\right)}^Y-1}}$$

(11)

where $C_{op}$ is operation and maintenance cost; $C_k$ is the annual operation and maintenance cost per unit power; $C_V$ is the annual operation and maintenance cost per unit capacity; $F$ is the present value coefficient; $r$ is the discount rate.

(3)

Life loss cost

$$C_{loss}=K\eta$$

(12)

where $C_{loss}$ is the life loss cost; $K$ is the life loss cost factor; $\eta$ is the number of daily cycles of energy storage.

(4)

Peak–valley electricity price difference income

$$W_{dp}=365\cdot E_B\cdot \Delta \lambda \cdot Y$$

(13)

where $W_{dp}$ is the yield of the peak–valley electricity price difference; $\Delta \lambda$ is the peak–valley electricity price difference, which is 0.7 $\mathrm{y}\mathrm{u}\mathrm{a}\mathrm{n}/\mathrm{k}\mathrm{W}·\mathrm{h}$ in the paper; $Y$ is the service life; the article stipulates 13 years.

Grid-Connected Volatility Index

The grid-connected rate of energy storage is defined as an indicator of the degree of output fluctuation of the power grid output combined system, as shown in Equation (13).

$$min\delta =\sum _{i=1}^3{k}_i{D}_i$$

(14)

where $\delta$ is the fluctuation index to measure the output, and $k_i$ is the scene weight coefficient.

The grid-connected volatility index is an important indicator for measuring the reliability of renewable energy integration, taking into account the weights of various typical scenarios to meet the demands of different situations.

Constraint Condition

Due to geographical restrictions or the constraints of power grid operation conditions, the scale of energy storage needs to be controlled within a certain range.

$$\left\{\begin{array}{c}{P}_{min}<P_{bat}<P_{max}\\ E_{min}<E_{bat}<E_{max}\end{array}\right.$$

(15)

where $P_{min}$ and $E_{min}$ are used to make the wind–photovoltaic joint output fluctuation meet the requirements of new energy fluctuation. $P_{max}$, $E_{max}$ indicates the maximum power and capacity allowed under geographical conditions or network requirements.

3.2. Model Solving

The energy storage optimization model considering the operation mode of electrochemical energy storage proposed in this paper can prevent the battery from frequent charging and discharging, optimize the operating state of the battery, reduce the operating loss of the battery, and improve the service life of the battery. In the actual solution process, the investment cost and the risk compensation cost of energy storage cannot be optimized at the same time, so the multi-objective algorithm is adopted.

The Gurobi-12.0.1 solver is used to solve the inner-layer model, and the output and output adjustment of electrochemical energy storage are obtained. The outer layer uses the NSGA-Ⅱ algorithm to optimize the storage capacity configuration scheme based on the capacity optimization objective, and the inner layer calls the Gurobi-12.0.1 solving model to solve the optimal operation scheme under the corresponding configuration capacity with the goal of getting as close as possible to the grid-connected target output. After the calculation of the lower layer, the optimal operation plan is returned to the upper layer. The upper-layer algorithm calculates the target value according to the capacity configuration plan and the optimal operation plan, and then searches for the optimal configuration capacity through the algorithm. 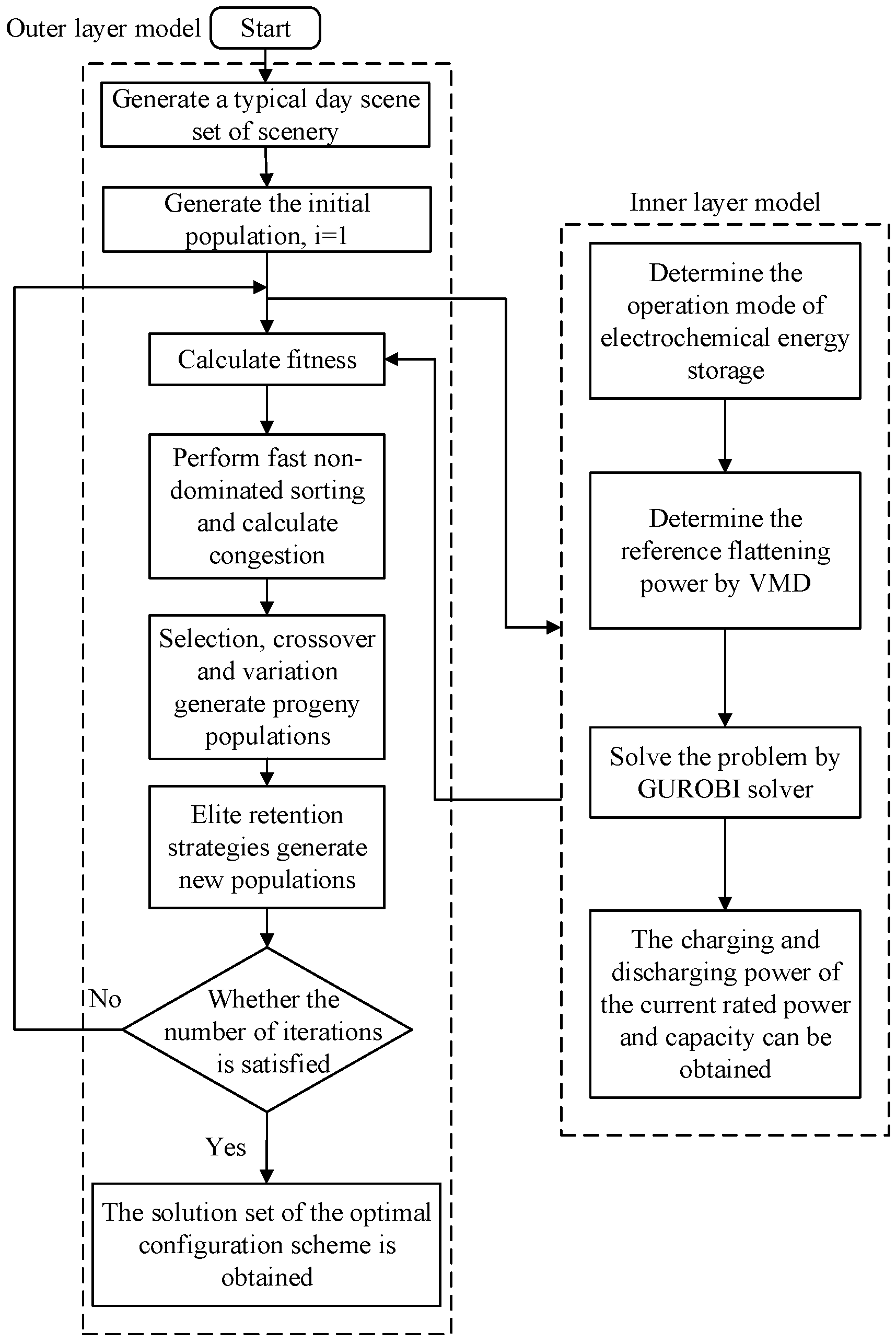Figure 2 is the flow chart of the two-layer optimization model.

The overall flow chart of the solution algorithm is shown in Figure 2:

The steps for solving the model are as follows:

(1)

Read typical daily wind and photovoltaic power data;

(2)

Generate an initial population, with a selected population size of 100, using the rated capacity and power of electrochemical energy storage as the fitness value of individuals;

(3)

Call the inner function to solve the benchmark output deviation of the energy storage and calculate the fitness value of each individual;

(4)

Rank all populations and set two parameters for each individual: non-dominated number $n_p$ and the individual domination set $S_p$. Place all individuals with $n_p$ equal to 0 into the initial layer, while decrementing $n_p$ by 1 for all individuals in the $S_p$ sets. Repeat to obtain $k$ non-dominated layers. Calculate the crowding distance of each layer, where the crowding distance of boundary individuals in each layer is infinite, and for the remaining individuals, the crowding distance is calculated as $i_d=\sum _{j=1}^m\left(\left|f_j^{i+1}-f_j^i\right|\right)$; f is the value of the $j-th$ objective function at the $i-th$ point;

(5)

Select, crossover, and mutate to generate offspring. During selection, individuals are compared, with non-dominated individuals winning, and in the case of equal domination, individuals with greater crowding distance winning;

(6)

Generate a new population. Employing an elitism retention strategy in the iteration process, combine the parent population $P\left(t\right)$ and the offspring population $Q\left(t\right)$ to form a new population $R\left(t\right)$, then layer R(t) and add it to the new population $P_{t+1}$ until the number of individuals in $P_{t+1}$ reaches $N_p$;

(7)

Select, crossover, and mutate. As in the previous selection, individuals are compared, with non-dominated individuals winning, and in the case of equal domination, individuals with greater crowding distance winning;

(8)

Repeat steps (3) to (7) until the total number of iterations meets the requirements, thus obtaining the Pareto optimal solution set.

4. Case Analysis

The scenario composition of the new energy side is shown in Figure 3. While responding to the conventional demand of the power grid, electrochemical energy storage can properly suppress and absorb the output of new energy.

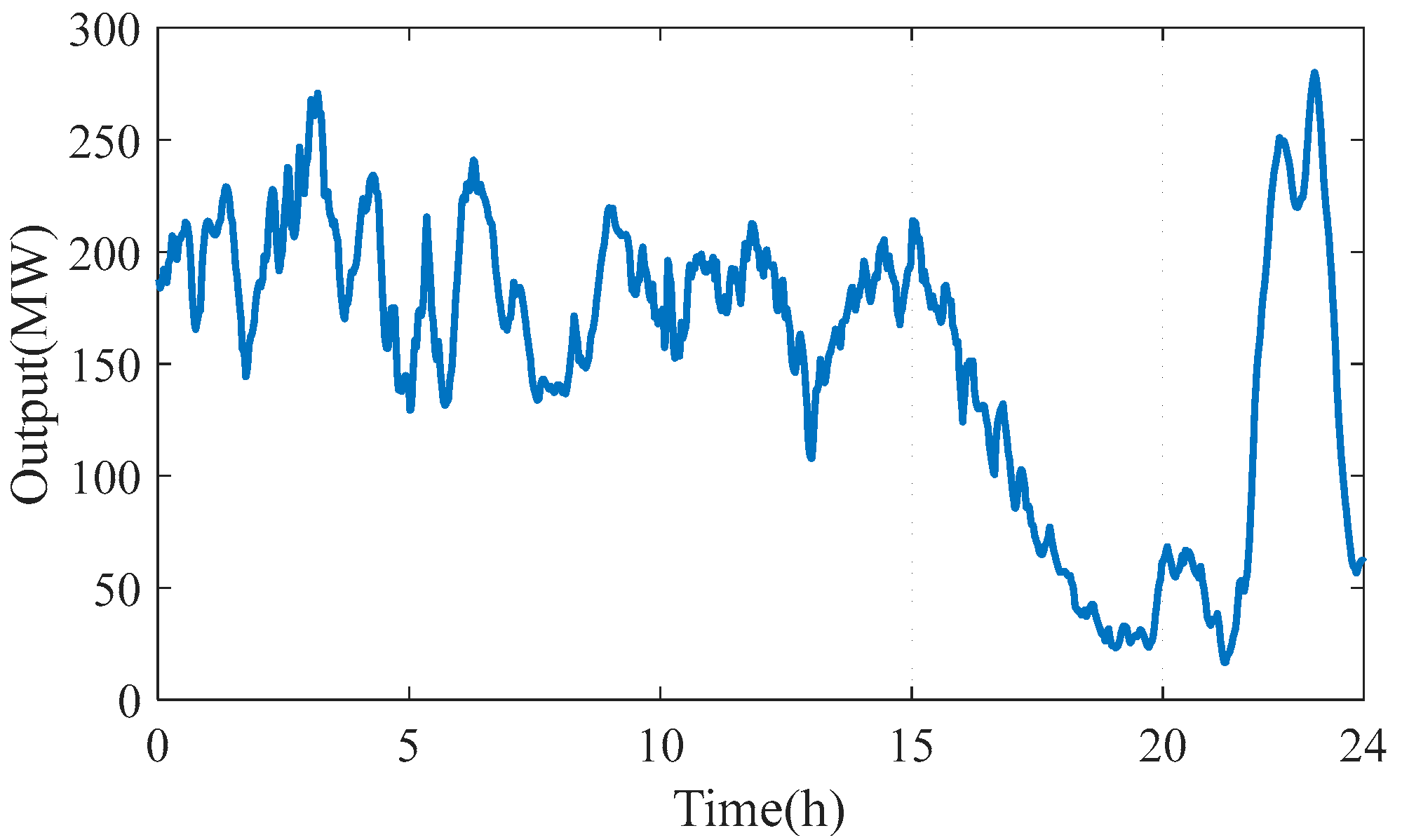
In this paper, the scene set in reference [16] is selected for example analysis. The combined wind–photovoltaic output data of scenario 1 are shown in Figure 4, and the wind–photovoltaic output before and after decomposition and the results of spectrum analysis can be obtained.

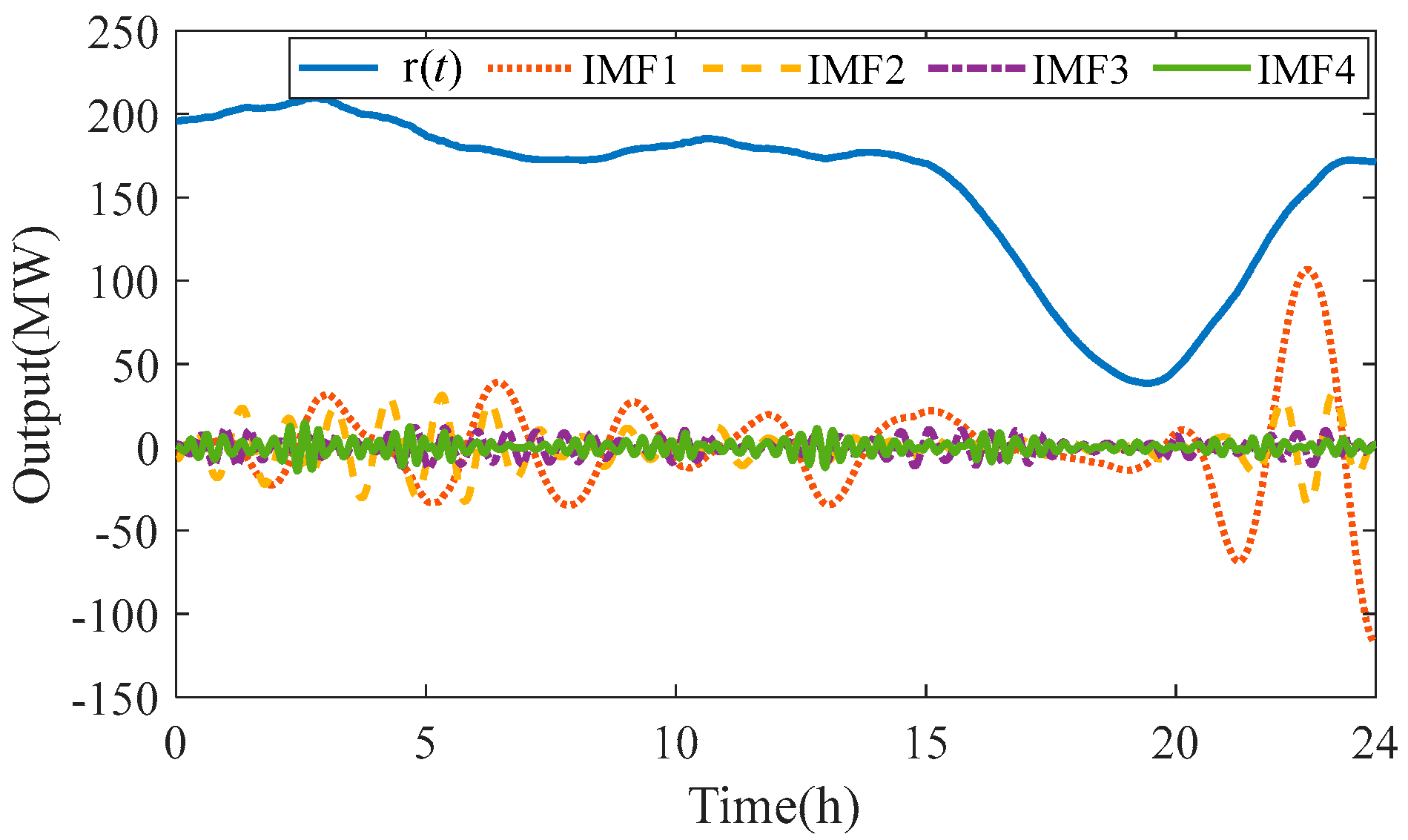
Here, for the convenience of display, the decomposition scale is set to 5, and then the output of the wind–photovoltaic combined system is decomposed through the VMD method, and the decomposed components are displayed on a graph. The decomposed components are shown in Figure 5.

As shown in Figure 6, the decomposed IMF (Intrinsic Mode Function) component is relatively clear, and the comparison of the change frequency between different components is obvious.

On the basis of retaining at least the remaining items, the boundary frequency between the middle frequency and the high frequency components can be roughly selected in 5 × 10⁻⁴ Hz~1.5 × 10⁻³ Hz, and the boundary frequency between the low frequency and the middle frequency is roughly 5 × 10⁻⁵ Hz~6 × 10⁻⁴ Hz. This will serve as a benchmark for processing the output scenarios of wind power and photovoltaic energy for each year.

4.1. Configuration Result Analysis

In this paper, the scale of wind power is 300 MW, the scale of photovoltaics is 150 MW [16], the cycle life of the energy storage battery is 5000 times [9], and the charging time of the electrochemical energy storage is set to be 0–5, the discharge time is 9–10, 14–18, and the benchmark output during charging is 0.8 times of the rated power. The reference output during discharge is 0.4 times the rated power, and the rest of the time is free charge and discharge time.

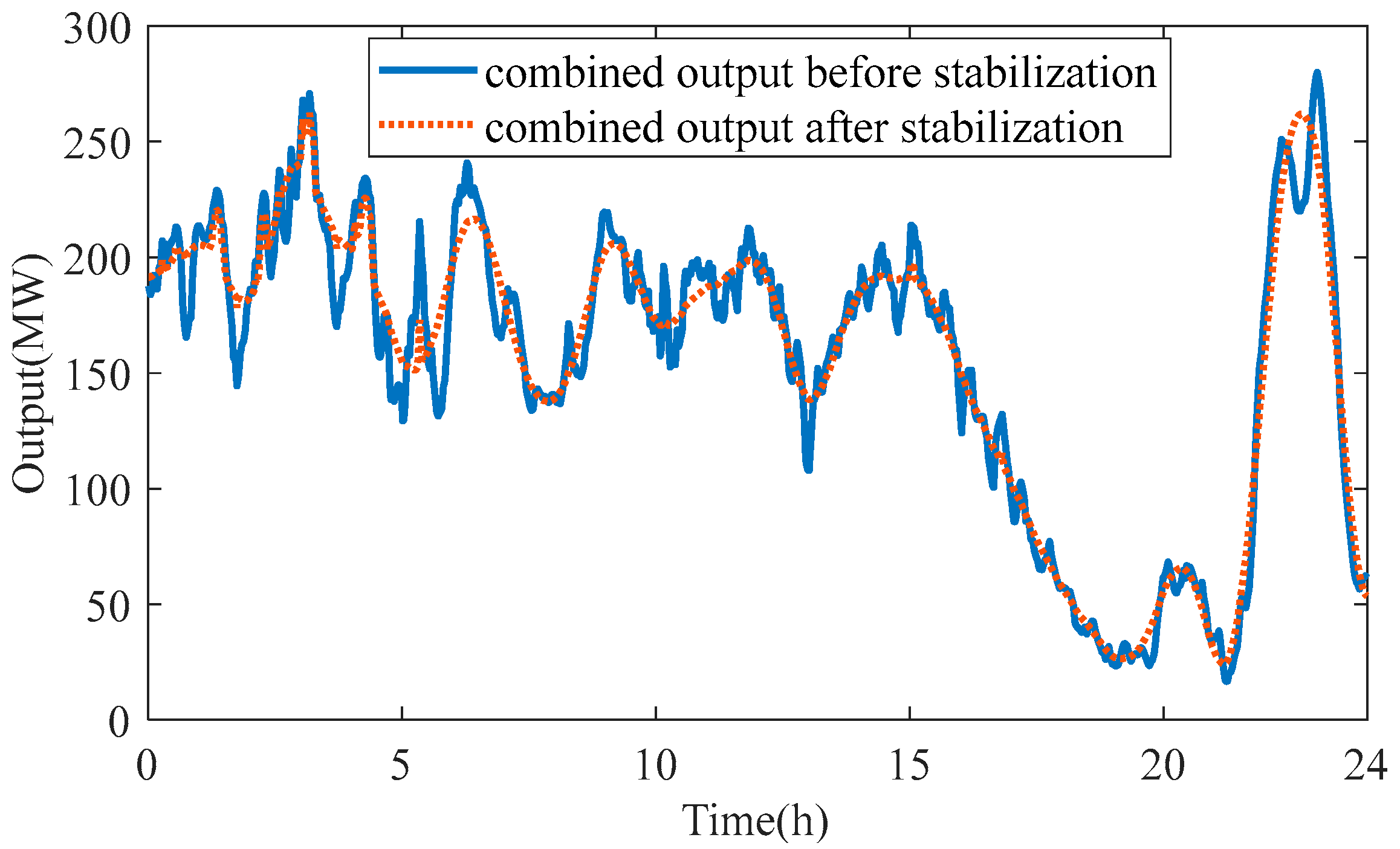
The upper target is the minimum comprehensive investment cost and the minimum grid-connected volatility, while the lower target is the minimum grid-connected volatility index of each scenario. Through the configuration model and algorithm established before, the configuration results were obtained, and the energy storage configuration scheme of 42.35 MW/80.55 MW·h in the solution set was selected for analysis.

Under the strategy of considering the energy storage operation mode, the battery service life is about 13 years, the comprehensive investment cost is CNY 212.516 million, the part of the income generated due to the peaking valley price difference is CNY 266.8825 million, the grid-connected volatility is 0.0338, and the output is obviously smooth. Taking scenario 1 as an example, the combined output before and after flattening under scenario 1 is shown in Figure 7:

4.2. Comparison of Whether or Not to Consider the Strategy of This Article

This paper will compare whether to consider the two schemes of electrochemical energy storage operation mode and compare the configuration results, grid-connected fluctuation index, comprehensive investment cost, and the number of energy storage cycles under the two schemes. Traditional strategies refer to those configurations that are not based on energy storage operational modes. Whether to consider the electrochemical energy storage operation mode of the two scheme configuration results are as follows in

Table 1. Comparison of configuration schemes for different strategies.

	The Strategy in This Paper	Traditional Strategy
$E_{bat}/\mathrm{M}\mathrm{W}·\mathrm{h}$	80.35	13.15
$P_{bat}/\mathrm{M}\mathrm{W}$	42.55	23.86
$C/CNY \mathrm{m}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{o}\mathrm{n}$	212.516	54.7178
${\delta }_{wave}$	0.0338	0.0335
$\mathrm{Daily} \mathrm{cycles}$	1	3
$W/CNY \mathrm{m}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{o}\mathrm{n}$	266.8825	0

:

When the grid-connected volatility is almost the same, considering the strategy proposed in this paper, it is necessary to configure the rated energy storage capacity of 80.35 MW· hand the rated power of 42.55 MW. Regardless of the strategy proposed in this paper, the rated capacity of energy storage needs to be configured at 13.15 MW· hand rated power at 23.86 MW. This article considers the strategy of energy storage operation modes. Although the costs are higher than those of strategies that do not consider energy storage operation modes, it generates additional revenue, resulting in a comprehensive benefit that is CNY 109.0842 million higher than that of strategies configured without a basis in energy storage operation modes. In addition, the strategy proposed in this paper only cycles once a day, while the traditional strategy cycles 3 times a day. Under the strategy considering the energy storage operation mode, the battery life is greatly improved, which is 3 times that of the traditional strategy, proving the feasibility of the strategy considering the electrochemical energy storage operation mode proposed in this paper.

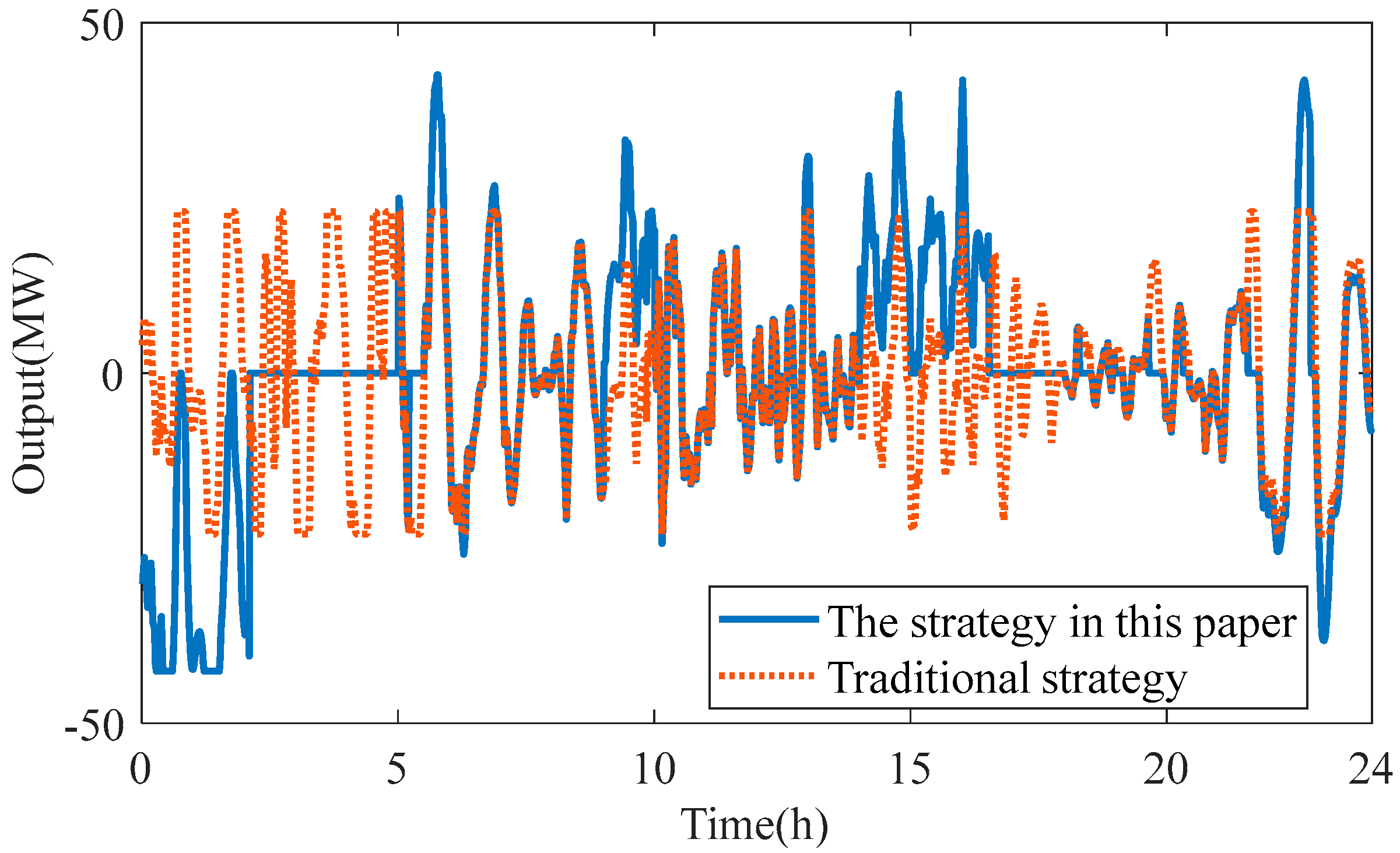
The energy storage output and SOC change curves under the two schemes are shown in Figure 8 and Figure 9. The strategy proposed in this paper is to consider the operation mode of electrochemical energy storage. After night charging, the charge state reaches the maximum value of 0.9, the energy storage output is 0, and then charge and discharge freely. When the battery is discharged, the charged state reaches the minimum value 0.1 and does not discharge. As can be seen from Figure 9, under the strategy proposed in this paper, the battery only cycles once, without considering the strategy of the energy storage operation mode. The SOC of the battery fluctuates greatly, and the number of cycles is 3 times.

4.3. Comparison of Two-Layer Model and Single-Layer Model

In this paper, the configuration results of the two-layer model and the single-layer model are compared; the results are presented in

Table 2. Comparison of single- and two-layer models.

	Two-Layer Model	Single-Layer Model
$E_{bat}/\mathrm{M}\mathrm{W}·\mathrm{h}$	80.35	61.97
$P_{bat}/\mathrm{M}\mathrm{W}$	42.55	32.58
$C/CNY \mathrm{m}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{o}\mathrm{n}$	212.516	163.6238
${\delta }_{wave}$	0.0338	0.0523
$W/CNY \mathrm{m}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{o}\mathrm{n}$	266.8825	205.8334

. In the two-layer configuration model, the operation of the inner layer is optimized, and the power and capacity of the energy storage are configured on the outer layer. The capacity planning and operation mode problems are optimized at the same time by alternating the inner and outer layers, and the rated capacity of the energy storage is 80.35 MW· h, the rated power is 42.55 MW, under this scheme, the cost of energy storage is CNY 212.516 million, the income is CNY 266.8825 million, and the grid-connected volatility is 0.0338. Although the optimal solution obtained by the single-layer configuration model can also achieve the purpose of smoothing the fluctuation of new energy, the rated capacity and rated power of the configuration are small, the rated capacity of the configured energy storage is 61.97 MW· h, the rated power is 32.58 MW, the cost of the single-layer model is 163.6238 million yuan, the income is CNY 205.8334 million, and the grid-connected volatility is 0.0523. It can be observed that the overall benefits of the two-layer model exceed those of the single-layer model by 22.36%, while the grid fluctuation rate has decreased by 1.85%. Although the investment cost of the single-layer model is relatively lower, its grid fluctuation rate is comparatively higher. Additionally, the dual-layer configuration model’s strategy can generate greater returns.

5. Conclusions

This paper studies the principle of energy storage configuration for electrochemical energy storage to suppress wind and wave fluctuations on the new energy side. Through the VMD method, the boundary frequency between medium frequency and low frequency, high frequency and medium frequency is divided, and the component of electrochemical energy storage that needs to be suppressed is formulated based on this. The operation mode of electrochemical energy storage is considered, and the grid-connected operation strategy of electrochemical energy storage is formulated based on this. The results of this paper are as follows:

(1)

Electrochemical energy storage on the new energy side can effectively smooth the fluctuation of new energy.

(2)

A strategy considering the operation mode of electrochemical energy storage is proposed, and the charge and discharge plan of energy storage is formulated. The charging and discharging power, operating state, daily cycle times, and peak–valley price difference of energy storage under the two schemes of energy storage operation mode were compared. It is concluded that the battery life of the proposed scheme is 3 times that of the traditional strategy. The effectiveness of the proposed strategy in improving battery life and generating additional benefits was verified.

(3)

A two-layer configuration model considering the service life, income, and volatility of electrochemical energy storage is proposed, and compared with the traditional single-layer configuration model, the effectiveness of the model in this paper is verified.

This paper only considers the energy storage operation mode of one charge and two discharges, without considering configurations under other operational modes. Future research could explore different operational modes and conduct comparisons. Moreover, this study overlooks the impact of depth of discharge on the cycle life of energy storage systems, which can affect the configuration outcomes. Future studies might take into account the influence of depth of discharge by employing more advanced life degradation models.