Aerodynamic Characteristics of Typical Operating Conditions and the Impact of Inlet Flow Non-Uniformity in a Multi-Stage Transonic Axial Compressor
Abstract
1. Introduction
2. Numerical Analysis
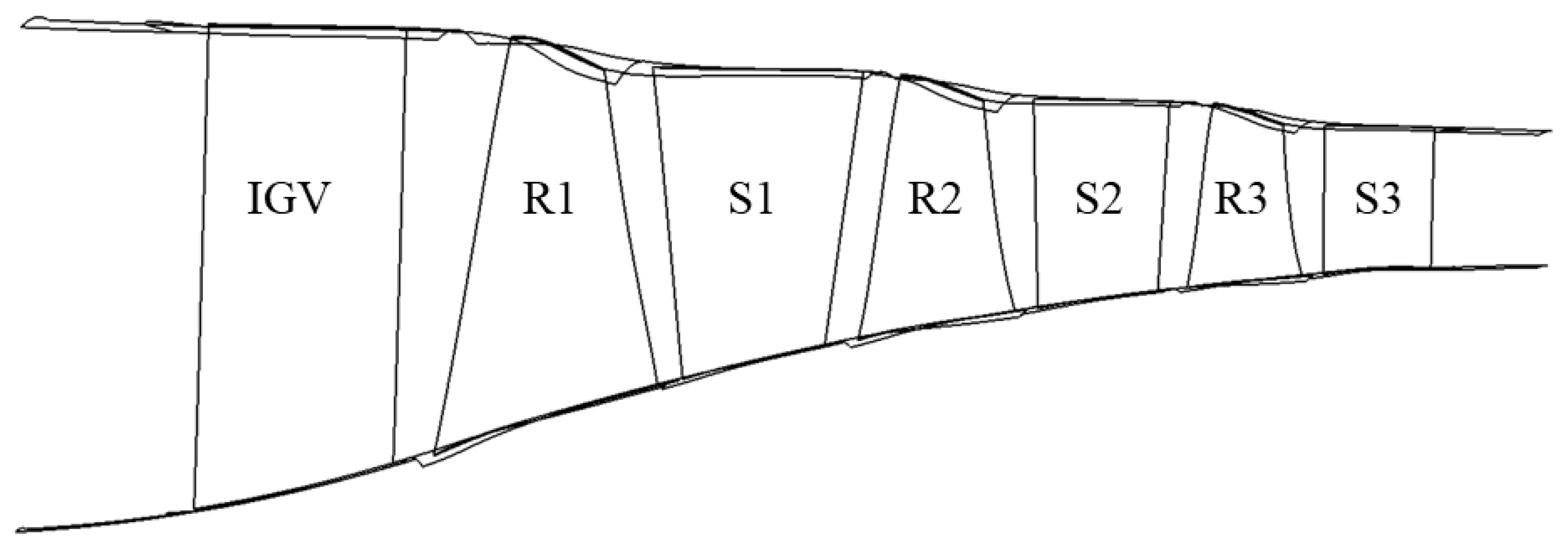
2.1. Physical Model
2.2. Numerical Model
2.3. Parameter Indicators
3. Verification of the Numerical Method
3.1. Boundary Conditions
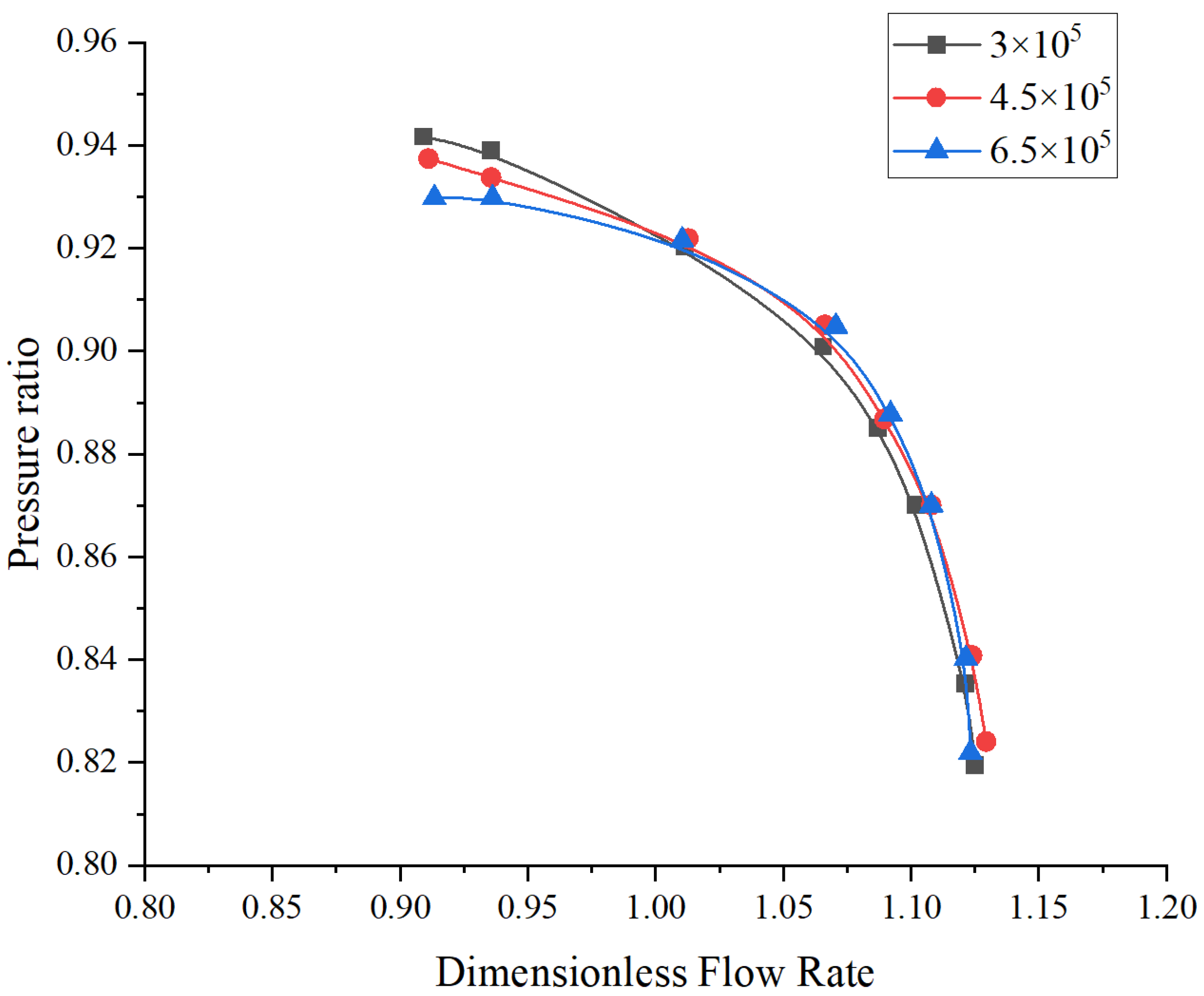
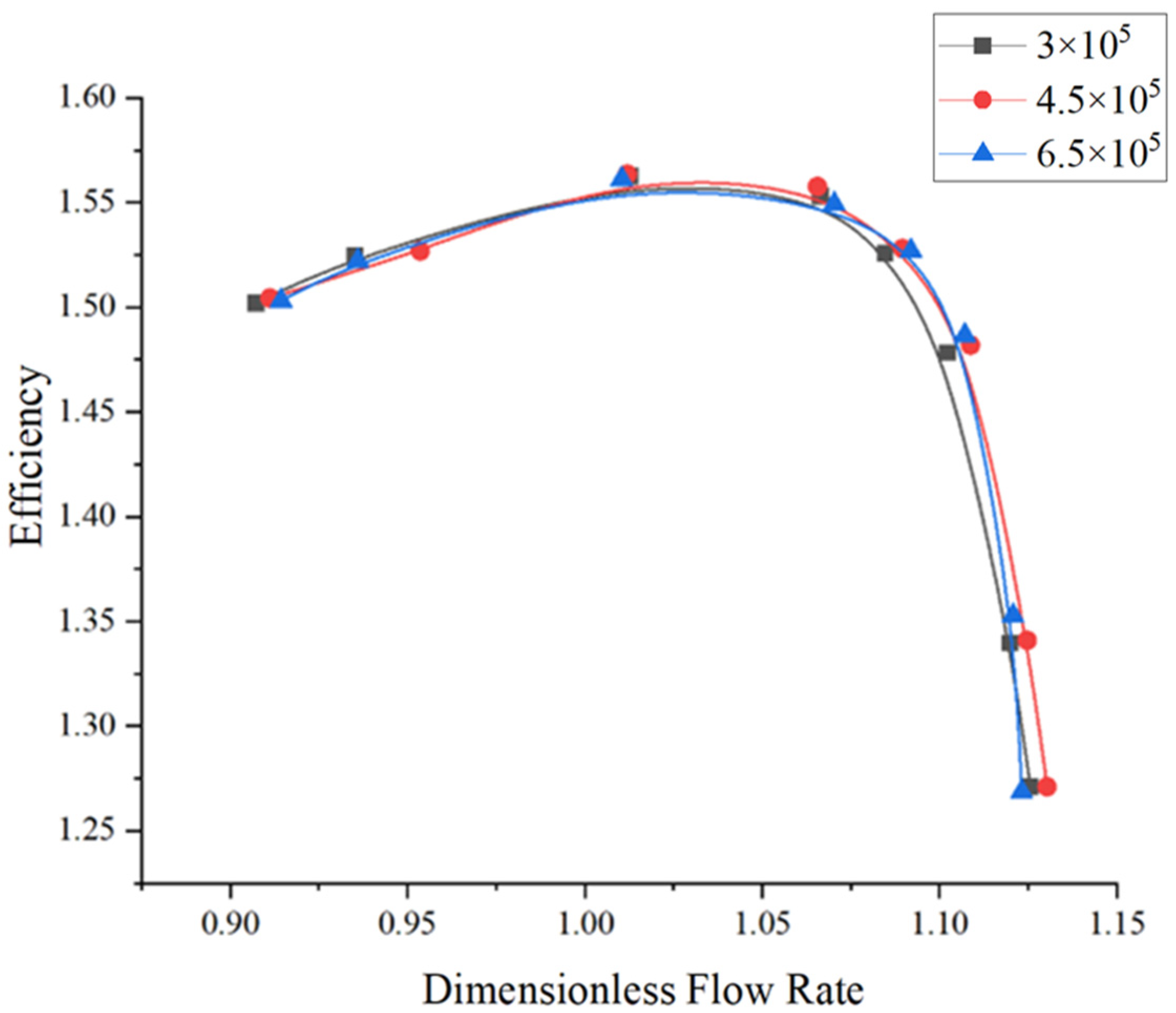
3.2. Numerical Model and Grid Independence Verification
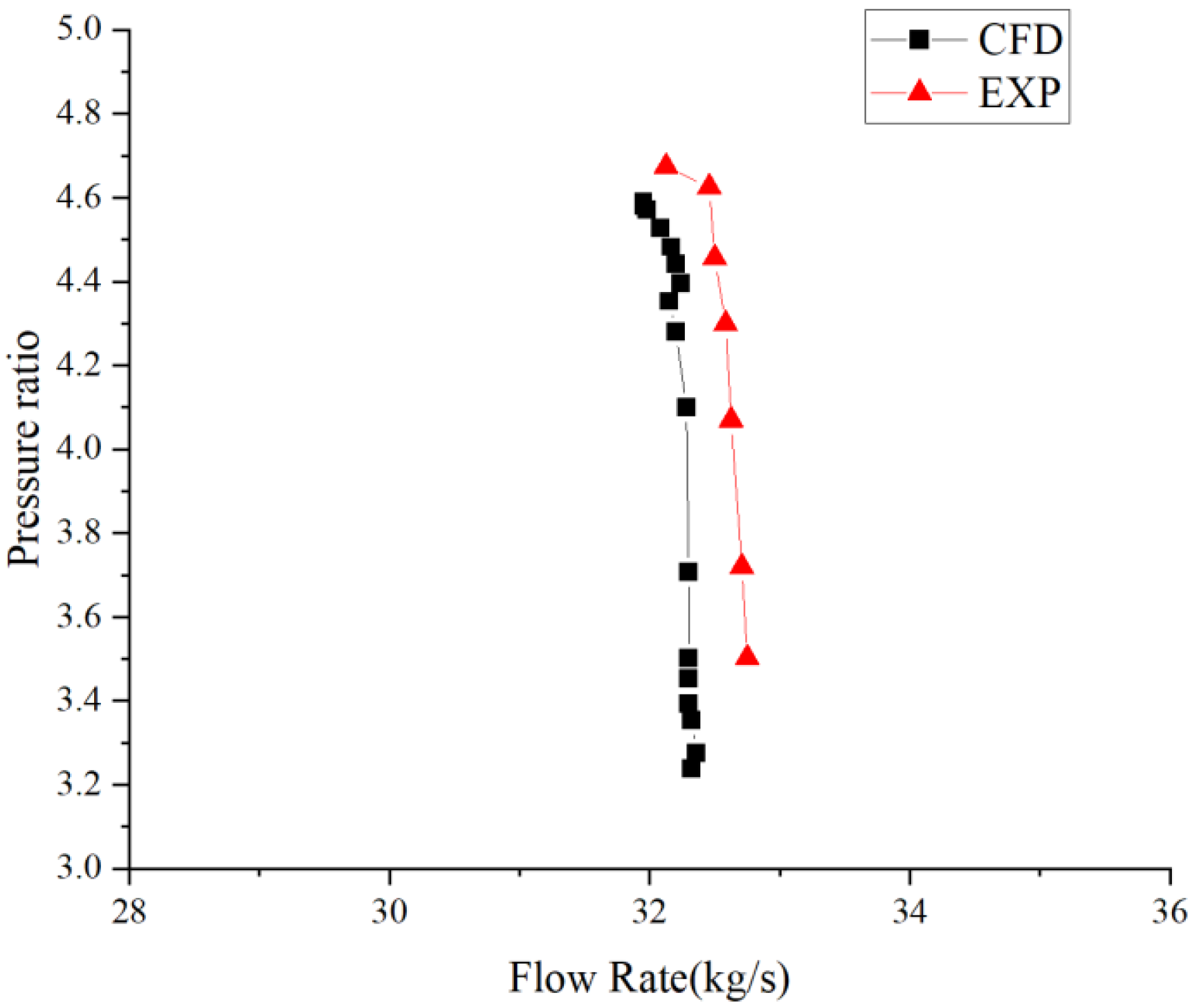
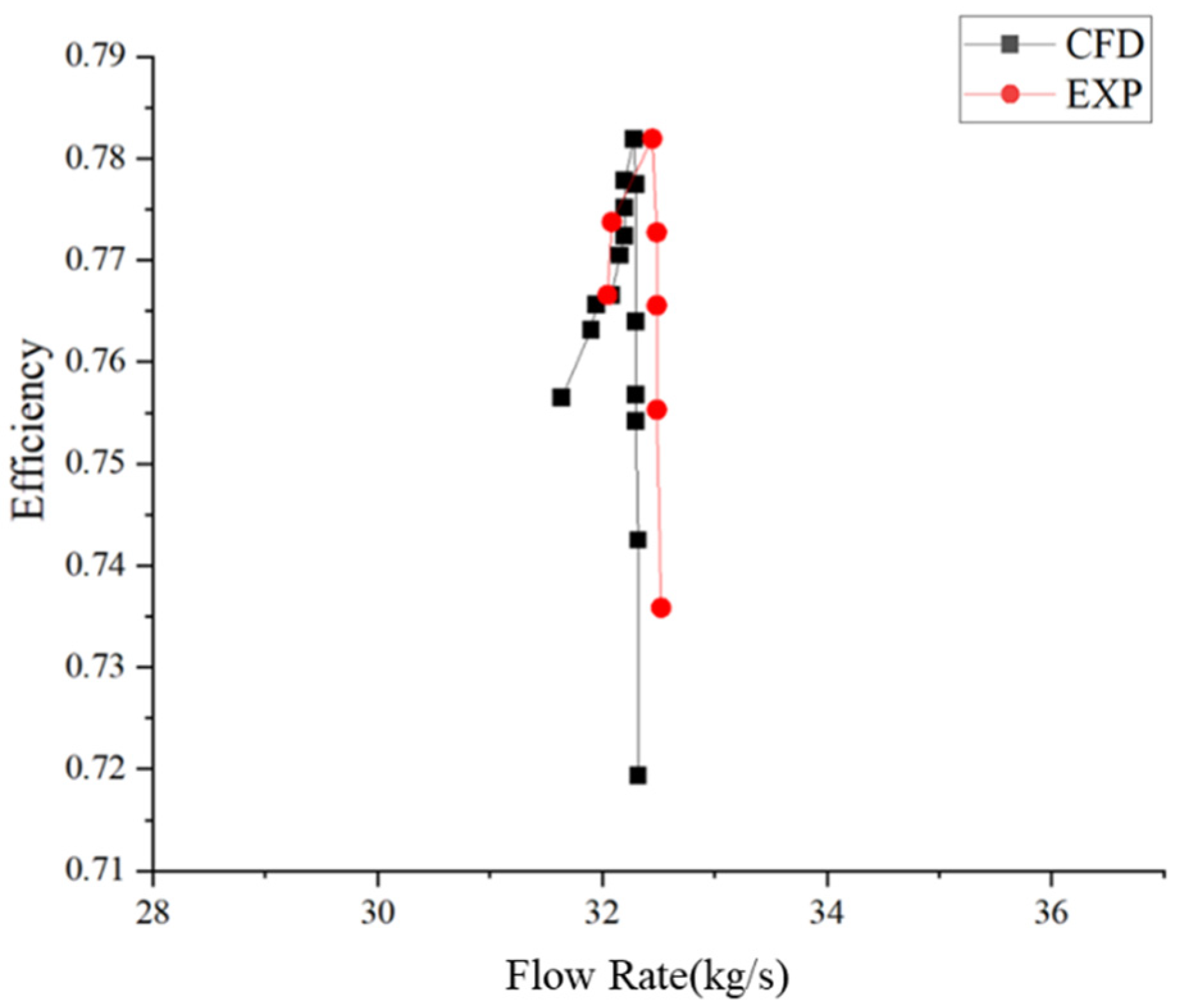
3.3. Feasibility Verification of Numerical Method
4. Results and Discussion
4.1. Simulation and Analysis of Compressor Exit Flow Field Under Different Typical Operating Conditions
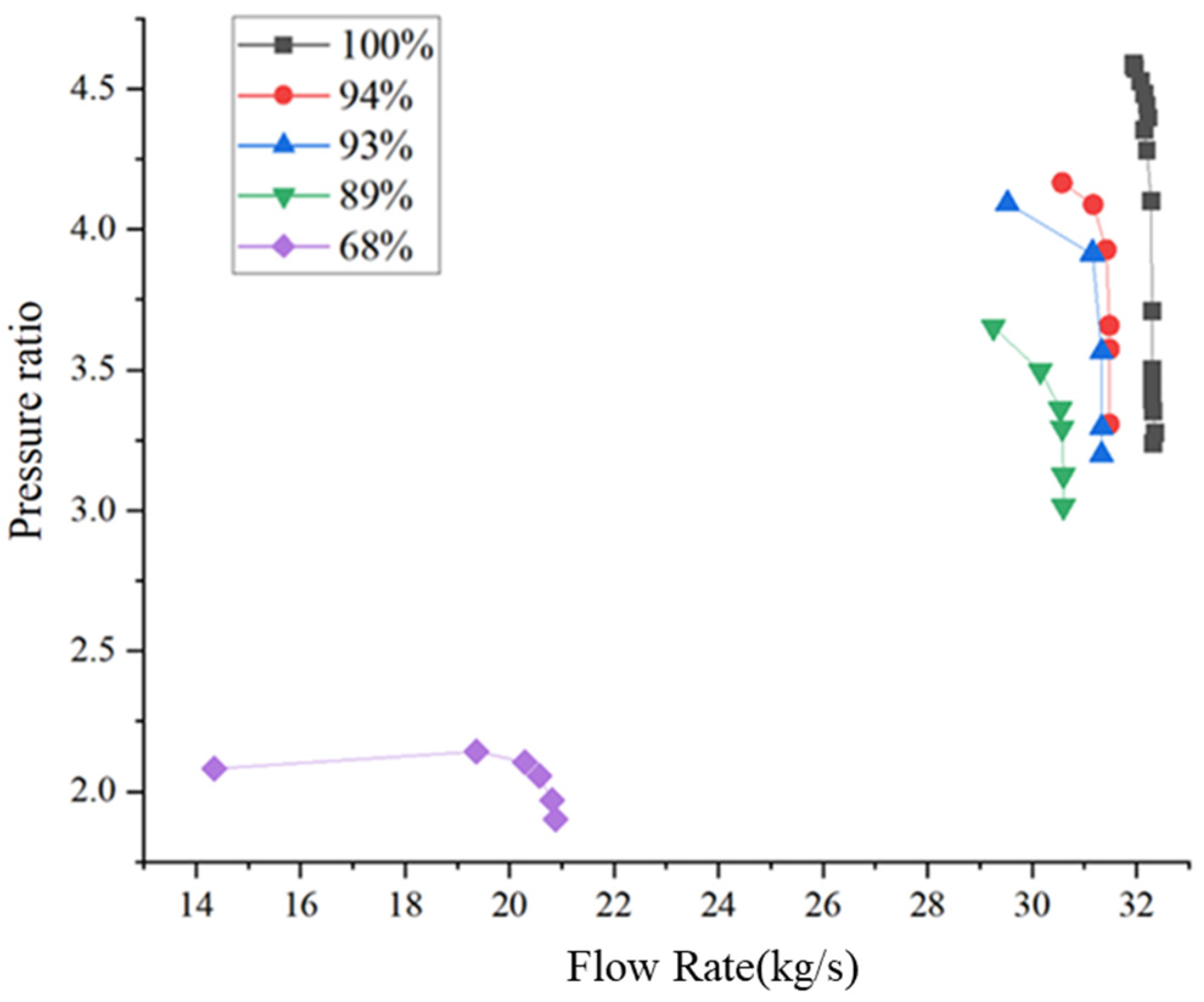
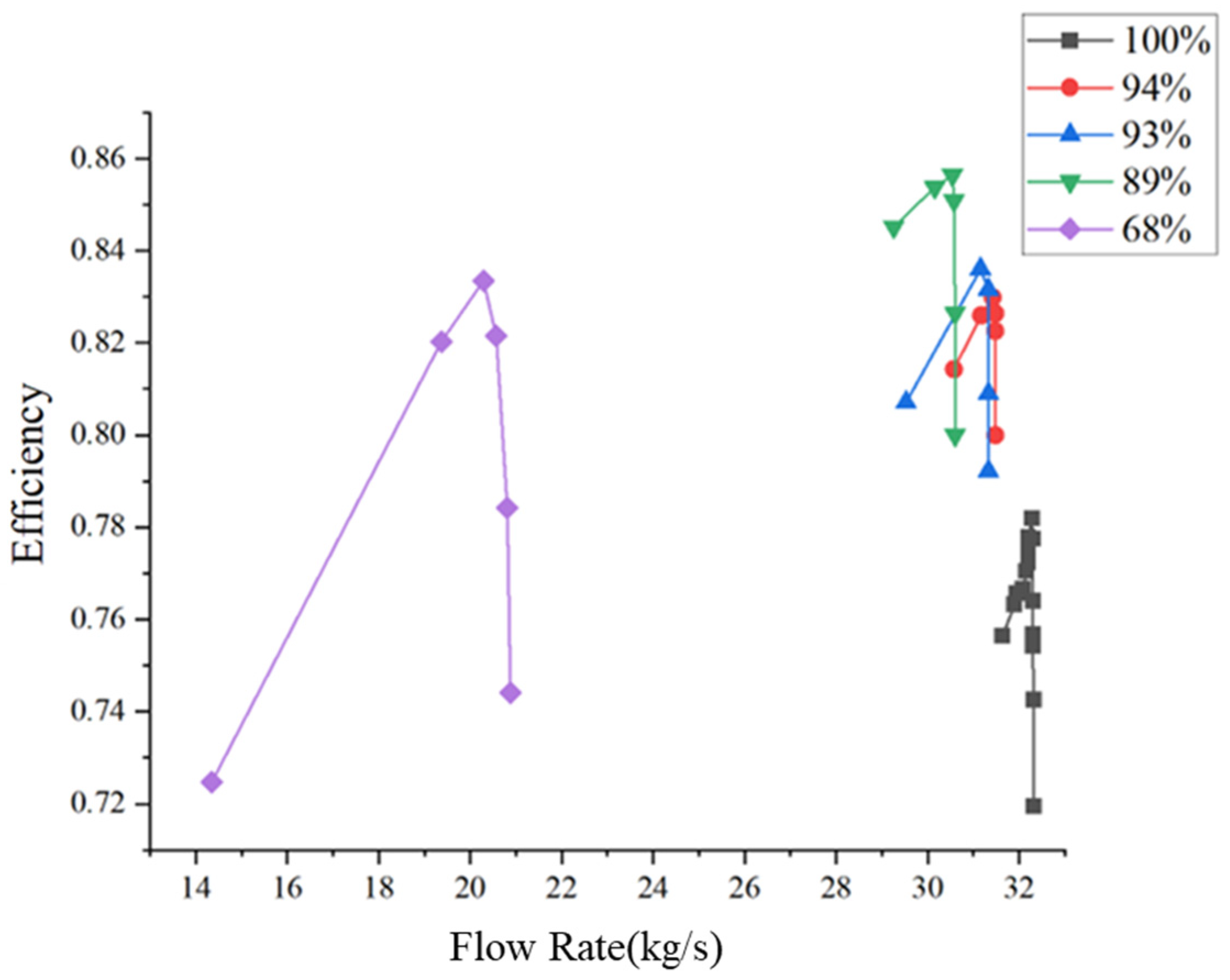
4.1.1. Analysis of Overall Compressor Performance Under Various Rotational Speed Conditions
4.1.2. Distribution Pattern of Total Velocity at the Compressor Exit Under Different Typical Operating Conditions
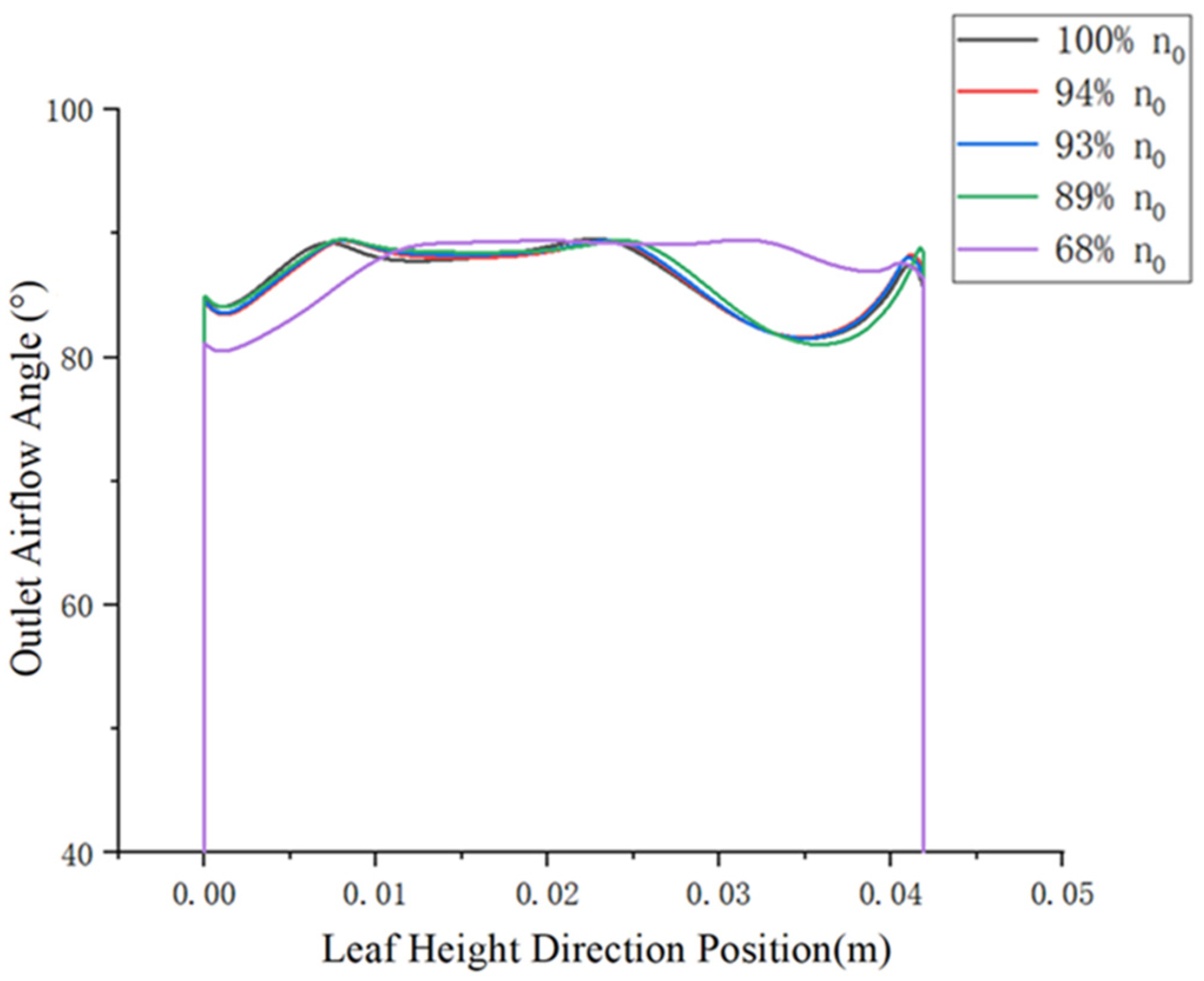
4.1.3. Distribution Pattern of Airflow Deflection Angle at the Compressor Exit Under Different Typical Operating Conditions
4.2. Effect of Non-Uniform Inlet Flow on Compressor Exit Flow Field Under Design Conditions
4.2.1. Configuration of Non-Uniform Inlet Flow Conditions
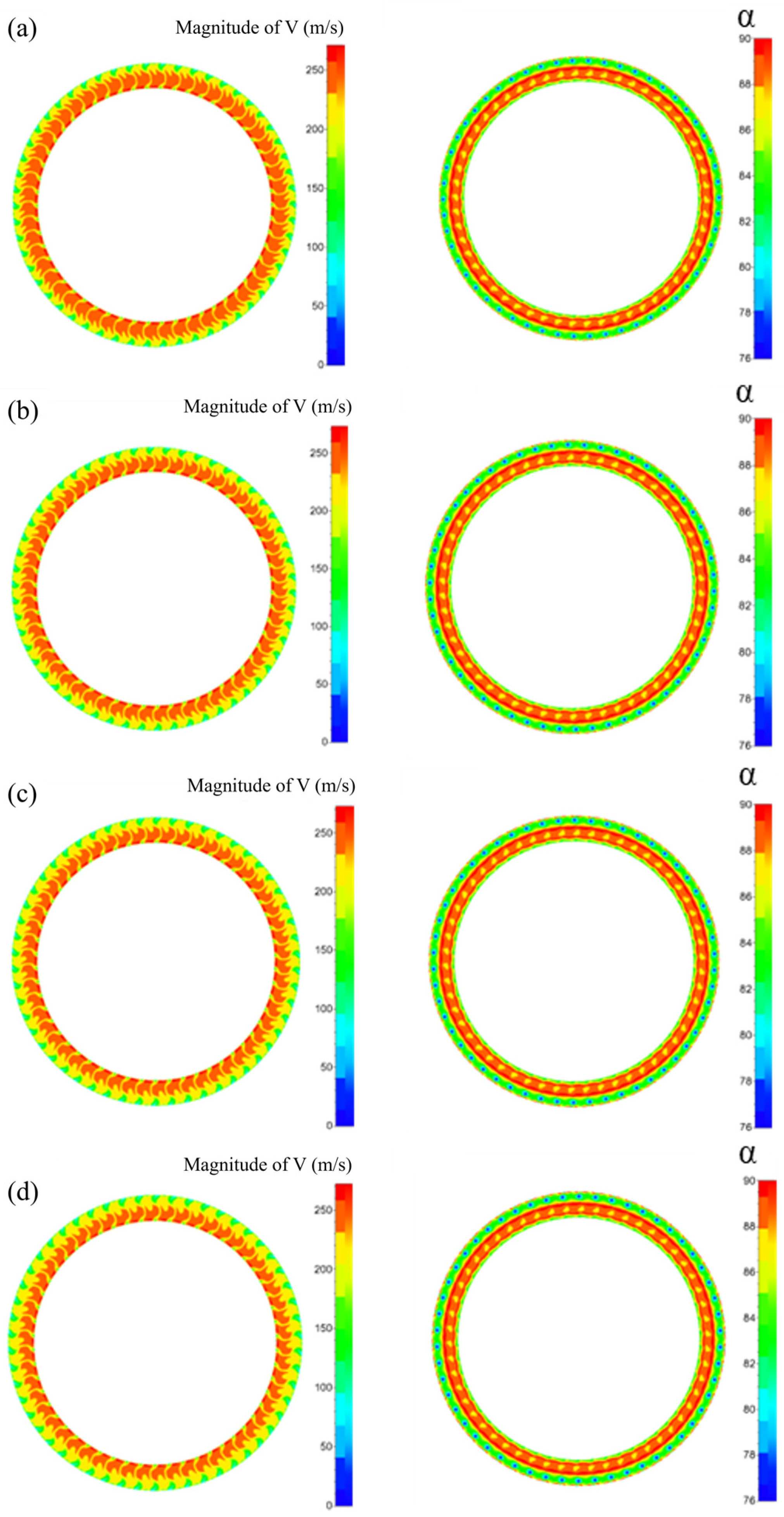
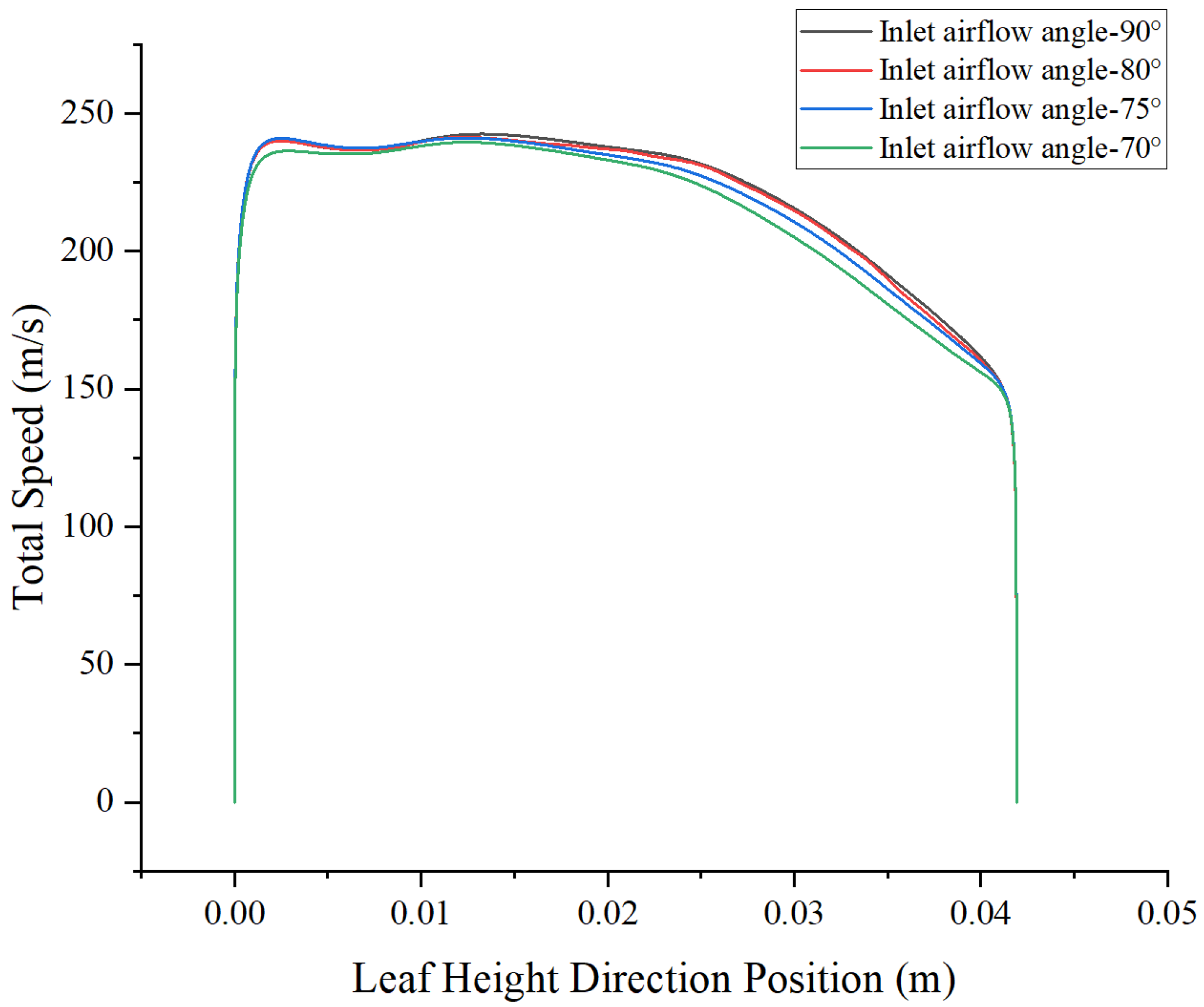
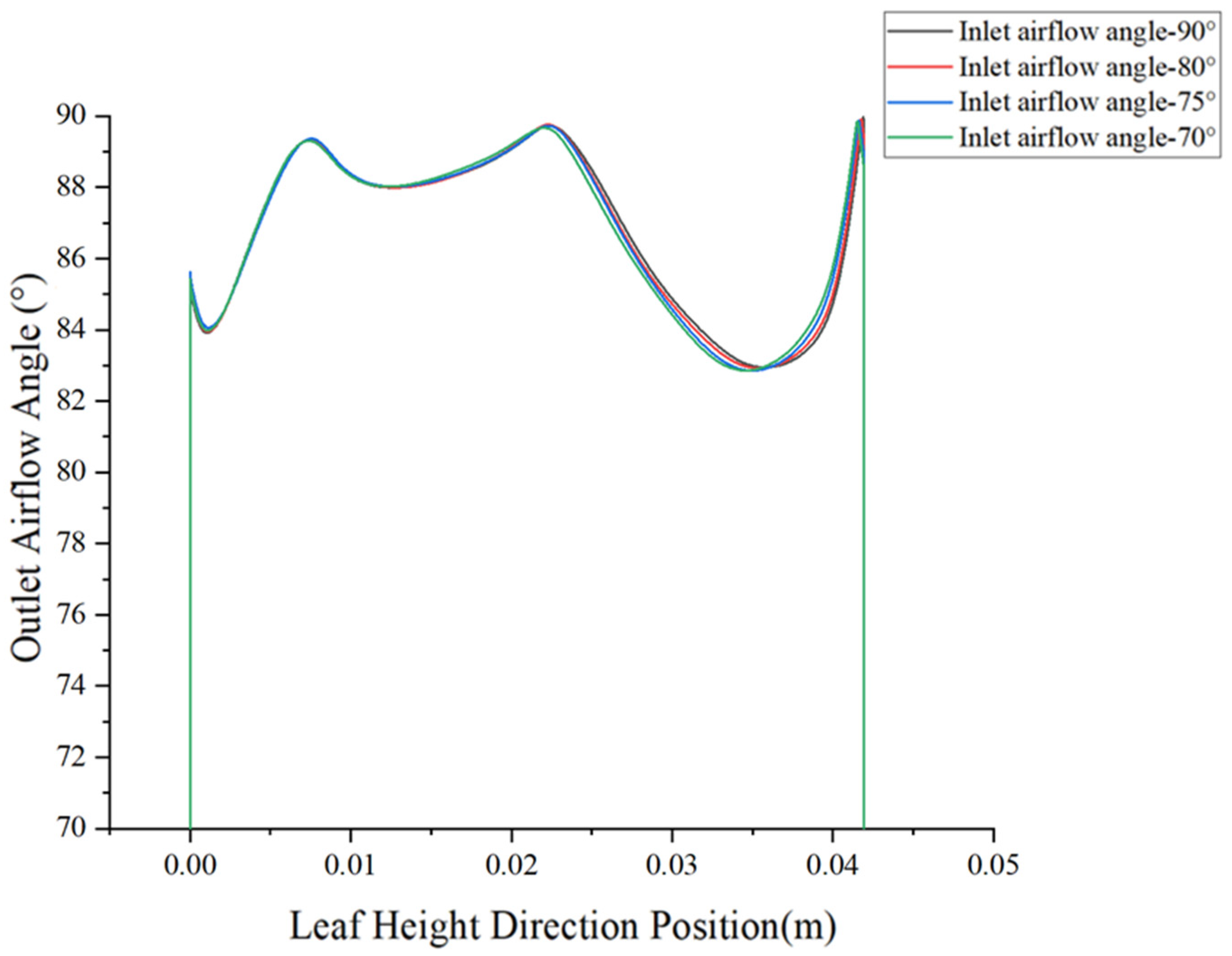
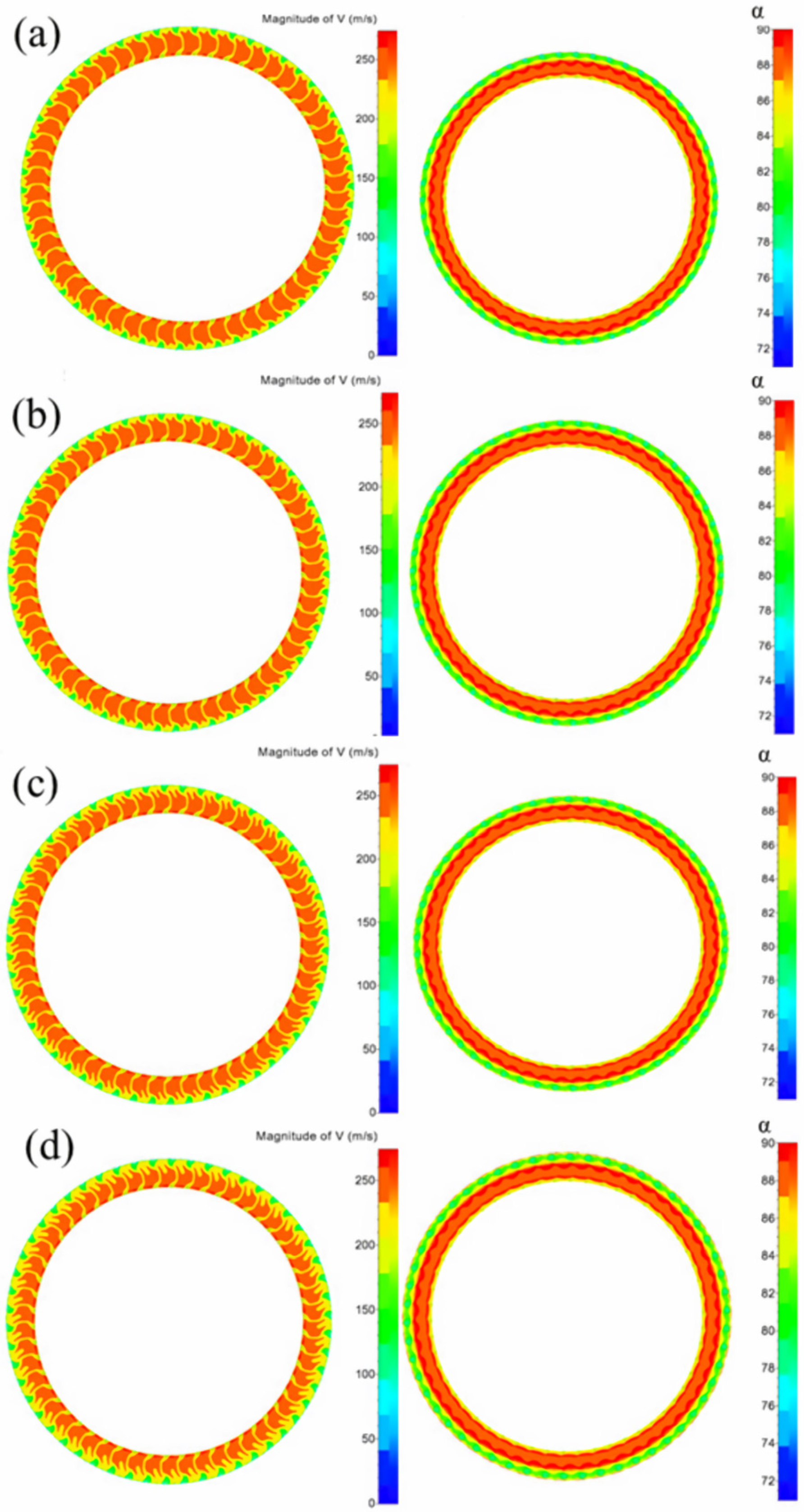
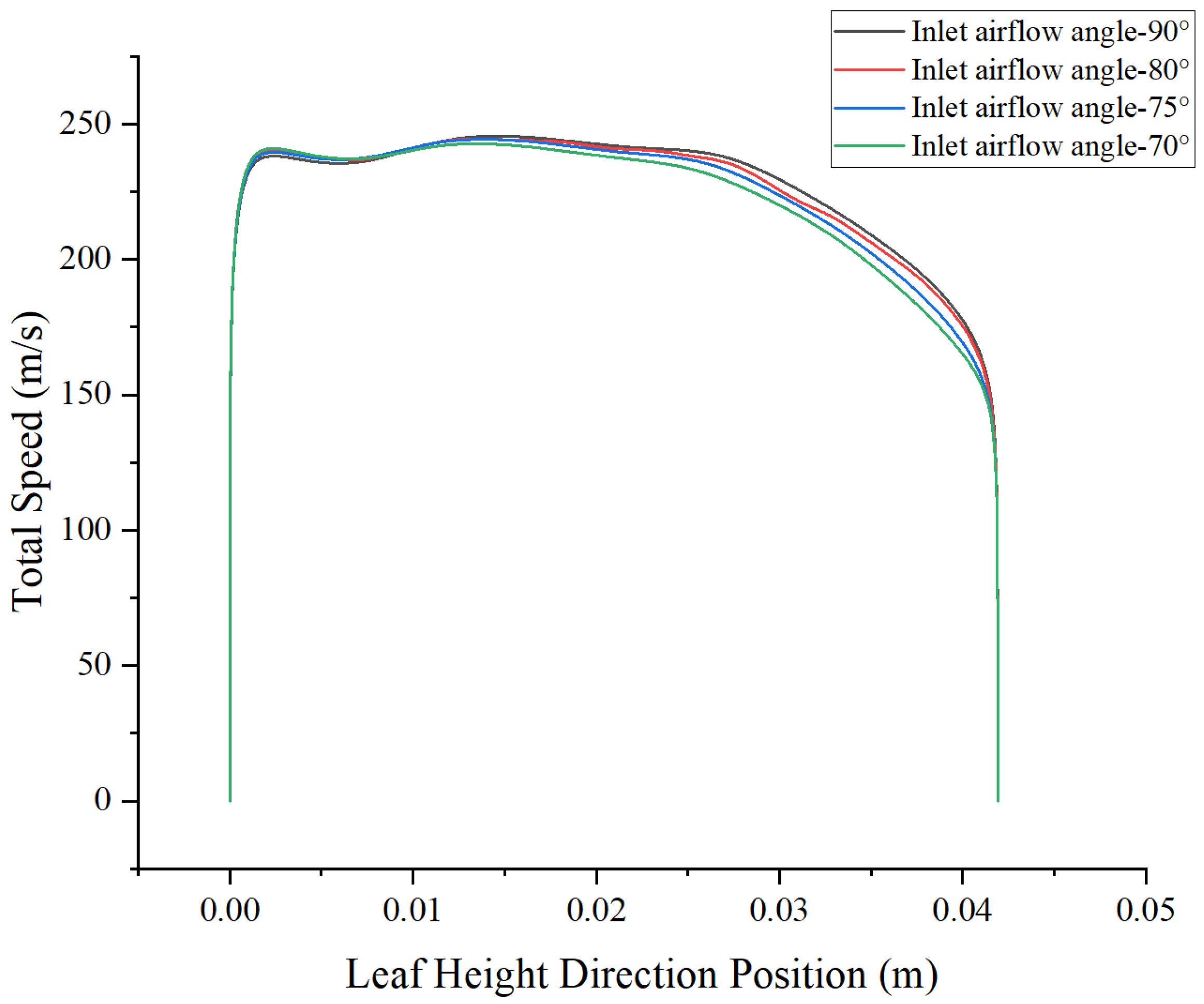
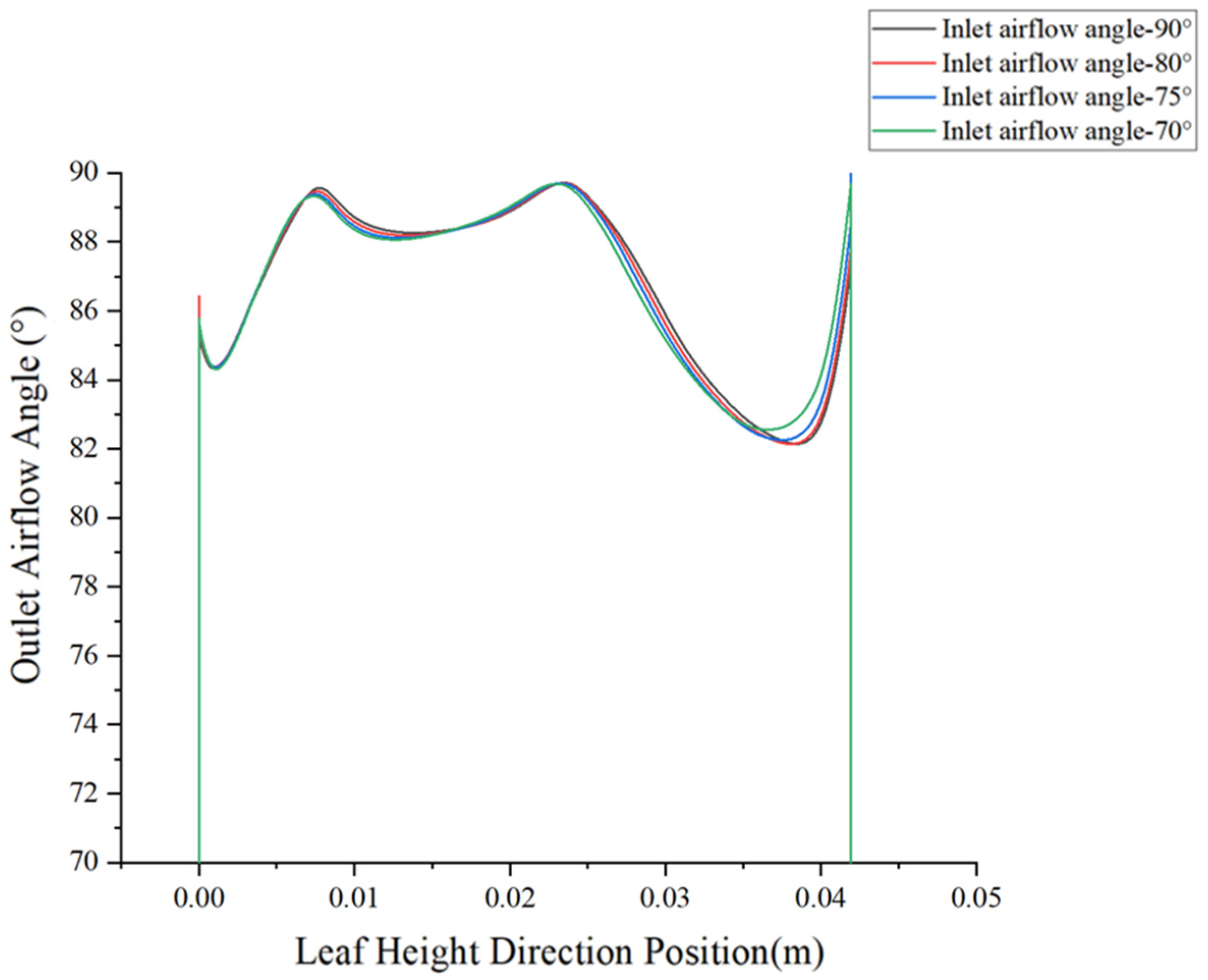
4.2.2. Effect of Different Inlet Airflow Angles at an Inlet Pressure of 1 atm
4.2.3. Effect of Different Inlet Airflow Angles at an Inlet Pressure of 1.05 atm
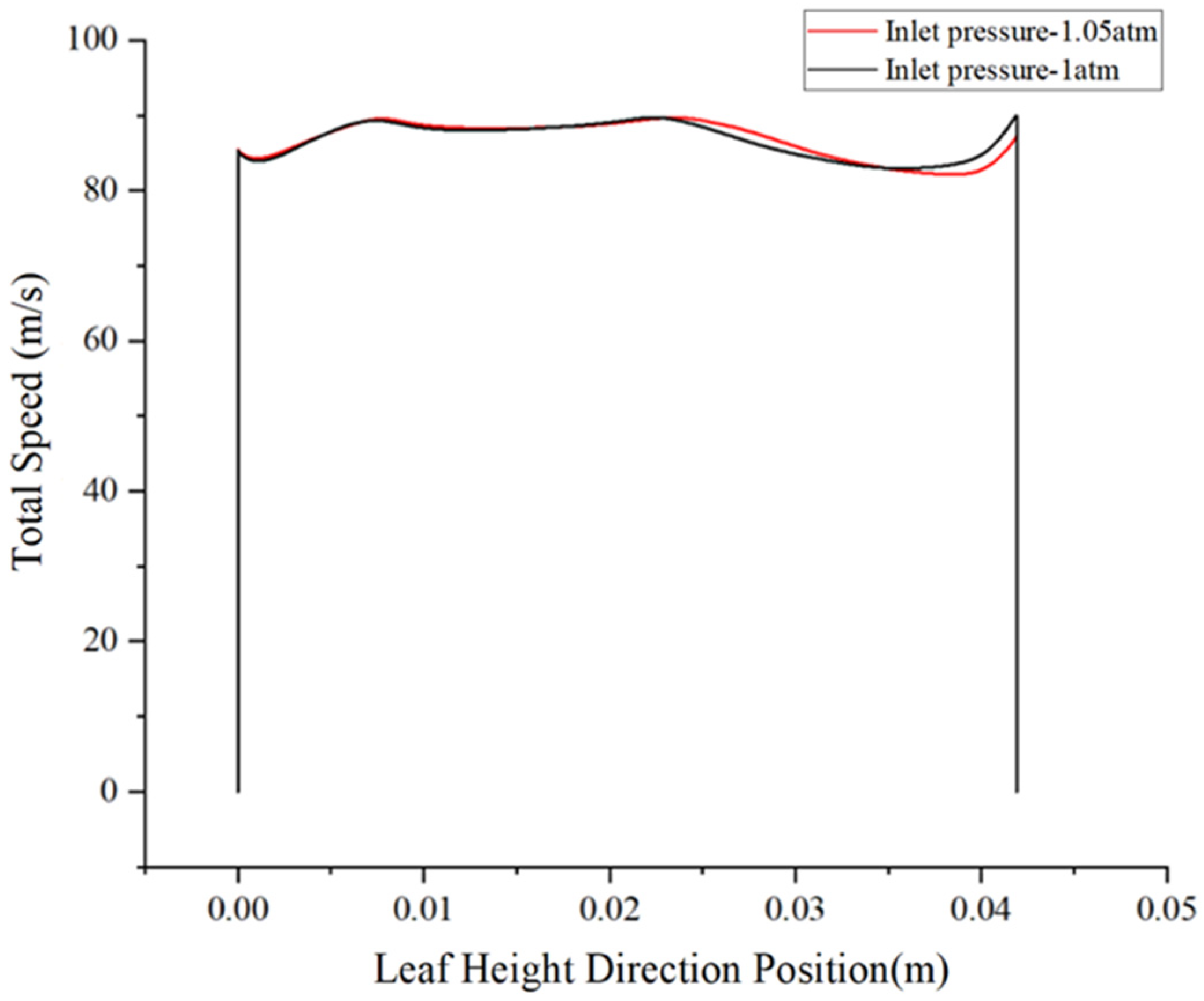
4.2.4. Effect of Different Compressor Inlet Pressures on the Exit Flow Field
4.2.5. Summary of the Effects of Inlet Flow Angle and Inlet Pressure on Exit Flow Field Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Semlitsch, B. Boundary conditions to represent the wave impedance characteristics of axial compressors. Appl. Acoust. 2023, 204, 109236. [Google Scholar] [CrossRef]
- Lamarque, N.; Poinsot, T. Boundary Conditions for Acoustic Eigenmodes Computation in Gas turbine Combustion Chambers. AIAA J. 2008, 46, 2282–2292. [Google Scholar] [CrossRef]
- Silva, C.F.; Durán, I.; Nicoud, F.; Moreau, S. Boundary Conditions for the Computation of Thermoacoustic Modes in Combustion Chambers. AIAA J. 2014, 52, 1180–1193. [Google Scholar] [CrossRef]
- Sun, Y. The Influence of Inlet Distortion on the Operating Characteristics of Transonic Axial-Flow Compressor. Master’s Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar]
- Mistry, C.S.; Pradeep, A.M. Investigations on the effect of inflow distortion on the performance of a high aspect ratio, low-speed contra-rotating fan stage. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference & Exposition, V06AT35A005, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Wartzek, F.; Schiffer, H.P.; Haug, J.P. Investigation of engine distortion interaction. In Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar]
- Zhang, L.; Liu, Y.; Sun, S. Numerical study on the effects of different total temperature inlet distortions on the aerodynamic performance and stability of the centrifugal compressor. Aerosp. Sci. Technol. 2025, 110292. [Google Scholar] [CrossRef]
- Gui, X.; Teng, J.; Liu, B.; Ning, F. Aviation Compressor Aerodynamic Thermodynamic Theory and Application; Shanghai Jiao Tong University Press: Shanghai, China, 2014. [Google Scholar]
- Liu, A.; Ju, Y.; Zhang, C.; Dai, R. Parallel steady/unsteady flow simulations of an 8.5-stage axial compressor. Aerosp. Sci. Technol. 2024, 145, 108853. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, B.; Wang, Y.; Nan, X. Numerical Simulation to Three-Dimensional Turbulent Flow in Multistage Axial Compressor Blade Row. J. Appl. Mech. 2007, 2, 21–25+170. [Google Scholar] [CrossRef]
- Jia, H.; Wu, H. Numerical simulation of three-dimensional flow field in transonic compressor rotor. Aeronaut. Comput. Tech. 2005, 35, 94–97. [Google Scholar]
- Wang, F.; Zhao, L.; He, L.; Zhang, M. Three-Dimensional CFD Flow Field Analysis and Aerodynamic Optimization of a Multi-Stage Axial Compressor. Therm. Turbine 2012, 41, 215–219. [Google Scholar]
- Zhang, L.; Liu, Y.; Sun, S. Numerical study on effects of total pressure distortion on unsteady effect of impeller-diffuser interaction in centrifugal compressor. Propuls. Technol. 2025, 1–14. [Google Scholar]
- Ma, N.; Nan, X.; Tang, F.; Zhang, J.; Liu, R. Numerical study on evolution mechanism of inlet total temperature distortion in an axi-centrifugal compressor. J. Propuls. Technol. 2024; online first. [Google Scholar]
- Tian, W.; Tu, B.; Hu, J. Numerical Simulation of Influence of Swirl Distortion and Total Pressure Distortion on Performance and Stability of Booster Stage. J. Nav. Aviat. Univ. 2025, 40, 213–227. [Google Scholar]
- Pan, T.; Yan, J.; Lu, H.; Li, Q. Impact of circumferential inlet distortion on different types of stall inceptions in a transonic compressor. Chin. J. Aeronaut. 2024, 37, 107–117. [Google Scholar] [CrossRef]
- Dong, J.; Wang, M. Effect on Stability of Compressor with Total Temperature and Pressure Distortions. J. Aerosp. Power 2003, 18, 788–793. [Google Scholar]
- Kikuchi, K.; Tamura, A.; Matsuo, Y.; Hirai, K.; Kodama, H.; Nozaki, O. Unsteady three-dimensional analysis of inlet distortion in turbomachinery. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997. [Google Scholar]
- Fidalgo, V.J.; Hall, C.A.; Colin, Y. A study of fan-distortion interaction within the NASA Rotor 67 transonic stage. ASME Turbo Expo Power Land Sea Air 2012, 134, 051011. [Google Scholar] [CrossRef]
- Sun, P.; Feng, G. Numerical simulation of effects of steady circumferential total pressure distortion on a small fan. Propuls. Technol. 2006, 27, 239–242. [Google Scholar]
- Sun, P.; Feng, G.; Kui, D. Numerical Simulation of the Impact of Total-pressure Distortion on the Aerodynamic Performance of Small-sized Fans. Therm. Power Eng. 2006, 21, 259–263. [Google Scholar]
- Gao, Q.; Yang, X.; Liu, S. Experiment on inlet distortion of high bypass ratio fan and booster. J. Aerosp. Power 2025, 40, 44–52. [Google Scholar]
- Wang, W.; He, T.; Sun, W.; Wang, X.; He, W.; Wang, B. Numerical Investigation of Bleed Rate on Performance of Multistage Axial Compressor. Gas Turbine Technol. 2024, 37, 1–10. [Google Scholar]
- Zhang, X.-W.; Ju, Y.-P.; Zhang, C.-H. Performance prediction and IGV-stator adjustment optimization of a multi-stage axial-flow compressor. J. Eng. Thermophys. 2020, 41, 1418–1427. [Google Scholar]
- Steinke, R.J. Design of 9.271-Pressure-Ratio Five-Stage Core Compressor and Overall Performance for First Three Stages. In NASA Technical Paper 2597; National Aeronautics and Space Administration: Cleveland, OH, USA, 1986. [Google Scholar]
- Liu, C. Aerodynamic Stability Numerical Simulation Method Study of Compressor Component Running in Gas Turbine Engine. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2012. [Google Scholar]
- Peng, Z. Principles of Aviation Gas Turbines; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Liu, X.; Guo, S.; Wang, Y.; Wang, D.; Wang, G.; Li, H. CFD-based unsteady simulation and performance analysis of scroll compressor. Int. J. Refrig. 2025, 170, 150–163. [Google Scholar] [CrossRef]
- Huang, P.; Bu, X.; Lin, G.; Wen, D. Numerical simulations of ice crystal icing within a 1.5-stage compressor in an aero-engine. Case Stud. Therm. Eng. 2025, 69, 106026. [Google Scholar] [CrossRef]
- Jiang, Q.; Yao, J.; Tan, Y.; Jiang, W. Design and Numerical Investigation of a Six-stage Industrial Axial Compressor Using Different Vortex Laws. Comput. Simul. 2024, 41, 33–41+87. [Google Scholar]
- Wang, L.; Mao, X.; Ma, G.; Liu, Y.; Gao, L. Investigation of unsteady characteristics in a counter-rotating compressor based on unsteady numerical simulation and mode decomposition methods. Aerosp. Sci. Technol. 2025, 158, 109848. [Google Scholar] [CrossRef]
- Milidonis, K.; Semlitsch, B.; Hynes, T. Effect of Clocking on Compressor Noise Generation. AIAA J. 2018, 56, 4225–4231. [Google Scholar] [CrossRef]
- Celik, I.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]








| Parameter | Value |
|---|---|
| Total pressure ratio | 4.474 |
| Total temperature ratio | 1.663 |
| Adiabatic efficiency | 0.799 |
| Polytropic efficiency | 0.836 |
| Mass flow rate (kg/s) | 29.71 |
| Rotational speed (r/min) | 16,042.3 |
| Tip speed (m/s) | 430.29 |
| Number of IGV blades | 26 |
| Number of stage 1 rotor blades | 28 |
| Number of stage 1 stator blades | 34 |
| Number of stage 2 rotor blades | 32 |
| Number of stage 2 stator blades | 46 |
| Number of stage 3 rotor blades | 39 |
| Number of stage 3 stator blades | 54 |
| Tip clearance (mm) | 0.408 |
| Inlet Pressure | Inlet Airflow Angle α (°) | |
|---|---|---|
| Non-uniform inlet | 1.05 atm | 90 |
| 80 | ||
| 75 | ||
| 70 | ||
| 1 atm | 90 | |
| 80 | ||
| 75 | ||
| 70 |
| Inlet Flow Angle (°) | Peak Exit Velocity (m/s) | Average Exit Velocity (m/s) | Average Flow Deflection Angle (°) | |
|---|---|---|---|---|
| 1 | 90 | 242.7 | 219.44 | 85.45 |
| 80 | 241 | 217.6 | 85 | |
| 75 | 240 | 215.5 | 84.5 | |
| 70 | 239 | 214.44 | 84.18 | |
| 1.05 | 90 | 245.6 | 227.033 | 84.86 |
| 80 | 244.5 | 225.661 | 84.5 | |
| 75 | 243.3 | 223.187 | 84.3 | |
| 70 | 242.7 | 221.736 | 84.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Li, H.; Liu, C.; Hu, Y.; Li, Y.; Yan, Y.; Zhang, C. Aerodynamic Characteristics of Typical Operating Conditions and the Impact of Inlet Flow Non-Uniformity in a Multi-Stage Transonic Axial Compressor. Processes 2025, 13, 1428. https://doi.org/10.3390/pr13051428
Jiang D, Li H, Liu C, Hu Y, Li Y, Yan Y, Zhang C. Aerodynamic Characteristics of Typical Operating Conditions and the Impact of Inlet Flow Non-Uniformity in a Multi-Stage Transonic Axial Compressor. Processes. 2025; 13(5):1428. https://doi.org/10.3390/pr13051428
Chicago/Turabian StyleJiang, Dong, Huadong Li, Chongyang Liu, Yang Hu, Yongbo Li, Yunfei Yan, and Chenghua Zhang. 2025. "Aerodynamic Characteristics of Typical Operating Conditions and the Impact of Inlet Flow Non-Uniformity in a Multi-Stage Transonic Axial Compressor" Processes 13, no. 5: 1428. https://doi.org/10.3390/pr13051428
APA StyleJiang, D., Li, H., Liu, C., Hu, Y., Li, Y., Yan, Y., & Zhang, C. (2025). Aerodynamic Characteristics of Typical Operating Conditions and the Impact of Inlet Flow Non-Uniformity in a Multi-Stage Transonic Axial Compressor. Processes, 13(5), 1428. https://doi.org/10.3390/pr13051428







