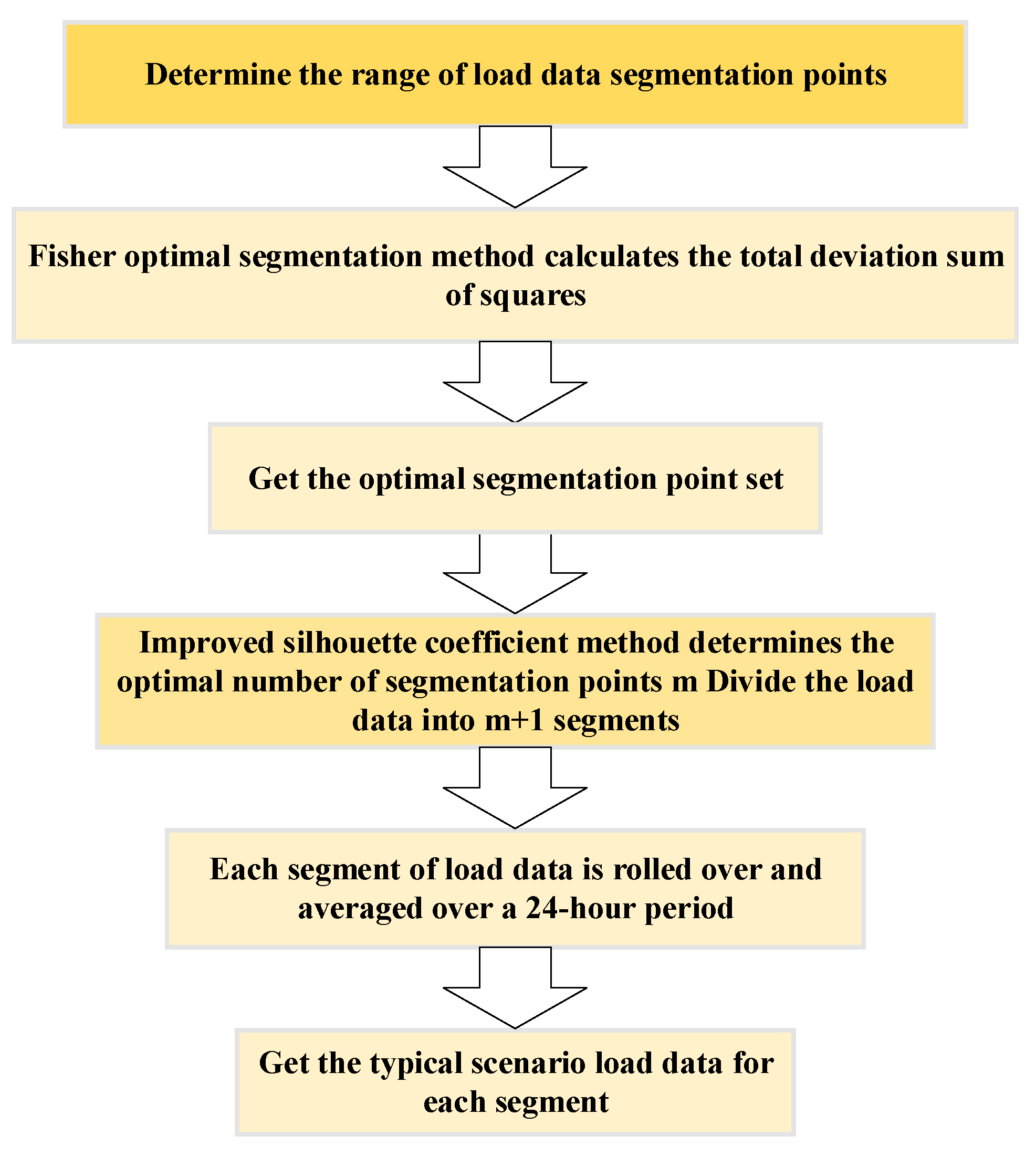
5.3.3. Analysis of Scenario 2 Results
The results of CES operation optimization after the introduction of demand response are presented in
Table 6. The implementation of demand response policies includes both price-based and incentive-based demand response, with different load types responding in various ways. The degree of low carbonization for typical days in summer and winter increased by 2563.08 and 785.11, respectively, compared to Scenario 1. Additionally, the economic benefits of the CES increased by CNY 113.2 and CNY 617.75, respectively.
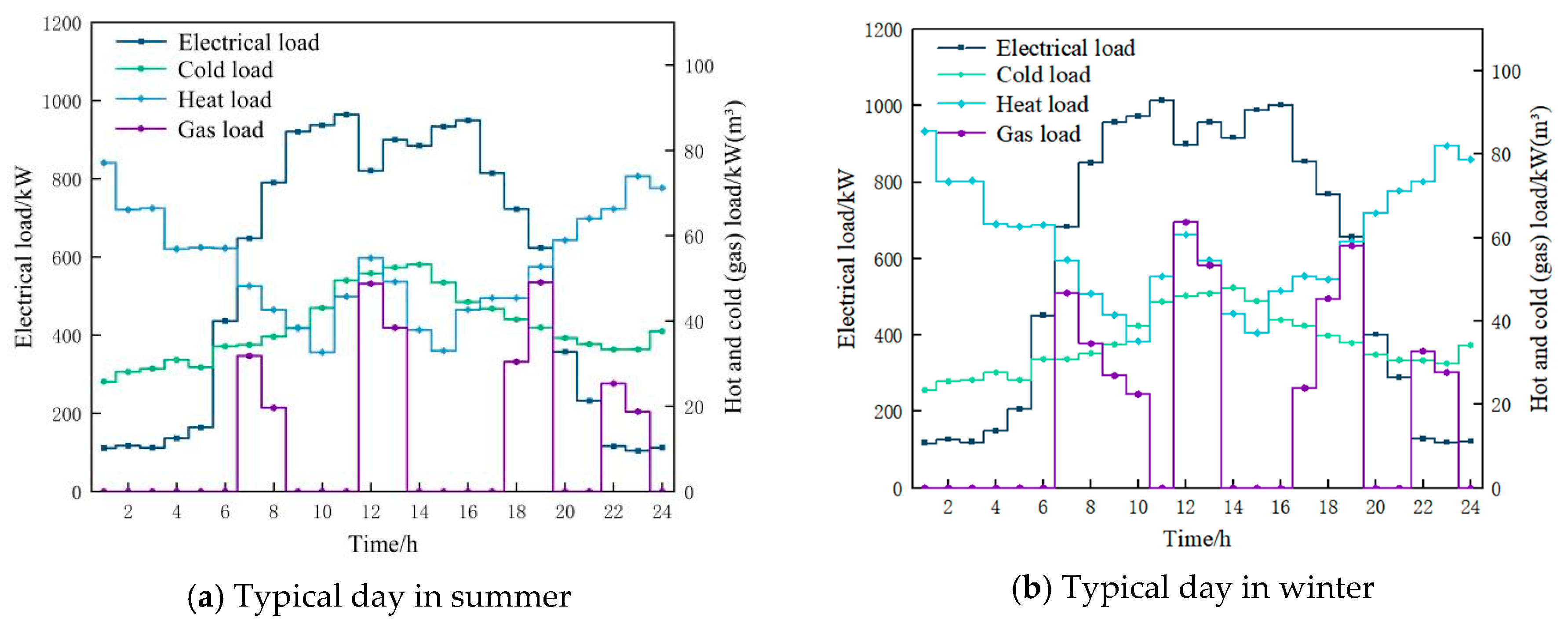
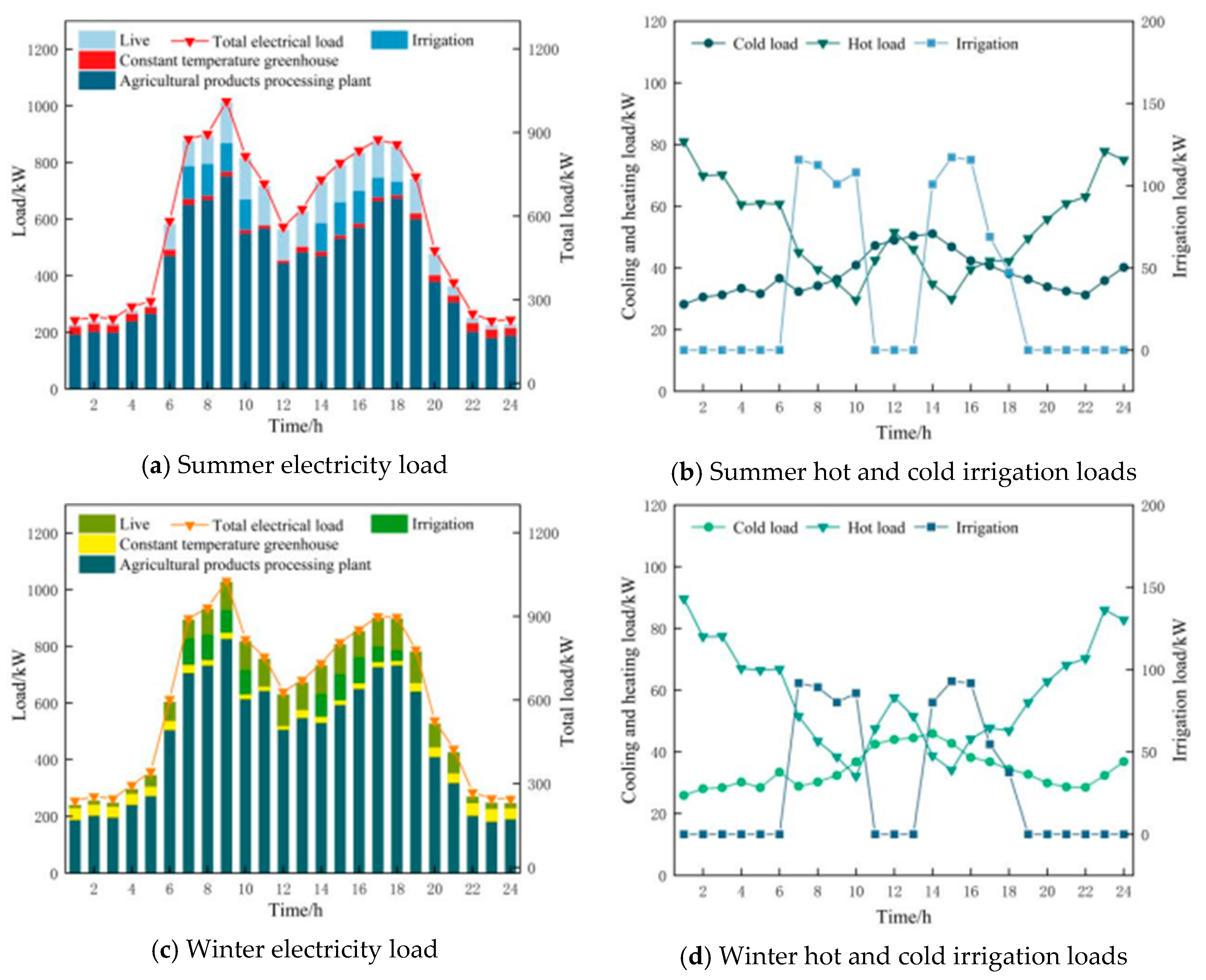
Figure 10a–d are the cooling, heating, and electricity load data on typical days in summer and winter after all types of loads participate in demand response.
As shown in
Figure 10a, agricultural product processing plants are the main component of the electricity load in each period, followed by rural life load and irrigation load. Constant temperature greenhouses require the least electricity load due to their simple energy use form. Compared with
Figure 10c, it can be seen that the electricity load demand of constant temperature greenhouses has increased. This is because the temperature is low in winter, and the constant temperature greenhouse needs to increase energy demand to maintain a constant temperature state. By comparing
Figure 10b,d, it can be seen that rural areas have higher irrigation and cooling load demands in summer than in winter. This is because the weather is hot and the temperature is high in summer, and the water evaporation is large. Agricultural irrigation and cold storage need to increase energy to maintain their load demand. At the same time, the heat load demand of agricultural product processing plants in winter is also increasing compared to summer.
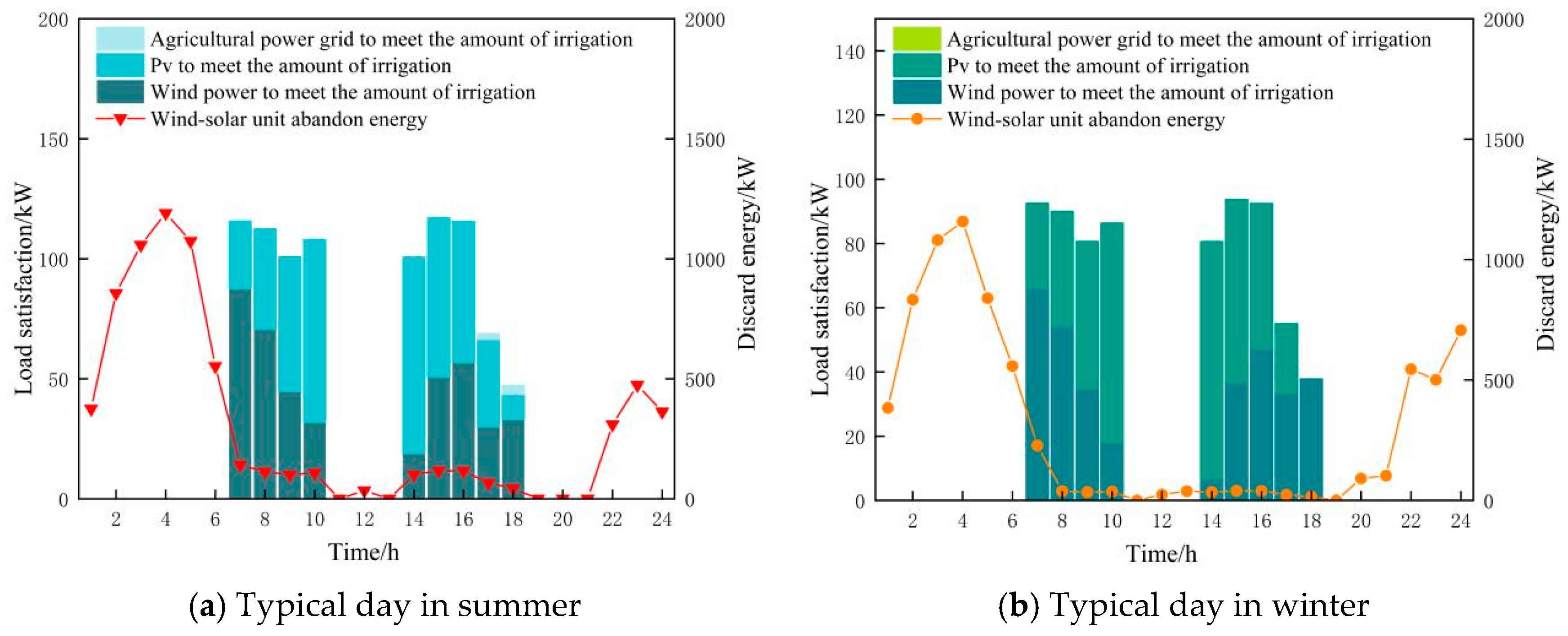
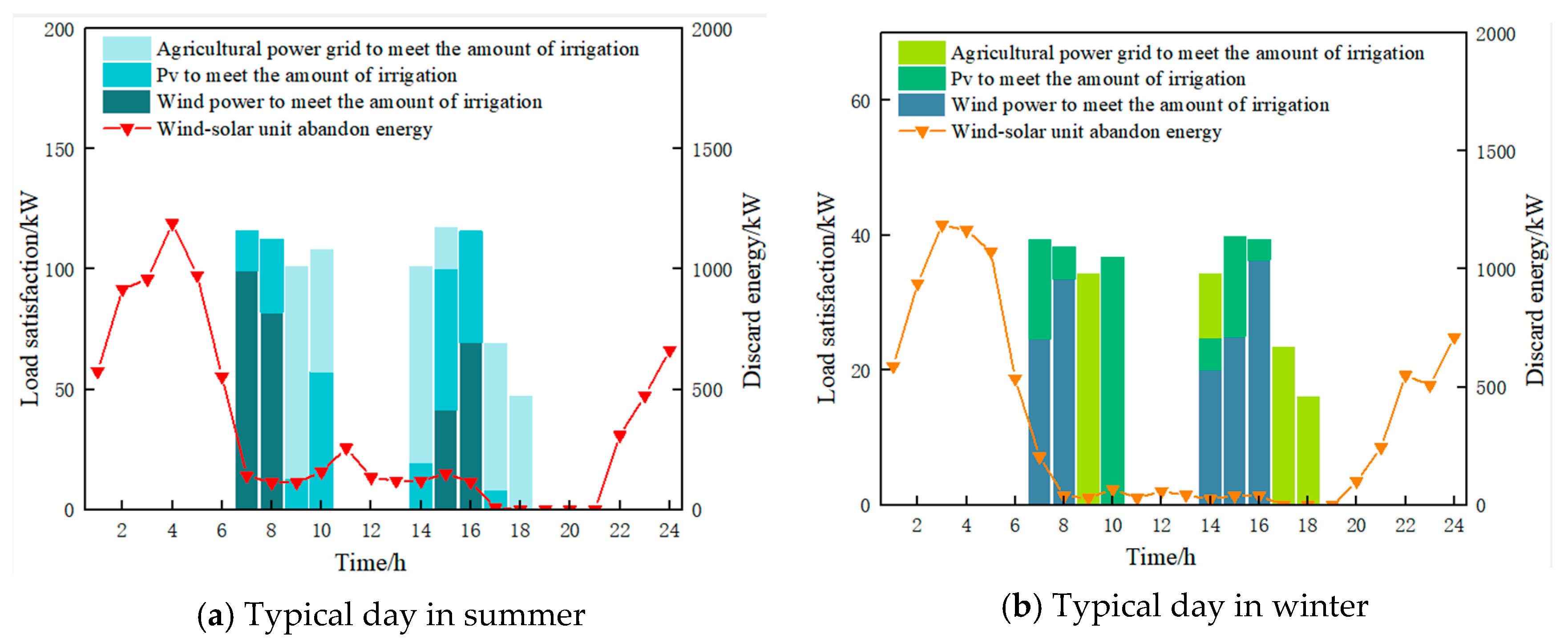
Figure 11 shows the optimization results of the CES for rural irrigation energy use on typical days in summer and winter and the wind and solar energy abandonment of the CES.
The consumption of clean energy on typical days in summer and winter is shown in
Figure 11. As shown in
Figure 11a,b, in addition to describing the consumption of wind and solar resources, it also shows the dispatch of each unit to meet the irrigation volume. During the nighttime period of 3:00–5:00, wind turbines generate a large amount of abandoned energy. This is due to the low demand for daily energy consumption of villagers and direct electricity load in the production park at night, and the abundant wind power resources at night. The low-carbonization degree of the clean energy system is high during this period. During the period of 9:00–17:00, the system requires high cooling and heating loads and electricity loads, so the wind and solar units have less abandoned energy and a higher consumption rate. At the same time, the clean energy system purchases electricity from the rural grid to meet the remaining load demand. The irrigation load during the period of 17:00–18:00 is mainly met by the rural grid. This is because this period is close to dusk, the photovoltaic power generation is reduced, and the heat load demand of the industrial park continues to increase. Therefore, the clean energy system purchases electricity from the rural grid to meet the remaining load. During the period of 6:00–8:00 and 16:00, the irrigation load is fully met by clean energy, achieving comprehensive low carbonization and creating benefits for the clean energy system. Comparing
Figure 11a,b, it can be seen that the energy required for irrigation in winter is relatively low in the rural power grid. This is because the irrigation demand is low during the entire scheduling cycle in winter, so the amount of electricity purchased by the CES from the rural power grid is relatively low, and the economic benefits of the CES in the typical winter scenario are relatively high.
5.3.4. Analysis of the Results of Scenario 3
Introducing energy storage devices based on the response of various load demands in Scenario 2, energy storage aggregators obtain benefits by buying at low prices and selling at normal prices, while optimizing the new energy consumption rate during the operation of the CES. The scheduling results of Scenario 3 are shown in
Table 7. The low-carbonization degree of the CES on typical summer and winter days is improved by 365.29 and 323.11 compared with Scenario 2, and the economic income of the CES is increased by CNY 5966.34 and CNY 5586.9. It can be seen from the scheduling results that the low-carbonization degree index of the CES on typical summer days is higher than that of typical winter days, while the economic benefit index is lower than that of typical winter days.
The main costs of the CES during the dispatch cycle after the introduction of energy storage devices are shown in
Table 8. Due to the large overall demand for irrigation load, cooling load, and living energy on typical summer days, the CES needs to purchase electricity from energy storage aggregators and rural power grids during certain periods, with purchase costs of CNY 554.32 and CNY 87.35, respectively. Therefore, the cost of purchasing electricity from external sources in summer is relatively high compared to winter, and the equipment depreciation cost is also higher. This is one of the reasons why the economic benefits of the CES on typical summer days are lower than those on typical winter days.
The optimized dispatch of the CES in a typical day is divided into two situations: living energy and production energy. The specific optimization results are as follows.
(1) Optimization results of living energy
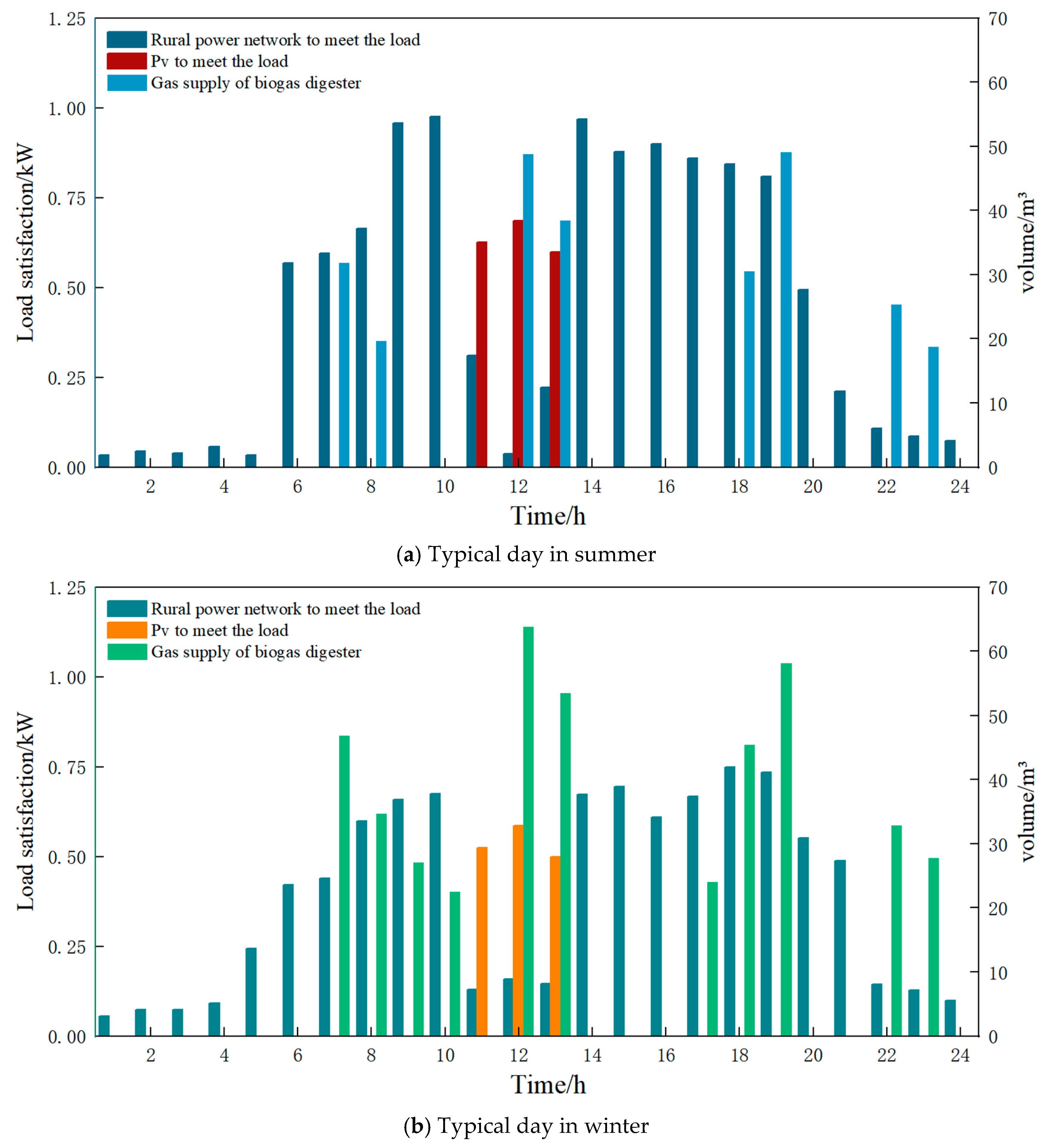
The daily energy supply and consumption of rural villagers in summer and winter are shown in
Figure 12a,b. The living electricity consumption is calculated per household, while the biogas demand is based on the entire village. Due to the regularity of rural living habits, electricity consumption is relatively low before 6:00 AM and after 8:00 PM, with peak electricity demand occurring between 9:00 AM and 7:00 PM. The biogas in the CES is directly used to meet the villagers’ daily cooking needs without being converted into electricity. The peak biogas demand period is from 12:00 PM to 1:00 PM and 6:00 PM to 7:00 PM. The daily cooling and heating load demand is met by the conversion unit in the CES. From 11:00 AM to 1:00 PM, photovoltaics supply the main electricity load demand, while the electricity load during the remaining periods is met by the rural power grid. Comparing
Figure 12a,b, it can be observed that the demand for cooking, heating, and lighting in winter is higher, resulting in greater biogas and electricity load demand in winter than in summer.
In summary, compared with the original rural energy supply, the introduction of clean energy significantly enhances the low-carbon level of living energy use, while also providing economic benefits for the clean energy system.
(2) Optimization results of production energy consumption
The CES provides energy for rural industrial parks. At the same time, various loads influence the optimization scheduling of CES units through response methods such as whole-section shifting, scattered scheduling, and peak reduction. The optimization results of production energy consumption in rural industrial parks are shown in
Figure 13,
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19 and
Figure 20.
The optimization results of CES production energy consumption on typical days in summer and winter are shown in
Figure 13a,b. Wind and solar energy meet most of the production electricity demand. As shown in
Figure 13a, during the period of 17:00–18:00 on a typical summer day, wind and solar units, biogas turbines, and rural power grids jointly meet the remaining electricity load demand. This is because the output of wind and solar units meets the high demand for cooling, heating, and irrigation loads during this period. During this time, the output of wind and solar units is almost entirely consumed, and the CES purchases electricity from the rural power grid to meet the remaining load. Throughout the scheduling period, biogas turbines meet a lower electricity load than wind and solar units. This is because the output of wind and solar units has a certain randomness and uncertainty. In order to ensure the environmental protection and economy of the CES, wind and solar resources are prioritized. Electric refrigeration units and electric boilers meet the cooling and heating loads, respectively, so their power consumption curves are consistent with the cooling and heating load curves. As shown in
Figure 13b, on a typical winter day, except for the reduction in energy consumption of electric refrigeration machines, the other load demands all increase. At the same time, due to the higher wind power output in winter, the load satisfied by wind and solar power on a typical winter day increases, while the load satisfied by the biogas unit decreases. Consequently, the CES does not need to purchase electricity from the rural grid.
The optimization results of the CES satisfying the cooling and heating loads on typical days in summer and winter are shown in
Figure 14a,b. In the 11:00–12:00 period of
Figure 14a, clean energy meets a relatively low heat load throughout the entire dispatch period, with the heat load mainly being met by wind turbines through electric refrigeration machines. In the 14:00–16:00 period, the cooling load is met by biogas units. This is because the output from wind and solar power is nearly fully absorbed during this period. In
Figure 14b, during the 8:00–11:00 period and the 13:00–16:00 period, wind power hardly meets the cooling and heating loads. During these periods, the cooling and heating loads are instead met by other clean energy units. This is due to the system’s electrical load being at a peak during this time and wind power resources being limited.
Figure 14.
Cooling and heating load optimization results.
Figure 14.
Cooling and heating load optimization results.
In the periods of 1:00–6:00 and 22:00–24:00 in
Figure 14a, and 0:00–5:00 and 20:00–24:00 in
Figure 14b, the cooling and heating loads are fully met by clean energy, achieving comprehensive low carbonization. As can be seen from both figures, the energy abandonment of wind and solar units increases during the 22:00–24:00 period, which sufficiently demonstrates the abundance of clean energy during this time. As a result, the cooling and heating loads are met in this period, ensuring comprehensive low carbonization.
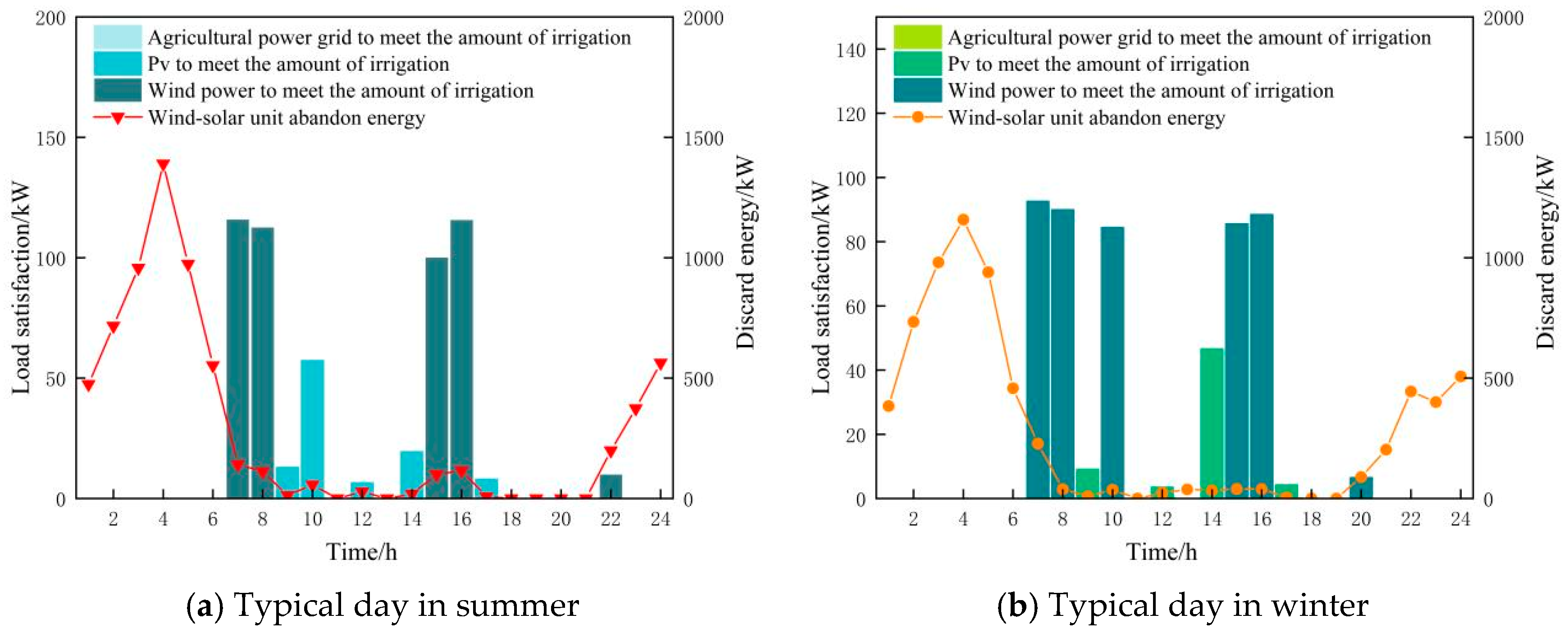
The consumption of clean energy in typical days during summer and winter in Scenario 3 is shown in
Figure 15. As illustrated in
Figure 13a,b, during the nighttime period of 3:00–5:00, wind turbines generate a large amount of abandoned energy, and the low-carbonization degree of the CES reaches its highest level during this period. In
Figure 15a, from 9:00 to 17:00, the abandoned energy of the CES wind and solar units is relatively small. During the period of 17:00–18:00, the CES purchases electricity from the rural power grid to meet the remaining load demand, with the irrigation load mainly supplied by the rural power grid and wind power. This is because this period is close to dusk, photovoltaic power generation decreases, and the heat load demand of the industrial park continues to rise. As a result, the CES purchases electricity from the rural power grid to fulfill the remaining load demand. In other periods, the irrigation load is fully met by clean energy, achieving comprehensive low carbonization and generating benefits for the CES. As shown in
Figure 15b, the abandoned energy in winter is higher than in summer throughout the entire scheduling period, with wind power abandonment being more pronounced during the 20:00–24:00 period.
Figure 15.
Irrigation energy consumption and clean energy consumption results.
Figure 15.
Irrigation energy consumption and clean energy consumption results.
Comparing
Figure 15 and
Figure 11, the total amount of wind and solar energy abandonment on typical days in summer and winter in Scenario 3 with the introduction of energy storage is less than the total abandoned energy in Scenario 2. This is because energy storage aggregators will purchase at low prices during periods of high abandoned energy and sell at normal prices when the CES needs to purchase electricity, thereby earning profits while improving the low-carbonization degree of the CES.
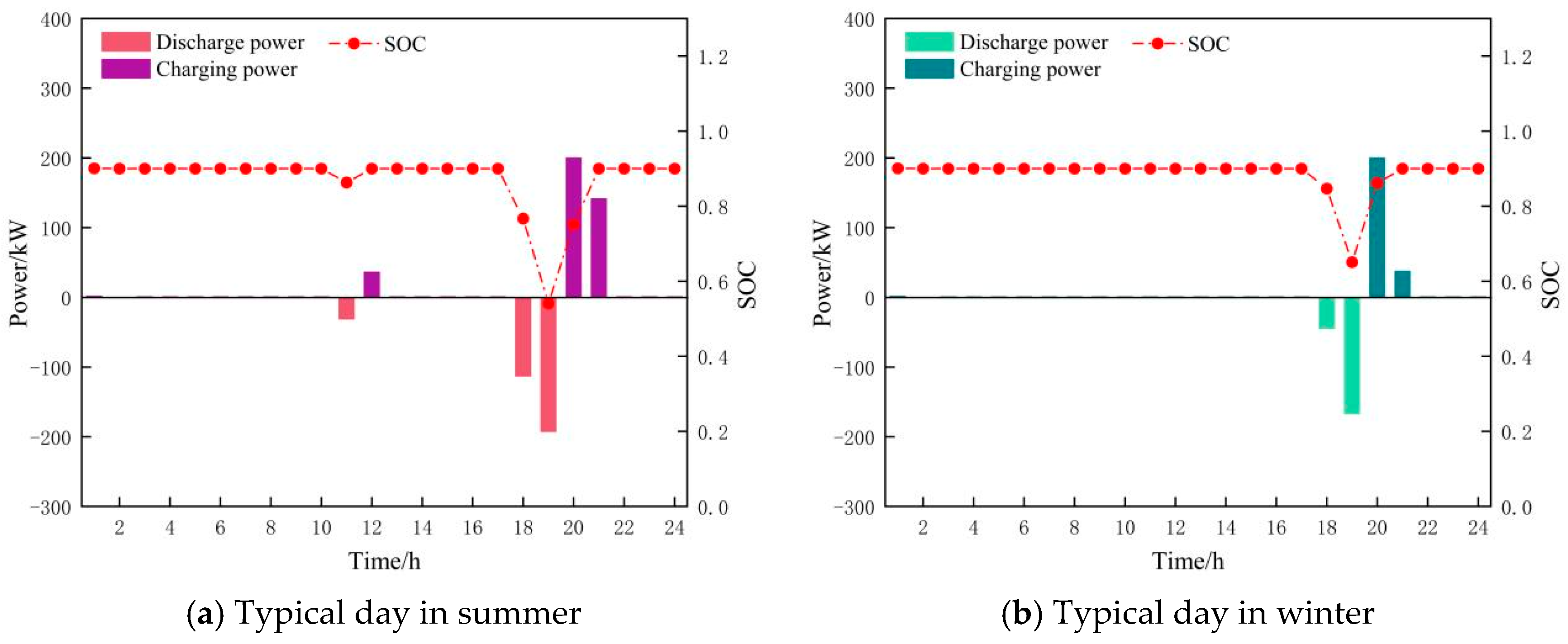
Figure 16a,b show the operating status of energy storage devices in Scenario 3 on typical days in summer and winter, respectively.
Figure 16.
Energy storage operation status.
Figure 16.
Energy storage operation status.
As shown in
Figure 16a,b, on typical days in different seasons, the energy storage device in the CES exhibits noticeable differences in charge and discharge patterns in response to changes in load demand and wind and solar resources. These differences highlight the critical role of energy storage in balancing energy supply and optimizing economic objectives. On typical summer days, the frequency and total amount of charge and discharge by the energy storage devices are relatively high. During the period of 3:00–8:00, the energy storage device remains in a state of continuous, small-scale charging. This phase corresponds to the nighttime period when wind power resources are abundant, but the load demand of the system is low, leading to the abandonment of some wind power resources. To avoid wasting this surplus energy, the CES stores the excess wind power through energy storage devices, thereby enhancing the utilization rate of wind power.
During the high-load periods of 9:00–11:00, 14:00–15:00, and 17:00–19:00, the energy storage system is continuously discharged. During these times, the load demand is high, and the available wind and solar resources are insufficient to meet the system’s requirements. The CES draws electricity from the energy storage device, which not only reduces the cost of electricity purchases but also helps to meet peak load demands, thus improving the overall economy of the system. In the period of 22:00–23:00, when wind power resources are abundant again and system load demand is relatively low, a significant amount of energy is abandoned. During this time, the CES purchases electricity at a low price and stores it, with the charging power of the energy storage system increasing substantially. This charging strategy effectively leverages the low electricity prices during off-peak hours and the abundant wind resources, thereby enhancing the efficiency of wind energy utilization.
On a typical winter day, the charging and discharging characteristics of energy storage are different from those in summer. First, during the period of 11:00–13:00, after the energy storage system has undergone a large amount of charging, it enters a 2 h small amount of charging stage. The reason for this phenomenon is that there is no irrigation load during this period, the overall load demand of the system decreases, and the abandoned energy increases. The CES chooses to store part of the abandoned energy. At the same time, the SOC of the energy storage device is close to saturation, so it enters a small amount of charging mode during the period of 12:00–13:00 to maintain battery health. During the period of 14:00–20:00, the energy storage continues to discharge. At this stage, the system’s cooling, heating, and electricity loads are all at peak, and the wind and solar resources are fully absorbed. The energy storage discharge helps to meet the peak load demand and reduce the pressure of external power purchase. Entering the nighttime period (20:00–23:00), wind power resources are abundant again, the load is low, and the energy storage device resumes charging, further improving the new energy consumption capacity of the CES and reserving sufficient electricity for the next dispatch cycle.
By comparing the energy storage operation characteristics on typical summer and winter days, it is evident that both the amount and frequency of energy storage charging and discharging are significantly higher in summer than in winter. This discrepancy is primarily due to the higher volatility of load demand during the summer months, combined with the weaker stability of wind and solar resources, particularly wind power. As a result, energy storage devices are required to charge and discharge more frequently in order to balance the load. In contrast, during the winter, wind power resources are more abundant, and the load demand is relatively stable. Consequently, the CES relies less on energy storage for electricity procurement, leading to a reduction in the frequency of charging and discharging events.
Overall, the integration of energy storage devices into the CES system has significantly enhanced the degree of low carbonization. The energy storage system is capable of flexibly charging and discharging in response to fluctuations in load demand and electricity market prices, which not only reduces reliance on external electricity sources but also mitigates the impact of peak load on the system. By capturing and storing wind and solar surplus energy, the system reduces renewable energy waste while simultaneously improving its economic performance. The real-time responsiveness of the energy storage device allows the CES to effectively manage the volatility and uncertainty associated with wind and solar power generation, optimizing resource utilization and boosting overall system efficiency.
5.3.5. Analysis of the Results of Scenario 4
Building upon the introduction of energy storage in Scenario 3, Scenario 4 introduces a high-level water tower, which is integrated with a drip irrigation system to fulfill irrigation requirements. The high-level water tower operates by using a water pump to store water during periods when the system energy supply is adequate, and releases water during irrigation periods. This coordinated operation with drip irrigation ensures efficient irrigation water supply. The scheduling results for Scenario 4 are presented in
Table 9. Compared to Scenario 3, the degree of low carbonization and economic benefits of the CES on a typical summer day are 4.32% and 2.18% higher, respectively, while on a typical winter day, the degree of low-carbonization and economic benefits are 3.94% and 3.34% higher. Notably, the low-carbonization degree and system economic benefits for a typical winter day exceed those of a typical summer day.
The main costs of the CES during the dispatching cycle, after the introduction of the high-level water tower, are shown in
Table 10. The integration of the high-level water tower significantly improves the energy utilization rate of the CES. As a result, the cost of purchasing electricity from the rural power grid during the entire dispatching cycle of the CES on typical days in both summer and winter is reduced to zero. The cost of purchasing electricity from energy storage amounts to CNY 183.95 in summer and CNY 115.6 in winter, both of which are substantially lower than the electricity purchase costs from energy storage in Scenario 3. This reduction is attributed to the high-level water tower’s ability to decrease the frequency and volume of energy storage charging. Additionally, the water release for irrigation from the high-level water tower reduces the CES’s reliance on electricity from energy storage, further lowering the overall electricity purchase costs. Despite this, the overall load demand for various energy types on typical summer days remains high, which results in a relatively higher cost in summer. Consequently, the system’s economic benefits are slightly lower in summer than in winter.
Figure 17 shows the satisfaction of irrigation load demand in summer and winter and the optimization results of irrigation load and compares the energy abandonment of wind and solar units in summer.
Figure 17.
Irrigation energy consumption and clean energy consumption results.
Figure 17.
Irrigation energy consumption and clean energy consumption results.
The consumption of clean energy on typical days in summer and winter in Scenario 4 is shown in
Figure 17. As illustrated in
Figure 17a,b, the CES no longer purchases electricity from the rural grid to meet the irrigation load on typical days in both summer and winter. This is due to the high-level water tower’s water storage and drainage irrigation method, which fully satisfies the irrigation demand, thereby eliminating the need for electricity purchases from the rural grid. When comparing
Figure 17 with
Figure 15, which represents Scenario 3 where energy storage is introduced, it can be observed that the total amount of wind and solar energy abandonment on typical days in both summer and winter is lower in Scenario 4. This improvement is because the high-level water tower utilizes periods of high wind and solar energy abandonment to pump and store water. During irrigation periods, the water tower releases water to meet the irrigation demand, thus reducing the electricity load required for drip irrigation. This approach not only decreases the reliance on electricity but also enhances the utilization of wind and solar resources, leading to improved low carbonization of the system.
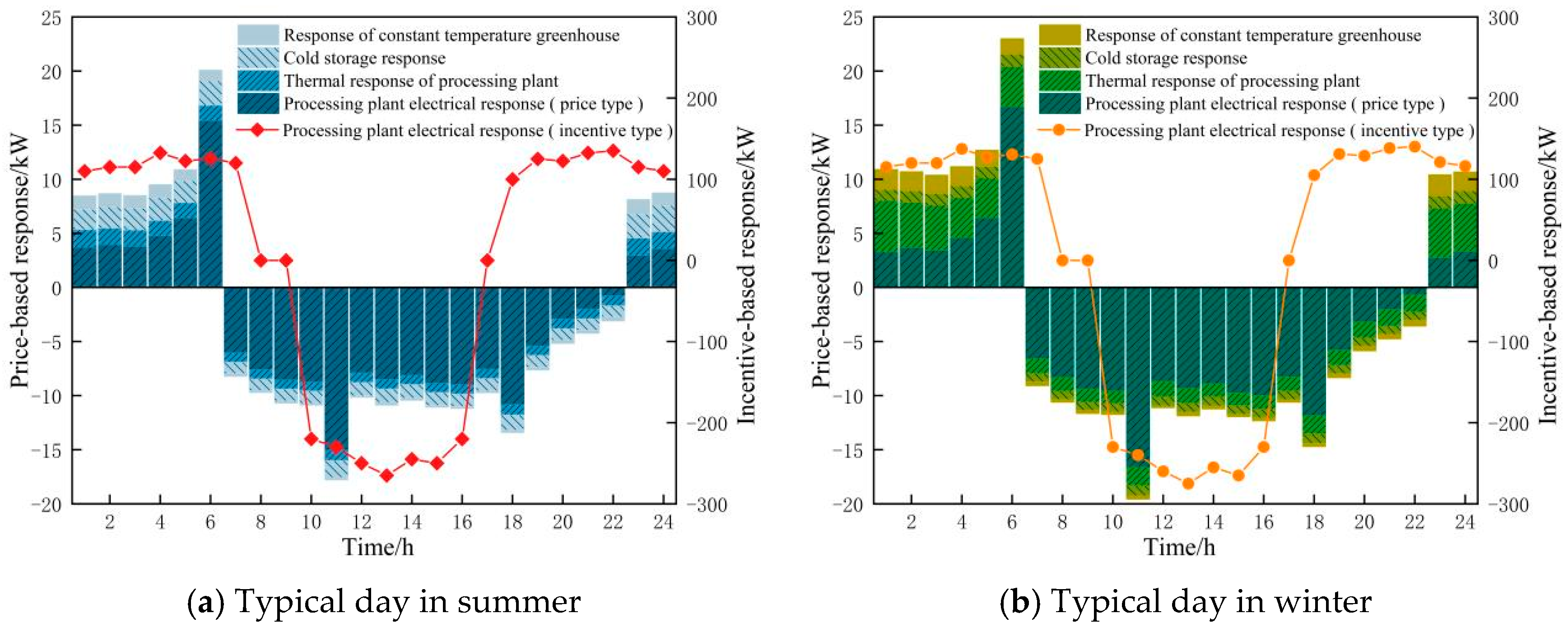
Figure 18 summarizes the response of various production loads in summer and winter under different participation methods.
Figure 18.
Production load response scheme.
Figure 18.
Production load response scheme.
In the summer, the load response is more pronounced during the 8:00–18:00 period, primarily due to the high daytime temperatures, which lead to increased cooling demand for cold storage and constant-temperature greenhouses. Additionally, the power load of the processing plant is also influenced by temperature fluctuations and production demands. In terms of price response, cold storage exhibits a more significant response during the day, as it increases electricity consumption to maintain the required temperature, while reducing load during periods of higher electricity prices (8:00–10:00, 14:00–16:00). Moreover, the incentive response is more active during the day in summer, particularly around 14:00 when the power load of the processing plant is most influenced by the incentive-based response. The price response of the processing plant’s power load is more substantial during the 6:00 and 11:00 periods, as the electricity prices in these periods are the lowest and highest, respectively, making the response more noticeable.
The load response in winter exhibits distinct characteristics compared to summer. The price response during the day is not as pronounced as in summer, and there is an increase in load during the night (18:00–24:00). This is primarily due to the lower temperatures at night in winter, which necessitate an increase in the heat load of constant temperature greenhouses and cold storage to maintain a stable temperature. Furthermore, the incentive response is more noticeable during the morning and evening peak periods. Specifically, the processing plant shows a larger response around 6:00 in the morning and 18:00 in the evening, helping to alleviate the morning and evening peak load demand. Comparing
Figure 18a,b, it is evident that the cooling load demand of cold storage on a typical summer day is higher than on a typical winter day, resulting in a greater cooling load response in summer. Conversely, the heating load required by the agricultural product processing plant on a typical winter day exceeds that of a typical summer day, so the heat load response of the processing plant in winter is also higher than in summer.
The constant-temperature greenhouse exhibits load response in both seasons, though the heat load demand is more pronounced in winter to maintain the necessary temperature for plant growth. The price-response strategy reduces energy consumption during the day and supplements it during the low electricity price period at night. The response pattern of cold storage differs significantly between summer and winter. In summer, the cooling demand during the day is higher, so the load response of cold storage is mainly concentrated during periods of low electricity prices, with the electricity price used as an incentive to increase the load. In winter, due to the lower ambient temperature, the load demand of cold storage decreases, leading to a reduced response intensity. The response of the processing plant is influenced by both price and incentive factors, displaying a diurnal periodic fluctuation. In summer, the power load response of the processing plant is more concentrated during the daytime, while in winter, it is primarily guided by incentives during the morning and evening, offering greater flexibility in its response.
It can be observed that the production load response strategies in both summer and winter effectively contribute to reducing peak power demand, smoothing the load curve and alleviating the operating pressure on the power grid. By optimizing electricity usage during low-electricity-price periods and minimizing consumption during high-price periods, this load response mechanism enhances the economic efficiency of the system. Additionally, the role of incentive-based responses is particularly significant during critical periods, further improving the effectiveness of load adjustments and adapting to seasonal variations. The implementation of this load response scheme aligns with the goal of promoting the consumption of clean energy. By increasing the load during low-electricity-price periods, the system maximizes the utilization of renewable energy and reduces reliance on rural power grids. Furthermore, the incentive response helps to guide the power consumption of the processing plant during periods of high wind and solar power generation, thereby enhancing the efficiency of clean energy use. These response schemes are tailored to the specific characteristics of rural loads, developing practical and feasible strategies based on their particular load demands. In contrast to the general approach in the literature [
17], which typically categorizes loads as simple electric loads for demand response, this approach is more practical and better suited to the unique conditions of rural areas.
Figure 19 illustrates the operating status of the high-level water tower and the irrigation water supply situation, depicting the fulfillment of irrigation load demands in both summer and winter. It also provides a detailed view of the operational status and water storage capacity of the high-level water tower during each period. This visual representation showcases how the high-level water tower effectively meets the irrigation needs by utilizing stored water during peak irrigation periods, thus optimizing water usage while reducing the dependency on electricity for irrigation purposes. The data also highlight the tower’s performance across different seasons, reflecting its contribution to improving energy utilization and system efficiency.
Figure 19.
High-level water tower operation status and irrigation water supply.
Figure 19.
High-level water tower operation status and irrigation water supply.
As shown in
Figure 19a, during a typical summer day, the high-level water tower operates with a low flow rate, performing small-scale pumping from 1:00 to 7:00 to replenish the water level. During the irrigation periods of 9:00 to 10:00, 14:00 to 15:00, and 17:00 to 18:00, the water tower discharges water to meet the irrigation demand. However, the water supply from the water tower during these periods does not fully satisfy the irrigation load, and additional irrigation demand is partially supplemented by drip irrigation. Additionally, the pumping volume of the water tower increases significantly during the 12:00 and 22:00 periods due to low electricity prices, which helps to reduce the operating costs of the water pump. Moreover, at the 22:00 period, abundant wind power abandonment occurs within the CES system, and the water tower’s pumping operation effectively utilizes this low-cost clean energy to store water for subsequent irrigation needs.
As shown in
Figure 19b, the amount of water pumped and drained by the high-level water tower on a typical winter day is lower than that on a typical summer day. During a typical winter day, the water tower continuously pumps a small amount of water from 1:00 to 7:00, drains water from 14:00 to 18:00 to meet irrigation needs, and pumps water until the water tower is full from 20:00 to 24:00. These operations are planned considering the abandonment of wind and solar energy and the electricity costs in each period. The operation strategy of the high-level water tower depends on the dynamic changes in electricity prices and the availability of wind and solar energy. By storing water during low-electricity-price periods, the system effectively utilizes wind and solar energy abandonment and reduces energy waste. On the other hand, draining water for irrigation during high-electricity-price periods not only satisfies the irrigation demand but also helps to avoid increased costs during peak periods. This strategy optimizes the efficiency of resource utilization, enhances the absorption rate of clean energy in the system, and ultimately brings significant economic benefits to the CES system.
Figure 20 illustrates the charging, discharging, and state of charge of the energy storage system at different times of day during both summer and winter and compares the operational differences between the two seasons.
Figure 20.
Energy storage operation status.
Figure 20.
Energy storage operation status.
Figure 20 shows the different response strategies of the energy storage system in summer and winter. In summer, the energy storage system balances the load by charging during low-load periods and discharging during high-load periods, reducing the need for electricity purchases. In winter, the system’s reliance on energy storage decreases due to the abundance of wind power resources. In Scenario 4, where a high-level water tower is introduced, the energy storage system is further optimized, reducing electricity purchase costs and increasing the absorption of clean energy.
Figure 20a shows that the energy storage system performs minimal charging operations from early morning to morning in summer (3:00–10:00), mainly due to low load demand at night and surplus wind and solar resources. The system charges during this period to provide power reserves for subsequent high-load periods. From morning to noon (11:00–12:00), the system exhibits alternating charging and discharging behavior, reflecting the volatility of electricity loads during this time. Around 11:00, the load is high, and the system relies on energy storage to balance the short-term power gap. At 12:00, the irrigation load temporarily disappears, increasing the amount of abandoned energy, which the energy storage system utilizes to charge. Simultaneously, the water tower pumps and stores a large amount of water, making full use of excess electricity for peak shaving and valley filling. During the evening peak period (18:00–19:00), the system load demand peaks for the day. With wind and solar resources nearly depleted, the energy storage system discharges a large amount to supplement the load demand and alleviate system pressure, ensuring stable electricity supply. During the night period (20:00–24:00), as the load demand gradually decreases and abandoned wind and solar energy increases, the energy storage system charges to utilize low-cost excess clean energy. Additionally, the high-level water tower stores water during this time to prepare for future demand. This charging and discharging strategy in summer enables flexible response during peak load periods and reserves electricity during valley periods, optimizing the system’s economic benefits.
As shown in
Figure 20b, the overall charge and discharge volume decreases in winter, primarily due to the relatively abundant wind power resources. The output of wind power can better meet load demand, reducing the need for the CES system to purchase electricity from energy storage aggregators. Compared to summer, the energy storage system in winter has a reduced charging period at night, as wind resources are more stable, allowing the system to rely more directly on wind power during the day, thereby reducing the need for charging. At the same time, the increase in load demand during winter has limited the discharge demand of the energy storage system during the evening peak, reflecting the change in reliance on energy storage at different times. In comparison to Scenario 3, Scenario 4, which introduces a high-level water tower, demonstrates a significant optimization of energy storage. The high-level water tower allows the CES system to store excess clean energy during low-electricity-price periods and release it when irrigation loads occur, providing auxiliary support to the system. This configuration improves the clean energy utilization rate and reduces the need for the CES to purchase electricity from energy storage aggregators. High-level water towers not only reduce the frequency of energy storage system charging and discharging but also decrease the cost of electricity purchases by regulating part of the irrigation load through water, thus improving the economic benefits of the CES. Additionally, due to the water tower’s regulation capacity, the energy storage system can reduce deep discharges, extend battery life, and further lower operating costs.
Based on the above analysis, in terms of carbon emission reduction, the low-carbonization degree in both summer and winter of the baseline scenario is not negative. After the introduction of the CES, the low-carbonization degree gradually increases and decreases with the expansion of system considerations. Among these, Scenario 2 performs better than Scenario 1, with the low-carbonization degree on typical summer days increasing by 108%. Scenario 4 achieves the highest low-carbonization degree after the introduction of high-level water towers. Economically, the baseline scenario results in negative returns, while Scenarios 1 and 2 yield lower returns. Scenario 3 shows a significant improvement over Scenario 2, and Scenario 4 maximizes economic benefits. Therefore, the optimization plan in Scenario 4 is prioritized.