Ultra-Low Frequency Oscillation in a Thermal Power System Induced by Doubly-Fed Induction Generators with Inertia Control

Abstract

Ultra-low frequency oscillation has been regarded as a typical instability issue in power systems consisting of hydro turbine synchronous generators due to the water hammer phenomenon. However, the increasing installation of renewable power generators gradually changes the stability mechanisms within multiple frequency bands. In this digest, a new kind of ultra-low frequency oscillation caused by doubly-fed induction generators (DFIGs) equipped with a df/dt controller in a thermal power generation system is introduced. To reveal the underlying mechanism, the motion equation model of the DFIG is constructed, and the simplified analytical model is proposed. The results show that when integrating a df/dt-controlled DFIG into a normal three-machine, nine-bus system, the damping ratio decreases to more than 0.2 when the virtual inertia parameter increases from 5 to 20, leading to a conflict between fast virtual inertial response and stability requirements. Other controllers related to active power regulation are also vital to stability. The frequency domain characteristics of the system are studied to illustrate the influence of key parameters on system stability. Finally, simulation verifications are conducted in MATLAB/Simulink.

1. Introduction

Ultra-low frequency, whose oscillation frequency (ULFO) is under 0.1 Hz, is an instability issue. This phenomenon is reported in Yunnan, Manitoba, Nordic power systems [1,2,3], and so on. The common point of these oscillation incidents is that the power systems have a high penetration of hydro turbines. The water hammer effect is considered the root cause of ULFO. Extensive efforts have been put into solving this problem. Reference [4] proposed a small-signal model for ultra-low frequency oscillations in hydroelectric units, and mechanistically analyzed the impacts of excitation regulation and a power system stabilizer (PSS) on ultra-low frequency oscillations in the system, identifying key influencing factors. Reference [5], through an analysis of hydro turbine governor damping characteristics, indicated that an excessively low ratio between proportional and integral parameters in governors could easily induce ultra-low frequency oscillations. Reference [6] examined the influence of governor dead-zone settings on ultra-low frequency oscillations. Reference [7] investigated the mechanism by which hydroelectric unit governor systems provide negative damping during oscillations, identifying governor parameters and water hammer effects as primary causes of oscillation induction.

These studies conducted modal analysis and influence factor investigations on ultra-low frequency oscillation issues in traditional power systems. Building upon this foundation, numerous studies have explored suppression measures for low-frequency oscillations in conventional power systems. Reference [8] suggested that ultra-low frequency oscillations could be suppressed by adjusting hydro turbine governor parameters, proposing a parameter design method based on structured singular value theory. Reference [9] developed an ultra-low frequency oscillation suppression method using governor additional damping control (GPSS). Reference [10] proposed a wide area detection method to adjust the operation mode of the governor of hydraulic turbines, and the governor can be disabled when necessary. Reference [11] proposed a proportional-resonant and lead–lag series power system stabilizer and utilized a deep reinforcement learning method to realize the parameter setting. Reference [12] employed a frequency-band partitioning control concept, extending the ultra-low frequency control range by adding low-pass branches to conventional PSS, thereby constructing a novel PSS control structure for ultra-low frequency oscillation suppression. It also proposed a robust parameter tuning algorithm considering frequency-band settings and system operational condition variations. Through an analysis of ultra-low frequency oscillation phenomena in a DC island system within the Yunnan Power Grid after asynchronous interconnection, a coordinated control method between governor systems and DC frequency controllers was presented.

With the continuous construction of renewable energy generation (REG), the stability characteristic has undergone significant evolution [13]. For ULFO issues, it is important to consider the impact of REG. Reference [14] investigated modeling and stability analysis of ultra-low frequency oscillation issues in wind-integrated power systems based on the conclusion of approximately unified system-wide frequency in ultra-low frequency bands and then constructed a unified frequency model for wind-integrated power systems. Reference [15] investigated the impact mechanism of inertia-controlled wind power on ultra-low frequency oscillations through small-signal modeling and root locus analysis while analyzing the influence of patterns of wind power parameters on such oscillations. Reference [16] investigated the operational mechanisms of different frequency control strategies on prime mover system damping variations and their impacts on frequency stability using damping torque analysis. However, the modeling only considered wind power frequency response components, omitting research on other electromechanical parts. Except for wind generation, photovoltaic generators can also be employed to suppress the ULFO by adding a lead–lag section in its control loop [17]. From these works, it can be concluded that REG can have a significant impact on the ULFO in hydro power systems.

However, since REG deeply influences the stability mechanism of the power system, it is unclear whether ULFO will exist in thermal power systems. In recent years, some ULFOs have occurred in systems with thermal power and wind power generation [18,19]; thus, this issue needs to be studied. This paper innovatively discovered that doubly-fed induction generators (DFIG) with df/dt virtual inertia control can induce ULFO in thermal power generation systems. By applying the average system frequency (ASF) model, a clear explanation is brought out. The main contribution of this paper is as follows:

(1)

The properties of the DFIG are depicted by the motion equation model, which can reasonably reflect the impact of controllers within the electromechanical timescale.

(2)

Based on the cognition that frequency waveforms are approximately equal during the ULFO process, a simplified analytical model is proposed by combining the motion equation model and the ASF model.

(3)

The ULFO mechanism is revealed through the perspective of the impact of DFIG equivalent inertia on system inertia.

(4)

The impact of key parameters on stability is analyzed through frequency domain characteristics.

The rest of this paper is organized as follows. In Section 2, the structure of the thermal power generator and the DFIG is introduced, and the motion equation models are established. In Section 3 the system model is constructed, and frequency domain analysis is conducted. The analysis is verified through simulation in Section 4, and the conclusions are drawn in Section 5.

2. Modeling of Generators

To investigate the studied issue, the model of the steam turbine-based synchronous generator and the doubly-fed induction generator should be established.

(a)

The model of the synchronous generator (SG)

The entire thermal power plant consists of a synchronous generator, an excitation system, a governor, and a reheat turbine. Since the voltage regulation is a local control, and the frequency variation in the whole system is approximately the same, the excitation system is neglected in the modeling process. The block diagram of the governor and the steam turbine is shown in Figure 1a,b.

Neglecting the impact of the dead band and limiter, the transfer function of the governor is

$$G_{\mathrm{GS}}\left(s\right)=-{\displaystyle \frac{1}{R\left(1+s{T}_1\right)\left(1+s{T}_3\right)}}$$

(1)

The transfer function of the steam turbine is

$$G_{\mathrm{TB}}\left(s\right)={\displaystyle \frac{1}{1+s{T}_{\mathrm{CH}}}}\left[{\displaystyle \frac{F_{\mathrm{LP}}+F_{\mathrm{IP}}\left(1+s{T}_{\mathrm{CO}}\right)}{\left(1+s{T}_{\mathrm{CO}}\right)\left(1+s{T}_{\mathrm{RH}}\right)}}+F_{\mathrm{HP}}{\displaystyle \frac{1+s\left(1+\lambda \right)T_{\mathrm{RH}}}{1+s{T}_{\mathrm{RH}}}}\right]$$

(2)

Denoting the inertia of the rotor by H, the motion equation model of the SG is

$$G_{\mathrm{SG}}\left(s\right)={\displaystyle \frac{1}{2H_{\mathrm{SG}}s-G_{\mathrm{GS}}\left(s\right)G_{\mathrm{TB}}\left(s\right)}}$$

(3)

(b)

The model of the DFIG

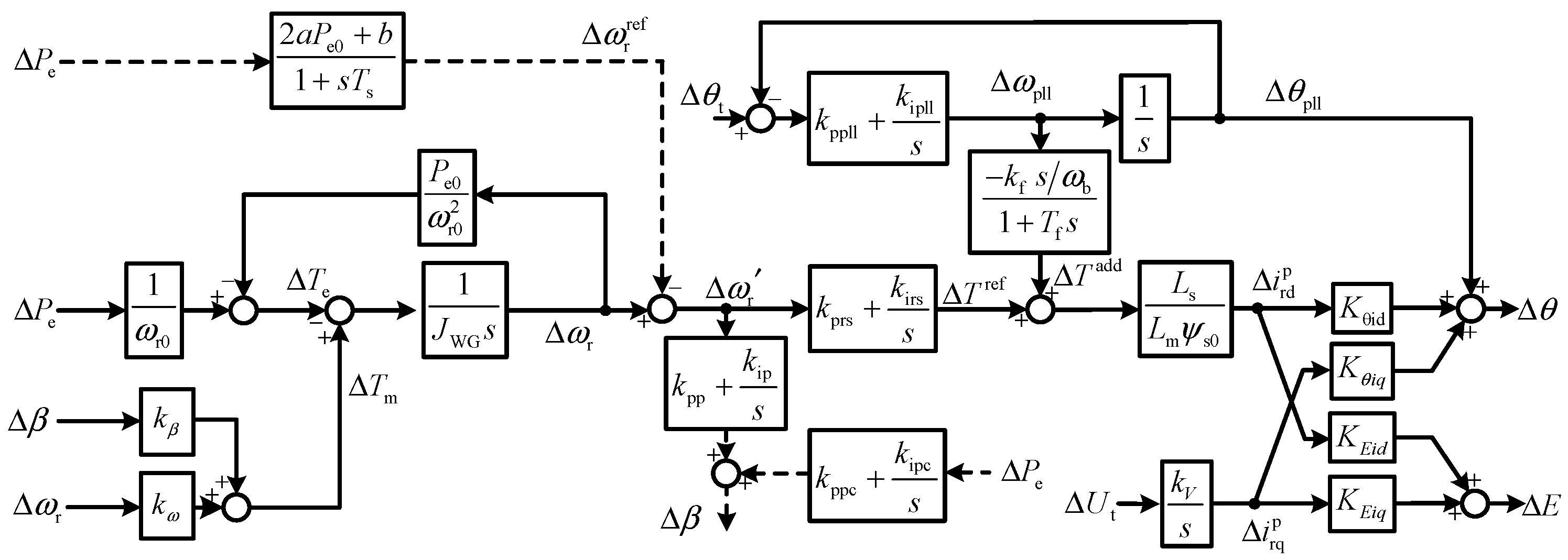
A DFIG is a complex piece of equipment combining both mechanical and electrical sections. The characteristics of the frequency band, maximum power point tracking (MPPT), rotor, pitch control, pitch compensation control, PLL, and terminal voltage control are preserved, while the dynamics of the current controller and the grid-side converter are ignored.

The MPPT relationship can be written as ${\omega }_{\mathrm{r}}^{\mathrm{r}\mathrm{e}\mathrm{f}}$ = ${aP}_{\mathrm{e}}^2$ + bP_e + c, where ${\omega }_{\mathrm{r}}^{\mathrm{r}\mathrm{e}\mathrm{f}}$ is the rotor speed reference value and P_e is the stator electromagnetic power, and the linearized form of the MPPT section is

$$\Delta {\omega }_{\mathrm{r}}^{\mathrm{ref}}={\displaystyle \frac{2a{P}_{\mathrm{e}0}+b}{1+s{T}_{\mathrm{s}}}}$$

(4)

where T_s is the time constant of the MPPT low-pass filter, and the subscript 0 represents the steady-state value.

When the wind speed is constant, the rotor dynamics can be represented by the following equation:

$$\left\{\begin{array}{l}\Delta T_{\mathrm{m}}=k_{\beta }\Delta \beta +k_{\omega }\Delta {\omega }_{\mathrm{r}}\\ \Delta T_{\mathrm{e}}={\displaystyle \frac{1}{{\omega }_{\mathrm{r}0}}}\Delta P_{\mathrm{e}}-{\displaystyle \frac{P_{\mathrm{e}0}}{{\omega }_{\mathrm{r}0}^2}}\Delta {\omega }_{\mathrm{r}}\\ \Delta {\omega }_{\mathrm{r}}={\displaystyle \frac{1}{J_{{\mathrm{WG}}^s}}}\left(\Delta T_{\mathrm{m}}-\Delta T_{\mathrm{e}}\right)\end{array}\right.$$

(5)

where Δβ is the pitch angle, ω_r is the rotor speed, J_WG is the rotor inertia, and k_β and k_ω are derived from the aerodynamic function of the wind turbine.

Denoting the proportional and integral parameter of the phase-locked loop (PLL) by K_ppll and K_ipll, the actual phase of the terminal voltage by θ_t, the frequency and phase output by the PLL by ω_pll and θ_pll, the linearized form of the PLL can be expressed as

$$\left\{\begin{array}{l}\Delta {\omega }_{\mathrm{pll}}=\left(k_{\mathrm{ppll}}+{\displaystyle \frac{k_{\mathrm{ipll}}}{s}}\right)\left(\Delta {\theta }_{\mathrm{t}}-\Delta {\theta }_{\mathrm{pll}}\right)\\ \Delta {\theta }_{\mathrm{pll}}={\displaystyle \frac{1}{s}}\Delta {\omega }_{\mathrm{pll}}\end{array}\right.$$

(6)

The df/dt controller has been proposed to enhance the inertial response of REG [20]. Denoting the inertia and time constant of the df/dt controller by k_f and T_f, the additional torque by T_add, and the nominal angular frequency of the power system by ω_b, the linearized function of the df/dt controller can be expressed as

$$\Delta T_{\mathrm{add}}=-{\displaystyle \frac{k_{\mathrm{f}}s}{{\omega }_{\mathrm{b}}\left(1+T_{\mathrm{f}}s\right)}}\Delta {\omega }_{\mathrm{pll}}$$

(7)

Denoting the PI parameter of the speed controller by k_prs and k_irs, the PI parameter of the pitch controller by k_pp and k_ip, and the PI parameter of the pitch compensation controller by k_ppc and k_ipc, the linearized functions of the three controllers are

$$\Delta T^{\mathrm{ref}}=\left(k_{\mathrm{prs}}+{\displaystyle \frac{k_{\mathrm{irs}}}{s}}\right)\left(\Delta {\omega }_{\mathrm{r}}-\Delta {\omega }_{\mathrm{r}}^{\mathrm{ref}}\right)$$

(8)

$$\Delta \beta ={\displaystyle \frac{1}{1+T_{\mathrm{p}}s}}\left[\left(k_{\mathrm{pp}}+{\displaystyle \frac{k_{\mathrm{ip}}}{s}}\right)\left(\Delta {\omega }_{\mathrm{r}}-\Delta {\omega }_{\mathrm{r}}^{\mathrm{ref}}\right)+\left(k_{\mathrm{ppc}}+{\displaystyle \frac{k_{\mathrm{ipc}}}{s}}\right)\Delta P_{\mathrm{e}}\right]$$

(9)

where T_p is the time constant of the pitch controller low-pass filter.

Since the dynamics of the current controller are ignored, the current references are regarded as equal to their actual values. Denoting the integral parameter of the terminal voltage control by k_V, the stator and mutual inductance by L_s and L_m, and the stator flux by ψ_s, the dq-axis current can be calculated as follows:

$$\left\{\begin{array}{l}\Delta i_{\mathrm{rd}}^{\mathrm{p}}={\displaystyle \frac{L_{\mathrm{s}}}{L_{\mathrm{m}}{\psi }_{\mathrm{s}0}}}\left(\Delta T_{\mathrm{add}}+\Delta T^{\mathrm{ref}}\right)\\ \Delta i_{\mathrm{rq}}^{\mathrm{p}}={\displaystyle \frac{k_{\mathrm{V}}}{s}}\Delta U_{\mathrm{t}}\end{array}\right.$$

(10)

where U_t is the amplitude of the terminal voltage, and the superscript p represents quantities in the PLL reference frame.

Similar to the SG, the interface of the DFIG to the grid is the internal voltage. Denoting the mutual reactance by X_m, the internal voltage E_d + jE_q can be expressed by (11) according to reference [21].

$$E_{\mathrm{d}}+j{E}_{\mathrm{q}}=j{X}_{\mathrm{m}}\left(i_{\mathrm{rd}}^{\mathrm{p}}+j{i}_{\mathrm{rq}}^{\mathrm{p}}\right)$$

(11)

The relationship between the rotor currents and the amplitude/phase of the internal voltage is algebraic, and is written as follows:

$$\left\{\begin{array}{l}\Delta \theta =K_{\mathsf{\theta }\mathrm{id}}\Delta i_{\mathrm{rd}}^{\mathrm{p}}+K_{\mathsf{\theta }\mathrm{iq}}\Delta i_{\mathrm{rq}}^{\mathrm{p}}\\ \Delta E=K_{\mathrm{Eid}}\Delta i_{\mathrm{rd}}^{\mathrm{p}}+K_{\mathrm{Eiq}}\Delta i_{\mathrm{rq}}^{\mathrm{p}}\end{array}\right.$$

(12)

where K_θid, K_θiq, K_Eid, and K_Eiq are linearization coefficients.

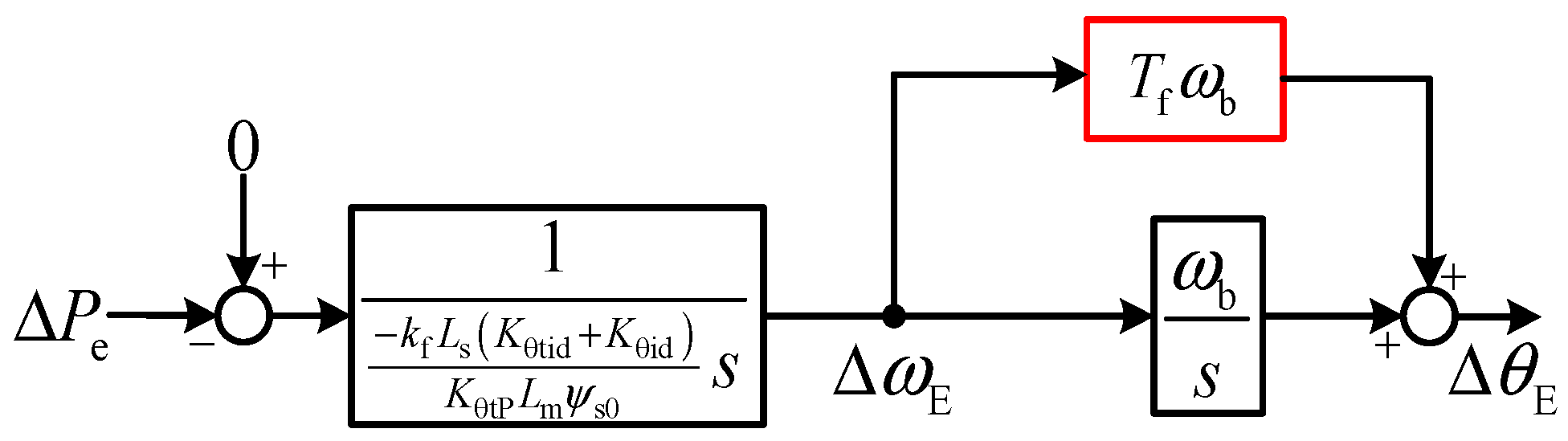
Combining (4)~(12), the linearized model of the DFIG is established, as shown in Figure 2.

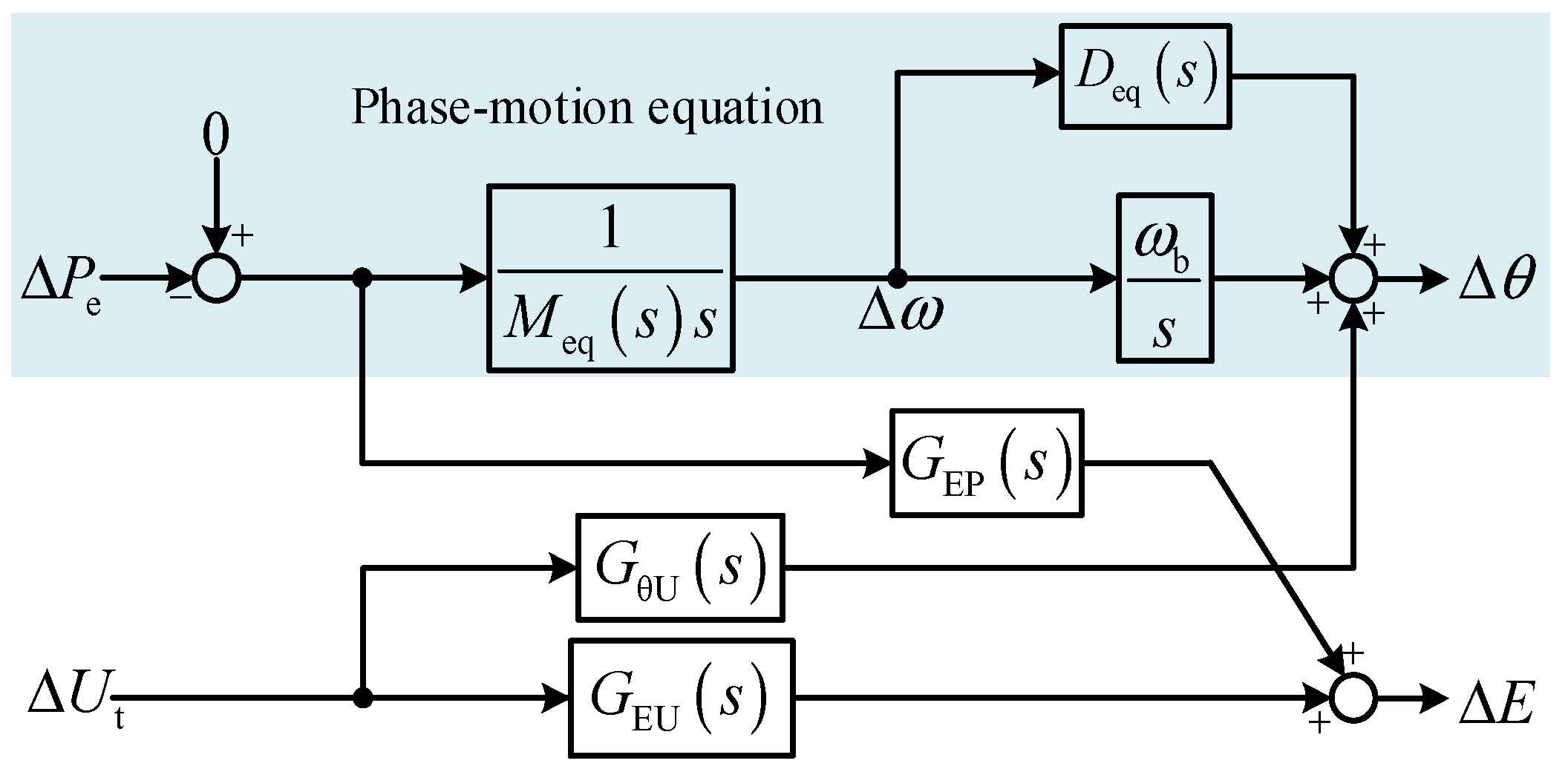
The linearized model of the DFIG can be reorganized in a form similar to the model of the SG [22,23]. To simplify the description, the motion equation model of the DFIG is directly given, as shown in Figure 3. M_eq(s) and D_eq(s) are called the equivalent inertia and damping of the DFIG.

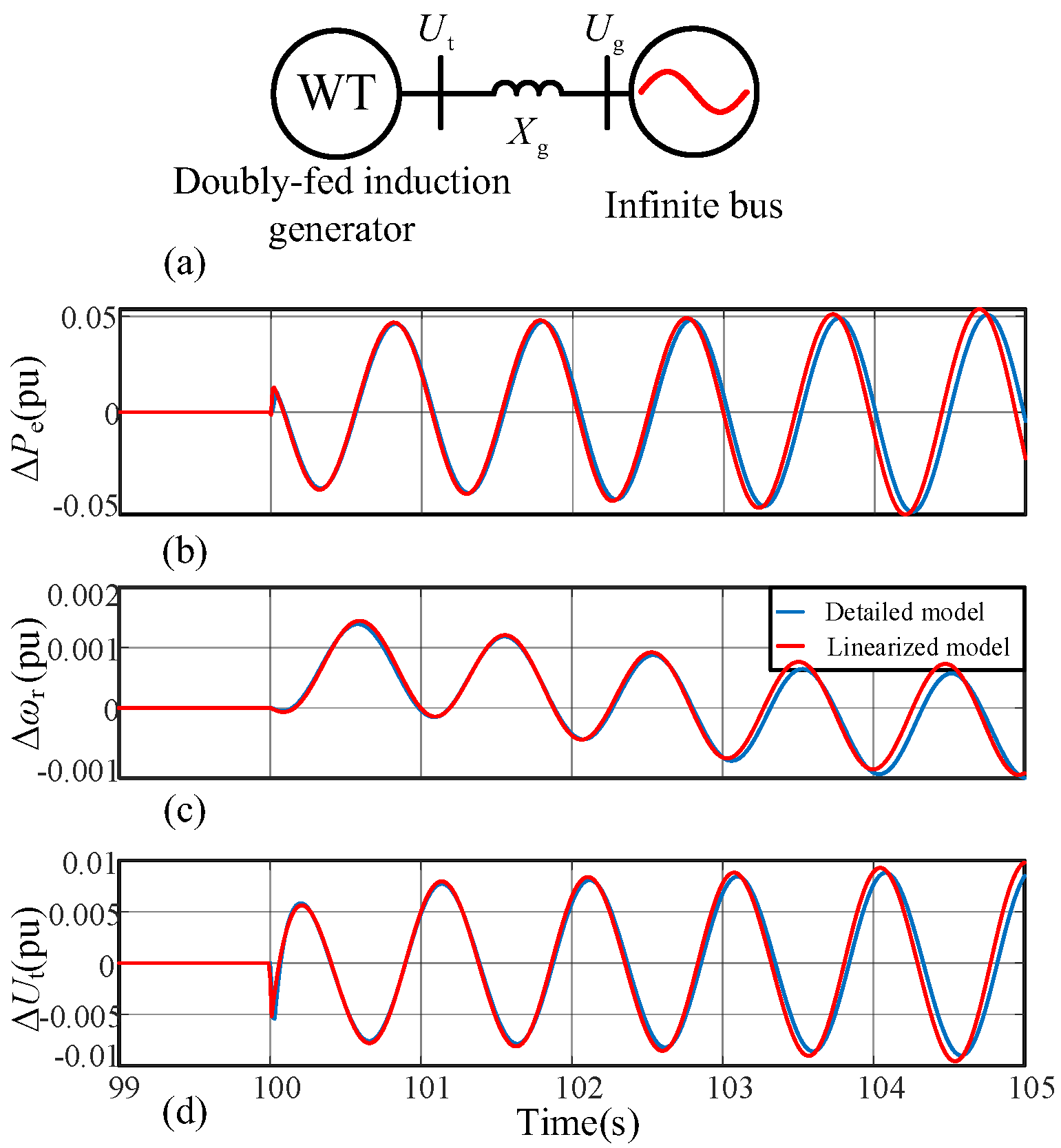
To verify the applicability of the proposed model for the DFIG, a single machine-infinite bus system is utilized, where a phase disturbance is added to the phase of the infinite bus. The response of the DFIG is shown in Figure 4. The results imply that the motion equation model is suitable for the ULFO study.

3. Mechanism Analysis

3.1. System Model

As stated in the previous section, the frequency waveforms of all devices during the ULFO tend to be the same; thus, the average system frequency model can be applied to derive a simple analytical model.

According to Figure 3, only the phase-motion equation branch is preserved during the system modeling process. The following quantity is defined in Equation (13):

$$M_{\mathrm{WT}}\left(s\right)={\displaystyle \frac{M_{\mathrm{eq}}\left(s\right)}{1+s{D}_{\mathrm{eq}}\left(s\right)/{\omega }_{\mathrm{b}}}}$$

(13)

The ASF model of the system can be represented by the block diagram shown in Figure 5, where $\overline{\omega }$ is the average frequency of the system, and G_GT(s) = −G_GS(s)G_TB(s).

3.2. Oscillation Mechanism

The oscillation mechanism can be revealed by analyzing the impact of M_WT(s) on the system inertia.

To provide a clear statement, it is first assumed that the speed control is very slow. In this case, the relationship between the unbalanced active power and internal voltage phase is shown in Figure 6. The relationship between ΔP_e and Δθ_E is not linked by integral sections. The existence of the term T_fω_b results in a proportional-integral relationship between the frequency and phase of the internal voltage. Thus, the equivalent inertia of the DFIG is not a constant. As shown in Figure 7, the equivalent inertia of the DFIG introduces a negative phase within the frequency band (0.1, 10) Hz; thus, the phase margin of the whole system is reduced, which increases the risk of ultra-low frequency oscillations.

Moreover, since the ULFO risk does not exist in a system consisting of only thermal power generators, it can be concluded that the negative phase introduced by the DFIG is very crucial for inducing the ULFO.

3.3. Key Influencing Parameters and Influence Trend

Every section that is contained in the phase-motion equation can have an impact on the stability. To conduct the quantitative analysis, the extended three-machine, nine-bus system is utilized, as shown in Figure 8. A DFIG-based wind farm is connected to the load 3 node through a transformer and a transmission line.

The open-loop transfer function of the system is defined by G_op(s), and the phase margin of the open-loop transfer function reflects the stability [24]. Its expression is as follows:

$$G_{\mathrm{op}}\left(s\right)={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{G}_{\mathrm{GT}i}\left(s\right)}}{2{\displaystyle \sum _{i=1}^n{H}_{\mathrm{SG}i}\left(s\right)s+M_{\mathrm{WT}}\left(s\right)s}}}$$

(14)

(a)

The impact of df/dt parameters on system stability

Decreasing the time constant T_f decreases the phase margin, illustrating that the stability deteriorates, as shown in Figure 9a. Increasing the virtual inertia k_f decreases the phase margin, as shown in Figure 9b, meaning that the system diverges more easily. The numerical results are shown in

Table 1. Damping ratio and oscillation frequency with different T_f.

Tf	Damping Ratio	Frequency (Hz)
20	0.613	0.0892
10	0.549	0.0873
5	0.428	0.0845
2	0.218	0.0838
1	0.105	0.0861
0.1	−0.0129	0.0912

and

Table 2. Damping ratio and oscillation frequency with different k_f.

kf	Damping Ratio	Frequency (Hz)
5	0.208	0.122
10	0.106	0.106
20	−0.0129	0.0912

.

(b)

The impact of speed control parameters on system stability

Several sets of speed control parameters were investigated. Since the speed control is a second-order section, the parameters shown in Figure 10a were selected to change the bandwidth. The phase margin first decreases and then increases, meaning the stability first weakens and then strengthens. The numerical results are shown in

Table 3. Damping ratio and oscillation frequency with different speed control bandwidth.

kprs, kirs	Damping Ratio	Frequency (Hz)
0.3, 0.006	0.408	0.0848
1, 0.067	0.285	0.0795
3, 0.6	−0.0129	0.0912
9, 5.4	0.278	0.128
30, 60	0.35	0.147

.

(c)

The impact of wind speed on system stability

As the wind speed changes, the operational region of the wind turbine switches, and the expression of M_WT(s) has a different expression, which may influence the stability. As shown in Figure 10b, within the MPPT region, with the wind speed increasing, the phase margin of the open-loop transfer function decreases, and the system stability becomes worse. Within the constant speed and constant power region, the phase margin increases with wind speed, and the stability is enhanced. The numerical results are shown in

Table 4. Damping ratio and oscillation frequency with different wind speeds.

Vw	Damping Ratio	Frequency (Hz)
9	0.0947	0.0998
10.5	0.0921	0.0923
11.5	0.159	0.0734
12	0.193	0.0737
13.5	−0.0129	0.0912
15	0.0311	0.0874
20	0.0684	0.0890

.

(d)

The impact of MPPT on system stability

When the wind turbine operates within the MPPT region, the electromagnetic and mechanical power are first filtered and then inputted into the MPPT calculation. Thus, the filter time constant can influence the stability. As shown in Figure 11a, the phase margin decreases with T_s, and the system becomes more unstable. The numerical results are shown in

Table 5. Damping ratio and oscillation frequency with different T_s.

Ts	Damping Ratio	Frequency (Hz)
1	0.251	0.113
2	0.18	0.11
5	0.0947	0.0998
10	0.0674	0.0914
20	0.0657	0.0853

.

(e)

The impact of the pitch control parameter on system stability

From Figure 11b, it can be seen that when the wind farm operates within the constant power region, the system becomes more stable with an increase in the pitch control parameter. The numerical results are shown in Table 5 and

Table 6. Damping ratio and oscillation frequency with different k_pp.

Kpp	Damping Ratio	Frequency (Hz)
100	−0.0603	0.0913
150	−0.0129	0.0912
200	0.0753	0.0823

.

(f)

The impact of the pitch compensation control parameter on system stability

The pitch compensation controller is a first-order section. The result in Figure 12 shows that when the bandwidth of the pitch compensation control increases, the system first becomes more unstable and then more stable. The numerical results are shown in

Table 7. Damping ratio and oscillation frequency with different pitch compensation control bandwidth.

kppc, kipc	Damping Ratio	Frequency (Hz)
0.3, 3	0.342	0.0829
1, 10	0.264	0.0772
3, 30	−0.0129	0.0912
9, 90	0.027	0.139
30, 300	0.156	0.152

.

4. Simulation Verification

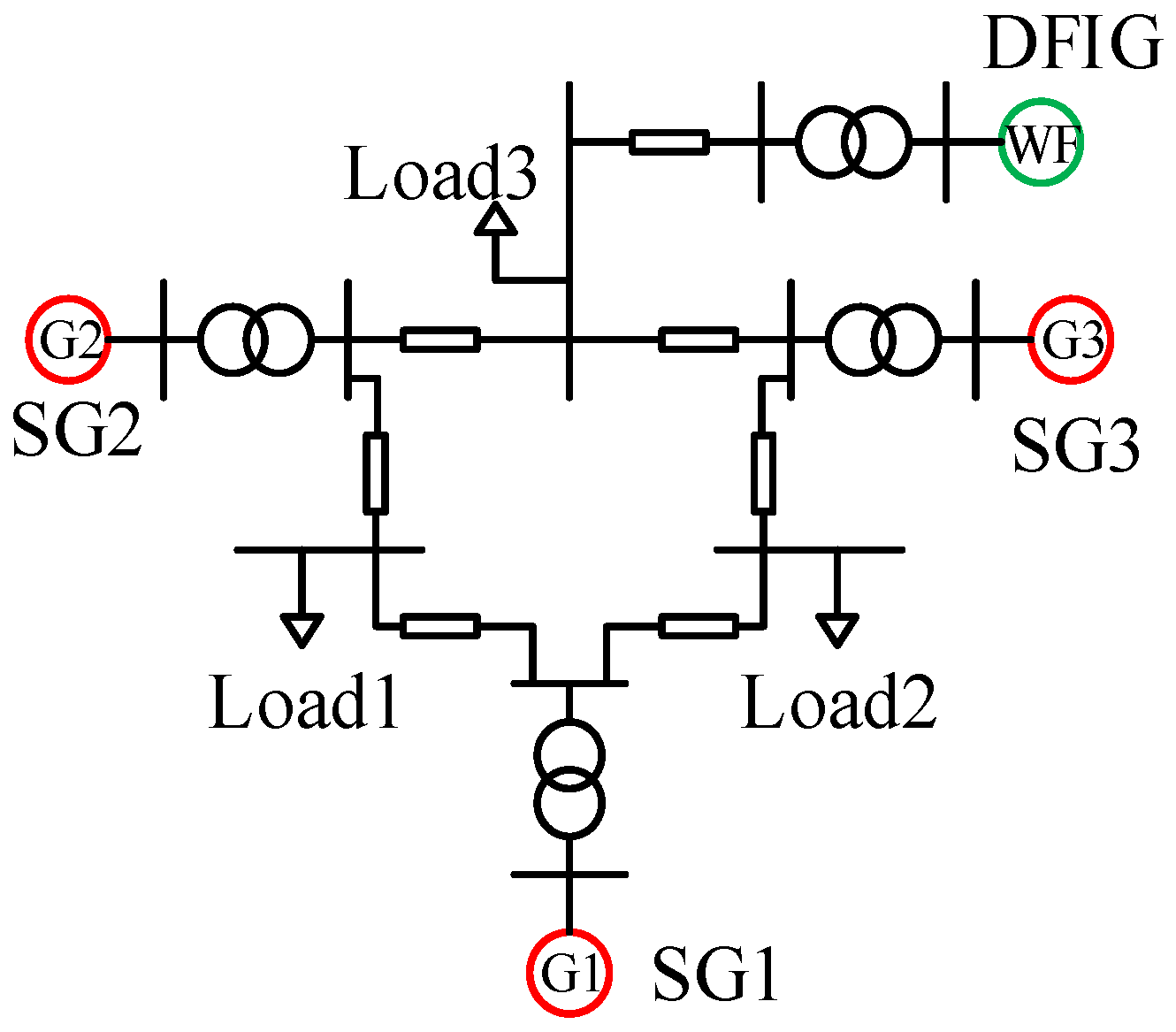
In order to verify the analysis in the previous section, simulations were conducted using MATLAB/Simulink R2021a. The studied system is identical to that shown in Figure 8.

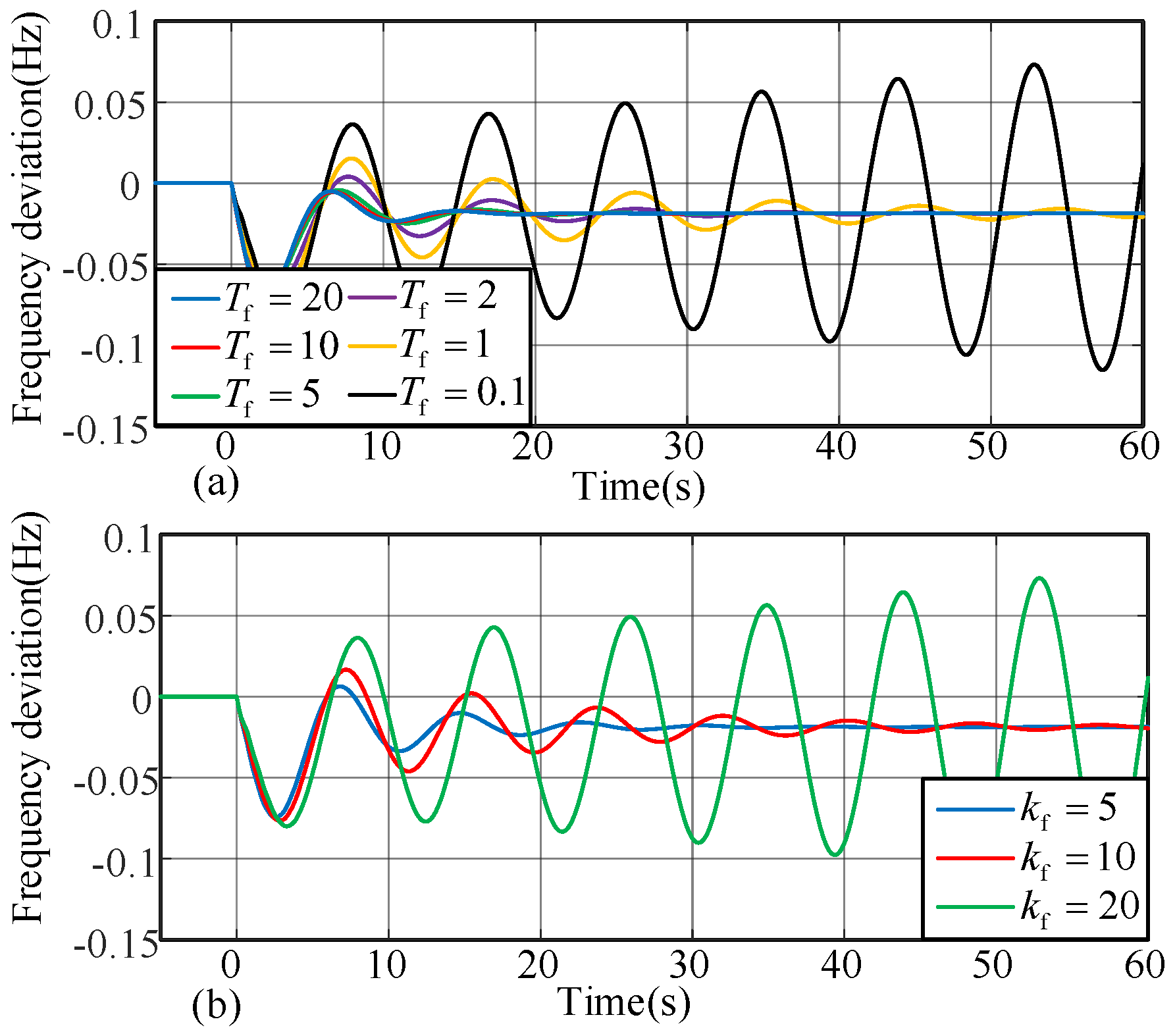
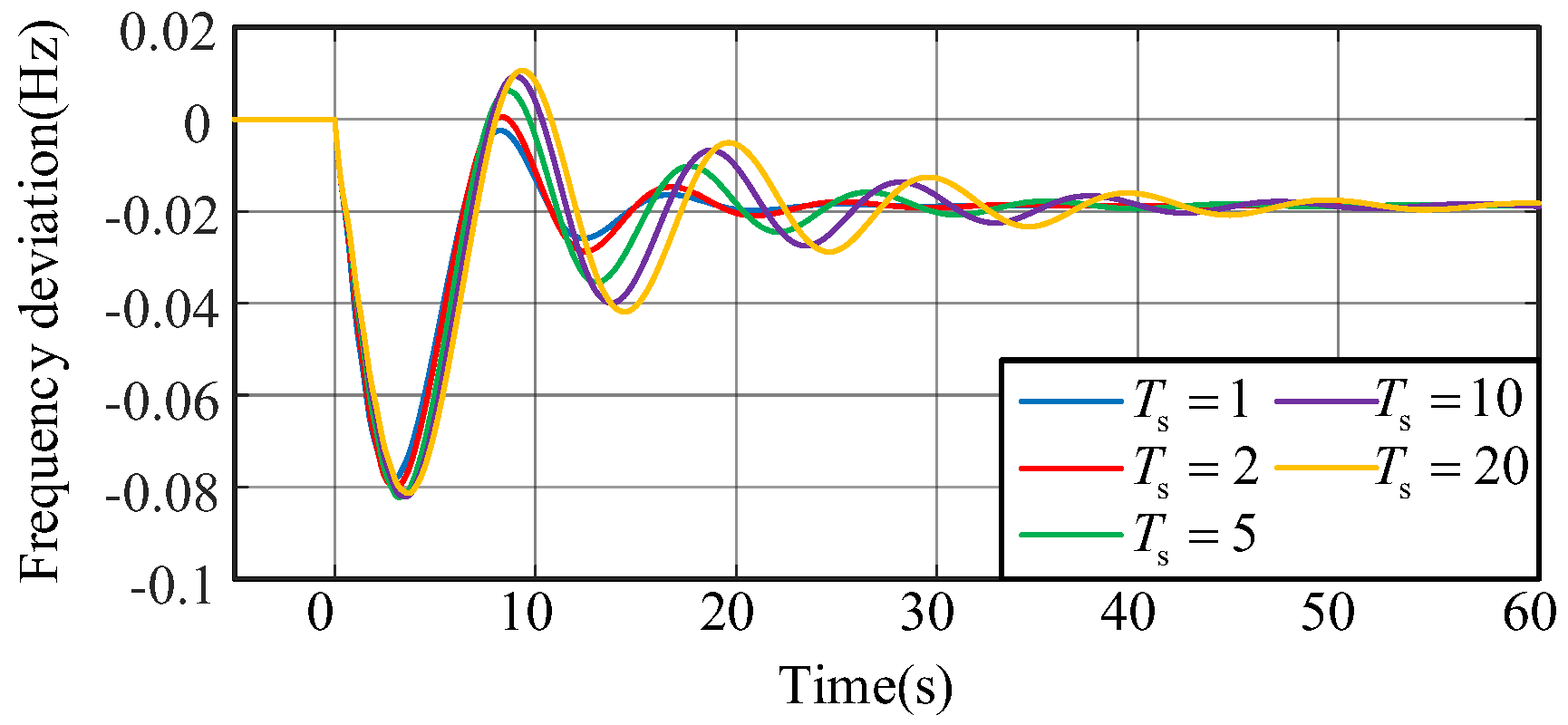
Figure 13 shows the simulation results when the time constant or the gain of the df/dt controller changes. It can be seen that the system is more stable with a larger time constant T_s and a smaller virtual inertia k_f.

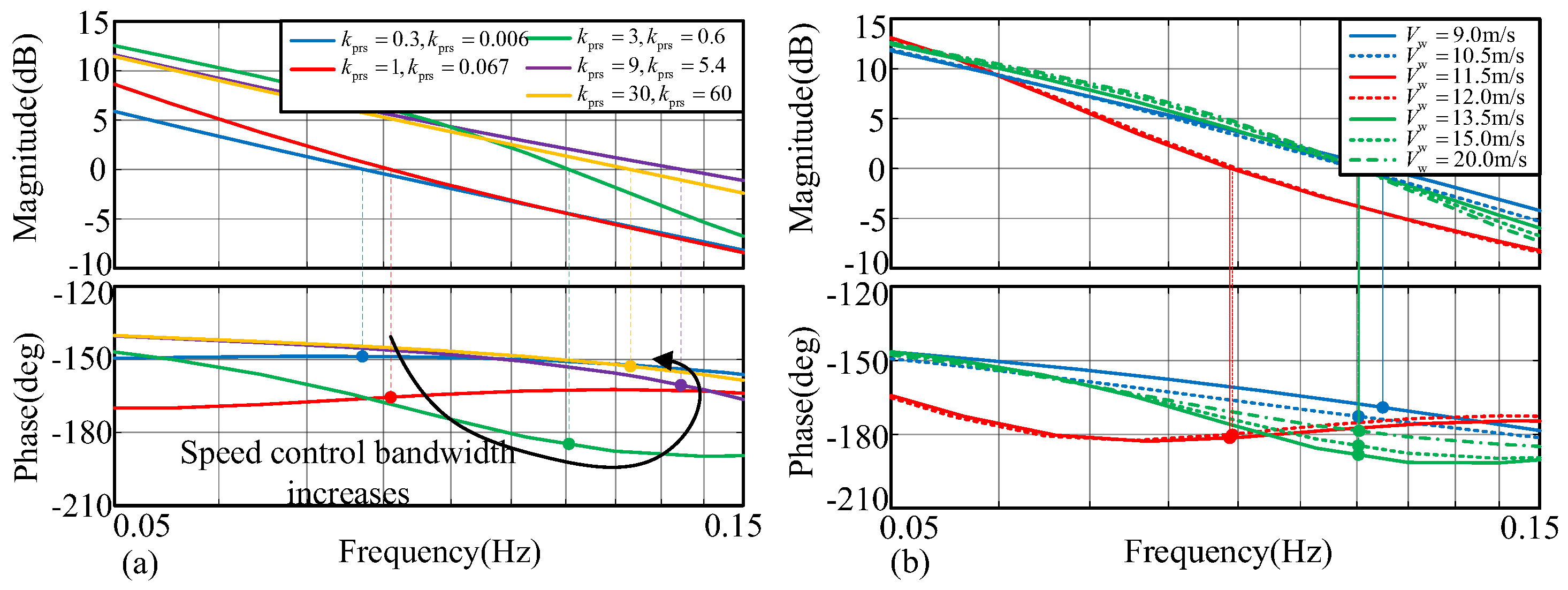
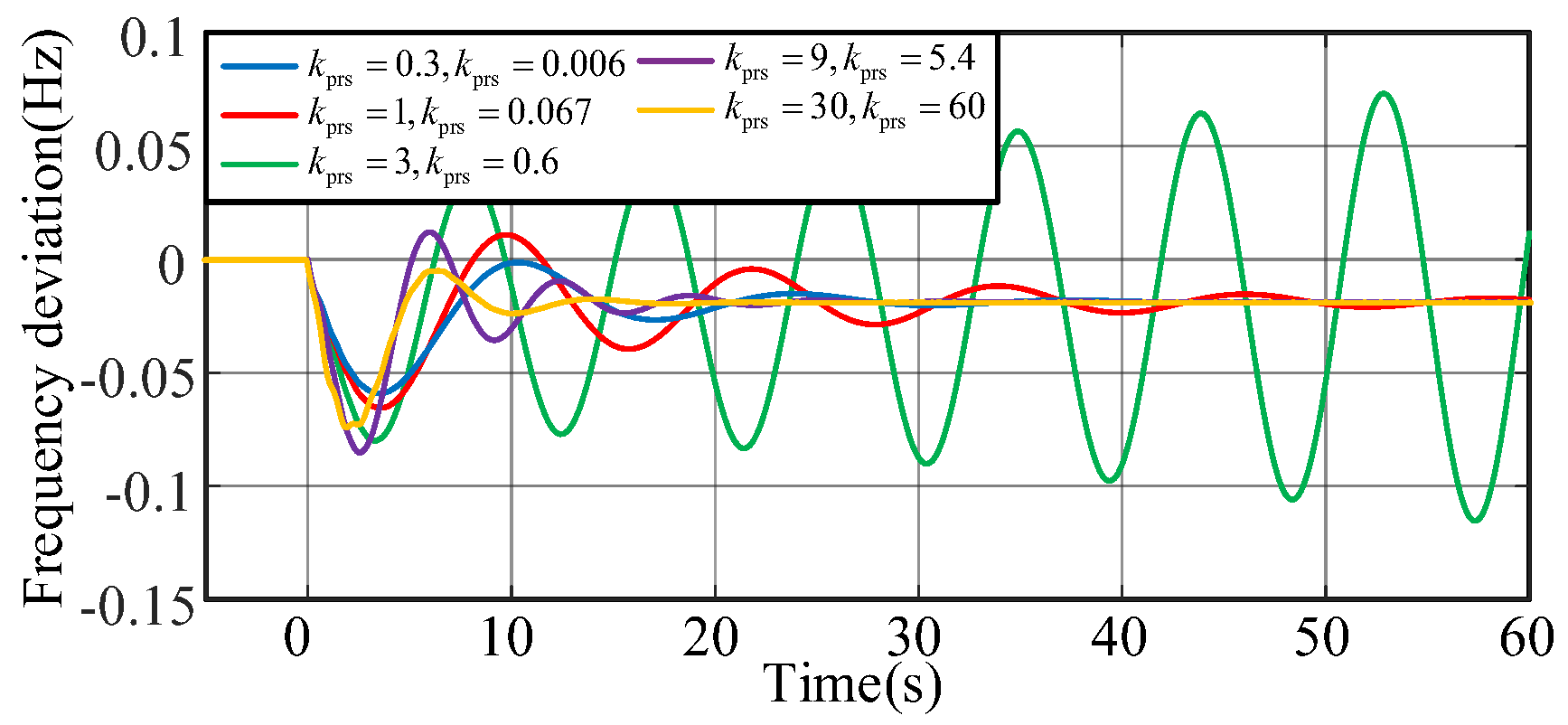
Figure 14 shows that the system becomes more unstable and then more stable when the bandwidth of the speed control increases.

Figure 15 shows the simulation results when the wind farm operates within different regions. When the wind speed increases, the power output of the wind farm is larger, and the system is more unstable, although the equivalent inertia of the DFIG varies.

Figure 16 illustrates that the system becomes more stable when the time constant of the low-pass filter of the MPPT increases.

When the pitch control parameter k_pp increases, the system becomes more stable, as shown in Figure 17.

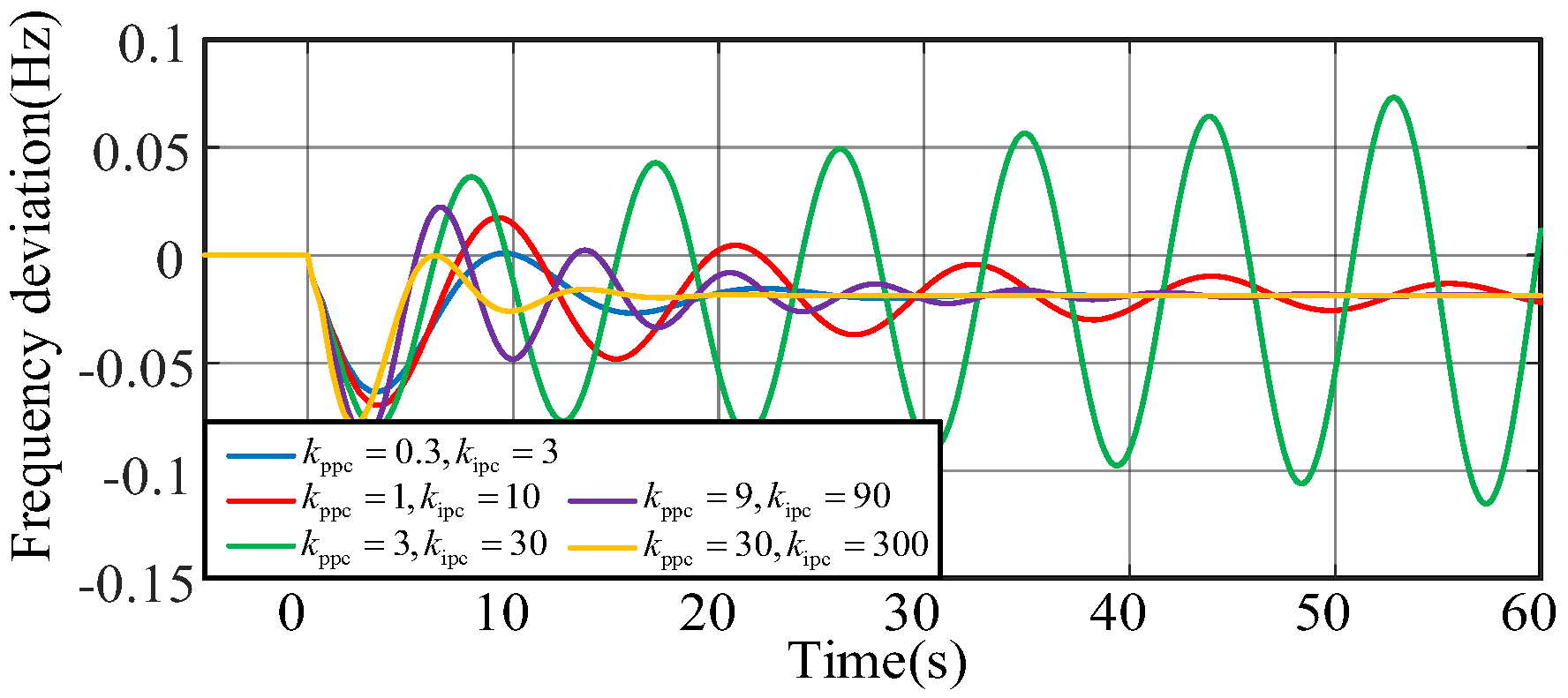
The influence of the bandwidth on pitch compensation control is shown in Figure 18. When the bandwidth increases, the system first becomes more unstable and then more stable.

The simulations above coincide with the analysis in Section 3, implying that the frequency domain analyses are correct.

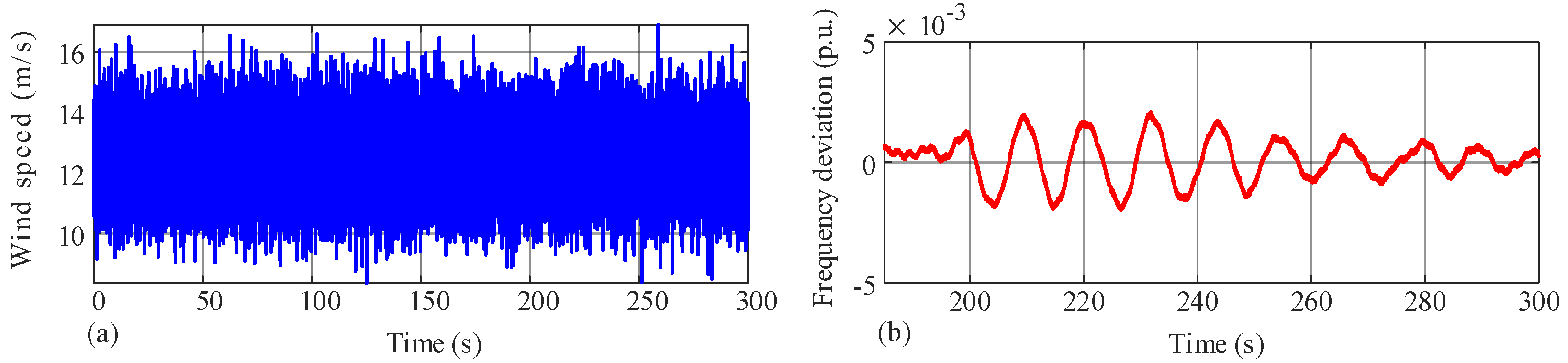
In reality, the wind speed is not constant. To simulate this effect on stability, the wind speed model is represented as follows:

$$V_{\mathrm{wind}}\left(t\right)=v_{\mathrm{average}}+v_{\mathrm{p}}\sin {\omega }_{\mathrm{wind}}t+v_{\mathrm{random}}$$

(15)

where v_average = 12.5 m/s, v_p = 0.5 m/s, ω_wind = π rad/s, and v_random is represented by a Gaussian-distributed random signal whose variance equals 1. A small load disturbance is added at t = 200 s, and the wind speed and system frequency response are shown in Figure 19. With the wind speed changing, the oscillation does not converge or diverge fast enough; thus, in the long period, the waveform is similar to an unattenuated oscillation.

To explore whether the ultra-low frequency oscillation may exist in other systems, the four-machine, two-area system is utilized, where the steam turbines in the left area are replaced by two DFIGs. The system topology is shown in Figure 20. At t = 150 s, a load disturbance is added to Load 1, and the simulation result is shown in Figure 21. It can be seen that although the simulation system has changed, this phenomenon still exists.

5. Conclusions

Various kinds of new oscillation instability issues occur when the capacity of REG increases. This paper focused on the ultra-low frequency oscillation risk in thermal power generation systems and discovered that DFIGs with df/dt virtual inertia controllers can induce this problem, which has not been reported or studied. By deriving the motion equation model of the DFIG, it was shown that the negative phase characteristic introduced by the equivalent inertia of the DFIG can reduce the phase margin of the entire system within the ultra-low frequency band, making the system lose stability more easily. Subsequently, key factors that influence the stability were analyzed through frequency domain characteristic analysis, depicting influencing trends. Especially, it should be noticed that the increase in the virtual inertia and the decrease in its time constant deteriorate the stability, creating a conflict between providing a fast inertial response and the stability requirement. Finally, time-domain simulations verified the consistency between electromagnetic transient model dynamics and frequency domain analyses.

Since the ULFO is introduced by the negative phase of the equivalent inertia of the DFIG, it is important to develop a method to mitigate this effect while preserving the ability of the fast inertial response. Future studies may include reshaping the equivalent inertia to satisfy both requirements or designing effective controllers for oscillation damping.