A Dual-Loop Modified Active Disturbance Rejection Control Scheme for a High-Purity Distillation Column
Abstract
1. Introduction
- (1)
- During the stable operation of the distillation process, open-loop experiments are carried out. The loop structure with an input, flow rate of boil-up (), and an output, light component’s composition in bottom product (), can be depicted approximately as a high-order inertial model. Likewise, the loop structure with an input, flow rate of reflux (), and an output, light component’s composition in top product (), can be depicted approximately as another high-order inertial model.
- (2)
- The dual-loop MADRC scheme for the high-purity distillation column is designed.
- (3)
2. Process Model for the Column
3. The Dual-Loop MADRC Scheme for the Column
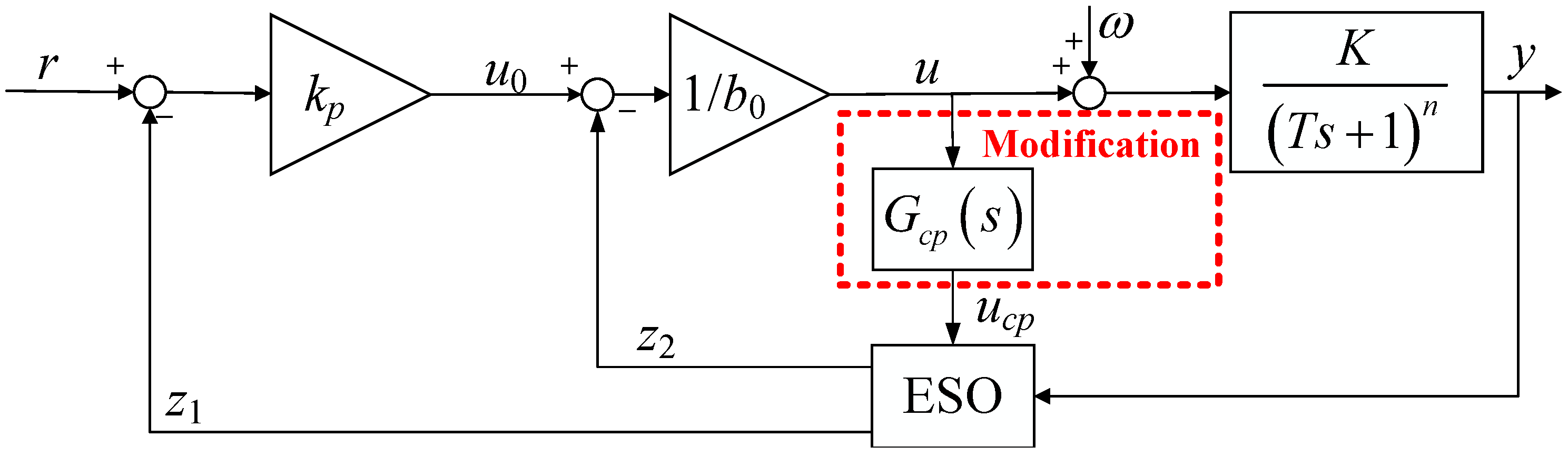
3.1. The Regular Design of Linear ADRC
3.2. The Design of MADRC for and
3.3. Stability Analysis of MADRC
4. The Tuning Rule of the Dual-Loop MADRC Scheme
5. Simulation and Experiment Validation
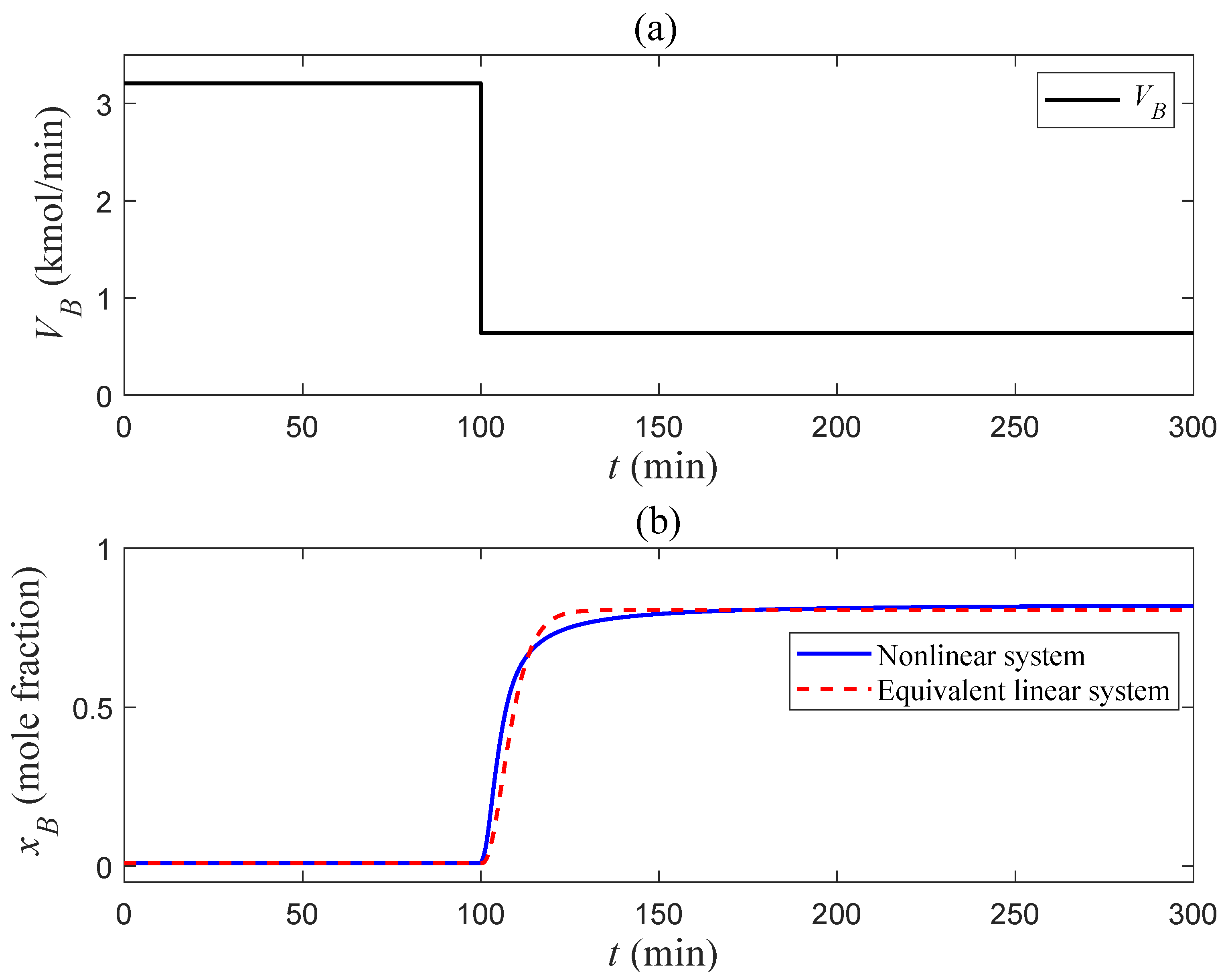
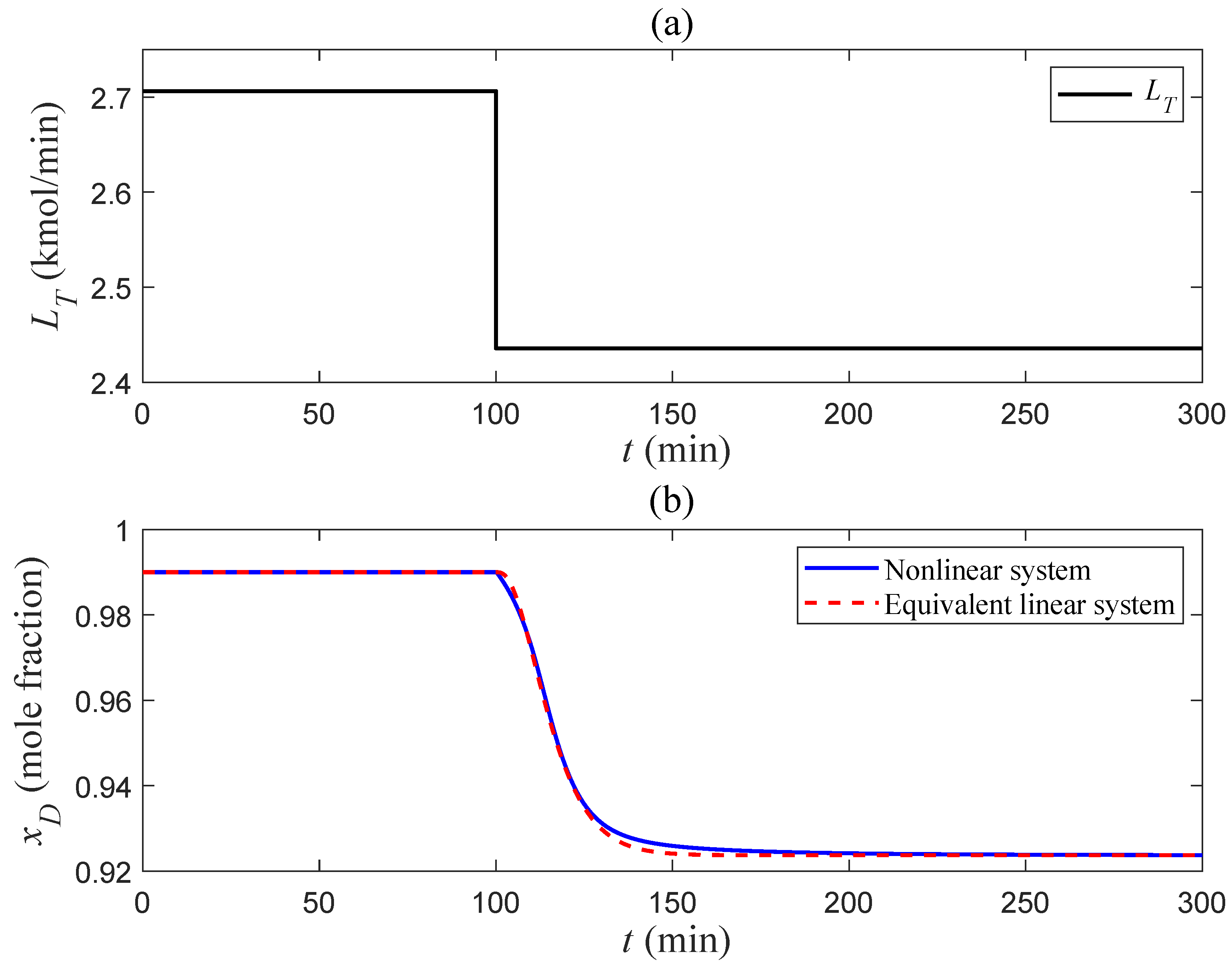
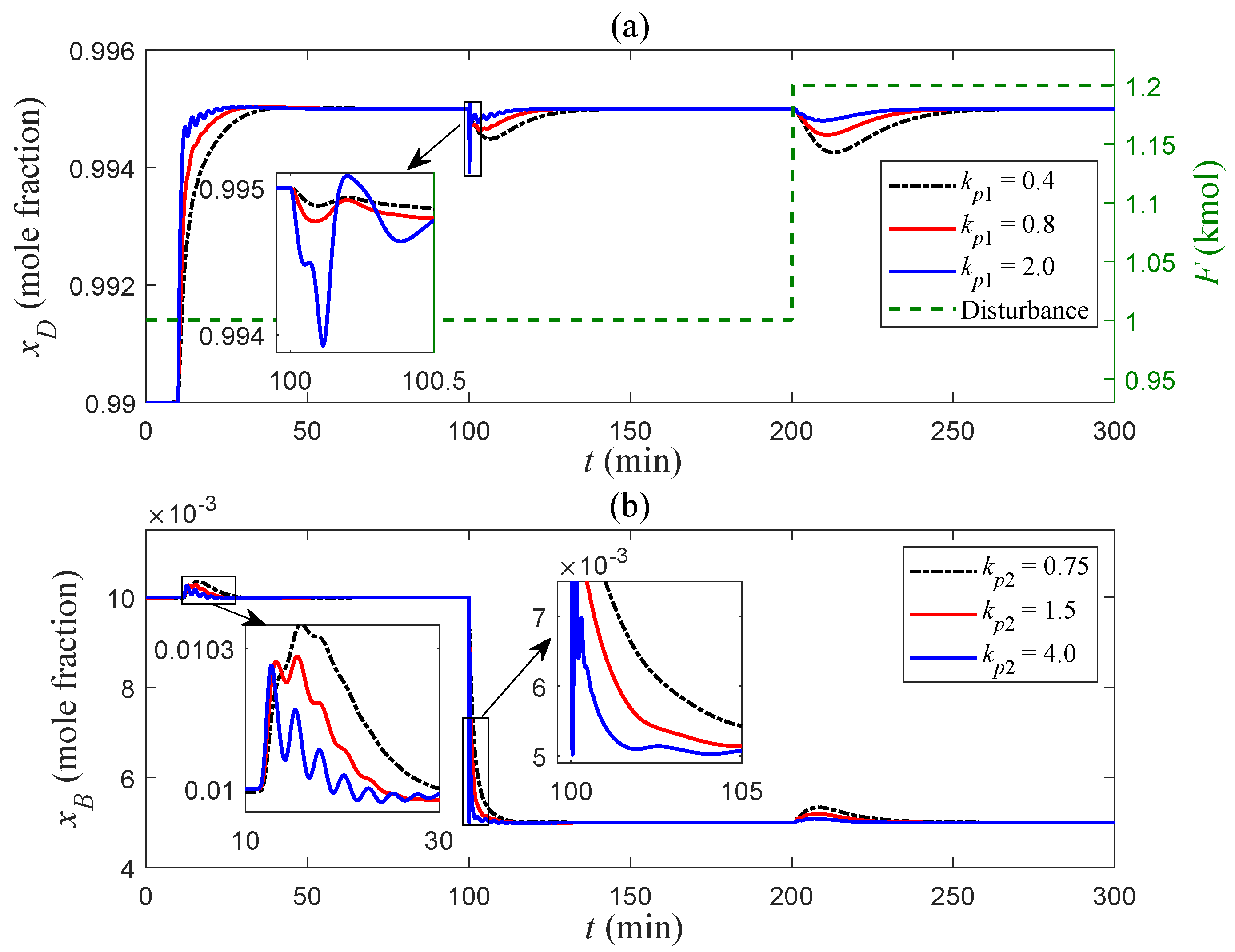
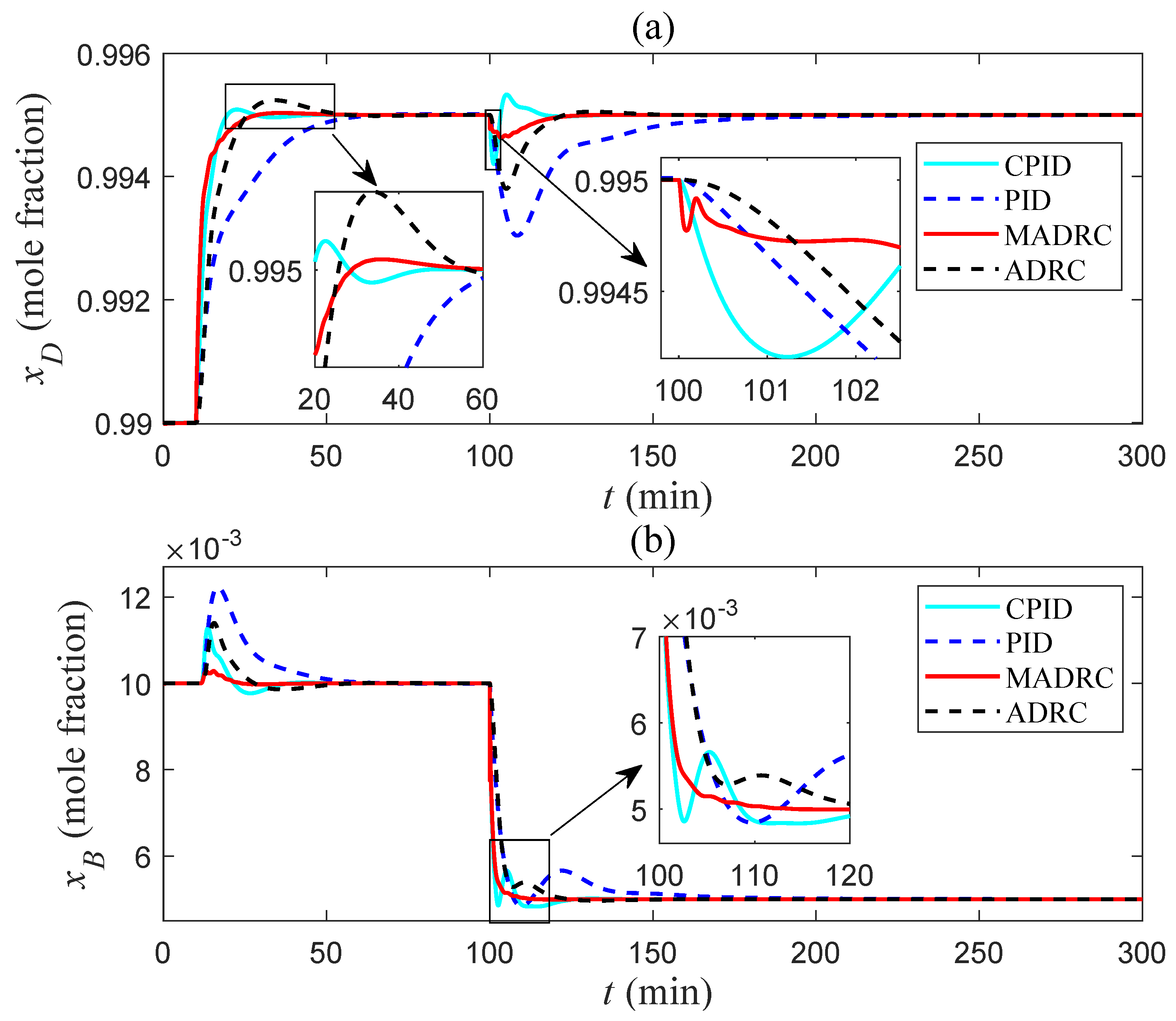
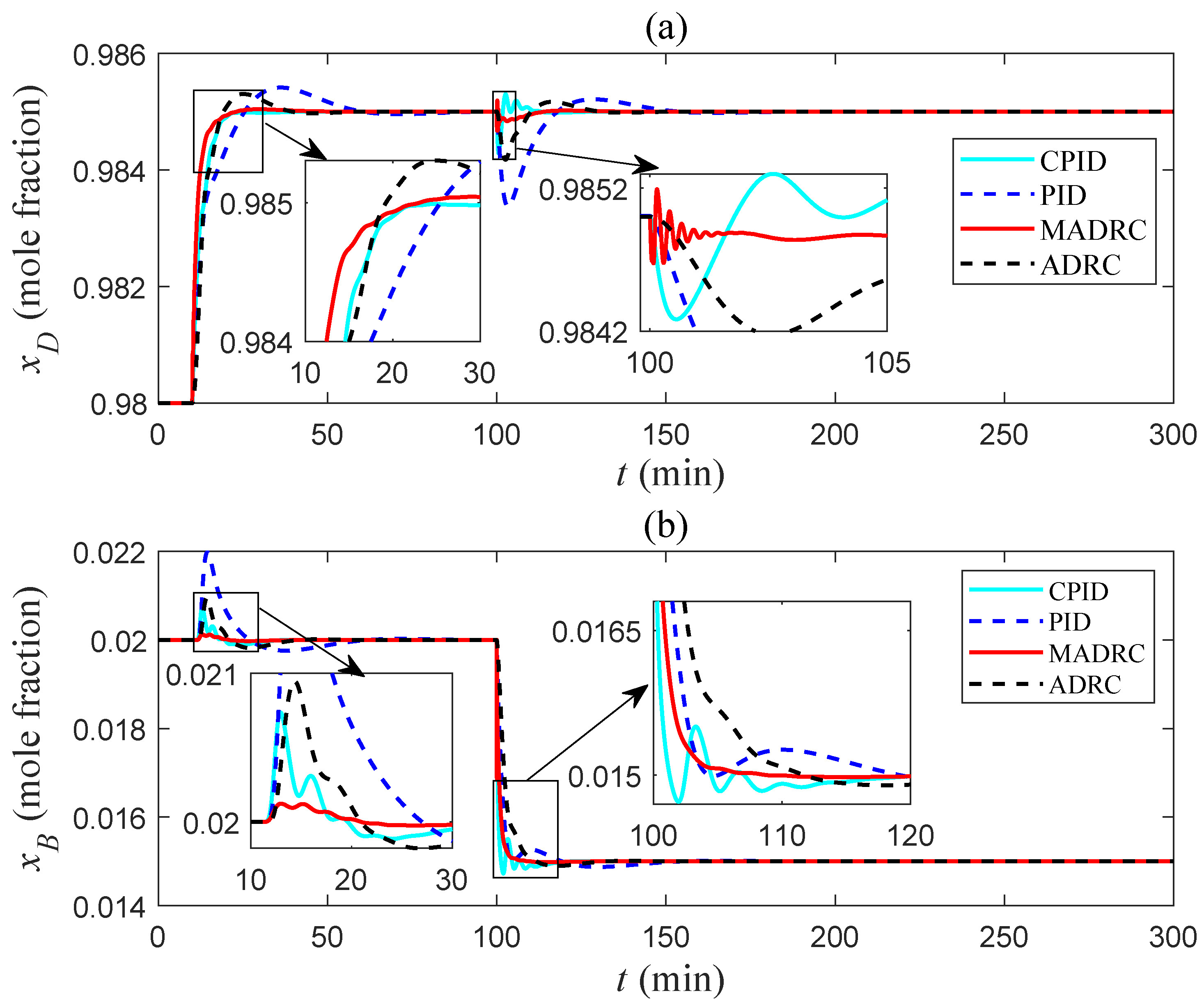
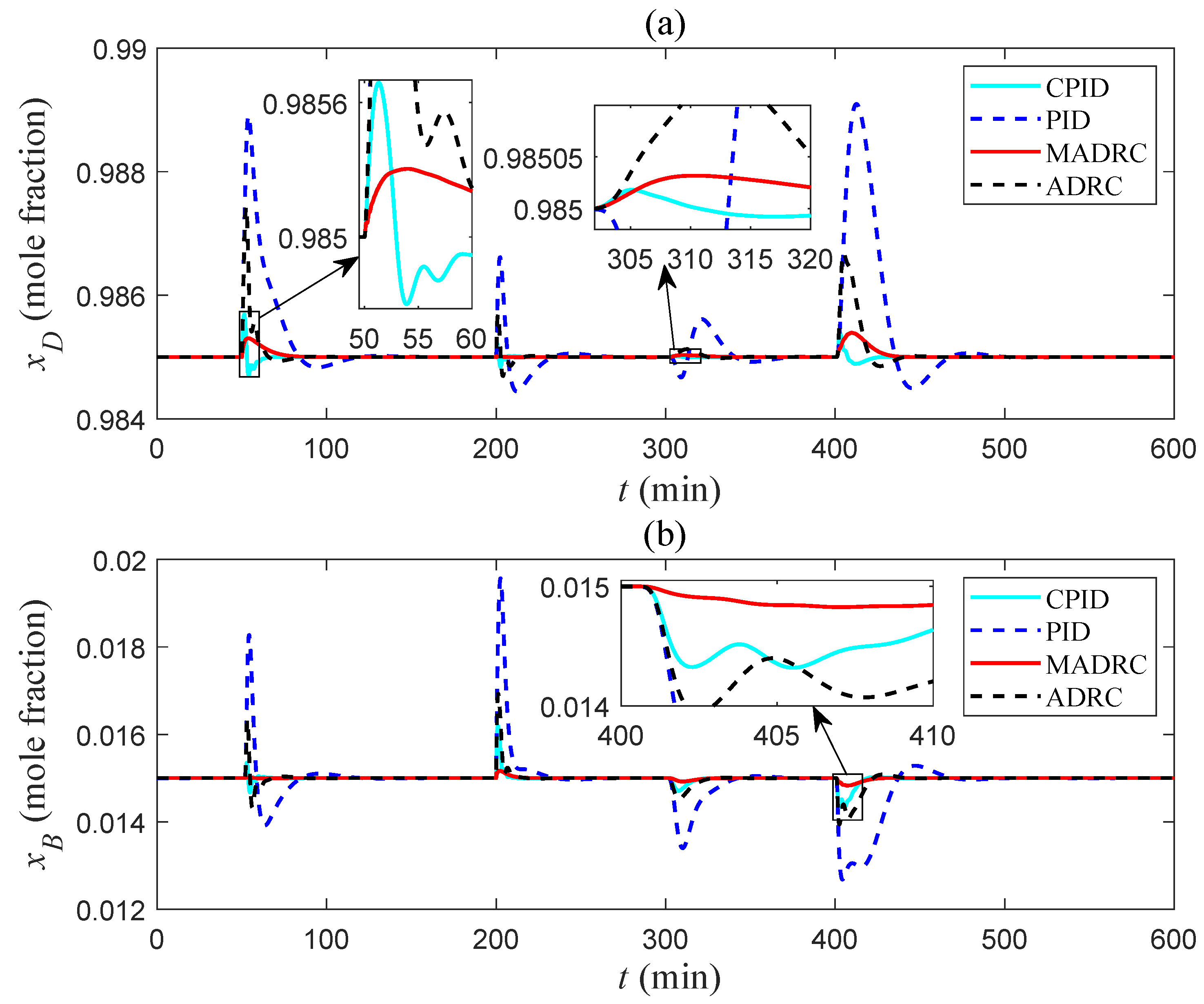
5.1. Simulation Validations
5.2. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, Y.; Huang, K.; Qian, X.; Chen, H.; Zang, L.; Zhang, L. Enhanced temperature difference control of distillation columns based on the averaged absolute variation magnitude. Chin. J. Chem. Eng. 2021, 29, 266–278. [Google Scholar] [CrossRef]
- Torres Cantero, C.A.; Pérez Zúñiga, R.; Martínez García, M.; Ramos Cabral, S.; Calixto-Rodriguez, M.; Valdez Martínez, J.S.; Mena Enriquez, M.G.; Pérez Estrada, A.J.; Ortiz Torres, G.; Sorcia Vázquez, F.d.J.; et al. Design and Control Applied to an Extractive Distillation Column with Salt for the Production of Bioethanol. Processes 2022, 10, 1792. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, X. Dynamics and control of high purity heat integrated distillation columns. Ind. Eng. Chem. Res. 2005, 44, 8806–8814. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, X. Nonlinear dynamic behaviors and control based on simulation of high-purity heat integrated air separation column. ISA Trans. 2015, 55, 145–153. [Google Scholar] [CrossRef]
- Karan, S.; Dey, C.; Mukherjee, S. Simple internal model control based modified Smith predictor for integrating time delayed processes with real-time verification. ISA Trans. 2022, 121, 240–257. [Google Scholar] [CrossRef]
- Tahir, N.M.; Zhang, J.; Armstrong, M. Control of heat-integrated distillation columns: Review, trends, and challenges for future research. Processes 2024, 13, 17. [Google Scholar] [CrossRef]
- Shi, X.; Zhao, H.; Fan, Z. Parameter optimization of nonlinear PID controller using RBF neural network for continuous stirred tank reactor. Meas. Control 2023, 56, 1835–1843. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef]
- Zangina, J.A.S.; Wang, W.; Qin, W.; Gui, W.; Zhang, Z.; Xu, S.; Liu, X. Model predictive control of a high-purity internal thermally coupled distillation column. Chem. Eng. Technol. 2021, 44, 1294–1301. [Google Scholar] [CrossRef]
- Ping, Z.; Li, Y.; Huang, Y.; Lu, J.G.; Wang, H. Global robust output regulation of a class of MIMO nonlinear systems by nonlinear internal model control. Int. J. Robust Nonlinear Control 2021, 31, 4037–4051. [Google Scholar] [CrossRef]
- Cheng, Y.; Gao, Z.; Sun, M.; Sun, Q. Cascade active disturbance rejection control of a high-purity distillation column with measurement noise. Ind. Eng. Chem. Res. 2018, 57, 4623–4631. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller-tuning. Proc. Amer. Control Conf. 2003, 4898–4996. [Google Scholar]
- Ren, J.; Chen, Z.; Sun, M.; Sun, Q.; Wang, Z. Proportion integral-type active disturbance rejection generalized predictive control for distillation process based on grey wolf optimization parameter tuning. Chin. J. Chem. Eng. 2022, 49, 234–244. [Google Scholar] [CrossRef]
- Ren, J.; Chen, Z.; Yang, Y.; Wang, Z.; Sun, M.; Sun, Q. A New Grey Wolf Optimizer Tuned Extended Generalized Predictive Control for Distillation Process. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5880–5890. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Li, D.; Liu, Y.; Chen, Y. Performance Analysis of Improved ADRCs for a Class of High-Order Processes With Verification on Main Steam Pressure Control. IEEE Trans. Ind. Electron. 2023, 70, 6180–6190. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, Z. Modified active disturbance rejection control for time-delay systems. ISA Trans. 2014, 53, 882–888. [Google Scholar] [CrossRef]
- Wu, Z.; He, T.; Li, D.; Xue, Y.; Sun, L.; Sun, L. Superheated steam temperature control based on modified active disturbance rejection control. Control Eng. Pract. 2019, 83, 83–97. [Google Scholar] [CrossRef]
- He, T.; Wu, Z.; Shi, R.; Li, D.; Sun, L.; Wang, L.; Zheng, S. Maximum Sensitivity-Constrained Data-Driven Active Disturbance Rejection Control with Application to Airflow Control in Power Plant. Energies 2019, 12, 231. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Adaptive Active Disturbance Rejection Control for Uncertain Current Ripples Suppression of PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 2320–2331. [Google Scholar] [CrossRef]
- Huang, C.; Zhuang, J. Error-Based Active Disturbance Rejection Control for Pitch Control of Wind Turbine by Improved Coyote Optimization Algorithm. IEEE Trans. Energy Convers. 2022, 37, 1394–1405. [Google Scholar] [CrossRef]
- Taqvi, S.A.A.; Zabiri, H.; Uddin, F.; Naqvi, M.; Tufa, L.D.; Kazmi, M.; Rubab, S.; Naqvi, S.R.; Maulud, A.S. Simultaneous fault diagnosis based on multiple kernel support vector machine in nonlinear dynamic distillation column. Energy Sci. Eng. 2022, 10, 814–839. [Google Scholar] [CrossRef]
- Skogestad, S.; Morari, M. LV-Control of a high-purity distillation column. Chem. Eng. Sci. 1988, 43, 33–48. [Google Scholar] [CrossRef]
- Kovari, B.; Pelenczei, B.; Knab, I.G.; Becsi, T. Beyond trial and error: Lane keeping with Monte Carlo Tree Search-driven optimization of Reinforcement Learning. Electronics 2024, 13, 2058. [Google Scholar] [CrossRef]
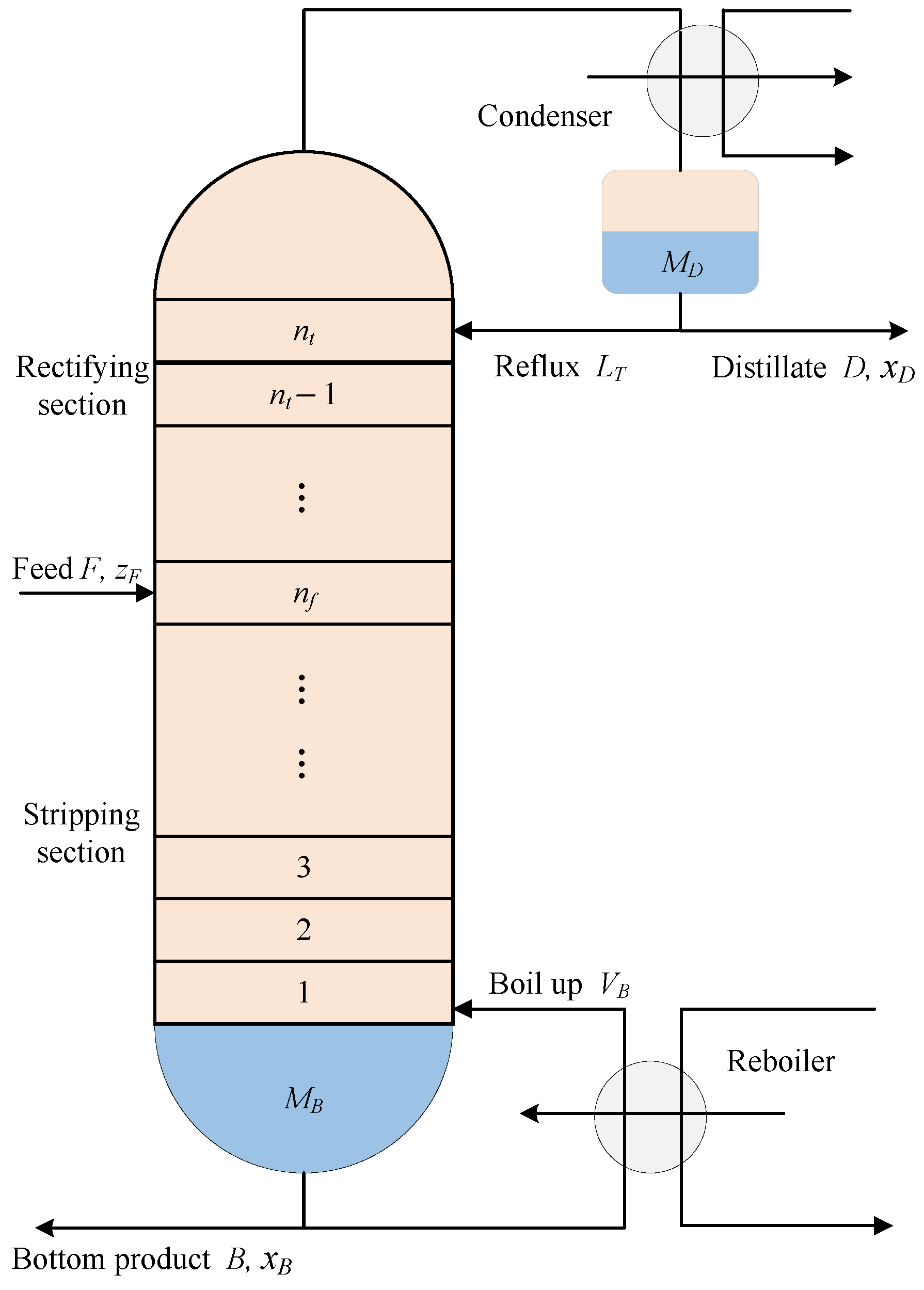









| Symbol | Nomenclature | Nominal Values |
|---|---|---|
| condenser stage | 41 | |
| feed stage | 21 | |
| F | feed flow rate, kmol/min | 1 |
| composition concentration of the feed | ||
| fluid content fraction within the feed | 1 | |
| D and B | flow rates of top and bottom products, kmol/min | |
| and | fluid holdup of condenser and reboiler fluid holdup, kmol | |
| and | light component’s composition in top and bottom products | and |
| and | flow rates of reflux and boil-up, kmol/min | and |
| fluid holdup on stage i, kmol | ||
| relative volatility | ||
| time constant, min | ||
| steam’s influence on fluid holdup | 0 |
| Control Scheme | Tuned Parameters |
|---|---|
| MADRC | |
| CPID | outer loop: |
| inner loop: | |
| ADRC | |
| PID |
| Control Scheme | Tuned Parameters |
|---|---|
| MADRC | |
| CPID | |
| ADRC | |
| PID |
| Control Scheme | |||||
|---|---|---|---|---|---|
| MADRC | |||||
| CPID | |||||
| ADRC | |||||
| PID | |||||
| Control Scheme | |||||
|---|---|---|---|---|---|
| MADRC | |||||
| CPID | |||||
| ADRC | |||||
| PID | |||||
| Control Scheme | |||||
|---|---|---|---|---|---|
| MADRC | |||||
| CPID | |||||
| ADRC | |||||
| PID | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Zhao, Y.; Li, Z.; Song, J.; Wu, Z.; Guo, J.; Zhang, J. A Dual-Loop Modified Active Disturbance Rejection Control Scheme for a High-Purity Distillation Column. Processes 2025, 13, 1359. https://doi.org/10.3390/pr13051359
Song X, Zhao Y, Li Z, Song J, Wu Z, Guo J, Zhang J. A Dual-Loop Modified Active Disturbance Rejection Control Scheme for a High-Purity Distillation Column. Processes. 2025; 13(5):1359. https://doi.org/10.3390/pr13051359
Chicago/Turabian StyleSong, Xudong, Yuedong Zhao, Zihao Li, Jingchao Song, Zhenlong Wu, Jingzhong Guo, and Jian Zhang. 2025. "A Dual-Loop Modified Active Disturbance Rejection Control Scheme for a High-Purity Distillation Column" Processes 13, no. 5: 1359. https://doi.org/10.3390/pr13051359
APA StyleSong, X., Zhao, Y., Li, Z., Song, J., Wu, Z., Guo, J., & Zhang, J. (2025). A Dual-Loop Modified Active Disturbance Rejection Control Scheme for a High-Purity Distillation Column. Processes, 13(5), 1359. https://doi.org/10.3390/pr13051359






