A Novel Process for the Design, Analysis, and Control of a Dual-Phase Motors with Independent Drive for a High Power Density
Abstract
1. Introduction
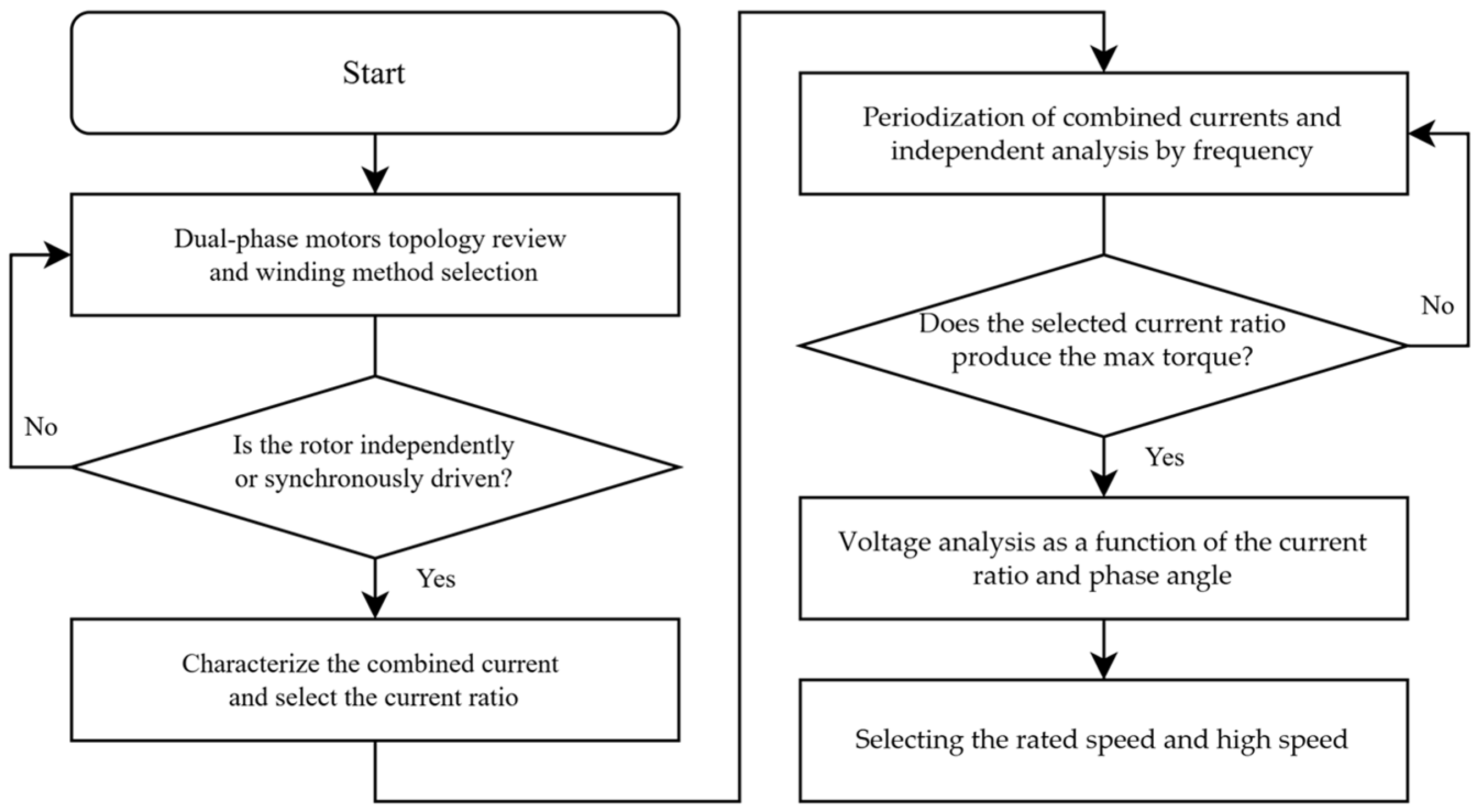
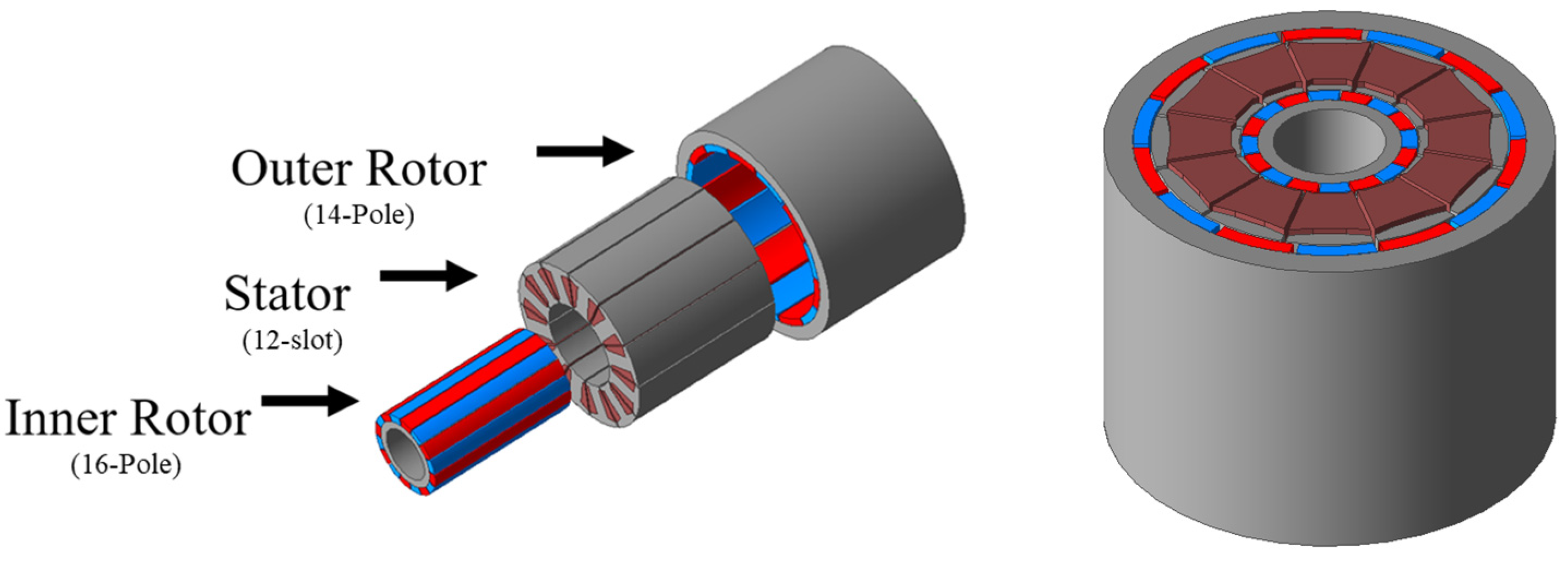
2. Definition and Design Process of the DPM
2.1. Definition of a DPM
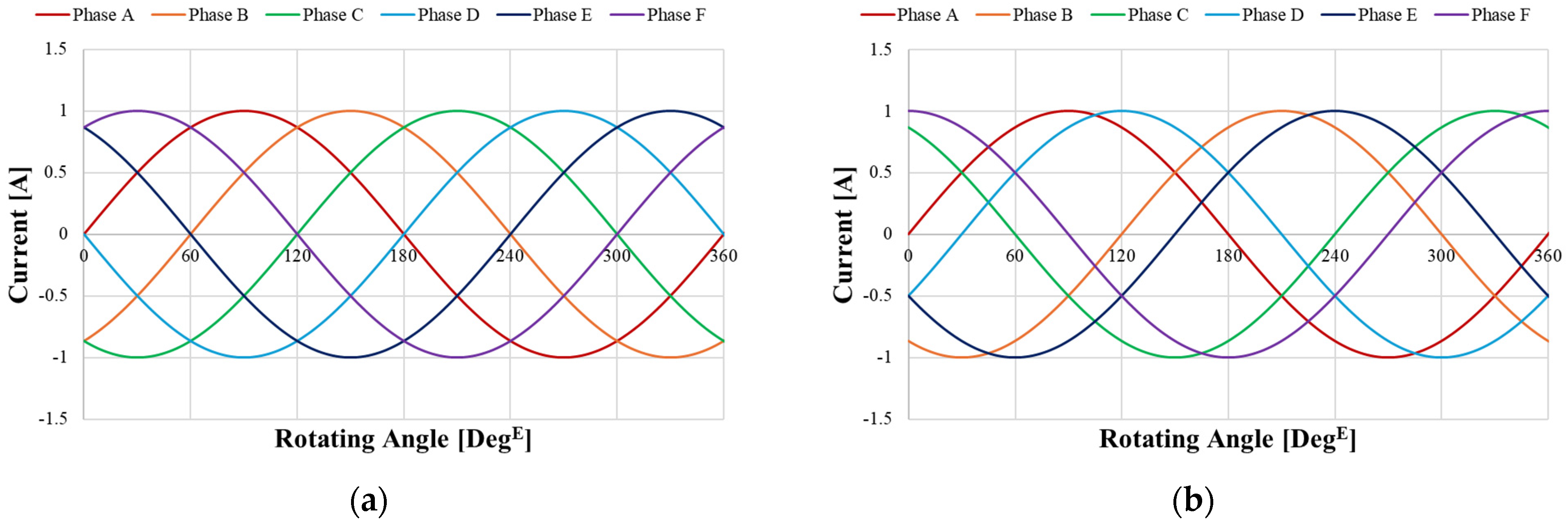
2.2. Phase Difference of the 6-Phase Current
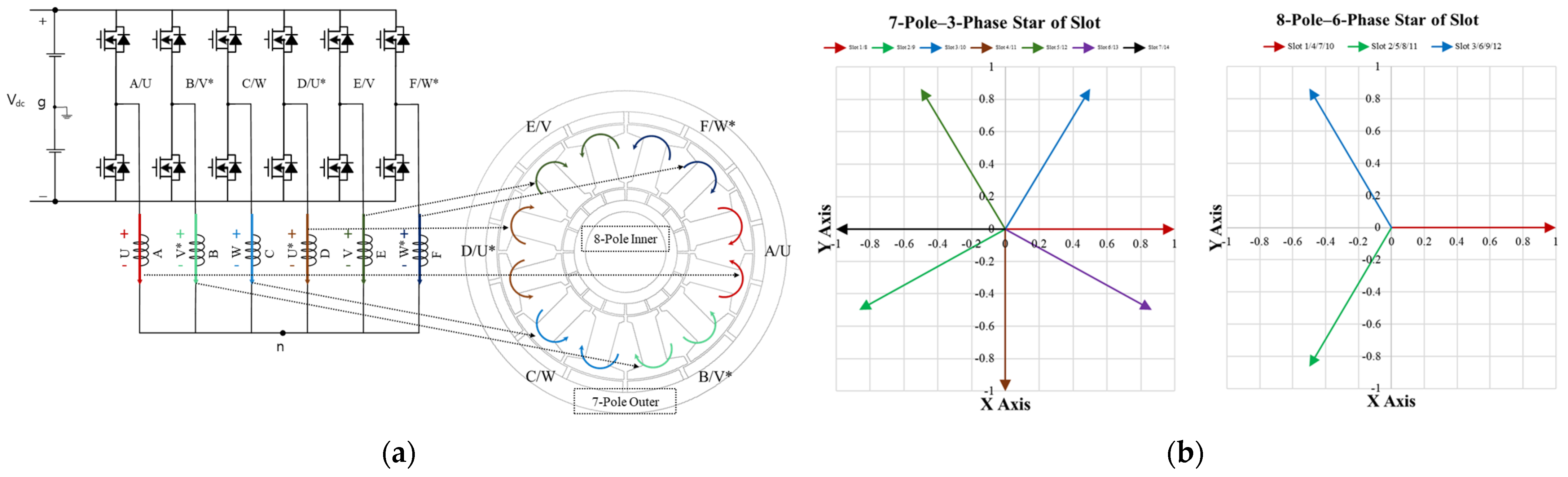
2.3. Winding Connection Method That Enables Independent Drive
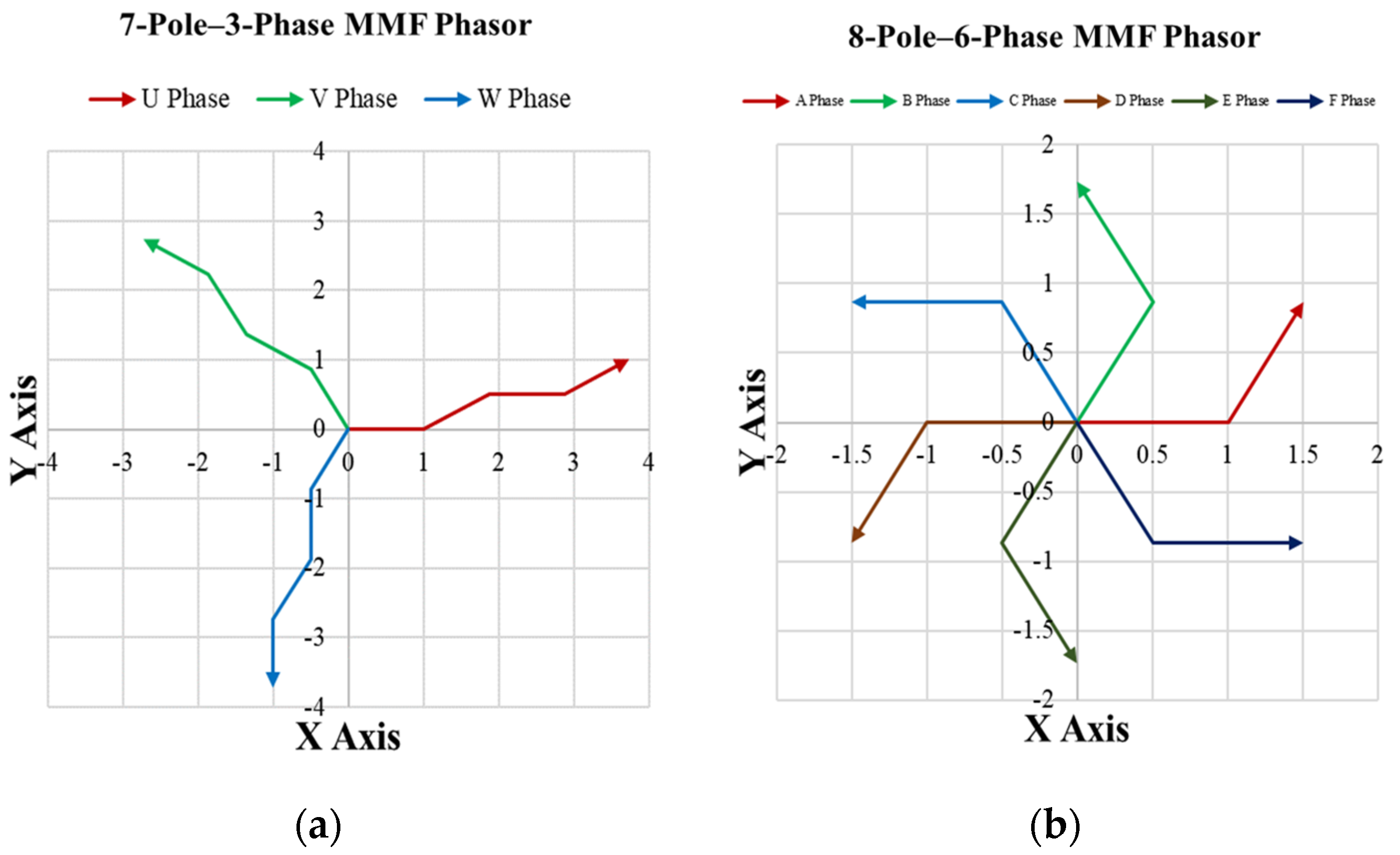
2.3.1. Basic Explanation of the Winding Factor
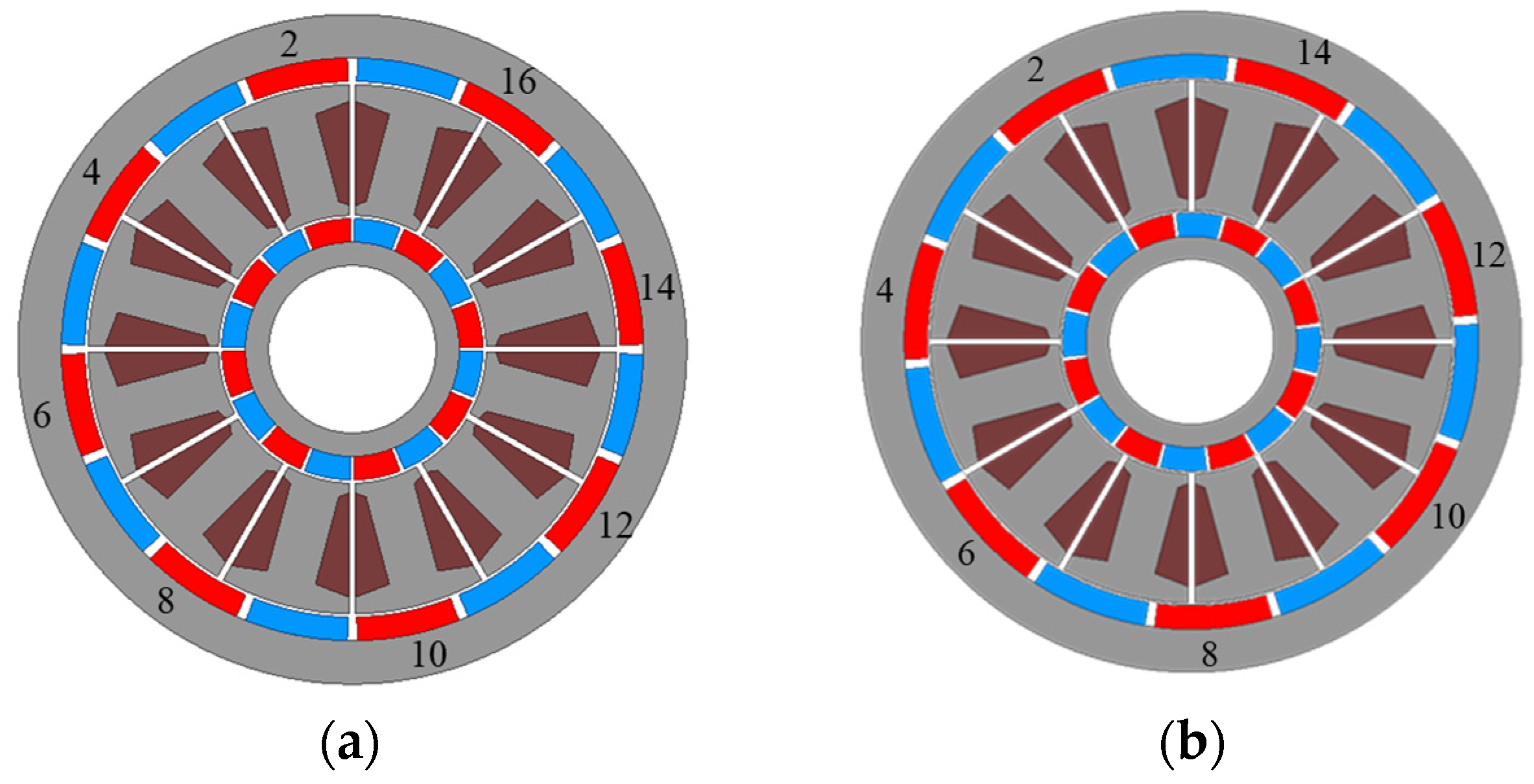
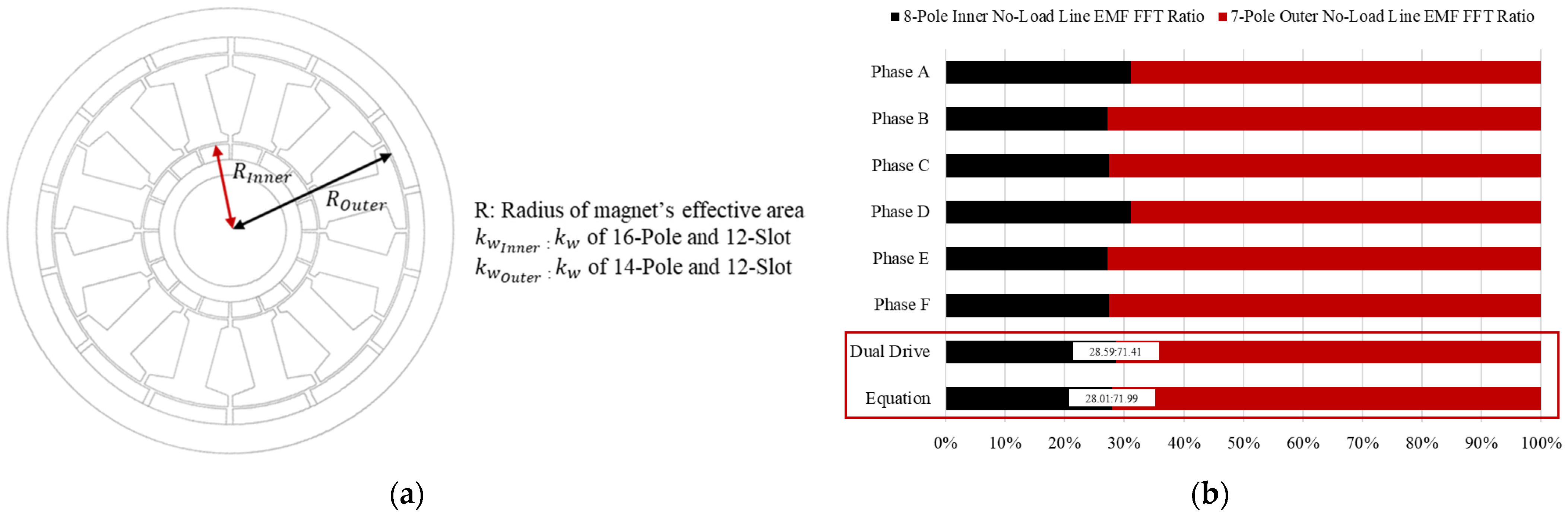
2.3.2. Selection of the Winding Method for the Independent Operation of the Inner Rotor and Outer Rotor
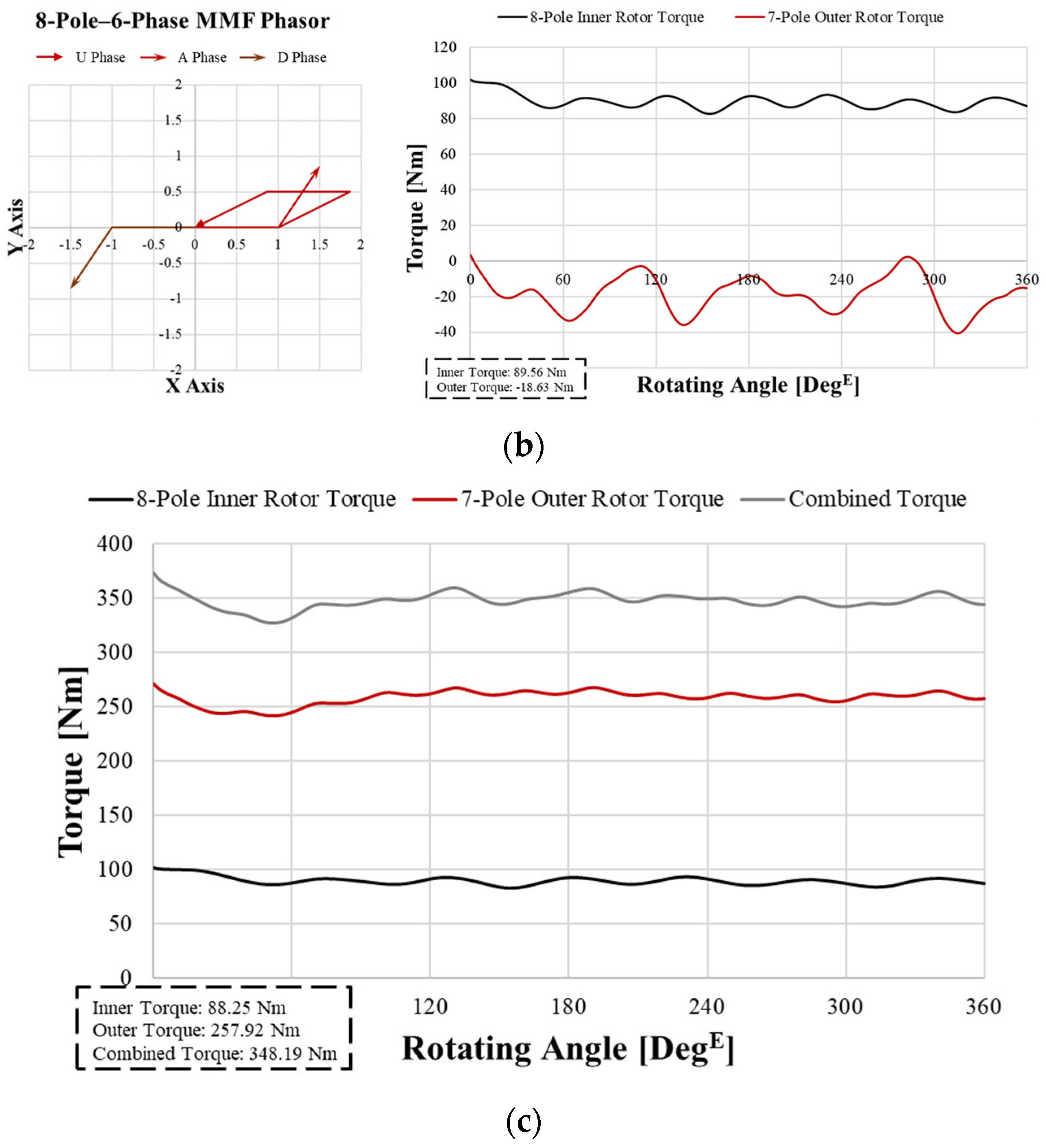
2.3.3. Analysis of Independent Operation in a DPM
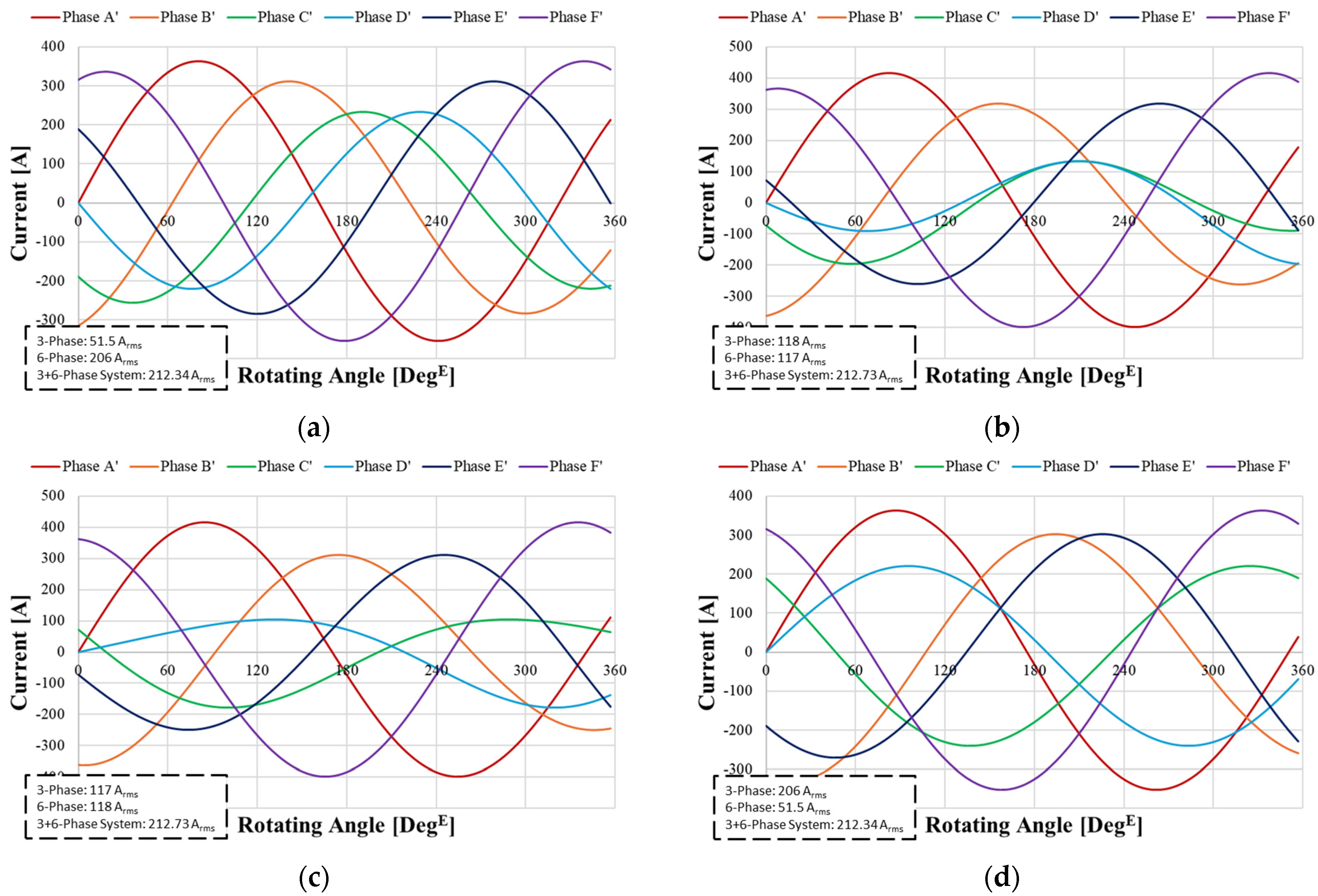
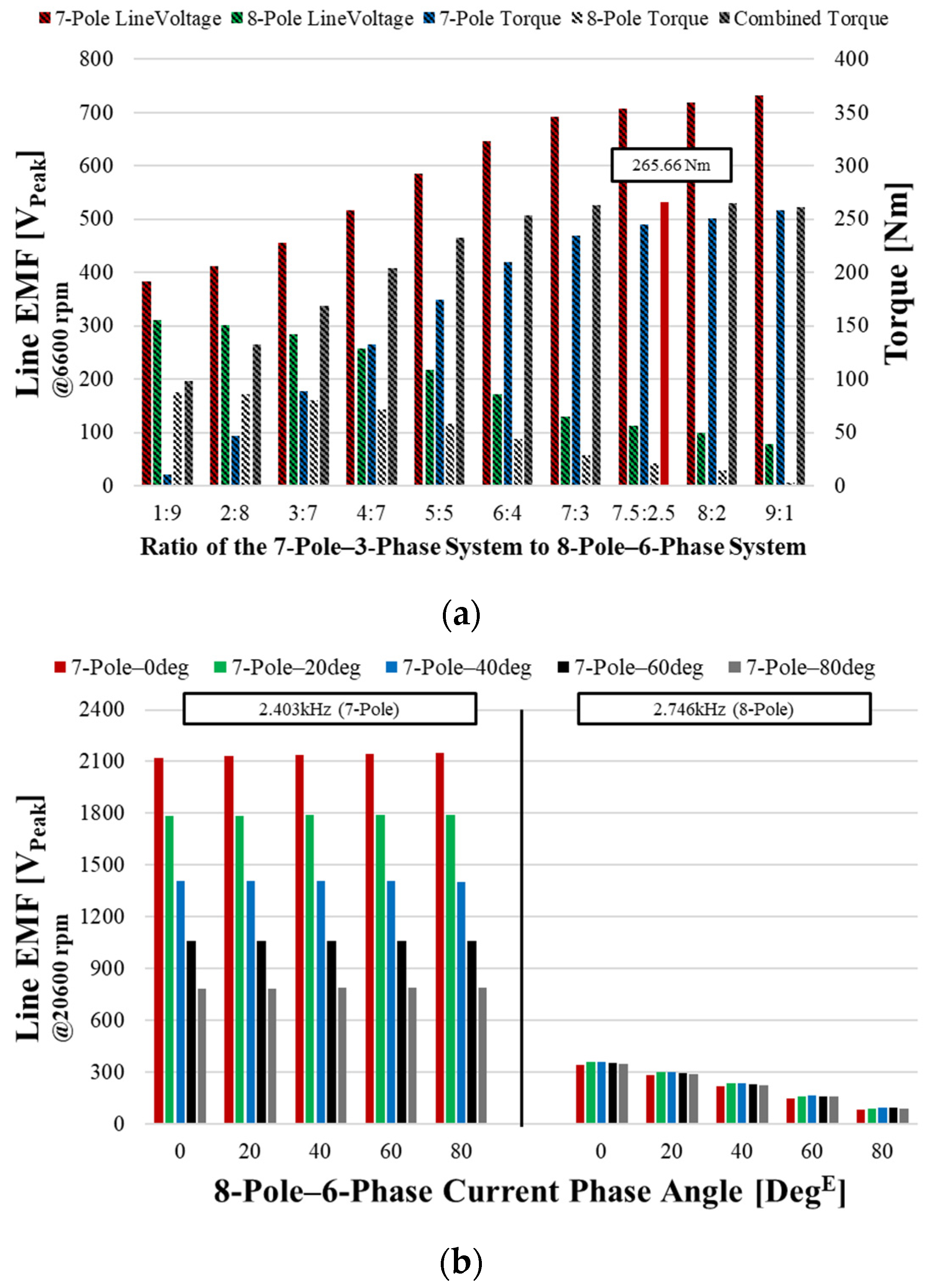
3. Defining the Combined Current and Selecting the Best Ratio of Currents
3.1. Current Features in DPM Subsections
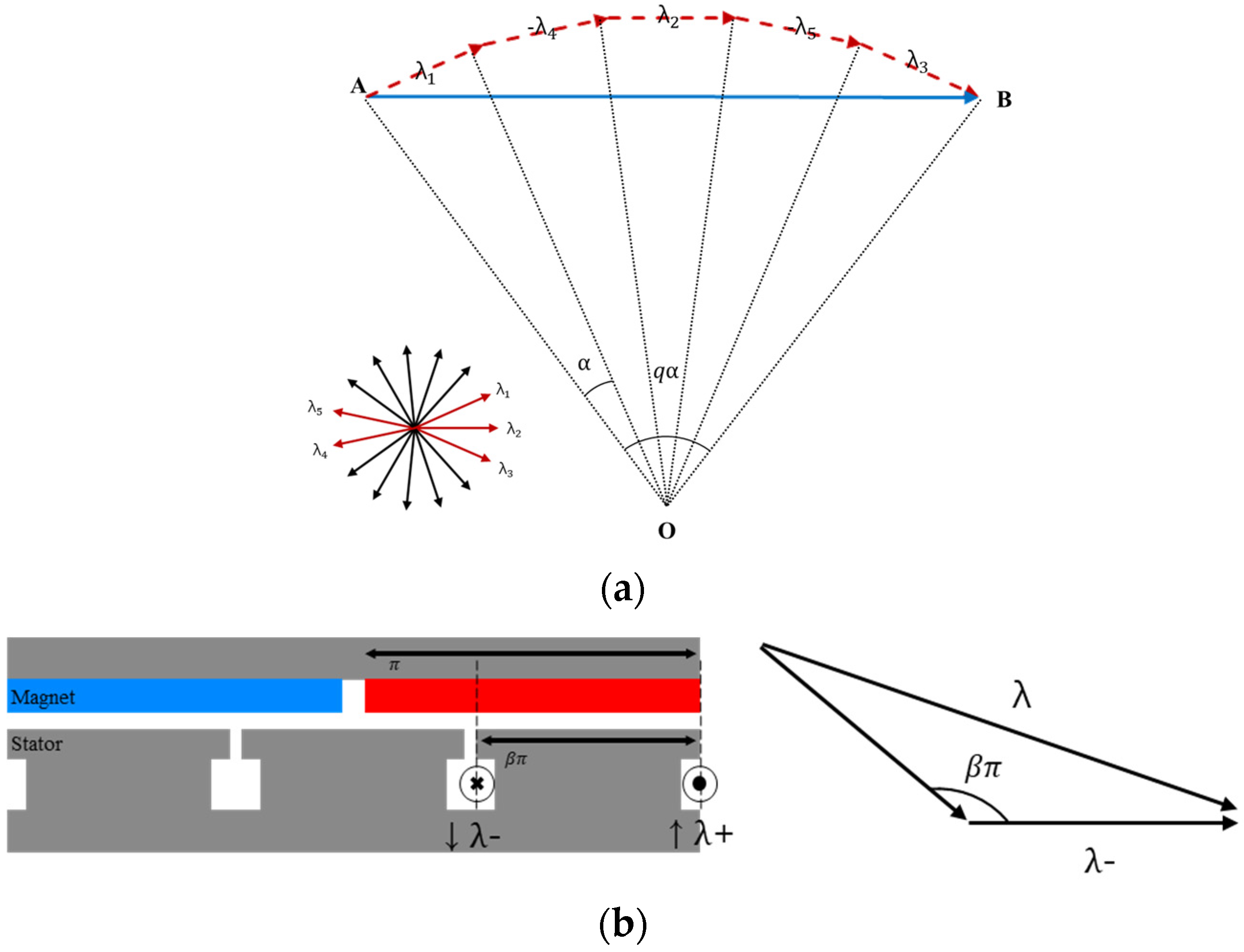
3.2. Current Ratio
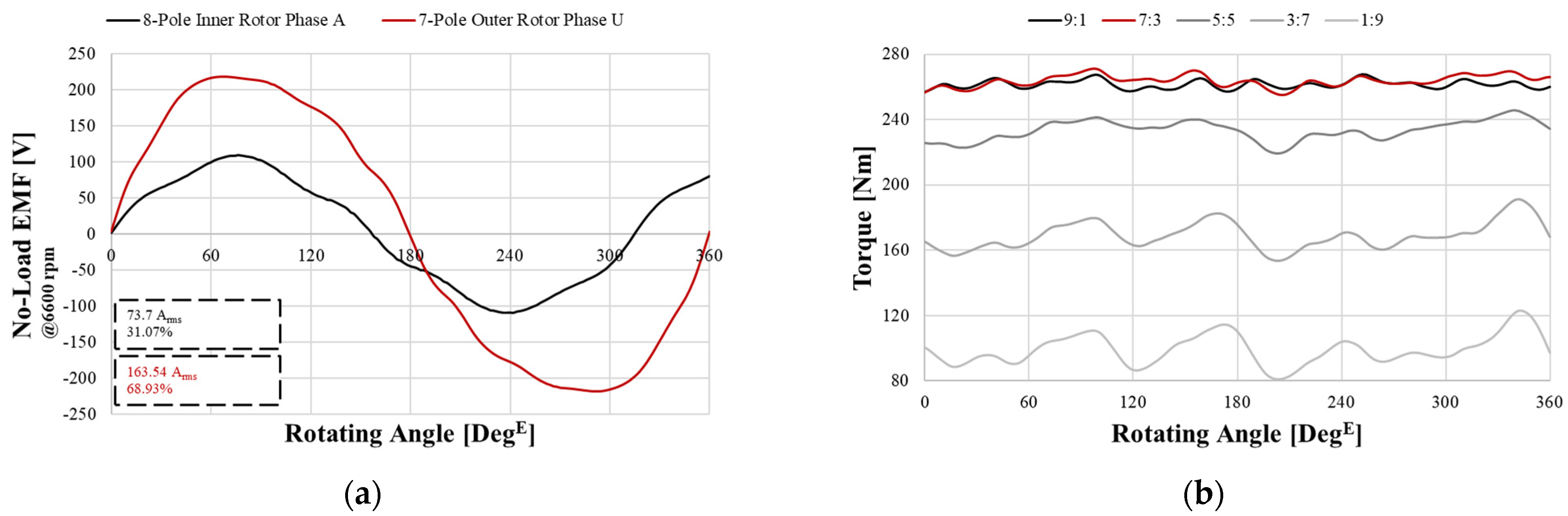
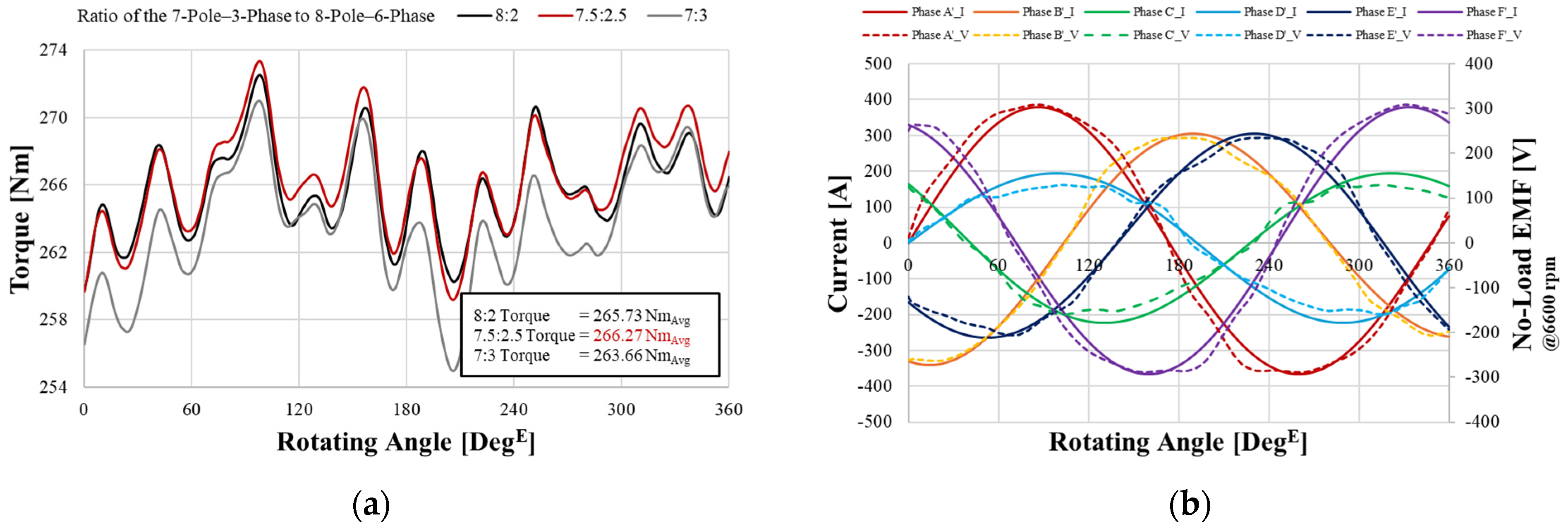
3.3. Determining the Combined Current and Matching with BEMF
4. Drive and Control of the DPM
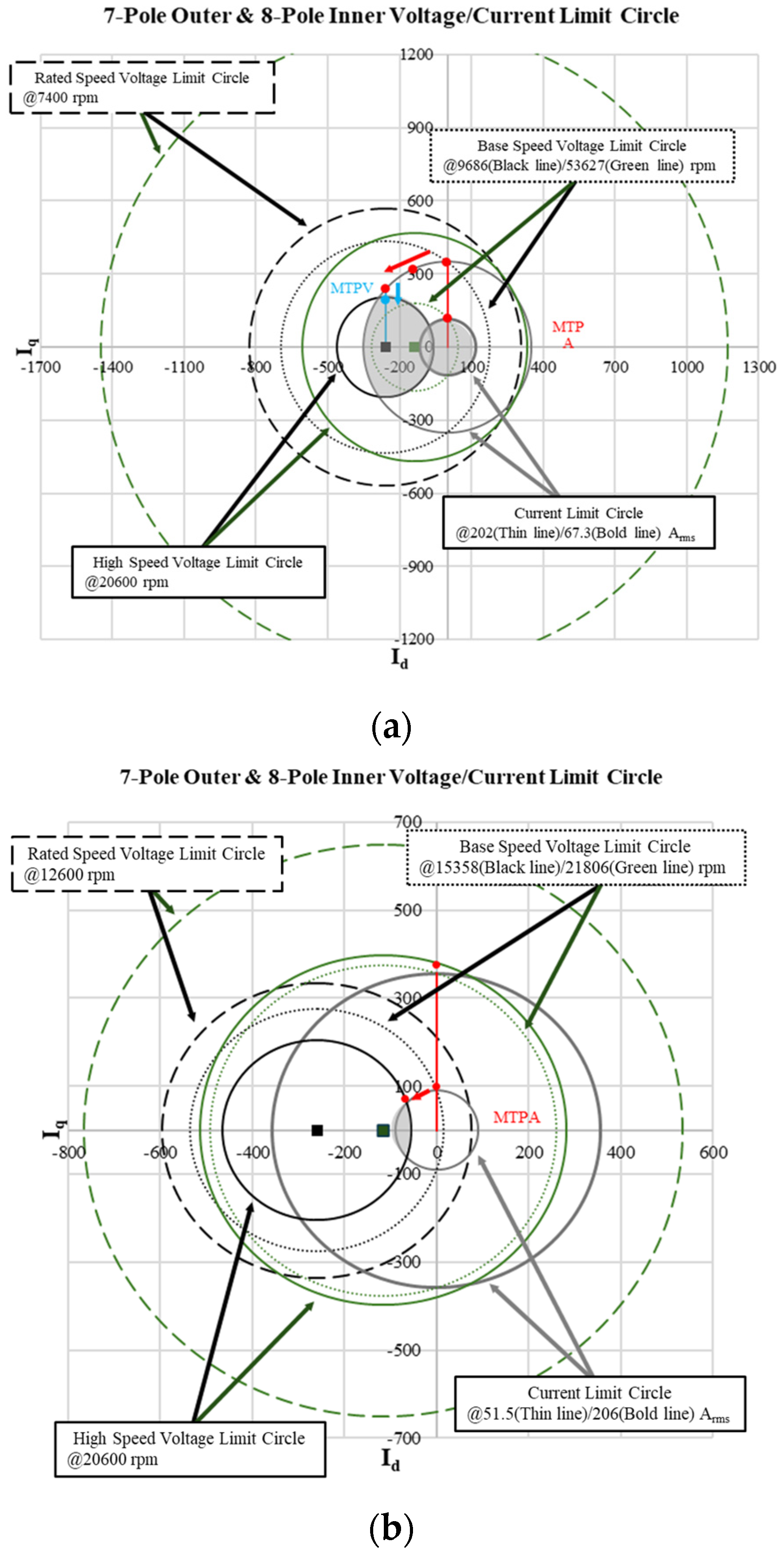
4.1. Rated Speed and High Speed of the DPM
4.2. Control Method for the DPM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, G.; Hu, C.; Zhou, Q.; Gao, W.; Zhang, Q. Multi-Objective Optimization for Outer Rotor Low-Speed Permanent Magnet Motor. Appl. Sci. 2022, 12, 8113. [Google Scholar] [CrossRef]
- Sirimanna, S.; Balachandran, T.; Haran, K. A Review on Magnet Loss Analysis, Validation, Design Considerations, and Reduction Strategies in Permanent Magnet Synchronous Motors. Energies 2022, 15, 6116. [Google Scholar] [CrossRef]
- Shou, J.; Ma, J.; Zhang, Z.; Qiu, L.; Xu, B.; Luo, C.; Li, B.; Fang, Y. Vibration and Noise Optimization of Variable-Frequency-Driven SPMSM Used in Compressor Based on Electromagnetic Analysis and Modal Characteristics. Energies 2022, 15, 7474. [Google Scholar] [CrossRef]
- Hayashi, S.; Kubota, Y.; Soma, S.; Ohtani, M.; Igarashi, H. Topology Optimization of Permanent Magnet Synchronous Motor Considering the Control System. IEEE Trans. Magn. 2022, 58, 8205605. [Google Scholar]
- Liu, C.; Xu, Y.; Zou, J.; Yu, G.; Zhuo, L. Permanent magnet shape optimization method for PMSM air gap flux density harmonics reduction. CES Trans. Electr. Mach. Syst. 2021, 5, 284–290. [Google Scholar] [CrossRef]
- Cavagnino, A.; Lazzari, M.; Profumo, F.; Tenconi, A. A comparison between the axial flux and the radial flux structures for PM synchronous motors. IEEE Trans. Ind. Appl. 2002, 38, 1517–1524. [Google Scholar] [CrossRef]
- Wang, C.; Han, J.; Zhang, Z.; Hua, Y.; Gao, H. Design and Optimization Analysis of Coreless Stator Axial-Flux Permanent Magnet In-Wheel Motor for Unmanned Ground Vehicle. IEEE Trans. Transp. Electrif. 2022, 8, 1053–1062. [Google Scholar] [CrossRef]
- Zhang, Z.; Profumo, F.; Tenconi, A. Axial Flux Versus Radial Flux PM Motors; SPEEDAM: Capri, Italy, 1996; pp. A4-19–A4-25. [Google Scholar]
- Aydin, M.; Huang, S.; Lipo, T.A. Torque quality and comparison of internal and external rotor axial flux surface-magnet disc machines. IEEE Trans. Ind. Electron. 2006, 53, 822–830. [Google Scholar] [CrossRef]
- Haddad, R.Z. Iron Loss Analysis in Axial Flux Permanent Magnet Synchronous Motors with Soft Magnetic Composite Core Material. IEEE Trans. Energy Convers. 2022, 37, 295–303. [Google Scholar] [CrossRef]
- Syed, Q.A.S.; Solovieva, V.; Hahn, I. Magnetization Characteristics and Loss Measurements of the Axial Flux Permanent Magnet Motor’s Stator. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1061–1066. [Google Scholar] [CrossRef]
- Demir, Y.; Aydin, M. A Novel Dual 3-Phase Permanent Magnet Synchronous Motor with Asymmetric Stator Winding. IEEE Trans. Magn. 2016, 52, 8105005. [Google Scholar] [CrossRef]
- Onsal, M.; Demir, Y.; Aydin, M. A New Nine-Phase Permanent Magnet Synchronous Motor with Consequent Pole Rotor for High-Power Traction Applications. IEEE Trans. Magn. 2017, 53, 8700606. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y. Maximum Torque Per Ampere (MTPA) Control for IPMSM Drives Based on a Variable-Equivalent-Parameter MTPA Control Law. IEEE Trans. Power Electron. 2019, 34, 7092–7102. [Google Scholar] [CrossRef]
- Liu, T.-H.; Chen, Y.; Dai, B.-C. MTPA control for an IPMSM drive system using high frequency injection method. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 181–186. [Google Scholar] [CrossRef]
- Bendjedia, M.; Tehrani, K.A.; Azzouz, Y. A new robust digital control of an induction motor supplied by a 3-level voltage inverter for electric vehicle applications. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–10. [Google Scholar] [CrossRef]
- Mondal, A.; Khan, J.; Prins, S.; Kumaravel, S. Control of Dual Motor Test Bench for Performance Testing of PMSM for Traction Application. In Proceedings of the 2023 IEEE Silchar Subsection Conference (SILCON), Silchar, India, 3–5 November 2023; pp. 1–6. [Google Scholar] [CrossRef]








| Pole | 3-Phase Winding Factor | 6-Phase Winding Factor |
|---|---|---|
| 7 | Kp = 0.97 | Kp = 0.97 |
| Kd = 0.97 | Kd = 0 | |
| Kw = 0.94 | Kw = 0 | |
| 8 | Kp = 0.87 | Kp = 0.87 |
| Kd = 0 | Kd = 0.87 | |
| Kw = 0 | Kw = 0.75 |
| Parameter | Data | Unit |
|---|---|---|
| Core | 20JNHF1300 | - |
| Magnet | N45SH | - |
| Outer rotor diameter | 200/133.66 | mm |
| Inner rotor diameter | 78/50 | mm |
| Air gap thickness | 1 | mm |
| Stack length | 148 | mm |
| Current density | 33 | A/mm2 |
| Wire diameter | 2.9 | mm |
| Number of parallel | 1 | - |
| Turns | 12 | - |
| Current | 212 | Arms |
| Voltage limit | 970 (at high speed) 795 (at base speed) | VPeak |
| Resistance | 21.7 | mΩ |
| Ratio | NRatio |
|---|---|
| 9 | 1.0123 |
| 8 | 1.062 |
| 7 | 1.183 |
| 6 | 1.444 |
| Ratio | Data | Equation (14) | |||||
|---|---|---|---|---|---|---|---|
| In EMF | Out EMF | In Ratio | Out Ratio | In | Out | ||
| Phases A/U | 73.7 | 163.5 | 31.07 | 68.93 | Kw | 0.75 | 0.94 |
| Phases B/V * | 59.8 | 160.9 | 27.08 | 72.92 | |||
| Phases C/W | 60.68 | 160.8 | 27.39 | 72.61 | 2piR | 245.04 | 502.65 |
| Phases D/U * | 73.71 | 163.5 | 31.07 | 68.93 | |||
| Phases E/V | 59.8 | 160.9 | 27.09 | 72.91 | Ratio | 28.01 | 71.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.-S.; Song, S.-W.; Lee, S.-H.; Jeon, S.-B.; Kim, W.-H. A Novel Process for the Design, Analysis, and Control of a Dual-Phase Motors with Independent Drive for a High Power Density. Processes 2025, 13, 930. https://doi.org/10.3390/pr13040930
Han H-S, Song S-W, Lee S-H, Jeon S-B, Kim W-H. A Novel Process for the Design, Analysis, and Control of a Dual-Phase Motors with Independent Drive for a High Power Density. Processes. 2025; 13(4):930. https://doi.org/10.3390/pr13040930
Chicago/Turabian StyleHan, Hyung-Sub, Si-Woo Song, Seung-Heon Lee, Su-Bin Jeon, and Won-Ho Kim. 2025. "A Novel Process for the Design, Analysis, and Control of a Dual-Phase Motors with Independent Drive for a High Power Density" Processes 13, no. 4: 930. https://doi.org/10.3390/pr13040930
APA StyleHan, H.-S., Song, S.-W., Lee, S.-H., Jeon, S.-B., & Kim, W.-H. (2025). A Novel Process for the Design, Analysis, and Control of a Dual-Phase Motors with Independent Drive for a High Power Density. Processes, 13(4), 930. https://doi.org/10.3390/pr13040930








