Comparison of Fixed Switching Frequency FCS-MPC Strategies Applied to a Multilevel Converter: A Case Study of a Hybrid Cascade Converter Based on 2L-VSI and H-Bridge Converters
Abstract
1. Introduction
2. System Description
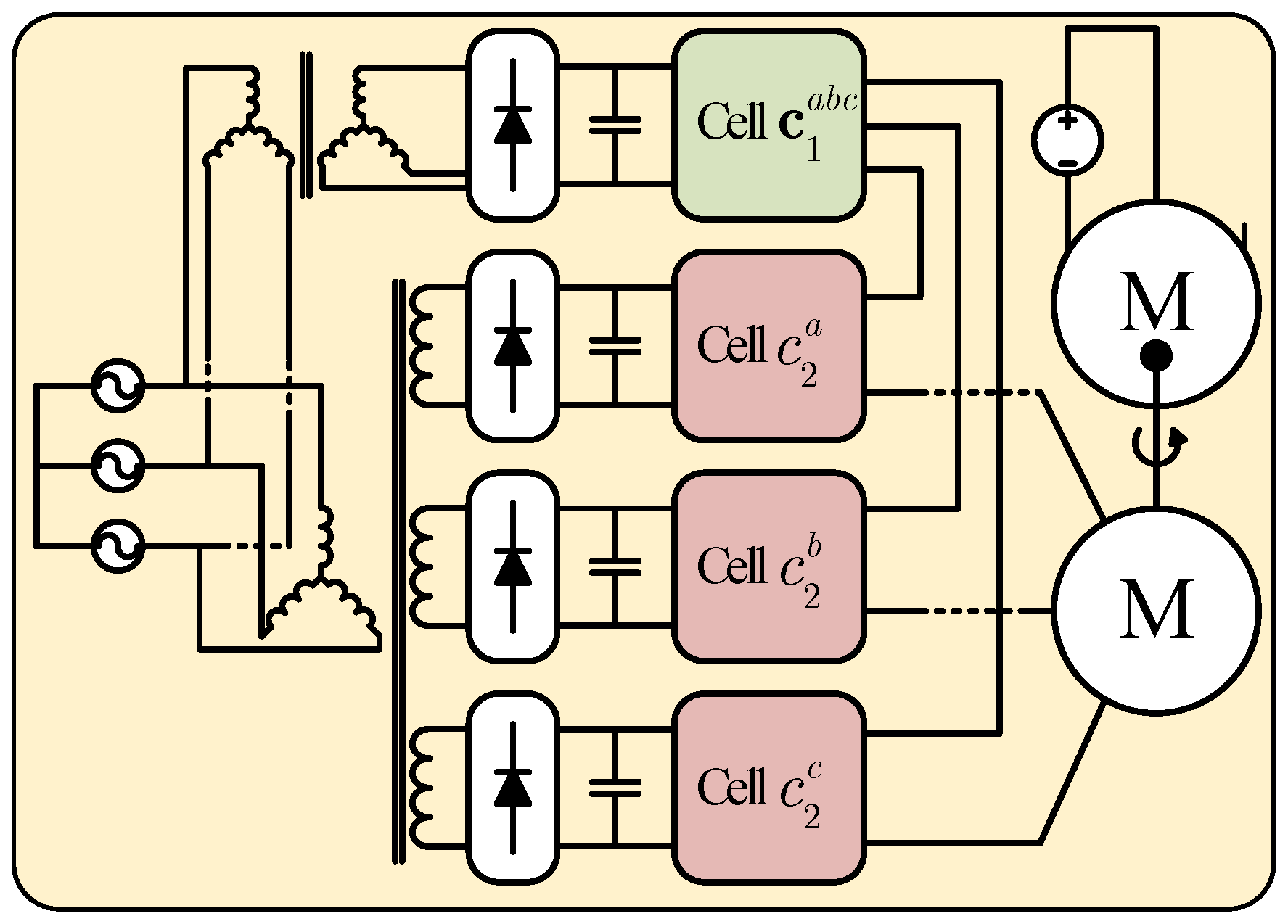
2.1. Hybrid Cascade Inverter
2.2. Motor Model Under the Field-Oriented Control Strategy
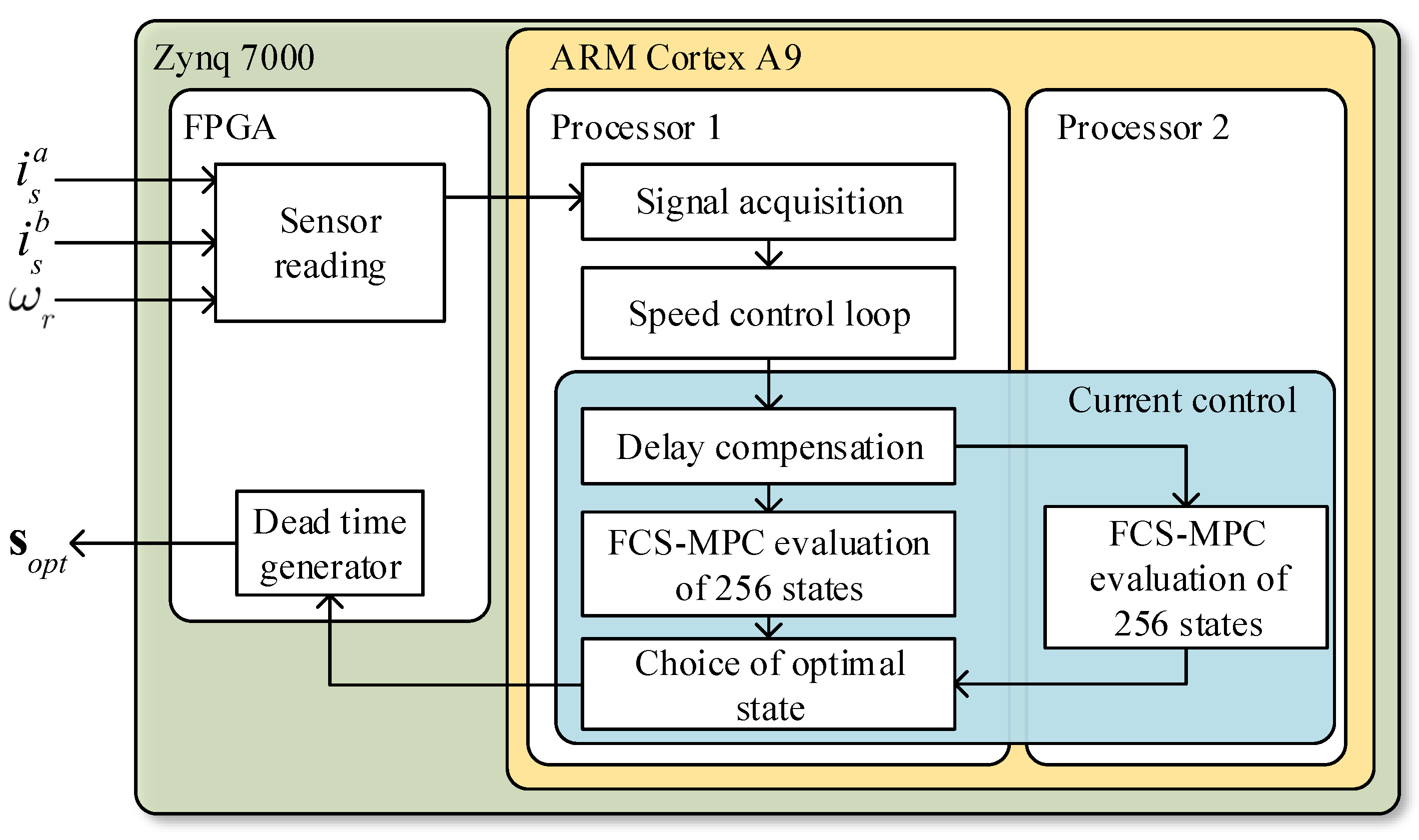
3. Finite-Control-Set Model Predictive Control
4. Proposals Under Evaluation
4.1. Input Restriction
4.2. Notch Filter
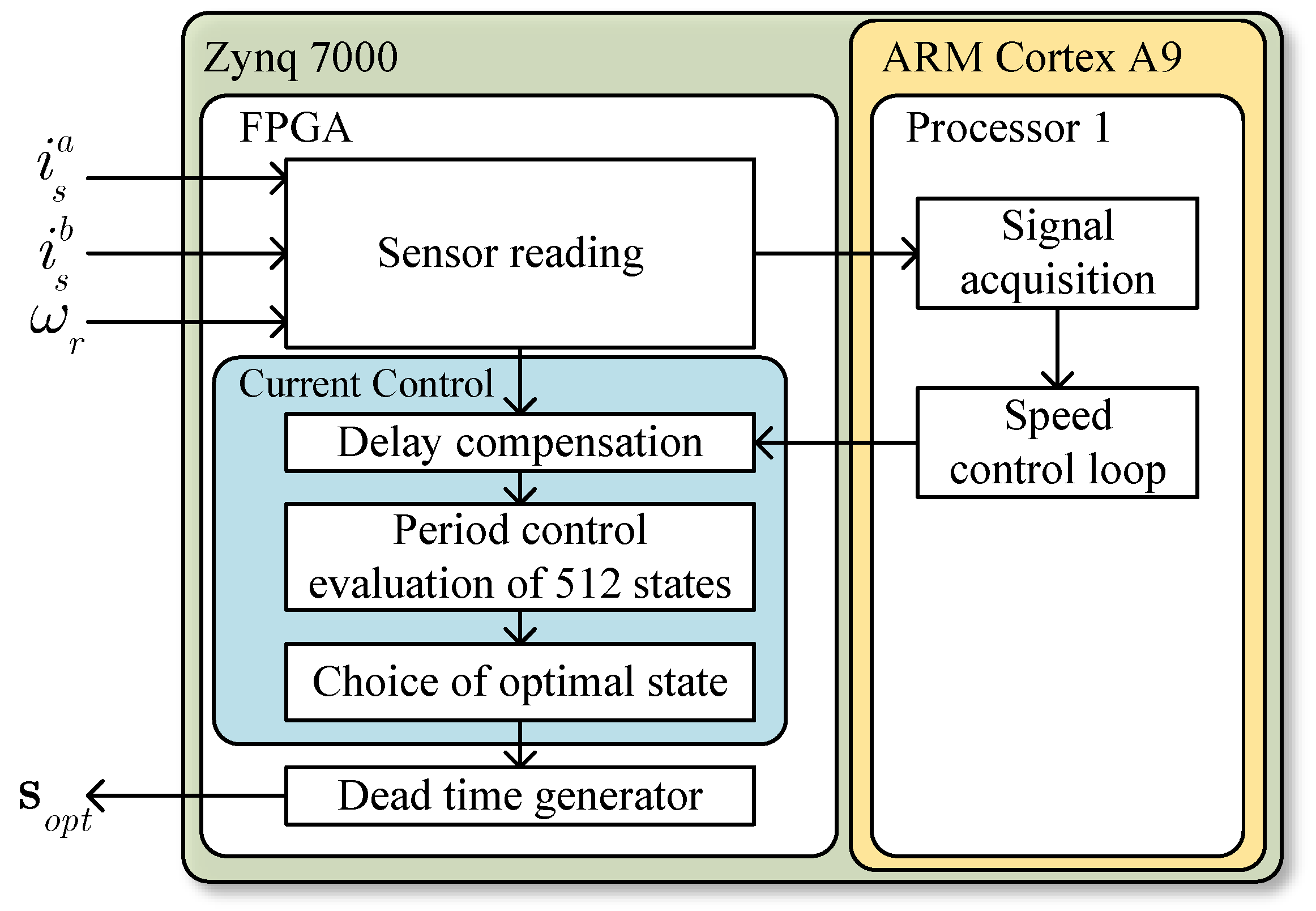
4.3. Period Control
4.4. PWM Restriction
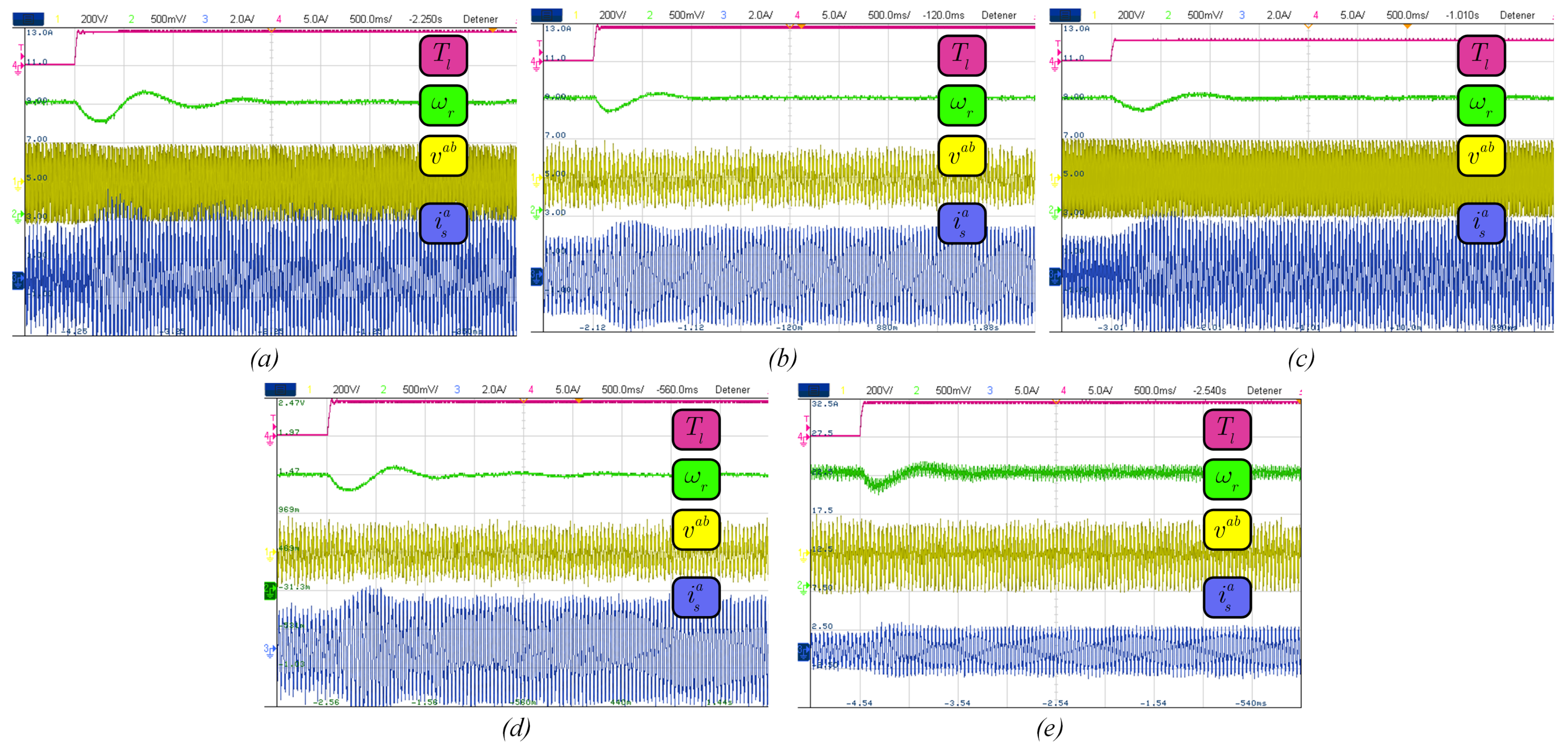
5. Experimental Results
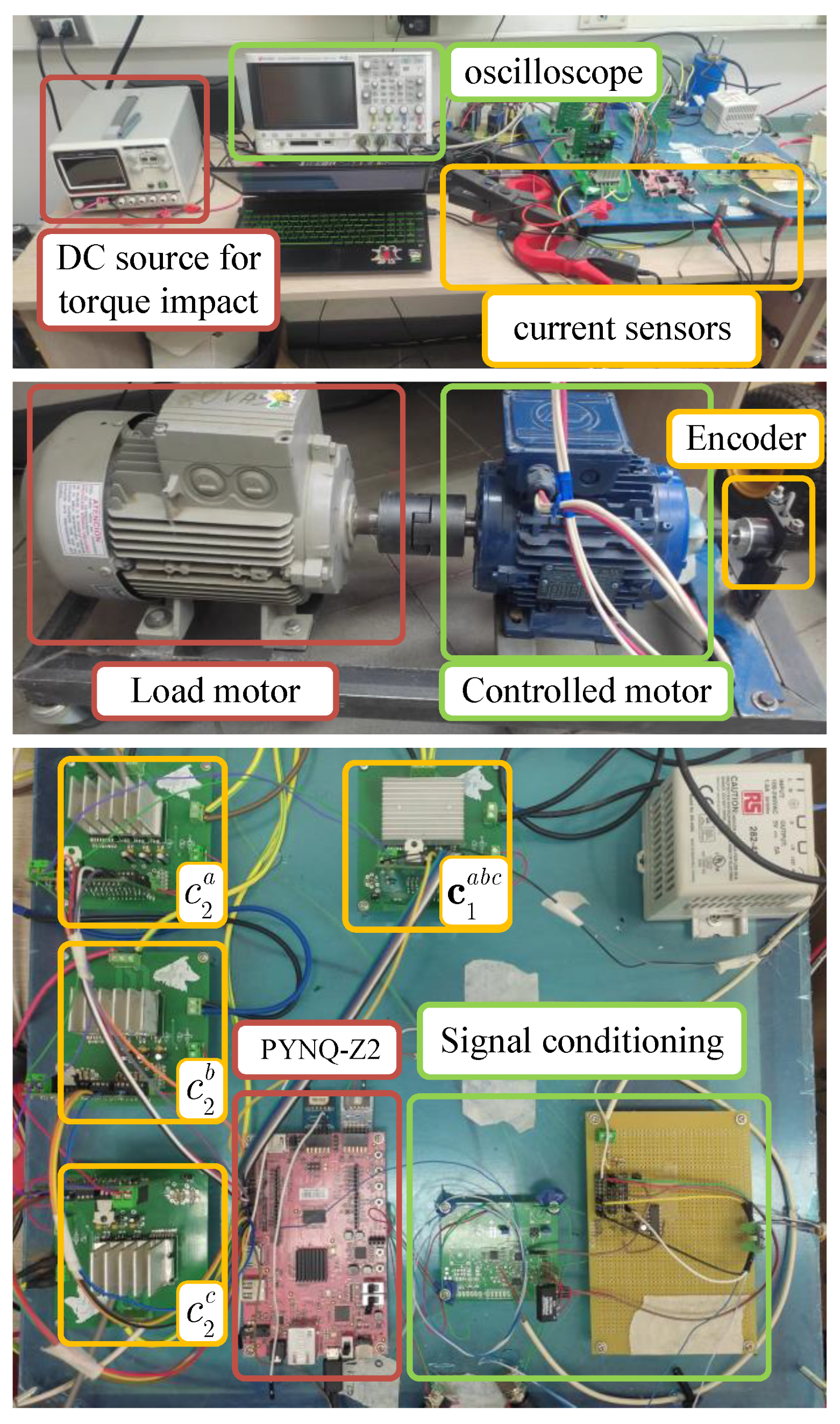
5.1. Hardware Implementation
5.2. Steady-State Performance
5.3. Dynamic Performance
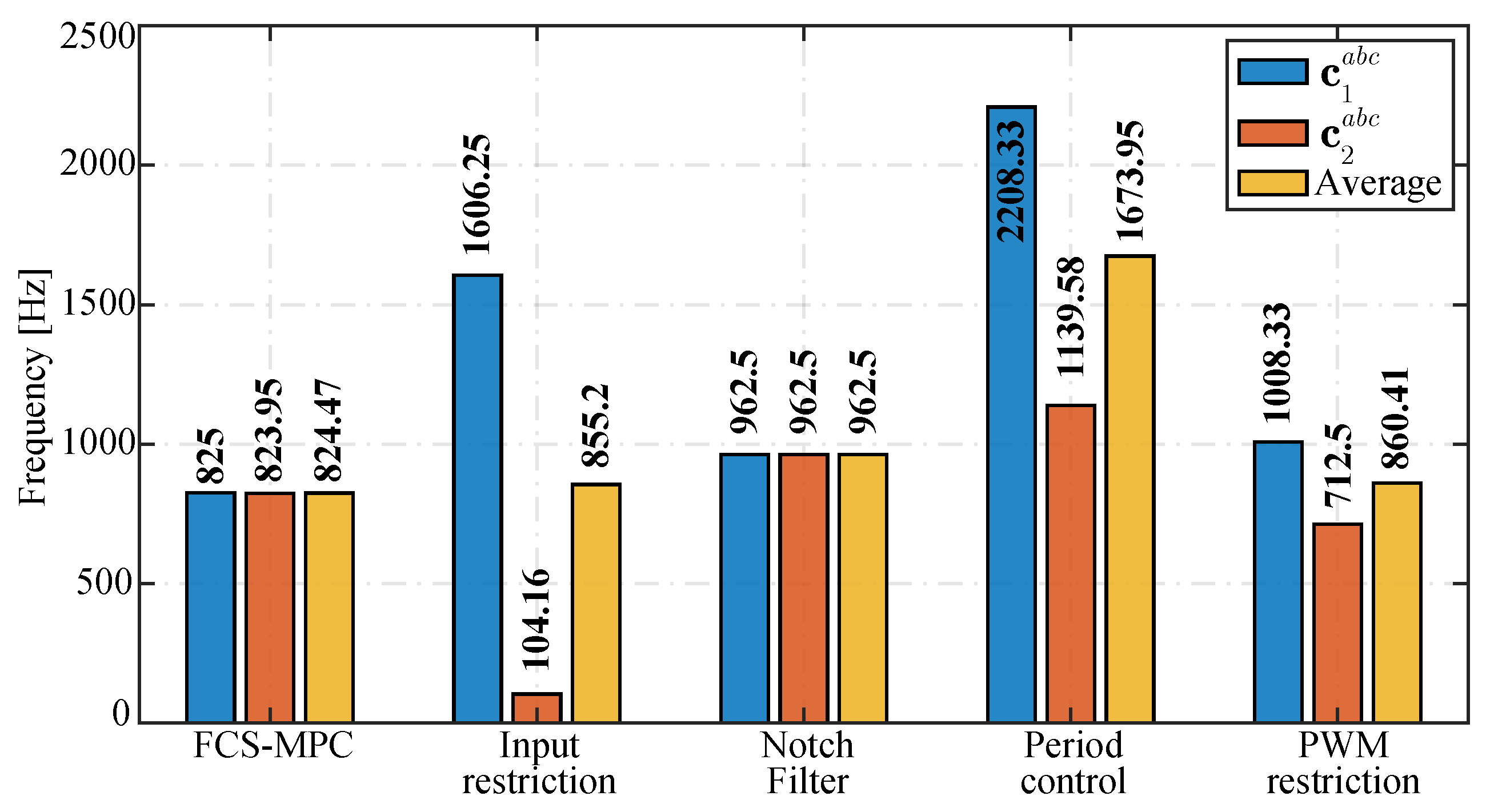
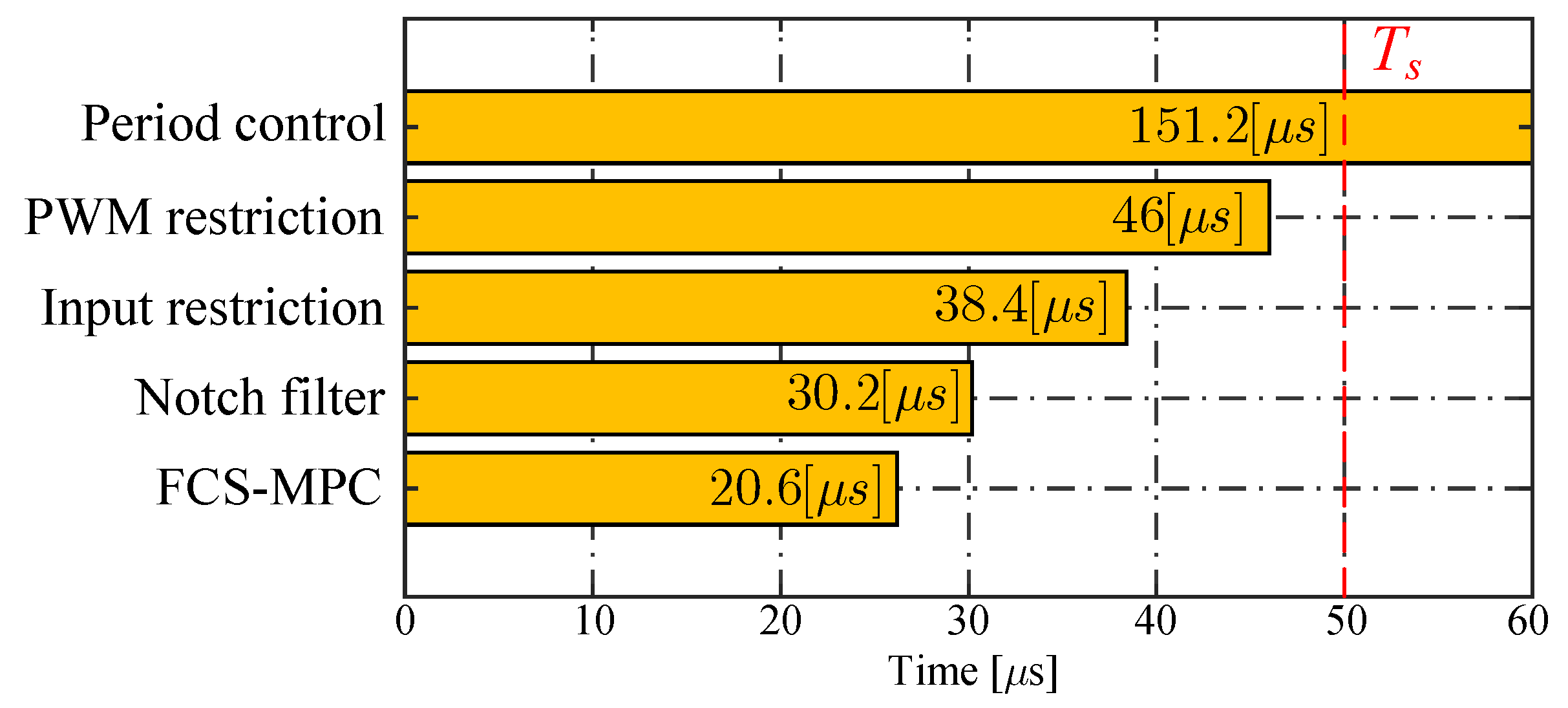
5.4. Computational Cost
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abu-Rub, H.; Holtz, J.; Rodriguez, J.; Baoming, G. Medium-voltage multilevel converters State of the art, challenges, and requirements in Industrial applications. IEEE Trans. Ind. Electron. 2010, 57, 2581–2596. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Pérez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Wu, B.; Pontt, J.o.; Kouro, S. Multilevel Voltage-Source-Converter Topologies for Industrial Medium-Voltage Drives. IEEE Trans. Ind. Electron. 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
- Du, Z.; Ozpineci, B.; Tolbert, L.M.; Chiasson, J.N. Inductorless DC-AC cascaded H-bridge multilevel boost inverter for electric/hybrid electric vehicle applications. In Proceedings of the IEEE Industry Applications Society, New Orleans, LA, USA, 23–27 September 2007; pp. 603–608. [Google Scholar] [CrossRef]
- Su, Y.C.; Wu, P.H.; Cheng, P.T. Design and Evaluation of a Control Scheme for the Hybrid Cascaded Converter in Grid Applications. IEEE Trans. Power Electron. 2020, 35, 3139–3147. [Google Scholar] [CrossRef]
- Bisht, N.; Das, A. A Circuit Topology of Cascaded H-Bridge STATCOM to Operate with Multiple Faulty Bypassed Cells. IEEE Trans. Ind. Appl. 2021, 57, 5345–5355. [Google Scholar] [CrossRef]
- Wiatr, P.; Kazmierkowski, M.P. Hybrid 5-level cascaded H-Bridge converter with model predictive controller. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 128–132. [Google Scholar] [CrossRef]
- Wiatr, P.; Kryński, A. Model predictive control of multilevel cascaded converter with boosting capability—Experimental results. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 589–599. [Google Scholar] [CrossRef][Green Version]
- Kouro, S.; Cortés, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model predictive control—A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Cortés, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive control in power electronics and drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Geyer, T.; Papafotiou, G.; Morari, M. Model predictive direct torque control—Part I: Concept, algorithm, and analysis. IEEE Trans. Ind. Electron. 2009, 56, 1894–1905. [Google Scholar] [CrossRef]
- Yaramasu, V.; Rivera, M.; Wu, B.; Rodriguez, J. Model predictive current control of two-level four-leg inverters—Part i: Concept, algorithm, and simulation analysis. IEEE Trans. Power Electron. 2013, 28, 3459–3468. [Google Scholar] [CrossRef]
- Cortés, P.; Rodríguez, J.; Quevedo, D.E.; Silva, C. Predictive Current Control Strategy with Imposed Load Current Spectrum. IEEE Trans. Power Electron. 2008, 23, 612–618. [Google Scholar] [CrossRef]
- Ramirez, R.O.; Baier, C.R.; Villarroel, F.; Espinoza, J.R.; Pou, J.; Rodriguez, J. A Hybrid FCS-MPC with Low and Fixed Switching Frequency without Steady-State Error Applied to a Grid-Connected CHB Inverter. IEEE Access 2020, 8, 223637–223651. [Google Scholar] [CrossRef]
- Moosavi, M.; Farivar, G.; Iman-Eini, H.; Shekarabi, S.M. A voltage balancing strategy with extended operating region for cascaded H-bridge converters. IEEE Trans. Power Electron. 2014, 29, 5044–5053. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Power Balance Optimization of Cascaded H-Bridge Multilevel Converters for Large-Scale Photovoltaic Integration. IEEE Trans. Power Electron. 2016, 31, 1108–1120. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Wu, X.; Yuan, Y.; Zhou, J. Parallel Implementation of Model Predictive Control for Multilevel Cascaded H-Bridge STATCOM With Linear Complexity. IEEE Trans. Ind. Electron. 2020, 67, 832–841. [Google Scholar] [CrossRef]
- Holtz, J. Advanced PWM and Predictive Control-An Overview. IEEE Trans. Ind. Electron. 2016, 63, 3837–3844. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Liegmann, E.; Makhamreh, H.; Heldwein, M.L.; Novak, M.; Rossi, M.; Abdelrahem, M.; Trabelsi, M.; Ahmed, M.; et al. Model-Predictive Control of Multilevel Inverters: Challenges, Recent Advances, and Trends. IEEE Trans. Power Electron. 2023, 38, 10845–10868. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Clare, J.C.; Degano, M.; Bifaretti, S. Modulated Model Predictive Control for a Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2015, 51, 1610–1620. [Google Scholar] [CrossRef]
- Rivera, M.; Perez, M.; Baier, C.; Munoz, J.; Yaramasu, V.; Wu, B.; Tarisciotti, L.; Zanchetta, P.; Wheeler, P. Predictive Current Control with fixed switching frequency for an NPC converter. In Proceedings of the IEEE International Symposium on Industrial Electronics, Buzios, Brazil, 3–5 June 2015; pp. 1034–1039. [Google Scholar] [CrossRef]
- Donoso, F.; Mora, A.; Cardenas, R.; Angulo, A.; Saez, D.; Rivera, M. Finite-Set Model-Predictive Control Strategies for a 3L-NPC Inverter Operating with Fixed Switching Frequency. IEEE Trans. Ind. Electron. 2018, 65, 3954–3965. [Google Scholar] [CrossRef]
- Alexandrou, A.D.; Adamopoulos, N.K.; Kladas, A.G. Development of a Constant Switching Frequency Deadbeat Predictive Control Technique for Field-Oriented Synchronous Permanent-Magnet Motor Drive. IEEE Trans. Ind. Electron. 2016, 63, 5167–5175. [Google Scholar] [CrossRef]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Rodriguez, J.; Leon, J.I. Switching Frequency Regulation for FCS-MPC Based on a Period Control Approach. IEEE Trans. Ind. Electron. 2018, 65, 5764–5773. [Google Scholar] [CrossRef]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Vazquez, S. Enhanced Switching Frequency Control in FCS-MPC for Power Converters. IEEE Trans. Ind. Electron. 2021, 68, 2470–2479. [Google Scholar] [CrossRef]
- Tomlinson, M.; Mouton, H.D.T.; Kennel, R.; Stolze, P. A Fixed Switching Frequency Scheme for Finite-Control-Set Model Predictive Control-Concept and Algorithm. IEEE Trans. Ind. Electron. 2016, 63, 7662–7670. [Google Scholar] [CrossRef]
- Urrutia, M.; Cárdenas, R.; Clare, J.C.; Watson, A. Circulating Current Control for the Modular Multilevel Matrix Converter Based on Model Predictive Control. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6069–6085. [Google Scholar] [CrossRef]
- Urrutia, M.; Cárdenas, R.; Clare, J.C.; Díaz, M.; Watson, A. Continuous Set Model Predictive Control for Energy Management of Modular Multilevel Matrix Converters. IEEE Trans. Power Electron. 2022, 37, 5731–5748. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, W.; Chen, Y.; Gao, N.; Chen, J.; Koutroulis, E.; Chung, H.S.H.; Liserre, M.; Blaabjerg, F. Enhanced Deadbeat Control-Model Predictive Control Strategy of Grid-Connected Power Converters With LCL Filter. IEEE Trans. Ind. Electron. 2024, 71, 15826–15834. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, L.; Liu, C.; Yang, Z.; Wu, X. Deadbeat Model Predictive Control for Modular Multilevel Matrix Converter Under Unbalanced Grid Conditions. IEEE Trans. Power Electron. 2025, 40, 1258–1271. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, H.; Li, C.; Lang, X.; Yeoh, S.S.; Yang, T.; Rivera, M.; Bozhko, S.; Wheeler, P. A Low-Complexity Optimal Switching Time-Modulated Model-Predictive Control for PMSM With Three-Level NPC Converter. IEEE Trans. Transp. Electrif. 2020, 6, 1188–1198. [Google Scholar] [CrossRef]
- Harbi, I.; Ahmed, M.; Hackl, C.M.; Rodriguez, J.; Kennel, R.; Abdelrahem, M. Low-Complexity Dual-Vector Model Predictive Control for Single-Phase Nine-Level ANPC-Based Converter. IEEE Trans. Power Electron. 2023, 38, 2956–2971. [Google Scholar] [CrossRef]
- Schuetz, D.; Osório, C.R.D.; Maccari, L.A.; Lima, D.M.; Carnielutti, F.d.M.; Montagner, V.F.; Pinheiro, H. Space Vector Modulated Model Predictive Control for Grid-Tied Converters. IEEE Trans. Ind. Inform. 2023, 19, 414–425. [Google Scholar] [CrossRef]
- Matias, M.A.; Vazquez, S.; Wilson-Veas, A.H.; Kouro, S.; Rojas, C.A.; Leon, J.I.; Franquelo, L.G. Extended Period Control Approach FCS-MPC for Three Phase NPC Power Converters. IEEE Trans. Power Electron. 2025, 40, 4927–4937. [Google Scholar] [CrossRef]
- Baier, C.R.; Ramirez, R.O.; Marciel, E.I.; Hernández, J.C.; Melín, P.E.; Espinosa, E.E. FCS-MPC Without Steady-State Error Applied to a Grid-Connected Cascaded H-Bridge Multilevel Inverter. IEEE Trans. Power Electron. 2021, 36, 11785–11799. [Google Scholar] [CrossRef]
- Aguirre, M.; Vazquez, S.; Alcaide, A.M.; Portillo, R.; Kouro, S.; Leon, J.I.; Franquelo, L.G. Period Control Approach Finite Control Set Model Predictive Control Switching Phase Control for Interleaved DC/DC Converters. IEEE Trans. Ind. Electron. 2024, 71, 8304–8312. [Google Scholar] [CrossRef]
- OPAL-RT. OP4512 SIMULATOR. 2024. Available online: https://www.opal-rt.com/simulator-platform-op4512/ (accessed on 3 January 2025).
- dSPACE. MicroLabBox. 2024. Available online: https://www.dspace.com/en/pub/home/products/hw/microlabbox.cfm (accessed on 3 January 2025).
- Plexim. RT Box 1. 2024. Available online: https://www.plexim.com/products/rt_box/rt_box_1 (accessed on 3 January 2025).
- Abughalieh, K.M.; Alawneh, S.G. A Survey of Parallel Implementations for Model Predictive Control. IEEE Access 2019, 7, 34348–34360. [Google Scholar] [CrossRef]
- Xu, F.; Guo, Z.; Chen, H.; Ji, D.; Qu, T. A Custom Parallel Hardware Architecture of Nonlinear Model-Predictive Control on FPGA. IEEE Trans. Ind. Electron. 2022, 69, 11569–11579. [Google Scholar] [CrossRef]
- MarketsandMarkets. Electric Motor Market Report. Latest Industry Trends 2026. 2025. Available online: https://www.marketsandmarkets.com/Market-Reports/electric-motor-market-alternative-fuel-vehicles-717.html (accessed on 3 January 2025).
- Williamson, S.S.; Rathore, A.K.; Musavi, F. Industrial Electronics for Electric Transportation: Current State-of-the-Art and Future Challenges. IEEE Trans. Ind. Electron. 2015, 62, 3021–3032. [Google Scholar] [CrossRef]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Cortes, P.; Rodriguez, J.; Silva, C.; Flores, A. Delay compensation in model predictive current control of a three-phase inverter. IEEE Trans. Ind. Electron. 2012, 59, 1323–1325. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, H.; Zhao, N.; Li, C.; Xu, D. Sensorless Control of IPMSM Drives Using a Pseudo-Random Phase-Switching Fixed-Frequency Signal Injection Scheme. IEEE Trans. Ind. Electron. 2018, 65, 7660–7671. [Google Scholar] [CrossRef]
- Leon, J.I.; Vazquez, S.; Franquelo, L.G. Multilevel Converters: Control and Modulation Techniques for Their Operation and Industrial Applications. Proc. IEEE 2017, 105, 2066–2081. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters; IEEE: Piscataway, NJ, USA, 2003; p. 744. [Google Scholar] [CrossRef]
- Instruments, T. F28379D LaunchPad development kit for C2000 Delfino MCU. 2024. Available online: https://www.ti.com/tool/LAUNCHXL-F28379D (accessed on 3 January 2025).
- Cortés, P.; Kouro, S.; Rocca, B.L.; Vargas, R.; Rodríguez, J.; León, J.I.; Vazquez, S.; Franquelo, L.G. Guidelines for weighting factors design in model predictive control of power converters and drives. In Proceedings of the IEEE International Conference on Industrial Technology, Churchill, VIC, Australia, 10–13 February 2009. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T. Guidelines for the Design of Finite Control Set Model Predictive Controllers. IEEE Trans. Power Electron. 2019, 8993, 7434–7450. [Google Scholar] [CrossRef]
- Xilinx, A. XUP PYNQ-Z2. 2024. Available online: https://www.amd.com/es/corporate/university-program/aup-boards/pynq-z2.html (accessed on 3 January 2025).
- Xilinx, A. High Level Design Features. 2024. Available online: https://www.xilinx.com/products/design-tools/vivado/high-level-design.html (accessed on 3 January 2025).


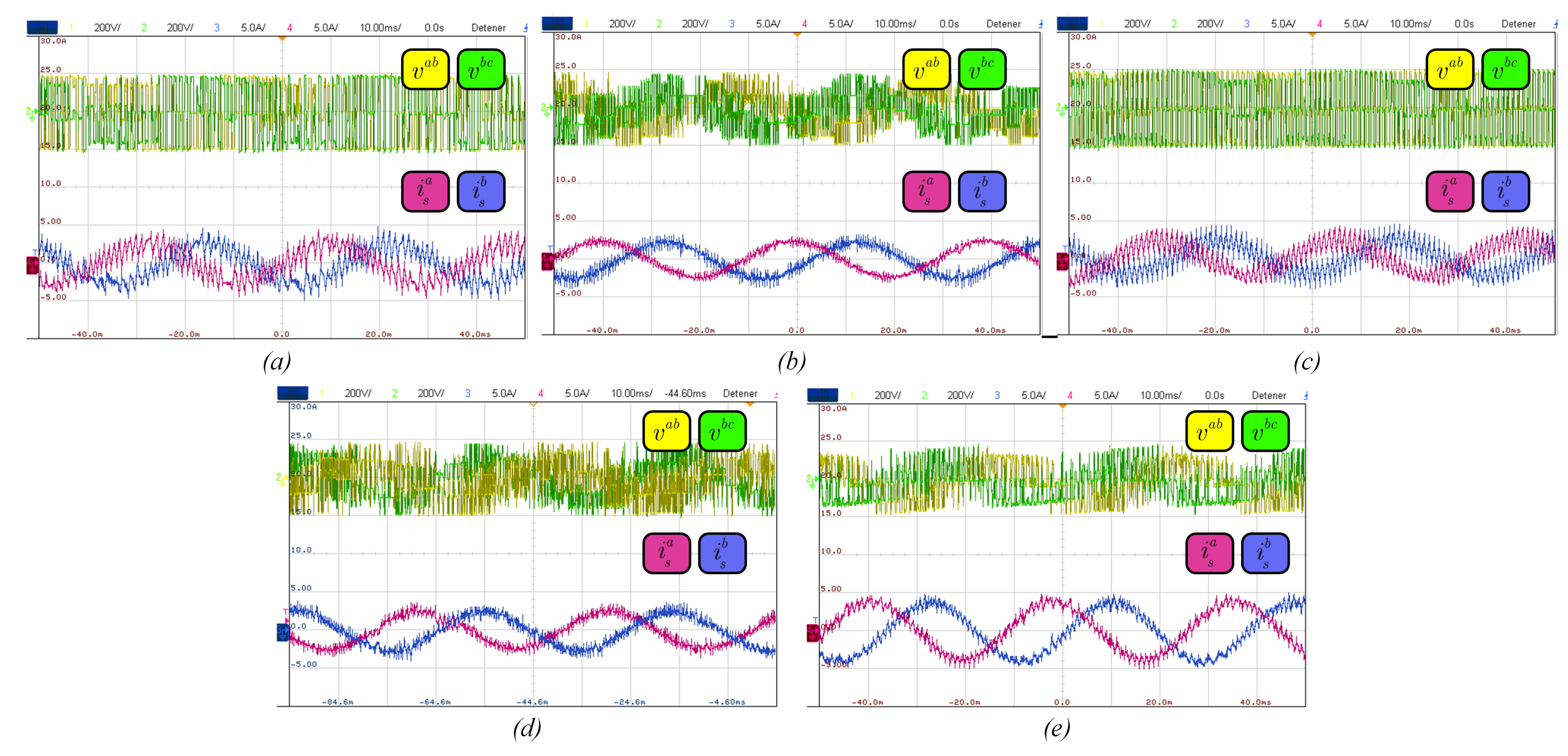

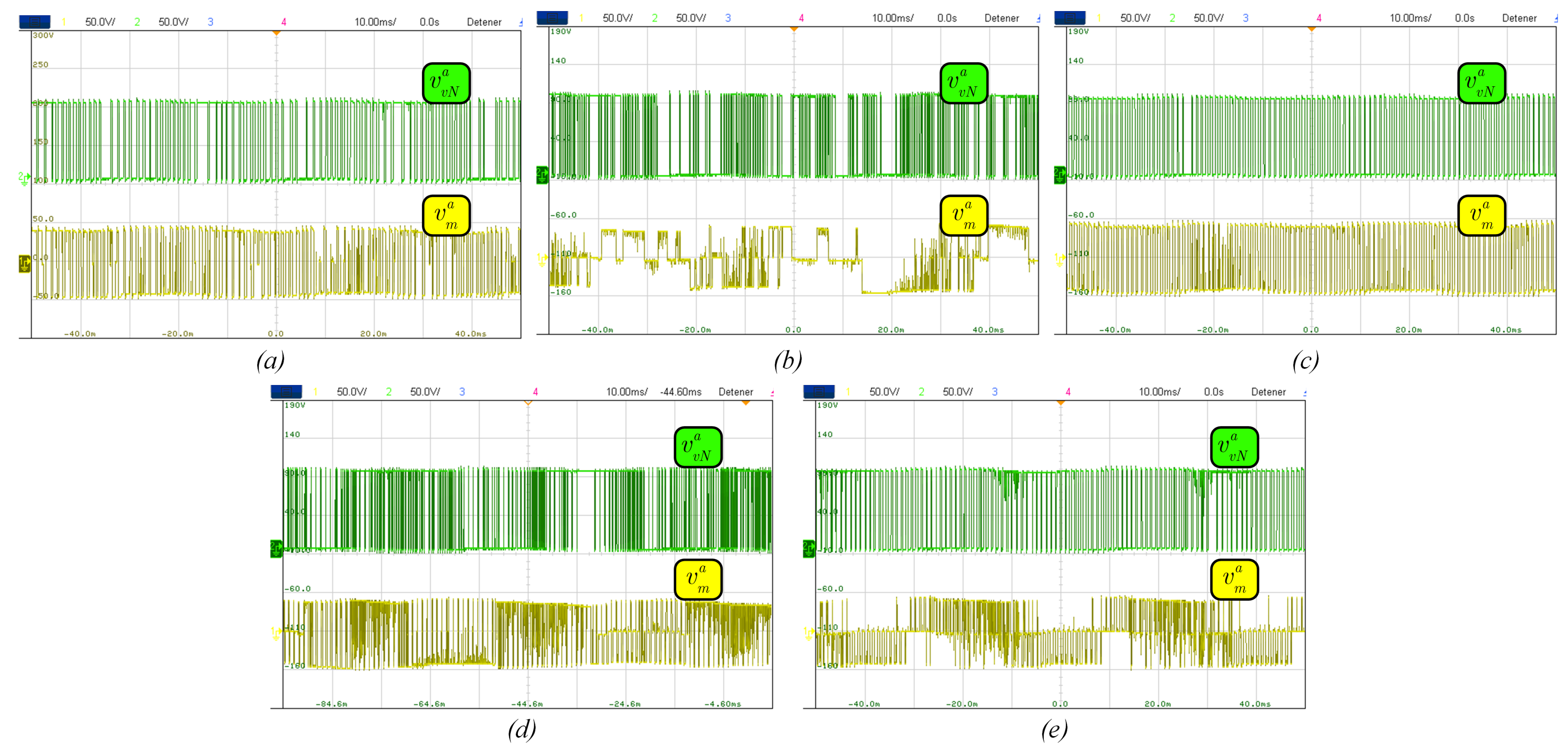


| Parameter | Description | Values of Controlled Motor | Values of Load Motor |
|---|---|---|---|
| Stator resistance | |||
| Rotor resistance | |||
| Stator inductance | H | H | |
| Rotor inductance | H | H | |
| Magnetizing inductance | 0.1175 H | H | |
| J | Moment of inertia | 0.05 kg·m2 | 0.1 kg·m2 |
| B | Inertia coefficient | 0.005 Nm/s | 0.005 Nm/s |
| p | Number of pole pairs | 2 | 2 |
| Nominal values | |||
| Voltage | 190 V | 400 V | |
| Frequency | 25 Hz | 50 Hz | |
| Speed | 74.874 rad/s | 148.7 rad/s | |
| Current | 4 A | A | |
| Current d | A | A | |
| Current q | A | A | |
| Torque | 1.338 Nm | 13.312 Nm |
| Parameter | Description | Value |
|---|---|---|
| Conventional FCS-MPC | ||
| Sampling time | 200 μs * | |
| Input restriction | ||
| Sampling time | 50 μs | |
| Weighting factor | ||
| Notch filter | ||
| Sampling time | 50 μs | |
| Filter coefficient | ||
| Filter coefficient | ||
| Filter coefficient | ||
| Filter coefficient | ||
| Filter coefficient | ||
| Period control | ||
| Sampling time | 50 μs | |
| Weighting factor | ||
| Period reference | 1 ms (40 p.u.) | |
| PWM restriction | ||
| Sampling time | 50 μs | |
| Weighting factor | 2 | |
| Proportional gain | ||
| Integral gain | ||
| Carrier frequency of H-bridge | 500 Hz (20 p.u.) ** | |
| Carrier frequency of 2L-VSI | 1000 Hz (40 p.u.) ** |
| Standard Error Mean | Mean Square Error | |||||||
|---|---|---|---|---|---|---|---|---|
| FCS-MPC | ||||||||
| Input restriction | ||||||||
| Notch filter | ||||||||
| Period control | ||||||||
| PWM restriction | ||||||||
| THD (%) | Amp. | THD (%) | Amp. | THD (%) | Amp. | THD (%) | Amp. | |
|---|---|---|---|---|---|---|---|---|
| FCS-MPC | ||||||||
| Input restriction | ||||||||
| Notch filter | ||||||||
| Period control | ||||||||
| PWM restriction | ||||||||
| Before Optimization | During Optimization | ||||||
|---|---|---|---|---|---|---|---|
| Sum | Mult. | Comp. | Sum | Mult. | Comp. | Total | |
| FCS-MPC | 8 | 14 | 0 | 3 | 4 | 0 | |
| Input restriction | 8 | 14 | 0 | 5 | N | ||
| Notch filter | 14 | 22 | 0 | 5 | 6 | 0 | |
| Period control | |||||||
| PWM restriction | 17 | 22 | N | 4 | 4 | N | |
| FCS-MPC | Input Restriction | Notch Filter | Period Control | PWM Restriction | |
|---|---|---|---|---|---|
| Switching frequency | Dependent on | * Dependent on weight factor | Dependent on the filter parameters | Dependent on weight factor | Dependent on carrier frequency ✓ |
| Harmonic spectrum | Spread | Spread | Concentrated ✓ | Concentrated ✓ | Concentrated ✓ |
| Power distribution | No | No | No | No | Yes ✓ |
| Computational cost | Low ✓ | Medium | Low ✓ | Very high | Medium |
| Standard mean error | Medium | Low ✓ | High | Medium | Very low ✓ |
| Mean square error | High | Low ✓ | Very high | Low ✓ | Low ✓ |
| Parameters to tune | 0 | 1 | Dependent on order filter | 1 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arévalo, M.E.; Ramírez, R.O.; Baier, C.R.; Villarroel, F.A.; Espinoza, J.R.; Urra-González, F.P. Comparison of Fixed Switching Frequency FCS-MPC Strategies Applied to a Multilevel Converter: A Case Study of a Hybrid Cascade Converter Based on 2L-VSI and H-Bridge Converters. Processes 2025, 13, 1214. https://doi.org/10.3390/pr13041214
Arévalo ME, Ramírez RO, Baier CR, Villarroel FA, Espinoza JR, Urra-González FP. Comparison of Fixed Switching Frequency FCS-MPC Strategies Applied to a Multilevel Converter: A Case Study of a Hybrid Cascade Converter Based on 2L-VSI and H-Bridge Converters. Processes. 2025; 13(4):1214. https://doi.org/10.3390/pr13041214
Chicago/Turabian StyleArévalo, Mauricio E., Roberto O. Ramírez, Carlos R. Baier, Felipe A. Villarroel, José R. Espinoza, and Fernando P. Urra-González. 2025. "Comparison of Fixed Switching Frequency FCS-MPC Strategies Applied to a Multilevel Converter: A Case Study of a Hybrid Cascade Converter Based on 2L-VSI and H-Bridge Converters" Processes 13, no. 4: 1214. https://doi.org/10.3390/pr13041214
APA StyleArévalo, M. E., Ramírez, R. O., Baier, C. R., Villarroel, F. A., Espinoza, J. R., & Urra-González, F. P. (2025). Comparison of Fixed Switching Frequency FCS-MPC Strategies Applied to a Multilevel Converter: A Case Study of a Hybrid Cascade Converter Based on 2L-VSI and H-Bridge Converters. Processes, 13(4), 1214. https://doi.org/10.3390/pr13041214









