A Prediction of the Monthly Average Daily Solar Radiation on a Horizontal Surface in Saudi Arabia Using Artificial Neural Network Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Regions and Datasets
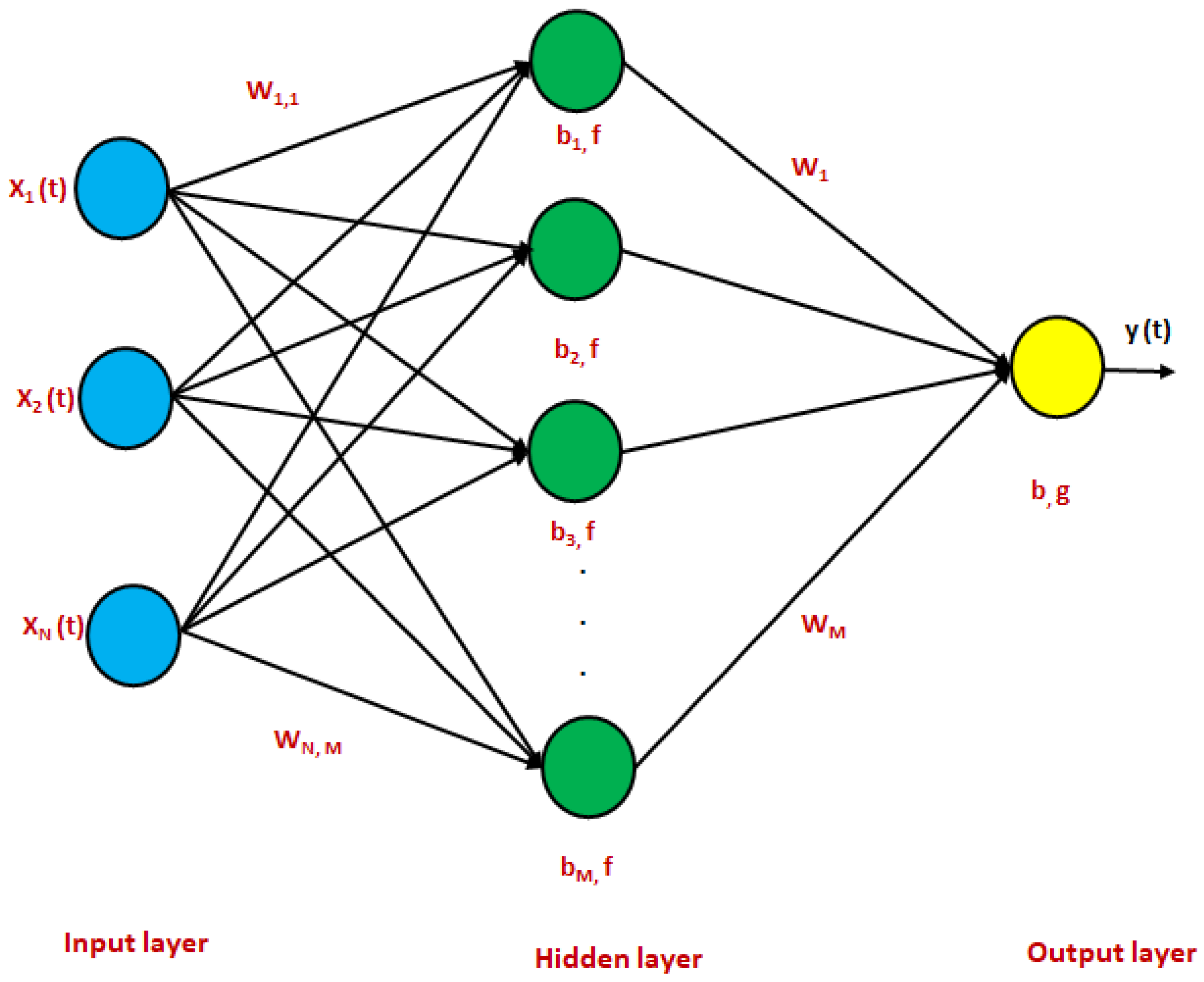
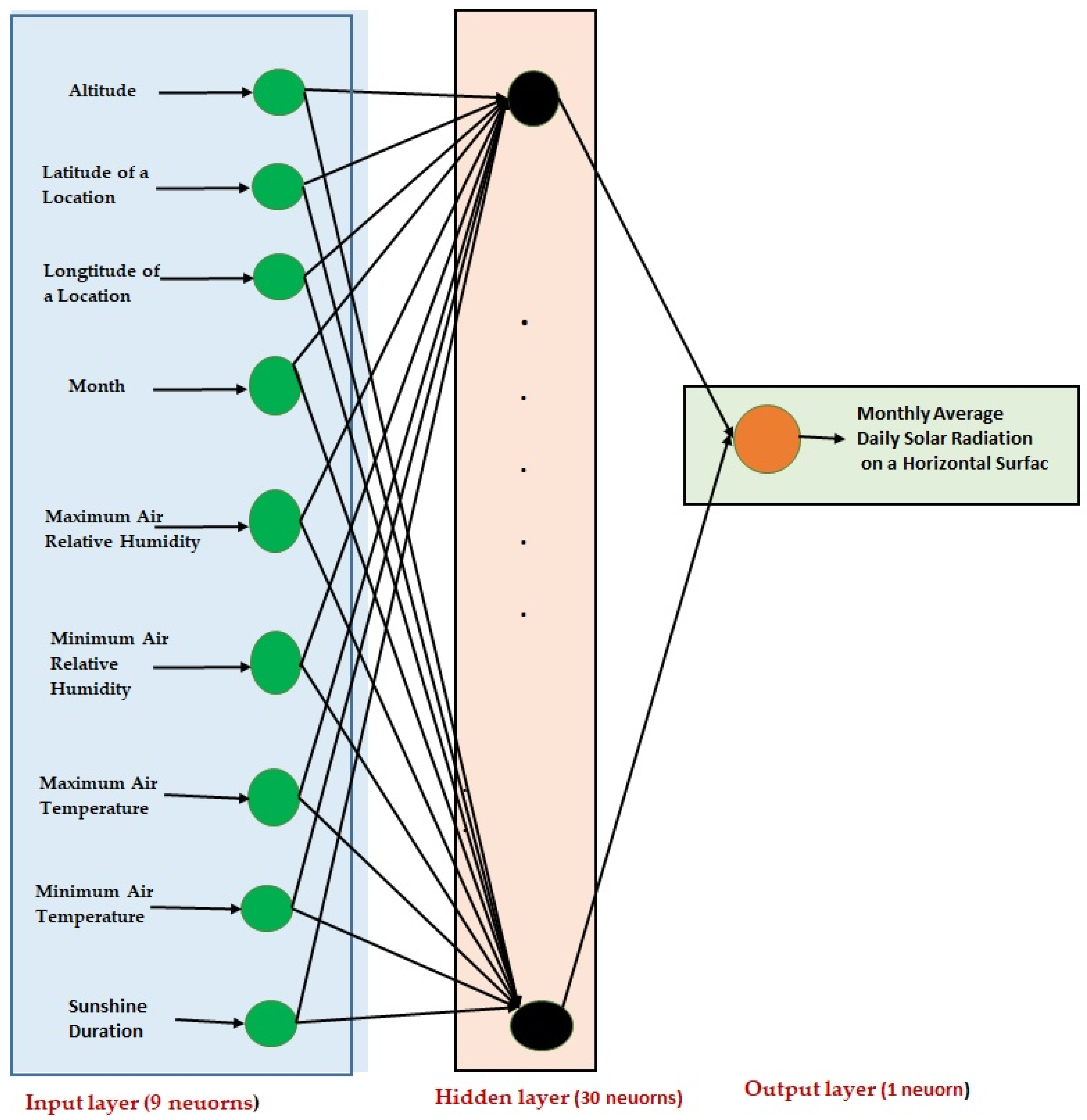
2.2. Building a Model to Estimate MADSR on Horizontal Surfaces Using an Artificial Neural Network Approach
2.3. Sensitivity Analysis of the Established ANN Model for Predicting the MADSR on Horizontal Surfaces
2.4. Validation Performance of the ANN Model
3. Results and Discussion
3.1. Solar Radiation and Input Parameters Analysis
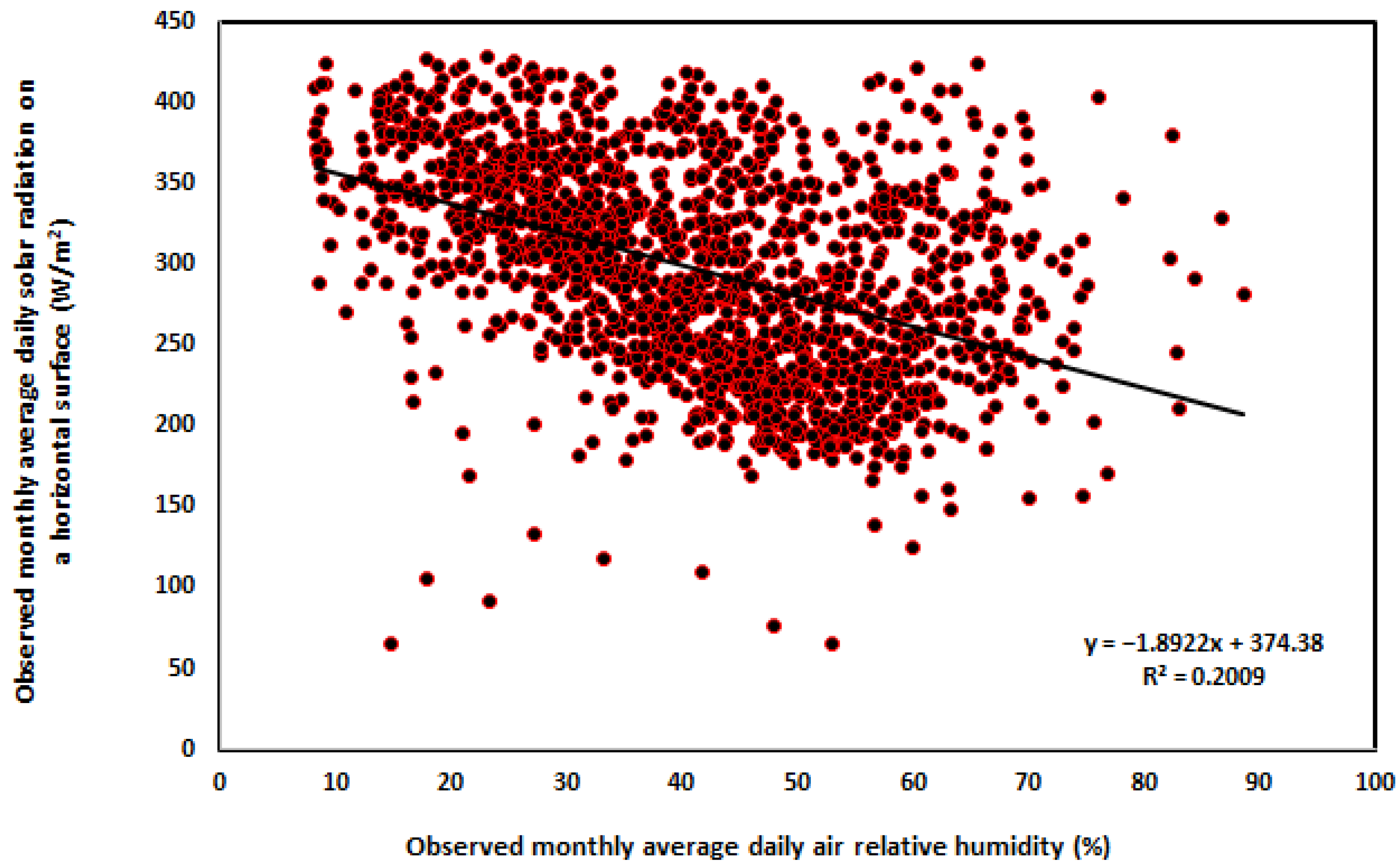
3.1.1. Air Relative Humidity
3.1.2. Air Temperature
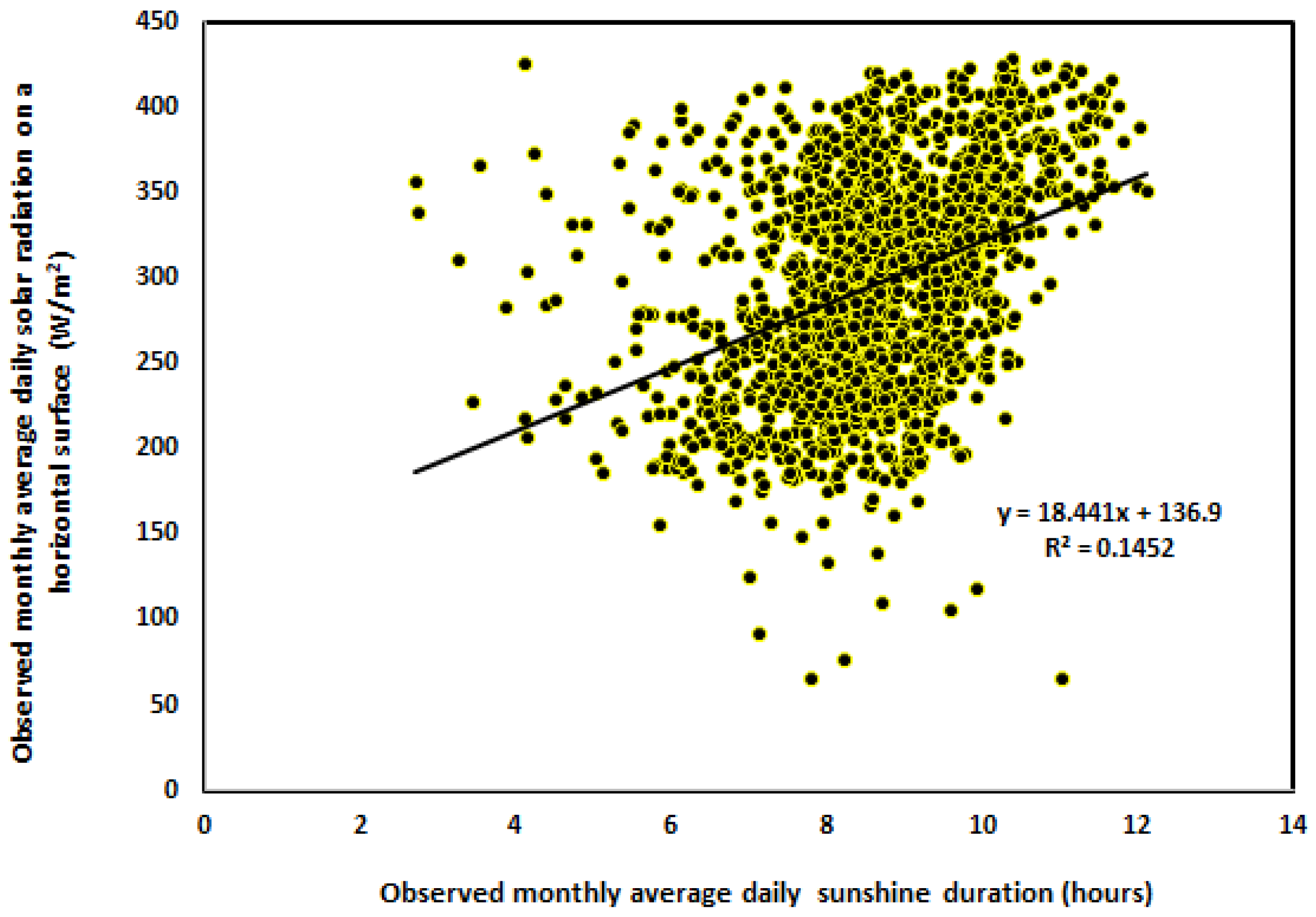
3.1.3. Sunshine Hours
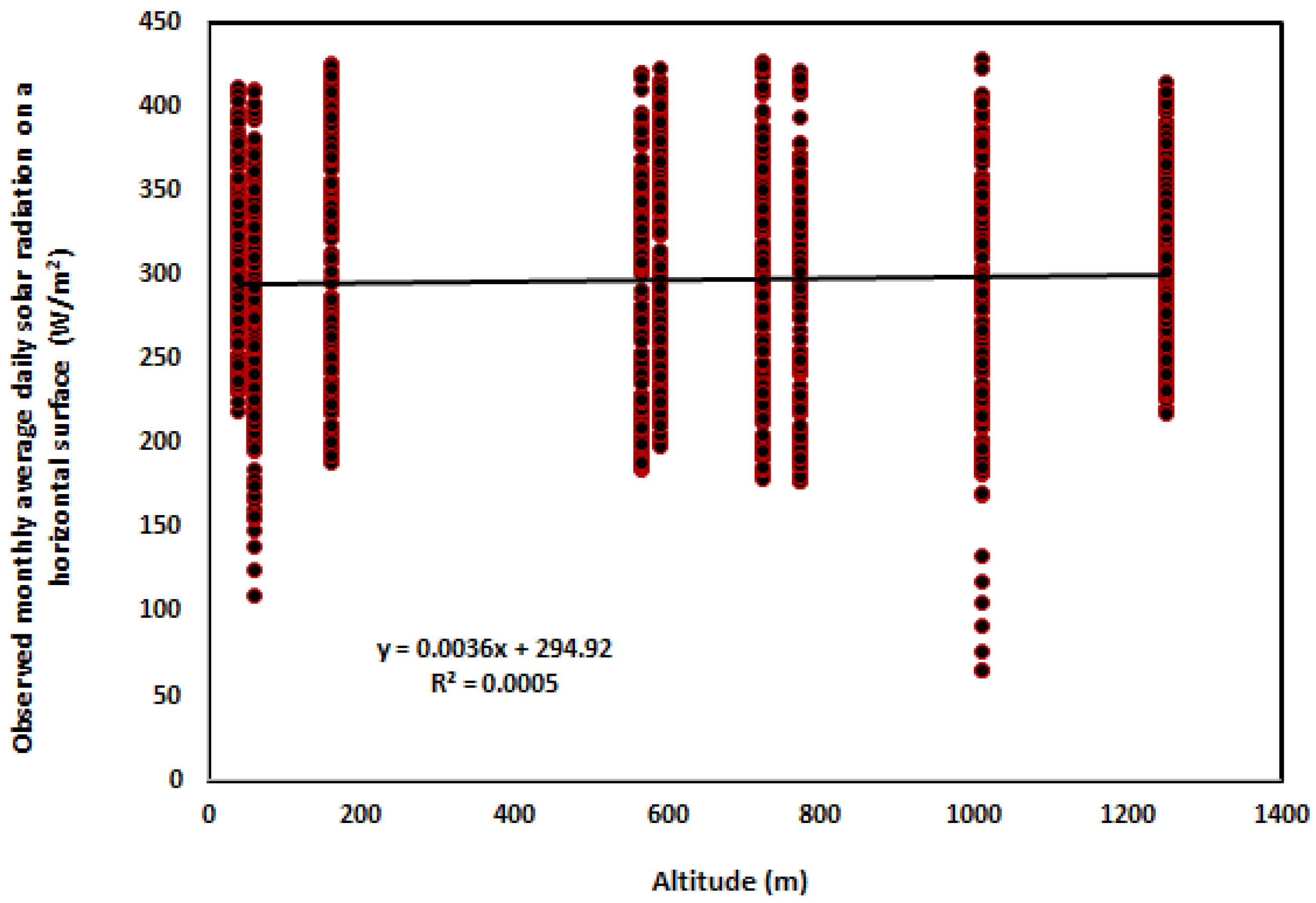
3.1.4. Altitude
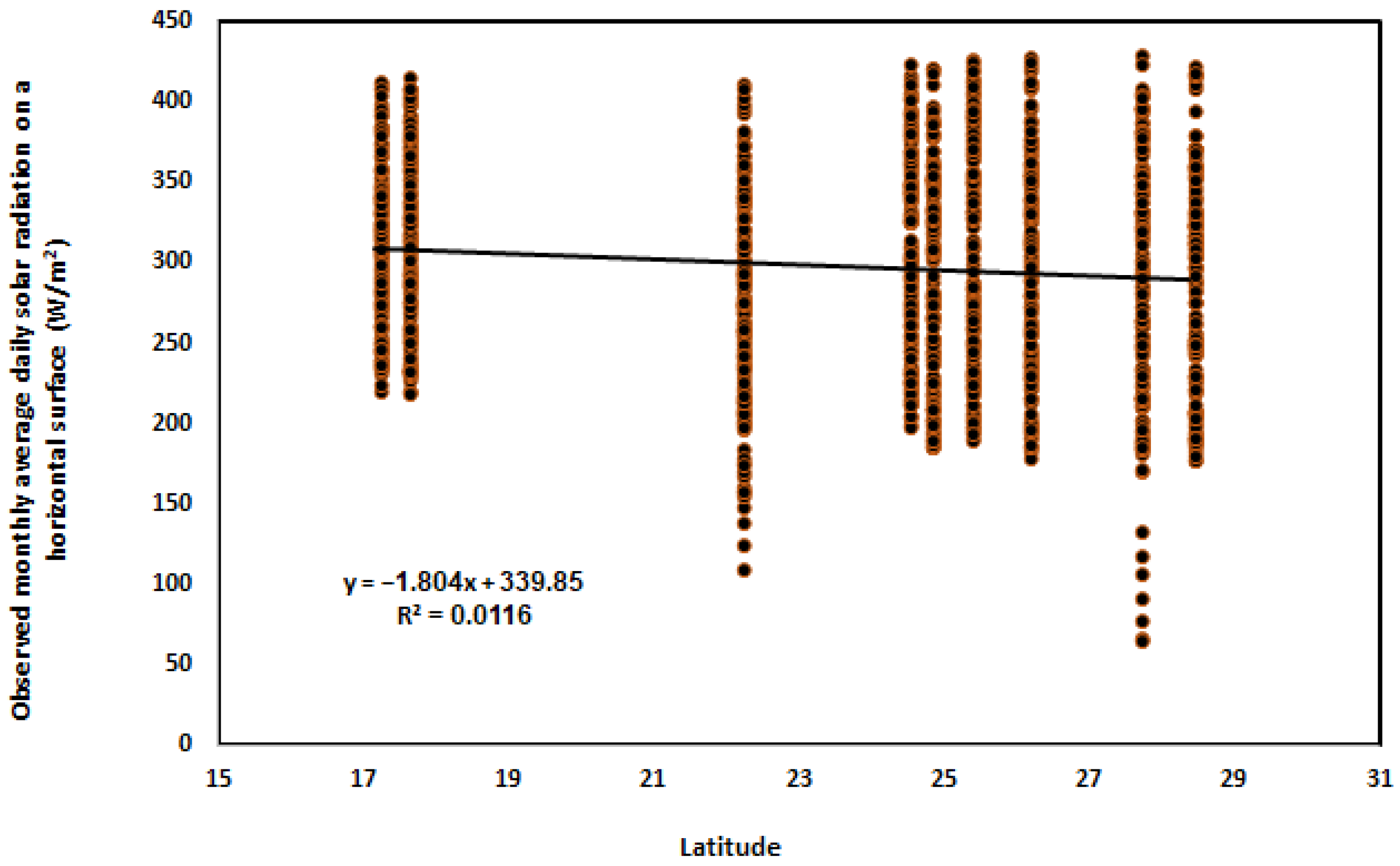
3.1.5. Latitude and Longitude Coordinates
3.1.6. Month of the Year
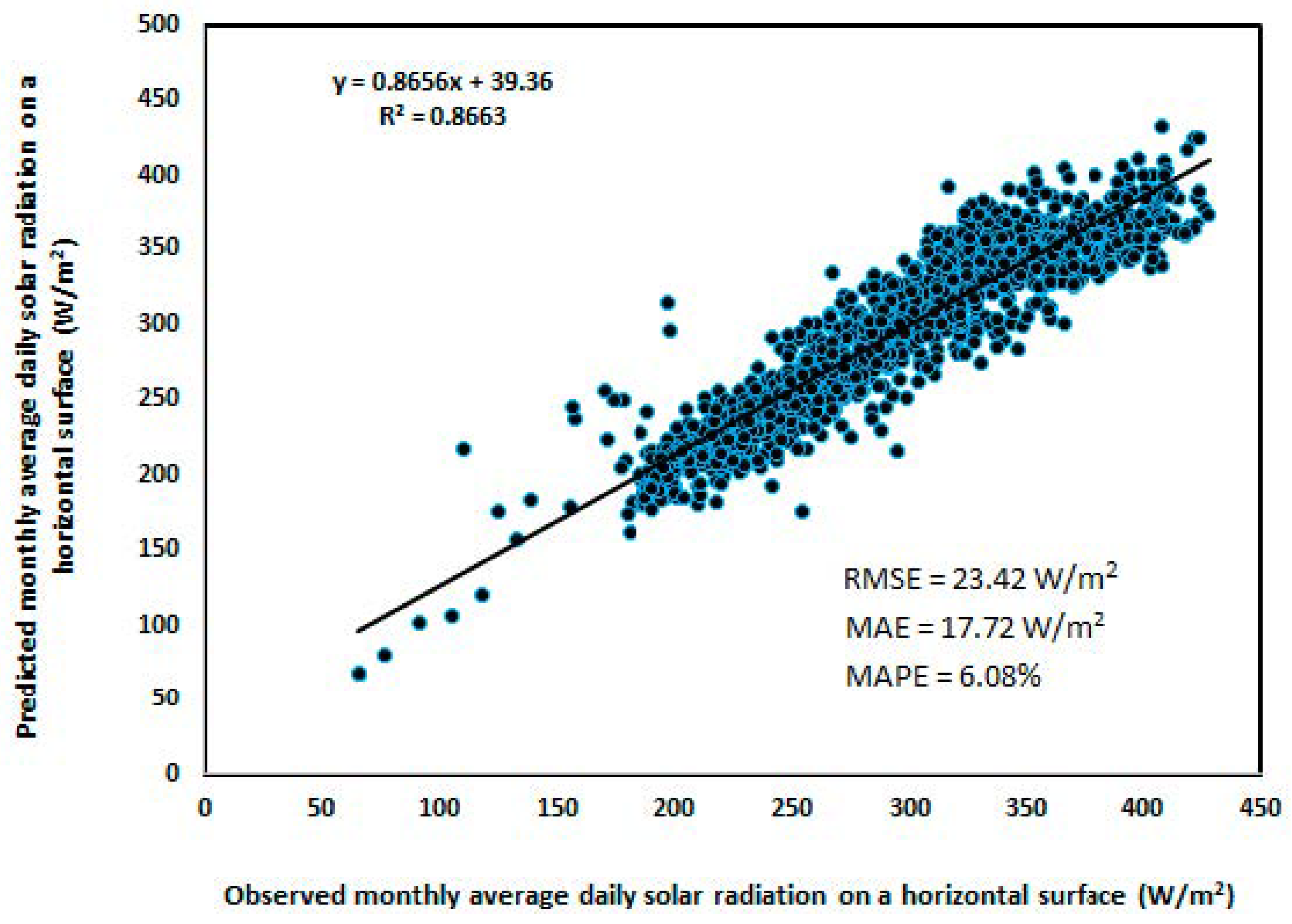
3.2. Performance of the Recognized ANN Model for MADSR on Horizontal Surface Prediction
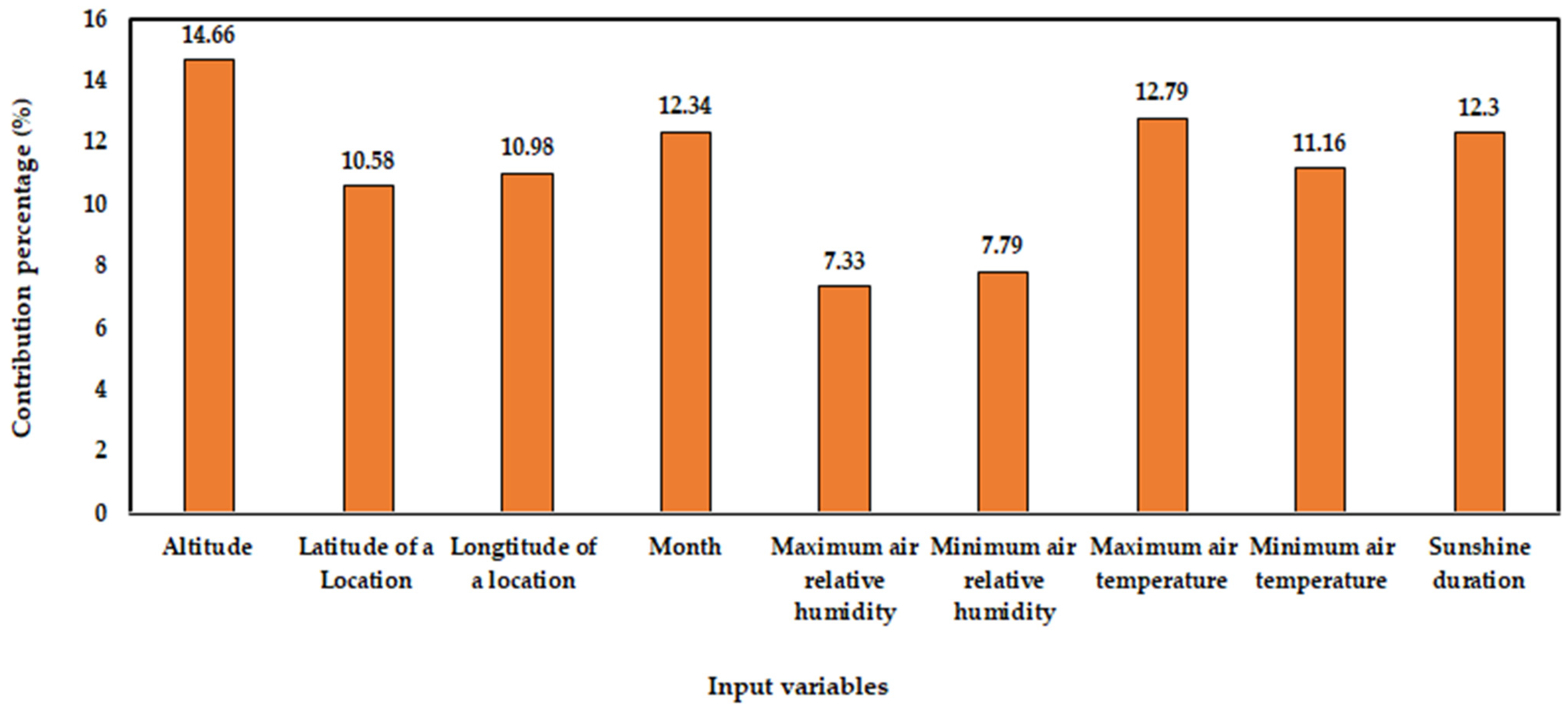
3.3. Contribution of Each Input Parameter to the Prediction of MADSR on a Horizontal Surface Using the Developed ANN Model
3.4. Utilizing Developed ANN Model Weights and Biases to Forecast MADSR on a Horizontal Surface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The International Energy Agency. Available online: https://www.iea.org/energy-system/renewables (accessed on 1 January 2025).
- Kannan, N.; Vakeesan, D. Solar energy for future world: A review. Renew. Sustain. Energy Rev. 2016, 62, 1092–1105. [Google Scholar] [CrossRef]
- Anupong, W.; Jweeg, M.J.; Alani, S.; Al-Kharsan, I.H.; Alviz-Meza, A.; Cárdenas-Escrocia, Y. Comparison of Wavelet Artificial Neural Network, Wavelet Support Vector Machine, and Adaptive Neuro-Fuzzy Inference System Methods in Estimating Total Solar Radiation in Iraq. Energies 2023, 16, 985. [Google Scholar] [CrossRef]
- Shafi, I.; Khan, H.; Farooq, M.S.; Diez, I.D.l.T.; Miró, Y.; Galán, J.C.; Ashraf, I. An Artificial Neural Network-Based Approach for Real-Time Hybrid Wind–Solar Resource Assessment and Power Estimation. Energies 2023, 16, 4171. [Google Scholar] [CrossRef]
- Ali, M.A.; Elsayed, A.; Elkabani, I.; Akrami, M.; Youssef, M.E.; Hassan, G.E. Optimizing Artificial Neural Networks for the Accurate Prediction of Global Solar Radiation: A Performance Comparison with Conventional Methods. Energies 2023, 16, 6165. [Google Scholar] [CrossRef]
- World Energy Resources: Solar World Energy Council. 2013. Available online: https://www.worldenergy.org/assets/images/imported/2013/10/WER_2013_8_Solar_revised.pdf (accessed on 1 January 2025).
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- Benghanem, M.; Mellit, A. Radial Basis Function Network-based prediction of global solar radiation data: Application for sizing of a stand-alone photovoltaic system at Al-Madinah, Saudi Arabia. Energy 2010, 35, 3751–3762. [Google Scholar] [CrossRef]
- Rodríguez, E.; Cardemil, J.M.; Starke, A.R.; Escobar, R. Modelling the Exergy of Solar Radiation: A Review. Energies 2022, 15, 1477. [Google Scholar] [CrossRef]
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Mohammadi, B.; Moazenzadeh, R. Performance Analysis of Daily Global Solar Radiation Models in Peru by Regression Analysis. Atmosphere 2021, 12, 389. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Al-Ghamdi, A.A.; Al-Hazmi, F.S.; Faidah, A.S. Estimation of global solar radiation on horizontal surfaces in Jeddah, Saudi Arabia. Energy Policy 2009, 37, 3645–3649. [Google Scholar] [CrossRef]
- Ali, M.A.; Elsayed, A.; Elkabani, I.; Akrami, M.; Youssef, M.E.; Hassan, G.E. Artificial Intelligence-Based Improvement of Empirical Methods for Accurate Global Solar Radiation Forecast: Development and Comparative Analysis. Energies 2024, 17, 4302. [Google Scholar] [CrossRef]
- Asif, M. Growth and sustainability trends in the GCC countries with particular reference to KSA and UAE. Renew. Renew. Sustain. Energy Rev. 2016, 55, 1267–1273. [Google Scholar] [CrossRef]
- Hepbasli, A.; Alsuhaibani, Z. A Key review on present status and future directions of solar energy studies and applications in Saudi Arabia. Renew. Sustain. Energy Rev. 2011, 15, 5021–5050. [Google Scholar] [CrossRef]
- Asif, M. Urban Scale Application of Solar PV to Improve Sustainability in the Building and the Energy Sectors of KSA. Sustainability 2016, 8, 1127. [Google Scholar] [CrossRef]
- Youssef, M.E.; Hassan, G.E.; Mohamed, Z.E.; Ali, M.A. Investigating the performance of different models in estimating global solar radiation. Adv. Nat. Appl. Sci. 2016, 10, 379–389. [Google Scholar]
- Hassan, G.E.; Youssef, M.E.; Ali, M.A.; Mohamed, Z.E.; Hanafy, A.A. Evaluation of different sunshine-based models for predicting global solar radiation-Case study: New Borg El-Arab City, Egypt. Therm. Sci. 2018, 22, 979–992. [Google Scholar] [CrossRef]
- Tao, H.; Ewees, A.A.; Al-Sulttani, A.O.; Beyaztas, U.; Hameed, M.M.; Salih, S.Q.; Armanuos, A.M.; Al-Ansari, N.; Voyant, C.; Shahid, S.; et al. Global solar radiation prediction over North Dakota using air temperature: Development of novel hybrid intelligence model. Energy Rep. 2021, 7, 136–157. [Google Scholar] [CrossRef]
- Ali, M.A.; Elsayed, A.; Elkabani, I.; Youssef, M.E.; Hassan, G.E. Modeling global solar radiation using ambient temperature. Clean. Energy Syst. 2024, 7, 100101. [Google Scholar] [CrossRef]
- Amrouche, B.; Le Pivert, X. Artificial neural network based daily local forecasting for global solar radiation. Appl. Energy 2014, 130, 333–341. [Google Scholar] [CrossRef]
- Ali, M.A.; Hassan, G.E.; Youssef, M.E. Assessment the Performance of Artificial Neural Networks in Estimating Global Solar Radiation. In Proceedings of the First International Conference on New Trends for Sustainable Energy—ICNTSE, Alexandria, Egypt, 1–3 October 2016; pp. 148–150. [Google Scholar]
- Alzahrani, A.; Shamsi, P.; Dagli, C.; Ferdowsi, M. Solar irradiance forecasting using deep neural networks. Proc. Comput. Sci. 2017, 114, 304–313. [Google Scholar] [CrossRef]
- Shboul, B.; AL-Arfi, I.; Michailos, S.; Ingham, D.; Ma, L.; Hughes, K.J.; Pourkashanian, M. A new ANN model for hourly solar radiation and wind speed prediction: A case study over the north & south of the Arabian Peninsula. Sustain. Energy Technol. Assess. 2021, 46, 101248. [Google Scholar] [CrossRef]
- Mfetoum, I.M.; Ngoh, S.K.; Molu, R.J.J.; Nde Kenfack, B.F.; Onguene, R.; Naoussi, S.R.D.; Tamba, J.G.; Bajaj, M.; Berhanu, M. A multilayer perceptron neural network approach for optimizing solar irradiance forecasting in Central Africa with meteorological insights. Sci. Rep. 2024, 14, 3572. [Google Scholar] [CrossRef]
- Besharat, F.; Dehghan, A.A.; Faghih, A.R. Empirical models for estimating global solar radiation: A review and case study. Renew. Sustain. Energy Rev. 2013, 21, 798–821. [Google Scholar] [CrossRef]
- Ali, M.A.; Elsayed, A.; Elkabani, I.; Youssef, M.E.; Hassan, G.E. Evaluation and performance comparison of different models for global solar radiation forecasting: A case study on five cities. Environ. Dev. Sustain. 2023. [Google Scholar] [CrossRef]
- Busu, C.; Busu, M. An Application of the Kalman Filter Recursive Algorithm to Estimate the Gaussian Errors by Minimizing the Symmetric Loss Function. Symmetry 2021, 13, 240. [Google Scholar] [CrossRef]
- Yoon, B.J. Hidden Markov Models and their Applications in Biological Sequence Analysis. Curr. Genom. 2009, 10, 402–415. [Google Scholar] [CrossRef]
- Demir, V. Evaluation of Solar Radiation Prediction Models Using AI: A Performance Comparison in the High-Potential Region of Konya, Türkiye. Atmosphere 2025, 16, 398. [Google Scholar] [CrossRef]
- Al-Salihi, A.M.; Kadum, M.M.; Mohammed, A.J. Estimation of global solar radiation on horizontal surface using routine meteorological measurements for different cities in Iraq. Asian J. Sci. Res. 2010, 3, 240–248. [Google Scholar] [CrossRef][Green Version]
- Gupta, S.; Singh, A.K.; Mishra, S.; Vishnuram, P.; Dharavat, N.; Rajamanickam, N.; Kalyan, C.N.S.; AboRas, K.M.; Sharma, N.K.; Bajaj, M. Estimation of Solar Radiation with Consideration of Terrestrial Losses at a Selected Location—A Review. Sustainability 2023, 15, 9962. [Google Scholar] [CrossRef]
- Hassan, M.A.; Almezhghwi, K.; Ghadedo, A. Solar Radiation Prediction in Libya Using Neural Networks. In Proceedings of the 2024 IEEE 4th International Maghreb Meeting of the Conference on Sciences and Techniques of Automatic Control and Computer Engineering (MI-STA), Tripoli, Libya, 19–21 May 2024; pp. 601–604. [Google Scholar] [CrossRef]
- Babatunde, O.M.; Munda, J.L.; Hamam, Y. Exploring the Potentials of Artificial Neural Network Trained with Differential Evolution for Estimating Global Solar Radiation. Energies 2020, 13, 2488. [Google Scholar] [CrossRef]
- González-Plaza, E.; García, D.; Prieto, J.-I. Monthly Global Solar Radiation Model Based on Artificial Neural Network, Temperature Data and Geographical and Topographical Parameters: A Case Study in Spain. Sustainability 2024, 16, 1293. [Google Scholar] [CrossRef]
- Chiteka, K.; Enweremadu, C.C. Prediction of global horizontal solar irradiance in Zimbabwe using artificial neural networks. J. Clean. Prod. 2016, 135, 701–711. [Google Scholar] [CrossRef]
- Nawab, F.; Hamid, A.S.A.; Ibrahim, A.; Sopian, K.; Fazlizan, A.; Fauzan, M.F. Solar irradiation prediction using empirical and artificial intelligence methods: A comparative review. Heliyon 2023, 9, e17038. [Google Scholar] [CrossRef]
- Alanazi, A.; Alanazi, M. Multicriteria Decision-Making for Evaluating Solar Energy Source of Saudi Arabia. Sustainability 2023, 15, 10228. [Google Scholar] [CrossRef]
- Khan, M.; Asif, M.; Stach, E. Rooftop PV Potential in the Residential Sector of the Kingdom of Saudi Arabia. Buildings 2017, 7, 46. [Google Scholar] [CrossRef]
- Almasoud, A.H.; Gandayh, H.M. Future of solar energy in Saudi Arabia. J. King Saud Univ. -Eng. Sci. 2015, 27, 153–157. [Google Scholar] [CrossRef]
- Pashiardis, S.; Pelengaris, A.; Kalogirou, S.A. Geographical Distribution of Global Radiation and Sunshine Duration over the Island of Cyprus. Appl. Sci. 2023, 13, 5422. [Google Scholar] [CrossRef]
- Mohandes, M.A.; Rehman, S. Estimation of sunshine duration in Saudi Arabia. J Renew Sustain. Energy 2013, 5, 033128. [Google Scholar] [CrossRef]
- El Alani, O.; Ghennioui, H.; Ghennioui, A.; Saint-Drenan, Y.V.; Blanc, P.; Hanrieder, N.; Dahr, F.E. A Visual Support of Standard Procedures for Solar Radiation Quality Control. Int. J. Renew. Energy Dev. 2021, 10, 401–414. [Google Scholar] [CrossRef]
- Available online: https://www.engr.scu.edu/~emaurer/tools/calc_solar_cgi.pl (accessed on 1 January 2025).
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Şenkal, O.; Kuleli, T. Estimation of solar radiation over Turkey using artificial neural network and satellite data. Appl. Energy 2009, 86, 1222–1228. [Google Scholar] [CrossRef]
- Hassan, G.E.; Ali, M.A. Performance Evaluation of Artificial Neural Networks in Estimating Global Solar Ra-diation, Case Study: New Borg El-arab City, Egypt. Int. J. Environ. Sci. Sustain. Dev. 2017, 2, 16. [Google Scholar]
- Choudhary, A.; Pandey, D.; Bhardwaj, S. A Review for the Development of ANN Based Solar Radiation Estimation Models; Springer: Singapore, 2021; Volume 194. [Google Scholar]
- Foggno Fotso, H.R.; Aloyem Kazé, C.V.; Kenmoe, G.D. Optimal Input Variables Disposition of Artificial Neural Networks Models for Enhancing Time Series Forecasting Accuracy. Appl. Artif. Intell. 2020, 34, 792–815. [Google Scholar] [CrossRef]
- Fazeli, H.; Soleimani, R.; Ahmadi, M.A.; Badrnezhad, R.; Mohammadi, A.H. Experimental Study and Modeling of Ultrafiltration of Refinery Effluents Using a Hybrid Intelligent Approach. J. Energy 2013, 27, 3523–3537. [Google Scholar] [CrossRef]
- Bounoua, Z.; Ouazzani Chahidi, L.; Mechaqrane, A. Estimation of daily global solar radiation using empirical and machine-learning methods: A case study of five Moroccan locations. Sustain. Mater. Technol. 2021, 28, e00261. [Google Scholar] [CrossRef]
- Kumar, S.; Kaur, T. Development of ANN Based Model for Solar Potential Assessment Using Various Meteoro-logical Parameters. Energy Procedia 2016, 90, 587–592. [Google Scholar] [CrossRef]
- Çelik, Ö.; Teke, A.; Yildirim, H.B. The optimized artificial neural network model with Levenberg-Marquardt algorithm for global solar radiation estimation in Eastern Mediterranean Region of Turkey. J. Clean. Prod. 2016, 116, 1–12. [Google Scholar] [CrossRef]
- Marzouq, M.; Bounoua, Z.; El Fadili, H.; Mechaqrane, A.; Zenkouar, K.; Lakhliai, Z. New daily global solar irra-diation estimation model based on automatic selection of input parameters using evolutionary artificial neural networks. J. Clean. Prod. 2019, 209, 1105–1118. [Google Scholar] [CrossRef]
- Bounoua, Z.; Mechaqrane, A. Prediction of Short-Term and Long-Term Hourly Global Horizontal Solar Irradiation Using Artificial Neural Networks Techniques in Fez City, Morocco; Springer: Singapore, 2021; Volume 681. [Google Scholar]
- Bounoua, Z.; Mechaqrane, A. Hourly and sub-hourly ahead global horizontal solar irradiation forecasting via a novel deep learning approach: A case study. Sustain. Mater. Technol. 2023, 36, e00599. [Google Scholar] [CrossRef]
- Vesta Services, Inc. Qnet2000 Shareware. Vesta Services. Inc. 1001 Green Bay Rd, STE 196. Winnetka. IL 60093, USA, 2000. QnetV2kt. Qnet v2000 for Windows, the Complete Solution for Backpropagation Neural Network. Available online: https://qnetv2kt.software.informer.com/ (accessed on 1 January 2025).
- Al-Sager, S.M.; Almady, S.S.; Marey, S.A.; Al-Hamed, S.A.; Aboukarima, A.M. Prediction of Specific Fuel Consumption of a Tractor during the Tillage Process Using an Artificial Neural Network Method. Agronomy 2024, 14, 492. [Google Scholar] [CrossRef]
- Bakas, I.; Kontoleon, K.J. Performance Evaluation of Artificial Neural Networks (ANN) Predicting Heat Transfer through Masonry Walls Exposed to Fire. Appl. Sci. 2021, 11, 11435. [Google Scholar] [CrossRef]
- Pratiwi, H.; Windarto, A.P.; Susliansyah, S.; Aria, R.R.; Susilowati, S.; Rahayu, L.K.; Fitriani, Y.; Merdekawati, A.; Rahadjeng, I.R. Sigmoid Activation Function in Selecting the Best Model of Artificial Neural Networks. Conf. Ser. J. Phys. 2020, 1471, 012010. [Google Scholar] [CrossRef]
- Kassem, Y.; Camur, H.; Adamu, M.T.; Chikowero, T.; Apreala, T. Prediction of Solar Irradiation in Africa us-ing Linear-Nonlinear Hybrid Models. Eng. Technol. Appl. Sci. Res. 2023, 13, 11472–11483. [Google Scholar] [CrossRef]
- Mrzygłód, B.; Hawryluk, M.; Janik, M.; Olejarczyk-Wożeńska, I. Sensitivity analysis of the artificial neural networks in a system for durability prediction of forging tools to forgings made of C45 steel. Int. J. Adv. Manuf. Technol. 2020, 109, 1385–1395. [Google Scholar] [CrossRef]
- Yousefi, M.; Esrafili, A.; Gholami, M.; Mohammadi, A.A.; Khan, N.A.; Baziar, M.; Oskoei, V. Modeling and analysis of the groundwater hardness variations process using machine learning procedure. Desalination Water Treat. 2021, 238, 135–141. [Google Scholar] [CrossRef]
- Al-Dosary, N.M.N.; Alnajjar, F.M.; Aboukarima, A.E.W.M. Estimation of wheel slip in 2WD mode for an agricultural tractor during plowing operation using an artificial neural network. Sci. Rep. 2023, 13, 5975. [Google Scholar] [CrossRef]
- Pizarroso, J.; Portela, J.; Munoz, A. NeuralSens: Sensitivity Analysis of Neural Networks. J. Stat. Softw. 2022, 102. [Google Scholar] [CrossRef]
- Qazi, A.; Fayaz, H.; Wadi, A.; Raj, R.G.; Rahim, N.A.; Khan, W.A. The artificial neural network for solar radiation prediction and designing solar systems: A systematic literature review. J. Clean. Prod. 2015, 104, 1–12. [Google Scholar] [CrossRef]
- Khoshnevisan, B.; Rafiee, S.; Omid, M.; Mousazadeh, H.; Sefeedpari, P. Prognostication of environmental indices in potato production using artificial neural networks. J. Clean. Prod. 2013, 52, 402–409. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Tasie, N.N.; Israel-Cookey, C.; Banyie, L.J. The Effect of Relative Humidity on the Solar Radiation Intensity in Port Harcourt, Nigeria. Int. J. Res. 2018, 5, 128–136. [Google Scholar]
- Shrestha, A.K.; Thapa, A.; Gautam, H. Solar Radiation, Air Temperature, Relative Humidity, and Dew Point Study: Damak, Jhapa, Nepal. Int. J. Photoenergy 2019, 2019, 8369231. [Google Scholar] [CrossRef]
- Regmi, S.; Adhikary, S. Solar energy potential in Kath-mandu Valley, Nepal. J. Hydrol. Meteorol. 2012, 8, 77–82. [Google Scholar] [CrossRef][Green Version]
- Poudyal, K.N.; Bhattarai, B.K.; Sapkota, B.K.; Kjeldstad, B.; Karki, N.R. Estimation of global solar radiation using pyranometer and NILU-UV irradiance meter at Pokhara Valley in Nepal. J. Inst. Eng. 2014, 9, 69–78. [Google Scholar] [CrossRef]
- Geerts, B. Empirical estimation of the monthly-mean daily temperature range. Theor. Appl. Climatol. 2002, 73, 101–132. [Google Scholar] [CrossRef]
- Villegas-Mier, C.G.; Rodriguez-Resendiz, J.; Álvarez-Alvarado, J.M.; Jiménez-Hernández, H.; Odry, Á. Optimized Random Forest for Solar Radiation Prediction Using Sunshine Hours. Micromachines 2022, 13, 1406. [Google Scholar] [CrossRef]
- Cañada, J. Global Solar Radiation in Pais Valenciano Using Sunshine Hours. Int. J. Ambient. Energy 1988, 9, 197–202. [Google Scholar] [CrossRef]
- Ibrahim, S.M.A. Predicted and Measured Global Solar Radiation in Egypt. Sol. Energy 1985, 35, 185. [Google Scholar] [CrossRef]
- Turton, S.M. The Relationship between Total Irradiation and Sunshine Duration in the Humid Tropics. Sol. Energy 1987, 38, 353. [Google Scholar] [CrossRef]
- Halouani, N.; Nguyen, C.T.; Vo-Ngoc, D. Calculation of Monthly Average Global Solar Radiation on Horizontal Surfaces using Daily Hours of Bright Sunshine. Sol. Energy 1993, 50, 247. [Google Scholar] [CrossRef]
- Atsbeha, A.K.; Gebremariam, G.G.; Gebreslassie, T.H. Analysis of sunshine hours data and estimation of global solar radiation for Mychew Tabia Smret station, Northern Ethiopia. Sustain. Energy Res. 2024, 11, 38. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Labban, A. The Solar Radiation Climate of Saudi Arabia. Climate 2023, 11, 75. [Google Scholar] [CrossRef]
- Dvorkin, A.Y.; Steinberger, E.H. A modeling the altitude effect on solar UV radiation. Sol. Energy 1999, 65, 181–187. [Google Scholar] [CrossRef]
- Aldobhani, A.M.S. Effect of Altitude and Tilt Angle on Solar Radiation in Tropical Regions. J. Sci. Technol. 2014, 19, 96–109. [Google Scholar]
- Bel, G.; Bandi, M.M. Geographic Dependence of the Solar Irradiance Spectrum at Intermediate to High Frequencies. Phys. Rev. Appl. 2019, 12, 024032. [Google Scholar] [CrossRef]
- Kopp, G. Daily solar flux as a function of latitude and time. Sol. Energy 2023, 249, 250–254. [Google Scholar] [CrossRef]
- Mohandes, M.A. Modeling global solar radiation using Particle Swarm Optimization (PSO). Sol. Energy 2012, 86, 3137–3145. [Google Scholar] [CrossRef]
- Sarkin, A.S.; Dindar, T. The Effect of Latitude Differences, Sunshine Periods, Solar Radiation Quantities and Air Temperatures on Solar Electricity Generation. J. Smart Grid Sustain. Energy Technol. 2017, 1, 20–23. [Google Scholar] [CrossRef]
- Chabane, F.; Arif, A.; Benramache, S. Prediction of the solar radiation map on Algeria by latitude and longitude coordinates. Tec. Ital. Ital. J. Eng. Sci. 2020, 64, 213–215. [Google Scholar] [CrossRef]
- Yadav, A.K.; Malik, H.; Chandel, S.S. Selection of most relevant input parameters using WEKA for artificial neural network based solar radiation prediction models. Renew. Sustain. Energy Rev. 2014, 31, 509–519. [Google Scholar] [CrossRef]
- Babar, B.; Graversen, R.; Boström, T. Solar radiation estimation at high latitudes: Assessment of the CMSAF databases, ASR and ERA5. Sol. Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Kafka, J.L.; Miller, M.A. A climatology of solar irradiance and its controls across the United States: Implications for solar panel orientation. Renew. Energy 2019, 135, 897–907. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J.; Nazarko, L.; Rabayah, H.S. Solar Radiation Forecasting: A Systematic Meta-Review of Current Methods and Emerging Trends. Energies 2024, 17, 3156. [Google Scholar] [CrossRef]
- Amiri, B.; Dizène, R.; Dahmani, K. Most relevant input parameters selection for 10-min global solar irradiation estimation on arbitrary inclined plane using neural networks. Int. J. Sustain. Energy 2020, 39, 779–803. [Google Scholar] [CrossRef]
- Bezari, S.; Adda, A.; Kherrour, S.; Zarrit, R. Artificial Neural Network Application for the Prediction of Global Solar Radiation Inside a Greenhouse. In Renewable Energy Resources and Conservation; Pong, P., Ed.; Green Energy and Technology; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Koumi Ngoh, S.; Ayina, O.; Monkam, L.; Kemajou, A. Estimation of the Global Solar Radiation Under Su-dan-Type Tropical Climate Using Artificial Neural Network Model. ISESCO J. Sci. Technol. 2013, 9, 22–33. [Google Scholar]
- Diez, F.J.; Navas-Gracia, L.M.; Chico-Santamarta, L.; Correa-Guimaraes, A.; Martínez-Rodríguez, A. Prediction of Horizontal Daily Global Solar Irradiation Using Artificial Neural Networks (ANNs) in the Castile and León Region, Spain. Agronomy 2020, 10, 96. [Google Scholar] [CrossRef]
- Dekker, J.; Nthontho, M.; Chowdhury, S.; Chowdhury, S.P. Investigating the effects of solar modelling using different solar irradiation data sets and sources within South Africa. Sol. Energy 2012, 86, 2354–2365. [Google Scholar] [CrossRef]
- Hussain, S.; Alili, A.A. A pruning approach to optimize synaptic connections and select relevant input parameters for neural network modelling of solar radiation. Appl. Soft Comput. 2017, 52, 898–908. [Google Scholar] [CrossRef]
- Al-rubaye, A.; Al-Khuzaie, M.M. Artificial Neural Networks for Solar Radiation Prediction: Case Study, Al-Qadisiyah, Iraq. J. Eng. Res. 2024, 20, 106–112. [Google Scholar] [CrossRef]





| Station ID | Station Setting | Altitude | Latitude | Longitude |
|---|---|---|---|---|
| (m) | (°N) | (°E) | ||
| 166 | Hofuf | 160 | 25.31 | 49.63 |
| 186 | Hail | 1010 | 27.63 | 41.72 |
| 215 | Khlais | 60 | 22.15 | 39.34 |
| 366 | Madinah | 590 | 24.47 | 39.60 |
| 405 | Najran | 1250 | 17.57 | 44.23 |
| 452 | Riyadh | 564 | 24.77 | 46.74 |
| 786 | Unaizah | 724 | 26.09 | 43.97 |
| 497 | Sabya | 40 | 17.15 | 42.68 |
| 769 | Tabuk | 773 | 28.38 | 36.57 |
| Criteria | Altitude | Latitude | Longitude | RHmax | RHmin | Tmax | Tmin | Sunshine Duration | MADSR on a Horizontal Surface |
|---|---|---|---|---|---|---|---|---|---|
| (m) | (°N) | (°E) | (%) | (%) | (°C) | (°C) | (hrs) | (W/m2) | |
| Minimum | 40 | 17.15 | 36.57 | 11.77 | 2.90 | 7.91 | 1.21 | 2.71 | 91.12 |
| Maximum | 1250 | 28.38 | 49.63 | 98.03 | 84.68 | 48.50 | 44.38 | 12.11 | 427.91 |
| Mean | 583.33 | 23.75 | 42.69 | 57.11 | 24.73 | 32.70 | 18.20 | 8.68 | 297.74 |
| Kurtosis coefficient | −1.10 | −0.85 | −0.66 | −0.92 | 2.34 | −0.67 | −0.70 | 1.15 | −0.89 |
| Skewness coefficient | 0.04 | −0.70 | 0.19 | −0.19 | 1.15 | −0.40 | −0.17 | −0.61 | −0.08 |
| Standard deviation | ±396.88 | ±3.82 | ±3.74 | ±20.51 | ±11.80 | ±7.69 | ±7.59 | ±1.32 | ±62.92 |
| Coefficient of variation (%) | 68.04 | 16.07 | 8.77 | 35.91 | 47.72 | 23.50 | 41.71 | 15.23 | 21.13 |
| Independent Variables (Inputs) | Dependent Variable (Output) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Altitude | Latitude of a Location | Longitude of a Location | Month | Maximum Air Relative Humidity | Minimum Air Relative Humidity | Maximum Air Temperature | Minimum Air Temperature | Sunshine Duration | MADSR on a Horizontal Surface |
| (m) | (°N) | (°E) | (-) | (%) | (%) | (°C) | (°C) | (hrs) | (W/m2) |
| 60 | 22.15 | 39.34 | 4.00 | 69.20 | 26.11 | 31.95 | 20.29 | 4.23 | 373.37 |
| 60 | 22.15 | 39.34 | 6.00 | 72.66 | 27.76 | 38.98 | 25.92 | 5.46 | 341.51 |
| 160 | 25.31 | 49.63 | 7.00 | 61.50 | 26.43 | 44.48 | 26.68 | 2.71 | 356.67 |
| 60 | 22.15 | 39.34 | 3.00 | 73.86 | 33.03 | 33.35 | 22.46 | 4.41 | 283.57 |
| 160 | 25.31 | 49.63 | 4.00 | 61.50 | 26.43 | 30.78 | 13.43 | 2.76 | 338.42 |
| 160 | 25.31 | 49.63 | 6.00 | 31.60 | 10.40 | 42.82 | 23.83 | 3.55 | 366.03 |
| 60 | 22.15 | 39.34 | 10.00 | 91.80 | 48.30 | 37.05 | 26.96 | 5.85 | 155.13 |
| 40 | 17.15 | 42.68 | 7.00 | 71.03 | 40.90 | 38.89 | 31.05 | 7.68 | 219.33 |
| Criteria | RHmean = (RHmax + RHmin)/2 | Tmean = (Tmax + Tmin)/2 |
|---|---|---|
| (%) | (°C) | |
| Minimum | 8.25 | 5.16 |
| Maximum | 88.63 | 40.18 |
| Mean | 40.92 | 25.45 |
| Kurtosis coefficient | −0.62 | −0.92 |
| Skewness coefficient | 0.11 | −0.39 |
| Standard deviation | 15.21 | 7.22 |
| Coefficient of variation (%) | 37.16 | 28.39 |
| Output Node | Training Dataset | Testing Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE, % | R2 | RMSE | MAE | MAPE, % | R2 | |
| MADSR on a horizontal surface (W/m2) | 23.42 | 17.72 | 6.08 | 0.8663 | 25.56 | 19.42 | 6.86 | 0.8404 |
| Neurons of the Hidden Layer | Wk,i = Values of the Weights Between the Input Layer and the Hidden Layer | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Altitude | Latitude of a Location | Longitude of a Location | Month of the Year | Maximum Air Relative Humidity | Minimum Air Relative Humidity | Maximum Air Temperature | Minimum Air Temperature | Sunshine Duration | |
| (m) | (°N) | (°E) | (-) | (%) | (%) | (°C) | (°C) | (hrs) | |
| 1 | 3.64325 | 2.28576 | −0.25279 | 5.50858 | 0.51658 | −1.40753 | −0.20721 | −1.07723 | −5.28737 |
| 2 | 2.49036 | −2.69125 | 5.43094 | 0.7631 | 6.26345 | −0.65875 | 0.28476 | 0.86126 | −2.80097 |
| 3 | −1.64653 | −1.14938 | 1.46635 | 1.25978 | 2.4062 | 2.7282 | −2.13758 | −0.95897 | 0.77022 |
| 4 | −0.53044 | 0.03591 | 0.46227 | −0.5588 | −0.21512 | 0.26658 | −0.70735 | −0.43342 | −0.19672 |
| 5 | 5.4611 | −4.91645 | 1.72194 | 3.61561 | 2.5249 | 0.94421 | 0.71735 | −2.47387 | 0.14065 |
| 6 | −6.29028 | −0.43053 | −1.94248 | −3.51798 | −3.79139 | −3.17707 | 9.42016 | −7.04497 | −1.87773 |
| 7 | −0.00832 | −0.3269 | −0.3298 | −0.58201 | −0.09475 | 0.01211 | −0.49445 | 0.1567 | −0.60397 |
| 8 | −0.33478 | −0.64099 | −0.50119 | −0.33641 | −1.31591 | −0.91474 | −0.54291 | 0.18722 | −0.47037 |
| 9 | −6.21581 | −3.66877 | 2.10548 | −2.69447 | −1.28158 | 1.20578 | 3.01061 | 0.6996 | 1.40528 |
| 10 | 0.60409 | −0.32921 | −0.13627 | −0.54768 | −1.52076 | −1.1733 | −0.92987 | −0.77138 | −0.45265 |
| 11 | −1.45994 | −3.11725 | −0.40443 | −2.59807 | −2.75322 | 0.01502 | 3.60163 | 4.51328 | −4.08795 |
| 12 | 1.17886 | −0.37657 | −0.04258 | −0.1527 | −2.2182 | −1.10148 | −0.07266 | −0.85642 | −0.59411 |
| 13 | −0.98345 | −0.45196 | −1.11988 | −0.78257 | −0.45077 | −1.16004 | −0.22656 | 1.37189 | −0.88922 |
| 14 | −1.88733 | 0.46629 | −1.21425 | −0.35606 | −1.07621 | −1.3007 | 1.50522 | 2.93697 | −5.01394 |
| 15 | 1.04717 | −0.43464 | 0.04443 | 0.76904 | −2.49212 | −1.08612 | −1.51021 | −0.77521 | −0.37857 |
| 16 | 3.72529 | −0.6257 | −1.66129 | −5.57553 | 3.36003 | −2.53558 | −0.4524 | −1.34861 | −1.05367 |
| 17 | 0.9423 | −5.18226 | 1.003 | 0.36262 | 0.36807 | 1.6469 | −1.12121 | 0.77612 | −3.08583 |
| 18 | −0.05788 | −0.78244 | −0.73355 | −0.96836 | 0.41526 | 0.23181 | 0.30208 | −0.60984 | −0.46381 |
| 19 | −2.78754 | 0.40895 | −6.73058 | −9.31486 | −0.66826 | 1.20828 | −0.85705 | 2.75672 | −3.88305 |
| 20 | 2.29984 | 0.06168 | 0.08106 | −1.64415 | −1.96686 | −0.88317 | 5.47203 | 2.54645 | 0.91788 |
| 21 | 5.50867 | −2.03377 | 0.92059 | −1.45215 | −1.41973 | −1.23092 | −0.77912 | −1.96309 | −0.25458 |
| 22 | −2.93377 | 1.51832 | −6.09499 | −14.3542 | 0.02584 | −0.58067 | 1.33162 | 2.92809 | −2.73823 |
| 23 | −0.23399 | 0.80378 | −1.85073 | 0.57925 | 2.92675 | −2.36815 | −0.97265 | −4.18414 | −0.16201 |
| 24 | −0.24979 | −0.79068 | 0.23047 | −0.25448 | 0.0499 | 0.14674 | −0.46218 | −0.02789 | −0.3555 |
| 25 | −0.14734 | −0.17937 | −0.27351 | −0.41305 | −0.37015 | −0.15855 | −0.25968 | −0.25839 | −0.46269 |
| 26 | 0.71323 | −0.05919 | 0.0652 | 0.30638 | −2.27481 | −0.77718 | −1.30538 | −1.36889 | −0.33638 |
| 27 | 4.24905 | 0.84893 | −6.92155 | −3.85277 | −6.98483 | −1.00357 | −0.04721 | 2.51823 | 2.33017 |
| 28 | −1.50534 | 0.61333 | −1.86707 | −13.4237 | 0.00806 | −1.72457 | 2.31237 | 1.06187 | 1.39098 |
| 29 | 3.13622 | −0.02797 | −1.49809 | −0.58727 | −5.56297 | −1.31044 | −3.10907 | −3.14824 | −0.30802 |
| 30 | −0.20973 | −0.13387 | −0.54791 | −0.09096 | −0.32142 | −0.06449 | 0.04704 | −0.54654 | −0.62289 |
| Neurons of the Hidden Layer | bi = Biases Values for the Hidden Layer | Wi,y = Values of the Weights Between the Output and the Hidden Layer | by = Biases Values for the Output Layer |
|---|---|---|---|
| MADSR on a Horizontal Surface (W/m2) | |||
| 1 | 0.66127 | −4.84465 | −2.02257 |
| 2 | −2.07533 | 4.91145 | |
| 3 | 0.10737 | 2.76182 | |
| 4 | −0.60728 | 0.57118 | |
| 5 | −3.19605 | −5.11818 | |
| 6 | 2.71403 | 8.89179 | |
| 7 | −0.67962 | −0.32213 | |
| 8 | 0.31858 | −1.66883 | |
| 9 | 0.39121 | −5.28378 | |
| 10 | 0.0176 | −1.66251 | |
| 11 | 2.84701 | 4.06481 | |
| 12 | −0.38936 | −2.38008 | |
| 13 | 0.67291 | −2.23174 | |
| 14 | 1.53701 | −5.22902 | |
| 15 | −0.04531 | −2.60486 | |
| 16 | −0.86453 | 3.80742 | |
| 17 | 2.05925 | 4.00986 | |
| 18 | −0.54964 | 1.09945 | |
| 19 | 8.40291 | −8.00214 | |
| 20 | −2.90448 | 3.40216 | |
| 21 | −0.52552 | −5.26179 | |
| 22 | 7.19436 | 8.8439 | |
| 23 | 2.37941 | 3.35191 | |
| 24 | −0.39484 | 0.43398 | |
| 25 | −0.51009 | −0.31124 | |
| 26 | −0.01125 | −2.00613 | |
| 27 | 0.75853 | 3.39389 | |
| 28 | 2.8514 | −8.06339 | |
| 29 | 4.60501 | 4.46458 | |
| 30 | −0.60488 | 0.17584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almasoud, W.A.; Al-Sager, S.M.; Almady, S.S.; Marey, S.A.; Al-Hamed, S.A.; Al-Janobi, A.A.; Aboukarima, A.M. A Prediction of the Monthly Average Daily Solar Radiation on a Horizontal Surface in Saudi Arabia Using Artificial Neural Network Approach. Processes 2025, 13, 1149. https://doi.org/10.3390/pr13041149
Almasoud WA, Al-Sager SM, Almady SS, Marey SA, Al-Hamed SA, Al-Janobi AA, Aboukarima AM. A Prediction of the Monthly Average Daily Solar Radiation on a Horizontal Surface in Saudi Arabia Using Artificial Neural Network Approach. Processes. 2025; 13(4):1149. https://doi.org/10.3390/pr13041149
Chicago/Turabian StyleAlmasoud, Waleed A., Saleh M. Al-Sager, Saad S. Almady, Samy A. Marey, Saad A. Al-Hamed, Abdulrahman A. Al-Janobi, and Abdulwahed M. Aboukarima. 2025. "A Prediction of the Monthly Average Daily Solar Radiation on a Horizontal Surface in Saudi Arabia Using Artificial Neural Network Approach" Processes 13, no. 4: 1149. https://doi.org/10.3390/pr13041149
APA StyleAlmasoud, W. A., Al-Sager, S. M., Almady, S. S., Marey, S. A., Al-Hamed, S. A., Al-Janobi, A. A., & Aboukarima, A. M. (2025). A Prediction of the Monthly Average Daily Solar Radiation on a Horizontal Surface in Saudi Arabia Using Artificial Neural Network Approach. Processes, 13(4), 1149. https://doi.org/10.3390/pr13041149






