A Novel Approach to Waterflooding Optimization in Irregular Well Patterns Using Streamline Simulation and 3D Visualization
Abstract
1. Introduction
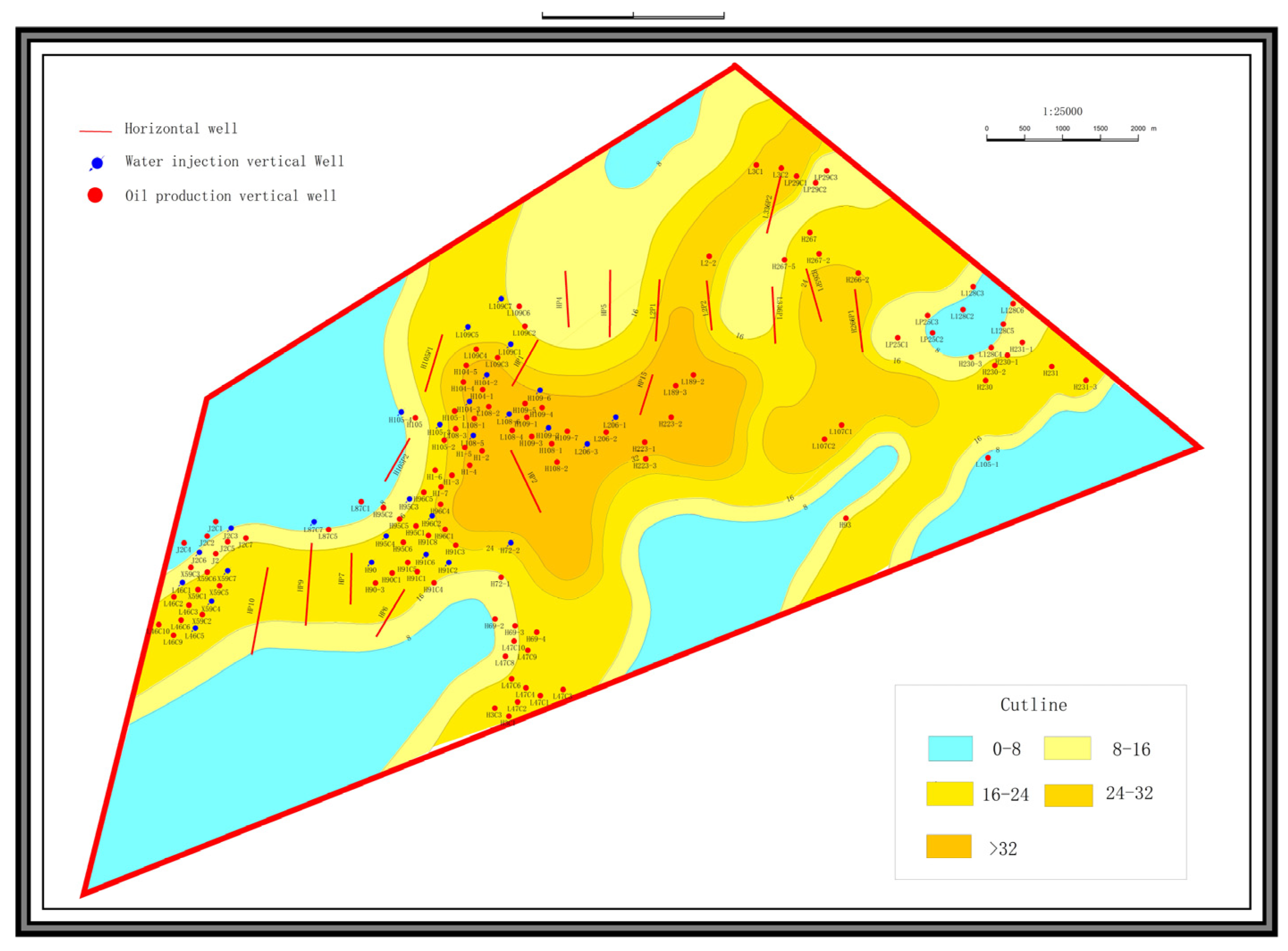
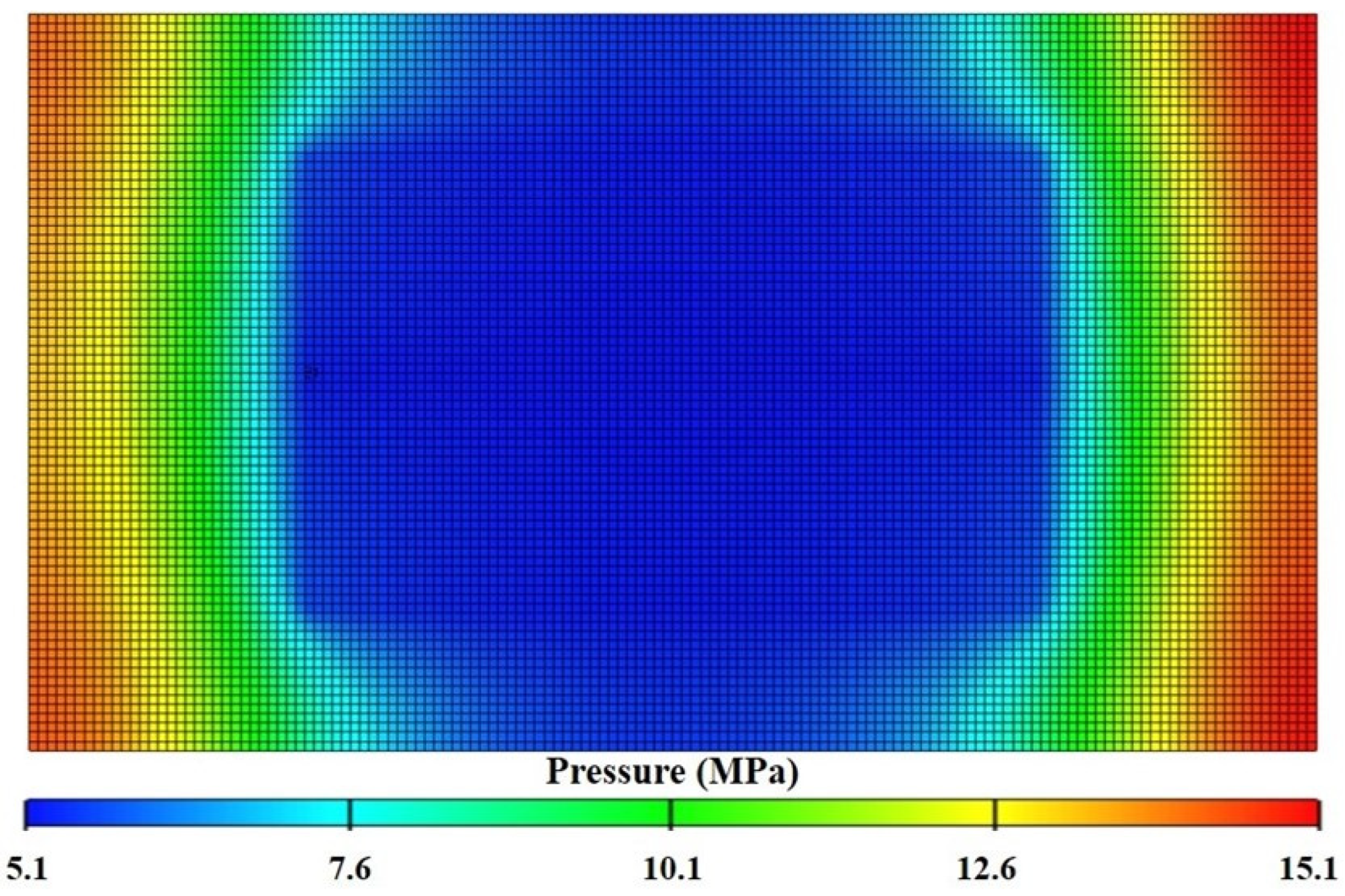
2. Reservoir Modeling
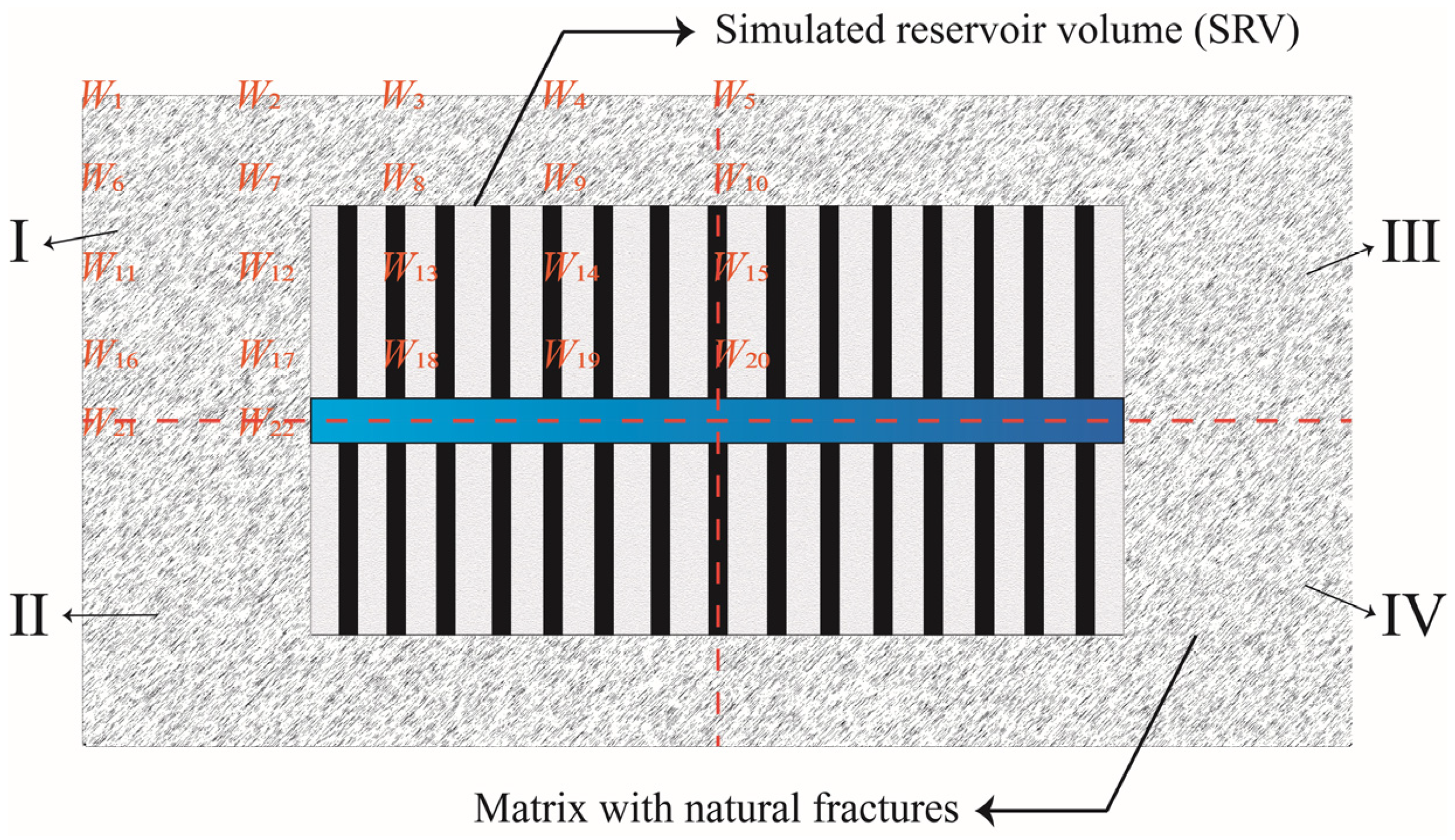
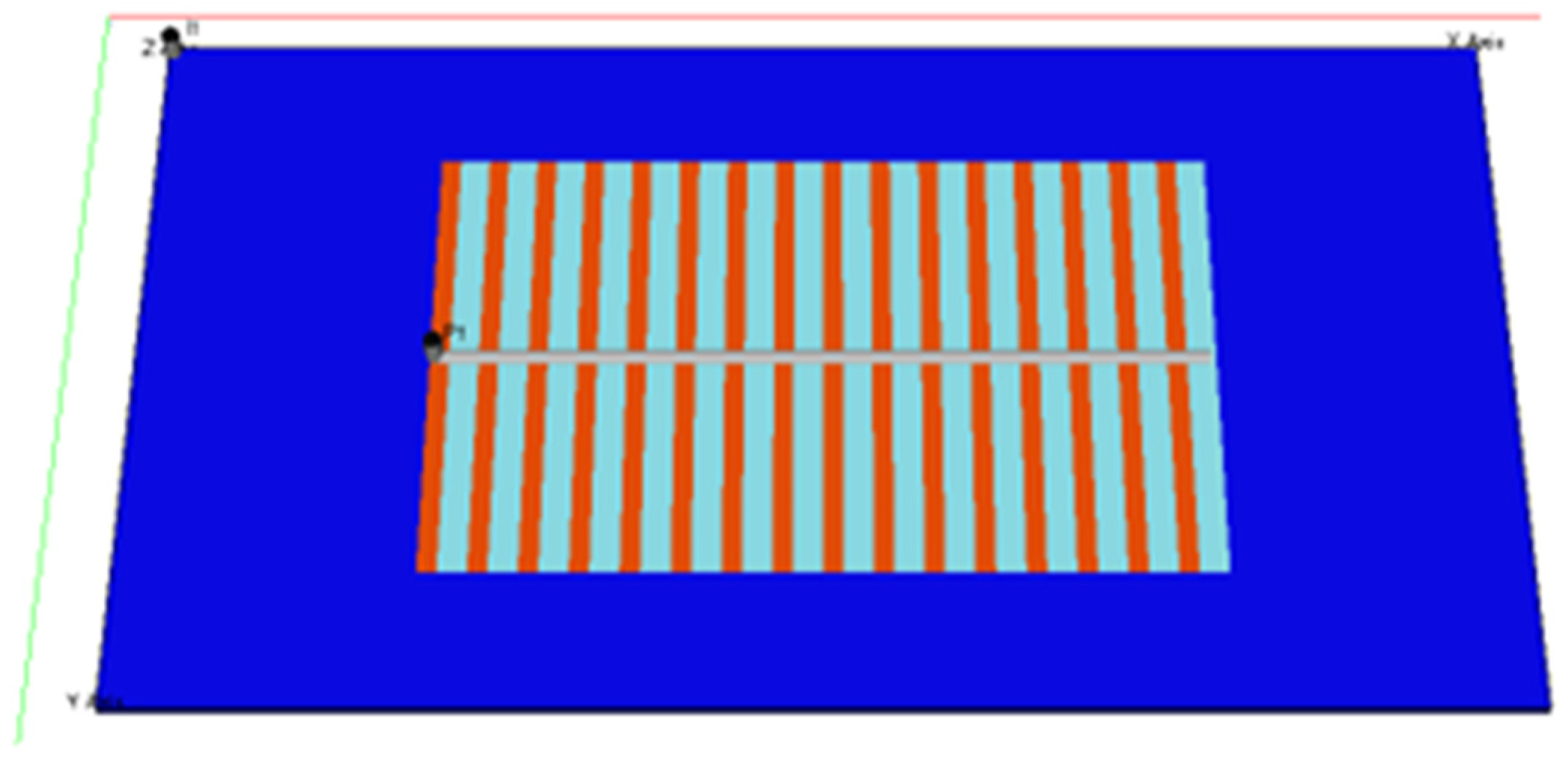
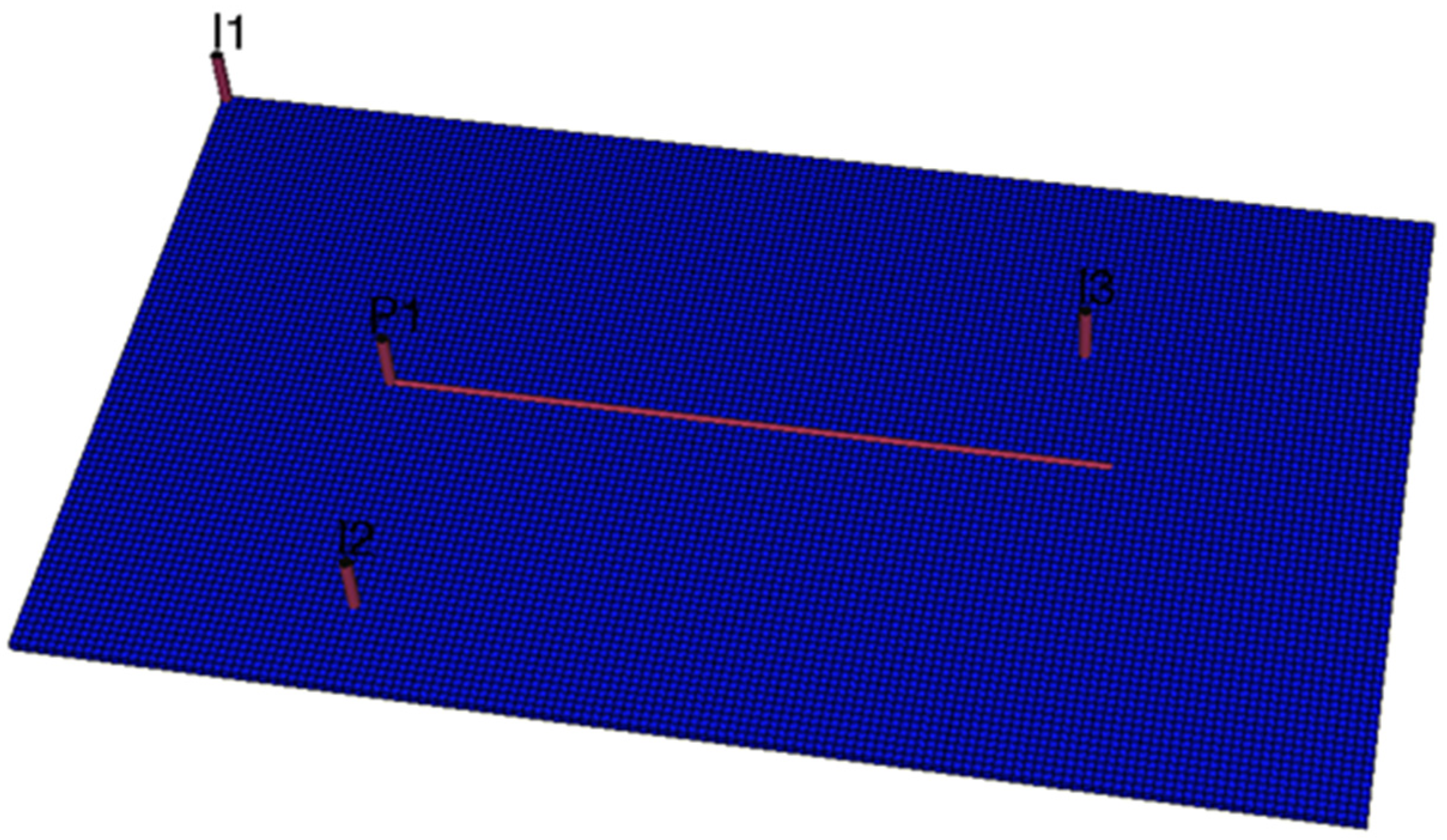
2.1. Modeling of a Combined Well Network of One-Injection-One-Production Water Straight
2.2. Establishment of the One-Injection-One-Production Streamline Model
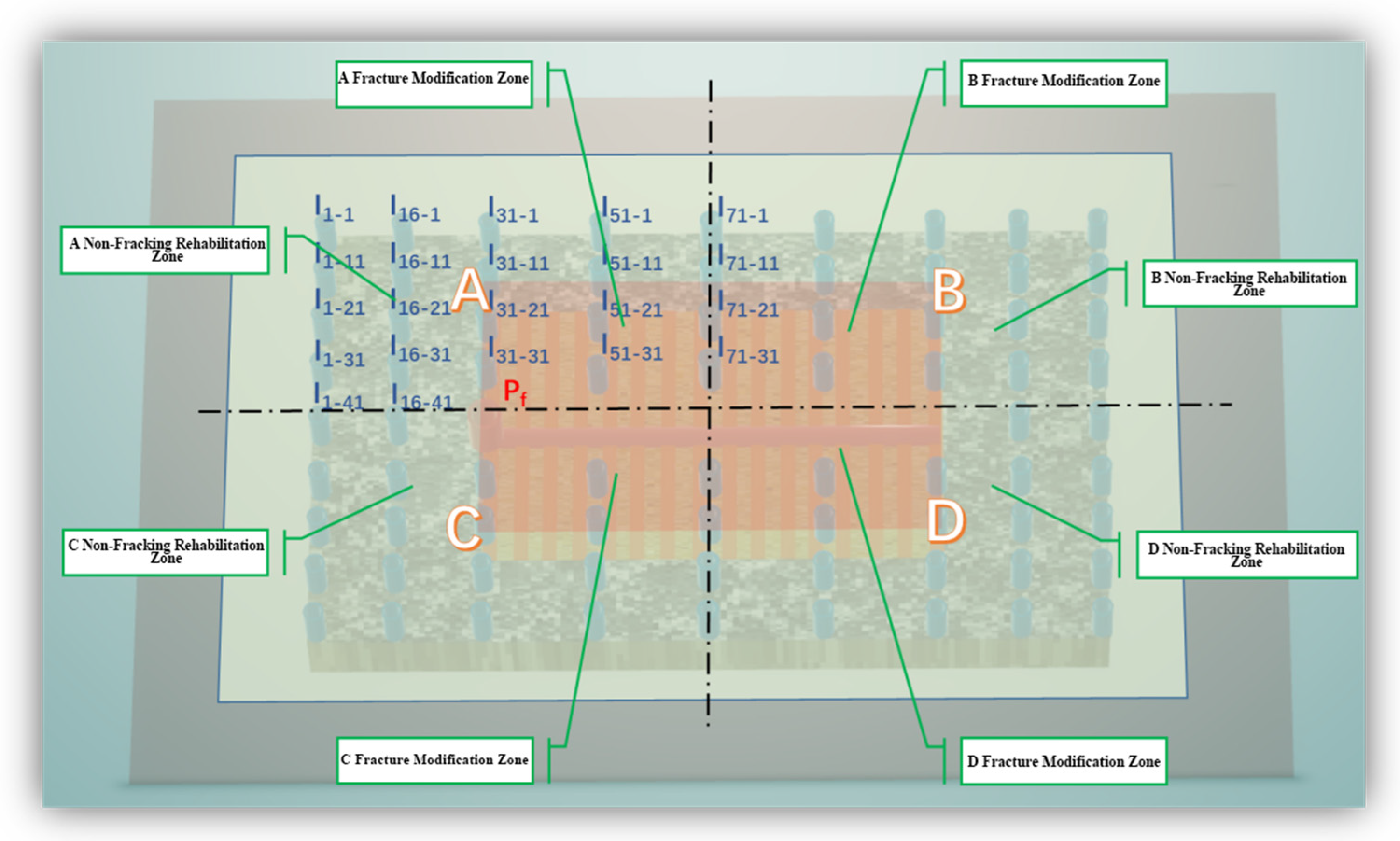
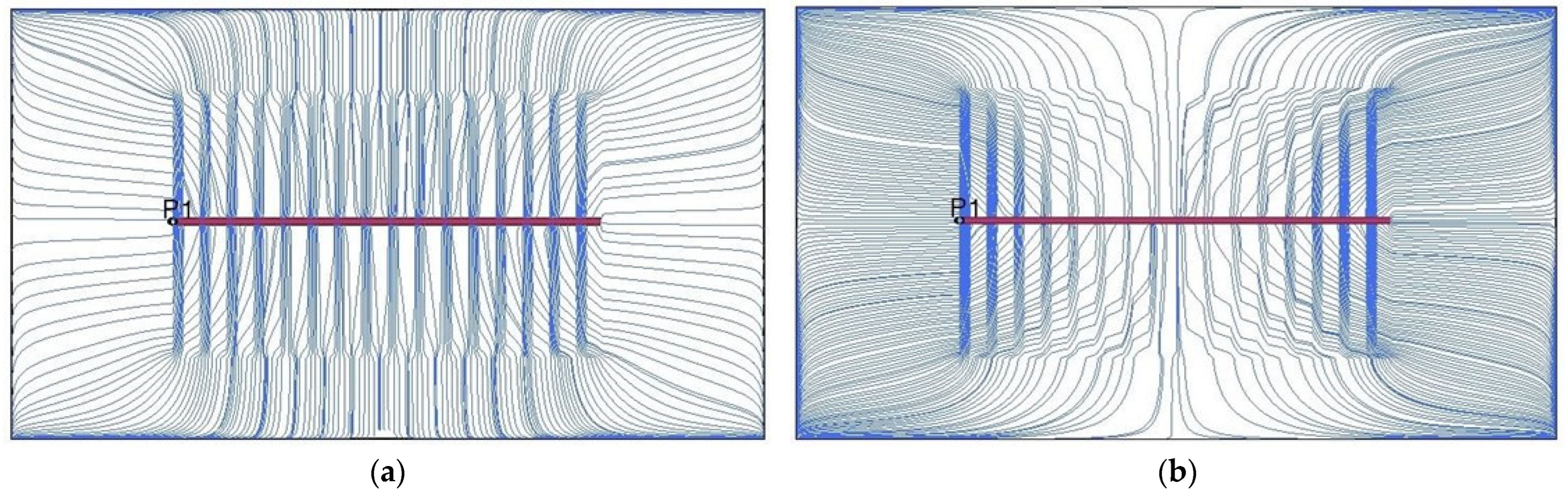
3. Classification of Water Injection Area
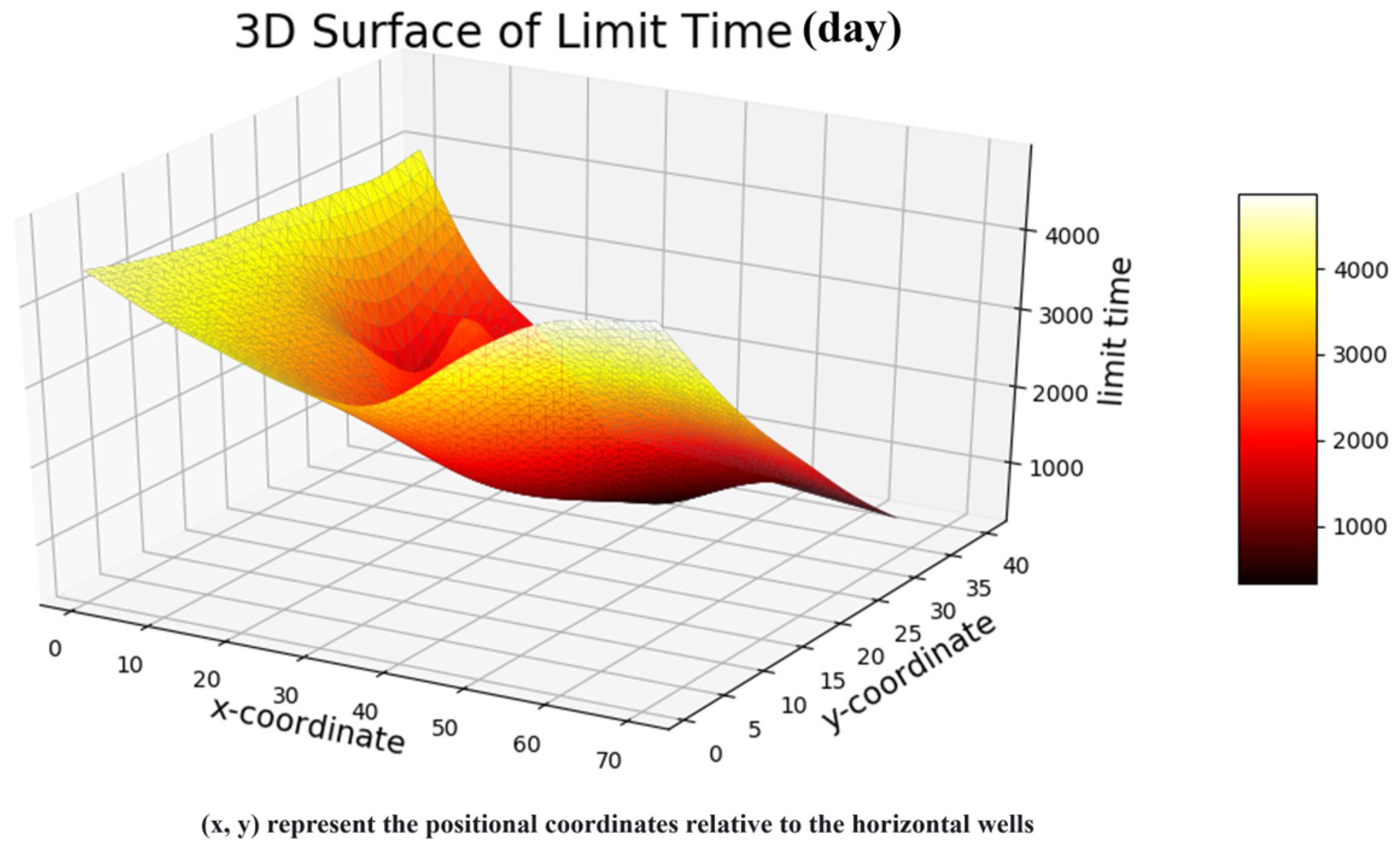
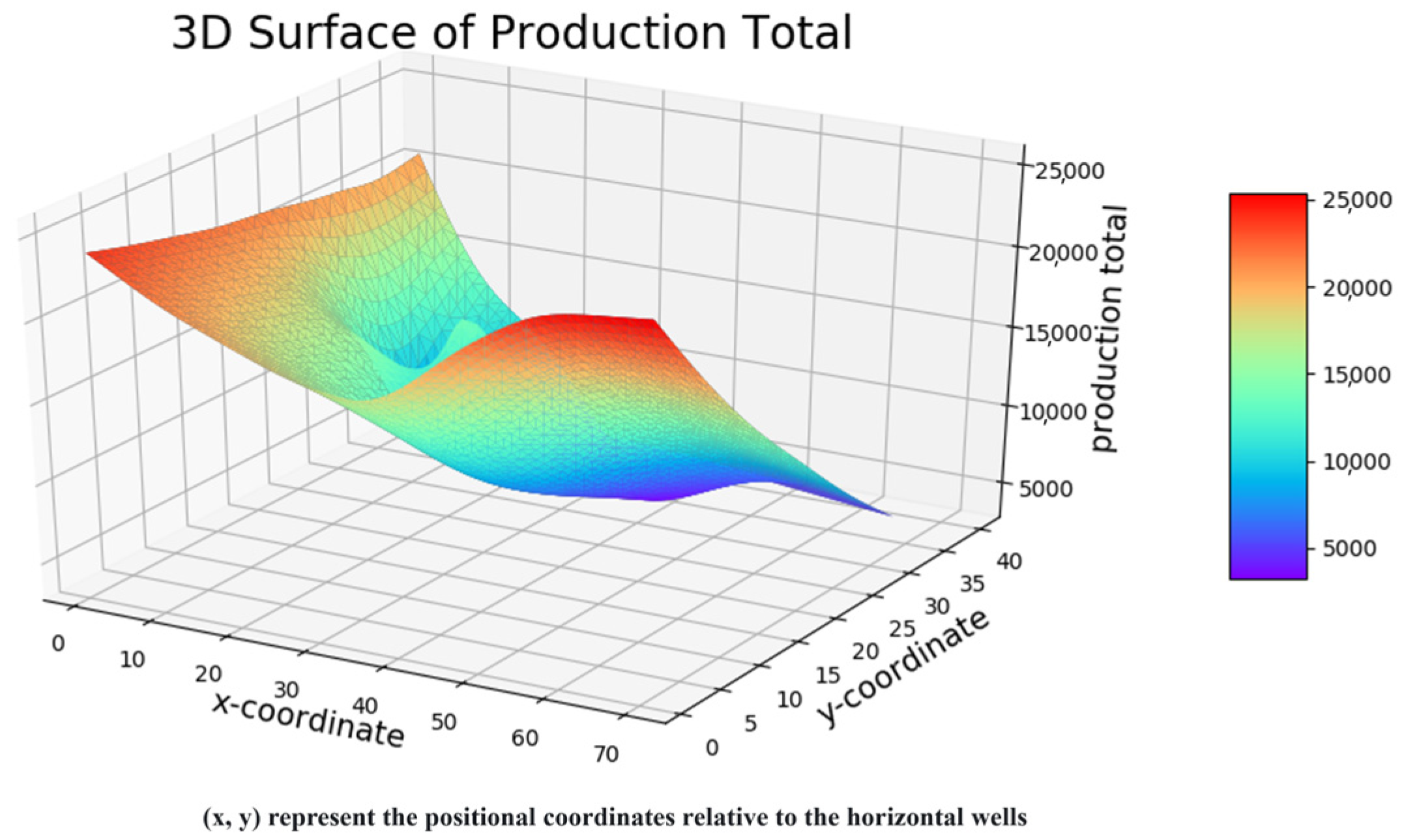
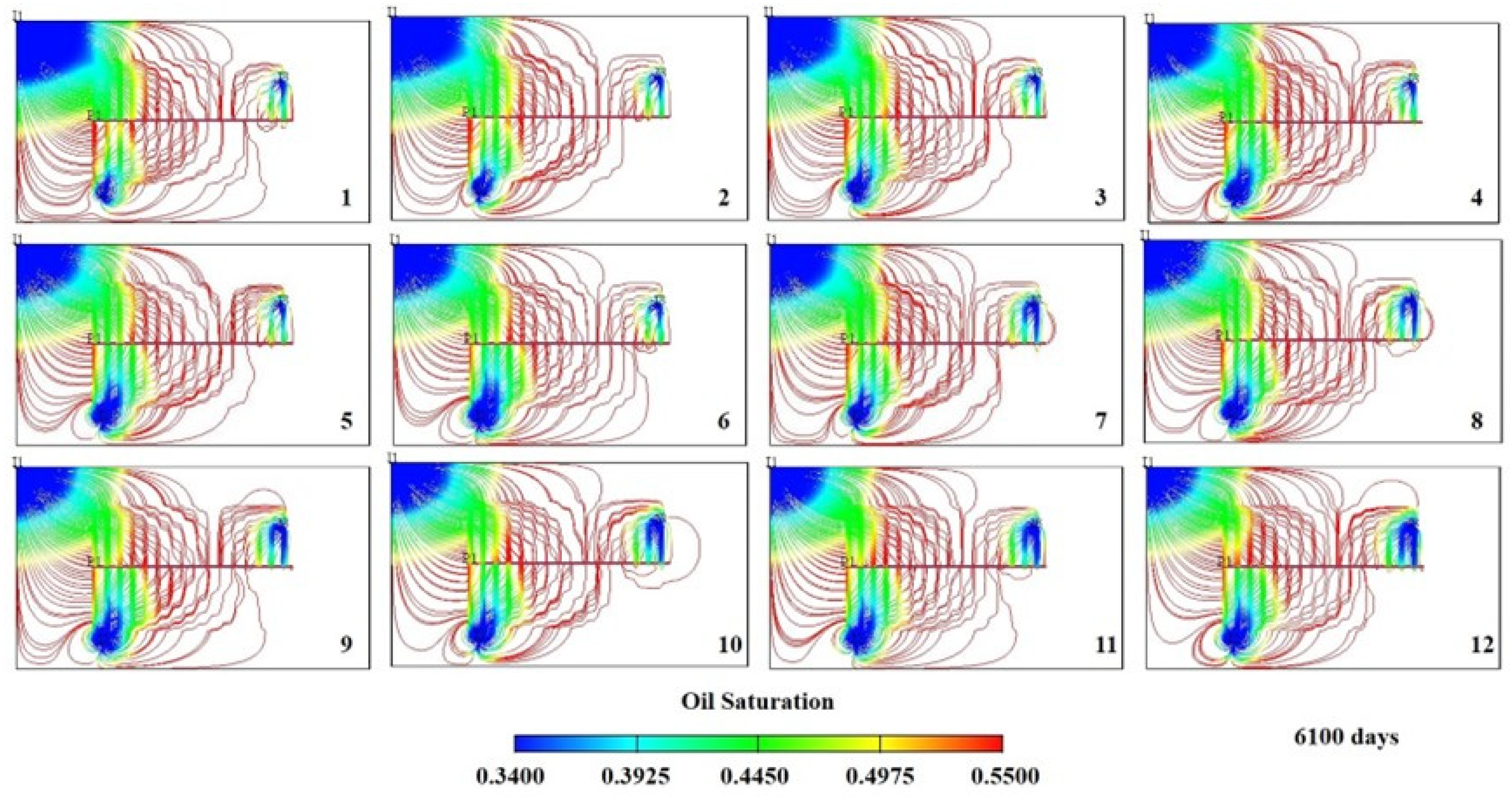
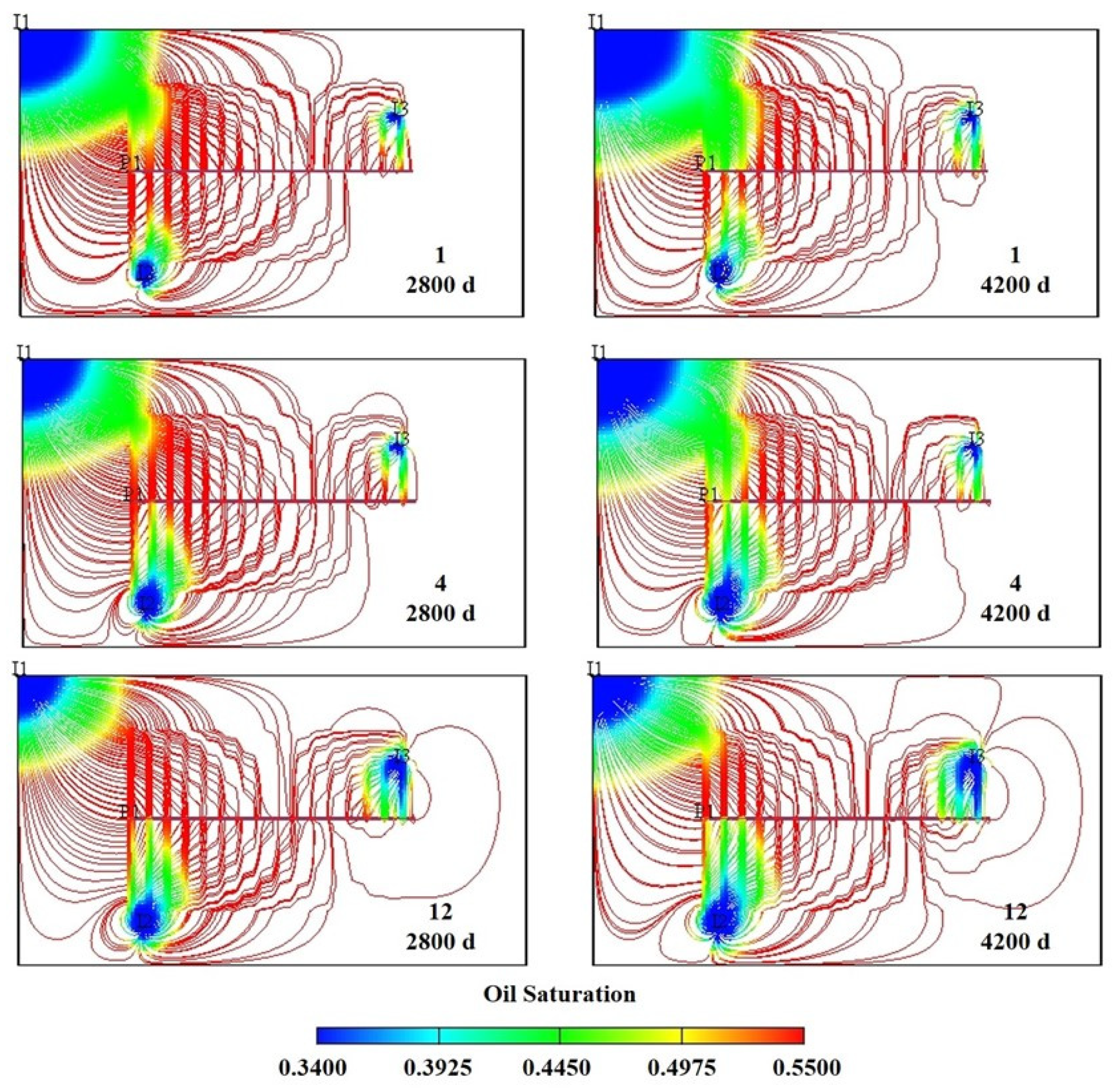
4. Water-Injection-Ratio Coefficient Optimization and Mechanism Analysis
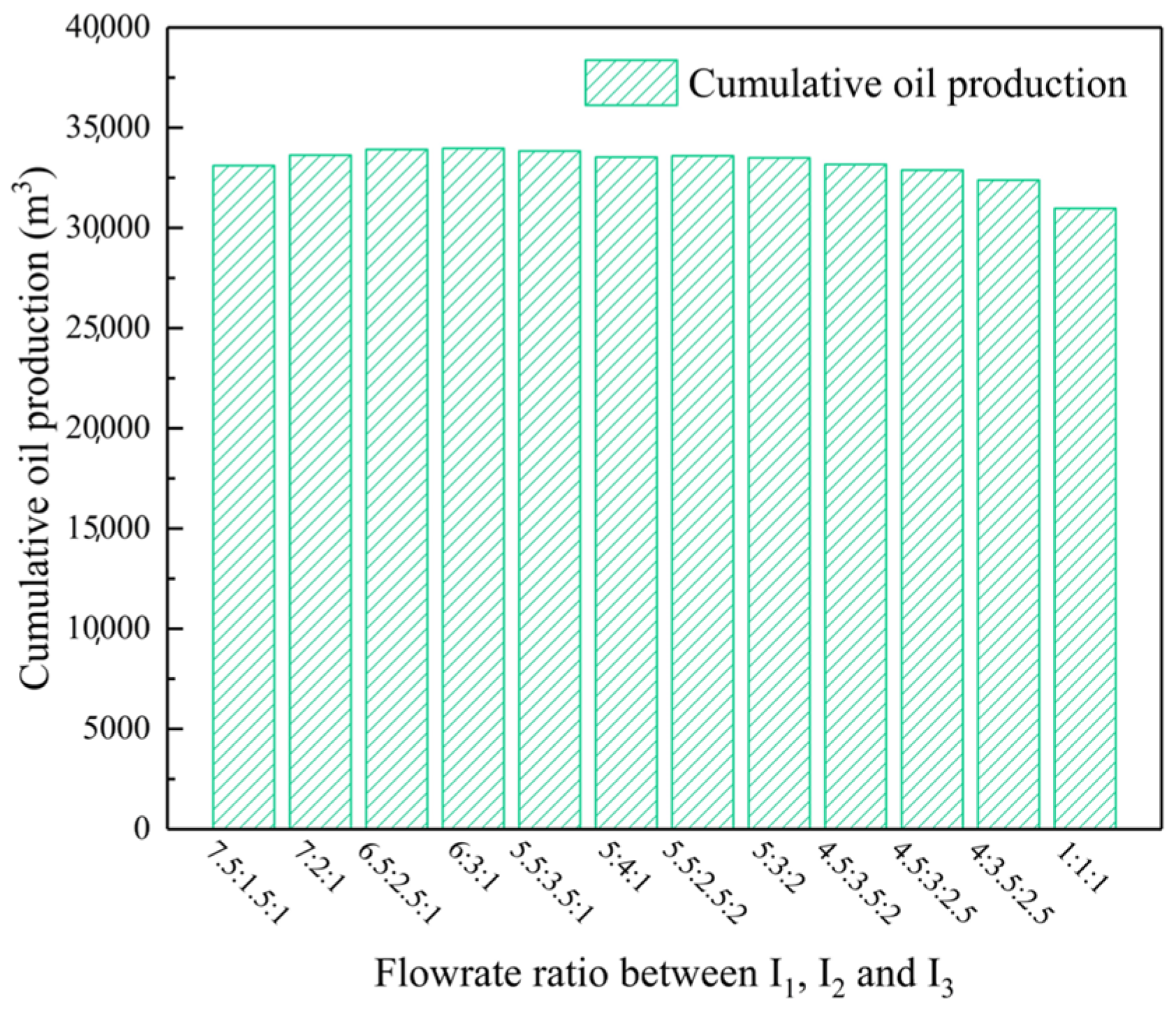
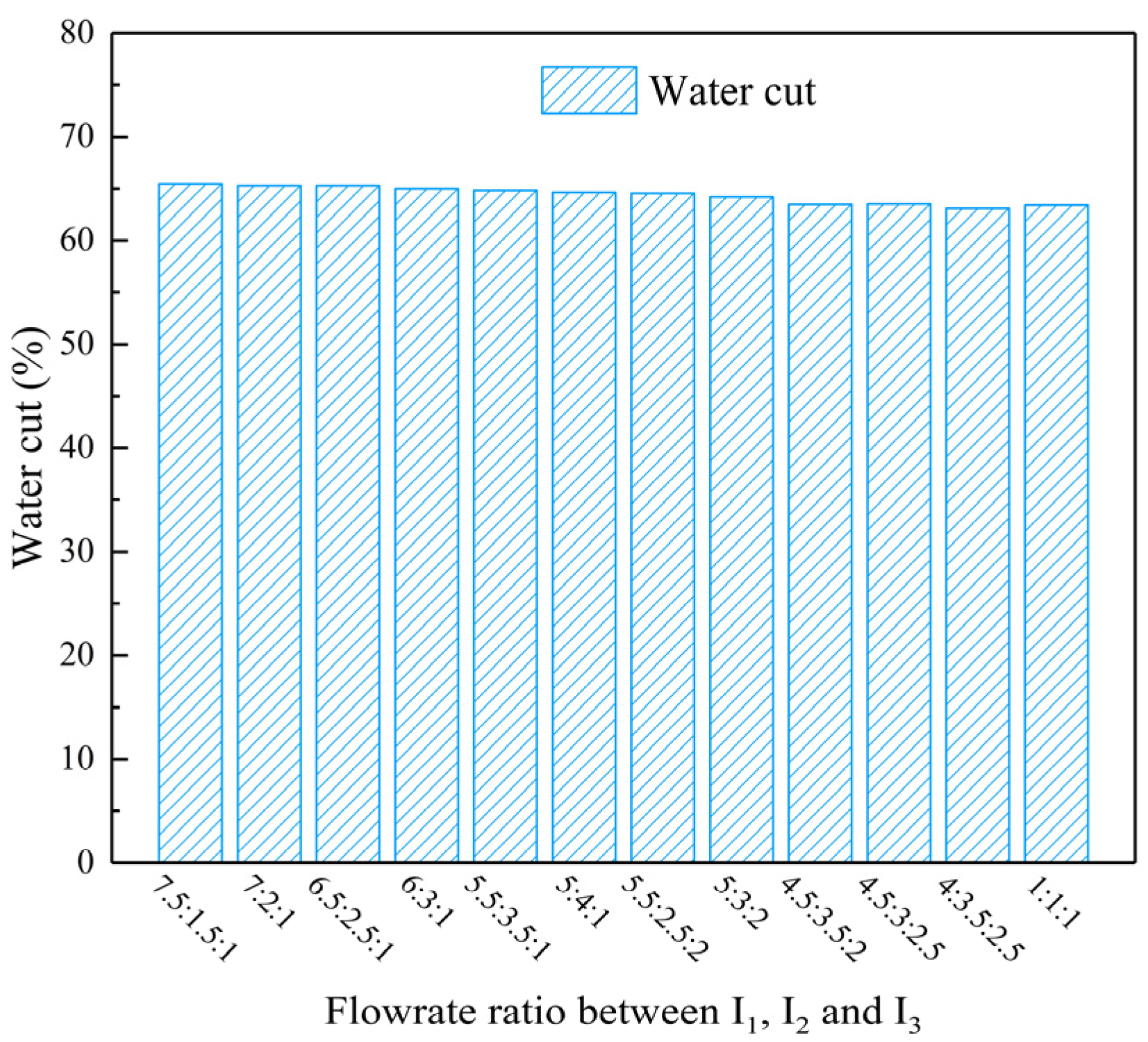
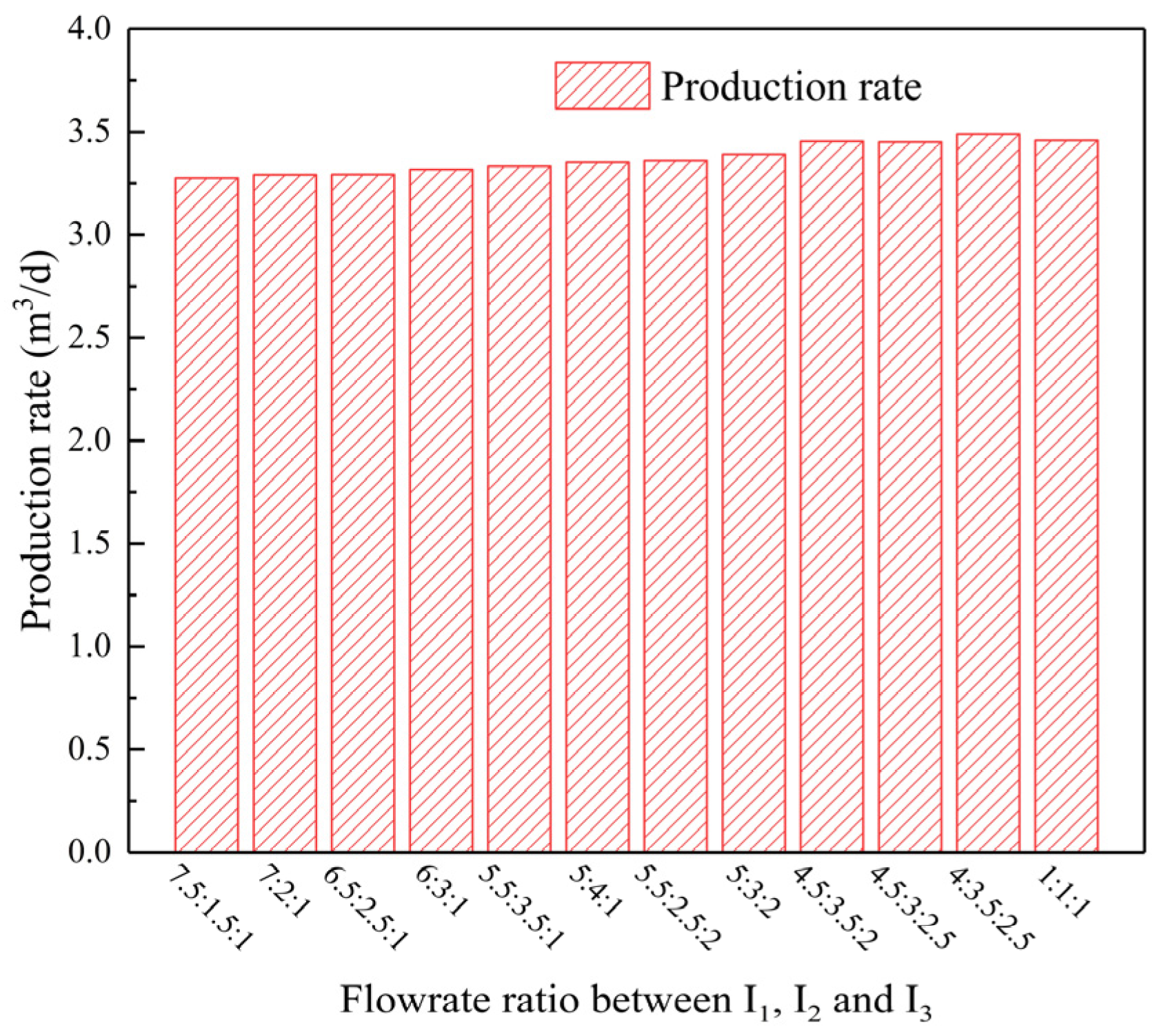
4.1. Water-Injection-Ratio Coefficient Optimization
4.2. Mechanism Analysis of Injection Intensity Classification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, S.; Zhu, R.; Wu, S.; Bai, B.; Yang, Z.; Cui, J. Exploration and development of continental tight oil in China. Petrol. Explor. Dev. 2018, 45, 790–802. [Google Scholar] [CrossRef]
- Tomassi, A.; de Franco, R.; Trippetta, F. High-resolution synthetic seismic modelling: Elucidating facies heterogeneity in carbonate ramp systems. Petrol. Geosci. 2025, 31, petgeo2024-047. [Google Scholar] [CrossRef]
- Yekeen, N.; Padmanabhan, E.; Idris, A.K.; Chauhan, P.S. Nanoparticles applications for hydraulic fracturing of unconventional reservoirs: A comprehensive review of recent advances and prospects. J. Pet. Sci. Eng. 2019, 178, 41–73. [Google Scholar] [CrossRef]
- Yu, H.; Rui, Z.; Chen, Z.; Lu, X.; Yang, Z.; Liu, J.; Qu, X.; Patil, S.; Ling, K.; Lu, J. Feasibility study of improved unconventional reservoir performance with carbonated water and surfactant. Energy 2019, 182, 135–147. [Google Scholar] [CrossRef]
- Jackson, M.D.; Vinogradov, J.; Hamon, G.; Chamerois, M. Evidence, mechanisms and improved understanding of controlled salinity waterflooding part 1: Sandstones. Fuel 2016, 185, 772–793. [Google Scholar] [CrossRef]
- Eyinla, D.S.; Leggett, S.; Badrouchi, F.; Emadi, H.; Adamolekun, O.J.; Akinsanpe, O.T. A comprehensive review of the potential of rock properties alteration during CO2 injection for EOR and storage. Fuel 2023, 353, 129219. [Google Scholar] [CrossRef]
- Sheng, J.J. Enhanced oil recovery in shale reservoirs by gas injection. J. Nat. Gas Sci. Eng. 2015, 22, 252–259. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wu, J.; Li, X.; Li, H.; Cheng, Y. Wellhead stability during development process of hydrate reservoir in the Northern South China Sea: Evolution and mechanism. Processes 2024, 13, 40. [Google Scholar] [CrossRef]
- Li, Y.; Xu, W.; Xiao, F.; Liu, L.; Liu, S.; Zhang, W. Optimization of a development well pattern based on production performance: A case study of the strongly heterogeneous Sulige tight sandstone gas field, Ordos Basin. Nat. Gas Ind. B 2015, 2, 95–100. [Google Scholar] [CrossRef][Green Version]
- Yu, R.; Bian, Y.; Wang, K.; Yang, Z.; Zhang, X. Numerical Simulation Study on Diamond-Shape Inverted Nine-Spot Well Pattern. Phys. Procedia 2012, 24, 390–396. [Google Scholar] [CrossRef][Green Version]
- Kou, Z.; Wang, H.; Alvarado, V.; McLaughlin, J.F.; Quillinan, S.A. Method for upscaling of CO2 migration in 3D heterogeneous geological models. J. Hydrol. 2022, 613, 128361. [Google Scholar] [CrossRef]
- Kou, Z.; Zhang, D.; Chen, Z.; Xie, Y. Quantitatively determine CO2 geosequestration capacity in depleted shale reservoir: A model considering viscous flow, diffusion, and adsorption. Fuel 2022, 309, 122191. [Google Scholar] [CrossRef]
- Wang, H.; Kou, Z.; Bagdonas, D.A.; Phillips, E.H.; Alvarado, V.; Johnson, A.C.; Jiao, Z.; McLaughlin, J.F.; Quillinan, S.A. Multiscale petrophysical characterization and flow unit classification of the Minnelusa eolian sandstones. J. Hydrol. 2022, 607, 127466. [Google Scholar] [CrossRef]
- Yue, P.; Xie, Z.; Liu, H.; Chen, X.; Guo, Z. Application of water injection curves for the dynamic analysis of fractured-vuggy carbonate reservoirs. J. Pet. Sci. Eng. 2018, 169, 220–229. [Google Scholar] [CrossRef]
- Strickland, T.A.; Crawford, P.B. Predicted areal sweep efficiency when using horizontal wells in five-spot patterns. Fuel 1991, 70, 1324–1326. [Google Scholar] [CrossRef]
- Abou-Kassem, J.H.; Islam, M.R.; Ali, S.M.F. Petroleum Reservoir Simulation, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 65–124. [Google Scholar] [CrossRef]
- Sepehrnoori, K.; Xu, Y.; Yu, W. EDFM for field-scale reservoir simulation with complex corner-point grids. Dev. Pet. Sci. 2020, 68, 191–237. [Google Scholar] [CrossRef]
- Xu, Y.; Fernandes, B.R.B.; Marcondes, F.; Sepehrnoori, K. Embedded discrete fracture modeling for compositional reservoir simulation using corner-point grids. J. Pet. Sci. Eng. 2019, 177, 41–52. [Google Scholar] [CrossRef]
- Ishibashi, T.; Watanabe, N.; Tamagawa, T.; Tsuchiya, N. Three-dimensional channeling flow within subsurface rock fracture networks suggested via fluid flow analysis in the Yufutsu fractured oil/gas reservoir. J. Pet. Sci. Eng. 2019, 178, 838–851. [Google Scholar] [CrossRef]
- Nelson, R.; Zuo, L.; Weijermars, R.; Crowdy, D. Applying improved analytical methods for modelling flood displacement fronts in bounded reservoirs (Quitman field, east Texas). J. Pet. Sci. Eng. 2018, 166, 1018–1041. [Google Scholar] [CrossRef]



| Items | Values |
|---|---|
| The length of horizontal well/m | 800 |
| Average porosity | 0.15 |
| Average permeability of matrix region/mD | 0.23 |
| Average permeability of fracturing | 200 |
| region/mD | |
| Fracture width/cm | 20 |
| Fracture half-length/m | 250 |
| Model Number | Streamline Distribution | Production Duration (Days) | Cumulative Oil Production (m3) |
|---|---|---|---|
| 1 |  | 4430 | 24,164 |
| 2 | 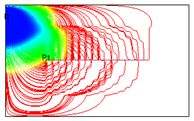 | 4160 | 22,756.62 |
| 3 | 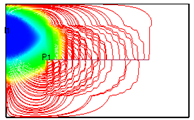 | 4080 | 21,886.51 |
| 4 | 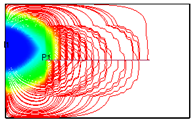 | 4050 | 21,303.44 |
| 5 |  | 4090 | 21,270.68 |
| 6 | 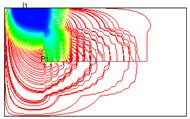 | 3800 | 20,511.72 |
| 7 | 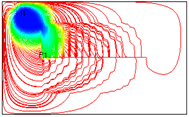 | 3110 | 17,141.04 |
| 8 |  | 2590 | 14,454.75 |
| 9 |  | 2130 | 11,816.99 |
| 10 | 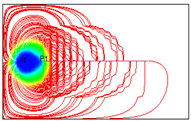 | 2000 | 10,928.94 |
| 11 |  | 3390 | 18,340.27 |
| 12 |  | 2220 | 12,409.64 |
| 13 |  | 1180 | 7410.55 |
| 14 | 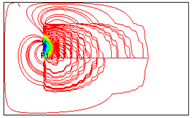 | 610 | 4646.06 |
| 15 |  | 4420 | 23,517.91 |
| 16 | 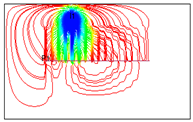 | 3170 | 17,082.34 |
| 17 |  | 2030 | 11,404.94 |
| 18 | 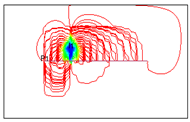 | 960 | 6185.23 |
| 19 |  | 5040 | 26,137.62 |
| 20 |  | 3410 | 18,142.48 |
| 21 | 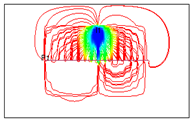 | 2130 | 11,818.11 |
| 22 | 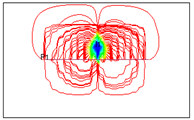 | 970 | 6232.69 |
| Number/# | IRC/R1 | IRC/R2 | IRC/R3 |
|---|---|---|---|
| 1 | 7.5 | 1.5 | 1 |
| 2 | 7 | 2 | 1 |
| 3 | 6.5 | 2.5 | 1 |
| 4 | 6 | 3 | 1 |
| 5 | 5.5 | 3.5 | 1 |
| 6 | 5 | 4 | 1 |
| 7 | 5.5 | 2.5 | 2 |
| 8 | 5 | 3 | 2 |
| 9 | 4.5 | 3.5 | 2 |
| 10 | 4.5 | 3 | 2.5 |
| 11 | 4 | 3.5 | 2.5 |
| 12 | 3.4 | 3.3 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Yu, J.; Qu, H.; Yin, S. A Novel Approach to Waterflooding Optimization in Irregular Well Patterns Using Streamline Simulation and 3D Visualization. Processes 2025, 13, 1114. https://doi.org/10.3390/pr13041114
Yin H, Yu J, Qu H, Yin S. A Novel Approach to Waterflooding Optimization in Irregular Well Patterns Using Streamline Simulation and 3D Visualization. Processes. 2025; 13(4):1114. https://doi.org/10.3390/pr13041114
Chicago/Turabian StyleYin, Hu, Jianing Yu, Hongjun Qu, and Siqi Yin. 2025. "A Novel Approach to Waterflooding Optimization in Irregular Well Patterns Using Streamline Simulation and 3D Visualization" Processes 13, no. 4: 1114. https://doi.org/10.3390/pr13041114
APA StyleYin, H., Yu, J., Qu, H., & Yin, S. (2025). A Novel Approach to Waterflooding Optimization in Irregular Well Patterns Using Streamline Simulation and 3D Visualization. Processes, 13(4), 1114. https://doi.org/10.3390/pr13041114






