Surrogate Modeling of Hydrogen-Enriched Combustion Using Autoencoder-Based Dimensionality Reduction
Abstract
1. Introduction
2. Construction of Dataset
2.1. Description of Physical Problem
2.2. Design of Experiment
3. Autoencoder-Based Reduced Order Models
4. Results and Discussion
4.1. Hyperparameter Optimization of CAEs
4.2. Hyperparameter Optimization of FCAEs
4.3. Comparisons Between CAE and FCAE
4.3.1. ROM Prediction
4.3.2. Computation Time
5. Conclusions
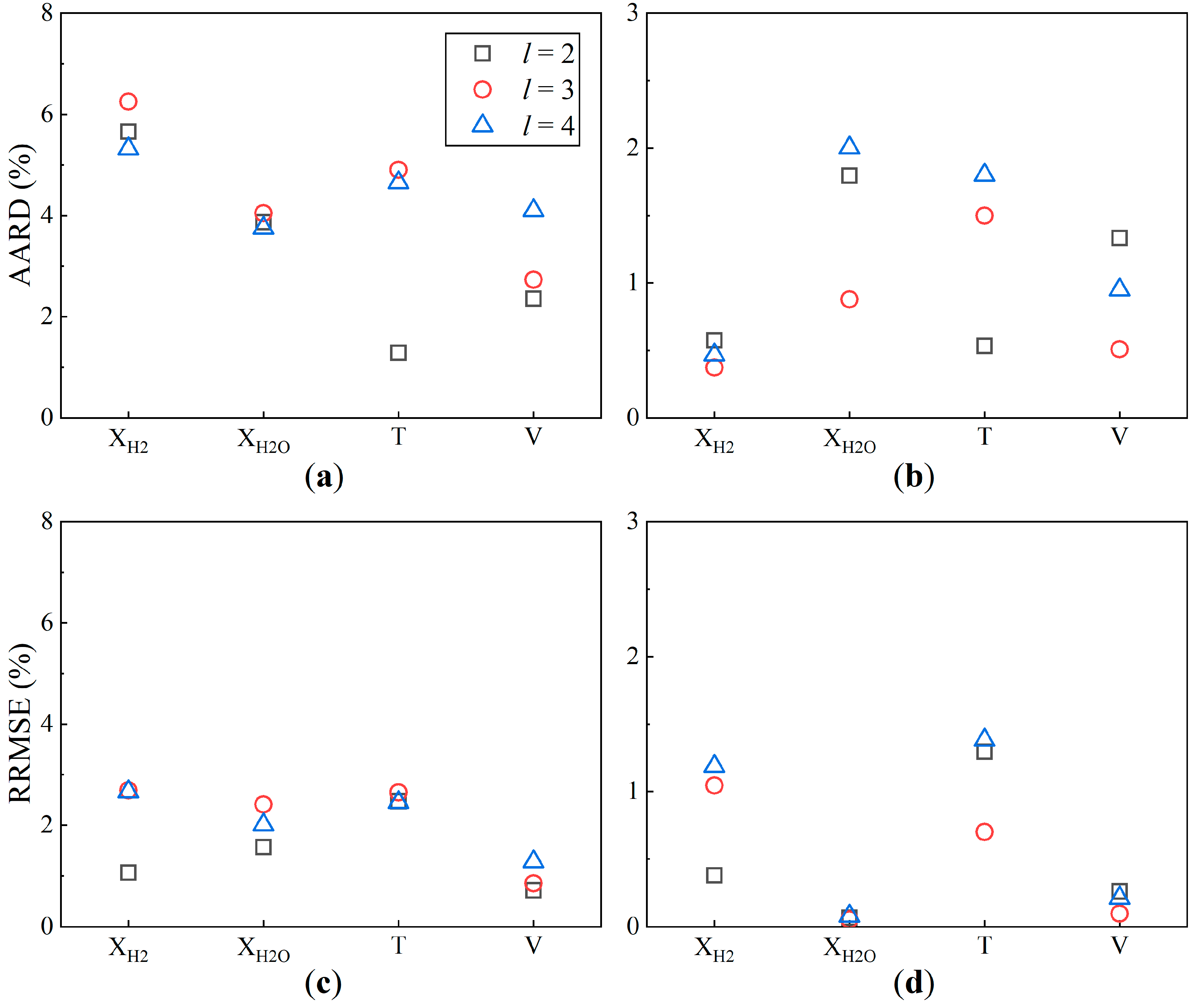
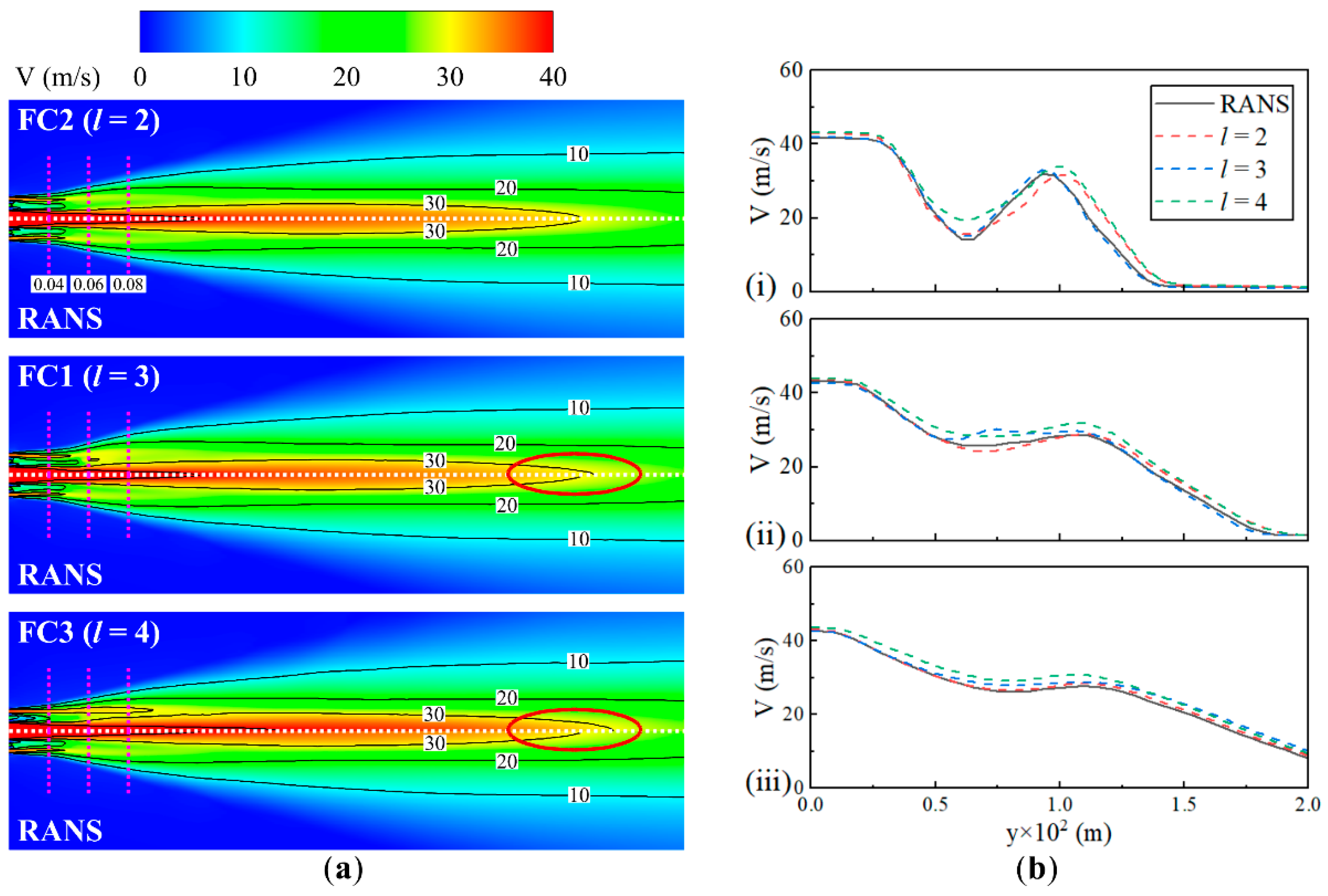
- For AE-based ROMs, deeper networks are essential for capturing features in strongly nonlinear flowfields, while fewer layers are more effective for weakly nonlinear flowfields to avoid overfitting, as indicated by the average reconstruction AARDs. Specifically, when predicting a temperature field with strong nonlinearity, the l = 2 CAE model exhibited an absolute RD consistently ranging from 15% to 30% in the flame anchoring region, which was considerably larger than that of the l = 3 and 4 models. In contrast, for weakly nonlinear predictions, an l = 2 configuration was more suitable.
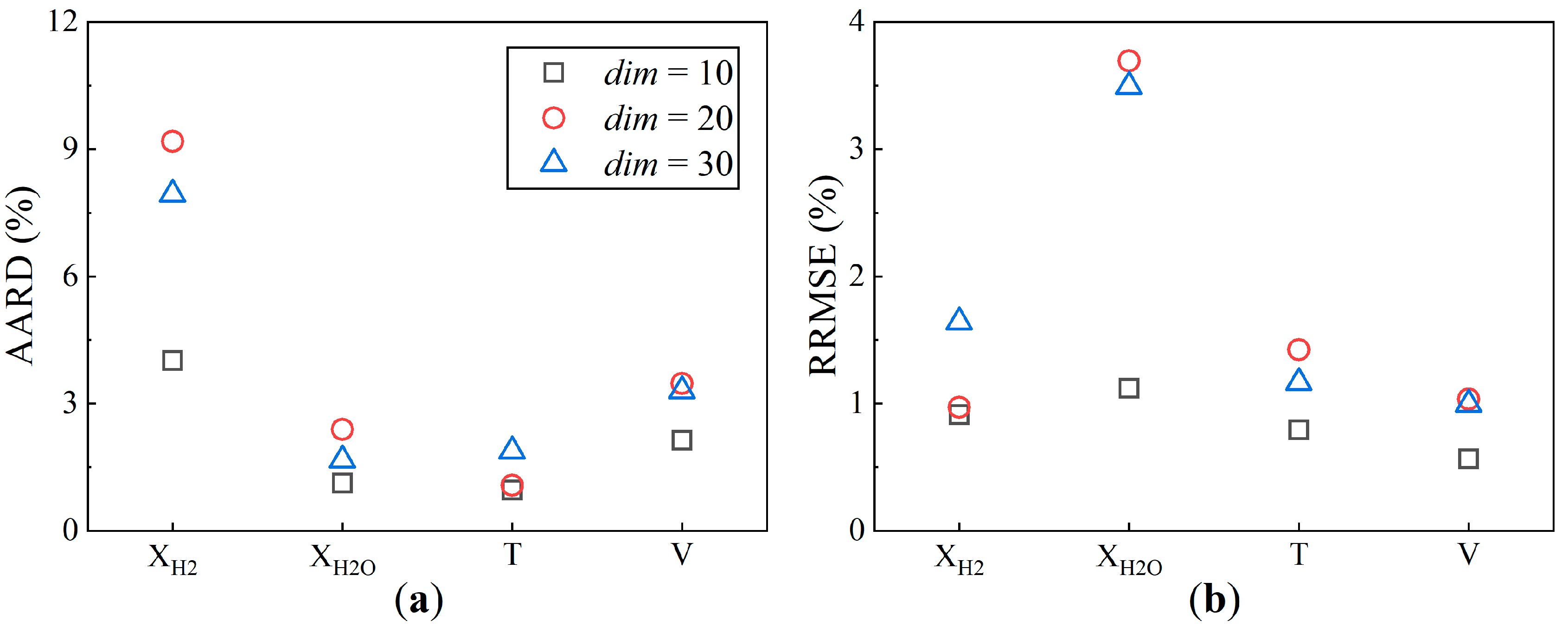
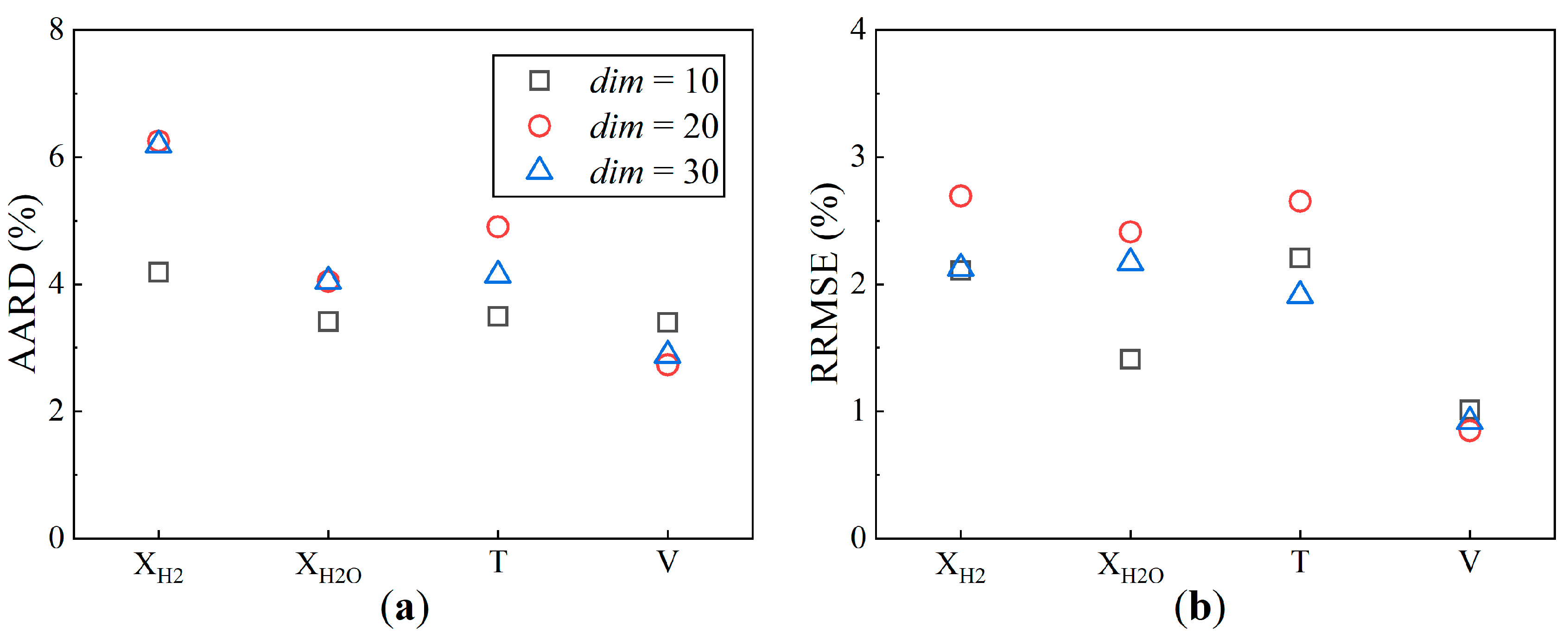
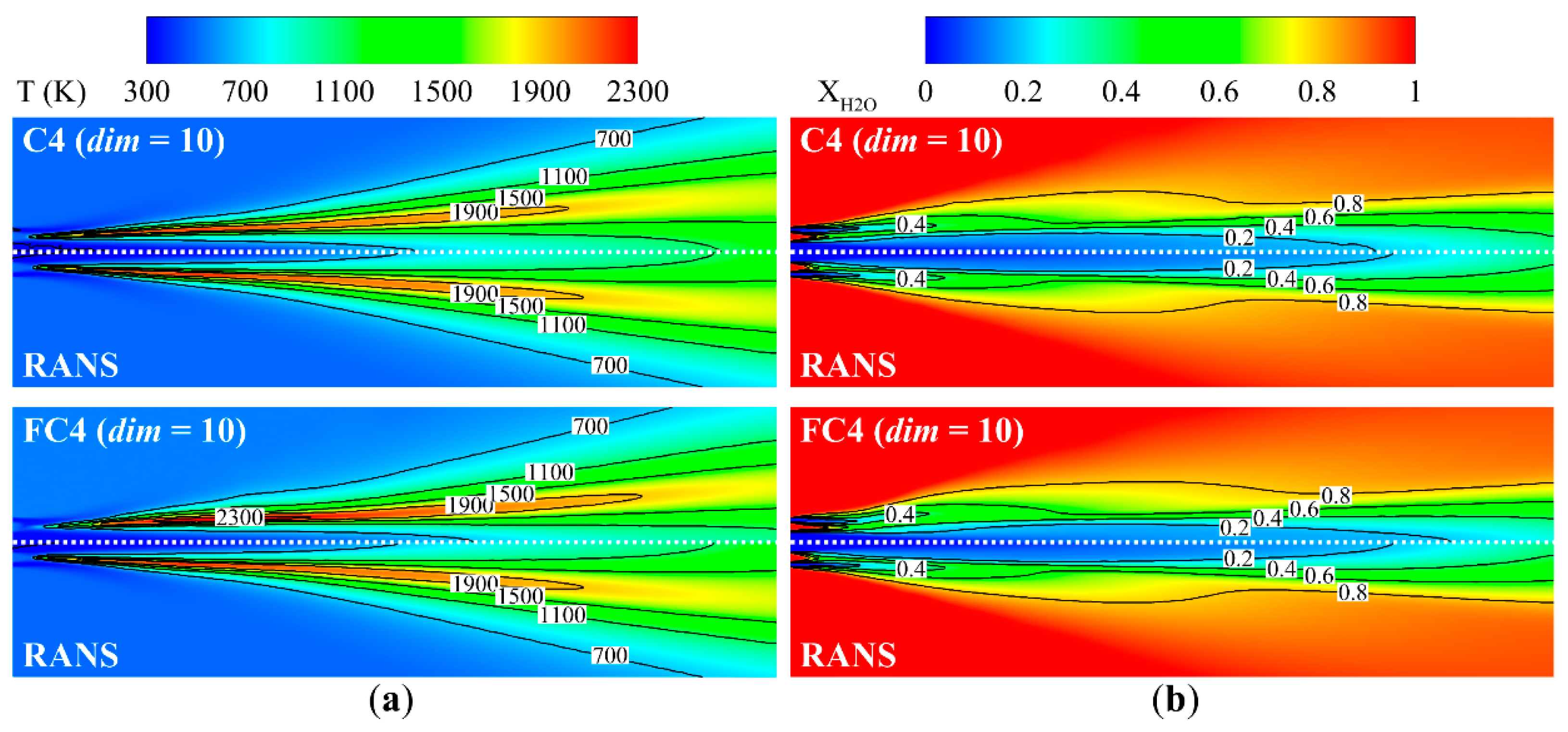
- AE-based ROMs with fewer dimensions may yield better performance for flowfields where nonlinearity is less pronounced, while they may lead to an increased local error in certain cases because of excessive feature compression. The prediction for demonstrated that the CAE model with a dim = 10 achieved a significantly lower AARD of 4.01%, representing about a 50% reduction compared to the dim = 20 and 30 models. However, when predicting regions with strong shear effects, the local errors of the dim = 10 and 20 CAE models were larger.
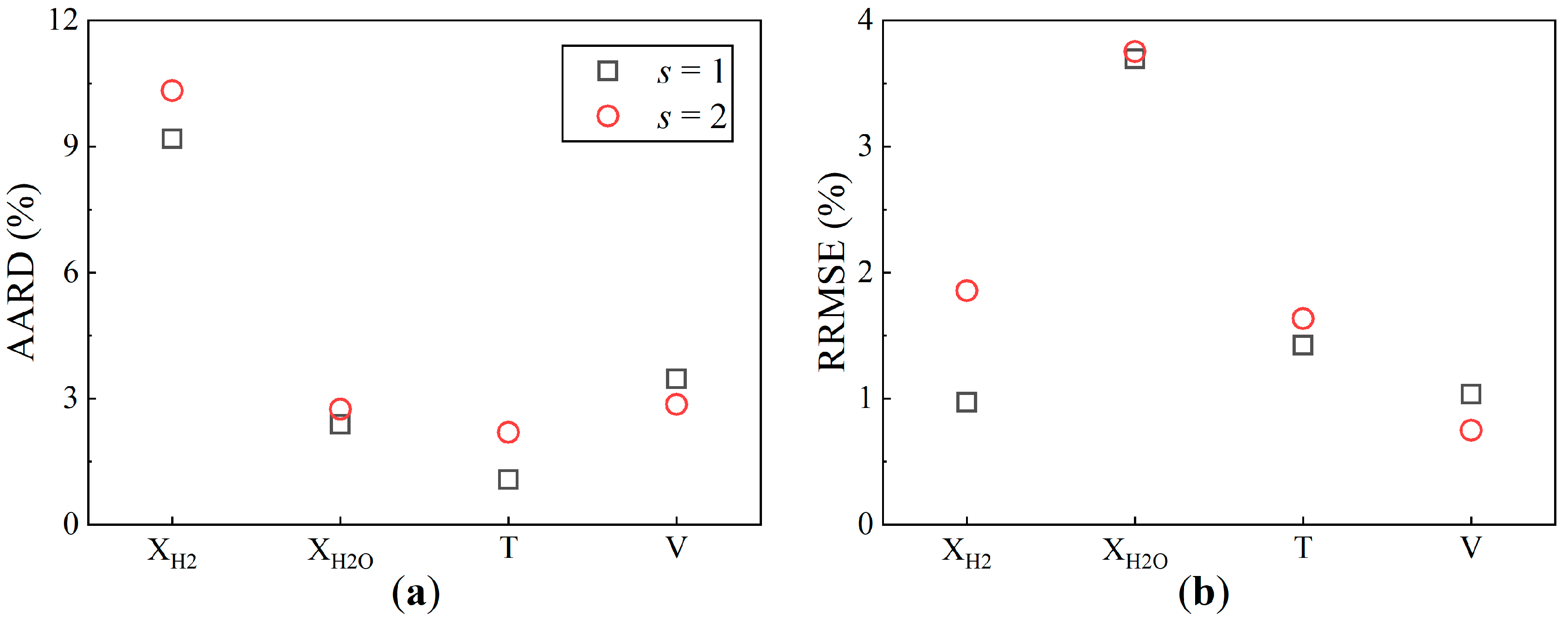
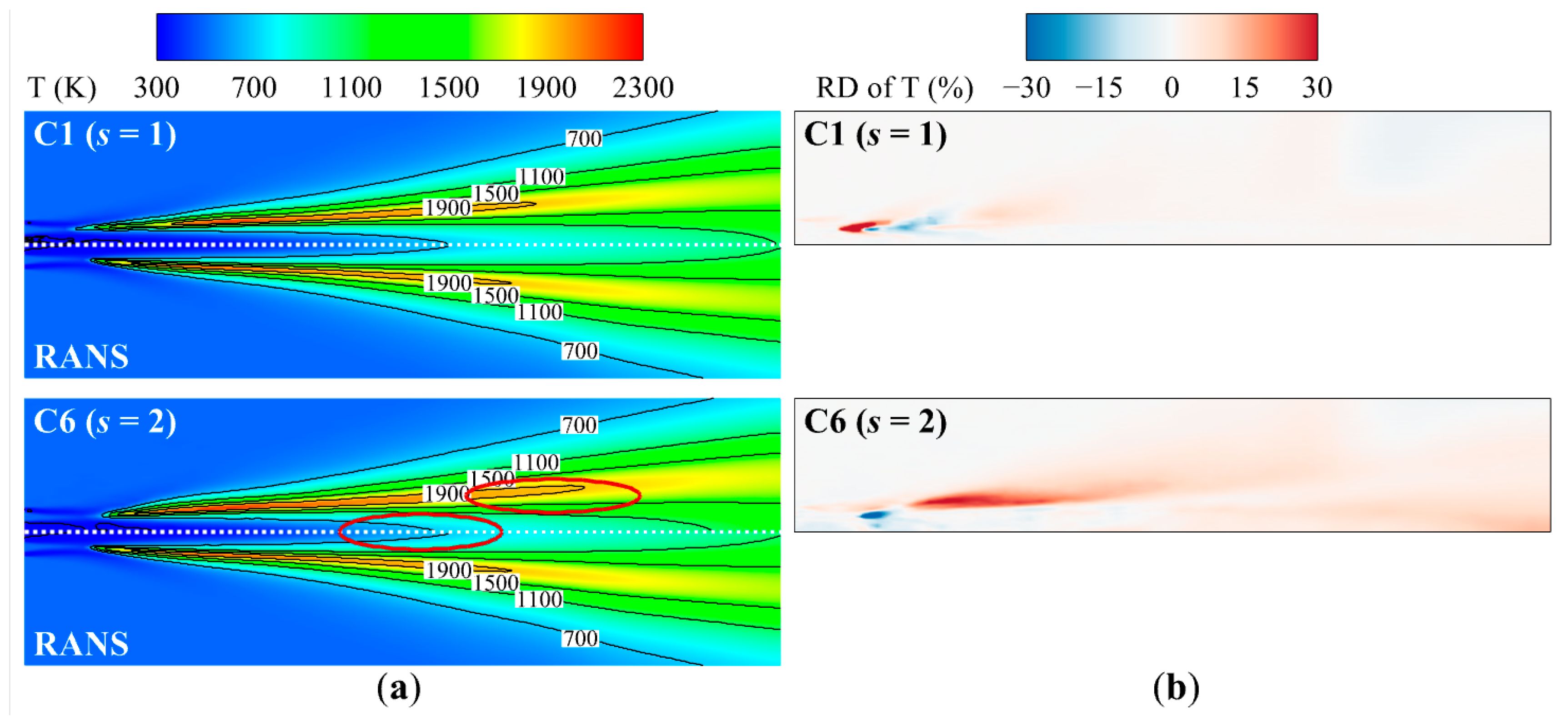
- The CAE-based model indicated a preferable general simulation capability with a smaller convolutional stride, as the s = 1 model contained approximately 21 times more training parameters than the s = 2 model.
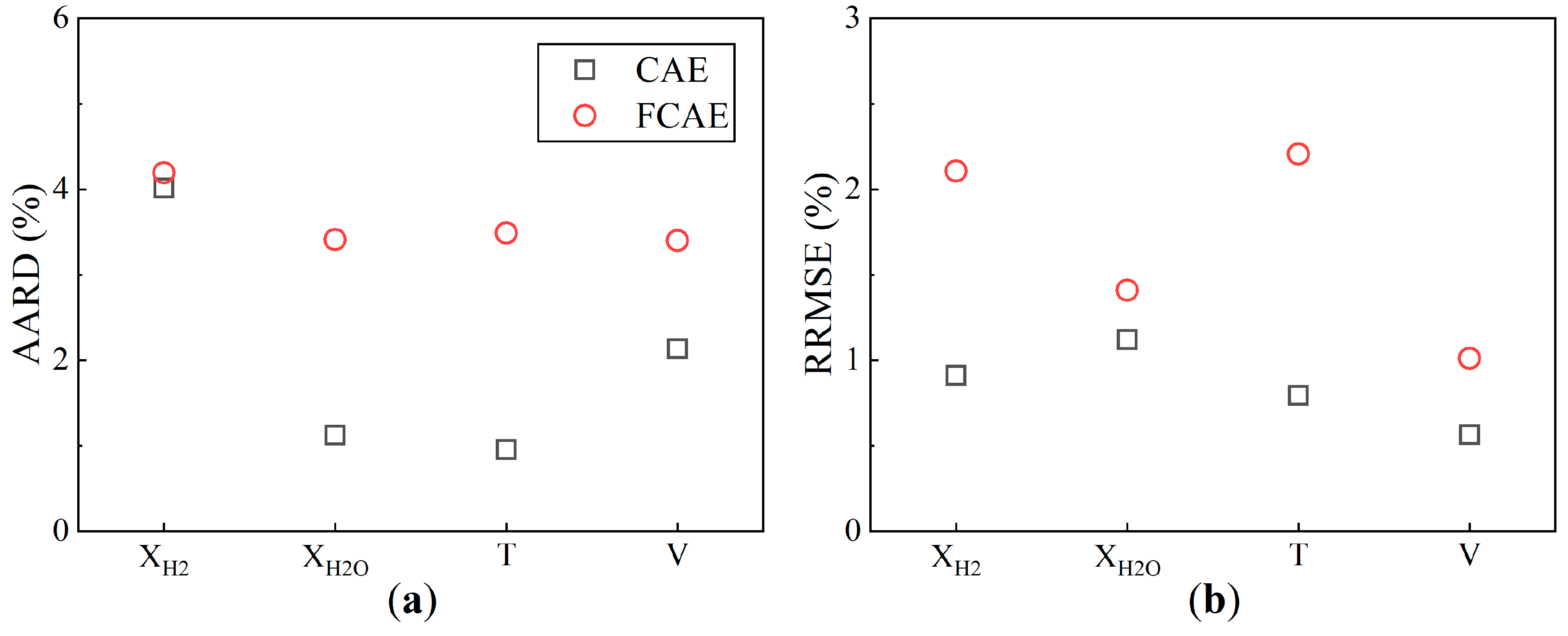
- Comparing the CAE- and FCAE-based models under the same number of network layers and latent vector dimensionality, the CAE-based model exhibits superior predictive accuracy and a shorter training time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su-Ungkavatin, P.; Tiruta-Barna, L.; Hamelin, L. Biofuels, electrofuels, electric or hydrogen?: A review of current and emerging sustainable aviation systems. Prog. Energy Combust. Sci. 2023, 96, 101073. [Google Scholar]
- Jin, U.; Kim, K.T. Hybrid rich-and lean-premixed ammonia-hydrogen combustion for mitigation of NOx emissions and thermoacoustic instabilities. Combust. Flame 2024, 262, 113366. [Google Scholar] [CrossRef]
- Tanneberger, T.; Schimek, S.; Paschereit, C.O.; Stathopoulos, P. Combustion efficiency measurements and burner characterization in a hydrogen-oxyfuel combustor. Int. J. Hydrogen Energy 2019, 44, 29752–29764. [Google Scholar]
- Abbas, T.; Chen, S.; Zhang, X.; Wang, Z. Coordinated optimization of hydrogen-integrated energy hubs with demand response-enabled energy sharing. Processes 2024, 12, 1338. [Google Scholar] [CrossRef]
- Hydrogen Gas Turbines. Available online: https://etn.global/wp-content/uploads/2020/01/ETN-Hydrogen-Gas-Turbines-report.pdf (accessed on 18 February 2025).
- Lieuwen, T.; McDonell, V.; Petersen, E.; Santavicca, D. Fuel flexibility influences on premixed combustor blowout, flashback, autoignition and instability. Turbo Expo Power Land Sea Air 2006, 42363, 601–615. [Google Scholar]
- Noble, D.; Wu, D.; Emerson, B.; Sheppard, S.; Lieuwen, T.; Angello, L. Assessment of current capabilities and near-term availability of hydrogen-fired gas turbines considering a low-carbon future. J. Eng. Gas Turbines Power 2021, 143, 041002. [Google Scholar] [CrossRef]
- Noble, D.R.; Zhang, Q.; Shareef, A.; Tootle, J.; Meyers, A.; Lieuwen, T. Syngas mixture composition effects upon flashback and blowout. Turbo Expo Power Land Sea Air 2006, 42363, 357–368. [Google Scholar]
- Ni, C.; Ding, S.; Li, J.; Chu, X.; Ren, Z.; Wang, X. Projection-based reduced order modeling of multi-species mixing and combustion. Phys. Fluids 2024, 36, 077168. [Google Scholar]
- Ding, S.; Ni, C.; Chu, X.; Lu, Q.; Wang, X. Reduced-order modeling via convolutional autoencoder for emulating combustion of hydrogen/methane fuel blends. Combust. Flame 2025, 274, 113981. [Google Scholar]
- Li, J.; Zhang, R.; Wang, H.; Xu, Z. Inverse problem of permeability field under multi-well conditions using TgCNN-based surrogate model. Processes 2024, 12, 1934. [Google Scholar] [CrossRef]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar]
- Eldred, M.; Dunlavy, D. Formulations for surrogate-based optimization with data fit, multifidelity, and reduced-order models. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; p. 7117. [Google Scholar]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.-X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar]
- Ma, T.; Lu, H.; Li, Q. Optimization design method based on parameter reduction and active subspaces: Redistribution of chordwise loading at blade tips in a transonic axial-flow fan. Phys. Fluids 2024, 36, 095103. [Google Scholar]
- Hou, C.K.J.; Behdinan, K. Dimensionality reduction in surrogate modeling: A review of combined methods. Data Sci. Eng. 2022, 7, 402–427. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar]
- Benner, P.; Gugercin, S.; Willcox, K. A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar]
- Wang, X.; Chang, Y.-H.; Li, Y.; Yang, V.; Su, Y.-H. Surrogate-based modeling for emulation of supercritical injector flow and combustion. Proc. Combust. Inst. 2021, 38, 6393–6401. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar]
- Milan, P.J.; Torelli, R.; Lusch, B.; Magnotti, G. Data-driven model reduction of multiphase flow in a single-hole automotive injector. At. Sprays 2020, 30, 401–429. [Google Scholar]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar]
- Xu, J.; Duraisamy, K. Multi-level convolutional autoencoder networks for parametric prediction of spatio-temporal dynamics. Comput. Methods Appl. Mech. Eng. 2020, 372, 113379. [Google Scholar]
- Hartman, D.; Mestha, L.K. A deep learning framework for model reduction of dynamical systems. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Hawaii, HI, USA, 27–30 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1917–1922. [Google Scholar]
- Agostini, L. Exploration and prediction of fluid dynamical systems using auto-encoder technology. Phys. Fluids 2020, 32, 067103. [Google Scholar]
- Zhang, Y.; Chen, Y.; Wang, J.; Pan, Z. Unsupervised deep anomaly detection for multi-sensor time-series signals. IEEE Trans. Knowl. Data Eng. 2021, 35, 2118–2132. [Google Scholar]
- Nakamura, T.; Fukami, K.; Hasegawa, K.; Nabae, Y.; Fukagata, K. Convolutional neural network and long short-term memory based reduced order surrogate for minimal turbulent channel flow. Phys. Fluids 2021, 33, 025116. [Google Scholar]
- Milano, M.; Koumoutsakos, P. Neural network modeling for near wall turbulent flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar]
- Lee, K.; Carlberg, K.T. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 2020, 404, 108973. [Google Scholar]
- Gruber, A.; Gunzburger, M.; Ju, L.; Wang, Z. A comparison of neural network architectures for data-driven reduced-order modeling. Comput. Methods Appl. Mech. Eng. 2022, 393, 114764. [Google Scholar]
- Ding, S.; Wang, L.; Lu, Q.; Wang, X. Data-driven surrogate modeling and optimization of supercritical jet into supersonic crossflow. Chin. J. Aeronaut. 2024, 37, 139–155. [Google Scholar]
- Wu, X.; Wu, S.; Tian, X.; Guo, X.; Luo, X. Effects of hyperparameters on flow field reconstruction around a foil by convolutional neural networks. Ocean Eng. 2022, 247, 110650. [Google Scholar]
- Fukami, K.; Hasegawa, K.; Nakamura, T.; Morimoto, M.; Fukagata, K. Model order reduction with neural networks: Application to laminar and turbulent flows. SN Comput. Sci. 2021, 2, 467. [Google Scholar]
- Lui, H.; Wolf, W. Convolutional neural networks for the construction of surrogate models of fluid flows. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–21 January 2021; p. 1675. [Google Scholar]
- Peng, J.-Z.; Chen, S.; Aubry, N.; Chen, Z.; Wu, W.-T. Unsteady reduced-order model of flow over cylinders based on convolutional and deconvolutional neural network structure. Phys. Fluids 2020, 32, 123609. [Google Scholar]
- Wang, L.; Xiao, H.; Yang, B.; Wang, X.-E. Steam dilution effect on laminar flame characteristics of hydrogen-enriched oxy-combustion. Int. J. Hydrogen Energy 2024, 71, 375–386. [Google Scholar]
- McGuinness, R.M.; Kleinberg, W.T. Oxygen Production. In Oxygen-Enhanced Combustion, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 92–125. [Google Scholar]
- Gregory, P.; Smith, D.M.G.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 18 February 2025).
- Undapalli, S.; Srinivasan, S.; Menon, S.-I. LES of premixed and non-premixed combustion in a stagnation point reverse flow combustor. Proc. Combust. Inst. 2009, 32, 1537–1544. [Google Scholar]
- Gopalakrishnan, P.; Bobba, M.; Seitzman, J.-I. Controlling mechanisms for low NOx emissions in a non-premixed stagnation point reverse flow combustor. Proc. Combust. Inst. 2007, 31, 3401–3408. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistic, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Mak, S.; Sung, C.-L.; Wang, X.; Yeh, S.-T.; Chang, Y.-H.; Joseph, V.R.; Yang, V.; Wu, C.J. An efficient surrogate model for emulation and physics extraction of large eddy simulations. J. Am. Stat. Assoc. 2018, 113, 1443–1456. [Google Scholar]
- Zhou, M.; Ni, C.; Sung, C.-L.; Ding, S.; Wang, X. Modeling of thermophysical properties and vapor-liquid equilibrium using Gaussian process regression. Int. J. Heat Mass Transf. 2024, 219, 124888. [Google Scholar]
- Cheng, J.C.; Wang, M. Automated detection of sewer pipe defects in closed-circuit television images using deep learning techniques. Autom. Constr. 2018, 95, 155–171. [Google Scholar]
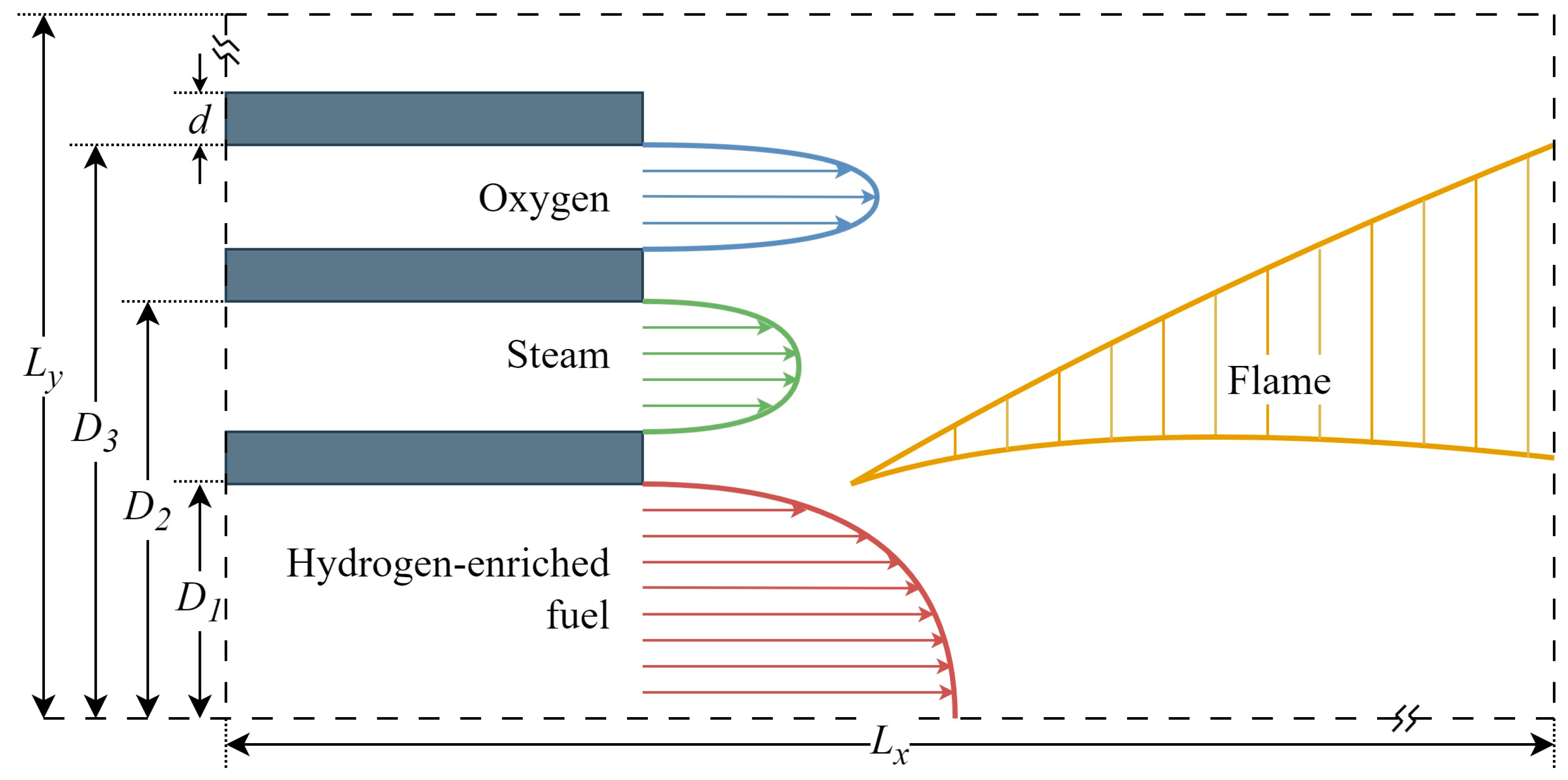
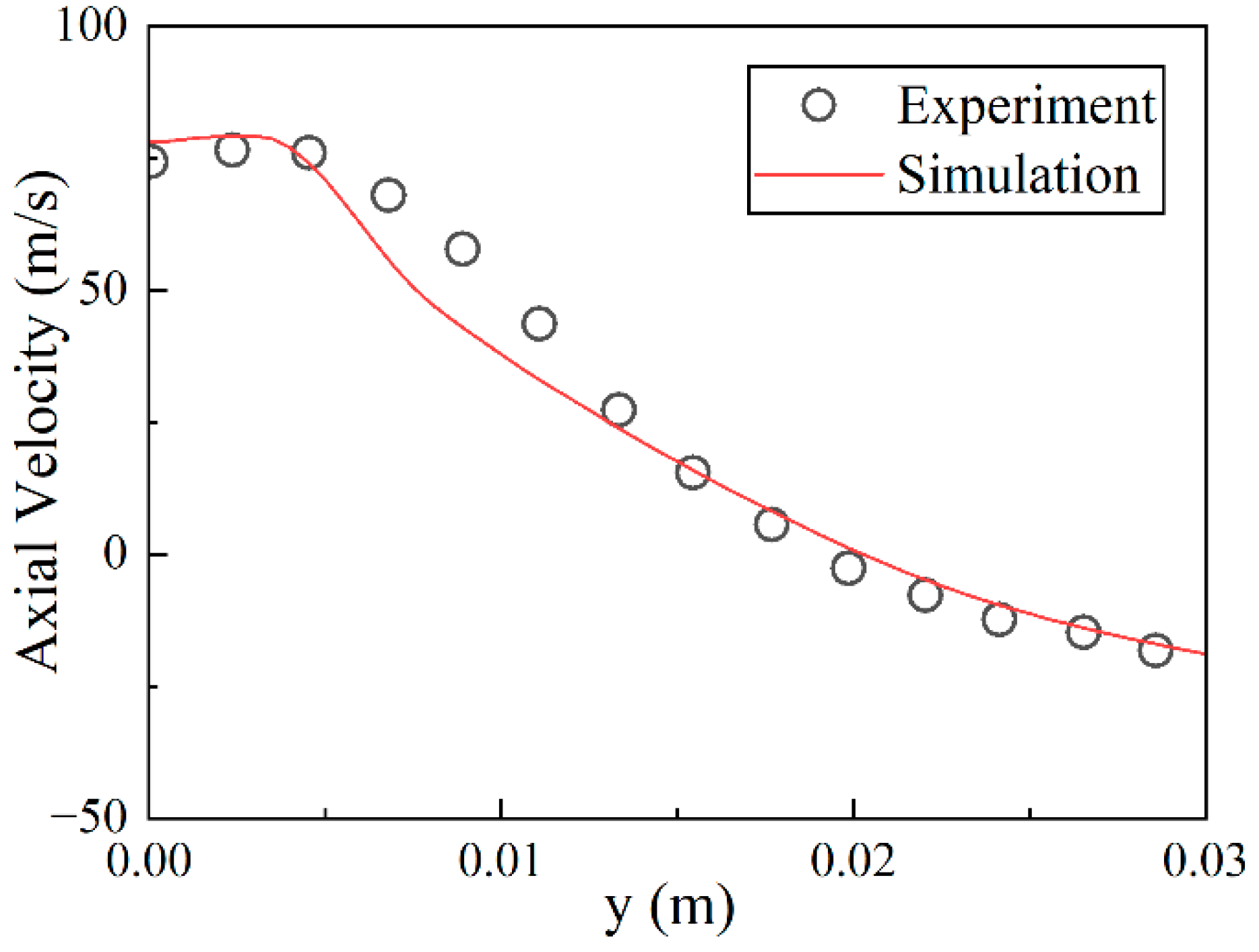


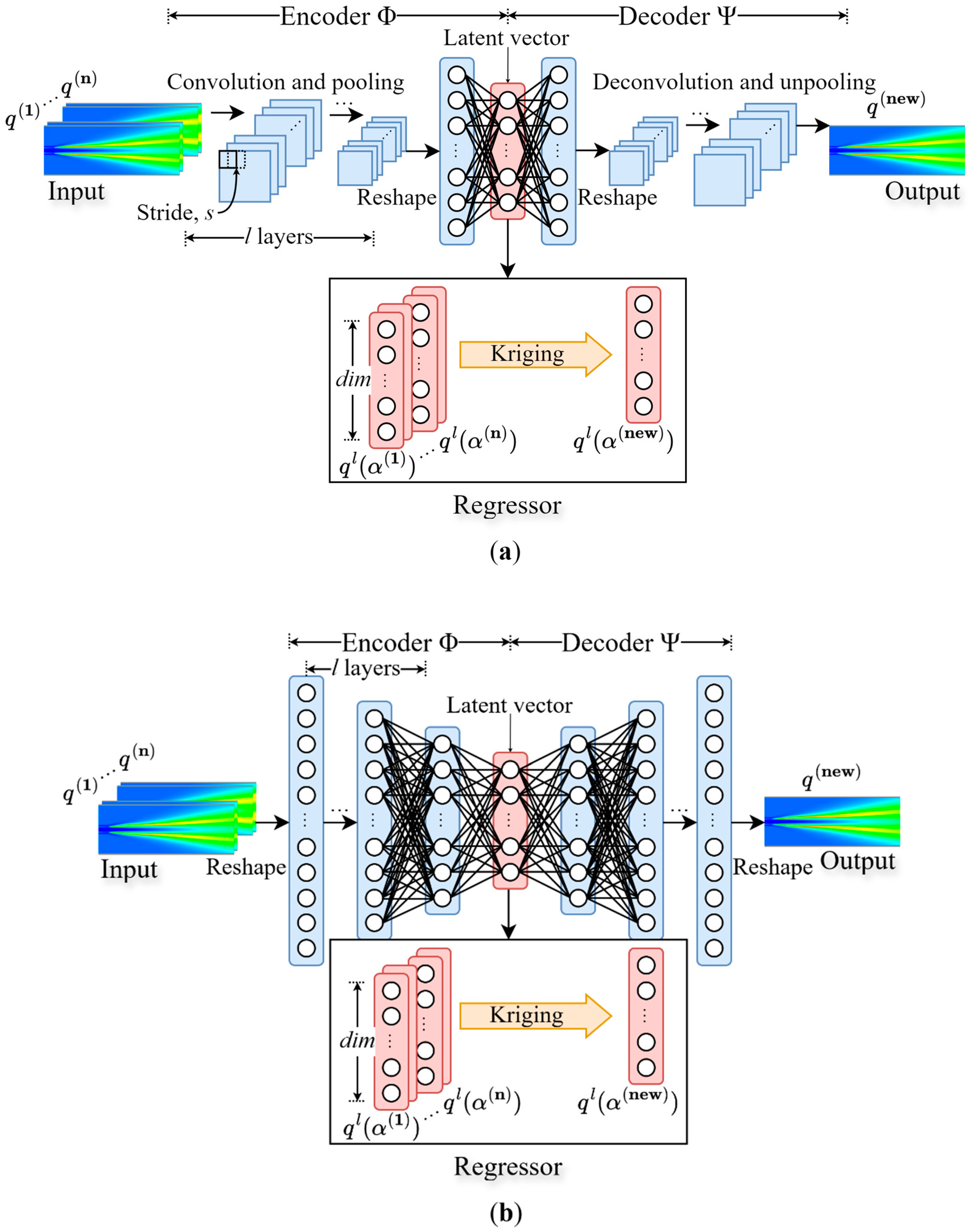
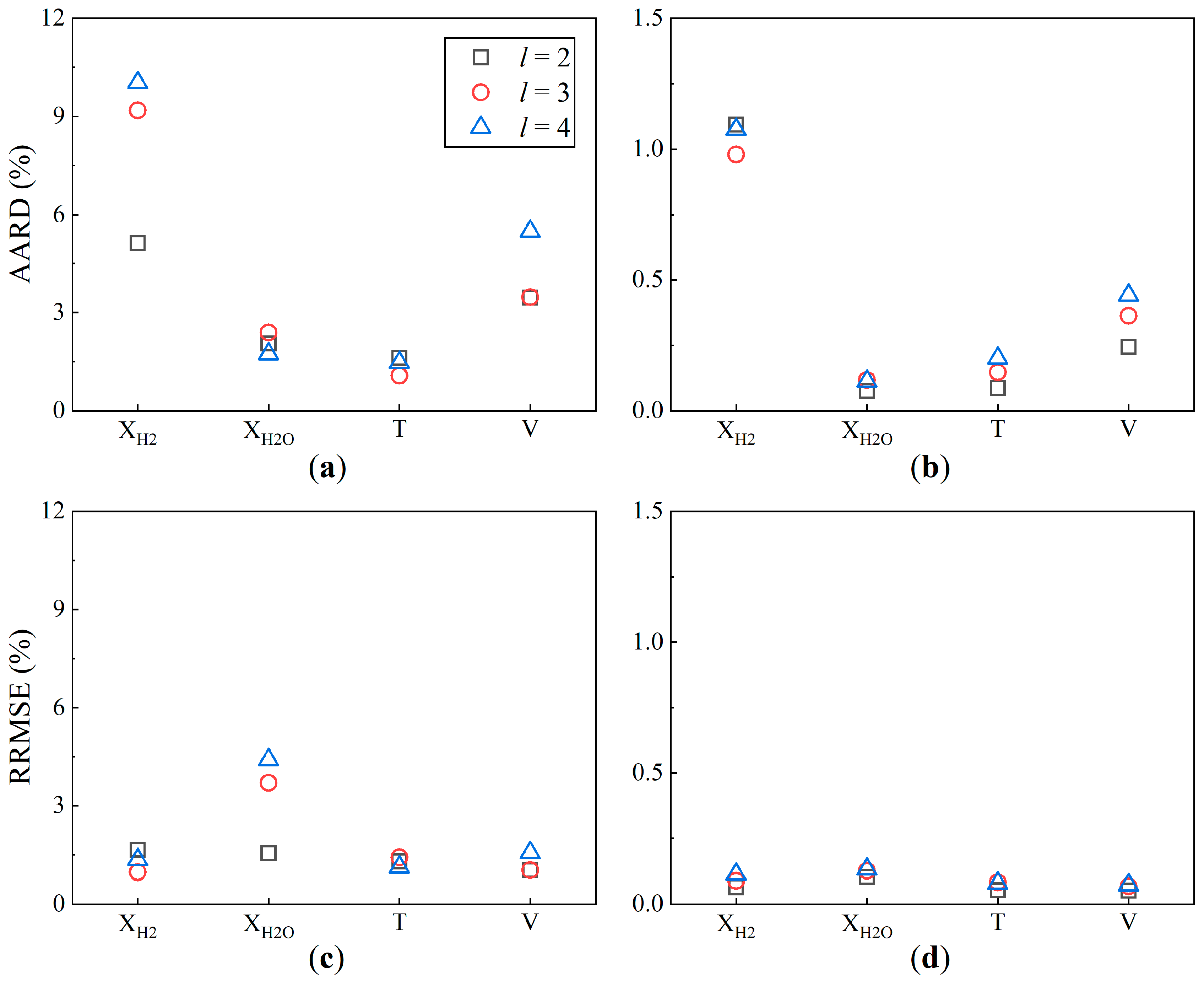



| Structures | Size (mm) |
|---|---|
| Outer Diameter of Fuel Nozzle, | 9 |
| Outer Diameter of Steam Nozzle, | 16 |
| Outer Diameter of Oxygen Nozzle, | 22 |
| Thickness of Nozzle Wall, | 1 |
| Axial Span of Computational Domain, | 360 |
| Radial Span of Computational Domain, | 160 |
| Model Number | L | Dim | S | |
|---|---|---|---|---|
| CAE | C1 | 3 | 20 | 1 |
| C2 | 2 | 20 | 1 | |
| C3 | 4 | 20 | 1 | |
| C4 | 3 | 10 | 1 | |
| C5 | 3 | 30 | 1 | |
| C6 | 3 | 20 | 2 | |
| FCAE | FC1 | 3 | 20 | / |
| FC2 | 2 | 20 | / | |
| FC3 | 4 | 20 | / | |
| FC4 | 3 | 10 | / | |
| FC5 | 3 | 30 | / |
| CAE-Based ROMs | Total Training Parameters | Training Time (s) |
|---|---|---|
| C1 | 1,476,229 | 59,671 |
| C2 | 5,772,837 | 143,168 |
| C3 | 433,381 | 47,530 |
| C4 | 779,899 | 54,783 |
| C5 | 2,172,559 | 66,424 |
| C6 | 69,893 | 8751 |
| AE | Total Training Parameters | Training Time (s) | Prediction Time (ms) | Simulation Time (CPUh) |
|---|---|---|---|---|
| C4 | 779,899 | 54,783 | 3.916 | 288–576 |
| FC4 | 293,473,046 | 1,892,767 | 11.860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Chu, X.; Ding, S.; Zhou, M.; Ni, C.; Wang, X. Surrogate Modeling of Hydrogen-Enriched Combustion Using Autoencoder-Based Dimensionality Reduction. Processes 2025, 13, 1093. https://doi.org/10.3390/pr13041093
Zhang L, Chu X, Ding S, Zhou M, Ni C, Wang X. Surrogate Modeling of Hydrogen-Enriched Combustion Using Autoencoder-Based Dimensionality Reduction. Processes. 2025; 13(4):1093. https://doi.org/10.3390/pr13041093
Chicago/Turabian StyleZhang, Lanfei, Xu Chu, Siyu Ding, Mingshuo Zhou, Chenxu Ni, and Xingjian Wang. 2025. "Surrogate Modeling of Hydrogen-Enriched Combustion Using Autoencoder-Based Dimensionality Reduction" Processes 13, no. 4: 1093. https://doi.org/10.3390/pr13041093
APA StyleZhang, L., Chu, X., Ding, S., Zhou, M., Ni, C., & Wang, X. (2025). Surrogate Modeling of Hydrogen-Enriched Combustion Using Autoencoder-Based Dimensionality Reduction. Processes, 13(4), 1093. https://doi.org/10.3390/pr13041093






