Numerical Simulation and Application of Coated Proppant Transport in Hydraulic Fracturing Systems
Abstract
1. Introduction
2. Coated Proppant Transport CFD-DEM Mathematics Model
2.1. CFD-DEM Mathematical Model
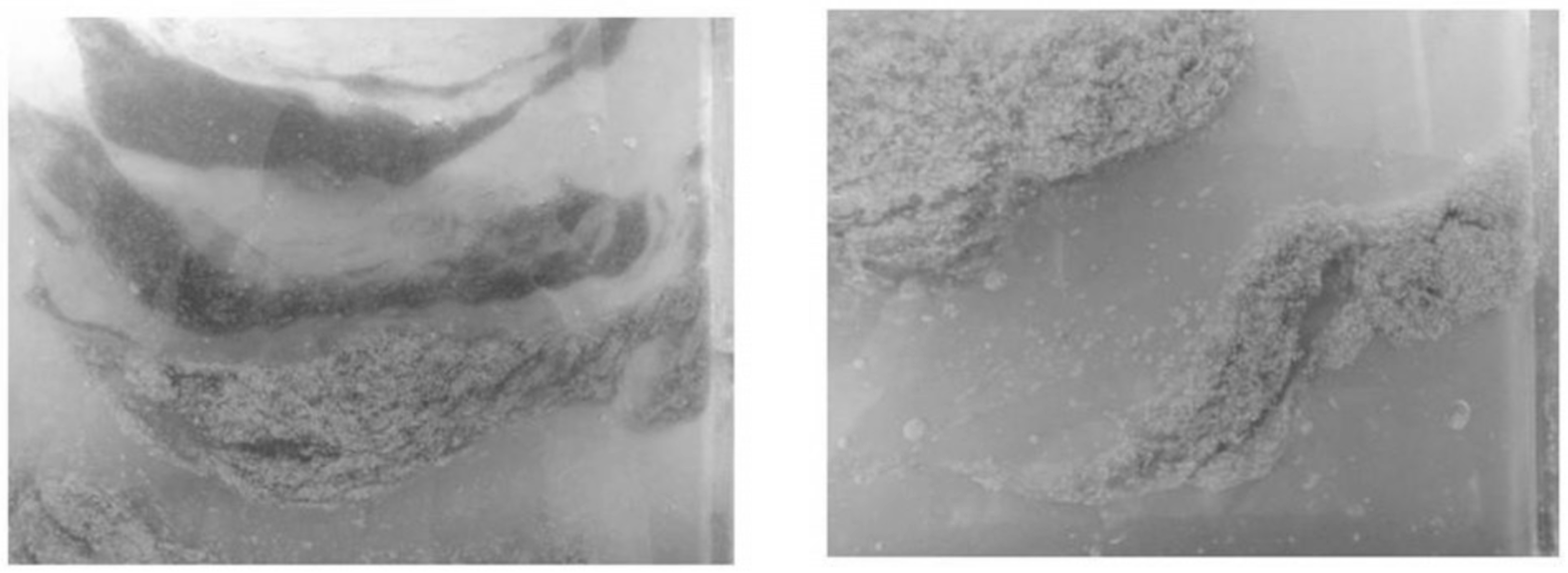
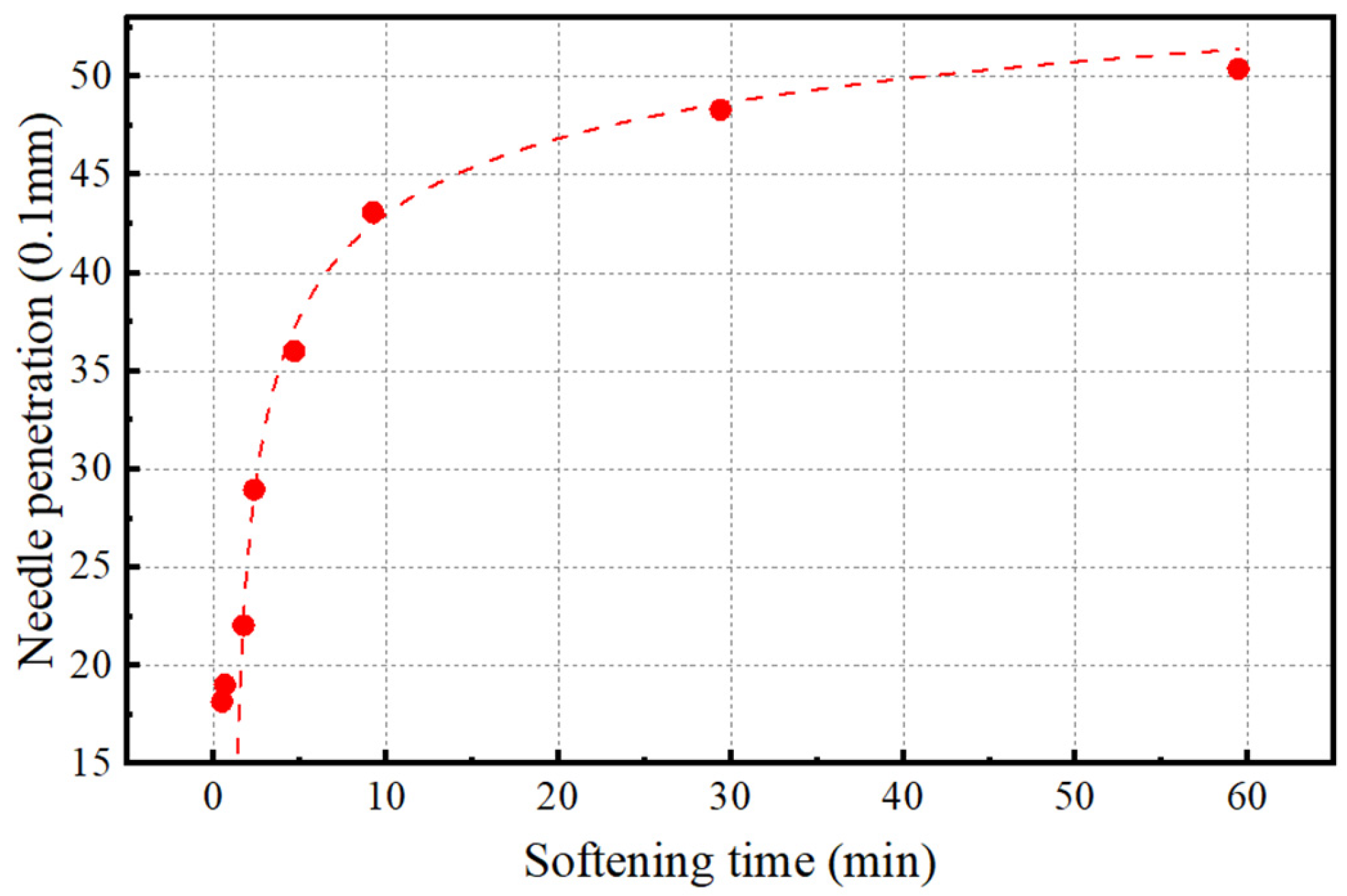
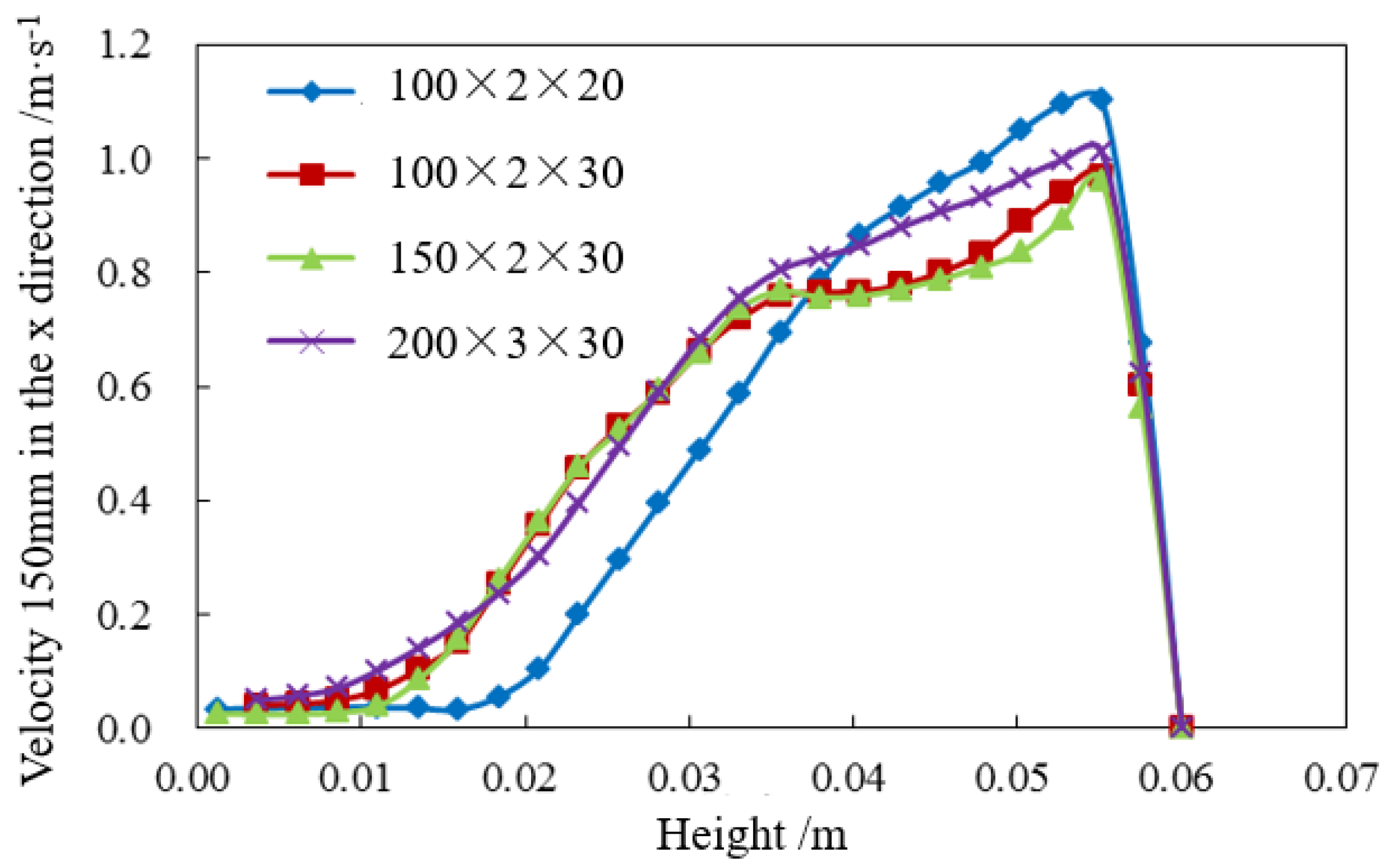
2.2. Model Parameters and Verification
3. Numerical Simulation Results and Applications
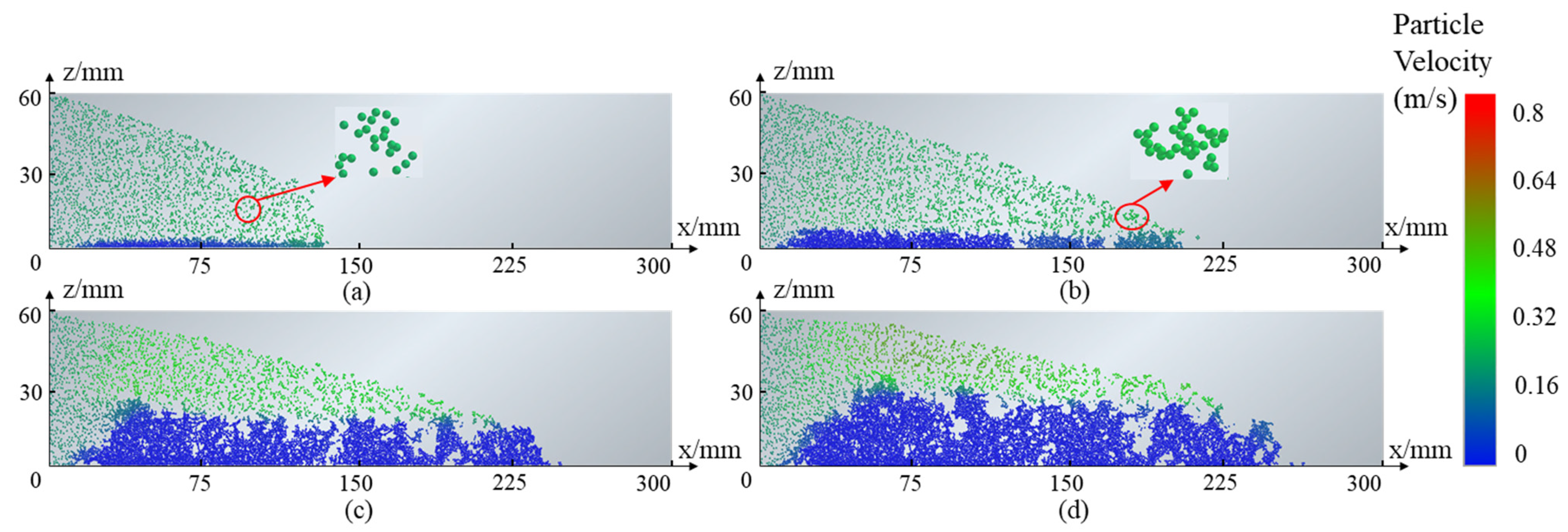
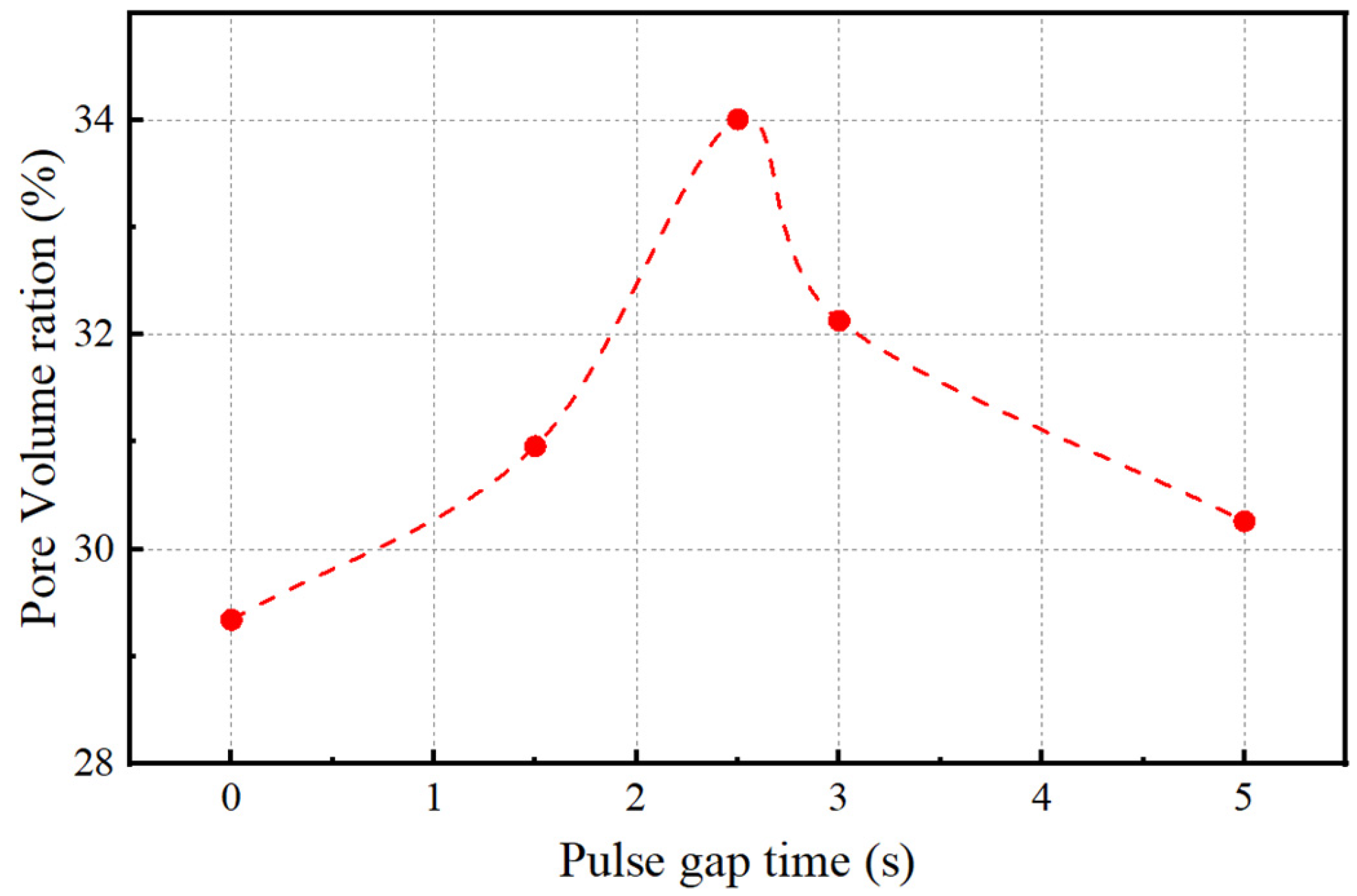
3.1. Transport Characteristics
3.2. Parametric Studies
3.3. Field Application
4. Conclusions
- (1)
- The two-phase flow coupling model based on the CFD-DEM approach taking into account the adhesive contact of coated proppant particles can better simulate the transport process of coated proppant in the fracture thanks to prior data and experimental verification.
- (2)
- The four stages of transportation in plane vertical cracks are separated by dynamic changes in the coated film proppant particles generating pillars. (1) The softening of proppant particles upon contact with fluid; (2) the positioning of the proppant pillars along the fracture height; and (3) the placement of the proppant pillars along the fracture length. The pore volume ratio can be raised by shortening the fourth stage time.
- (3)
- Field results show that compared with conventional continuous sand fracturing, the amount of proppant after treatment with viscous resin film is reduced by 35%, and the proppant particles can self-aggregate during transportation to form “sand clusters” to form highly conductive fracture channels.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Cao, J.; Han, H.; Nian, J.; Guo, L. Adaptability Analysis of Commonly Used Production Prediction Models for Shale Oil and Gas Wells. Unconv. Oil Gas Resour. 2019, 6, 48–57. [Google Scholar]
- Lin, H.; Deng, J.; Xie, T.; Huo, H.; Chen, Z. Effect of Formation Anisotropy on Wellbore Stability of Hard Brittle Shale. J. Northeast. Pet. Univ. 2021, 45, 85–94. [Google Scholar]
- Wang, H.; Feng, M.A.; Tong, X.; Liu, Z.; Zhang, X.; Wu, Z.; Li, D.; Wang, B.; Xie, Y.; Yang, L. Assessment of Global Unconventional Oil and Gas Resources. Pet. Explor. Dev. 2016, 43, 925–940. [Google Scholar]
- Zhao, J.; Zhao, X.; Zhao, J.; Cao, L.; Hu, Y.; Liu, X. Coupled Model for Simulating Proppant Distribution in Extending Fracture. Eng. Fract. Mech. 2021, 253, 107865. [Google Scholar]
- Qian, B.; Yin, C.; Zhu, J.; Chen, X. Research and Practice of the Impulse Sand Fracturing Technology. Nat. Gas Ind. B 2015, 2, 334–340. [Google Scholar] [CrossRef]
- Inyang, U.A.; Nguyen, P.D.; Cortez, J. Development and Field Applications of Highly Conductive Proppant-Free Channel Fracturing Method. In Proceedings of the SPE Unconventional Resources Conference/Gas Technology Symposium, The Woodlands, TX, USA, 1–3 April 2014; SPE: Richardson, TX, USA, 2014; p. D031S006R006. [Google Scholar]
- McDaniel, B.W.; Weaver, J.D. Fracture Stimulate and Effectively Prop Fracs: The Conductivity Challenges of Liquids Production from Ultralow-Permeability Formations. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar]
- Sahai, R.; Moghanloo, R.G. Proppant Transport in Complex Fracture Networks–A Review. J. Pet. Sci. Eng. 2019, 182, 106199. [Google Scholar] [CrossRef]
- Zeng, J.; Li, H.; Zhang, D. Numerical Simulation of Proppant Transport in Hydraulic Fracture with the Upscaling CFD-DEM Method. J. Nat. Gas Sci. Eng. 2016, 33, 264–277. [Google Scholar] [CrossRef]
- Zhang, G.; Li, M.; Gutierrez, M. Simulation of the Transport and Placement of Multi-Sized Proppant in Hydraulic Fractures Using a Coupled CFD-DEM Approach. Adv. Powder Technol. 2017, 28, 1704–1718. [Google Scholar] [CrossRef]
- Xu, J.; Gao, R.; Yang, L.; Liu, Z.; Ding, Y.; Wang, Z.; Mo, S. A 3D Tortuous Fracture Network Construction Approach to Analyze Proppant Distribution in Post-Fractured Shale. J. Pet. Sci. Eng. 2022, 208, 109676. [Google Scholar] [CrossRef]
- Akhshik, S.; Rajabi, M. Simulation of Proppant Transport at Intersection of Hydraulic Fracture and Natural Fracture of Wellbores Using CFD-DEM. Particuology 2022, 63, 112–124. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD–DEM Simulation of Fluid–Particle Interaction in Geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Ren, L.; Lin, C.; Zhao, J.; Lin, R.; Wu, J.; Wu, J.; Hu, Z. Numerical Simulation of Coated Proppant Transport and Placement in Hydraulic Fractures Based on CFD-DEM. Pet. Sci. Technol. 2024, 42, 3334–3354. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, G.; Ge, J.; Liao, K.; Jiang, P.; Pei, H.; Li, X. Surface Modified Proppants Used for Porppant Flowback Control in Hydraulic Fracturing. Colloids Surf. A Physicochem. Eng. Asp. 2016, 507, 18–25. [Google Scholar] [CrossRef]
- Wen, Q.; Yang, Y.; Wang, F. Experimental Study on an Innovative Proppant Placement Method for Channel Fracturing Technique. J. China Univ. Pet. Ed. Nat. Sci. 2016, 40, 112–117. [Google Scholar]





| Parameters | Symbol | Unit | Values |
|---|---|---|---|
| Domain size | - | mm | 300 × 60 × 2 |
| CFD mesh size | - | mm | 3 × 2 × 1 |
| Proppant: | |||
| Shear modulus | Ep | MPa | 1 × 102 |
| Poisson’s ratio | vp | - | 0.25 |
| Fractured model: | |||
| Shear modulus | Ep | MPa | 7.85 × 103 |
| Poisson’s ratio | vp | - | 0.12 |
| Proppant–proppant contact: | |||
| Restitution coefficient | e1 | - | 0.3 |
| Static friction coefficient: | μs1 | - | 0.5 |
| Rolling friction coefficient: | μr2 | - | 0.1 |
| Proppant–fractured contact: | |||
| Restitution coefficient | e2 | - | 0.24 |
| Static friction coefficient: | μs2 | - | 0.194 |
| Rolling friction coefficient: | μr2 | - | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Q.; Yang, H.; He, S.; Deng, P.; Yang, X.; Lin, C.; Sun, Z.; Ren, L.; Yin, H.; He, B.; et al. Numerical Simulation and Application of Coated Proppant Transport in Hydraulic Fracturing Systems. Processes 2025, 13, 1062. https://doi.org/10.3390/pr13041062
Du Q, Yang H, He S, Deng P, Yang X, Lin C, Sun Z, Ren L, Yin H, He B, et al. Numerical Simulation and Application of Coated Proppant Transport in Hydraulic Fracturing Systems. Processes. 2025; 13(4):1062. https://doi.org/10.3390/pr13041062
Chicago/Turabian StyleDu, Qiang, Hua Yang, Shipeng He, Pingxuan Deng, Xun Yang, Chen Lin, Zhiyun Sun, Lan Ren, Hanxiang Yin, Bencheng He, and et al. 2025. "Numerical Simulation and Application of Coated Proppant Transport in Hydraulic Fracturing Systems" Processes 13, no. 4: 1062. https://doi.org/10.3390/pr13041062
APA StyleDu, Q., Yang, H., He, S., Deng, P., Yang, X., Lin, C., Sun, Z., Ren, L., Yin, H., He, B., & Lin, R. (2025). Numerical Simulation and Application of Coated Proppant Transport in Hydraulic Fracturing Systems. Processes, 13(4), 1062. https://doi.org/10.3390/pr13041062




