Abstract
To address the risk of annular pressure relief channel blockage caused by solid deposition in the B and C annulus of deepwater wells, solid deposition tests were conducted on deepwater drilling fluid systems. The test results provided the solid settling heights of different drilling fluid systems and the post-settling solid seepage characteristics. Based on the parameters of solid seepage characteristics and considering the impact of solid deposition in annular fluids, a predictive analysis method for annular pressure buildup under seepage conditions was established, and case studies were performed. The results indicate that the settling height showed the following trend: oil-based drilling fluid > EZFLOW drilling fluid > HEM drilling fluid. In contrast, the post-settling solid permeability exhibited the opposite trend, EZFLOW drilling fluid > HEM drilling fluid > oil-based drilling fluid, with the maximum permeability reaching 2216 mD. Under the condition of solid deposition in annular fluids, as the viscosity of annular fluids decreases and the formation permeability and open-hole section length increase, the viscous forces of fluid flow decrease, and the seepage contact area with the formation increase, leading to an increase in annular fluid seepage flow. Reducing the viscosity of drilling fluids and increasing the open-hole section length of the cementing can enhance the pressure release capability of the B and C annulus in deepwater wells. However, due to the influence of solid deposition, the seepage flow rate is significantly lower than the pressure reduction rate under non-solid deposition conditions, and there is a risk of pressure relief failure after solid settlement.
1. Introduction
Global deepwater oil and gas resources are abundant, with deepwater and ultra-deepwater reserves accounting for 30% of the world’s total. With the continuous advancement of their exploitation, the wellbore service environment has become increasingly harsh. Under extreme high-temperature, high-pressure, and highly corrosive conditions, the issue of annular pressure buildup in deepwater wells has become prominent [1,2]. Additionally, due to the unique characteristics of deepwater wells, a subsea wellhead with a Christmas tree is typically employed for oil and gas production, and a casing seal assembly is installed at the wellhead. This design prevents pressure relief operations in any annulus other than the A annulus. A special wellbore structure is usually adopted, where the cement returns to a level below the upper casing shoe, allowing the formation to release pressure in the B and C annuli. However, during long-term production, solid deposition of drilling fluids in the annuli poses a risk of blocking the pressure relief channels, preventing the release of high annular pressure, and severely threatening field production safety [3]. Therefore, it is necessary to analyze annular pressure under the influence of solid deposition in deepwater well annuli, optimize the wellbore structure design, and ensure safe field production [4].
Currently, scholars at home and abroad have conducted extensive research on the causes, prediction, and safety control of annular pressure buildup. In 2020, Wang Yanbin et al. [5] developed a prediction method for annular pressure buildup in deepwater wells based on changes in the physical properties of annular fluids and the coupling effect between fluid and annular volume. In 2022, Arthur P. et al. [6] established a calculation method for annular thermal expansion pressure considering the influence of nitrogen injection into the annulus. In 2022, Wang Hao et al. [7] proposed a dynamic annular pressure prediction model that accounts for cement sheath seepage and the varying thermophysical properties of annular fluids. In 2023, Zhang Zhi et al. [8] developed an annular pressure buildup prediction model based on transient heat transfer in the wellbore, considering changes in fluid thermodynamic properties under high temperature and high pressure. In 2023, Wu Yi et al. [9] introduced a method for predicting and controlling annular pressure buildup in deepwater wells, taking into account the seepage performance of the cement sheath. In 2024, Xie Renjun et al. [10] established an annular pressure recovery model based on elastic deformation theory, considering the deformation effects of the casing-cement sheath-formation system. Existing research has provided a relatively clear understanding of the mechanisms of annular pressure buildup (APB) in deepwater wells, including its causes, prediction methods, and safety management. Current APB prediction methods primarily focus on scenarios such as the thermal expansion of annular fluids, high-pressure fluid migration through the cement sheath, and tubing leaks. However, in the context of the unique wellbore design of deepwater wells, Annular B and C are often directly connected to the formation, and there is a risk of solid deposition in the annular fluids [11]. Research on APB prediction under the coupled effects of fluid seepage and thermal expansion in such scenarios is limited. Therefore, this paper, based on the wellbore design of deepwater wells, addresses the risk of depressurization channel clogging due to solid deposition in Annular B and C. By conducting solid deposition tests on deepwater drilling fluid systems, the solid-phase seepage characteristics of different drilling fluid systems after deposition were obtained. Based on these characteristics and considering the coupling effects of seepage under solid deposition and fluid thermal expansion, a prediction method for APB in deepwater wells under solid deposition was established. This method can analyze the risk of APB due to solid deposition in annular fluids, ensuring on-site safety production.
2. Prediction of Annular Pressure Buildup Due to Seepage in Deepwater Wells
During the production process of deepwater wells, the temperature in the annular space of the wellbore increases, leading to changes in annular pressure. This causes the annular volume to change due to the thermal expansion and ballooning effects of the fluid, resulting in annular pressure [12]. The magnitude of this pressure depends on the fluid’s ability to change volume under varying temperature and pressure conditions. Assuming the annular space is a closed system, the trapped annular pressure under the effects of temperature and ballooning can be expressed as [13,14]:
where Δp is the trapped annular pressure in MPa, V is the closed annular volume in m3, βt is the fluid expansion coefficient in 1/°C, βp is the fluid compression coefficient in MPa−1, ΔT is the increase in temperature of the annular fluid in °C, and ΔV is the increase in annular volume in m3.
For deepwater wells, when the cement returns to a depth below the upper casing shoe, the annular fluid can undergo mass changes through the open-hole section of the annulus, thereby mitigating the annular pressure caused by fluid thermal expansion. As the annular pressure increases, under the pressure difference, unstable seepage occurs between the formation and the annular fluid. Assuming the annular fluid is a single-phase incompressible fluid, the formation is an isotropic homogeneous medium, and the seepage process follows Darcy’s flow, the one-dimensional radial flow stress diffusion equation is described as follows [15]:
where r is the radius in m, k is the permeability in mD, φ is the porosity (dimensionless), μ is the fluid viscosity in mPa·s, c is the comprehensive compression coefficient in MPa−1, and t is the seepage time in s.
The initial conditions and pressure boundary under formation seepage are given as follows:
where PD is the formation pressure in MPa, rw is the wellbore radius in m, q is the seepage flow rate in m3/s, h is the length of the open-hole section in m, and P(r) is the pressure at a distance r from the well center in MPa.
Substituting Equation (3) yields
where Pa is the annulus pressure during seepage with the formation in MPa, and η is the pressure conductivity coefficient in cm2/s.
Integrating Equation (4) gives
Here, due to the exponential integral function
where G(x) is the exponential integral function, which is inherently dimensionless.
Expressing the integral part with the exponential integral function, the calculation formula for unstable seepage between the formation and annular fluid is obtained as follows [16,17]:
The exponential integral function can be expanded into an infinite series as follows [18]:
Therefore, when r2/4ηt < 0.01, the higher-order terms can be omitted, and Equation (8) can be simplified as follows:
In the actual process of annular fluid seepage, the seepage time t > 86,400 s, and the seepage radius r < 1 m. Therefore, the value of r2/(4ηt) is much less than 0.01. Substituting this into Equation (7), we can derive
When sedimentation occurs in the annular drilling fluid, solid deposits accumulate at the bottom of the annulus, affecting the unstable seepage between the annulus and the formation and reducing the seepage flow rate of the annular fluid. Under the pressure difference between the annular pressure at the top of the solid deposit and the formation pressure, fluid seepage occurs through the solid deposit. According to Darcy’s law, the seepage flow rate is as follows [19]:
where qc is the seepage flow rate through the solid deposit in m3/s, Δh is the height of the solid deposit in m, Pc is the annular pressure at the solid deposit in MPa, and A is the cross-sectional area of annular seepage in m2.
When the seepage flow rate through the solid deposit equals the unstable seepage flow rate, the seepage process reaches a steady state, and the steady-state seepage flow rate q of the annular fluid can be solved. Therefore, the calculation formula for the annular pressure caused by the mass change in the annular fluid during seepage is as follows [20]:
where Δt is the time of formation seepage change under annular pressure in s, and ΔpM is the annular pressure caused by the mass change in the annular fluid during seepage in MPa.
Considering the influence of solid deposition, the annular pressure coupling the seepage-thermal-pressure effects is [21]
The annular pressure buildup consists of three components: thermal expansion caused by fluid temperature increase, annular volume change, and fluid mass change caused by formation seepage. By iteratively calculating the coupled annular pressure model, the variation of annular pressure can be obtained.
3. Testing of Solid Deposition Characteristics in Annular Drilling Fluid
To obtain the solid deposition characteristics of annular drilling fluid, a core flow test system is used to conduct tests on the solid deposition of annular drilling fluid. This aims to measure the permeability of the deposited solids and accurately predict the annular pressure buildup under the influence of solid deposition [22].
- (1)
- Experimental Method and Procedure
The experiments utilized drilling fluids commonly employed in deepwater wells: EZFLOW drilling fluid, HEM drilling fluid, and oil-based drilling fluid. Their main components and properties are detailed in Table 1.

Table 1.
Performance parameters and composition of drilling fluid.
To obtain the seepage capacity of solid deposits from different drilling fluid systems, core samples were prepared using the deposited solids of the drilling fluids. High-temperature-resistant fluororubber tubes with an outer diameter of Φ25 mm and a length of 50–60 mm were used to create the core samples. The fluororubber tubes were rinsed and then placed in a high-temperature drying oven at 100 °C for 30 min to remove moisture from the tube walls. The drilling fluids were sequentially poured into the fluororubber tubes and baked at 70 °C for 20 h, followed by baking at 120 °C for another 20 h to reduce the bubbles inside the tubes and simulate natural sedimentation and drying. After the baking process, the excess rubber tubing at both ends of the samples was removed to control the sample length to 50 mm [23].
A core fluid flow testing apparatus, as shown in Figure 1, was employed. The core sample was held in place using a core clamping device, and a constant rate Q of gas with a dynamic viscosity of ηQ was injected through a steady-flow pump. The flow rate changes within a unit of time were recorded. When the recorded flow rate matched the injection flow rate Q from the steady-flow pump, the flow was considered to have reached a steady state. Pressures at both ends of the core sample were measured using pressure gauges, and the pressure difference Δp was calculated. Based on Darcy’s principle, the permeability of the core sample could then be determined [24].
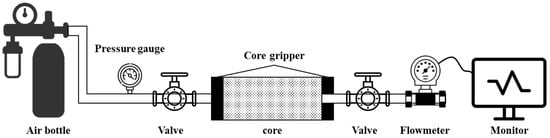
Figure 1.
Schematic diagram of the core permeability test device.
Based on the test results and Darcy’s law, the permeability of the deposited solids was calculated as follows:
where Q represents the flow rate through the sample in m3/s, As is the cross-sectional area of the sample in m2, l denotes the length of the sample in m, ηQ is the viscosity coefficient of the fluid in Pa·s, and Δp indicates the pressure difference between the upstream and downstream of the sample in Pa.
The experiment involved solid deposits from three commonly used drilling fluid systems: EZFLOW, oil-based, and HEM. For each type of solid deposit, three parallel core samples were prepared, and their seepage performance was measured individually.
- (2)
- Results
The permeability of solid sediments from three types of drilling fluid systems was measured using a core permeability testing device, and the results are shown in Figure 2. As indicated in the figure, the average permeability values of HEM, EZFLOW, and oil-based drilling fluid solid sediments were 2216 mD, 542 mD, and 16 mD, respectively, with the order HEM drilling fluid > EZFLOW drilling fluid > oil-based drilling fluid.
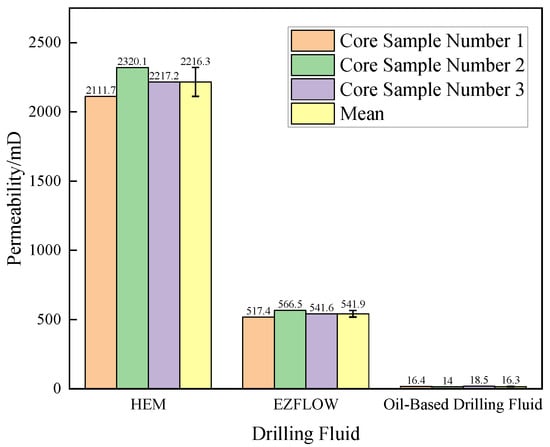
Figure 2.
Core permeability of solid sediments in different drilling fluid systems.
After obtaining the permeability of solid sediments from different drilling fluid systems, these values were substituted into Equations (10)–(12) to calculate the annular pressure induced by seepage under different drilling fluid systems.
4. Case Study
Well X is a deepwater high-temperature/high-pressure (HPHT) gas well located in the South China Sea, with a water depth of 910.0 m, a well depth of 4300 m, a bottomhole temperature of approximately 140 °C, and a formation pressure of 64.00 MPa. The drilling fluid system used is HEM drilling fluid. The cement top for Annulus B is 3350 m, and for Annulus C, it is 2150 m. The specific parameters of the annulus strings and fluids are listed in Table 2.

Table 2.
Technical parameters of annulus strings and fluids.
4.1. Prediction of Annulus Pressure
Based on the production planning calculations of this well, the variation of wellbore temperature distribution with production time is obtained, as shown in Figure 3. From Figure 3, it can be observed that the extraction of high-temperature fluid from the bottom of the well leads to an increase in wellbore temperature. The maximum annular temperatures at the wellhead reach 39.11 °C and 20.61 °C, respectively. The increase in wellbore temperature causes thermal expansion of the annular fluids, resulting in annular pressure. However, as production time increases, both production rate and bottomhole pressure decrease, leading to a corresponding reduction in wellbore annular temperature.
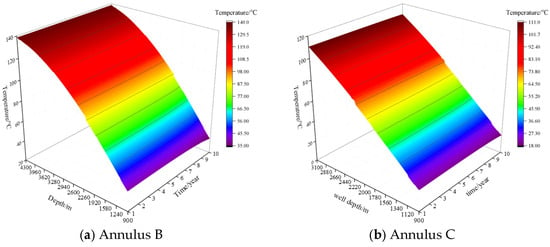
Figure 3.
Temperature distribution in wellbore annulus.
Based on annulus temperature changes and formation fluid parameters in the wellbore, the pressure variations in Annuli B and C over time under different conditions were calculated using Equations (2)–(12), as shown in Figure 4. It can be observed that, under the influence of temperature effects alone, heat from the high-temperature formation fluid is transferred outward through the tubing from Annular B to Annular C, resulting in a greater temperature change in Annular B compared to Annular C. Consequently, the pressure in Annular B is higher than in Annular C, with the maximum pressures in Annuli B and C reaching 17.44 MPa and 9.40 MPa, respectively. As production time increased, production rate and bottomhole pressure decreased, and the rate of temperature rise in the annuli slowed down, resulting in a corresponding reduction in annulus pressure. When the cement top exceeded the upper casing shoe, forming an open-hole section at the bottom of the annulus, unstable seepage occurred between the annulus and the formation. Due to the high porosity and permeability of the formation, annulus fluid flowed into the formation through seepage, releasing annulus pressure. Since the pressure difference between Annular B and the formation is greater than that between Annular C and the formation, under the same permeability and time conditions, the seepage flow rate from Annular B exceeds that from Annular C. Consequently, the pressure drop in Annular B is greater than in Annular C, and the pressures in Annuli B and C decreased to a minimum of 9.54 MPa and 5.65 MPa, representing reductions of 34.62% and 26.50%, respectively. This indicated that the formation could effectively release annulus pressure and reduce safety risks. However, after drilling fluid settling occurred, solid-phase deposits accumulated at the bottom of the annulus with low permeability, hindering fluid seepage and reducing the seepage flow rate, which decreased the annulus pressure release capability. Under the same time frame, the pressures in Annuli B and C only decreased to 13.61 MPa and 7.20 MPa, with reductions of 6.72% and 6.24%, respectively.
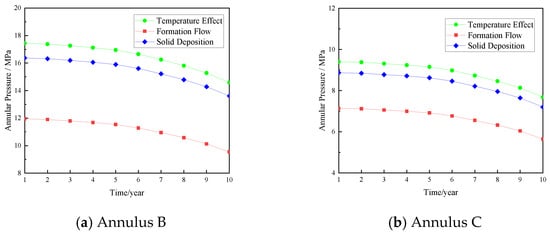
Figure 4.
Annulus pressure changes under different considerations.
4.2. Different Drilling Fluid Systems
The impact of solid-phase deposits from three drilling fluid systems (HEM, EZFLOW, and oil-based) on annulus pressure was analyzed, as shown in Figure 5. Under conditions of drilling fluid solid-phase deposition, the pressures in Annuli B and C decreased due to seepage after 30 days. However, the reduction in pressure was diminished due to the influence of solid-phase deposits, which reduced the seepage flow rate. Since the permeability of solid-phase deposits follows the order EZFLOW drilling fluid > HEM drilling fluid > oil-based drilling fluid, the pressure reduction in the EZFLOW drilling fluid was the greatest. Furthermore, due to differences in the wellhead pressure and fluid density between Annular B and Annular C, the seepage pressure differences between these annuli and the formation vary. Consequently, the pressure reduction in Annular B is greater than in Annular C, with decreases of 9.89 MPa and 5.89 MPa in Annuli B and C, representing reductions of 43.30% and 37.34%, respectively. For HEM drilling fluid, the pressure decreased by 14.34 MPa and 7.85 MPa, with reductions of 17.78% and 16.52%, while for oil-based drilling fluid, the pressure decreased by 17.32 MPa and 9.34 MPa, with reductions of only 0.66% and 0.65%. Therefore, when using drilling fluid types with poor solid-phase permeability, there is a risk of being unable to release annulus pressure after solid-phase settling occurs.
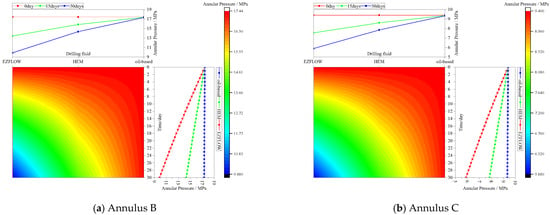
Figure 5.
Variation of annulus pressure under different drilling fluid systems.
4.3. Different Formation Permeability
The influence of solid-phase deposition on the annulus pressure under different formation permeabilities was analyzed, as shown in Figure 6. After the solid-phase deposition of annulus fluid, the seepage flow rate increased with higher formation permeability, allowing more annulus fluid to be released into the formation. Consequently, the rate of pressure reduction increased with higher permeability. However, from the relationship curve between permeability and annular pressure, it can be observed that as permeability increases, the annular pressure decreases, but the extent of the decrease gradually diminishes with increasing permeability. Permeability and annular pressure exhibit a logarithmic decay relationship. When formation permeability increased from 10 mD to 160 mD, the pressure in Annulus B decreased from 17.44 MPa to 15.88 MPa and 8.46 MPa, with reductions increasing from 8.96% to 51.48%. Similarly, the pressure in Annulus C decreased from 9.40 MPa to 8.74 MPa and 5.12 MPa, with reductions increasing from 6.97% to 45.58%. However, due to the greater pressure difference in Annular B compared to Annular C, the reduction rate in Annular B was larger than in Annular C. At the same time, due to the influence of solid-phase deposition, the rate of pressure release was significantly lower than that under conditions without solid-phase deposition.
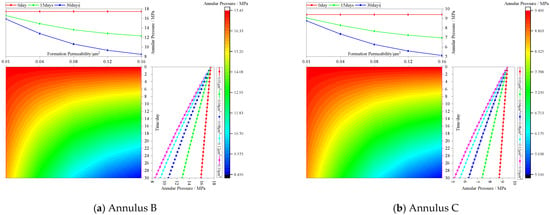
Figure 6.
Variation of annulus pressure under different formation permeabilities.
4.4. Different Drilling Fluid Viscosities
The influence of solid-phase deposition on annulus pressure under different drilling fluid viscosities was analyzed, as shown in Figure 7. As drilling fluid viscosity increased, the viscous force of fluid flow increased, reducing the seepage flow rate and slowing the rate of pressure reduction. However, from the relationship curve between fluid viscosity and annular pressure, it can be observed that as fluid viscosity increases, the annular pressure also increases, but the rate of increase gradually diminishes with higher fluid viscosity. Fluid viscosity and annular pressure exhibit a logarithmic growth relationship. When drilling fluid viscosity increased from 1 mPa·s to 9 mPa·s, the pressure in Annulus B decreased from 17.44 MPa to 9.89 MPa and 16.40 MPa, with reductions decreasing from 43.30% to 5.98%. Similarly, the pressure in Annulus C decreased from 9.40 MPa to 5.89 MPa and 8.89 MPa, with reductions decreasing from 37.34% to 5.31%. Reducing drilling fluid viscosity can enhance the pressure release capability in deepwater Annuli B and C.
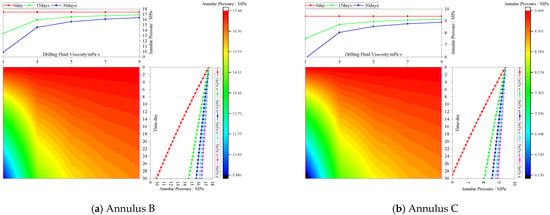
Figure 7.
Annulus pressure changes under different drilling fluid viscosities.
4.5. Different Open-Hole Length
The influence of solid-phase deposition on annulus pressure under different open-hole lengths was analyzed, as shown in Figure 8. As the length of the open-hole section increased, the contact area between the annulus drilling fluid and the formation increased, enhancing the seepage flow rate and the rate of pressure reduction. However, from the relationship curve between open-hole length and annular pressure, it can be observed that as the open-hole length increases, the annular pressure decreases, but the rate of decrease gradually diminishes with greater open-hole length. Open-hole length and annular pressure exhibit a logarithmic decay relationship. When the open-hole length increased from 50 m to 250 m, the pressure in Annulus B decreased from 17.44 MPa to 14.05 MPa and 8.99 MPa, with reductions increasing from 19.42% to 48.46%. Similarly, the pressure in Annulus C decreased from 9.40 MPa to 8.41 MPa and 6.14 MPa, with reductions increasing from 10.51% to 34.70%.
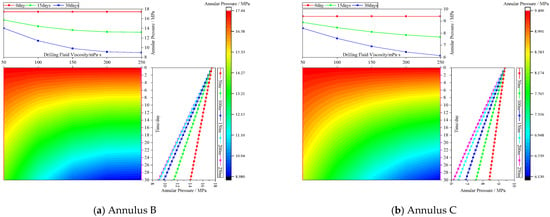
Figure 8.
Annulus pressure changes under different open-hole lengths.
5. Conclusions
- (1)
- To address the risk of annulus pressure release channel blockage due to solid-phase deposition in Annuli B and C of deepwater wells, solid-phase deposition tests were conducted on deepwater drilling fluid systems. The sedimentation height and post-settling permeability of different drilling fluid systems were obtained, showing that the permeability follows the order EZFLOW drilling fluid > HEM drilling fluid > oil-based drilling fluid, with the highest permeability reaching 2216 mD. Based on the deposition tests and considering the impact of solid-phase deposition in annulus fluids, a predictive analysis method was established for annulus pressure under the influence of solid-phase deposition and seepage in Annuli B and C. This method can effectively evaluate the pressure release risks in deepwater Annuli B and C. However, the method does not account for the influence of downhole high temperature and confining pressure on solid-phase deposition and fluid seepage behavior. Additionally, the model is based on idealized conditions and requires further optimization to better represent real downhole scenarios. Addressing these factors is essential to enhance the accuracy and applicability of the model in practical field operations.
- (2)
- Under the influence of temperature effects alone, the annulus pressure was relatively high. When an open-hole section existed at the bottom of the annulus, unstable seepage occurred between the annulus and the formation, allowing annulus fluid to flow into the formation and effectively release annulus pressure, reducing it by 34.62% and mitigating the risk of annulus pressure buildup. However, after the solid deposition of drilling fluid in the annulus, the solid media accumulates at the bottom of the annulus, leading to reduced permeability and hindering the seepage of the annular fluid. As a result, the seepage flow rate decreases, and the ability to release annular pressure is diminished, with a pressure reduction of only 6.25%. This creates a risk of failing to release annular pressure. Additionally, since the pressure and fluid density in Annular B are higher than in Annular C, the pressure differential effect becomes more pronounced, leading to a greater reduction in pressure in Annular B compared to Annular C.
- (3)
- As drilling fluid viscosity decreased and formation permeability and open-hole length increased, the viscous force of fluid flow decreased, the seepage area expanded, and the seepage flow rate increased, leading to a higher rate of annulus pressure reduction. Reducing drilling fluid viscosity and increasing the length of the open-hole section in the cement can enhance the pressure release capability in deepwater Annuli B and C, with a maximum reduction of up to 49.91%.
Author Contributions
Investigation, Y.D.; Data curation, Z.Z.; Writing—original draft, J.D.; Writing—review and editing, J.L. and J.D.; Project administration, X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (Grant No. U22A20164 and 52074234), Science and Technology Cooperation Project of the CNPC-SWPU Innovation Alliance (2020CX040100).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
This work was supported by Southwest Petroleum University. The authors gratefully acknowledge all contributors.
Conflicts of Interest
Authors Liu Jinming, Song Xuefeng and Ding Yida are employed by the CNOOC EnerTech-Drilling & Production Co, Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Zhong, L.; Zhiming, Y.; Deqiang, T. Research Progress on Well Control Risk Management Technology for Deep Sea and Ultra-deep Water Drilling. Drill. Prod. Technol. 2024, 47, 8–17. [Google Scholar]
- Yang, J.; Li, L.; Song, Y.; Tong, G.; Zhang, M.; Zhang, H. Current status and prospects of offshore oil and gas drilling technology development in China. Acta Pet. Sin. 2024, 44, 2308. [Google Scholar]
- Sultan, N.W.; Faget, J.B.P.; Fjeldheim, M.; Sinet, J.C. Real-Time Casing Annulus Pressure Monitoring in a Subsea HP/HT Exploration Well. Presented at the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008; p. OTC-19286-MS. [Google Scholar]
- Cheng, X.; Xue, D.; Zhang, L.; Ma, X.; Zheng, C. Challenges and Countermeasures of Deep-water Downhole Production and Injection Technology in the South China Sea. Sci. Technol. Eng. 2023, 23, 3123–3133. [Google Scholar]
- Wang, Y.B.; Zeng, J.; Gao, D.L. Effect of annular pressure on the fatigue damage of deepwater subsea wellheads. Nat. Gas Ind. 2020, 40, 116–123. [Google Scholar]
- da Veiga, A.P.; Martins, I.O.; Barcelos, J.G.; Ferreira, M.V.D.; Alves, E.B.; da Silva, A.K.; Hasan, A.R.; Barbosa, J.R., Jr. Predicting thermal expansion pressure buildup in a deepwater oil well with an annulus partially filled with nitrogen. J. Pet. Sci. Eng. 2022, 208, 109275. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Li, J.; Sun, T. Study on annular pressure buildup phenomenon in subsea wells considering the effect of cement. Energy Sci. Eng. 2022, 10, 81–95. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiang, S.; Yuan, Z.; Tang, H. A coupling prediction model of annular pressure build-up for deepwater oil and gas wells during transient-state testing. Geoenergy Sci. Eng. 2023, 230, 212162. [Google Scholar] [CrossRef]
- Xie, R.; Zhang, L. A New Prediction Model of Annular Pressure Buildup for Offshore Wells. Appl. Sci. 2024, 14, 9768. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, J.; Yang, J.; Zhang, T.; Zou, X.; Zhang, X.; Xu, G. Research on Wellbore Integrity Assurance Technology for Deepwater High-Pressure Oil and Gas Wells. Energies 2023, 16, 2230. [Google Scholar] [CrossRef]
- Calcada, L.A.; Scheid, C.M.; da Cruz Meleiro, L.A.; Oechsler, B.F.; Fagundes, F.M.; Santos, N.B.C.; de Oliveira Arouca, F.; Damasceno, J.J.R.; Souza, E.; Waldmann, A.T. Designing fluid properties to minimize barite sag and its impact on annular pressure build up mitigation in producing offshore wells. In Proceedings of the OTC Brasil, Rio de Janeiro, Brazil, 5 October 2017. [Google Scholar]
- Ding, L.; Dai, X.; Li, S.; Zhang, Q. Prediction Model of Sustained Annular Pressure Considering Thermodynamic Characteristics of Annular Liquid. Sci. Technol. Eng. 2023, 23, 8642–8649. [Google Scholar]
- Ma, Y.; Zhang, X.; Huo, H. Prediction and control of annulus pressure in Bohai condensate gas field. China Offshore Oil Gas 2023, 35, 117–127. [Google Scholar]
- Maiti, S.; Gupta, H.; Vyas, A.; Kulkarni, S.D. Evaluating precision of annular pressure buildup (APB) estimation using machine-learning tools. SPE Drill. Complet. 2022, 37, 93–103. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Zheng, Y.; Zhang, B.; Luo, F.; Yang, Y. Prediction and Analysis of Influencing Factors of Annular Pressure in Gas Storage Wells. Sci. Technol. Eng. 2023, 23, 14574–14580. [Google Scholar]
- Hu, Z.; Xin, L.; Xin, J. Full-scale Simulation Experiment of Trapped Annular Thermal Expansion Pressure. Sci. Technol. Eng. 2021, 21, 6663–6669. [Google Scholar]
- Zhang, B.; Lu, N.; Guo, Y.; Wang, Q.; Cai, M.; Lou, E. Modeling and Analysis of Sustained Annular Pressure and Gas Accumulation Caused by Tubing Integrity Failure in the Production Process of Deep Natural Gas Wells. J. Energy Resour. Technol.—Trans. ASME 2022, 144, 063005. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, J.; Gao, D. Assessment on the sustained casing pressure (SCP) with consideration of the infiltration of formation fluid into the annulus of deepwater wells. J. Pet. Sci. Eng. 2020, 189, 106999. [Google Scholar] [CrossRef]
- Zhang, Z.; Zeng, W.; Peng, X.; Wang, B.; Li, H.Y.; Shi, T.H. Mechanism study on sustained casing pressure caused by gas migration in annulus. Drill. Prod. Technol. 2014, 37, 39–41+8. [Google Scholar]
- Zhang, B.; Xu, Z.; Lu, N.; Liu, H.; Liu, J.; Hu, Z.; Xie, J.; Wang, K. Characteristics of sustained annular pressure and fluid distribution in high pressure and high temperature gas wells considering multiple leakage of tubing string. J. Pet. Sci. Eng. 2021, 196, 108083. [Google Scholar] [CrossRef]
- Ding, L.; Yang, X.; Chen, W.; Li, S.; Zhang, Q. Prediction of annulus liquid level depth in high-temperature and high-pressure gas wells based on sustained casing pressure. Meas. J. Int. Meas. Confed. 2022, 193, 110991. [Google Scholar] [CrossRef]
- Kacimov, A.R.; Marketz, F.; Pervez, T. Analytical solutions for one-phase seepage flows impeded by wellbore seals. J. Pet. Sci. Eng. 2009, 64, 67–76. [Google Scholar] [CrossRef]
- Khormali, A.; Petrakov, D.G.; Farmanzade, A.R. Prediction and Inhibition of Inorganic Salt Formation under Static and Dynamic Conditions—Effect of Pressure, Temperature, and Mixing Ratio. Int. J. Technol. 2016, 7, 943. [Google Scholar] [CrossRef]
- Skadsem, H.J. Fluid Migration Characterization of Full-Scale Annulus Cement Sections Using Pressure-Pulse-Decay Measurements. J. Energy Resour. Technol. 2022, 144, 13. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).