Study on Prediction of Wellbore Collapse Pressure of the Coal Seam Considering a Weak Structure Plane
Abstract
1. Introduction
2. Experimental Content
2.1. Coal Sample Microstructure
2.2. Coal Sample Preparation
2.3. Mechanical Experimental Scheme
2.4. Mechanical Experiment Results
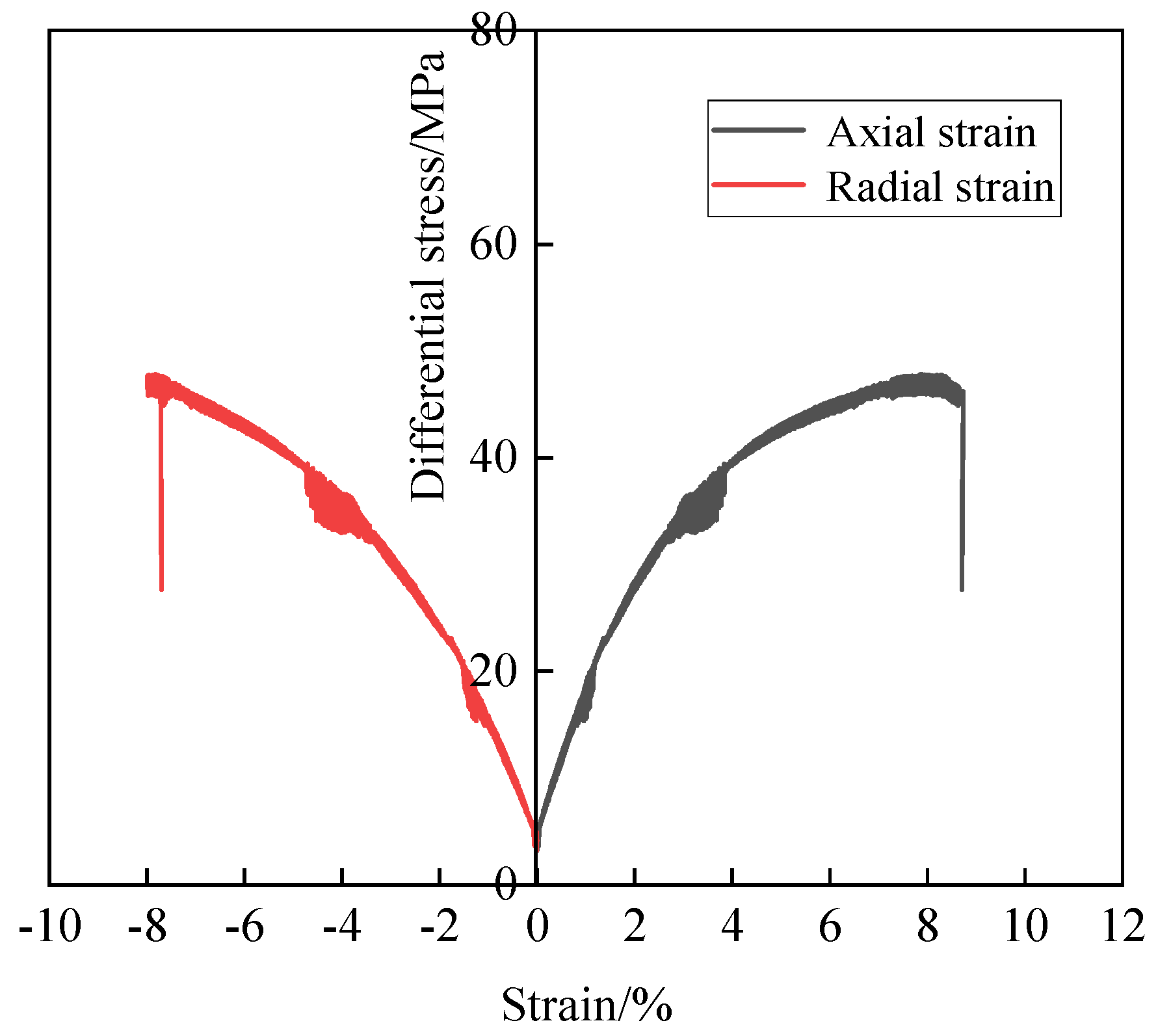
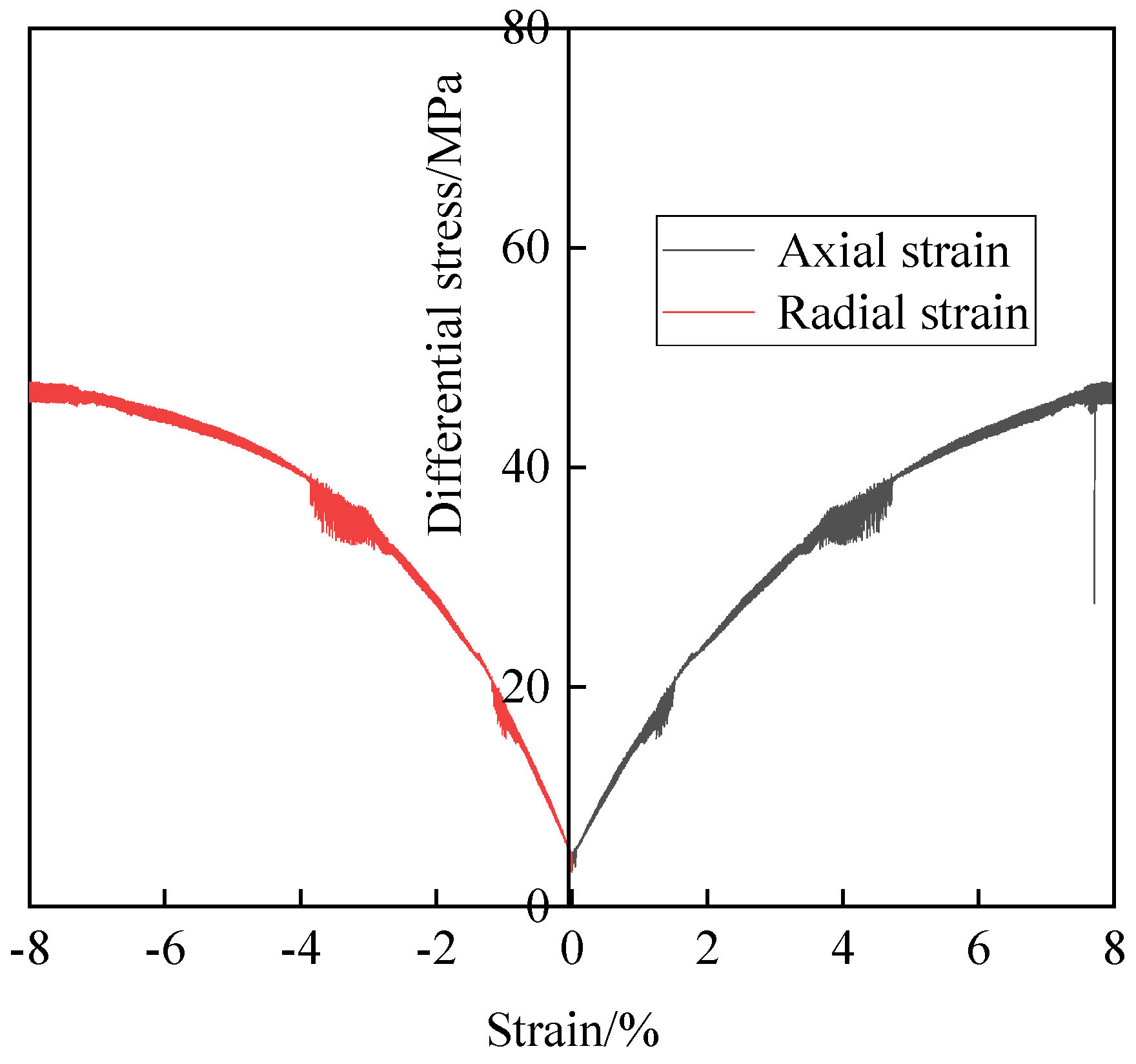
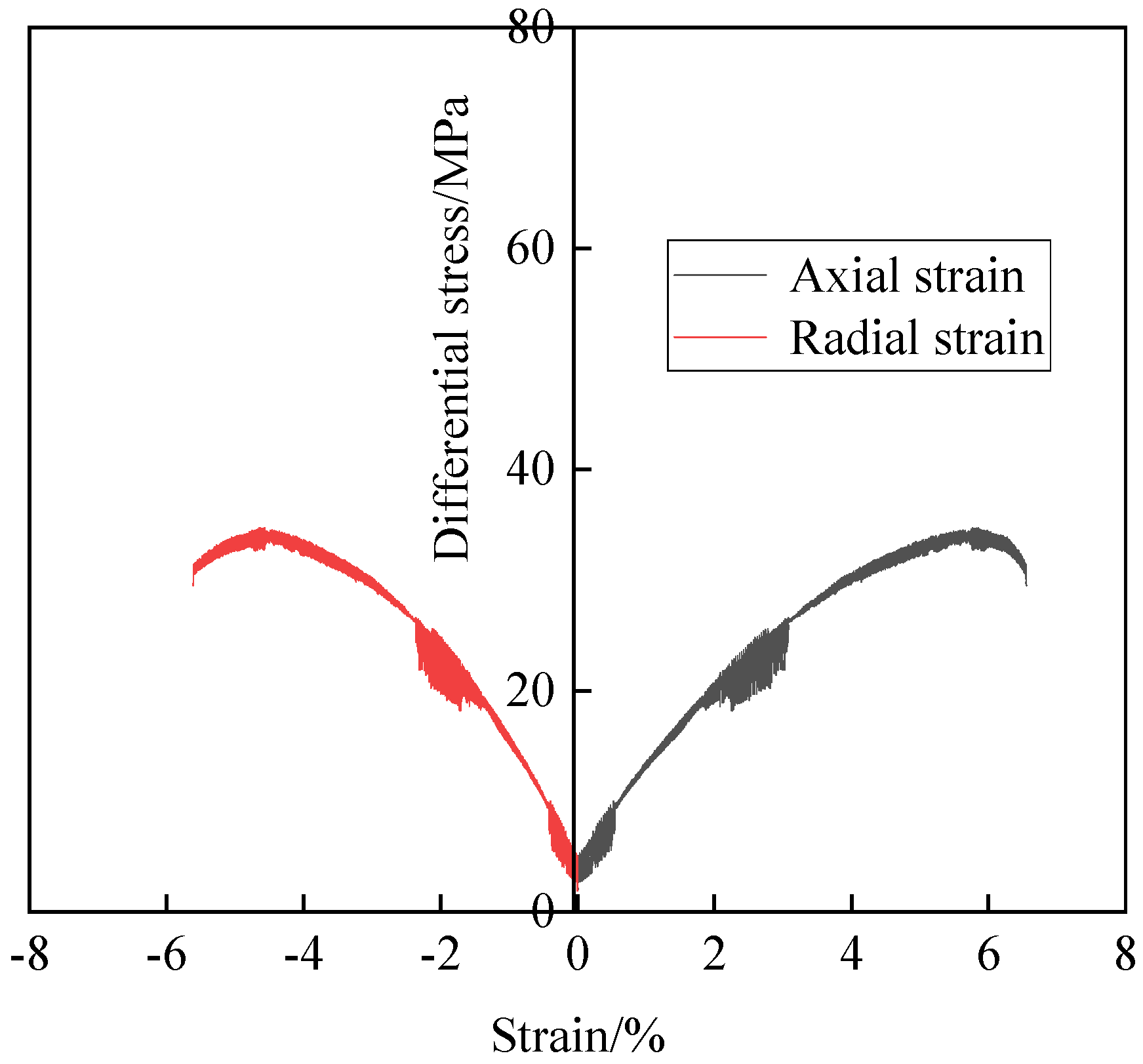
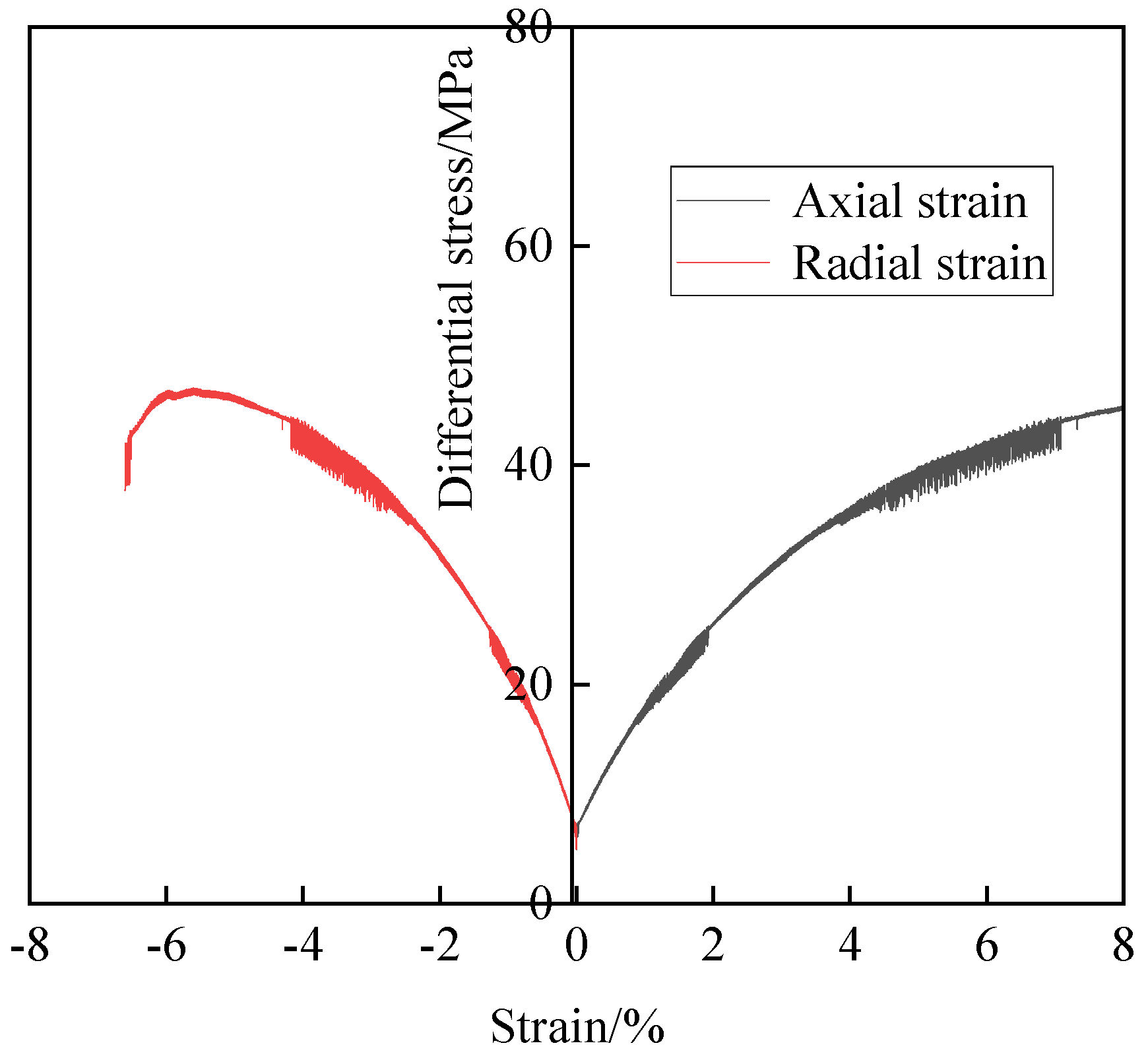
2.4.1. Stress–Strain Curve Characteristics
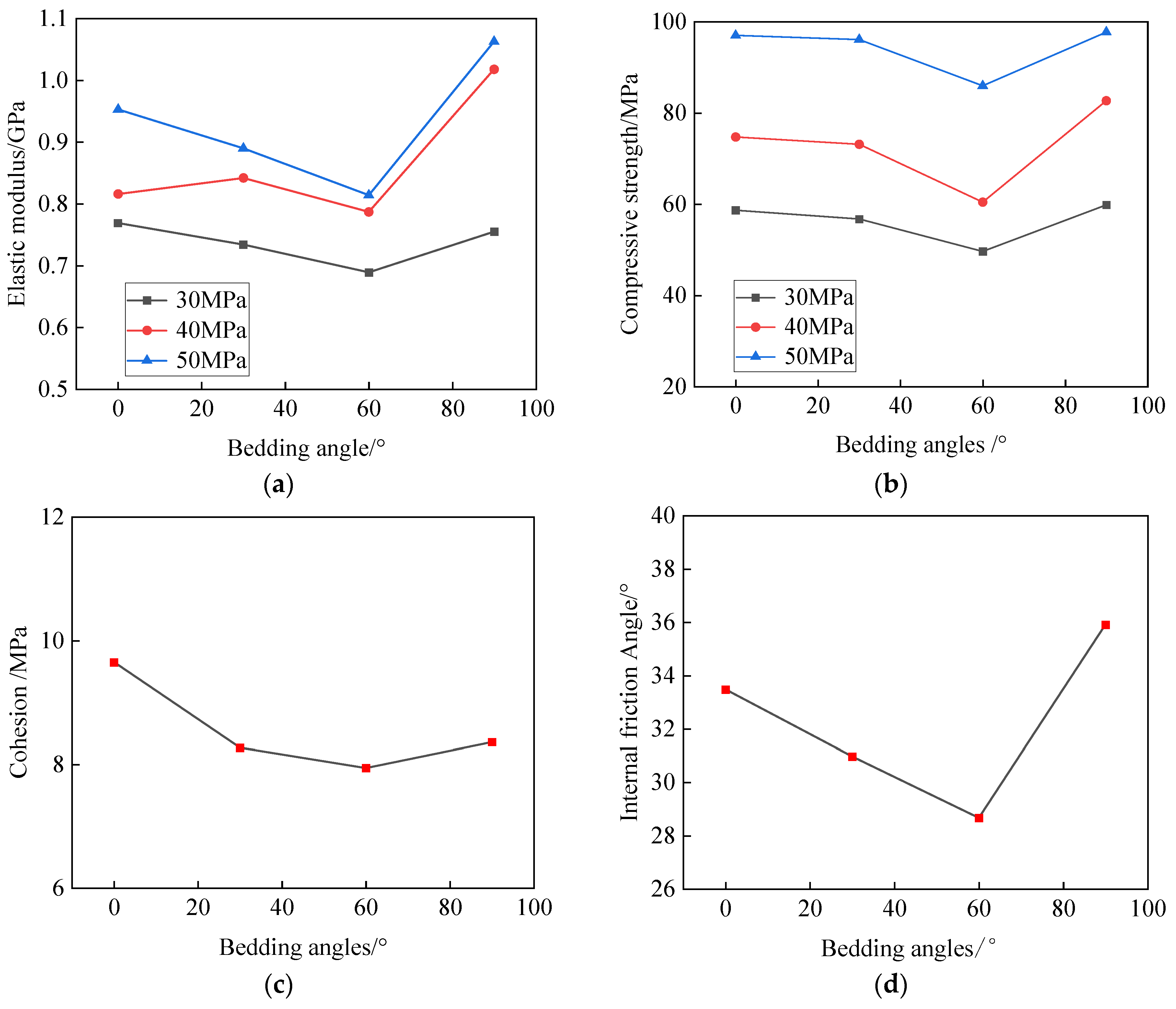
2.4.2. Variation Characteristics of Mechanical Parameters with Bedding Angle
3. Wellbore Collapse Pressure Prediction Model Considering Weak Structure Plane
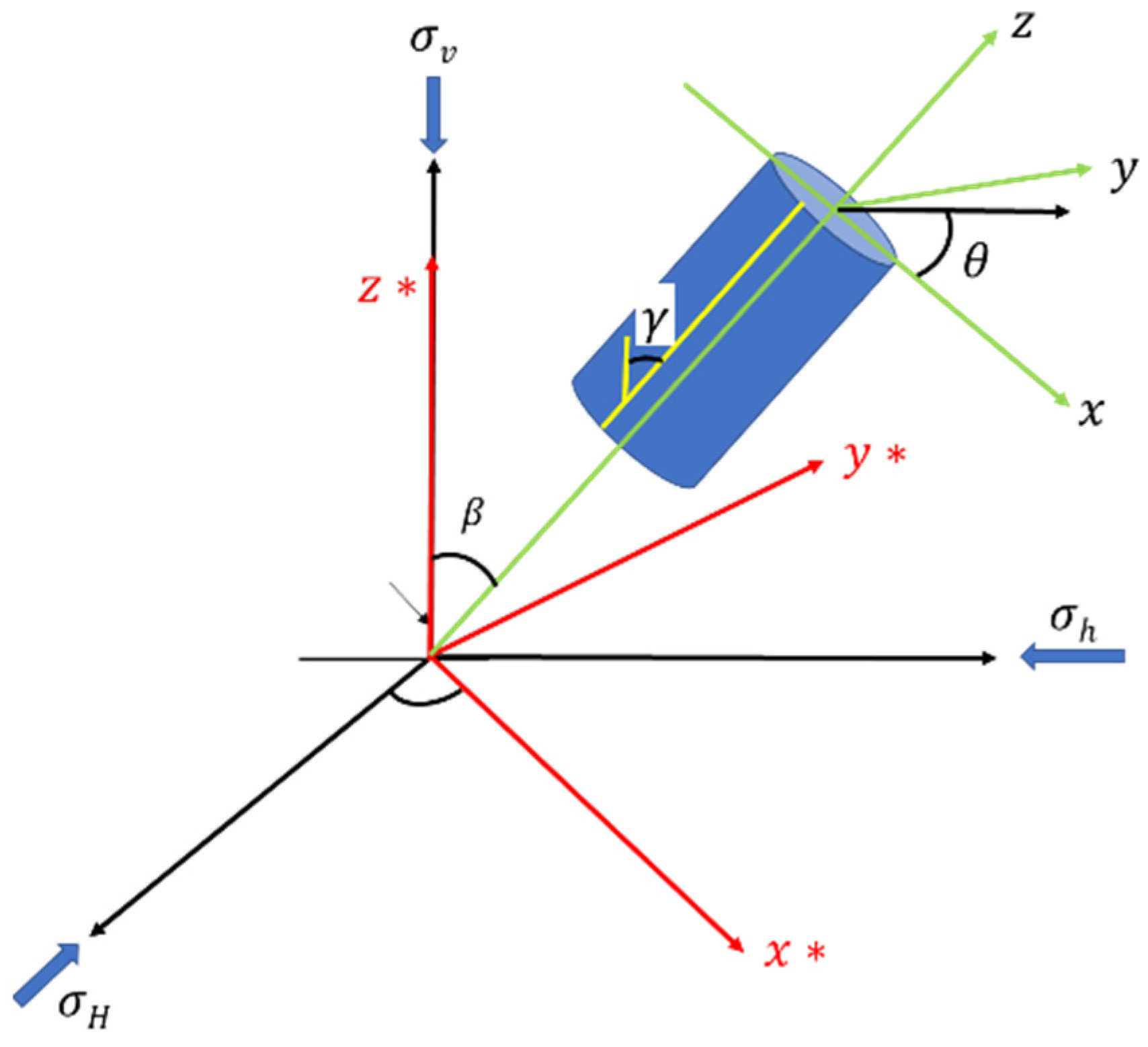
3.1. Wellbore Stress Distribution Transformation
3.2. Strength Criterion of the Coal Formation Considering the Weak Structure Plane
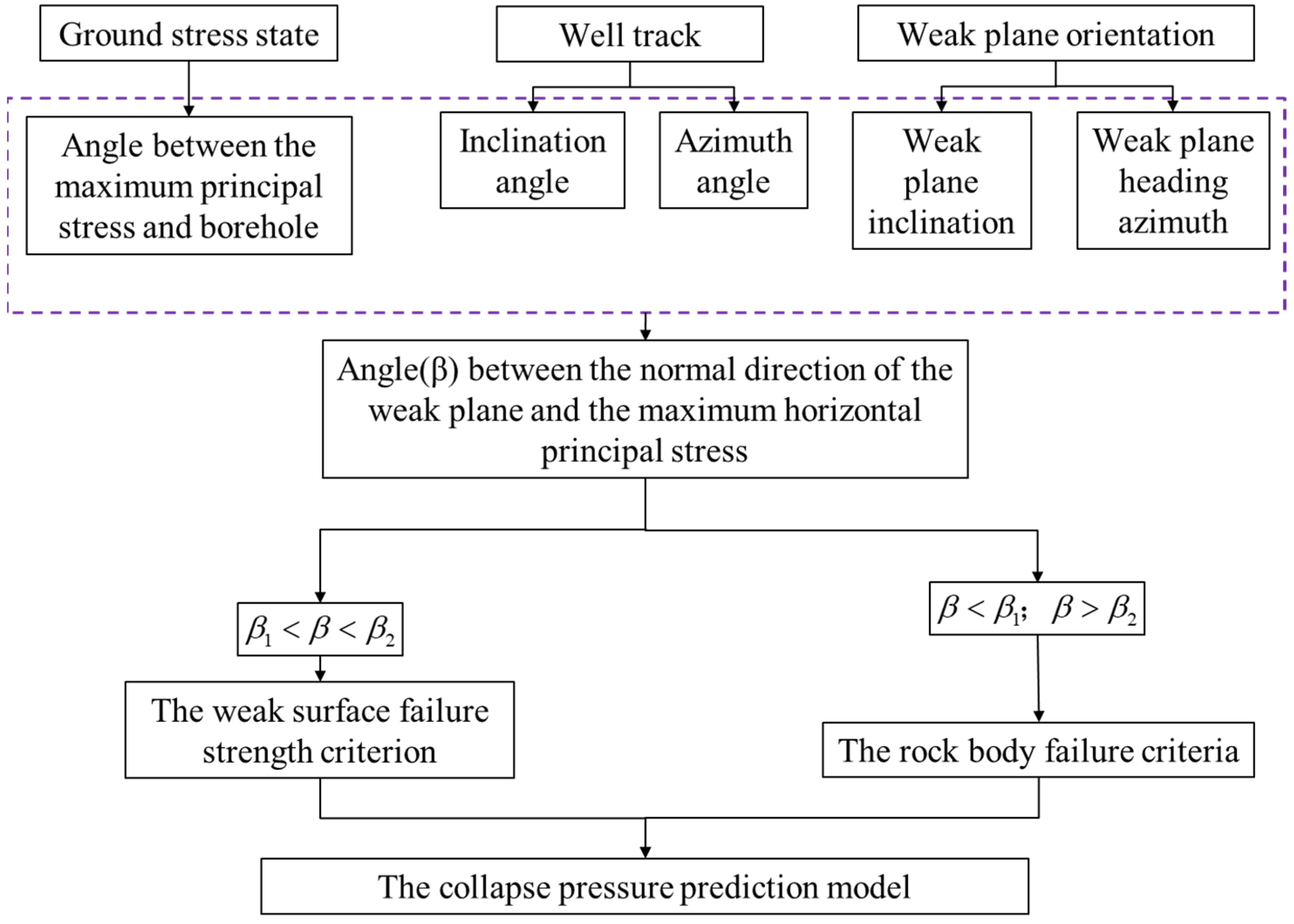
3.3. Process of Solving the Collapse Pressure Considering the Weak Structure Plane
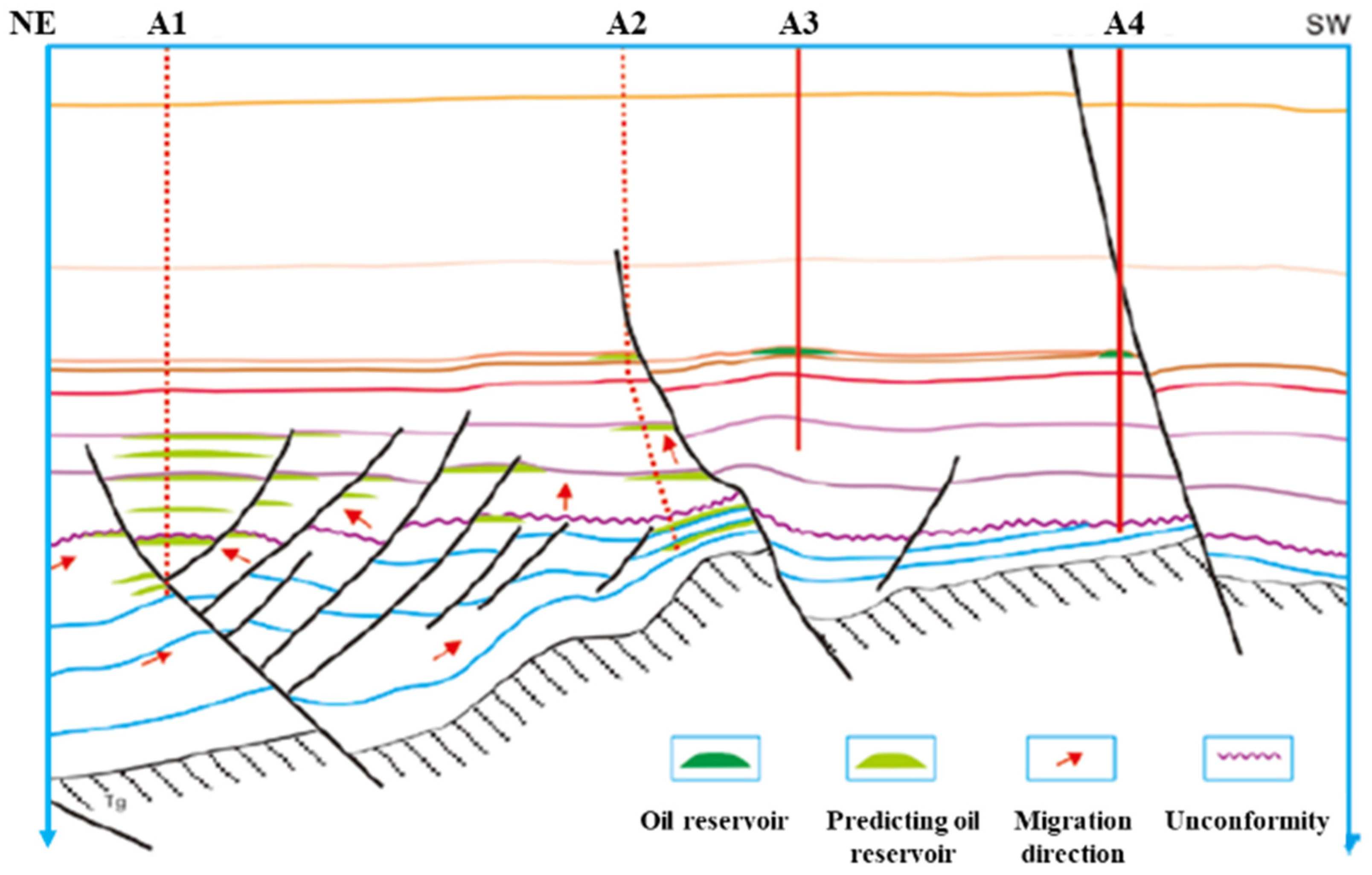
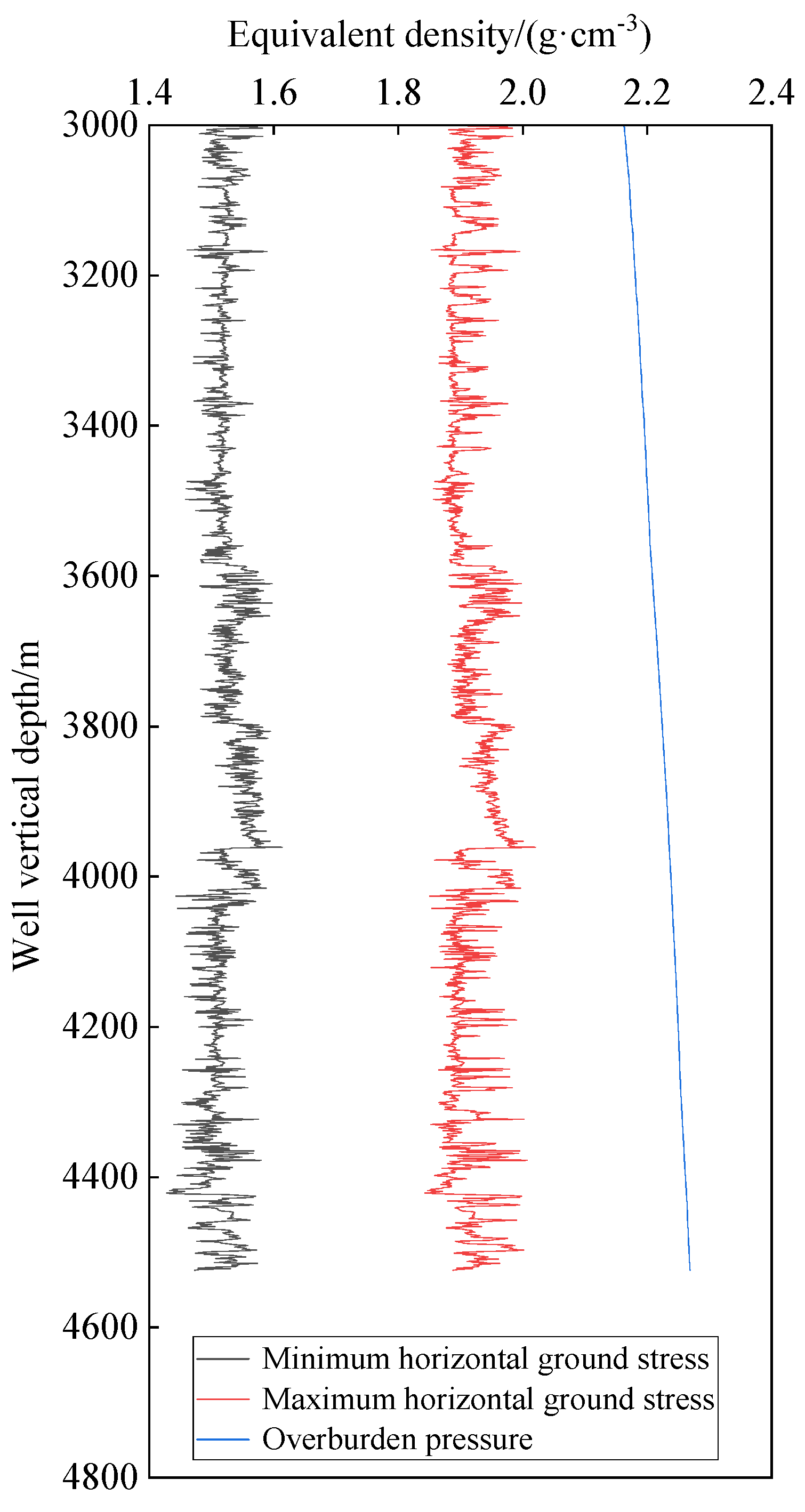
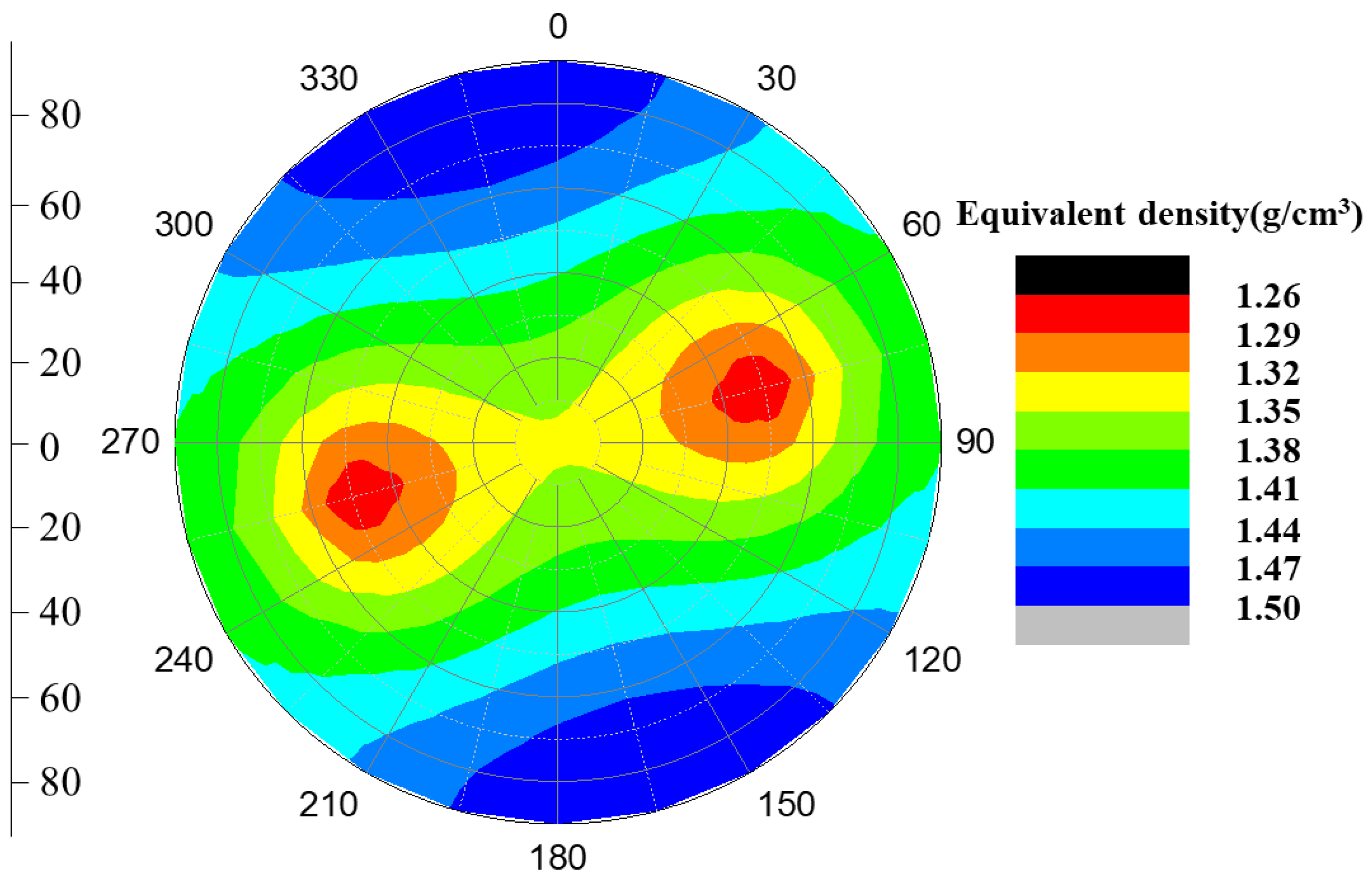
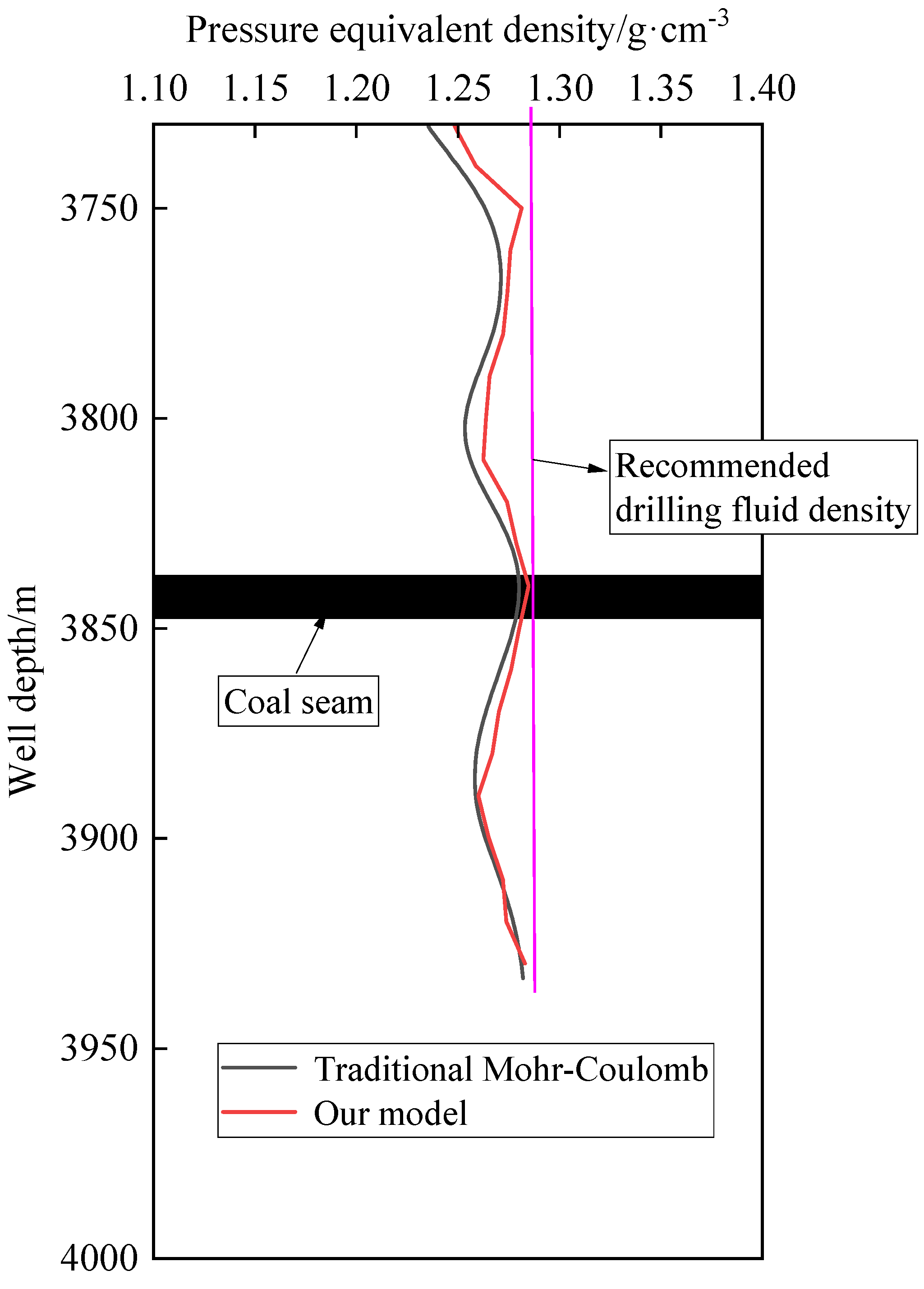
4. Field Application of the Collapse Pressure Prediction Model
5. Conclusions
- (1)
- The fracture structure of coal and rock samples is obvious and well-developed. The pores are irregular in shape and have a certain connectivity among them. The good development of pores improves the connectivity and permeability of coal and rock samples but degrades the mechanical properties of the coal rock;
- (2)
- With the increase of confining pressure, the compressive strength and elastic modulus of the coal rock show an increasing trend. With the increase of bedding angle, the compressive strength, elastic modulus, cohesion, and internal friction angle of the coal rock all decrease first and then increase, and the change curve presents an asymmetric “V” shape. When the bedding angle is 60°, the mechanical parameter value of coal and rock is the smallest, and 60° is the critical point when the mechanical parameter of the coal rock changes with the bedding angle;
- (3)
- Compared with the traditional wellbore collapse pressure prediction model without considering the weak structural plane, the collapse pressure obtained by the new model considering the change of mechanical parameters of the weak structural plane is higher;
- (4)
- Comparing with the coal seam data of the well drilled in the field, it is suggested that the drilling fluid density of this coal seam should be moderately increased to 1.28 g/cm3 during actual drilling, so as to reduce the occurrence of leakage accidents while ensuring the low risk of borehole collapse and instability.
6. Research Limitations and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holt, R.M.; Fjær, E.; Stenebråten, J.F.; Nes, O.M. Brittleness of shales: Relevance to borehole collapse and hydraulic fracturing. J. Pet. Sci. Eng. 2015, 131, 200–209. [Google Scholar] [CrossRef]
- Heng, S.; Yang, C.; Zhang, B.; Guo, Y.; Wang, L.; Wei, Y. Experimental study on anisotropy characteristics of shale. Rock Soil Mech. 2015, 36, 609–616. [Google Scholar]
- Yan, C.; Deng, J.; Hu, L.; Chen, Z.; Yan, X.; Lin, H.; Tan, Q.; Yu, B. Brittle failure of shale under uniaxial compression. Arab. J. Geosci. 2015, 8, 2467–2475. [Google Scholar]
- Ong, S.H.; Roegiers, J.-C. Fracture Initiation from Inclined Wellbores in Anisotropic Formations; SPE-29993-MS; Society of Petroleum Engineers (SPE): Richardson, TX, USA, 1995; p. 13. [Google Scholar]
- Wang, Z. Seismic anisotropy in sedimentary rocks, part 2: Laboratory data. Geophysics 2002, 67, 1423–1440. [Google Scholar] [CrossRef]
- Jaeger, J.C. Shear Failure of Anistropic Rocks. Geol. Mag. 1960, 97, 65–72. [Google Scholar] [CrossRef]
- Qi, W.; Wu, H.; Xie, X.; Lou, Y.; Liu, H. Study on formation rock characteristic sand bore hole collapse period in northern Jiangsu Basin. China Offshore Oil Gas 2024, 36, 108–118. [Google Scholar]
- Han, Z.; Liu, H.; Zhang, J.; Yang, H.; Shen, X.; Yang, Q. Research on the mechanical propertie sand borehole stability of deep brittle shale. Spec. Oil Gas Reserv. 2020, 27, 167–174. [Google Scholar]
- Larki, E.; Ayatizadeh Tanha, A.; Khosravi, M.; Fazaeilzadeh, M. Feasibility study of underbalanced drilling using geomechanical parameters and finite element method. J. Pet. Explor. Prod. Technol. 2023, 13, 407–426. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, M.; Chen, Z.; Zhao, H. Mechanical model of vertical well wall stability in weak surface formation. Drill. Prod. Technol. 1999, 3, 1314+97. [Google Scholar]
- Jin, Y.; Chen, M.; Liu, G.; Li, J. Wellbore stability analysis of inclined well in weak surface formation. J. Univ. Pet. (Nat. Sci. Ed.) 1999, 46–48. [Google Scholar]
- Ma, T.; Chen, P. Wellbore stability analysis of layered shale horizontal Wells. J. Cent. South Univ. (Nat. Sci. Ed.) 2015, 46, 1375–1383. [Google Scholar]
- Amadei, B. Rock Anisotropy and the Theory of Stress Measurements; Springer: Berlin/Heidelberg, Germany, 1983; p. 2. [Google Scholar]
- Aadnoy, B.S. Modelling of the Stability of Highly Inclined Boreholes in Anisotropic Rock Formations; SPE-16526-MS; Society of Petroleum Engineers (SPE): Richardson, TX, USA, 1987. [Google Scholar]
- Pei, J. Strength of Transversely Isotropic Rocks. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
- Li, X.; Yi, L.; Yang, Z. Computational model of horizontal well wall pseudo-three-dimensional stress field in transvertically isotropic formation. Chin. J. Rock Mech. Eng. 2017, 36, 1452–1459. [Google Scholar]
- Gao, L.; Shi, X.; Liu, J.; Chen, X. Simulation-based three-dimensional model of wellbore stability in fractured formation using discrete element method based on formation microscanner image: A case study of Tarim Basin, China. J. Nat. Gas Sci. Eng. 2022, 97, 104341. [Google Scholar] [CrossRef]
- Li, W. Wellbore Stability Analysis and Risk Assessment Based on Uncertainty of Lithology Parameters. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2020. [Google Scholar]
- Ma, T.; Yang, Z.; Chen, P. Wellbore stability analysis of fractured formations based on Hoek-Brown failure criterion. Int. J. Oil Gas Coal Technol. 2018, 17, 143–171. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Rice, J.R.; Cleary, M.P. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev. Geophys. 1976, 14, 227. [Google Scholar] [CrossRef]
- Yew, C.H.; Liu, G. Pore Fluid and Wellbore Stabilities; SPE-22381-MS; Society of Petroleum Engineers (SPE): Richardson, TX, USA, 1992; p. 9. [Google Scholar]
- Cui, L.; Cheng, A.H.-D.; Abousleiman, Y. Poroelastic Solution for an Inclined Borehole. J. Appl. Mech. 1997, 64, 32. [Google Scholar] [CrossRef]
- Cui, L.; Abousleiman, Y.; Cheng, A.H.-D.; Roegiers, J.C. Time-Dependent Failure Analysis of Inclined Boreholes in Fluid-Saturated Formations. J. Energy Resour. Technol. 1999, 121, 31. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Z.; Zhuang, Z.; Hwang, K.-C.; Wang, Y.; Yang, L.; Yang, H. Cylindrical Borehole Failure in a Poroelastic Medium. J. Appl. Mech. 2016, 83, 061005. [Google Scholar] [CrossRef]
- Huang, R.; Chen, M.; Deng, J.; Wang, K.; Chen, Z. Coupling study of wellbore stability mechanics and chemistry of mud shale. Drill. Fluid Complet. Fluids 1993, 03, 18–24+28. [Google Scholar]
- Mody, F.K.; Hale, A.H. Borehole-Stability Model to Couple the Mechanics and Chemistry of Drilling-Fluid/Shale Interactions. J. Pet. Technol. 1993, 45, 1093–1101. [Google Scholar] [CrossRef]
- Yu, M.; Chenevert, M.E.; Sharma, M.M. Chemical–mechanical wellbore instability model for shales: Accounting for solute diffusion. J. Pet. Sci. Eng. 2003, 38, 131–143. [Google Scholar] [CrossRef]
- Zeynali, M.E. Mechanical and physico-chemical aspects of wellbore stability during drilling operations. J. Pet. Sci. Eng. 2012, 82–83, 120–124. [Google Scholar] [CrossRef]
- Liang, L.; Ding, Y.; Liu, X.; Xu, L. Study on stable percolation-mechanical coupling of hard brittle shale. Spec. Oil Gas Reserv. 2016, 23, 140–143+158. [Google Scholar]
- Zhang, S.; Wang, H.; Qiu, Z.; Cao, W.; Huang, H.; Chen, Z. Calculation method of coupled fluid-solid-chemical safety density window in shale wellbore. Pet. Explor. Dev. 2019, 46, 1197–1205. [Google Scholar]
- Deng, Y.; He, S.; Deng, X.; Peng, Y.; He, S.; Tang, M. Study on wellbore instability of layered shale gas horizontal Wells under dynamic coupling. Pet. Drill. Tech. 2020, 48, 26–33. [Google Scholar]
- Wang, H.F. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Coussy, O. Poromechanics, 2nd ed.; Wiley: Chichester, UK; Hoboken, NJ, USA, 2004. [Google Scholar]
- Fjaer, E. Petroleum Related Rock Mechanics, 2nd ed.; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA, 2008. [Google Scholar]
- Chen, M. Petroleum Engineering Rock Mechanics; Science Press: Beijing, China, 2008. [Google Scholar]
- Huang, Z.; Zeng, W.; Gu, Q.; Wu, Y.; Zhong, W.; Zhao, K. Investigations of variations in physical and mechanical properties of granite, sandstone, and marble after temperature and acid solution treatments. Constr. Build. Mater. 2021, 307, 124943. [Google Scholar] [CrossRef]
- Liu, G.; Chen, Y.; Du, X.; Wang, S.; Fernández-Steeger, T.M. Evolutionary analysis of heterogeneous granite microcracks based on digital image processing in grain-block model. Materials 2022, 15, 1941. [Google Scholar] [CrossRef]
- Tong, H.; Chen, Y.; Du, X.; Chen, S.; Pan, Y.; Wang, S.; Peng, B.; Azzam, R.; Fernandez-Steeger, T.M. A State-Dependent Elasto-Plastic Model for Hydrate-Bearing Cemented Sand Considering Damage and Cementation Effects. Materials 2024, 17, 972. [Google Scholar] [CrossRef]


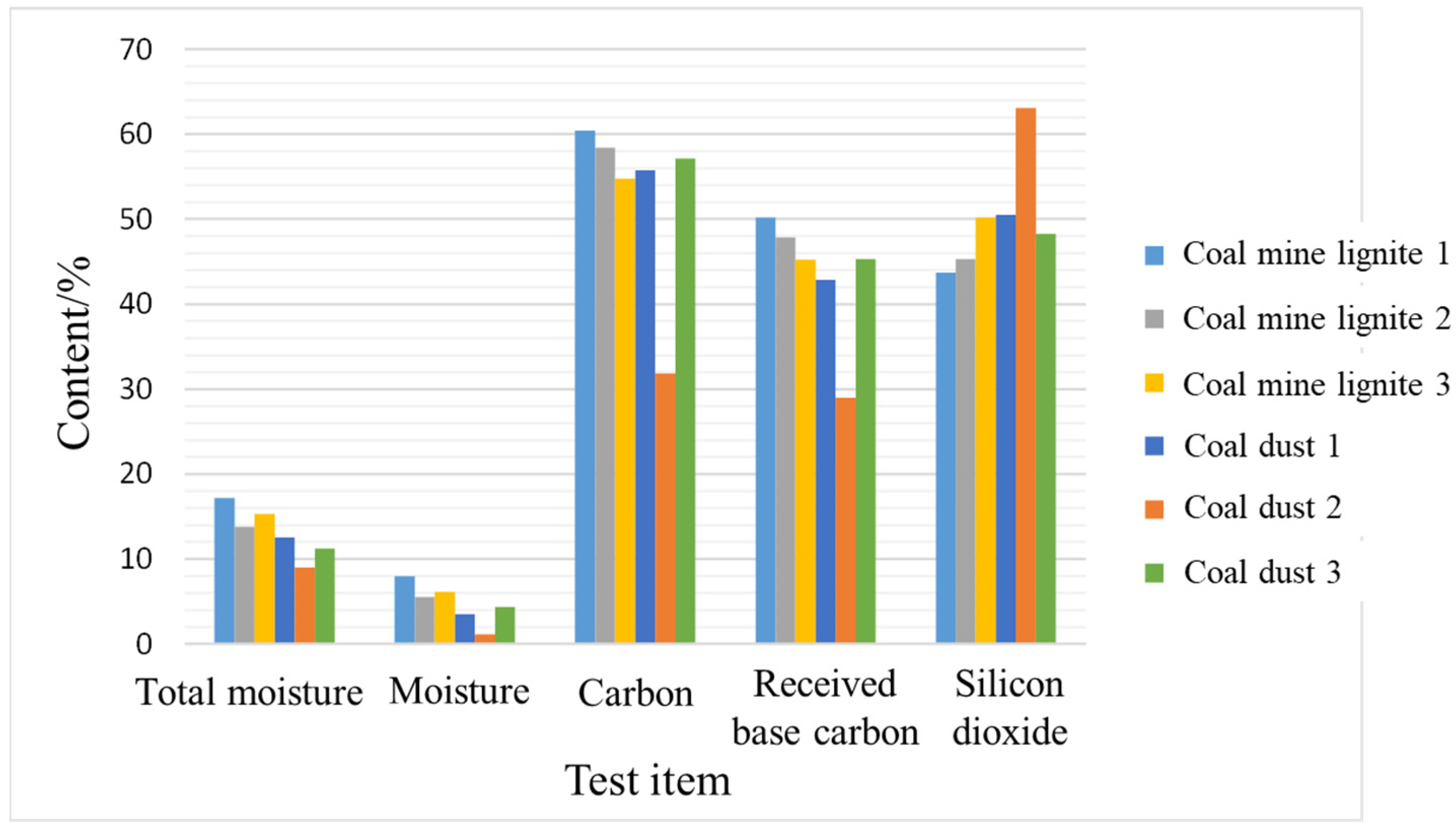




| Research Category | Researcher | Research Content | Inadequate Research |
|---|---|---|---|
| Experimental study on mechanical properties of rock with weak structure plane | Holt [1], Yan [3], Ong [4], Roegiers [6], Wang [5] et al. | The influence of weak structure plane on elastic modulus and failure form of rock was studied. | In particular, the characteristics of coal and rock cohesion and internal friction angle change with a weak structural plane are lacking. |
| Research on the prediction model of isotropic borehole collapse pressure | Qi [7], Han [8], Larki, E [9] et al. | Based on rock mechanics parameters and empirical formulas, calculation models of isotropic formation collapse pressure were established. | The influence of rock anisotropy on formation collapse pressure is not considered. |
| Study on formation collapse pressure model considering rock anisotropy | Jin [10,11], Ma [12], Amadei [13], Aadony [14], Pei [15], Li [16] et al. | Prediction models of formation collapse pressure considering rock elastic modulus, Poisson ratio, and other mechanical parameters were established. | In particular, the coal seam collapse pressure calculation model that fully considers the characteristics of cohesion, internal friction angle, and elastic modulus with a weak plane is lacking. |
| Core Label | Peak Load/mN | Minimum Elastic Modulus/GPa | Robustness Coefficient/GPa | Fracture Toughness/MPa·m0.5 |
|---|---|---|---|---|
| Coal mine lignite 1 | 50 | 1.26 | 0.121 | 0.072 |
| Coal mine lignite 2 | 50 | 1.34 | 0.132 | 0.081 |
| Coal mine lignite 3 | 50 | 1.24 | 0.118 | 0.072 |
| Coal dust 1 | 50 | 1.17 | 0.112 | 0.069 |
| Coal dust 2 | 50 | 1.29 | 0.120 | 0.072 |
| Coal dust 3 | 50 | 1.31 | 0.126 | 0.075 |
| Core Label | Bedding Angle/° | Diameter/mm | Height/mm | Quantity/g | Confining Pressure/MPa |
|---|---|---|---|---|---|
| M-1 | 0 | 24.61 | 49.97 | 29.16 | 30 |
| M-2 | 30 | 24.58 | 48.97 | 28.23 | 30 |
| M-3 | 60 | 24.70 | 49.60 | 29.07 | 30 |
| M-4 | 90 | 24.60 | 49.60 | 29.43 | 30 |
| M-5 | 0 | 24.62 | 49.91 | 29.37 | 40 |
| M-6 | 30 | 24.71 | 50.00 | 29.17 | 40 |
| M-7 | 60 | 24.70 | 49.54 | 29.09 | 40 |
| M-8 | 90 | 24.70 | 50.08 | 29.25 | 40 |
| M-9 | 0 | 24.69 | 50.32 | 29.28 | 50 |
| M-10 | 30 | 24.68 | 50.72 | 29.19 | 50 |
| M-11 | 60 | 24.52 | 50.20 | 28.95 | 50 |
| M-12 | 90 | 24.96 | 49.67 | 29.35 | 50 |
| Elastic Modulus/GPa | Bedding Angle/° | Cohesion/MPa | Internal Friction Angle/° |
|---|---|---|---|
| 0.83 | 45 | 8.24 | 30.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Chen, K.; Li, J.; Xue, L.; Han, Z. Study on Prediction of Wellbore Collapse Pressure of the Coal Seam Considering a Weak Structure Plane. Processes 2025, 13, 803. https://doi.org/10.3390/pr13030803
Li D, Chen K, Li J, Xue L, Han Z. Study on Prediction of Wellbore Collapse Pressure of the Coal Seam Considering a Weak Structure Plane. Processes. 2025; 13(3):803. https://doi.org/10.3390/pr13030803
Chicago/Turabian StyleLi, Dongsheng, Kaiwei Chen, Jian Li, Liang Xue, and Zhongying Han. 2025. "Study on Prediction of Wellbore Collapse Pressure of the Coal Seam Considering a Weak Structure Plane" Processes 13, no. 3: 803. https://doi.org/10.3390/pr13030803
APA StyleLi, D., Chen, K., Li, J., Xue, L., & Han, Z. (2025). Study on Prediction of Wellbore Collapse Pressure of the Coal Seam Considering a Weak Structure Plane. Processes, 13(3), 803. https://doi.org/10.3390/pr13030803





