Next Article in Journal
Optimization of Triazine Desulfurization Injection Rate and Injection Process for the Xiangguosi Underground Gas Storage
Previous Article in Journal
Editorial for the Special Issue: Sustainable and Intelligent Energy Systems and Processes—Recent Advances and Challenges
Previous Article in Special Issue
Shear Mechanical Properties and Acoustic Emission Characteristics of the Interface of a Surrounding-Rock–Backfill Composite
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 13
Issue 12
10.3390/pr13123909
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental Investigation on Fracture Behaviors of Straight-Wall Tunnels with Defects of Insufficient Lining Thickness

by
Wei Han
1,2,
Xuze Du
1,2,
Yihan Du
1,2,*,
Jiapeng Yue
1,2,
Bo Huang
1,2 and
Hui Liu
1,2
1
School of Architecture and Civil Engineering, Anhui Polytechnic University, Wuhu 241000, China
2
Engineering Research Center of Anhui Green Building and Digital Construction, Anhui Polytechnic University, Wuhu 241000, China
*
Author to whom correspondence should be addressed.
Processes 2025, 13(12), 3909; https://doi.org/10.3390/pr13123909
Submission received: 29 October 2025 / Revised: 22 November 2025 / Accepted: 27 November 2025 / Published: 3 December 2025
(This article belongs to the Special Issue Optimization of Complex Engineering Systems and Application of Advanced Digital and Intelligent Technologies)
Browse Figures
Versions Notes

Abstract

Fractures in straight-wall linings is a common disease that seriously affects the integrity and service life of tunnels. The presence of insufficient lining thickness can be regarded as one of the most important factors causing fractures. In this study, the fracture behaviors of straight-wall tunnels with insufficient lining thickness under progressive compressive loading were investigated. First, the fracture characteristics and failure mode were explored. Subsequently, the deformation behaviors were investigated by digital image correlation (DIC) technology. Finally, the fracture pattern was systematically discussed. The results show that the deformation intensifies in the areas with insufficient lining thickness, which is prone to induce cracks. As the ratio or range of insufficient thickness increases, the severity of fractures intensifies and the failure mode tends to be more complex. In addition, whether the lining comes into contact with the surrounding rock in the area with insufficient thickness has a significant impact on the failure mode. Furthermore, the more serious the defect is, the more obvious the spalling phenomenon will be. Moreover, the failure mode of straight-wall tunnels can basically be attributed to the combined effect of the fractures of defect zones, arch feet and tunnel floor.

1. Introduction

Straight-wall tunnels have been widely applied due to their advantages, such as simple structure and convenient construction [1,2]. However, typical diseases, such as water leakage, cracking, and spalling, often occur during tunnel operation [3,4,5,6,7,8]. Insufficient lining thickness can be regarded as one of the dominant inducements governing the formation of tunnel diseases [9,10]. Therefore, exploring the influence of insufficient lining thickness on the fracture characteristics of straight-wall tunnels is important for guiding reinforcement.
Extensive investigations have been conducted for the factors causing the defect of insufficient lining thickness, and can be classified as improper design [11], improper construction [12,13], and improper operation [14]. It can be observed that insufficient lining thickness occurs throughout the entire process from construction to operation, seriously affecting the durability of the tunnel [15]. Regarding the effect of insufficient lining thickness on the mechanical behavior of tunnels, the variation law of the lining safety factor with insufficient thickness was explored [16,17]. Lin et al. [18] numerically investigated the deformation characteristics of horseshoe-shaped tunnels with local insufficient lining thickness, and a tunnel damage prediction model was established. Chen et al. [19] explored the mechanical behavior and lining deterioration in horseshoe-shaped tunnels with insufficient lining thickness. Wang et al. [20] conducted model tests to investigate the deformation behavior and failure process of circular tunnel lining with insufficient thickness, and a thickness control standard of secondary lining defects was also proposed. Liu et al. [21] investigated the fracture behaviors of horseshoe-shaped tunnels with insufficient lining thickness using the cohesive zone model method, and the cracking characteristics were also statistically analyzed. Han et al. [22] numerically explored the cracking characteristics of horseshoe-shaped tunnels with local insufficient thickness. Liu et al. [23] performed the numerical evaluation on the damage behavior of horseshoe-shaped tunnels with insufficient lining thickness, and the maintenance method was also discussed. Gong [24] evaluated the safety state and cracking behavior of horseshoe-shaped tunnels under the influence of insufficient lining thickness. Sui et al. [25] studied the cracking characteristics of a straight-wall tunnel structure with void defects, and the characteristic of crack propagation was explored. In addition, DIC technology is a non-contact optical observation system that acquires displacement information by analyzing the pictures before and after the deformation [26]. DIC technology has been widely applied to investigate the fracture characteristics of rocks [27,28,29], concrete structures [30,31,32]. Particularly, Zhu et al. [33] explored the cracking behaviors of tunnel linings using 3D DIC photogrammetry.
For the fracture behaviors of tunnel structures with insufficient lining thickness, most research mainly focused on the horseshoe-shaped tunnels, whereas information on the straight-wall tunnels is rather limited. However, straight-wall tunnels are also prone to cracking in actual engineering, and the fracture degree is also quite pronounced, as shown in Figure 1 [34]. In addition, although experimental methods can visually provide the cracking behavior of the lining, the DIC technology that can reveal the failure mechanism of defective concrete lining has not been fully applied. Therefore, the focus of this study is to experimentally explore the fracture behaviors of straight-wall tunnels with insufficient lining thickness. This research also has guiding significance for the reinforcement of straight-wall tunnels with defects.

2. Model Test

2.1. Similar Material

Based on the similarity ratio design method, this study conducted similarity model tests with the straight-wall tunnel as the object. The geometric similarity ratio is set to 40. According to the similarities theory, other physical similarities are determined as follows: the weight similarity ratio is 1, Poisson’s ratio similarity ratio is 1, the internal friction angle similarity ratio is 1, and the elastic modulus similarity ratio is 40. The lining material was prepared by mixing gypsum and water in different proportions and then tested to ensure that the similarity ratio requirements were met, as shown in Figure 2. It should be indicated that the gypsum can well meet the similarity requirements with the concrete prototype in the physical model test [35]. To achieve the requirements for the similarity material parameters, the optimal mass ratio of water to gypsum was finally determined to be 1:0.8. The similarity material parameters for the lining model, ultimately determined based on the above similarity ratio relationships, are listed in Table 1.
The surrounding rock material was made of a mixture of Barite powder, Quartz sand and Vaseline. The configuration of the surrounding rock filling materials can be shown in Table 2. Then, the mixing ratio of the proportioned materials to Vaseline is 1:0.07. The physical and mechanical parameters of similar materials for the surrounding rock are shown in Table 3.

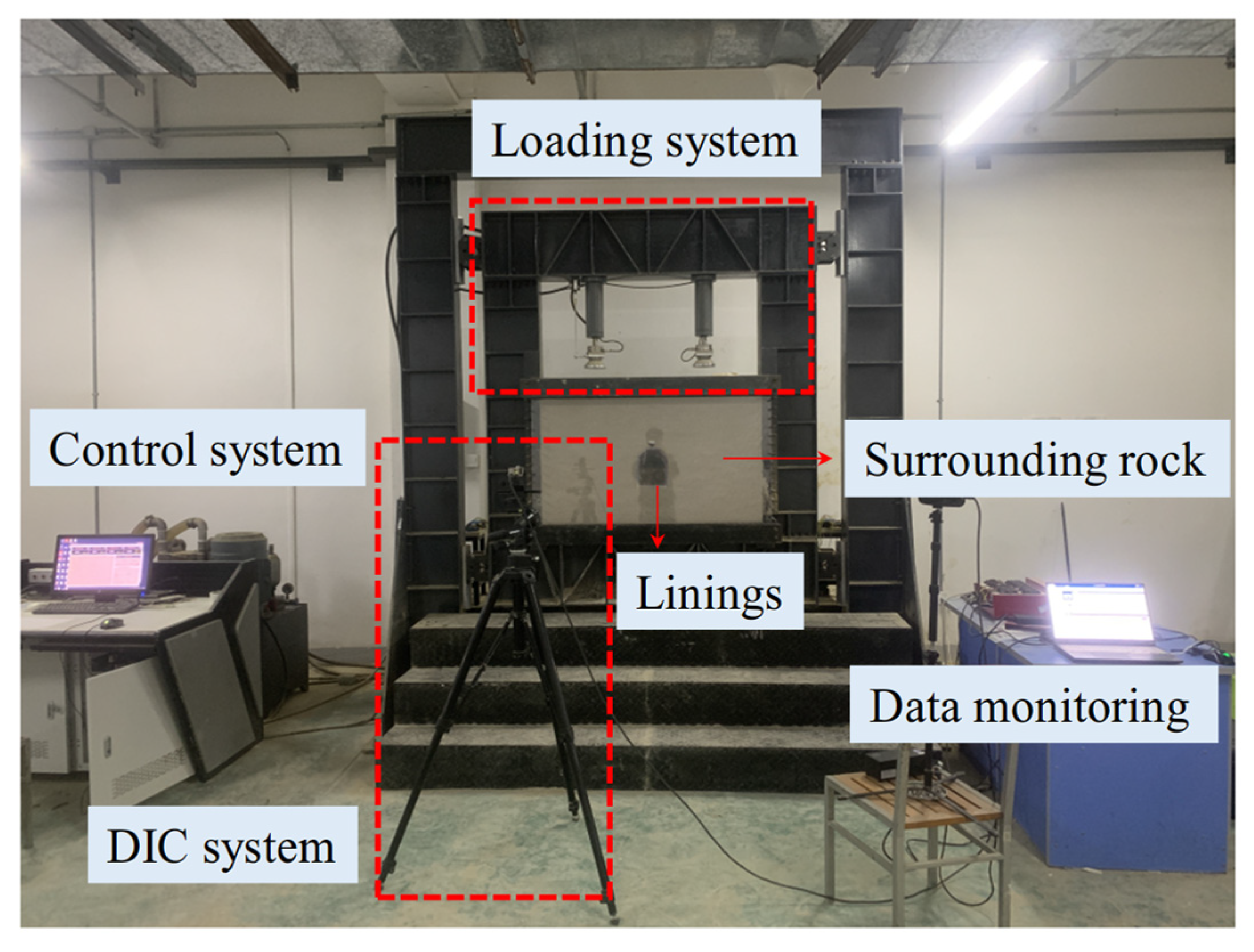
2.2. Loading Equipment

As can be shown in Figure 3, the loading device consists of a model test box, a loading system and a data acquisition system. The dimensions of the test box are 1200 mm (length) × 150 mm (width) × 900 mm (height). It mainly has three functions: accommodating materials of surrounding rock, accommodating tunnel models, and providing reaction force for loading devices. Regarding boundary conditions, the left and right surfaces and the lower surface of the model are fixed, while the upper surface is subjected to compressive loading. The mentioned boundary conditions were also applied in the implementation of tunnel model tests [36]. The progressive loading is applied through two hydraulic devices configured at the top, which support computer operation. The loading system is installed on the top and is used to apply axial pressure to the lining. The equipment integrates a hydraulic jack, a highly sensitive pressure sensor, and a rectangular loading plate. The hydraulic jack is controlled by a computer to output the required pressure and transmits the pressure data in real time to the computer connected to the pressure indicator for processing. During the experiment, DIC technique was carried out simultaneously.

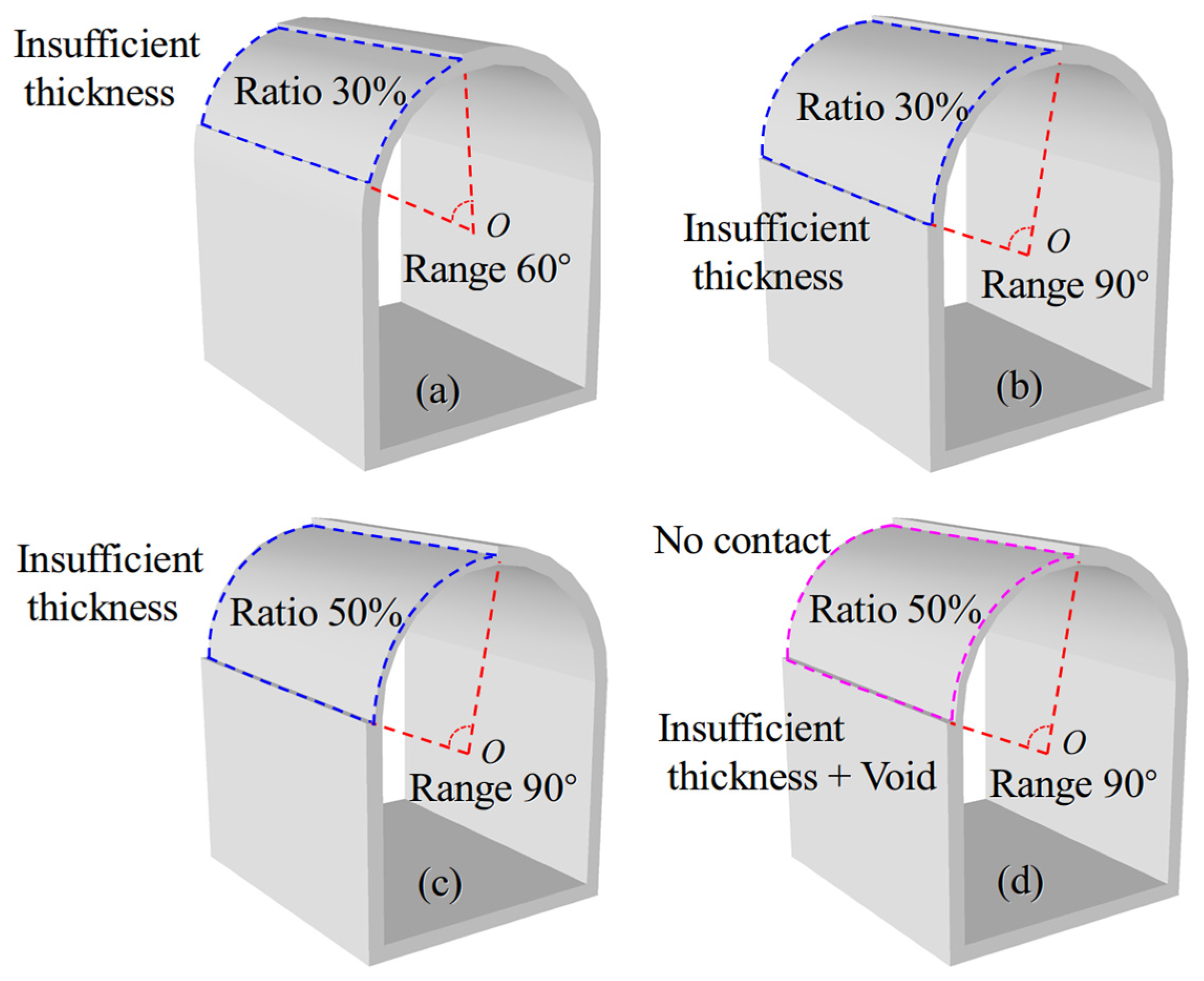
2.3. Design of Experimental Scheme

In this study, the manufacturing process of the tunnel model with insufficient lining thickness can be illustrated in Figure 4. First, foam of different thicknesses and ranges is adhered to the lining mold to form a specific thinning ratio and insufficient thickness range. The prepared lining material is then poured into the lining mode to form a straight-wall tunnel lining structure, as shown in Figure 4a,b. Subsequently, to observe the deformation characteristics of the lining through DIC, high-standard speckle patterns were fabricated on the lining, as shown in Figure 4c. Then, the surrounding rock material was prepared and fill into the model, as shown in Figure 4d. Next, position and place the lining model. That is, after the surrounding rock fills to a certain thickness, place the prefabricated lining at the designated position, as shown in Figure 4e. Finally, the surrounding rock is compacted, and the monitoring equipment is calibrated, as shown in Figure 4f.
This study mainly focuses on the existence of influence of insufficient lining thickness on the cracking characteristics of straight-wall tunnel structures. In the model test, the thinning areas are all fixed in the left shoulder, whereas the main considered influencing factors include the ratio of insufficient lining thickness, the defect range, and whether the thinning area is in contact with the surrounding rock. The experimental design includes five cases, as listed in Table 4. In case 1, the lining is normal and is used for comparative analysis. In Cases 2 and 3, the ratio of insufficient lining thickness is fixed as 0.3, and the defect ranges are 60° and 90°, respectively. In Case 4, the defect range is set as 90°, but the ratio of insufficient lining thickness is 50%. In Case 5, the defect range is still 90°, and the ratio of insufficient lining thickness is also 50%, but the defect area does not contact the surrounding rock. The schematic of the defective lining can be depicted in Figure 5.

3. Experimental Results

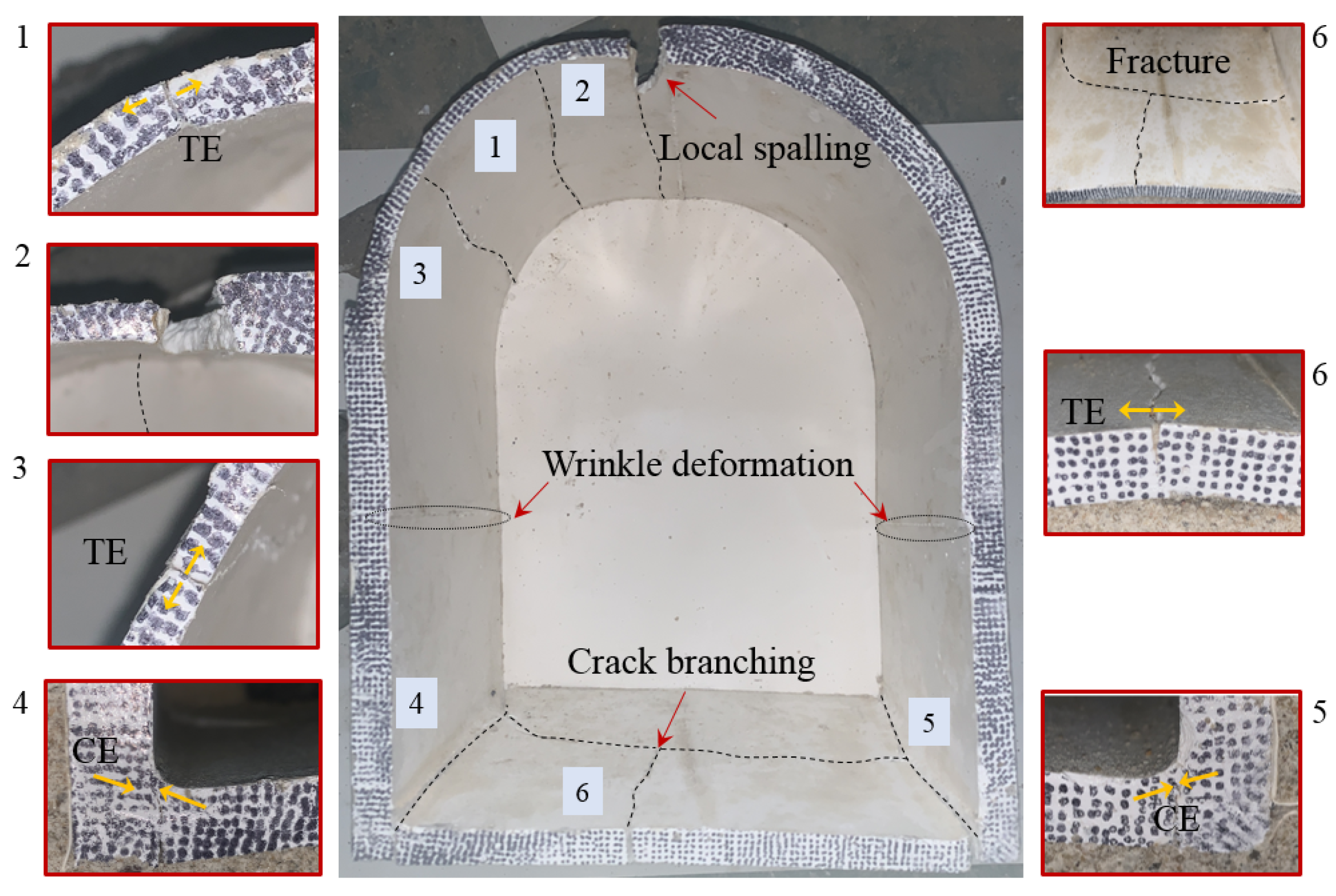
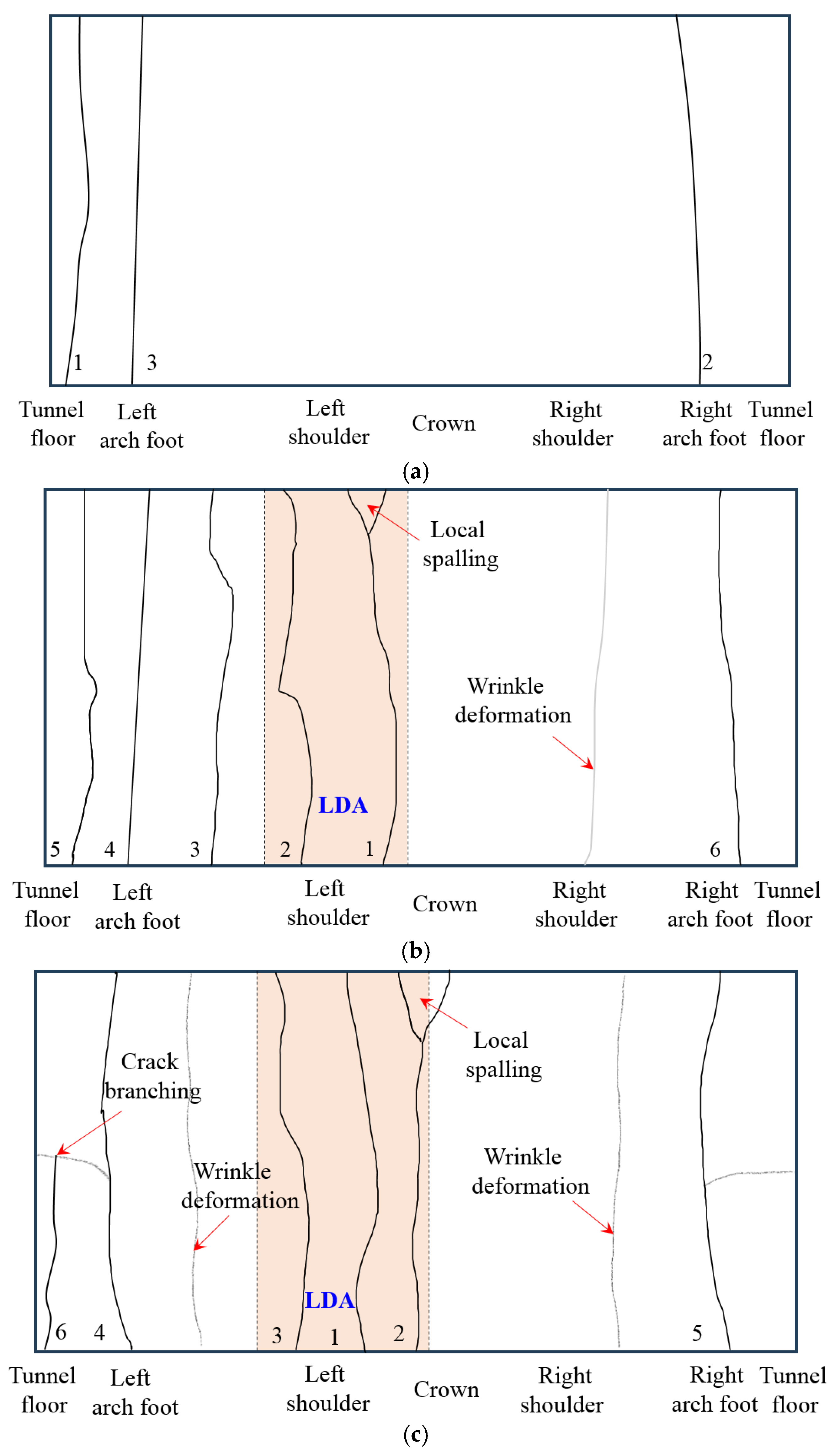
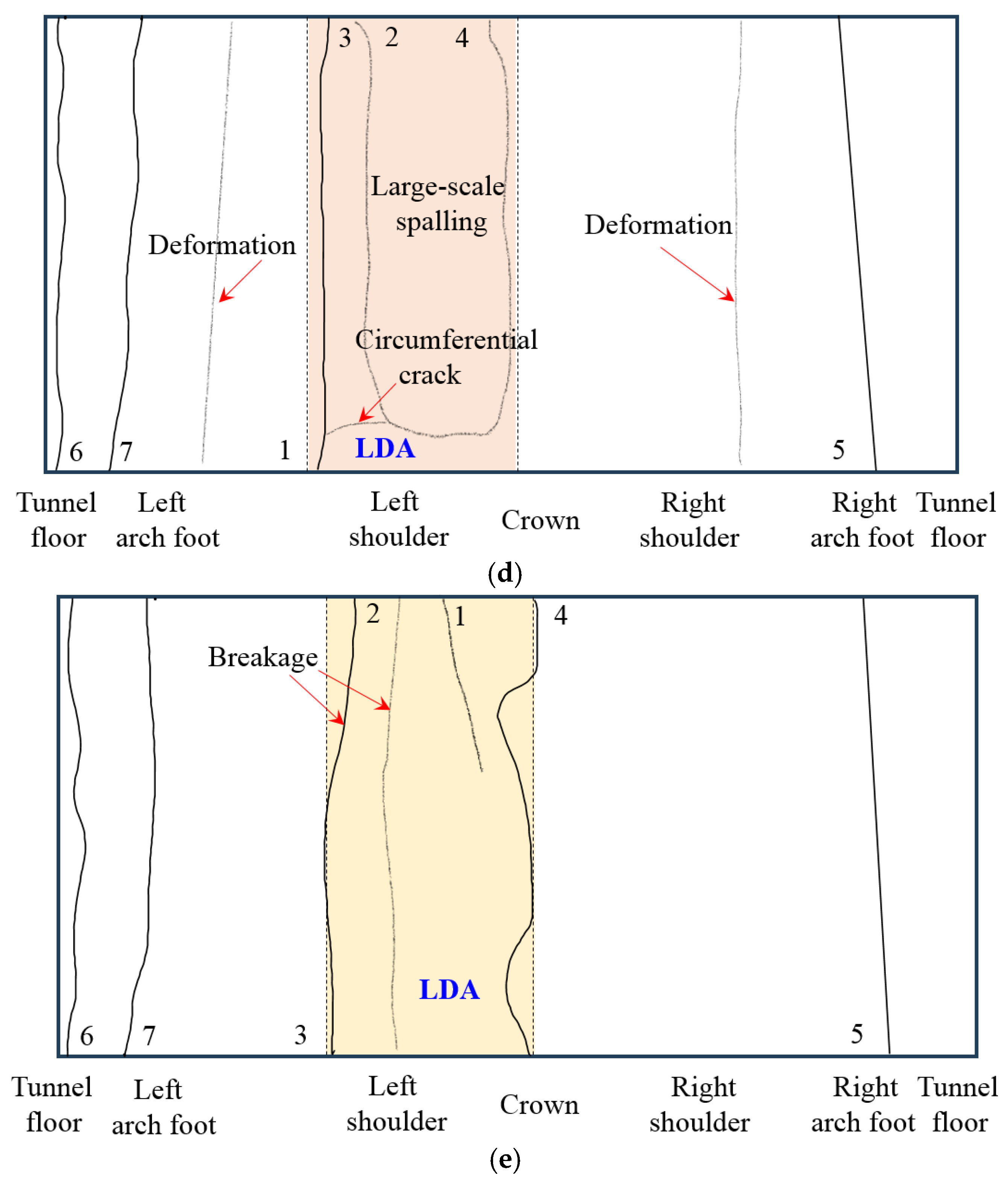
3.1. Fracture Characteristics

The fracture characteristics of straight-wall tunnel linings without defects can be presented in Figure 6. It should be pointed out that the cracking sequence is marked with numbers. The arrow represents the deformation direction. Meanwhile, the cracking causes of the compression effect, tensile effect, and shear slip effect can be, respectively, abbreviated as CE, TE, and SSE. As shown in Figure 6, the lining is in a compressed state and shows a distinct deformation towards the interior of the tunnel. With the gradual increase in external loads, the failure process shows obvious phased characteristics: Firstly, the area of the floor enters the failure stage, showing obvious uplift deformation towards the inner side of the tunnel. Subsequently, damage occurs successively on both sides of the arch feet, with cracks distributed on the outer surface of the arch feet. These cracks exhibit a characteristic “∨” pattern of propagation, and the width of the cracks shows a decreasing trend along the propagation direction. With the continuous increase in load, the propagation rate of cracks accelerates significantly, and the crack depth continues to increase, but the deformation characteristics of the “∨” pattern are basically maintained. The cracks in the tunnel floor develop most significantly, eventually completely penetrating the thickness of the lining, resulting in the overall fracture of the structure. Although the cracks at the arch feet on both sides have not completely penetrated the lining, they have caused serious structural damage, with obvious wrinkling and concrete peeling on the inner surface. It is worth noting that, except for the two key failure areas of the arch feet and the tunnel floor, although the rest of the lining deforms into the tunnel interior under the ultimate load, no significant fracture occurs. The fracture phenomenon indicates that the failure of tunnel linings without defects has obvious localized characteristics, and its failure mode is mainly controlled by the mechanical properties of key parts such as the tunnel floor and arch feet. In general, the tunnel floor and the arch feet on both sides of the straight-wall tunnel are severely deformed and damaged, while the deformation in other parts is relatively small and no significant cracking occurs.
When the ratio of insufficient lining thickness is 30% and the defect range is 60°, the crack distribution and failure mode of the straight-wall tunnel structure can be shown in Figure 7. The results show that several major fractures occur in the defective lining, mainly distributed at the areas with insufficient lining thickness, shoulders, arch feet and tunnel floor. Specifically, at the location near the crown where the tunnel lining thickness is insufficient, TE cracking occurs first, forming fracture 1, accompanied by local spalling. As the load continued to increase, fracture 2 occurs in the insufficient thickness area of the left shoulder. It can be found that during the propagation of the crack along the longitudinal direction, the crack path shows obvious tortuosity and eventually forms a through fracture. From the crack morphology, it can be clearly observed that this fracture suffers significant SSE. Then, fracture 3 occurs on the left side wall, presenting a significant inner side TE, resulting in obvious local crushing and spalling. In addition, the penetrating fractures appear at the arch feet on both sides, but there are significant differences in the morphology of the cracks. Specifically, the fracture path at the left arch foot propagates along the bottom surface of the side wall, while the fracture path at the right arch foot propagates obliquely along the junction between the tunnel floor and the right side wall. In addition, it can be observed that the degree of cracking on the right half of the lining is smaller than that on the side where the thickness is insufficient. Therefore, areas with the insufficient lining thickness seriously affect the local load-bearing capacity of the tunnel, making it a weak area in the structure.
When the ratio of insufficient lining thickness is 30% and the defect range is 90°, the crack distribution and failure mode of the straight-wall tunnel structure can be shown in Figure 8. It can be seen that there are several major fractures and large deformation areas in the lining structure. Specifically, there are three main cracks in the area with insufficient thickness, and the remaining cracks are distributed in the arch foot and the tunnel floor area. Firstly, the TE on the outer surface of the tunnel structure where the lining thickness is insufficient leads to the fracture 1, and wrinkles appear on the inner surface of the tunnel structure. Fracture 2 originates from the inner surface of the crown, showing a distinct opening trend, and is accompanied by local spalling in the later stage of expansion. With the increase in load, the wrinkling phenomenon on the inner surface structure of the lining corresponding to the left shoulder becomes more obvious, forming through fracture 3. The cracks at the arch feet on both sides and the cracks in the middle of the tunnel floor converge on the inner side of the structure, that is, cracks 4, 5, and 6 converge, causing the tunnel floor to be crushed and damaged. Overall, compared with the crack phenomena observed within the defect range of 60°, the cracks are more significant in terms of density, propagation length, depth, and potential threat to the structure.
When the ratio of insufficient lining thickness is 50% and the defect range is 90°, the crack distribution and failure mode of the straight-wall tunnel structure can be presented in Figure 9. It should be pointed out that in this model, the lining and the surrounding rock are in contact in the insufficient thickness zone. It is noted that several main fractures occur in the straight-wall linings. Among them, 4 cracks appear in the area where the lining thickness is insufficient, and 3 main cracks occur at the arch feet and the tunnel floor. Specifically, crack 1 appears on the inner surface of the structure due to the TE, slightly below the left shoulder. As the load increases, the areas with insufficient lining thickness are significantly compressed, resulting in the successive appearance of 2, 3, and 4 on the inner surface of the lining. In addition, cracks 5, 6, and 7 occur at the positions of the arch feet and the tunnel floor. Particularly noteworthy is that the lining failure at the insufficient thickness section becomes more complex. The deformation at the insufficient thickness area intensifies significantly with the increase in load, causing crack 2 and crack 3 to intersect and resulting in local spalling of the insufficient thickness section in the lining structure. In the areas where the lining thickness is insufficient, the deformation gradually intensifies, resulting in circumferential cracks. The propagation of cracks severely undermines the integrity of the structure, especially when cracks 2, 3 and 4 eventually penetrate completely, resulting in a large-scale spalling.
As for the ratio of insufficient lining thickness is 50% and the defect range is 90°, the failure mode of the lining can be presented in Figure 10. It should be indicated that the lining and the surrounding rock in this section are not in contact at the insufficient lining thickness zone. As the load increases, fractures 1, 2, 3 and 4 successively form in areas with insufficient thickness. Since the surrounding rock and the lining do not come into direct contact in the defect area, local voids are formed. The existence of voids leads to a tendency for the defect area to deform towards the surrounding rock, which results in significant TE on the outer side of the surrounding rock, thereby causing the formation of fractures 1 and 2. On the contrary, in the area with insufficient thickness at the edge, the lining is subjected to obvious CE, resulting in the formation of fractures 3 and 4. Both fractures 5 and 7 occur on the outer surface of the lining, while fracture 6 appears on the inner surface of the lining, which is caused by the uplift of the tunnel floor. As the load continues to increase, a connecting crack forms between fractures 2 and 3. Under continuous loading, the defective parts of the structure come into partial contact with the surrounding rock, generating compressive action within the structure. This led to significant deformation at fracture 3, resulting in fracture failure at this location. Subsequently, the inward deformation of the lining became increasingly obvious, and the depth of the cracks at the arch feet and tunnel floor gradually increased.

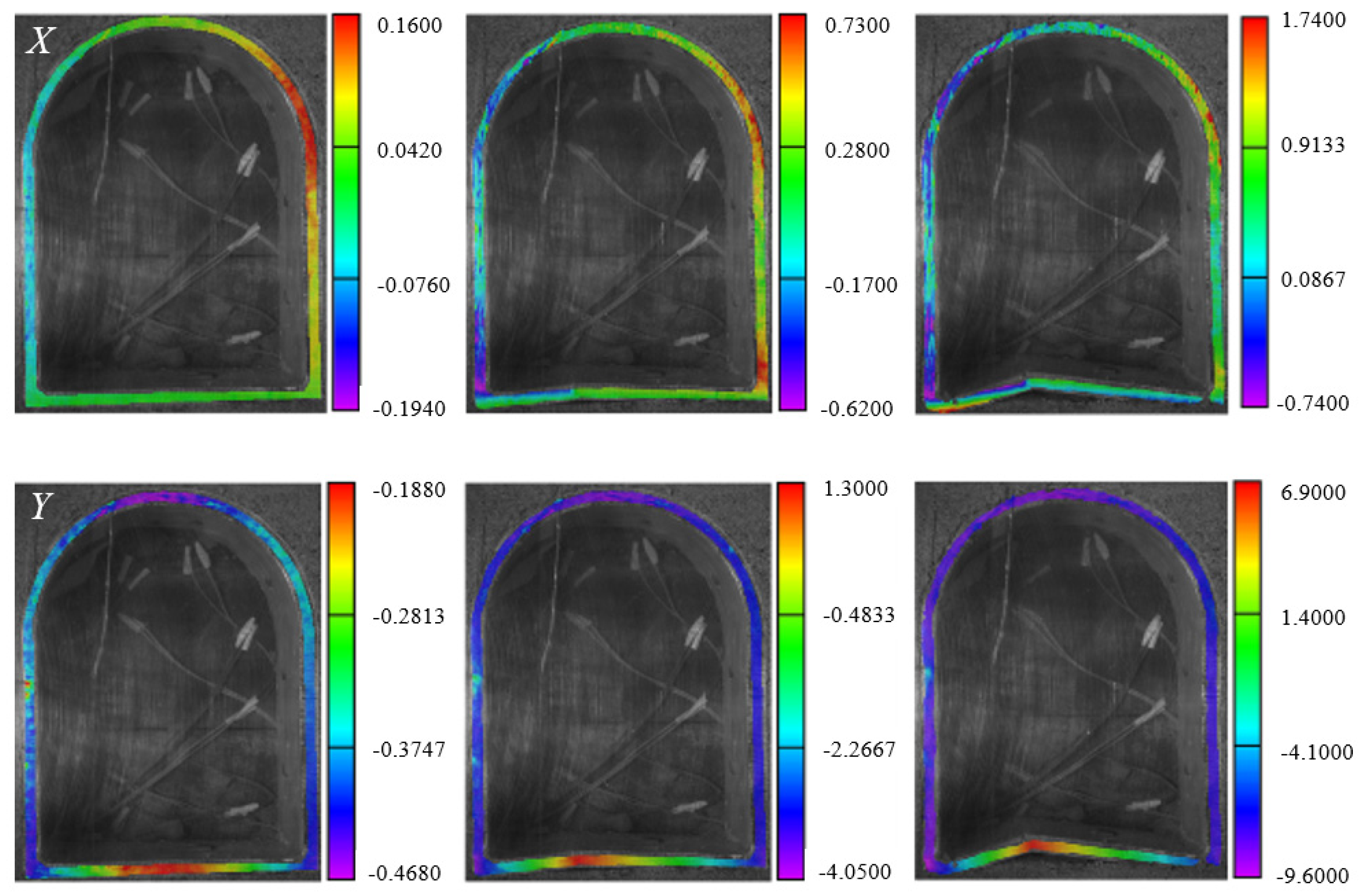
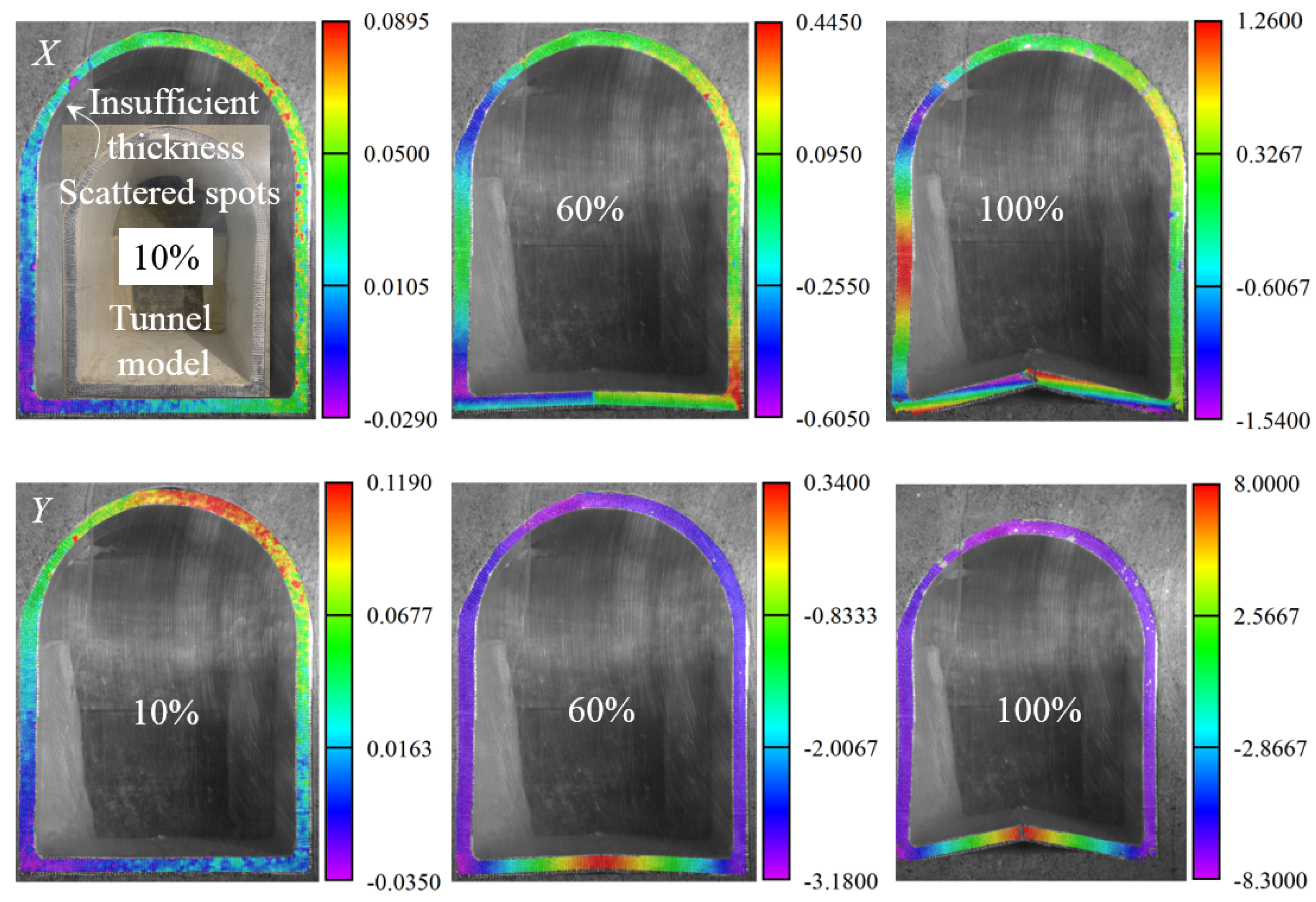
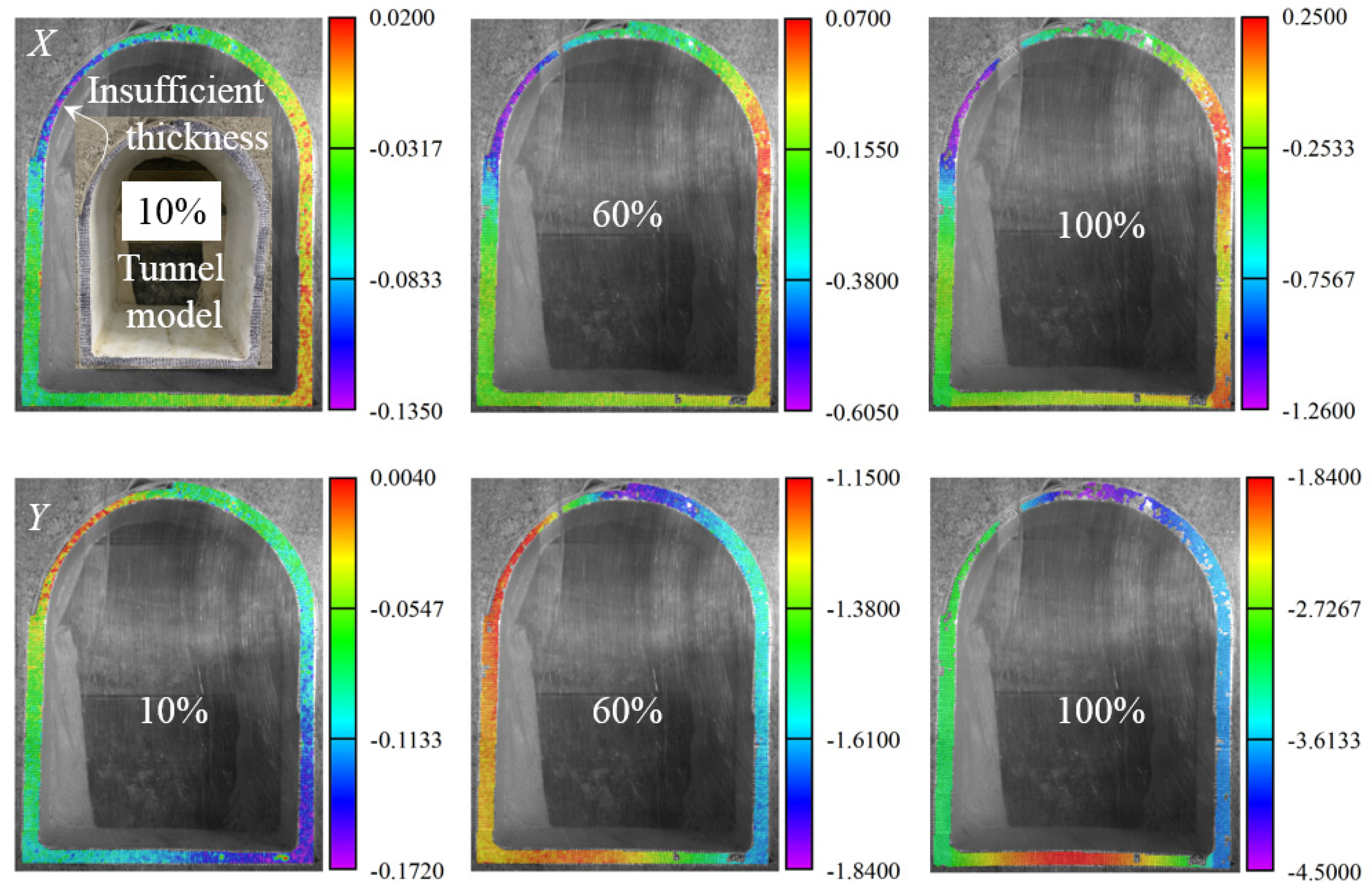
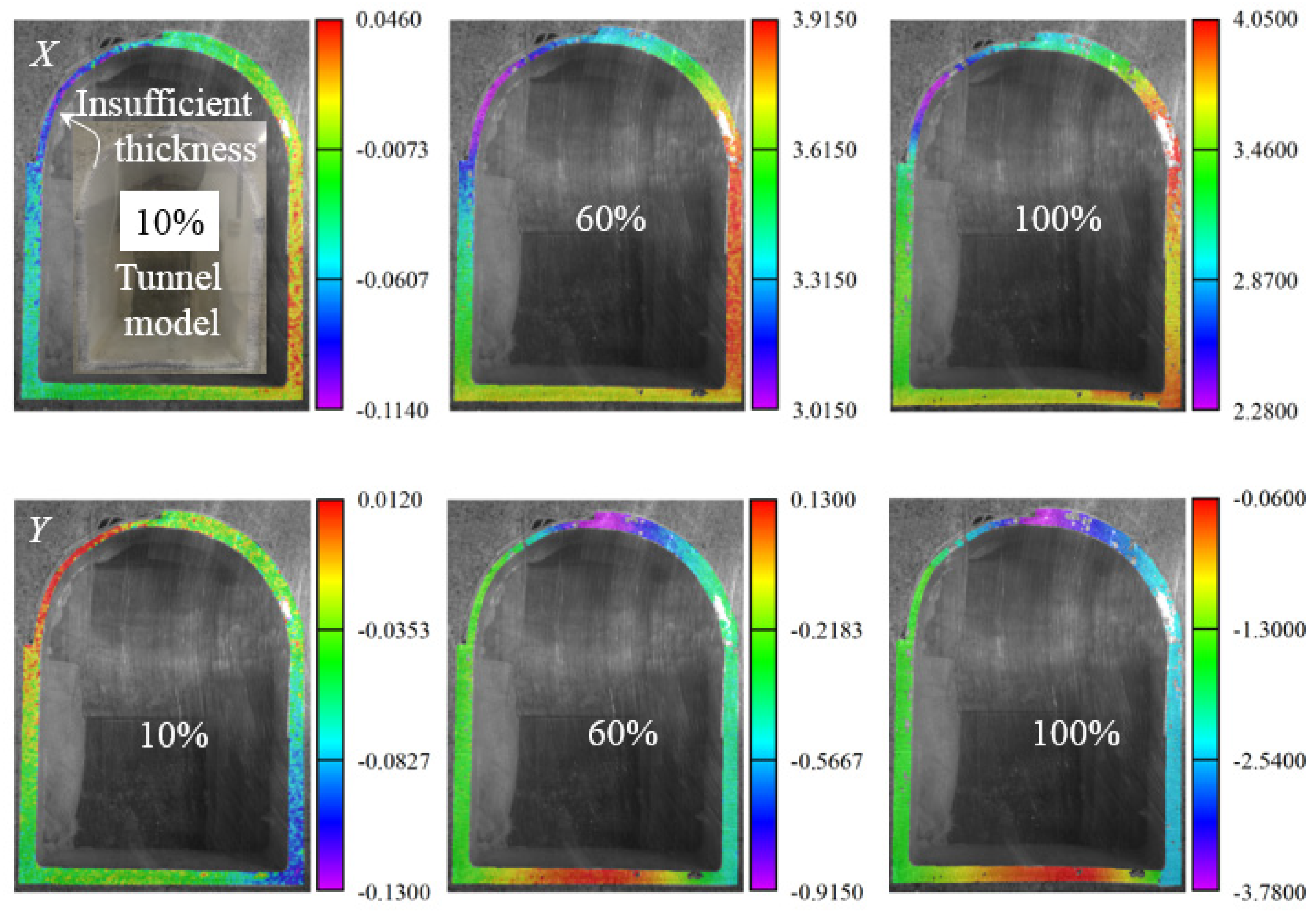
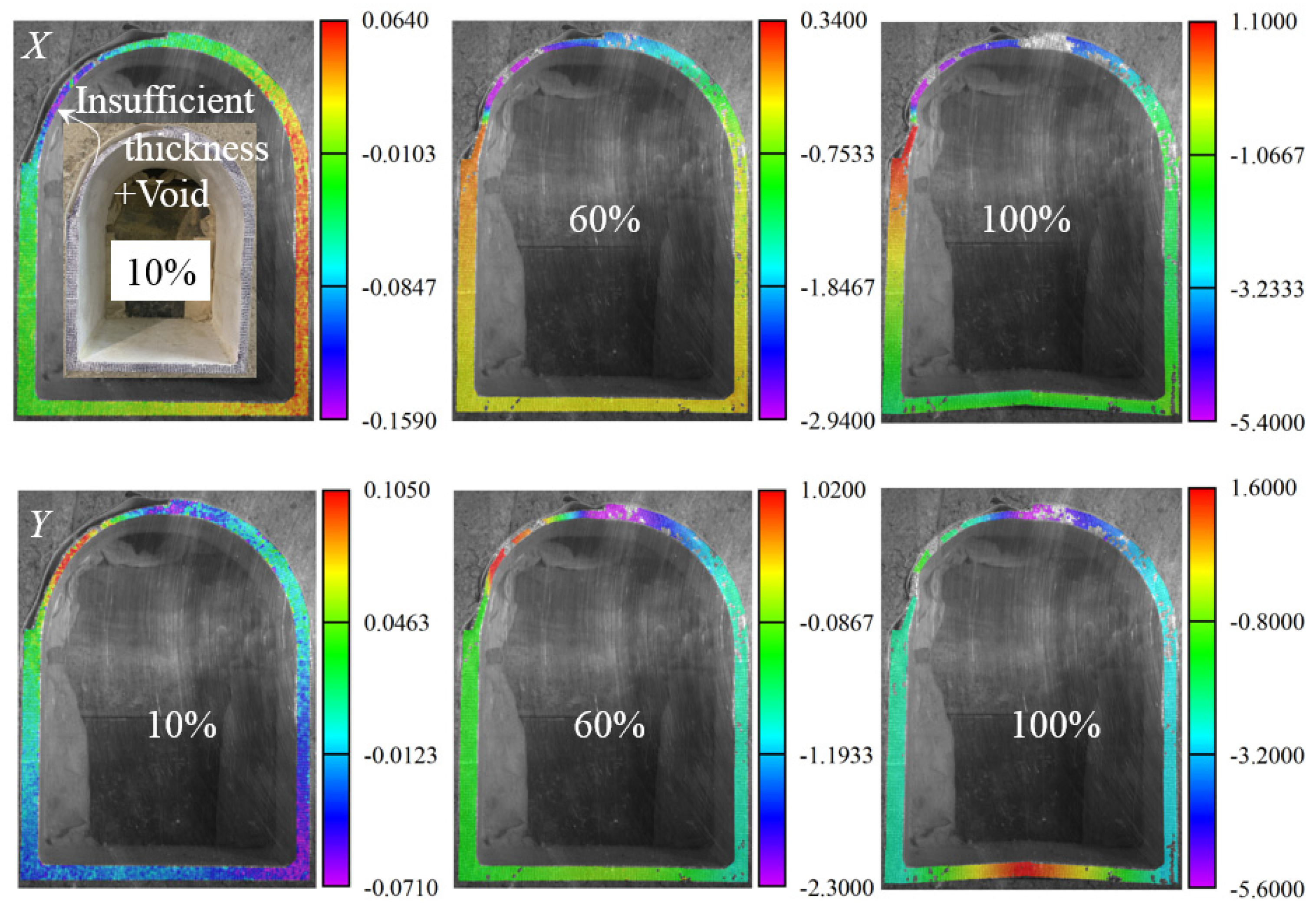
3.2. Deformation Behaviors

In this section, the evolution of the displacement in the straight-wall tunnel lining was investigated. The displacement results at loading levels of 10%, 60% and 100% were presented. For each case, the displacement fields were described separately from the perspectives of both the X and Y directions. The deformation characteristics of straight-wall tunnel linings without defects can be shown in Figure 11. When the loading level is 10%, the deformation of the lining in the X direction is mainly concentrated at the shoulder and straight-wall positions. The displacement gradually decreases to both sides at the shoulder, indicating that the structure deforms from both sides to the outer side. As the load continues to increase, the displacement becomes uneven, mainly concentrated at the top and bottom of the straight-wall. When the loading level increases from 60% to 100%, the displacement increases significantly and the structural deformation becomes more obvious. In addition, from the perspective of displacement characteristics in the Y direction, as the load increases, the tunnel floor warps upward and undergoes significant deformation, leading to structural fracture of the tunnel floor.
When the ratio of insufficient lining thickness is 30% and the defect range is 60°, the deformation characteristics of straight-wall tunnel linings can be shown in Figure 12. From the perspective of X direction, as the load increases, the structure deforms towards the interior of the lining where the lining thickness is insufficient. During the initial loading stage, the outward deformation of the structures on both sides relative to the lining is relatively small. With the continuous increase in the load, displacement concentration occurs on the left side wall, resulting in significant deformation in this area. As shown in the Y-direction, the displacement is most obvious at the tunnel floor. Due to the compression of the structures on both sides, the tunnel floor protrudes significantly inward. In addition, the displacements at other positions increase with the increase in the loading.
When the ratio of insufficient lining thickness is 30% and the defect range is 90°, the deformation characteristics of straight-wall tunnel linings can be shown in Figure 13. It can be seen that in the X direction, the displacement of the lining gradually increases as the load intensifies. The structure on the right side of the lining basically deforms in the positive X direction. The displacement characteristics in the Y direction can also be shown in Figure 13. As the load further increases, the structure at the insufficient lining thickness zone deforms towards the negative Y-direction, exhibiting substantial displacement changes.
When the ratio of insufficient lining thickness is 50% and the defect range is 90°, the deformation characteristics of straight-wall tunnel linings can be shown in Figure 14. The variation law of displacement in the X direction is basically similar to that observed when the ratio of insufficient lining thickness is 30%. However, the increase in the ratio of insufficient lining thickness leads to a further reduction in the local structural stiffness, thereby causing a decrease in the load-bearing capacity of the left structure and also an increase in the displacement of the right structure. Furthermore, from the Y direction displacement distribution, as the load increases, the deformation near the defect transitions into the interior of the lining.
When the lining and the surrounding rock do not come into contact in the defective zone, the ratio of insufficient lining thickness is 50%, and the defect range is 90°, the deformation characteristics of straight-wall tunnel linings can be shown in Figure 15. It is evident that combined defects significantly influence the deformation behavior. The presence of insufficient thickness reduces the local structural stiffness, resulting in pronounced changes in deformation values at the defect location as the load increases. The side walls on both sides deform towards the inner lining, and the displacement change on the left side is basically greater than that on the right side. When the lining structure at the void location comes into contact with the surrounding rock, the direction of deformation changes. Other areas exhibiting significant deformation are primarily the crown and the tunnel floor.

4. Discussion

In this section, the fracture patterns of tunnel structure with insufficient lining thickness were discussed and presented in Figure 16. The perspective here unfolds along the tunnel floor, focusing on clarifying the distribution characteristics of lining cracks and their relationship with the distribution of insufficient thickness. From the displacement distribution of lining structure, the deformation is affected by the weakening of the local stiffness of the lining structure, forming a significantly large deformation area (LDA). Meanwhile, the degree of lining spalling is significantly affected by the characteristics of the defects. Specifically, case 4 exhibits extensive spalling, while cases 2 and 3 show only local spalling. Although the presence of the void in case 5 suppresses spalling to some extent within the defect zone, it leads to a significant breakage phenomenon. In addition, at locations with insufficient lining thickness, the significant reduction in stiffness makes these areas more prone to cracking compared to other regions. Concretely, the number of main fractures in the lining at the defect area is 2, 3, and 4, respectively, when the range of insufficient lining thickness is 60°, 90° (defect ratio is 30%), and 90° (defect ratio is 50%). Furthermore, significant cracking occurs at the arch feet; thus, both the defect range and ratio have an insignificant impact on cracking at the arch foot for straight-wall tunnels. Consequently, the higher the defect ratio, the more prone the defective zone is to spalling; the larger the defect range, the more significant the spalling within the defect zone. In addition, the larger the defect area, the more cracks will appear in the defect area.

5. Conclusions

In this paper, a comprehensive investigation on the fracture behavior of straight-wall tunnels with insufficient lining thickness was conducted. The main conclusions can be drawn as follows:
(1)
Insufficient lining thickness leads to significant changes in the lining failure mode of straight-wall tunnels. As the ratio of insufficient thickness increases or the range of insufficient thickness increases, the failure mode gradually becomes more complex. The area with insufficient lining thickness becomes the core area of fracture, accompanied by phenomena such as spalling and crushing.
(2)
Whether the defect comes into contact with the surrounding rock significantly affects the failure characteristics. In cases where the defect does not come into contact with the surrounding rock, a combination of voids and insufficient thickness is formed, resulting in the superposition of stress concentration effects in the defect area. The tensile effect formed by the voids interacts with the shear failure caused by insufficient thickness, forming a relatively complex failure mode.
(3)
The ratio and range of insufficient lining thickness significantly alter the deformation characteristics of the straight-wall tunnel structure. In areas with insufficient thickness, the displacement changes are more obvious, which is prone to induce large deformation areas, and the deformation basically increases with the increase in the ratio and range of insufficient lining thickness.
(4)
The failure mechanism of lining structures with insufficient thickness begins with tensile-shear failure at defective areas, progressively propagates to compressive failure at the arch foot and tensile failure in the tunnel floor, ultimately forming a collaborative failure mode through the combined action of various components.

Author Contributions

W.H.: Writing—original draft, Software, Data curation, Funding acquisition. X.D.: Writing—original draft, Data curation. Y.D.: Writing—review & editing, Methodology, Conceptualization, Funding acquisition. J.Y.: Data curation, Investigation. B.H.: Data curation, Investigation. H.L.: Data curation, Investigation. All authors have read and agreed to the published version of the manuscript.

Funding

This work described in this paper is fully funded by the Anhui Provincial Natural Science Foundation (grant No. 2508085QE198); Anhui Province Housing Urban Rural Development Science Technology Plan Project (grant No. 2025-YF013); Natural Science Research Project of Colleges and Universities in Anhui Province (grant No. 2024AH050107); Wuhu Science and Technology Plan Project (grant No. 2024kj030); the Start Fund of Talent Introduction of Anhui Polytechnic University (grant No. 2023YQQ016).

Data Availability Statement

Data will be made available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Wang, Y.; Zhang, Y.J.; Chen, L.; Zhu, X.M.; Huang, X.; Xu, H.; Zhang, Z.; Luo, Z.M. Mechanical characterization and dynamic fracture behavior of twin straight-wall-top-arch tunnels under impact loading. Theo. Appl. Fract. Mec. 2025, 139, 105042. [Google Scholar] [CrossRef]
  2. Gao, J.; Wang, X.S.; Cong, Y.; Li, Q.Q.; Pan, Y.Q.; Ding, X.L. Critical Failure Characteristics of a Straight-Walled Arched Tunnel Constructed in Sandstone under Biaxial Loading. Processes 2024, 12, 841. [Google Scholar] [CrossRef]
  3. Fan, S.Y.; Jia, W.R.; Xie, J.S.; Feng, Z.N.; Tian, S.S.; Li, S.G. Study on the disaster mechanism and treatment measures of invert uplift cracking of in-service tunnel-A case research. Constr. Build. Mater. 2025, 471, 140772. [Google Scholar] [CrossRef]
  4. Asakura, T.; Kojima, Y. Tunnel maintenance in Japan. Tunn. Undergr. Space Technol. 2003, 18, 161–169. [Google Scholar] [CrossRef]
  5. Wang, B.X.; He, N.N.; Xu, F.; Du, Y.L.; Xu, H.B. Visual detection method of tunnel water leakage diseases based on feature enhancement learning. Tunn. Undergr. Space Technol. 2024, 153, 106009. [Google Scholar] [CrossRef]
  6. Liu, D.J.; Wang, F.; Hu, Q.F.; Hang, H.W.; Zuo, J.P.; Tian, C.; Zhang, D.M. Structural responses and treatments of shield tunnel due to leakage: A case study. Tunn. Undergr. Space Technol. 2020, 103, 103471. [Google Scholar] [CrossRef]
  7. Li, J.W.; Xu, F.; Du, Y.L.; Liu, X.T.; Ma, J.W.; Zhu, S.N. Evaluation method of tunnel cracking disease under biased pressure based on enhanced image fractal features. Constr. Build. Mater. 2024, 441, 137530. [Google Scholar] [CrossRef]
  8. Hao, S.J.; Fei, R.Z. Optimisation Study on Crack Resistance of Tunnel Lining Concrete Under High Ground Temperature Environment. Geotech. Geol. Eng. 2022, 40, 3985–4006. [Google Scholar] [CrossRef]
  9. Ma, W.B.; Chai, J.F. Development Status of Disease Detection, Monitoring, Evaluation and Treatment Technology of railway Tunnels in Operation. Tunn. Constr. 2019, 39, 1553–1562. [Google Scholar] [CrossRef]
  10. Li, B.; Lei, M.F.; Li, W.H. Safety influence of operating highway tunnel caused by sturcture disease. J. Railw. Sci. Eng. 2011, 8, 40–45. [Google Scholar]
  11. Ye, Z.J. The Influence of Poor Contact State between Tunnel Lining and Surrounding Rock on the Safety of Lining Structure. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
  12. Zhang, X.; Su, J.; Xu, Y.J.; Min, B. Experimental and numerical investigation the effects of insufficient concrete thickness on the damage behaviour of multi-arch tunnel. Structures 2021, 33, 2628–2638. [Google Scholar] [CrossRef]
  13. Zhao, Y.C.; Li, Y.L.; Wei, M.; Duan, J.C. Discussion on causes of and preventive measures against tunnel lining voids and inadequate thickness. Modern Tunn. Technol. 2019, 56, 40–43. [Google Scholar] [CrossRef]
  14. Li, K.; Xie, X.Y.; Zhai, J.L.; Zhou, B.; Huang, C.F.; Wang, C. Tunnel lining defects identification using TPE-CatBoost algorithm with GPR data: A model test study. Tunn. Undergr. Space Technol. 2025, 157, 106275. [Google Scholar] [CrossRef]
  15. Han, W.; Jiang, Y.J.; Wang, G.; Liu, C.Z.; Koga, D. Review of health inspection and reinforcement design for typical tunnel quality defects of voids and insufficient lining thickness. Tunn. Undergr. Space Technol. 2023, 137, 105110. [Google Scholar] [CrossRef]
  16. Li, M.; Chen, H.K. Experimental research on tunnel health criterion of deficiency in lining thickness. Rock Soil Mech. 2011, 32, 570–577. [Google Scholar] [CrossRef]
  17. Zhang, C.P.; Zhang, X.; Feng, G.; Zhang, D.L. Influence of insufficient lining thickness on the safety of a tunnel structure. Modern Tunn. Technol. 2017, 54, 137–143, 169. [Google Scholar] [CrossRef]
  18. Lin, J.; Zhu, J.L.; Huang, S.L.; Xiao, Q.; Huang, Y.B.; Lei, S.D.; Zhou, P. Numerical study on tunnel deformation under local thickness reduction in tunnel linings and destruction prediction. China J. Geotech. Eng. 2024, 46, 177–182. [Google Scholar] [CrossRef]
  19. Chen, X.; Lin, Z.; Feng, W.L.; Yang, H.Y.; Xiang, Y.H. Evolution of structural safety for tunnel arch crown linings under the coupled influence of void and insufficient thickness. Structures 2024, 68, 107125. [Google Scholar] [CrossRef]
  20. Wang, S.M.; Wang, Y.; Lin, Z.Y.; Song, Z.H.; Wang, X.M.; Peng, X.Y. Analysis of the influence of the thickness insufficiency in secondary lining on the mechanical properties of Double-layer lining of shield tunnel. Eng. Fail. Anal. 2022, 141, 106663. [Google Scholar] [CrossRef]
  21. Liu, J.; Zhang, X.S.; Lv, G.H.; Wang, K.; Han, B.; Xie, Q.Y. Study on Crack Development of Concrete Lining with Insufficient Lining Thickness Based on CZM Method. Materials 2021, 14, 7862. [Google Scholar] [CrossRef] [PubMed]
  22. Han, W.; Jiang, Y.J.; Li, N.B.; Luan, H.J.; Wu, X.L. Study on cracking behavior of tunnel linings with the diseases of void and lining insufficient thickness. IOP Conf. Ser. Earth Environ. Sci. 2019, 861, 042113. [Google Scholar] [CrossRef]
  23. Liu, S.H.; Shi, Y.; Sun, R.; Yang, J.S. Damage behavior and maintenance design of tunnel lining based on numerical evaluation. Eng. Fail. Anal. 2020, 109, 104209. [Google Scholar] [CrossRef]
  24. Gong, Y.P. Study on the Tunnel Structure Safety under the Impact of the Lining Thickness Deficiency. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
  25. Sui, J.H.; Che, Z.J.; Li, W.H.; Zhang, S.L.; Yuan, C.F.; Cheng, D.G. Study on the structural cracking mechanism under the influence of voids behind straight-wall tunnel lining. J. Qingdao Univ. Technol. 2022, 43, 11–19. [Google Scholar]
  26. Xu, Y.; Fan, Y.; Wang, Q.Y.; Zhou, S.W. Fracture process analysis of polypropylene fiber reinforced concrete based on DIC. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2024, 52, 103–111. [Google Scholar] [CrossRef]
  27. Ge, Y.X.; Ren, G.F.; Li, X.P.; Zhang, C.; Zhang, L.W.; Xu, C.; Zhang, C.R. Study on mechanical properties and failure behavior of jointed gypsum rock under uniaxial compression using AE and DIC techniques. Results in Eng. 2025, 27, 106024. [Google Scholar] [CrossRef]
  28. Wang, P.T.; Liu, Q.R.; Zhang, Y.S.; Huang, Z.J. Identifying rock fracture precursor by multivariate analysis based on the digital image correlation technique. Theor. Appl. Fract. Mec. 2023, 126, 103987. [Google Scholar] [CrossRef]
  29. Li, D.Y.; Zhu, Q.Q.; Zhou, Z.L.; Li, X.B.; Ranjith, P.G. Fracture analysis of marble specimens with a hole under uniaxial compression by digital image correlation. Eng. Fract. Mech. 2017, 183, 109–124. [Google Scholar] [CrossRef]
  30. Zhu, K.Y.; Liu, Y.Z.; Ren, X.C.; Pan, B. Panoramic deformation measurement and crack identification in concrete with deep-learning-based multi-camera DIC. Measurement 2025, 256, 118133. [Google Scholar] [CrossRef]
  31. Zhu, S.S.; Zhou, Z.F.; Zhang, Z.; Liu, Z.Q.; Hou, X. Evaluation of low-temperature fracture and damage of asphalt concrete using SCB test combined with DIC. Eng. Fract. Mech. 2025, 321, 111135. [Google Scholar] [CrossRef]
  32. Ma, W.; Gao, D.Y.; Ding, C.; Wang, L.; Tang, J.Y. Whole process analysis on splitting tensile behavior and damage mechanism of 3D/4D/5D steel fiber reinforced concrete using DIC and AE techniques. Constr. Build. Mater. 2024, 457, 139295. [Google Scholar] [CrossRef]
  33. Zhu, Y.T.; Zhang, Z.X.; Zhu, Y.F.; Huang, X.; Zhuang, Q.W. Capturing the cracking characteristics of concrete lining during prototype tests of a special-shaped tunnel using 3D DIC photogrammetry. Eur. J. Environ. Civ. En. 2018, 22, 179–199. [Google Scholar] [CrossRef]
  34. Che, Z.J. Study on the Safety of the Straight Wall Tunnel under the Condition of Void behind the Lining. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2020. [Google Scholar] [CrossRef]
  35. Guo, R.; Zhang, M.; Xie, H.; He, C.; Fang, Y.; Wang, S. Model test study of the mechanical characteristics of the lining structure for an urban deep drainage shield tunnel. Tunn. Undergr. Space Technol. 2019, 91, 103014. [Google Scholar] [CrossRef]
  36. Min, B. Study on the Cracking Characteristic of Asymmetric Double-Arch Tunnel Linings and Its Influence on Structural Bearing Capacity. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar] [CrossRef]
Processes 13 03909 g001
Figure 1. Cracking phenomenon of straight-wall tunnel linings [34]: (a) cracking at the crown and shoulder; (b) cracking at the side wall.
Figure 1. Cracking phenomenon of straight-wall tunnel linings [34]: (a) cracking at the crown and shoulder; (b) cracking at the side wall.
Processes 13 03909 g001
Processes 13 03909 g002
Figure 2. Preparation and testing of similar materials: (a) Water; (b) Gypsum material; (c) Strength test of gypsum test.
Figure 2. Preparation and testing of similar materials: (a) Water; (b) Gypsum material; (c) Strength test of gypsum test.
Processes 13 03909 g002
Processes 13 03909 g003
Figure 3. Experimental loading device.
Figure 3. Experimental loading device.
Processes 13 03909 g003
Processes 13 03909 g004
Figure 4. Preparation process of the tunnel model with insufficient lining thickness: (a) Lining mold; (b) Lining model with insufficient thickness; (c) Fabrication of speckle pattern; (d) Filling the surrounding rock; (e) Place the lining at the designed position; (f) Tunnel model.
Figure 4. Preparation process of the tunnel model with insufficient lining thickness: (a) Lining mold; (b) Lining model with insufficient thickness; (c) Fabrication of speckle pattern; (d) Filling the surrounding rock; (e) Place the lining at the designed position; (f) Tunnel model.
Processes 13 03909 g004
Processes 13 03909 g005
Figure 5. Schematic of defective linings: (a) Case 2; (b) Case 3; (c) Case 4; (d) Case 5.
Figure 5. Schematic of defective linings: (a) Case 2; (b) Case 3; (c) Case 4; (d) Case 5.
Processes 13 03909 g005
Processes 13 03909 g006
Figure 6. Fracture characteristics of lining structure without defects (Case 1).
Figure 6. Fracture characteristics of lining structure without defects (Case 1).
Processes 13 03909 g006
Processes 13 03909 g007
Figure 7. Fracture characteristics of Case 2.
Figure 7. Fracture characteristics of Case 2.
Processes 13 03909 g007
Processes 13 03909 g008
Figure 8. Fracture characteristics of Case 3.
Figure 8. Fracture characteristics of Case 3.
Processes 13 03909 g008
Processes 13 03909 g009
Figure 9. Fracture characteristics of Case 4.
Figure 9. Fracture characteristics of Case 4.
Processes 13 03909 g009
Processes 13 03909 g010
Figure 10. Fracture characteristics of Case 5.
Figure 10. Fracture characteristics of Case 5.
Processes 13 03909 g010
Processes 13 03909 g011
Figure 11. Deformation behavior of straight-wall tunnel linings without defects.
Figure 11. Deformation behavior of straight-wall tunnel linings without defects.
Processes 13 03909 g011
Processes 13 03909 g012
Figure 12. Deformation behavior of case 2.
Figure 12. Deformation behavior of case 2.
Processes 13 03909 g012
Processes 13 03909 g013
Figure 13. Deformation behavior of case 3.
Figure 13. Deformation behavior of case 3.
Processes 13 03909 g013
Processes 13 03909 g014
Figure 14. Deformation behavior of case 4.
Figure 14. Deformation behavior of case 4.
Processes 13 03909 g014
Processes 13 03909 g015
Figure 15. Deformation behavior of case 5.
Figure 15. Deformation behavior of case 5.
Processes 13 03909 g015
Processes 13 03909 g016aProcesses 13 03909 g016b
Figure 16. Fracture modes of straight-wall tunnels with insufficient lining thickness: (a) case 1; (b) case 2; (c) case 3; (d) case 4; (e) case 5.
Figure 16. Fracture modes of straight-wall tunnels with insufficient lining thickness: (a) case 1; (b) case 2; (c) case 3; (d) case 4; (e) case 5.
Processes 13 03909 g016aProcesses 13 03909 g016b
Table 1. Physical and mechanical parameters of linings.
Table 1. Physical and mechanical parameters of linings.
MechanicalElastic
Modulus (GPa)		Compressive Strength (MPa)Tensile Strength (MPa)Bulk Density (kN/m3)Poisson’s Ratio
Original Prototype30.021.02.01250.2
Table 2. Composition of filling materials of the surrounding rock.
Table 2. Composition of filling materials of the surrounding rock.
Material150 Mesh Barite Powder600 Mesh
Barite Powder		10 Mesh
Quartz Sand		40 Mesh Quartz Sand
Weight ratio16.248.521.610.7
Table 3. Physical and mechanical parameters of the surrounding rock.
Table 3. Physical and mechanical parameters of the surrounding rock.
MaterialsElastic Modulus/GPaCohesion/
MPa		Bulk Density/
kN/m3		Internal Friction Angle/°Poisson’s Ratio
Original
Prototype		0.8518018220.32
Model0.0214.618220.32
Table 4. Design of experimental scheme.
Table 4. Design of experimental scheme.
CasesRatio of Insufficient Lining Thickness Defect RangeContact Stage
Case100Yes
Case 20.360°Yes
Case 30.390°Yes
Case 40.590°Yes
Case 50.590°No
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Han, W.; Du, X.; Du, Y.; Yue, J.; Huang, B.; Liu, H. Experimental Investigation on Fracture Behaviors of Straight-Wall Tunnels with Defects of Insufficient Lining Thickness. Processes 2025, 13, 3909. https://doi.org/10.3390/pr13123909

AMA Style

Han W, Du X, Du Y, Yue J, Huang B, Liu H. Experimental Investigation on Fracture Behaviors of Straight-Wall Tunnels with Defects of Insufficient Lining Thickness. Processes. 2025; 13(12):3909. https://doi.org/10.3390/pr13123909

Chicago/Turabian Style

Han, Wei, Xuze Du, Yihan Du, Jiapeng Yue, Bo Huang, and Hui Liu. 2025. "Experimental Investigation on Fracture Behaviors of Straight-Wall Tunnels with Defects of Insufficient Lining Thickness" Processes 13, no. 12: 3909. https://doi.org/10.3390/pr13123909

APA Style

Han, W., Du, X., Du, Y., Yue, J., Huang, B., & Liu, H. (2025). Experimental Investigation on Fracture Behaviors of Straight-Wall Tunnels with Defects of Insufficient Lining Thickness. Processes, 13(12), 3909. https://doi.org/10.3390/pr13123909

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop