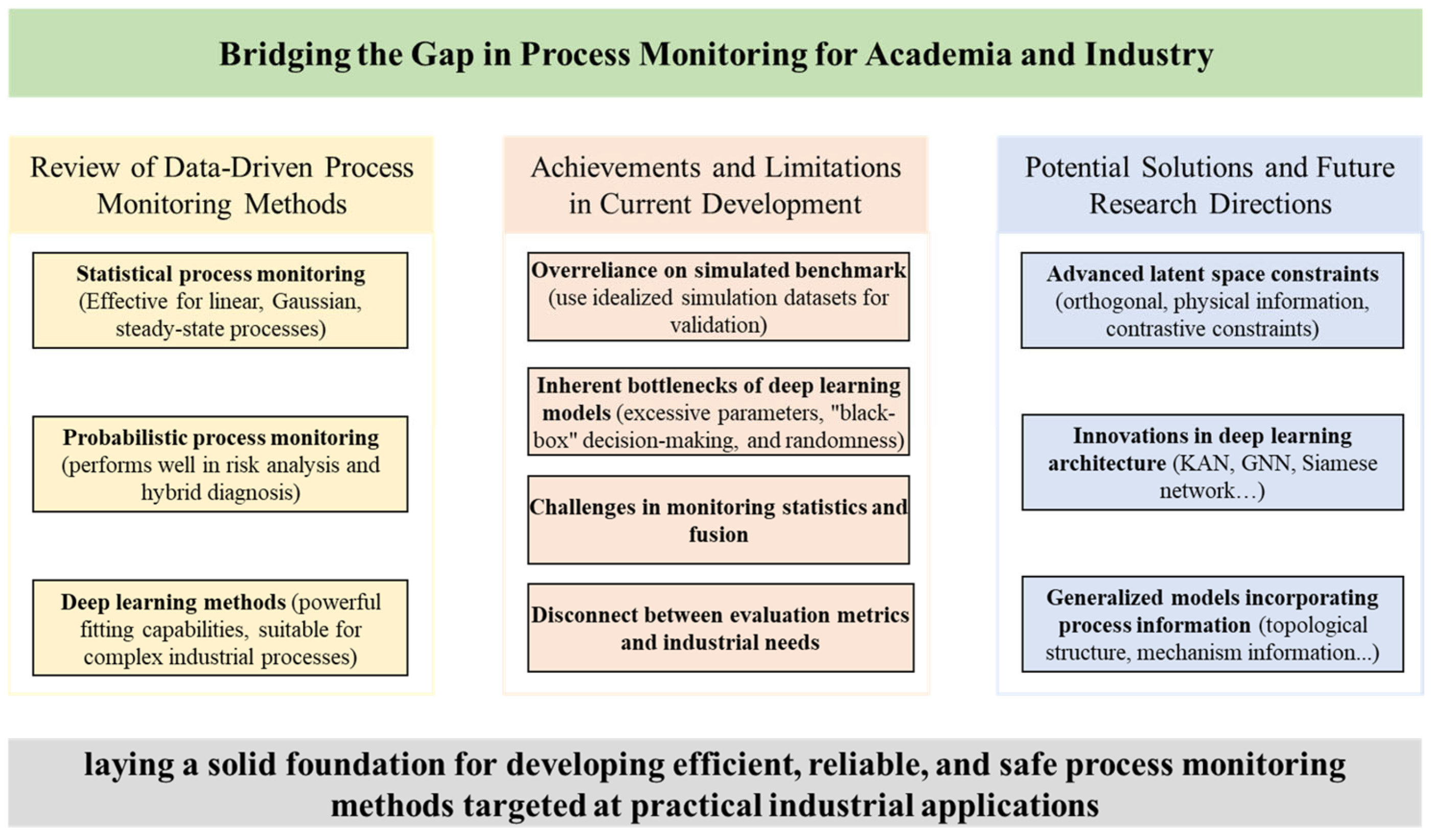
Bridging the Gap in Chemical Process Monitoring: Beyond Algorithm-Centric Research Toward Industrial Deployment
Abstract
1. Introduction
2. Data-Driven Process Monitoring
2.1. Statistical Process Monitoring Methods
2.2. Probabilistic Process Monitoring Methods
2.3. Deep Learning Methods
3. Current Limitations and Achievements in the Development of Data-Driven Process Monitoring Models
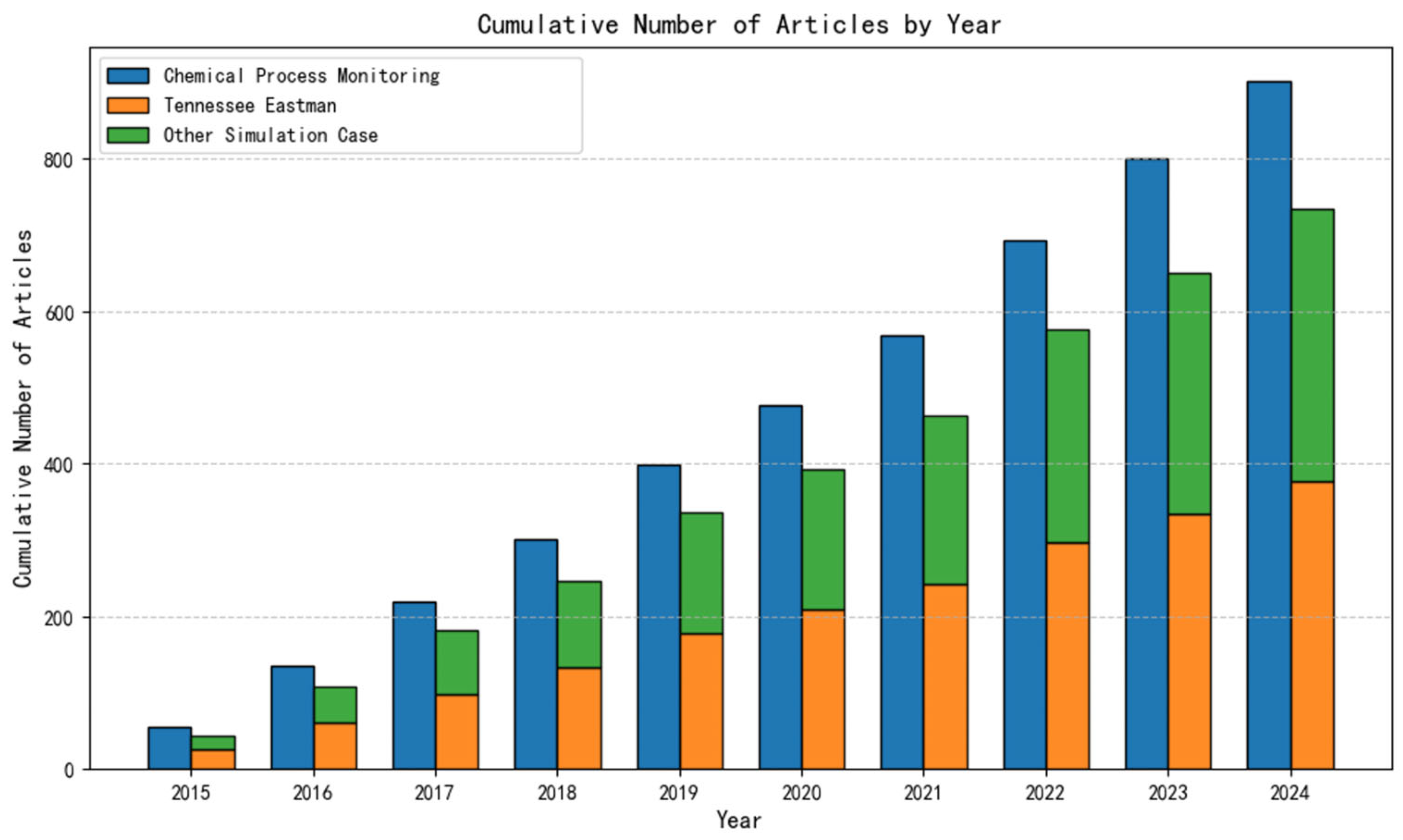
3.1. Overreliance on Simulated Benchmarks
3.2. Limitations of Deep Learning Models in Data-Driven Process Monitoring: Complexity, Interpretability, and the Path Forward
4. Research on the Establishment of Monitoring Statistics
4.1. Establishment of Monitoring Statistics
4.2. Fusion Statistics
4.3. Residual Statistics of Deep Learning Models
5. Evaluation Metrics for Process Monitoring Models
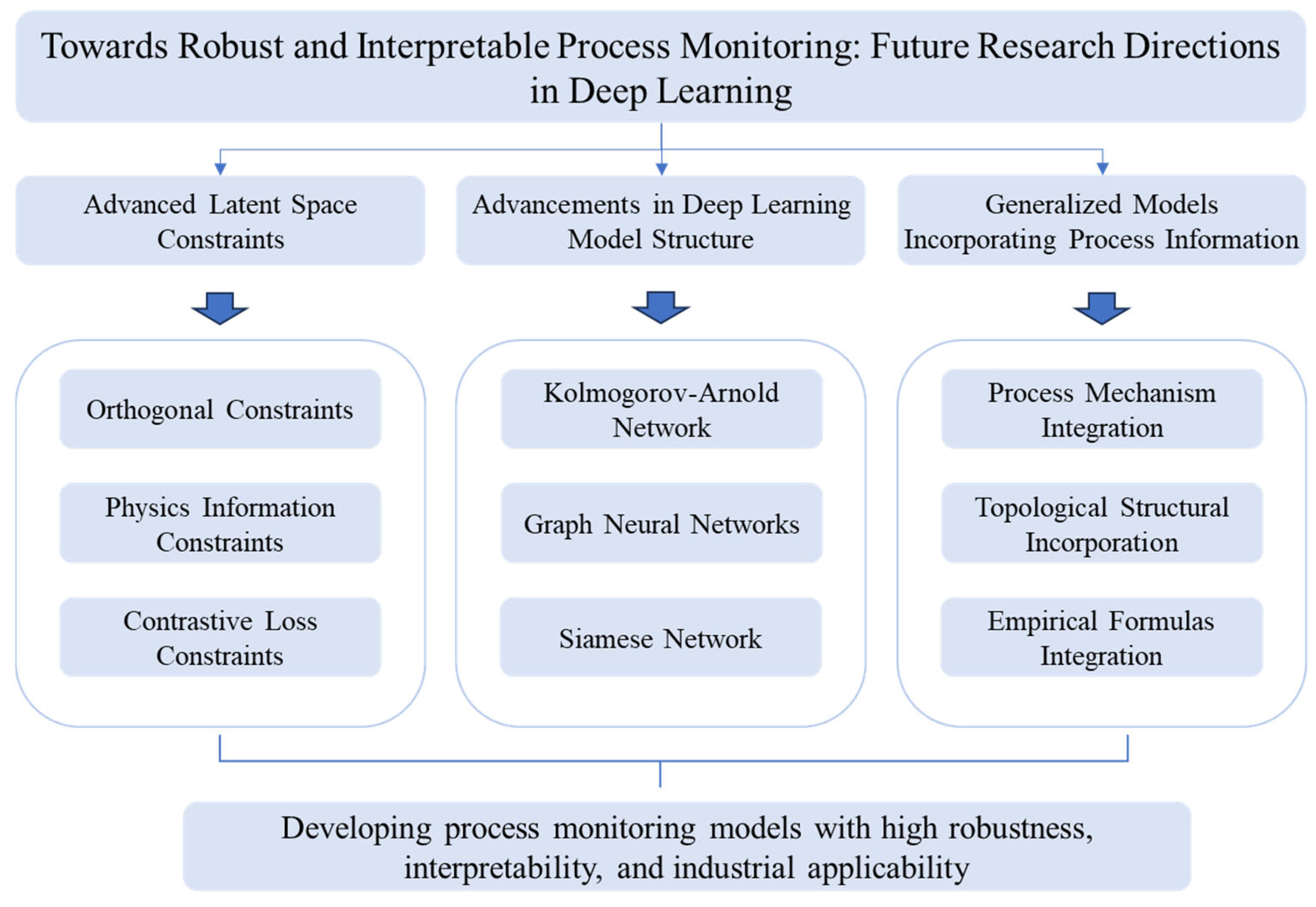
6. Future Research Suggestions
6.1. Advanced Latent Space Constraints for Deep Learning Models
6.2. Advancements in Deep Learning Model Structure for Process Monitoring
6.3. Generalized Models Incorporating Process Information
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, Y.; Wang, H.; Khan, F.; Zhao, J. Abnormal situation management for smart chemical process operation. Curr. Opin. Chem. Eng. 2016, 14, 49–55. [Google Scholar] [CrossRef]
- Isermann, R.; Ballé, P. Trends in the application of model-based fault detection and diagnosis of technical processes. Control Eng. Pract. 1997, 5, 709–719. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H. A Review on Basic Data-Driven Approaches for Industrial Process Monitoring. IEEE Trans. Ind. Electron. 2014, 61, 6418–6428. [Google Scholar] [CrossRef]
- Ge, Z. Review on data-driven modeling and monitoring for plant-wide industrial processes. Chemom. Intell. Lab. Syst. 2017, 171, 16–25. [Google Scholar] [CrossRef]
- Alauddin, M.; Khan, F.; Imtiaz, S.; Ahmed, S. A Bibliometric Review and Analysis of Data-Driven Fault Detection and Diagnosis Methods for Process Systems. Ind. Eng. Chem. Res. 2018, 57, 10719–10735. [Google Scholar] [CrossRef]
- Zhang, H.-D.; Zheng, X.-P. Characteristics of hazardous chemical accidents in China: A statistical investigation. J. Loss Prev. Process Ind. 2012, 25, 686–693. [Google Scholar] [CrossRef]
- Ji, C.; Sun, W. A Review on Data-Driven Process Monitoring Methods: Characterization and Mining of Industrial Data. Processes 2022, 10, 335. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X.; Huang, B. Review and Perspectives of Data-Driven Distributed Monitoring for Industrial Plant-Wide Processes. Ind. Eng. Chem. Res. 2019, 58, 12899–12912. [Google Scholar] [CrossRef]
- Quiñones-Grueiro, M.; Prieto-Moreno, A.; Verde, C.; Llanes-Santiago, O. Data-driven monitoring of multimode continuous processes: A review. Chemom. Intell. Lab. Syst. 2019, 189, 56–71. [Google Scholar] [CrossRef]
- Qin, S.J. Survey on data-driven industrial process monitoring and diagnosis. Annu. Rev. Control 2012, 36, 220–234. [Google Scholar] [CrossRef]
- Kresta, J.V.; MacGregor, J.F.; Marlin, T.E. Multivariate statistical monitoring of process operating performance. Can. J. Chem. Eng. 1991, 69, 35–47. [Google Scholar] [CrossRef]
- MacGregor, J.F. Statistical Process Control of Multivariate Processes. IFAC Proc. Vol. 1994, 27, 427–437. [Google Scholar] [CrossRef]
- Dong, Y.; Qin, S.J. A novel dynamic PCA algorithm for dynamic data modeling and process monitoring. J. Process Control 2018, 67, 1–11. [Google Scholar] [CrossRef]
- Ku, W.; Storer, R.H.; Georgakis, C. Disturbance detection and isolation by dynamic principal component analysis. Chemom. Intell. Lab. Syst. 1995, 30, 179–196. [Google Scholar] [CrossRef]
- Li, G.; Liu, B.; Qin, S.J.; Zhou, D. Dynamic latent variable modeling for statistical process monitoring. IFAC Proc. Vol. 2011, 44, 12886–12891. [Google Scholar] [CrossRef]
- Qin, S.J.; Dong, Y.; Zhu, Q.; Wang, J.; Liu, Q. Bridging systems theory and data science: A unifying review of dynamic latent variable analytics and process monitoring. Annu. Rev. Control 2020, 50, 29–48. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Y.; Huang, D.; Cai, B.; Wang, Q. Rebooting kernel CCA method for nonlinear quality-relevant fault detection in process industries. Process Saf. Environ. Prot. 2021, 149, 619–630. [Google Scholar] [CrossRef]
- Apsemidis, A.; Psarakis, S.; Moguerza, J.M. A review of machine learning kernel methods in statistical process monitoring. Comput. Ind. Eng. 2020, 142, 106376. [Google Scholar] [CrossRef]
- Choi, S.W.; Park, J.H.; Lee, I.-B. Process monitoring using a Gaussian mixture model via principal component analysis and discriminant analysis. Comput. Chem. Eng. 2004, 28, 1377–1387. [Google Scholar] [CrossRef]
- Liu, J.; Liu, T.; Chen, J. Sequential local-based Gaussian mixture model for monitoring multiphase batch processes. Chem. Eng. Sci. 2018, 181, 101–113. [Google Scholar] [CrossRef]
- Tong, C.; Lan, T.; Shi, X. Ensemble modified independent component analysis for enhanced non-Gaussian process monitoring. Control Eng. Pract. 2017, 58, 34–41. [Google Scholar] [CrossRef]
- Lee, J.-M.; Yoo, C.; Lee, I.-B. Statistical process monitoring with independent component analysis. J. Process Control 2004, 14, 467–485. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, C. Exponential Stationary Subspace Analysis for Stationary Feature Analytics and Adaptive Nonstationary Process Monitoring. IEEE Trans. Ind. Inf. 2021, 17, 8345–8356. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C.; Huang, B. Recursive cointegration analytics for adaptive monitoring of nonstationary industrial processes with both static and dynamic variations. J. Process Control 2020, 92, 319–332. [Google Scholar] [CrossRef]
- Rao, J.; Ji, C.; Wang, J.; Sun, W.; Romagnoli, J.A. High-Order Nonstationary Feature Extraction for Industrial Process Monitoring Based on Multicointegration Analysis. Ind. Eng. Chem. Res. 2024, 63, 9489–9503. [Google Scholar] [CrossRef]
- Amin, M.T.; Imtiaz, S.; Khan, F. Process system fault detection and diagnosis using a hybrid technique. Chem. Eng. Sci. 2018, 189, 191–211. [Google Scholar] [CrossRef]
- Weber, P.; Medina-Oliva, G.; Simon, C.; Iung, B. Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas. Eng. Appl. Artif. Intell. 2012, 25, 671–682. [Google Scholar] [CrossRef]
- Amin, M.T.; Khan, F.; Imtiaz, S. Fault detection and pathway analysis using a dynamic Bayesian network. Chem. Eng. Sci. 2019, 195, 777–790. [Google Scholar] [CrossRef]
- Amin, M.T.; Khan, F.; Ahmed, S.; Imtiaz, S. A data-driven Bayesian network learning method for process fault diagnosis. Process Saf. Environ. Prot. 2021, 150, 110–122. [Google Scholar] [CrossRef]
- Amin, M.T.; Khan, F.; Ahmed, S.; Imtiaz, S. A novel data-driven methodology for fault detection and dynamic risk assessment. Can. J. Chem. Eng. 2020, 98, 2397–2416. [Google Scholar] [CrossRef]
- Kong, X.; Ge, Z. Deep Learning of Latent Variable Models for Industrial Process Monitoring. IEEE Trans. Ind. Inf. 2021, 18, 6778–6788. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Shardt, Y.A.W.; Wang, Y.; Yang, C. Deep Learning with Spatiotemporal Attention-Based LSTM for Industrial Soft Sensor Model Development. IEEE Trans. Ind. Electron. 2021, 68, 4404–4414. [Google Scholar] [CrossRef]
- Arunthavanathan, R.; Khan, F.; Ahmed, S.; Imtiaz, S. A deep learning model for process fault prognosis. Process Saf. Environ. Prot. 2021, 154, 467–479. [Google Scholar] [CrossRef]
- Adedigba, S.A.; Khan, F.; Yang, M. Dynamic failure analysis of process systems using neural networks. Process Saf. Environ. Prot. 2017, 111, 529–543. [Google Scholar] [CrossRef]
- Venkatasubramanian, V. The promise of artificial intelligence in chemical engineering: Is it here, finally. AlChE J. 2019, 65, 466–478. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Yin, K.; Kavuri, S.N. A review of process fault detection and diagnosis Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 27, 293–311. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N. A review of process fault detection and diagnosis Part II: Qualitative models and search strategies. Comput. Chem. Eng. 2003, 27, 313–326. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N.; Yin, K. A review of process fault detection and diagnosis Part III: Process history based methods. Comput. Chem. Eng. 2003, 27, 327–346. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Gao, F. Review of Recent Research on Data-Based Process Monitoring. Ind. Eng. Chem. Res. 2013, 52, 3543–3562. [Google Scholar] [CrossRef]
- Melo, A.; Câmara, M.M.; Clavijo, N.; Pinto, J.C. Open benchmarks for assessment of process monitoring and fault diagnosis techniques: A review and critical analysis. Comput. Chem. Eng. 2022, 165, 107964. [Google Scholar] [CrossRef]
- Lee, J.M.; Qin, S.J.; Lee, I.B. Fault detection of non-linear processes using kernel independent component analysis. Can. J. Chem. Eng. 2007, 85, 526–536. [Google Scholar] [CrossRef]
- Kaneko, H.; Arakawa, M.; Funatsu, K. Development of a new soft sensor method using independent component analysis and partial least squares. AlChE J. 2009, 55, 87–98. [Google Scholar] [CrossRef]
- Kano, M.; Hasebe, S.; Hashimoto, I.; Ohno, H. Statistical process monitoring based on dissimilarity of process data. AlChE J. 2002, 48, 1231–1240. [Google Scholar] [CrossRef]
- Fazai, R.; Mansouri, M.; Abodayeh, K.; Nounou, H.; Nounou, M. Online reduced kernel PLS combined with GLRT for fault detection in chemical systems. Process Saf. Environ. Prot. 2019, 128, 228–243. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X. Nonlinear process fault pattern recognition using statistics kernel PCA similarity factor. Neurocomputing 2013, 121, 298–308. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, I.-B. Nonlinear dynamic process monitoring based on dynamic kernel PCA. Chem. Eng. Sci. 2004, 59, 5897–5908. [Google Scholar] [CrossRef]
- Zhou, L.; Li, G.; Song, Z.; Qin, S.J. Autoregressive Dynamic Latent Variable Models for Process Monitoring. IEEE Trans. Control Syst. Technol. 2017, 25, 366–373. [Google Scholar] [CrossRef]
- Wang, J.; He, Q.P. Multivariate statistical process monitoring based on statistics pattern analysis. Ind. Eng. Chem. Res. 2010, 49, 7858–7869. [Google Scholar] [CrossRef]
- He, Q.P.; Wang, J. Statistics pattern analysis: A new process monitoring framework and its application to semiconductor batch processes. AlChE J. 2011, 57, 107–121. [Google Scholar] [CrossRef]
- Ji, H. Statistics Mahalanobis distance for incipient sensor fault detection and diagnosis. Chem. Eng. Sci. 2021, 230, 116233. [Google Scholar] [CrossRef]
- Shang, J.; Chen, M.; Zhang, H. Fault detection based on augmented kernel Mahalanobis distance for nonlinear dynamic processes. Comput. Chem. Eng. 2018, 109, 311–321. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Sun, W. Orthogonal projection based statistical feature extraction for continuous process monitoring. Comput. Chem. Eng. 2024, 183, 108600. [Google Scholar] [CrossRef]
- Khan, F.; Haddara, M. Risk-based maintenance (RBM): A quantitative approach for maintenance/inspection scheduling and planning. J. Loss Prev. Process Ind. 2003, 16, 561–573. [Google Scholar] [CrossRef]
- Arunraj, N.S.; Maiti, J. Risk-based maintenance—Techniques and applications. J. Hazard. Mater. 2007, 142, 653–661. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.T.; Khan, F.; Ahmed, S.; Imtiaz, S. Risk-based fault detection and diagnosis for nonlinear and non-Gaussian process systems using R-vine copula. Process Saf. Environ. Prot. 2021, 150, 123–136. [Google Scholar] [CrossRef]
- Yu, H.; Khan, F.; Garaniya, V. Risk-based fault detection using Self-Organizing Map. Reliab. Eng. Syst. Saf. 2015, 139, 82–96. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P. Safety analysis in process facilities: Comparison of fault tree and Bayesian network approaches. Reliab. Eng. Syst. Saf. 2011, 96, 925–932. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P. Risk-based design of process systems using discrete-time Bayesian networks. Reliab. Eng. Syst. Saf. 2013, 109, 5–17. [Google Scholar] [CrossRef]
- Yu, H.; Khan, F.; Garaniya, V. Modified Independent Component Analysis and Bayesian Network-Based Two-Stage Fault Diagnosis of Process Operations. Ind. Eng. Chem. Res. 2015, 54, 2724–2742. [Google Scholar] [CrossRef]
- Gharahbagheri, H.; Imtiaz, S.A.; Khan, F. Root Cause Diagnosis of Process Fault Using KPCA and Bayesian Network. Ind. Eng. Chem. Res. 2017, 56, 2054–2070. [Google Scholar] [CrossRef]
- Gonzalez, R.; Huang, B.; Lau, E. Process monitoring using kernel density estimation and Bayesian networking with an industrial case study. ISA Trans. 2015, 58, 330–347. [Google Scholar] [CrossRef] [PubMed]
- Bi, X.; Wu, D.; Xie, D.; Ye, H.; Zhao, J. Large-scale chemical process causal discovery from big data with transformer-based deep learning. Process Saf. Environ. Prot. 2023, 173, 163–177. [Google Scholar] [CrossRef]
- Cervantes-Bobadilla, M.; García-Morales, J.; Saavedra-Benítez, Y.I.; Hernández-Pérez, J.A.; Adam-Medina, M.; Guerrero-Ramírez, G.V.; Escobar-Jímenez, R.F. Multiple fault detection and isolation using artificial neural networks in sensors of an internal combustion engine. Eng. Appl. Artif. Intell. 2023, 117, 105524. [Google Scholar] [CrossRef]
- Ma, F.; Ji, C.; Wang, J.; Sun, W. Early identification of process deviation based on convolutional neural network. Chin. J. Chem. Eng. 2023, 56, 104–118. [Google Scholar] [CrossRef]
- Heo, S.; Lee, J.H. Fault detection and classification using artificial neural networks. IFAC PapersOnLine 2018, 51, 470–475. [Google Scholar] [CrossRef]
- Yu, J.; Yan, X. Whole Process Monitoring Based on Unstable Neuron Output Information in Hidden Layers of Deep Belief Network. IEEE Trans. Cybern. 2020, 50, 3998–4007. [Google Scholar] [CrossRef]
- Barreto, N.E.M.; Rodrigues, R.; Schumacher, R.; Aoki, A.R.; Lambert-Torres, G. Artificial Neural Network Approach for Fault Detection and Identification in Power Systems with Wide Area Measurement Systems. J. Control. Autom. Electr. Syst. 2021, 32, 1617–1626. [Google Scholar] [CrossRef]
- Li, B.; Delpha, C.; Diallo, D.; Migan-Dubois, A. Application of Artificial Neural Networks to photovoltaic fault detection and diagnosis: A review. Renew. Sustain. Energy Rev. 2021, 138, 110512. [Google Scholar] [CrossRef]
- Cordoni, F.; Bacchiega, G.; Bondani, G.; Radu, R.; Muradore, R. A multi–modal unsupervised fault detection system based on power signals and thermal imaging via deep AutoEncoder neural network. Eng. Appl. Artif. Intell. 2022, 110, 104729. [Google Scholar] [CrossRef]
- Han, S.; Yang, L.; Duan, D.; Yao, L.; Gao, K.; Zhang, Q.; Xiao, Y.; Wu, W.; Yang, J.; Liu, W.; et al. A novel fault detection and identification method for complex chemical processes based on OSCAE and CNN. Process Saf. Environ. Prot. 2024, 190, 322–334. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Sakurada, M.; Yairi, T. Anomaly detection using autoencoders with nonlinear dimensionality reduction. In Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis, Gold Coast, Australia, 2 December 2014; pp. 4–11. [Google Scholar]
- Jang, K.; Hong, S.; Kim, M.; Na, J.; Moon, I. Adversarial Autoencoder Based Feature Learning for Fault Detection in Industrial Processes. IEEE Trans. Ind. Inf. 2022, 18, 827–834. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Robust Monitoring and Fault Isolation of Nonlinear Industrial Processes Using Denoising Autoencoder and Elastic Net. IEEE Trans. Control Syst. Technol. 2020, 28, 1083–1091. [Google Scholar] [CrossRef]
- Lee, S.; Kwak, M.; Tsui, K.-L.; Kim, S.B. Process monitoring using variational autoencoder for high-dimensional nonlinear processes. Eng. Appl. Artif. Intell. 2019, 83, 13–27. [Google Scholar] [CrossRef]
- Cacciarelli, D.; Kulahci, M. A novel fault detection and diagnosis approach based on orthogonal autoencoders. Comput. Chem. Eng. 2022, 163, 107853. [Google Scholar] [CrossRef]
- Bi, X.; Zhao, J. A novel orthogonal self-attentive variational autoencoder method for interpretable chemical process fault detection and identification. Process Saf. Environ. Prot. 2021, 156, 581–597. [Google Scholar] [CrossRef]
- Wan, F.; Guo, G.; Zhang, C.; Guo, Q.; Liu, J. Outlier Detection for Monitoring Data Using Stacked Autoencoder. IEEE Access 2019, 7, 173827–173837. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Aliabadi, M.M.; Emami, H.; Dong, M.; Huang, Y. Attention-based recurrent neural network for multistep-ahead prediction of process performance. Comput. Chem. Eng. 2020, 140, 106931. [Google Scholar] [CrossRef]
- Ren, J.; Ni, D. A batch-wise LSTM-encoder decoder network for batch process monitoring. Chem. Eng. Res. Des. 2020, 164, 102–112. [Google Scholar] [CrossRef]
- Cheng, F.; He, Q.P.; Zhao, J. A novel process monitoring approach based on variational recurrent autoencoder. Comput. Chem. Eng. 2019, 129, 106515. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Sun, W. Profitability related industrial-scale batch processes monitoring via deep learning based soft sensor development. Comput. Chem. Eng. 2023, 170, 108125. [Google Scholar] [CrossRef]
- Hong, F.; Ji, C.; Rao, J.; Chen, C.; Sun, W. Hourly ozone level prediction based on the characterization of its periodic behavior via deep learning. Process Saf. Environ. Prot. 2023, 174, 28–38. [Google Scholar] [CrossRef]
- Zhang, S.; Qiu, T. A dynamic-inner convolutional autoencoder for process monitoring. Comput. Chem. Eng. 2022, 158, 107654. [Google Scholar] [CrossRef]
- Yu, J.; Liu, X.; Ye, L. Convolutional Long Short-Term Memory Autoencoder-Based Feature Learning for Fault Detection in Industrial Processes. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Zhang, S.; Qiu, T. Semi-supervised LSTM ladder autoencoder for chemical process fault diagnosis and localization. Chem. Eng. Sci. 2022, 251, 117467. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
- Bayram, B.; Duman, T.B.; Ince, G. Real time detection of acoustic anomalies in industrial processes using sequential autoencoders. Expert Syst. 2021, 38, e12564. [Google Scholar] [CrossRef]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. Adv. Neural Inf. Process. Syst. 2017, 30, 4965597. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H.; Long, M.; Wang, J.; Yu, P.S. Memory in memory: A predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9154–9162. [Google Scholar]
- Ji, C.; Ma, F.; Wang, J.; Sun, W.; Zhu, X. Statistical method based on dissimilarity of variable correlations for multimode chemical process monitoring with transitions. Process Saf. Environ. Prot. 2022, 162, 649–662. [Google Scholar] [CrossRef]
- Leite, D.; Andrade, E.; Rativa, D.; Maciel, A.M.A. Fault Detection and Diagnosis in Industry 4.0: A Review on Challenges and Opportunities. Sensors 2024, 25, 60. [Google Scholar] [CrossRef]
- Ma, F.; Ji, C.; Xu, M.; Wang, J.; Sun, W. Spatial Correlation Extraction for Chemical Process Fault Detection Using Image Enhancement Technique aided Convolutional Autoencoder. Chem. Eng. Sci. 2023, 278, 118900. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Wang, J.; Sun, W. Real-Time Industrial Process Fault Diagnosis Based on Time Delayed Mutual Information Analysis. Processes 2021, 9, 1027. [Google Scholar] [CrossRef]
- Rojas, L.; Peña, Á.; Garcia, J. AI-Driven Predictive Maintenance in Mining: A Systematic Literature Review on Fault Detection, Digital Twins, and Intelligent Asset Management. Appl. Sci. 2025, 15, 3337. [Google Scholar] [CrossRef]
- Patil, A.; Soni, G.; Prakash, A. Data-driven approaches for impending fault detection of industrial systems: A review. Int. J. Syst. Assur. Eng. Manag. 2022, 15, 1326–1344. [Google Scholar] [CrossRef]
- Aghaee, M.; Mishra, A.; Krau, S.; Tamer, I.M.; Budman, H. Artificial intelligence applications for fault detection and diagnosis in pharmaceutical bioprocesses: A review. Curr. Opin. Chem. Eng. 2024, 44, 101025. [Google Scholar] [CrossRef]
- Bi, J.; Wang, H.; Yan, E.; Wang, C.; Yan, K.; Jiang, L.; Yang, B. AI in HVAC fault detection and diagnosis: A systematic review. Energy Rev. 2024, 3, 100071. [Google Scholar] [CrossRef]
- Liu, Y.; Jafarpour, B. Graph attention network with Granger causality map for fault detection and root cause diagnosis. Comput. Chem. Eng. 2024, 180, 108453. [Google Scholar] [CrossRef]
- Lv, F.; Bi, X.; Xu, Z.; Zhao, J. Causality-embedded reconstruction network for high-resolution fault identification in chemical process. Process Saf. Environ. Prot. 2024, 186, 1011–1033. [Google Scholar] [CrossRef]
- Yao, K.; Shi, H.; Song, B.; Tao, Y. A Temporal correlation topology graph model based on Mode-intrinsic and Mode-specific characterization using differentiated decoupling module with Distribution independence constraints for Multimode adaptive process monitoring. Process Saf. Environ. Prot. 2025, 199, 107207. [Google Scholar] [CrossRef]
- Zheng, Y.; Hu, C.; Wang, X.; Wu, Z. Physics-informed recurrent neural network modeling for predictive control of nonlinear processes. J. Process Control 2023, 128, 103005. [Google Scholar] [CrossRef]
- Bai, Y.-t.; Wang, X.-y.; Jin, X.-b.; Zhao, Z.-y.; Zhang, B.-h. A Neuron-Based Kalman Filter with Nonlinear Autoregressive Model. Sensors 2020, 20, 299. [Google Scholar] [CrossRef]
- Jackson, J.E.; Mudholkar, G.S. Control Procedures for Residuals Associated with Principal Component Analysis. Technometrics 1979, 21, 341–349. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, X.; Deng, X. Batch Process Monitoring Based on Multiway Global Preserving Kernel Slow Feature Analysis. IEEE Access 2017, 5, 2696–2710. [Google Scholar] [CrossRef]
- Li, G.; Qin, S.J.; Yuan, T. Data-driven root cause diagnosis of faults in process industries. Chemom. Intell. Lab. Syst. 2016, 159, 1–11. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, Z.; Yan, S.; Cao, Z. Data-driven Soft Sensing for Batch Processes Using Neural Network-based Deep Quality-Relevant Representation Learning. IEEE Trans. Artif. Intell. 2022, 4, 602–611. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Shimizu, S.; Ma, J.; Jin, Q. Siamese Neural Network Based Few-Shot Learning for Anomaly Detection in Industrial Cyber-Physical Systems. IEEE Trans. Ind. Inf. 2021, 17, 5790–5798. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Sun, W.; Palazoglu, A. Industrial Process Fault Detection Based on Siamese Recurrent Autoencoder. Comput. Chem. Eng. 2025, 192, 108887. [Google Scholar] [CrossRef]
- Shao, J.-D.; Rong, G.; Lee, J.M. Generalized orthogonal locality preserving projections for nonlinear fault detection and diagnosis. Chemom. Intell. Lab. Syst. 2009, 96, 75–83. [Google Scholar] [CrossRef]
- Koenig, B.C.; Kim, S.; Deng, S. KAN-ODEs: Kolmogorov–Arnold network ordinary differential equations for learning dynamical systems and hidden physics. Comput. Methods Appl. Mech. Eng. 2024, 432, 117397. [Google Scholar] [CrossRef]
- Shen, S.; Lu, H.; Sadoughi, M.; Hu, C.; Nemani, V.; Thelen, A.; Webster, K.; Darr, M.; Sidon, J.; Kenny, S. A physics-informed deep learning approach for bearing fault detection. Eng. Appl. Artif. Intell. 2021, 103, 104295. [Google Scholar] [CrossRef]
- Jia, M.; Hu, J.; Liu, Y.; Gao, Z.; Yao, Y. Topology-Guided Graph Learning for Process Fault Diagnosis. Ind. Eng. Chem. Res. 2023, 62, 3238–3248. [Google Scholar] [CrossRef]

| Category | Specific Method Implementation | Key Findings | Research Gaps | Way Forward |
|---|---|---|---|---|
| Statistical Process Monitoring Methods | PCA (linear projection via variance-covariance analysis) | Effective for steady, linear, Gaussian-distributed process data | Fails to handle nonlinearity, dynamics, and non-Gaussian data | Integrate kernel tricks or dynamic constraints for complex data characteristics |
| ICA (linear projection for extracting independent components) | Superior to PCA for non-Gaussian process data | Limited to linear relationships; unable to capture process dynamics | Combine with dynamic modeling to address time-series autocorrelation | |
| PLS (linear projection focusing on input-output variable correlation) | Reliable for feature extraction in input-output associated processes | Inadequate for nonlinear industrial processes | Apply kernel transformation to extend to nonlinear scenarios | |
| KPCA (kernel trick to map data to high-dimensional linear space) | Addresses nonlinearity in process data | Causes significant dimensionality increase; unsuitable for large-scale processes | Optimize kernel function to reduce computational complexity | |
| KPLS (kernel trick integrated with PLS for nonlinear input-output correlation) | Enhances nonlinear feature extraction for input-output processes | High computational cost limits real-time industrial application | Design lightweight kernel variants for efficient online monitoring | |
| DKPCA (hybrid of DPCA and KPCA for nonlinear dynamic processes) | Simultaneously handles process nonlinearity and dynamics | Dimensionality explosion in large-scale industrial systems | Incorporate feature selection to reduce redundant dimensions | |
| Auto-regressive PCA (autoregression model built on latent variables) | Captures process dynamics without data augmentation | Only considers unified time delay; ignores variable-specific dynamic differences | Adapt time-delay parameters for variables with distinct dynamic/periodic features | |
| DPCA (data augmentation to capture process autocorrelation) | Improves monitoring of dynamic processes via time-series extension | Limited to 1-step delay; unable to model complex dynamics | Extend to multi-step delay adaptation for periodic processes | |
| Dynamic-inner PCA (autoregression model on latent variables) | Avoids data augmentation while capturing dynamics | Fails to adapt to variable-specific dynamic performances | Develop variable-adaptive autoregressive coefficients | |
| SPA (Statistics Pattern Analysis, monitoring statistical features of variables) | Enables incipient fault detection via feature-level monitoring | Prone to feature redundancy; reduces fault detectability | Integrate feature selection to eliminate redundancy and enhance sensitivity | |
| Statistics Mahalanobis distance; Augmented kernel Mahalanobis distance | Improves incipient fault detection accuracy | Feature redundancy compromises monitoring performance | Optimize feature fusion strategies to balance comprehensiveness and conciseness | |
| Probabilistic Process Monitoring Methods | BN (Bayesian Network for risk-based maintenance, RBM) | Excels at uncertainty handling and risk quantification | Requires fault/disturbance data for causal network construction | Develop unsupervised BN training for imbalanced industrial data |
| RBM methodology (risk estimation, evaluation, maintenance planning) | Provides systematic risk-based process management framework | Lacks direct integration with real-time fault detection | Integrate real-time data streams for dynamic risk updating | |
| RBM applied to power-generating plants | Validates RBM feasibility in energy sector processes | Limited generalizability to other industrial domains (e.g., chemical) | Customize risk metrics for domain-specific process characteristics | |
| RBM applied to ethylene oxide production facilities | Demonstrates RBM effectiveness in chemical process safety management | Relies on sufficient fault data for risk model calibration | Incorporate transfer learning to address fault data scarcity | |
| R-vine copula (probabilistic model for risk-based FDD) | Enhances risk-based fault detection/diagnosis (FDD) accuracy | Requires sufficient fault samples for model training | Develop semi-supervised copula models for imbalanced data scenarios | |
| Self-organizing map, probabilistic analysis (risk-based fault detection) | Combines clustering and probability for risk-oriented fault detection | Limited adaptability to multimodal process data | Integrate adaptive clustering to handle multimodal industrial dynamics | |
| Hybrid PCA and BN | Identifies root causes and fault propagation pathways | Shallow fusion of statistical and probabilistic advantages | Develop deep fusion frameworks for enhanced fault tracing | |
| Modified ICA and BN (two-stage hybrid FDD) | Improves fault detection and propagation tracing accuracy | Limited to linear process features (via ICA) | Combine nonlinear feature extractors (e.g., KICA) with BN | |
| Hybrid KPCA and BN | Addresses nonlinear processes in probabilistic FDD | Computational complexity of KPCA limits real-time application | Optimize KPCA-BN integration for efficient online monitoring | |
| Hybrid HMM and BN for fault prognosis | Enables fault progression prediction via temporal probabilistic modeling | HMM suffers from gradient issues in long-time-series training | Integrate LSTM units to enhance temporal feature learning | |
| Multivariate fault probability integration in FDD | Improves FDD performance via comprehensive probability quantification | Over-reliance on fault data for probability calibration | Develop unsupervised probability estimation for unlabeled industrial data | |
| Deep Learning Methods | Deep learning (multi-layer neural networks for nonlinear/time-varying chemical processes) | Strong data fitting ability for complex industrial processes | High parameter demand; requires large-scale training data | Design lightweight networks to reduce data/parameter dependency |
| ANN (residue-based fault detection via neural network prediction) | Enables fault detection via prediction residual analysis | Poor interpretability; “black-box” limitation | Incorporate attention mechanisms to enhance feature interpretability | |
| Residual-based CNN and PCA | Captures local spatial features and enables dimensionality reduction | CNN’s local feature focus ignores global process relationships | Combine CNN with global feature extractors (e.g., transformer) | |
| ANN with unstable hidden layer neurons (multi-layer feature integration) | Enhances fault detection via comprehensive multi-layer feature fusion | Unstable neurons increase model training randomness | Optimize hidden layer activation functions for stability | |
| Hybrid KPCA and DNN | Combines nonlinear feature extraction (KPCA) and deep fitting (DNN) | High computational cost of hybrid model | Simplify model structure while retaining complementary advantages | |
| Adaptive BN and ANN | Tackles nonlinear/non-Gaussian/multimodal process FDD | Adaptive mechanism lacks robustness to extreme process deviations | Improve adaptability via online parameter updating | |
| AE (encoder–decoder structure for nonlinear feature extraction) | Models almost any nonlinearity via activation functions | Relies on reconstruction error; limited interpretability | Introduce orthogonal constraints to enhance feature interpretability | |
| AE (process monitoring via reconstruction error measurement) | Enables effective fault detection via input-output reconstruction | Insensitive to subtle incipient faults | Optimize loss function to enhance sensitivity to minor deviations | |
| Adversarial AE (latent variables constrained to specific distribution) | Improves latent feature representation of original data manifold | Adversarial training increases computational complexity | Simplify adversarial mechanism for industrial applicability | |
| Denoising AE (feature extraction from noisy input data) | Enhances robust monitoring in noisy industrial environments | Denoising process may lose fault-related weak signals | Balance denoising and fault signal preservation | |
| VAE (variational AE for nonlinear/nonnormal process data) | Simultaneously handles process nonlinearity and nonnormality | Complex variational inference limits real-time monitoring | Optimize inference algorithm for efficient online application | |
| Orthogonal AE (orthogonal constraints in loss function) | Reduces feature redundancy via orthogonalization | Orthogonal constraints may increase training difficulty | Adjust constraint strength to balance redundancy reduction and training stability | |
| Orthogonal self-attentive VAE | Enhances model interpretability and fault identification via self-attention | Complex structure increases computational cost | Simplify attention mechanism for lightweight deployment | |
| SAE (Stacked Autoencoder, multilayer structure for generalization) | Improves model generalization via deep feature extraction | Deep structure exacerbates “black-box” problem | Incorporate symbolic regression (e.g., KAN) for interpretability | |
| VAE (latent features constrained to normal distribution) | Stabilizes latent feature distribution for reliable monitoring | Normal distribution assumption may mismatch complex industrial data | Adopt flexible distribution constraints (e.g., nonparametric) | |
| RNN (memory unit for capturing time-series dynamic features) | Models process dynamics via temporal state transfer | Prone to gradient explosion/vanishing in long time-series | Replace with LSTM/GRU to address gradient issues | |
| LSTM (gate units for gradient preservation in dynamic feature extraction) | Solves RNN gradient issues; captures long-term temporal dependencies | High computational cost for large-scale time-series | Optimize LSTM cell structure for lightweight deployment | |
| GRU (simplified gate units for dynamic feature extraction) | Balances monitoring performance and computational efficiency | Less effective for ultra-long time-series than LSTM | Extend with attention to enhance long-range dependency capture | |
| Attention-based LSTM (catalyst activity prediction for methanol reactor) | Improves targeted feature extraction via attention mechanism | Limited to specific process (catalyst activity prediction) | Generalize attention weights for diverse industrial processes | |
| LSTM-AE (LSTM integrated with AE for batch process time dependencies) | Captures temporal dependencies in batch process data | Less effective for continuous process dynamics | Adapt to continuous processes via sliding window time-series processing | |
| VRAE (Variational Recurrent AE, VAE + RNN/GRU for nonlinearity/dynamics) | Simultaneously handles process nonlinearity and temporal dynamics | Complex structure increases training complexity | Simplify variational component for industrial applicability | |
| Differential RNN (embedded difference unit for short-term time-varying info) | Captures short-term dynamic changes in industrial processes | Ignores long-term temporal dependencies | Combine with LSTM to balance short/long-term dynamic feature extraction | |
| Multi-order difference embedded LSTM | Enhances capture of data periodicity in dynamic processes | Multi-order difference increases computational load | Optimize difference order selection for efficiency-performance balance | |
| Dynamic inner AE (vector autoregressive model on latent variables) | Captures process dynamics via latent variable autoregression | Limited to linear autoregressive relationships | Extend to nonlinear autoregression for complex dynamics | |
| Convolutional LSTM AE (forget gates for long-term time dependence) | Extracts long-term temporal dependencies via gated convolution | High parameter count increases memory consumption | Prune redundant parameters for lightweight deployment | |
| Semi-supervised LSTM ladder AE (labeled + unlabeled data training) | Boosts diagnostic accuracy via semi-supervised learning | Relies on sufficient labeled data for performance | Enhance unsupervised learning capability for scarce labeled data scenarios | |
| ConvLSTM (convolution + LSTM for spatiotemporal feature extraction) | Captures both spatial relationships and temporal dynamics | 3D convolution variant has excessive parameters | Optimize convolution kernel size to reduce parameter count | |
| ConvLSTM (real-time acoustic anomaly detection in industrial processes) | Validates ConvLSTM for industrial anomaly detection | Limited to acoustic data; lacks generalization to multi-variable processes | Extend input adaptation for diverse industrial sensor data | |
| PredRNN (addresses layer-independent memory in ConvLSTM) | Improves spatiotemporal feature integration via enhanced memory mechanism | Deep structure increases training difficulty | Simplify memory mechanism for stable industrial application | |
| PredRNN++ (causal LSTM + Gradient highway unit for deep time modeling) | Alleviates gradient propagation issues in deep spatiotemporal models | High complexity limits real-time deployment | Optimize highway unit for efficient gradient flow and low latency |
| Research Direction | Key Challenges | Potential Solutions | Expected Outcomes |
|---|---|---|---|
| Latent Space Optimization | Avoiding feature redundancy; Defining constrained latent features without fault labels | Orthogonal constraints; Siamese network structures | To extract more discriminative and interpretable features for improved fault detection |
| Model Structure Innovation | High computational cost; Limited interpretability | KAN; Symbolic regression and pruning | To develop inherently interpretable deep learning models |
| Process-Information Fusion | Systematic encoding of domain knowledge; Balancing physical constraints with data-driven flexibility | Construction of secondary variables; PINN; GNN | To create models with superior generalization for industrial environments |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, C.; Ma, F.; Rao, J.; Wang, J.; Sun, W. Bridging the Gap in Chemical Process Monitoring: Beyond Algorithm-Centric Research Toward Industrial Deployment. Processes 2025, 13, 3809. https://doi.org/10.3390/pr13123809
Ji C, Ma F, Rao J, Wang J, Sun W. Bridging the Gap in Chemical Process Monitoring: Beyond Algorithm-Centric Research Toward Industrial Deployment. Processes. 2025; 13(12):3809. https://doi.org/10.3390/pr13123809
Chicago/Turabian StyleJi, Cheng, Fangyuan Ma, Jingzhi Rao, Jingde Wang, and Wei Sun. 2025. "Bridging the Gap in Chemical Process Monitoring: Beyond Algorithm-Centric Research Toward Industrial Deployment" Processes 13, no. 12: 3809. https://doi.org/10.3390/pr13123809
APA StyleJi, C., Ma, F., Rao, J., Wang, J., & Sun, W. (2025). Bridging the Gap in Chemical Process Monitoring: Beyond Algorithm-Centric Research Toward Industrial Deployment. Processes, 13(12), 3809. https://doi.org/10.3390/pr13123809








