Role of Shear-Thinning-Induced Viscosity Heterogeneity in Regulating Fingering Transition of CO2 Flooding Within Porous Media
Abstract
1. Introduction
2. Numerical Modeling
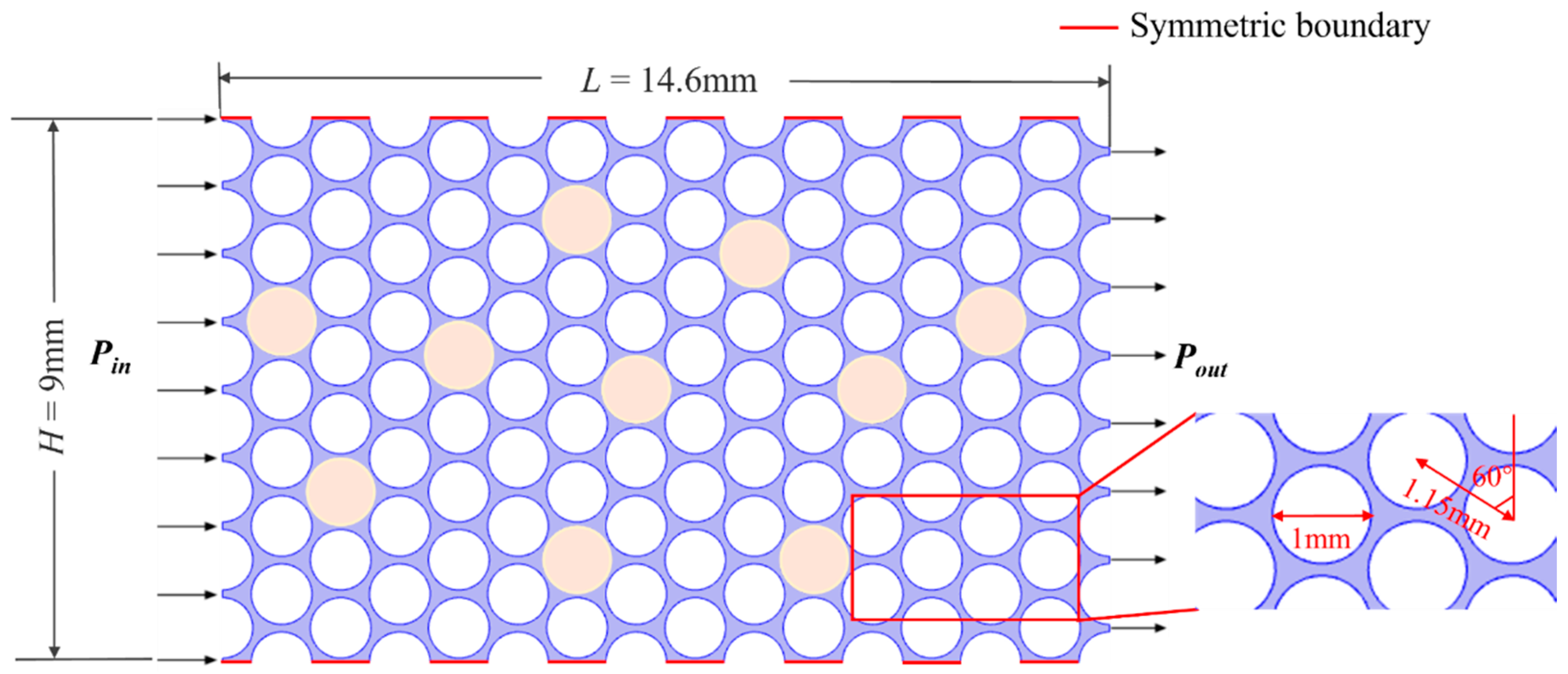
2.1. Geometric Model
2.2. Governing Equations
2.3. Boundary and Initial Conditions
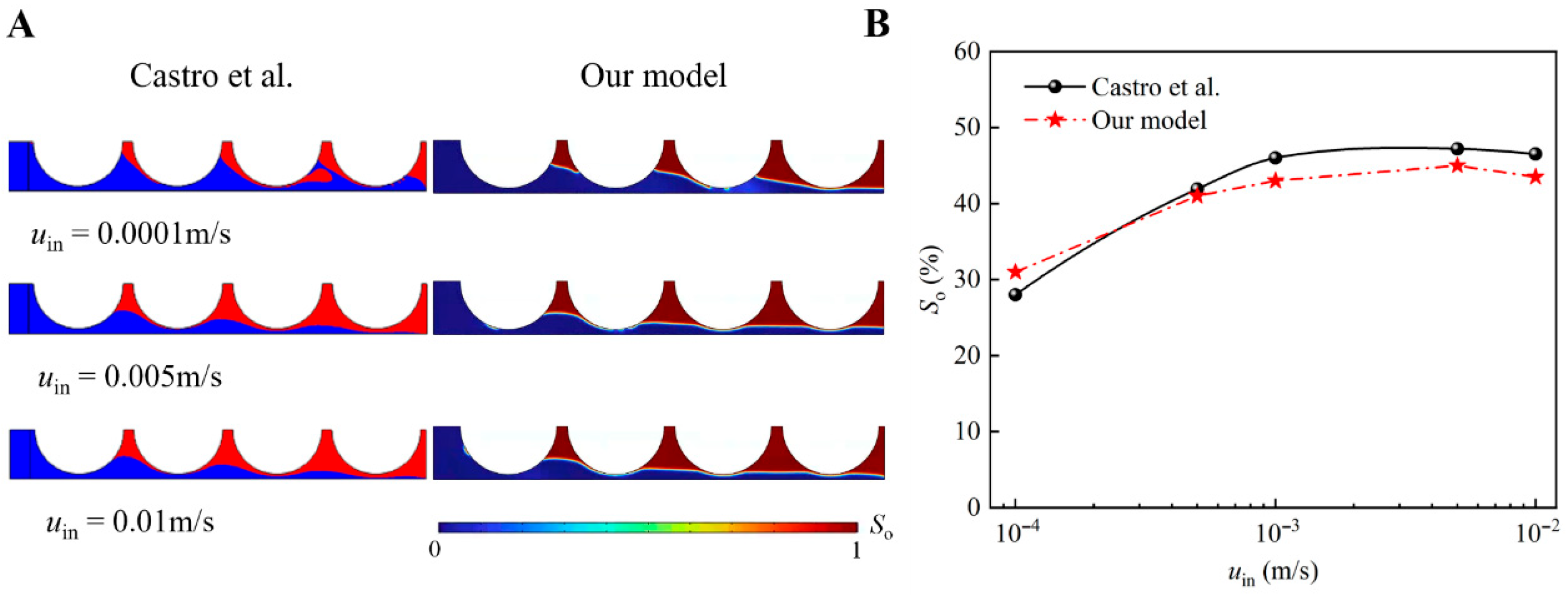
2.4. Model Validation
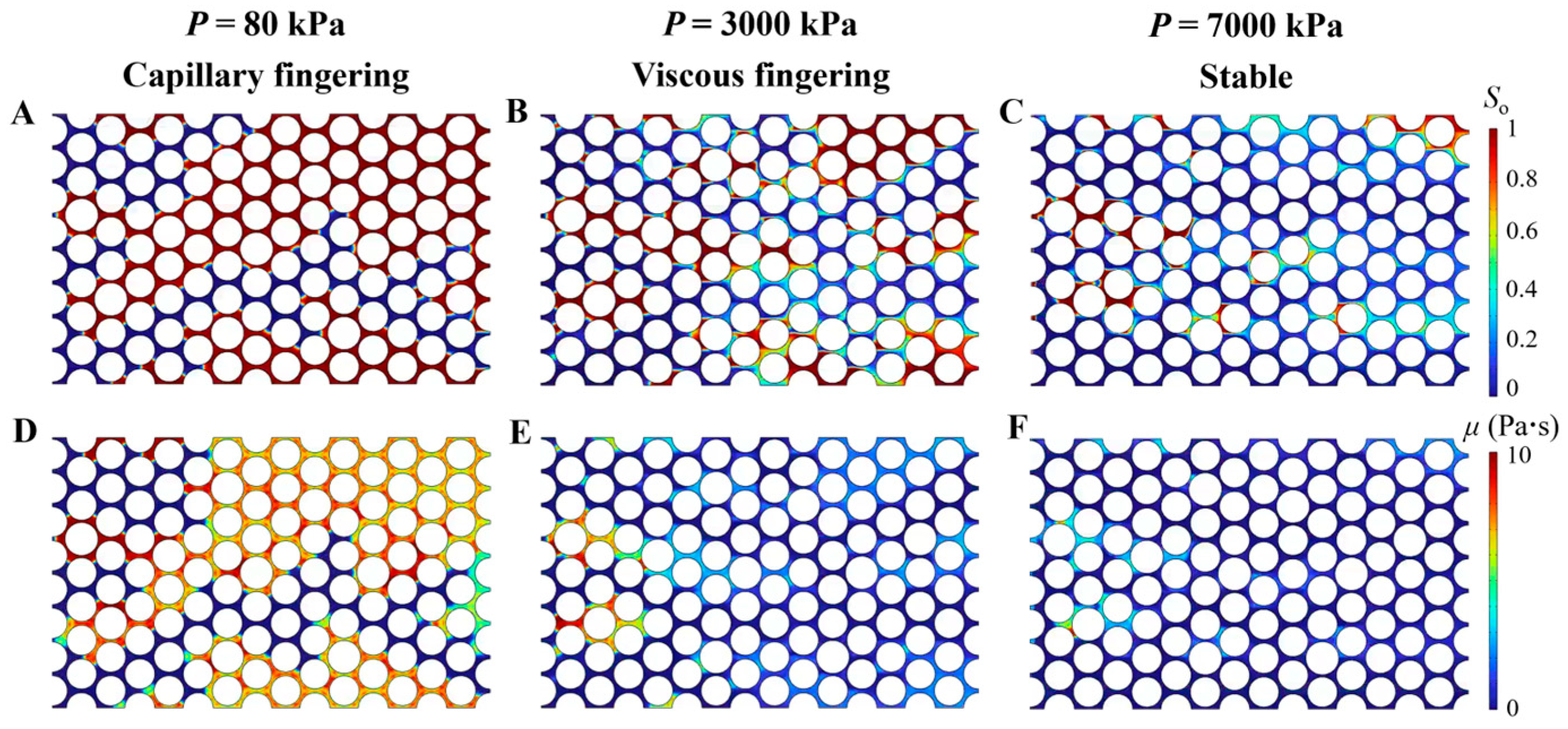
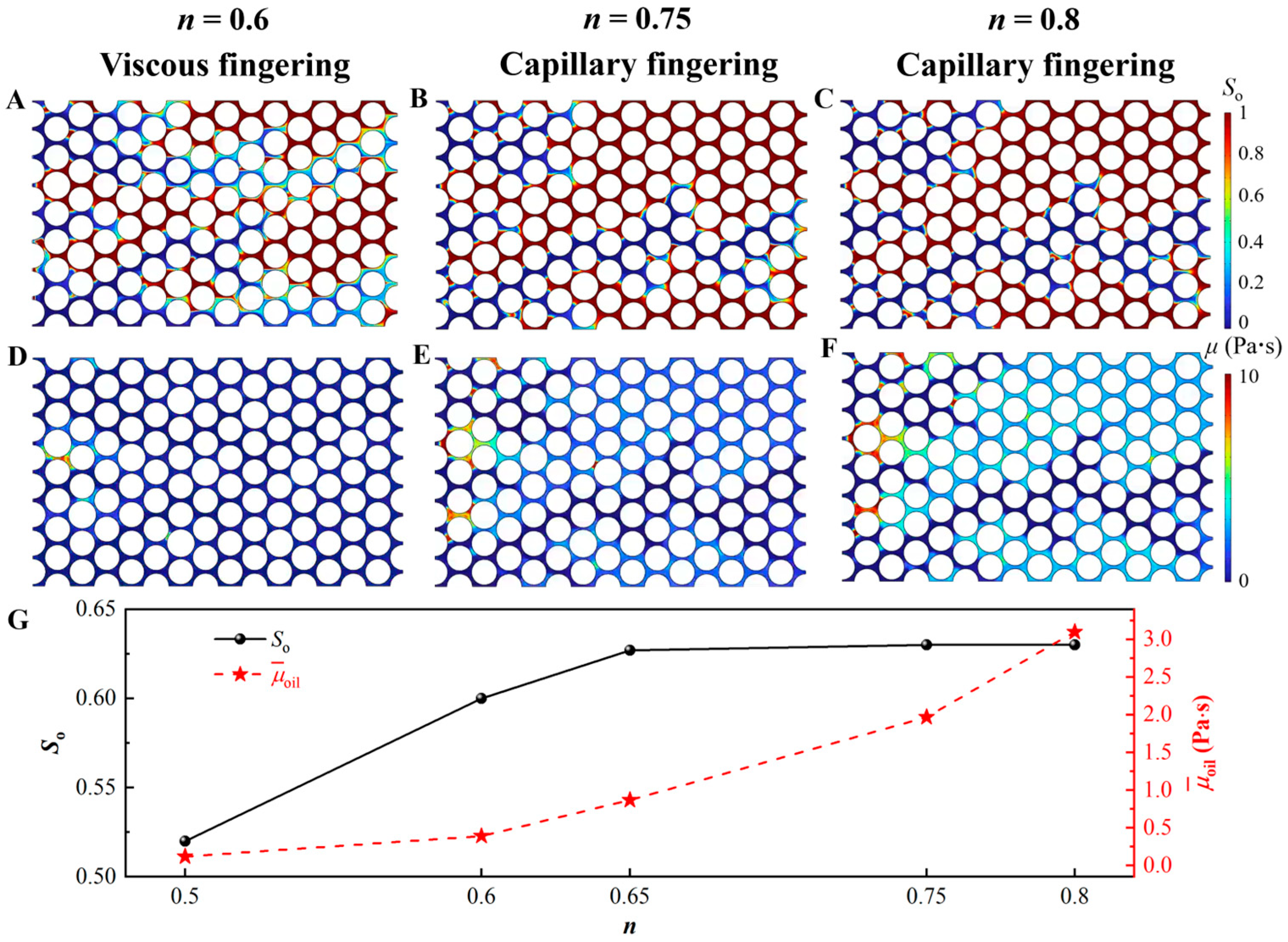
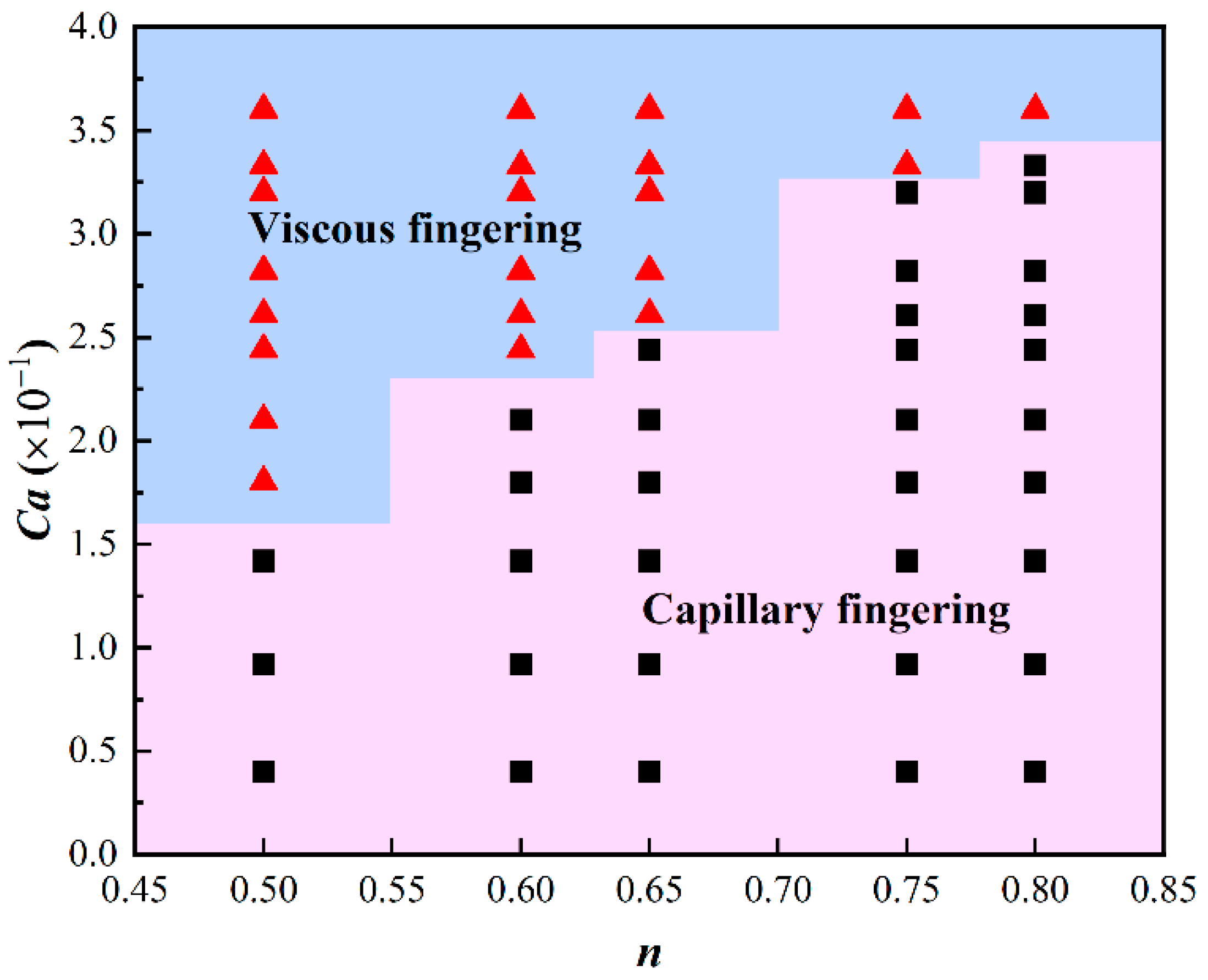
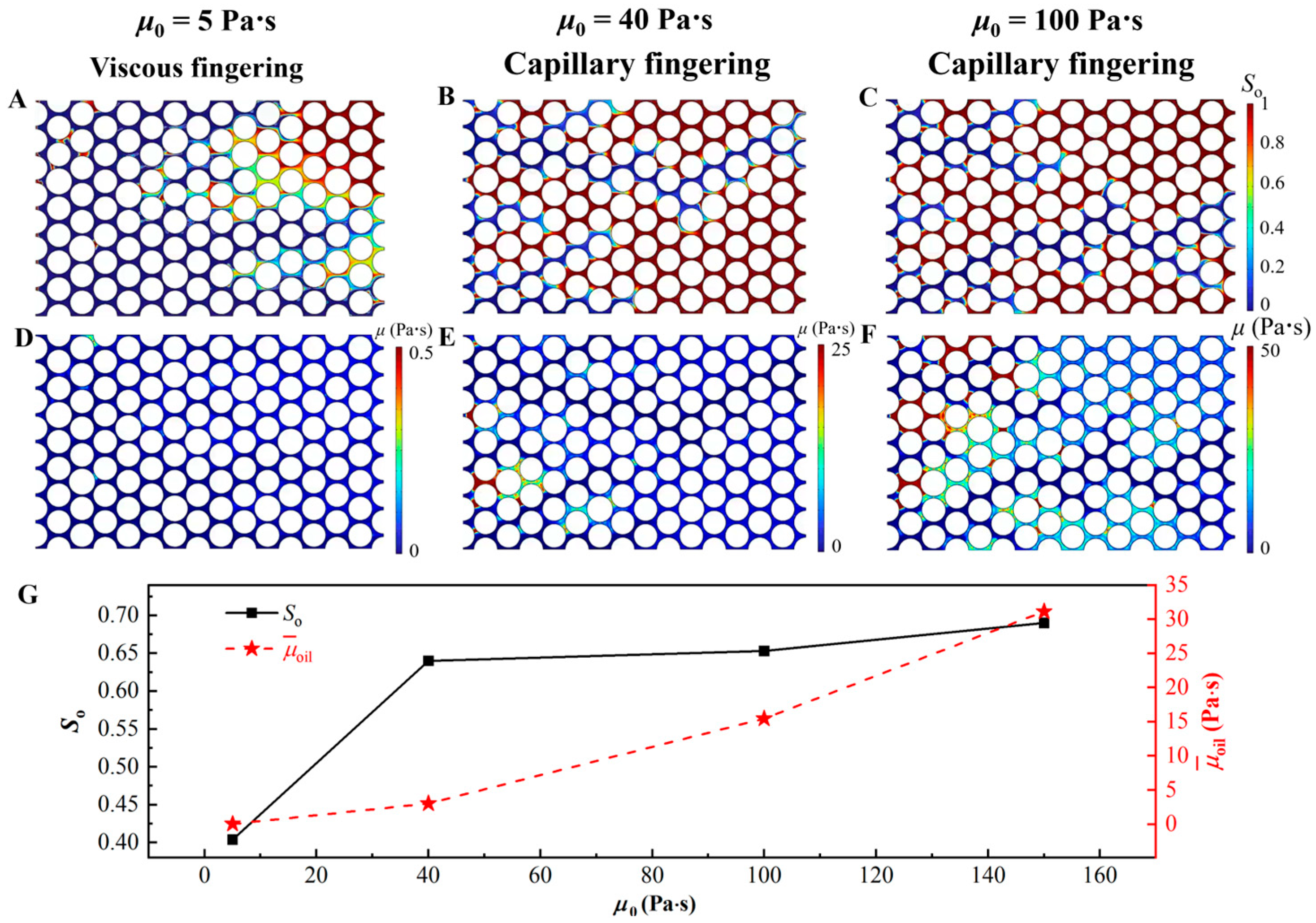
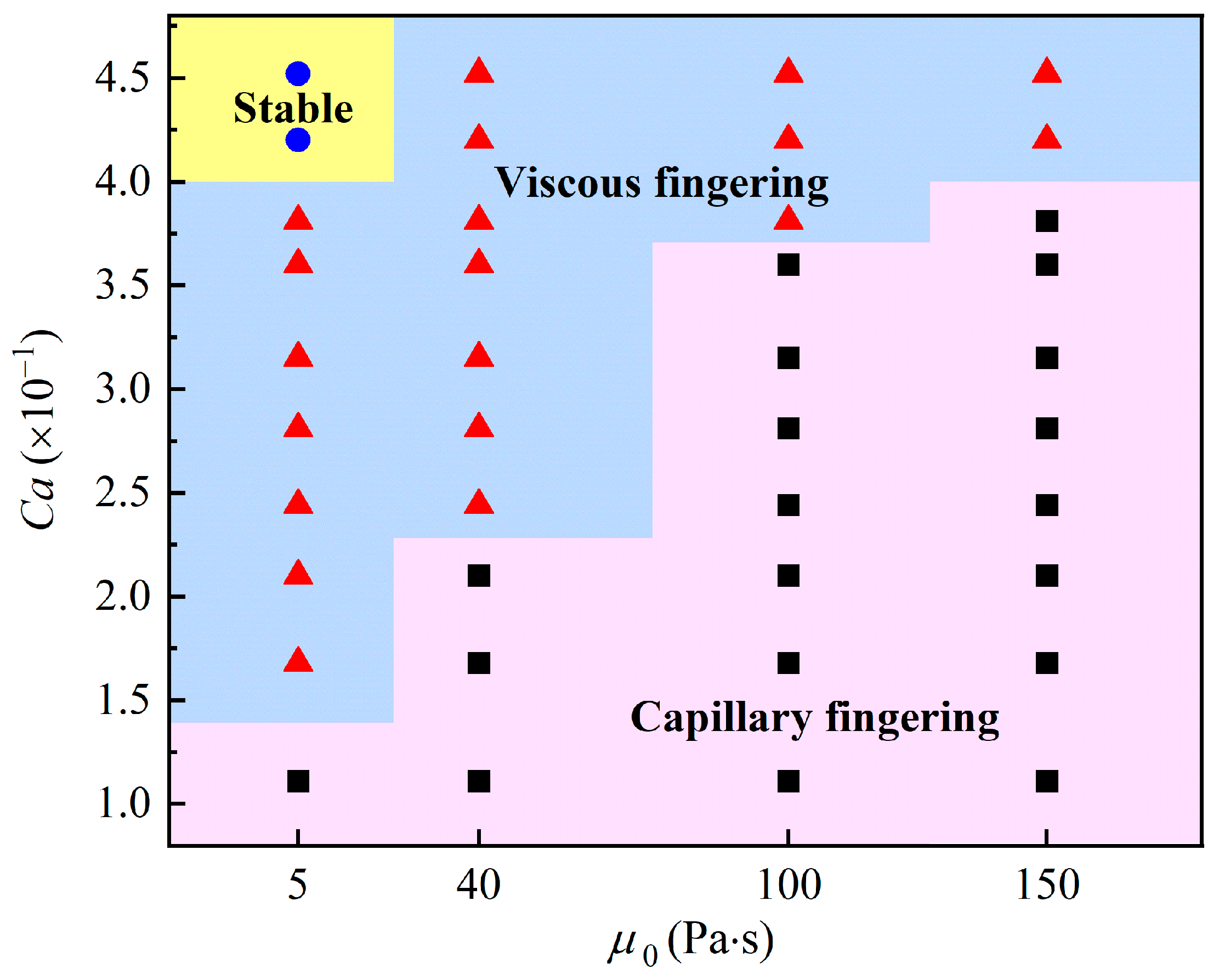
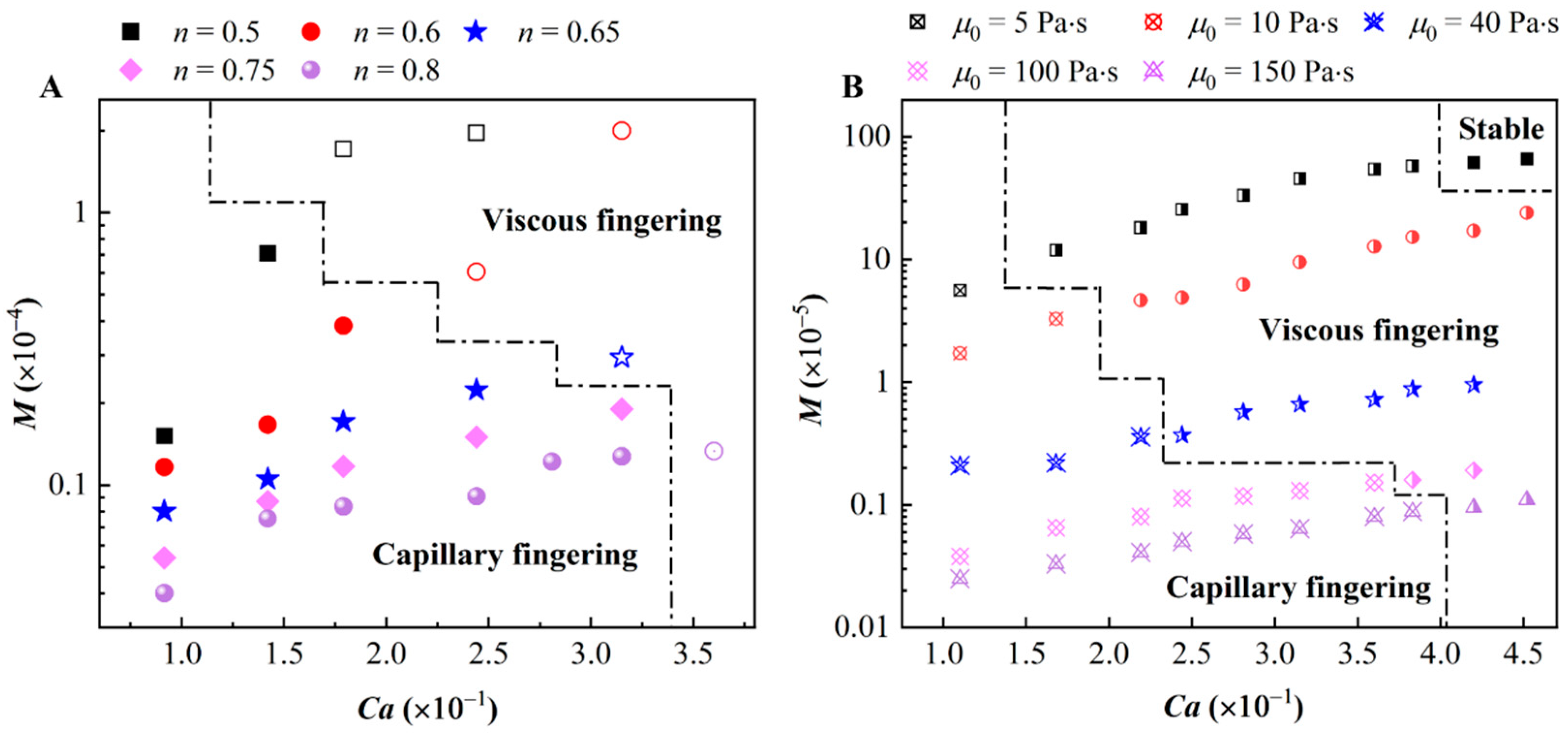
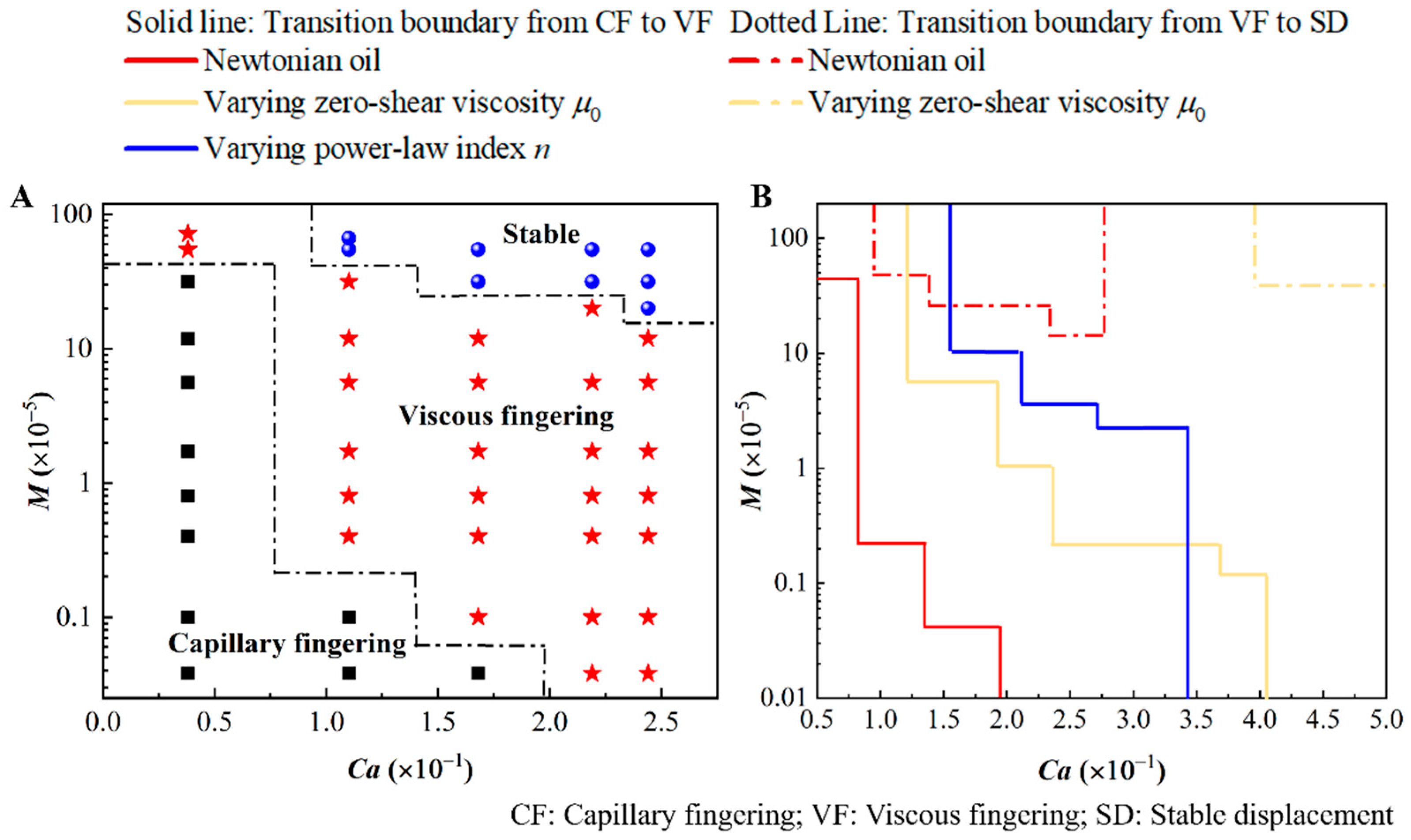
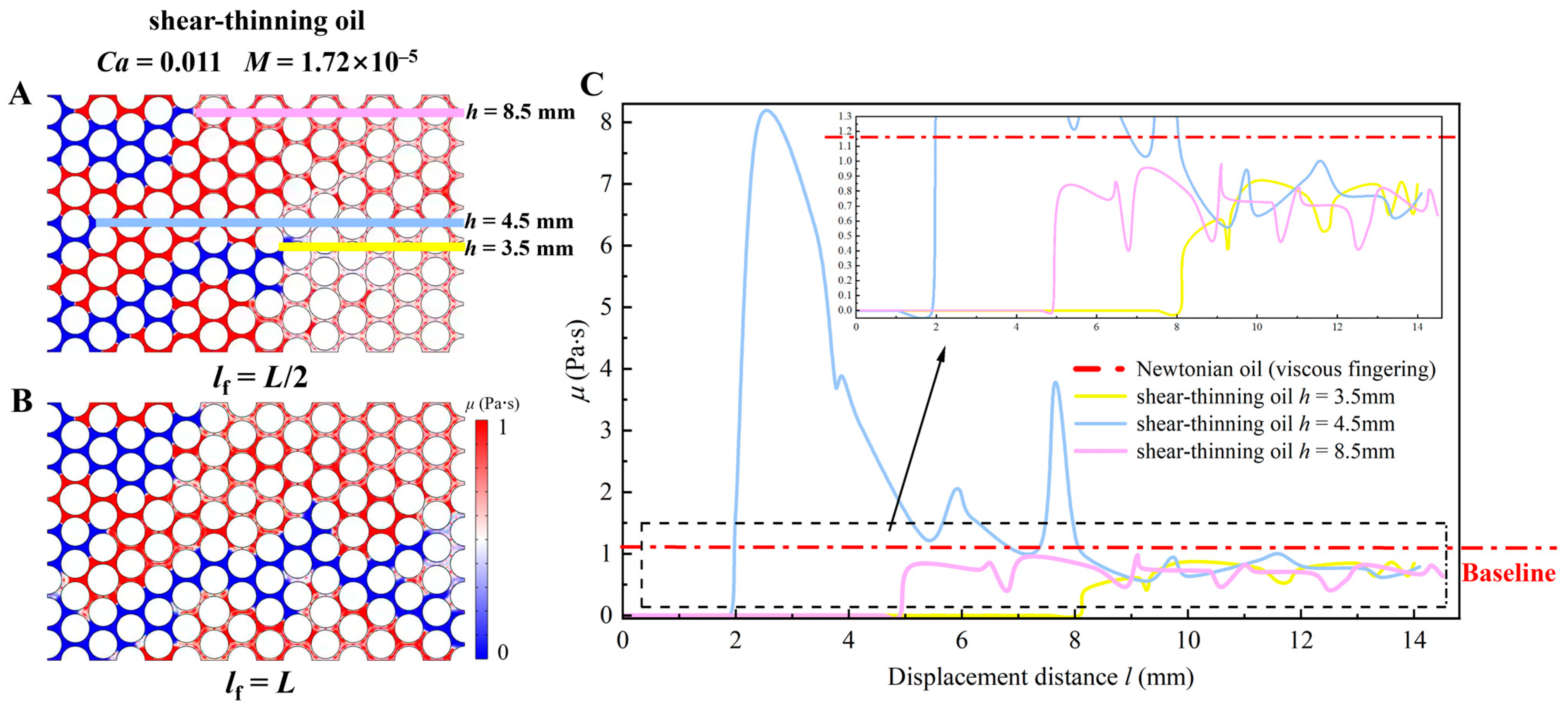
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Ma, S.; Liu, X.; Liu, J.; Lu, Y.; Zhao, P.; Kassabi, N.; Hamdi, E.; Elsworth, D. Coal measure gas resources matter in China: Review, challenges, and perspective. Phys. Fluids 2024, 36, 071301. [Google Scholar] [CrossRef]
- Lu, H.; Xi, D.; Cheng, Y.F. Hydrogen production in integration with CCUS: A realistic strategy towards net zero. Energy 2025, 315, 134398. [Google Scholar] [CrossRef]
- Jiang, K.; Ashworth, P.; Zhang, S.; Liang, X.; Sun, Y.; Angus, D. China’s carbon capture, utilization and storage (CCUS) policy: A critical review. Renew. Sustain. Energy Rev. 2020, 119, 109601. [Google Scholar] [CrossRef]
- He, L.; He, W.; Wang, S.; Lou, R.; Ren, T.; Cui, H.; Tao, Y.; Yuan, Y. Transport dynamics of droplets encapsulated by an elastic interface in pore throats. Phys. Fluids 2024, 36, 092101. [Google Scholar] [CrossRef]
- Qian, C.; Rui, Z.; Liu, Y.; Zhou, K.; Du, K.; Zhao, Y.; Zou, J.; Song, K.; Li, X. Microfluidic investigation on microscopic flow and displacement behavior of CO2 multiphase system for CCUS-EOR in heterogeneous porous media. Chem. Eng. J. 2025, 505, 159135. [Google Scholar] [CrossRef]
- Wang, L.; He, Y.; Wang, Q.; Liu, M.; Jin, X. Multiphase flow characteristics and EOR mechanism of immiscible CO2 water-alternating-gas injection after continuous CO2 injection: A micro-scale visual investigation. Fuel 2020, 282, 118689. [Google Scholar] [CrossRef]
- Hill, L.B.; Li, X.; Wei, N. CO2-EOR in China: A comparative review. Int. J. Greenh. Gas Control. 2020, 103, 103173. [Google Scholar] [CrossRef]
- He, L.; Ren, S.; Zhang, H. Fingering crossover and enhanced oil recovery mechanism of water-alternating-CO2 injection. Phys. Fluids 2023, 35, 053322. [Google Scholar] [CrossRef]
- Zhang, N.; Wei, M.; Bai, B. Statistical and analytical review of worldwide CO2 immiscible field applications. Fuel 2018, 220, 89–100. [Google Scholar] [CrossRef]
- Salmo, I.C.; Sorbie, K.S.; Skauge, A.; Alzaabi, M.A. Immiscible Viscous Fingering: Modelling Unstable Water–Oil Displacement Experiments in Porous Media. Transp. Porous Media 2022, 145, 291–322. [Google Scholar] [CrossRef]
- Ren, J.; Xiao, W.; Pu, W.; Tang, Y.; Bernabé, Y.; Cheng, Q.; Zheng, L. Characterization of CO2 miscible/immiscible flooding in low-permeability sandstones using NMR and the VOF simulation method. Energy 2024, 297, 131211. [Google Scholar] [CrossRef]
- Zakirov, T.R.; Khramchenkov, M.G. Pore-scale study of the anisotropic effect on immiscible displacement in porous media under different wetting conditions and capillary numbers. J. Pet. Sci. Eng. 2022, 208, 109484. [Google Scholar] [CrossRef]
- Xiao, L.; Zhu, G.; Zhang, L.; Yao, J.; Sun, H. Effects of pore-size disorder and wettability on forced imbibition in porous media. J. Pet. Sci. Eng. 2021, 201, 108485. [Google Scholar] [CrossRef]
- Wu, D.S.; Hu, R.; Lan, T.; Chen, Y.F. Role of Pore-Scale Disorder in Fluid Displacement: Experiments and Theoretical Model. Water Resour. Res. 2021, 57, e2020WR028004. [Google Scholar] [CrossRef]
- He, L.; Zhao, F.; He, W.; Ren, S.K.; Lou, R.; Song, B.Y. Fingering inhibition triggered by CO2 dissolution and viscosity reduction in water-alternating-CO2 injection. Int. J. Heat Fluid Flow 2024, 110, 109646. [Google Scholar] [CrossRef]
- He, L.; Wang, S.; Yuan, Y. Deformation dynamics of rear concave droplet enclosed by nanoparticle surfactants in a capillary. Phys. Fluids 2023, 35, 122112. [Google Scholar] [CrossRef]
- Zhang, M.; Li, B.; Zheng, L.; Xin, Y.; Xing, W.; Li, Z. Experimental study on CO2 flooding within a fractured low-permeability reservoir: Impact of high injection rate. Fuel 2025, 384, 134002. [Google Scholar] [CrossRef]
- Suo, S.; Liu, M.C.; Gan, Y. Fingering patterns in hierarchical porous media. Phys. Rev. Fluids 2020, 5, 034301. [Google Scholar] [CrossRef]
- Sorbie, K.S.; Al Ghafri, A.Y.; Skauge, A.; Mackay, E.J. On the Modelling of Immiscible Viscous Fingering in Two-Phase Flow in Porous Media. Transp. Porous Media 2020, 135, 331–359. [Google Scholar] [CrossRef]
- Chang, C.; Kneafsey, T.J.; Tokunaga, T.K.; Wan, J.; Nakagawa, S. Impacts of Pore Network-Scale Wettability Heterogeneity on Immiscible Fluid Displacement: A Micromodel Study. Water Resour. Res. 2021, 57, e2021WR030302. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1958, 245, 312–329. [Google Scholar] [CrossRef]
- Verma, P.; Hung, S.-W.; Mao, J.-J.; Chen, C.-Y. Impact of an intermediate layer on immiscible viscous fingering instability in radial Hele-Shaw cell. Int. J. Heat Mass Transf. 2025, 245, 127010. [Google Scholar] [CrossRef]
- Lenormand, R.; Touboul, E.; Zarcone, C. Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 2006, 189, 165–187. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, Y.; Yin, M.; Zhang, S.; Song, Y.; Zhao, Y. Fluorescence visualization dynamics of carbonated water injection processes in homogeneous glass micromodels. J. Mol. Liq. 2024, 414, 126164. [Google Scholar] [CrossRef]
- Beteta, A.; Sorbie, K.; Skauge, A.; Skauge, T. Immiscible viscous fingering: The effects of wettability/capillarity and scaling. Transp. Porous Media 2024, 151, 85–118. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.-Q.; Peng, C.; Jiao, P.; Loh, W.L.; Wang, Q. Insight into evolution of invasive patterns on fingering phenomenon during immiscible two-phase flow through pore structure. Pet. Sci. 2024, 21, 3307–3325. [Google Scholar] [CrossRef]
- Singh, P.; Mondal, S. Role of the process conditions on three-dimensional viscous fingering: Impact on enhanced oil recovery and geological storage. Int. J. Multiph. Flow 2025, 184, 105110. [Google Scholar] [CrossRef]
- Yang, J.; Mukunoki, T.; Oxarango, L. 3D Visualization of Viscous Fingering in Miscible Fluids Flow in Porous Materials. Transp. Porous Media 2025, 152, 21. [Google Scholar] [CrossRef]
- Tsuji, T.; Jiang, F.; Christensen, K.T. Characterization of immiscible fluid displacement processes with various capillary numbers and viscosity ratios in 3D natural sandstone. Adv. Water Resour. 2016, 95, 3–15. [Google Scholar] [CrossRef]
- Chen, Y.F.; Fang, S.; Wu, D.S.; Hu, R. Visualizing and quantifying the crossover from capillary fingering to viscous fingering in a rough fracture. Water Resour. Res. 2017, 53, 7756–7772. [Google Scholar] [CrossRef]
- Ahmadikhamsi, S.; Golfier, F.; Oltean, C. Impact of surfactant addition on non-Newtonian fluid behavior during viscous fingering in Hele-Shaw cell. Phys. Fluids 2020, 32, 012103. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Luu, D.V.; Nguyen, X.B. Viscoplastic effects on a non-Newtonian fluid flow in rock fracture. AIP Adv. 2025, 15, 035331. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.-Q.; Peng, C.; He, H. Discussion on pore-to-field scale evolution of invasive pattern in immiscible two-phase flow with pseudoplastic behavior in porous media. Phys. Fluids 2025, 37, 023106. [Google Scholar] [CrossRef]
- Wang, W.; Liu, P.; Zhou, C.; Bate, B.; Chen, Y. Numerical pore-scale investigation of two-phase displacement with non-Newtonian defending fluid. Phys. Fluids 2024, 36, 093105. [Google Scholar] [CrossRef]
- Lee, Y.H.; Wang, J.; Kannaiyan, R.; Su, Y.; Gates, I.D. Air invasion into three-dimensional foam induces viscous fingering instabilities. Sci. Rep. 2024, 14, 2892. [Google Scholar] [CrossRef]
- Cao, L.; Lv, M.; Li, C.; Sun, Q.; Wu, M.; Xu, C.; Dou, J. Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing. Reserv. Sci. 2025, 1, 36–51. [Google Scholar] [CrossRef]
- Li, M.; Liu, J.; Xia, Y. Risk Prediction of Gas Hydrate Formation in the Wellbore and Subsea Gathering System of Deep-Water Turbidite Reservoirs: Case Analysis from the South China Sea. Reserv. Sci. 2025, 1, 52–72. [Google Scholar] [CrossRef]
- Wu, J.; Ansari, U. From CO2 Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs. Reserv. Sci. 2025, 1, 19–35. [Google Scholar] [CrossRef]
- Shi, Y.; Tang, G.H. Non-Newtonian rheology property for two-phase flow on fingering phenomenon in porous media using the lattice Boltzmann method. J. Non-Newton. Fluid Mech. 2016, 229, 86–95. [Google Scholar] [CrossRef]
- Yang, X.; Tang, Y.; Li, M.; Li, C.; Wang, M.; Li, X.; Zhao, J. Effect of shear-thinning of non-Newtonian fluid on the crossover from capillary fingering to viscous fingering in porous media. Phys. Lett. A 2022, 449, 128364. [Google Scholar] [CrossRef]
- Omrani, S.; Green, C.; Sahimi, M.; Niasar, V. Anomalies of solute transport in flow of shear-thinning fluids in heterogeneous porous media. Phys. Fluids 2024, 36, 076629. [Google Scholar] [CrossRef]
- Al-Qenae, A.; Shokri, J.; Shende, T.; Sahimi, M.; Niasar, V. Enhanced dispersion in shear-thinning fluid flow through porous media. Phys. Rev. Fluids 2025, 10, 063802. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Abdallah, K.B.; Li, L.; Hamdi, E.; Liu, J. Multiphase flow controlled by synergistic injection-production pressure: Enabling CO2 geo-sequestration with additional gas recovery from vertically heterogeneous depleted shale reservoirs. Fuel 2025, 398, 135591. [Google Scholar] [CrossRef]
- Lu, Z.H.; Li, K.; Liu, X.B.; Zhao, P.; Liu, J. Low-field NMR application in the characterization of CO2 Geological storage and utilization related to shale gas reservoirs: A brief review. Front. Earth Sci. 2023, 17, 739–751. [Google Scholar] [CrossRef]
- He, L.; Zhao, F.; Shang, X.; Lou, R.; Sun, P.; Song, B.; Cui, H.; Tao, Y. Detachment dynamics of sessile droplets triggered by interaction forces between oil and wall in a microchannel. Phys. Fluids 2024, 36, 052107. [Google Scholar] [CrossRef]
- He, L.; Wang, S.; Han, S.; Yuan, Y.; Yuan, Y.; Shang, X. Shear-thinning stimulative fluid breakup in 3D pore-throat. Chem. Eng. Res. Des. 2024, 201, 362–371. [Google Scholar] [CrossRef]
- Georgiadis, A.; Llovell, F.; Bismarck, A.; Blas, F.J.; Galindo, A.; Maitland, G.C.; Trusler, J.; Jackson, G. Interfacial tension measurements and modelling of (carbon dioxide+n-alkane) and (carbon dioxide+water) binary mixtures at elevated pressures and temperatures. J. Supercrit. Fluids 2010, 55, 743–754. [Google Scholar] [CrossRef]
- Barrufet, M.A.; Salem, S.K.E.S.; Tantawy, M.; Iglesias-Silva, G.A. Liquid Viscosities of Carbon Dioxide + Hydrocarbons from 310 K to 403 K. J. Chem. Eng. Data 1996, 41, 436–439. [Google Scholar] [CrossRef]
- He, L.; Liang, W.; Zhao, F.; Yuan, Y.; Lou, R.; Ren, T.; Liu, W. Role of thermal Marangoni effect on droplet jetting induced by surface acoustic waves. Therm. Sci. Eng. Prog. 2025, 68, 104248. [Google Scholar] [CrossRef]
- He, L.; Liang, W.; Yuan, K.; Lou, R.; Ren, T.; Liu, W. Facilitating droplets detachment in microchannels via surface acoustic wave. Phys. Fluids 2025, 37, 082126. [Google Scholar] [CrossRef]
- de Castro, A.R.; Goyeau, B. Numerical analysis of the pore-scale mechanisms controlling the efficiency of immiscible displacement of a pollutant phase by a shear-thinning fluid. Chem. Eng. Sci. 2022, 251, 117462. [Google Scholar] [CrossRef]
| Symbol | ρg | ρoil | μg | μ0 | μ∞ | n | λ |
|---|---|---|---|---|---|---|---|
| Unit | kg/m3 | kg/m3 | Pa·s | Pa·s | Pa·s | — | s |
| Value | 142.7 | 718.9 | 2 × 10−5 | 5~150 [47] | 0.01 | 0.2~0.8 | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; He, W.; Zhao, F.; He, L. Role of Shear-Thinning-Induced Viscosity Heterogeneity in Regulating Fingering Transition of CO2 Flooding Within Porous Media. Processes 2025, 13, 3771. https://doi.org/10.3390/pr13123771
Shi W, He W, Zhao F, He L. Role of Shear-Thinning-Induced Viscosity Heterogeneity in Regulating Fingering Transition of CO2 Flooding Within Porous Media. Processes. 2025; 13(12):3771. https://doi.org/10.3390/pr13123771
Chicago/Turabian StyleShi, Wei, Wenjing He, Fengyu Zhao, and Long He. 2025. "Role of Shear-Thinning-Induced Viscosity Heterogeneity in Regulating Fingering Transition of CO2 Flooding Within Porous Media" Processes 13, no. 12: 3771. https://doi.org/10.3390/pr13123771
APA StyleShi, W., He, W., Zhao, F., & He, L. (2025). Role of Shear-Thinning-Induced Viscosity Heterogeneity in Regulating Fingering Transition of CO2 Flooding Within Porous Media. Processes, 13(12), 3771. https://doi.org/10.3390/pr13123771






